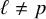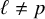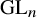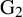1 Introduction
1.1 Galois deformations
Fix a local field F with residue characteristic
![]() $\ell $
. Fix a prime
$\ell $
. Fix a prime
![]() $p \neq \ell $
and a reductive group scheme G (with connected fibers) over the ring of integers
$p \neq \ell $
and a reductive group scheme G (with connected fibers) over the ring of integers
![]() $\mathcal {O}$
in a p-adic field. Let k be the residue field of
$\mathcal {O}$
in a p-adic field. Let k be the residue field of
![]() $\mathcal {O}$
and
$\mathcal {O}$
and
![]() $\Gamma _F$
the absolute Galois group of F.
$\Gamma _F$
the absolute Galois group of F.
Given a G-valued representation of
![]() $\Gamma _F$
over k (i.e., a continuous homomorphism
$\Gamma _F$
over k (i.e., a continuous homomorphism
![]() ${\overline {\rho }}: \Gamma _F \to G(k)$
), Tillouine[Reference TilouineTil96] introduced a Galois lifting ring
${\overline {\rho }}: \Gamma _F \to G(k)$
), Tillouine[Reference TilouineTil96] introduced a Galois lifting ring
![]() $R_{{\overline {\rho }}}^\square $
(building on work of Mazur treating the
$R_{{\overline {\rho }}}^\square $
(building on work of Mazur treating the
![]() $\operatorname {\mathrm {GL}}_n$
case [Reference MazurMaz89, Reference MazurMaz97]). These lifting rings and the associated formal schemes are central in many modern developments in number theory, and it is important to
$\operatorname {\mathrm {GL}}_n$
case [Reference MazurMaz89, Reference MazurMaz97]). These lifting rings and the associated formal schemes are central in many modern developments in number theory, and it is important to
-
• understand whether
 ${\overline {\rho }}$
lifts to characteristic zero; and
${\overline {\rho }}$
lifts to characteristic zero; and -
• understand the geometry of
 $\operatorname {\mathrm {Spf}}(R_{{\overline {\rho }}}^{\square })$
, especially to find formally smooth components and understand how they intersect.
$\operatorname {\mathrm {Spf}}(R_{{\overline {\rho }}}^{\square })$
, especially to find formally smooth components and understand how they intersect.
(There are similar questions in the complementary situation when
![]() $\ell = p$
, but the analysis is quite different and is connected with p-adic Hodge theory.) Work on these questions originally focused on the case that
$\ell = p$
, but the analysis is quite different and is connected with p-adic Hodge theory.) Work on these questions originally focused on the case that
![]() $G = \operatorname {\mathrm {GL}}_n$
(especially
$G = \operatorname {\mathrm {GL}}_n$
(especially
![]() $\operatorname {\mathrm {GL}}_2$
), but recent developments in the Langlands program have made it increasingly important to understand general reductive groups G. For example, progress on these questions can be used to
$\operatorname {\mathrm {GL}}_2$
), but recent developments in the Langlands program have made it increasingly important to understand general reductive groups G. For example, progress on these questions can be used to
-
• produce ‘nice’ lifts of global mod-p representations to characteristic zero [Reference RamakrishnaRam02, Reference Hamblen and RamakrishnaHR08, Reference PatrikisPat16, Reference BooherBoo19b, Reference TangTan19, Reference Fakhruddin, Khare and PatrikisFKP21, Reference Fakhruddin, Khare and PatrikisFKP22];
-
• investigate
 $\ell \neq p$
versions of the Breuil-Mézard conjecture [Reference ShottonSho18, Reference ShottonSho22, Reference ShottonSho23];
$\ell \neq p$
versions of the Breuil-Mézard conjecture [Reference ShottonSho18, Reference ShottonSho22, Reference ShottonSho23]; -
• establish potential automorphy theorems and automorphy lifting theorems over global function fields for general G [Reference Böckle, Harris, Khare and ThorneBHKT19, Reference Böckle, Feng, Harris, Khare and ThorneBFH+22].
Theorem 1.1. (see Theorems 6.1 and 6.20)
Let
![]() ${\overline {\rho }} : \Gamma _F \to G(k)$
be a continuous homomorphism. Suppose p is large enough for the root datum of G (see Remark 6.21). Then there exists a continuous homomorphism
${\overline {\rho }} : \Gamma _F \to G(k)$
be a continuous homomorphism. Suppose p is large enough for the root datum of G (see Remark 6.21). Then there exists a continuous homomorphism
![]() $\rho : \Gamma _F \to G(\mathcal {O})$
lifting
$\rho : \Gamma _F \to G(\mathcal {O})$
lifting
![]() ${\overline {\rho }}$
such that
${\overline {\rho }}$
such that
![]() $C_{G}(\rho (I_F))$
is
$C_{G}(\rho (I_F))$
is
![]() $\mathcal {O}$
-smooth. Moreover, there is a canonical
$\mathcal {O}$
-smooth. Moreover, there is a canonical
![]() $\mathcal {O}$
-formally smooth irreducible component
$\mathcal {O}$
-formally smooth irreducible component
![]() $\operatorname {\mathrm {Spf}} R_{{\overline {\rho }}}^{\operatorname {m.r.}, \square }$
of
$\operatorname {\mathrm {Spf}} R_{{\overline {\rho }}}^{\operatorname {m.r.}, \square }$
of
![]() $\operatorname {\mathrm {Spf}} R_{{\overline {\rho }}}^{\square }$
.
$\operatorname {\mathrm {Spf}} R_{{\overline {\rho }}}^{\square }$
.
We call
![]() $R_{{\overline {\rho }}}^{\operatorname {m.r.},\square }$
the minimally ramified lifting ring and the associated Galois representations minimally ramified. Previous work about the smoothness of (components of)
$R_{{\overline {\rho }}}^{\operatorname {m.r.},\square }$
the minimally ramified lifting ring and the associated Galois representations minimally ramified. Previous work about the smoothness of (components of)
![]() $R_{{\overline {\rho }}}^{\square }$
has been for classical groups [Reference Clozel, Harris and TaylorCHT08, Reference BooherBoo19a] or about the generic fiber [Reference Booher and PatrikisBP19, Reference Bellovin and GeeBG19] or has had strong dependencies between
$R_{{\overline {\rho }}}^{\square }$
has been for classical groups [Reference Clozel, Harris and TaylorCHT08, Reference BooherBoo19a] or about the generic fiber [Reference Booher and PatrikisBP19, Reference Bellovin and GeeBG19] or has had strong dependencies between
![]() $\ell $
and p [Reference Dat, Helm, Kurinczuk and MossDHKM24, §5].
$\ell $
and p [Reference Dat, Helm, Kurinczuk and MossDHKM24, §5].
The existence of lifts of
![]() ${\overline {\rho }}$
without the smooth centralizer condition also follows from
${\overline {\rho }}$
without the smooth centralizer condition also follows from
![]() $\mathbf {Z}_p$
-flatness of
$\mathbf {Z}_p$
-flatness of
![]() $R_{{\overline {\rho }}}^{\square }$
, a consequence of results about moduli of Langlands parameters in [Reference Dat, Helm, Kurinczuk and MossDHKM24], [Reference Fargues and ScholzeFS24] and [Reference ZhuZhu21] which are established using completely different techniques. In [Reference Dat, Helm, Kurinczuk and MossDHKM24], one ingredient in the proof of
$R_{{\overline {\rho }}}^{\square }$
, a consequence of results about moduli of Langlands parameters in [Reference Dat, Helm, Kurinczuk and MossDHKM24], [Reference Fargues and ScholzeFS24] and [Reference ZhuZhu21] which are established using completely different techniques. In [Reference Dat, Helm, Kurinczuk and MossDHKM24], one ingredient in the proof of
![]() $\mathbf {Z}_p$
-flatness is to find a finite extension
$\mathbf {Z}_p$
-flatness is to find a finite extension
![]() $\mathcal {O}'$
of
$\mathcal {O}'$
of
![]() $\mathcal {O}$
such that
$\mathcal {O}$
such that
![]() ${\overline {\rho }}$
lifts to
${\overline {\rho }}$
lifts to
![]() $\rho : \Gamma _F \to G(\mathcal {O}')$
. The lifts produced in [Reference Dat, Helm, Kurinczuk and MossDHKM24] are different than those produced using our method: they have finite image, and we do not expect the centralizers of the inertia to be
$\rho : \Gamma _F \to G(\mathcal {O}')$
. The lifts produced in [Reference Dat, Helm, Kurinczuk and MossDHKM24] are different than those produced using our method: they have finite image, and we do not expect the centralizers of the inertia to be
![]() $\mathcal {O}$
-smooth.
$\mathcal {O}$
-smooth.
Our initial motivation for this project was to produce characteristic zero lifts of global
![]() ${\overline {\rho }} : \Gamma _K \to G(k)$
that are geometric in the sense of the Fontaine-Mazur conjecture when K is a number field, using variations on a local-to-global lifting result going back to Ramakrishna [Reference RamakrishnaRam02]. As a sample application of Theorem 1.1, we give a lifting result for the exceptional group of type
${\overline {\rho }} : \Gamma _K \to G(k)$
that are geometric in the sense of the Fontaine-Mazur conjecture when K is a number field, using variations on a local-to-global lifting result going back to Ramakrishna [Reference RamakrishnaRam02]. As a sample application of Theorem 1.1, we give a lifting result for the exceptional group of type
![]() $G_2$
, making use of [Reference Fakhruddin, Khare and PatrikisFKP21, Theorem A] (a generalization of the local-to-global lifting result) and [Reference LinLin20b, Theorem C] (giving local lifts at p). For a representation
$G_2$
, making use of [Reference Fakhruddin, Khare and PatrikisFKP21, Theorem A] (a generalization of the local-to-global lifting result) and [Reference LinLin20b, Theorem C] (giving local lifts at p). For a representation
![]() ${\overline {\rho }} : \Gamma \to G(k)$
, let
${\overline {\rho }} : \Gamma \to G(k)$
, let
![]() ${\overline {\rho }}(\mathfrak {g})$
denote the Lie algebra of
${\overline {\rho }}(\mathfrak {g})$
denote the Lie algebra of
![]() $G_k$
with
$G_k$
with
![]() $\Gamma $
acting via the composition of
$\Gamma $
acting via the composition of
![]() ${\overline {\rho }}$
and the adjoint action.
${\overline {\rho }}$
and the adjoint action.
Corollary 1.2. Let G be the exceptional split group
![]() $G_2$
over
$G_2$
over
![]() $\mathbf Z$
. Let p be a sufficiently large prime, and let
$\mathbf Z$
. Let p be a sufficiently large prime, and let
![]() ${\overline {\rho }} \colon \Gamma _{\mathbf Q} \to G(\overline {\mathbf F}_p)$
be a continuous representation. Assume that
${\overline {\rho }} \colon \Gamma _{\mathbf Q} \to G(\overline {\mathbf F}_p)$
be a continuous representation. Assume that
-
•
 ${\overline {\rho }}$
is odd (i.e.
${\overline {\rho }}$
is odd (i.e.
 $\dim \mathrm {H}^0(\Gamma _{\mathbf {R}}, {\overline {\rho }}(\mathfrak {g}))=\dim \mathrm {Flag}_{G}$
).
$\dim \mathrm {H}^0(\Gamma _{\mathbf {R}}, {\overline {\rho }}(\mathfrak {g}))=\dim \mathrm {Flag}_{G}$
). -
•
 ${\overline {\rho }}|_{\Gamma _{\mathbf Q(\zeta _p)}}$
is absolutely irreducible (i.e., its image in
${\overline {\rho }}|_{\Gamma _{\mathbf Q(\zeta _p)}}$
is absolutely irreducible (i.e., its image in
 $G(\bar {k})$
is not contained in any proper parabolic subgroup of G).
$G(\bar {k})$
is not contained in any proper parabolic subgroup of G).
Then
![]() ${\overline {\rho }}$
lifts to a
${\overline {\rho }}$
lifts to a
![]() $\rho \colon \Gamma _{\mathbf Q} \to G(\overline {\mathbf {Z}}_p)$
which is geometric in the sense of the Fontaine–Mazur conjecture.
$\rho \colon \Gamma _{\mathbf Q} \to G(\overline {\mathbf {Z}}_p)$
which is geometric in the sense of the Fontaine–Mazur conjecture.
The proof is given in Appendix C. All that is needed from Theorem 1.1 is the existence of local lifts at places away from p, which follows as above from [Reference Dat, Helm, Kurinczuk and MossDHKM24, Reference Fargues and ScholzeFS24, Reference ZhuZhu21].
Remark 1.3. We emphasize that
![]() $\mathcal {O}$
-smoothness of the centralizer of the inertia in Theorem 1.1 is crucial for establishing the existence of a formally smooth component of the universal lifting ring; see Theorem 6.16. Besides producing minimally ramified lifts, our method can also produce lifts with other inertial types and sometimes establish smoothness of the component of the deformation ring containing the lift. We do not systematically explore this, as this is not the focus of this work, but we do build flexibility into our results in Section 6 and give a simple illustration in Example 6.10. This is of interest when studying generalizations of the
$\mathcal {O}$
-smoothness of the centralizer of the inertia in Theorem 1.1 is crucial for establishing the existence of a formally smooth component of the universal lifting ring; see Theorem 6.16. Besides producing minimally ramified lifts, our method can also produce lifts with other inertial types and sometimes establish smoothness of the component of the deformation ring containing the lift. We do not systematically explore this, as this is not the focus of this work, but we do build flexibility into our results in Section 6 and give a simple illustration in Example 6.10. This is of interest when studying generalizations of the
![]() $\ell \neq p$
version of the Breuil-Mézard conjecture and the irreducible components of the moduli of Langlands parameters as in [Reference ShottonSho18, Reference ShottonSho22, Reference ShottonSho23].
$\ell \neq p$
version of the Breuil-Mézard conjecture and the irreducible components of the moduli of Langlands parameters as in [Reference ShottonSho18, Reference ShottonSho22, Reference ShottonSho23].
Remark 1.4. The Galois lifting space for
![]() ${\overline {\rho }}$
is a formal completion of the moduli spaces of [Reference Dat, Helm, Kurinczuk and MossDHKM24], [Reference Fargues and ScholzeFS24, §VIII] and [Reference ZhuZhu21] at
${\overline {\rho }}$
is a formal completion of the moduli spaces of [Reference Dat, Helm, Kurinczuk and MossDHKM24], [Reference Fargues and ScholzeFS24, §VIII] and [Reference ZhuZhu21] at
![]() ${\overline {\rho }}$
. To make this precise, one can apply [Reference ZhuZhu21, Lemma 2.4.10] to the various moduli spaces of Galois representations and Weil-Deligne representations studied and compared in [Reference ZhuZhu21, §3.1]. Then the main results in these papers show that the Galois lifting spaces are flat local complete intersections, and [Reference Dat, Helm, Kurinczuk and MossDHKM24, §5] provides some results on generic smoothness.
${\overline {\rho }}$
. To make this precise, one can apply [Reference ZhuZhu21, Lemma 2.4.10] to the various moduli spaces of Galois representations and Weil-Deligne representations studied and compared in [Reference ZhuZhu21, §3.1]. Then the main results in these papers show that the Galois lifting spaces are flat local complete intersections, and [Reference Dat, Helm, Kurinczuk and MossDHKM24, §5] provides some results on generic smoothness.
In this language, Theorem 1.1 shows in particular that the underlying reduced subscheme of the mod-p fiber of the moduli space
![]() ${\mathscr H}_W$
of Weil-Deligne representations is smooth away from the intersections of components for large p, and even at a point of intersection, there is some smooth component passing through this point. Indeed, Theorem 1.1 asserts that every point lies in a formally smooth irreducible component of
${\mathscr H}_W$
of Weil-Deligne representations is smooth away from the intersections of components for large p, and even at a point of intersection, there is some smooth component passing through this point. Indeed, Theorem 1.1 asserts that every point lies in a formally smooth irreducible component of
![]() $\operatorname {\mathrm {Spf}} R_{{\overline {\rho }}}^{\square }$
, whose mod-p fiber is therefore a smooth localization of the underlying reduced subscheme of an irreducible component of the mod-p fiber of
$\operatorname {\mathrm {Spf}} R_{{\overline {\rho }}}^{\square }$
, whose mod-p fiber is therefore a smooth localization of the underlying reduced subscheme of an irreducible component of the mod-p fiber of
![]() ${\mathscr H}_W$
. As our bound on p is independent of the size of the residue field of F, it applies in situations where the mod-p fibers of the above moduli space are not reduced (see [Reference Dat, Helm, Kurinczuk and MossDHKM24, Proposition 5.26], and note that the banality of p depends on the size of the residue field of F by [Reference Dat, Helm, Kurinczuk and MossDHKM24, Lemma 5.28]). See Remark 6.23 for a slight reinterpretation of our main result in terms of this moduli space.
${\mathscr H}_W$
. As our bound on p is independent of the size of the residue field of F, it applies in situations where the mod-p fibers of the above moduli space are not reduced (see [Reference Dat, Helm, Kurinczuk and MossDHKM24, Proposition 5.26], and note that the banality of p depends on the size of the residue field of F by [Reference Dat, Helm, Kurinczuk and MossDHKM24, Lemma 5.28]). See Remark 6.23 for a slight reinterpretation of our main result in terms of this moduli space.
Remark 1.5. In [Reference Böckle, Feng, Harris, Khare and ThorneBFH+22, Section 4.3], an automorphy lifting theorem for G-valued Galois representations over global function fields is established, assuming that the mod-p residual automorphic Galois representation has suitably large image and that the local deformation problems are balanced in the sense of [Reference Böckle, Feng, Harris, Khare and ThorneBFH+22, Definition 3.4]. Section 5 of loc. cit. shows that the unrestricted local condition at a place of ramification is balanced (and hence formally smooth) if p is larger than an ineffective constant depending on the automorphic representation using global arguments. In contrast, Theorem 1.1 produces a natural balanced local deformation condition in the general case with an effective lower bound on p depending only on the root datum of G (see Remark 6.21 for this lower bound).
1.2 Weakly reductive group schemes
To prove Theorem 1.1, we will directly adapt the argument of [Reference Clozel, Harris and TaylorCHT08] (which dealt with
![]() $G = \operatorname {\mathrm {GL}}_n$
) to a general G. For clarity, we will outline (a reinterpretation of) the argument from [Reference Clozel, Harris and TaylorCHT08] which constructs a canonical lift of
$G = \operatorname {\mathrm {GL}}_n$
) to a general G. For clarity, we will outline (a reinterpretation of) the argument from [Reference Clozel, Harris and TaylorCHT08] which constructs a canonical lift of
![]() ${\overline {\rho }}: \Gamma _F \to \operatorname {\mathrm {GL}}(V \otimes _{\mathcal {O}} k)$
up to conjugacy, where V is a finite free
${\overline {\rho }}: \Gamma _F \to \operatorname {\mathrm {GL}}(V \otimes _{\mathcal {O}} k)$
up to conjugacy, where V is a finite free
![]() $\mathcal {O}$
-module of rank n. Let
$\mathcal {O}$
-module of rank n. Let
![]() $\Lambda _F$
be the maximal prime-to-p closed subgroup of the inertia subgroup
$\Lambda _F$
be the maximal prime-to-p closed subgroup of the inertia subgroup
![]() $I_F$
of
$I_F$
of
![]() $\Gamma _F$
.
$\Gamma _F$
.
-
1. Lift
 ${\overline {\rho }}|_{\Lambda _F}$
to a representation
${\overline {\rho }}|_{\Lambda _F}$
to a representation
 $\rho _0: \Lambda _F \to \operatorname {\mathrm {GL}}(V)$
. Let
$\rho _0: \Lambda _F \to \operatorname {\mathrm {GL}}(V)$
. Let
 $V = \bigoplus _i V_i \otimes _{\mathcal {O}} W_i$
be the isotypic decomposition of V.
$V = \bigoplus _i V_i \otimes _{\mathcal {O}} W_i$
be the isotypic decomposition of V. -
2. Show that if
 $p> n$
, then there is a unique extension of the
$p> n$
, then there is a unique extension of the
 $\Lambda _F$
-representation
$\Lambda _F$
-representation
 $\bigoplus _i V_i$
to a representation
$\bigoplus _i V_i$
to a representation
 $\tau = (\tau _i): I_F \to \prod _i \operatorname {\mathrm {GL}}(V_i)$
such that
$\tau = (\tau _i): I_F \to \prod _i \operatorname {\mathrm {GL}}(V_i)$
such that
 $\det (\tau _i(\sigma ))$
is of finite prime-to-p order for all
$\det (\tau _i(\sigma ))$
is of finite prime-to-p order for all
 $\sigma \in I_F$
and all i.
$\sigma \in I_F$
and all i. -
3. Choosing an identification
 $I_F/\Lambda _F \cong \mathbf {Z}_p$
and a splitting
$I_F/\Lambda _F \cong \mathbf {Z}_p$
and a splitting
 $I_F/\Lambda _F \to I_F$
, show that there is a unipotent element
$I_F/\Lambda _F \to I_F$
, show that there is a unipotent element
 $u_0 \in \prod _i \operatorname {\mathrm {GL}}(W_i \otimes _{\mathcal {O}} k)$
such that
$u_0 \in \prod _i \operatorname {\mathrm {GL}}(W_i \otimes _{\mathcal {O}} k)$
such that
 ${\overline {\rho }}(n) = u_0^n$
for all
${\overline {\rho }}(n) = u_0^n$
for all
 $n \in \mathbf {Z}_p$
. Show that
$n \in \mathbf {Z}_p$
. Show that
 $u_0$
lifts uniquely up to conjugacy to a section
$u_0$
lifts uniquely up to conjugacy to a section
 $u \in \prod _i \operatorname {\mathrm {GL}}(W_i)$
with the same Jordan block decomposition on both fibers, and define
$u \in \prod _i \operatorname {\mathrm {GL}}(W_i)$
with the same Jordan block decomposition on both fibers, and define
 $\rho _1: I_F = \Lambda _F \rtimes \mathbf {Z}_p \to \operatorname {\mathrm {GL}}(V)$
by
$\rho _1: I_F = \Lambda _F \rtimes \mathbf {Z}_p \to \operatorname {\mathrm {GL}}(V)$
by  $$\begin{align*}\rho_1(\lambda n) = \tau(\lambda n) u^n. \end{align*}$$
$$\begin{align*}\rho_1(\lambda n) = \tau(\lambda n) u^n. \end{align*}$$
-
4. Using the uniqueness assertions of (2) and (3), finally extend
 $\rho _1$
to
$\rho _1$
to
 $\rho : \Gamma _F \to \operatorname {\mathrm {GL}}(V)$
.
$\rho : \Gamma _F \to \operatorname {\mathrm {GL}}(V)$
.
To adapt this argument for general G in place of
![]() $\operatorname {\mathrm {GL}}_n$
, one first needs to interpret the objects appearing. For instance, in steps 2 and 3, we need analogs of
$\operatorname {\mathrm {GL}}_n$
, one first needs to interpret the objects appearing. For instance, in steps 2 and 3, we need analogs of
![]() $\prod _i \operatorname {\mathrm {GL}}(V_i)$
and
$\prod _i \operatorname {\mathrm {GL}}(V_i)$
and
![]() $\prod _i \operatorname {\mathrm {GL}}(W_i)$
. The main observation is that when
$\prod _i \operatorname {\mathrm {GL}}(W_i)$
. The main observation is that when
![]() $G = \operatorname {\mathrm {GL}}(V)$
, the centralizer
$G = \operatorname {\mathrm {GL}}(V)$
, the centralizer
![]() $\mathfrak {C} = C_G(\Lambda _F)$
is equal to
$\mathfrak {C} = C_G(\Lambda _F)$
is equal to
![]() $\prod _i \operatorname {\mathrm {GL}}(W_i)$
, while the double centralizer
$\prod _i \operatorname {\mathrm {GL}}(W_i)$
, while the double centralizer
![]() $\Delta = C_G(C_G(\Lambda _F))$
is equal to
$\Delta = C_G(C_G(\Lambda _F))$
is equal to
![]() $\prod _i \operatorname {\mathrm {GL}}(V_i)$
. From this perspective, it is natural to study
$\prod _i \operatorname {\mathrm {GL}}(V_i)$
. From this perspective, it is natural to study
![]() $\mathfrak {C} = C_G(\Lambda _F)$
and
$\mathfrak {C} = C_G(\Lambda _F)$
and
![]() $\Delta = C_G(C_G(\Lambda _F))$
for general G, which we formalize using the notion of a decomposition type. This provides a structure for extending a prime-to-p inertial type to a G-valued representation of
$\Delta = C_G(C_G(\Lambda _F))$
for general G, which we formalize using the notion of a decomposition type. This provides a structure for extending a prime-to-p inertial type to a G-valued representation of
![]() $\Gamma _F$
. It is also necessary to understand the abelianization morphism
$\Gamma _F$
. It is also necessary to understand the abelianization morphism
![]() $\Delta \to \Delta ^{\mathrm {{ab}}}$
(the analog of the determinant) and the center
$\Delta \to \Delta ^{\mathrm {{ab}}}$
(the analog of the determinant) and the center
![]() $Z(\Delta )$
(the analog of the group of scalar matrices). We must, therefore, understand representability and smoothness properties of the
$Z(\Delta )$
(the analog of the group of scalar matrices). We must, therefore, understand representability and smoothness properties of the
![]() $\mathcal {O}$
-group schemes
$\mathcal {O}$
-group schemes
![]() $\mathfrak {C}$
,
$\mathfrak {C}$
,
![]() $\Delta $
,
$\Delta $
,
![]() $\Delta ^{\mathrm {{ab}}}$
, and
$\Delta ^{\mathrm {{ab}}}$
, and
![]() $Z(\Delta )$
.
$Z(\Delta )$
.
Remark 1.7. In step 3, it is also necessary to find a suitable meaning of ‘the same Jordan block decomposition on both fibers’ for a unipotent section of a general G and to show a suitable conjugacy result for these. This has been handled in [Reference CotnerCot22a]; see also [Reference HardestyHar18] for similar results.
Unlike the case
![]() $G = \operatorname {\mathrm {GL}}_n$
, it is not evident that
$G = \operatorname {\mathrm {GL}}_n$
, it is not evident that
![]() $\Delta $
is smooth (or even representable), and it is usually not true that
$\Delta $
is smooth (or even representable), and it is usually not true that
![]() $\mathfrak {C}$
and
$\mathfrak {C}$
and
![]() $\Delta $
are reductive group schemes; they often have disconnected fibers. This causes serious difficulties when working integrally, and the theory developed in [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11] is not sufficient to handle this situation. These difficulties are well known to experts, and we describe some pathologies in Examples 2.16, 2.20 and 2.28.
$\Delta $
are reductive group schemes; they often have disconnected fibers. This causes serious difficulties when working integrally, and the theory developed in [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11] is not sufficient to handle this situation. These difficulties are well known to experts, and we describe some pathologies in Examples 2.16, 2.20 and 2.28.
In order to handle the families of disconnected reductive groups that are relevant to us, we introduce the notion of weak reductivity. Recall [Reference ConradCon14, Proposition 3.1.3] that if S is a scheme and G is a smooth affine S-group scheme with (possibly disconnected) reductive fibers, then the relative identity component
![]() $G^0$
is a reductive group scheme, and
$G^0$
is a reductive group scheme, and
![]() $G/G^0$
is an étale separated S-group scheme of finite presentation.
$G/G^0$
is an étale separated S-group scheme of finite presentation.
Definition 1.8. Over a scheme S, a weakly reductive group scheme is a smooth affine S-group scheme G such that
![]() $G^0$
is reductive and the component group
$G^0$
is reductive and the component group
![]() $G/G^0$
is finite étale over S with order invertible on S.
$G/G^0$
is finite étale over S with order invertible on S.
We emphasize the condition that
![]() $G/G^0$
is of order invertible on S; if this assumption is omitted, such a smooth affine G is often called geometrically reductive or generalized reductive. However, as we show in Examples 2.20, 2.28 and 2.16, general geometrically reductive smooth affine group schemes are more pathological than their reductive counterparts.
$G/G^0$
is of order invertible on S; if this assumption is omitted, such a smooth affine G is often called geometrically reductive or generalized reductive. However, as we show in Examples 2.20, 2.28 and 2.16, general geometrically reductive smooth affine group schemes are more pathological than their reductive counterparts.
Theorem 1.9 (Corollary 3.5, Corollary 3.7, Proposition 2.19, Proposition 2.27).
Let S be a scheme, and let G be a weakly reductive S-group scheme.
-
1. If
 $\Lambda $
is a finite étale group scheme acting on G whose order is invertible on S, then the fixed point scheme
$\Lambda $
is a finite étale group scheme acting on G whose order is invertible on S, then the fixed point scheme
 $\mathfrak {C} = C_G(\Lambda )$
is weakly reductive. If
$\mathfrak {C} = C_G(\Lambda )$
is weakly reductive. If  is pretty goodFootnote
1
for
is pretty goodFootnote
1
for
 $G_s$
for all
$G_s$
for all
 $s \in S$
, then the centralizer
$s \in S$
, then the centralizer
 $\Delta = C_G(\mathfrak {C})$
is weakly reductive.
$\Delta = C_G(\mathfrak {C})$
is weakly reductive. -
2. If H is a simple reductive group scheme acting on G and
 $(\dim G/\operatorname {\mathrm {rank}} H)!$
is invertible on S, then the fixed point scheme
$(\dim G/\operatorname {\mathrm {rank}} H)!$
is invertible on S, then the fixed point scheme
 $C_G(H)$
is weakly reductive.
$C_G(H)$
is weakly reductive. -
3. The center
 $Z(G)$
is a group scheme of multiplicative type, and it is smooth if
$Z(G)$
is a group scheme of multiplicative type, and it is smooth if
 $Z(G^0)$
is smooth.
$Z(G^0)$
is smooth. -
4. The derived group
 ${\mathscr D}(G)$
(in the sense of fppf group sheaves) is represented by a weakly reductive S-group scheme, and the abelianization
${\mathscr D}(G)$
(in the sense of fppf group sheaves) is represented by a weakly reductive S-group scheme, and the abelianization
 $G^{\mathrm {ab}} = G/{\mathscr D}(G)$
of G is a smooth group scheme of multiplicative type.
$G^{\mathrm {ab}} = G/{\mathscr D}(G)$
of G is a smooth group scheme of multiplicative type.
The main new input in the proof of Theorem 1.9 is an analysis of schemes of homomorphisms between weakly reductive group schemes. If S is a scheme and G and H are S-group schemes, we let
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
denote the functor which sends an S-scheme
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
denote the functor which sends an S-scheme
![]() $S'$
to the set of
$S'$
to the set of
![]() $S'$
-homomorphisms
$S'$
-homomorphisms
![]() $H_{S'} \to G_{S'}$
. In [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. XXIV, Corollaire 7.2.3], it is proved that if H is a reductive S-group scheme and G is a smooth affine S-group scheme, then
$H_{S'} \to G_{S'}$
. In [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. XXIV, Corollaire 7.2.3], it is proved that if H is a reductive S-group scheme and G is a smooth affine S-group scheme, then
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable by a separated S-scheme locally of finite presentation. Usually
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable by a separated S-scheme locally of finite presentation. Usually
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is usually not quasi-compact or flat over S (see Example 2.4). However, we will show in Theorem 2.2 that
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is usually not quasi-compact or flat over S (see Example 2.4). However, we will show in Theorem 2.2 that
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is always a disjoint union of finitely presented S-affine S-schemes. Proving this involves revisiting the proof of representability of
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is always a disjoint union of finitely presented S-affine S-schemes. Proving this involves revisiting the proof of representability of
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
in [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11], using ind-quasi-affine descent and affineness results for schemes of tori in [Reference RaynaudRay70]. Over a field, this affineness result was proved in [Reference BrionBri21, Theorem 6.3], and in general, it strengthens affineness results from [Reference RomagnyRom22, Theorem 3.1.4].
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
in [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11], using ind-quasi-affine descent and affineness results for schemes of tori in [Reference RaynaudRay70]. Over a field, this affineness result was proved in [Reference BrionBri21, Theorem 6.3], and in general, it strengthens affineness results from [Reference RomagnyRom22, Theorem 3.1.4].
Let us give a sense of some key steps in the proof of Theorem 1.9, starting with part (2).
-
1. Use known cohomology vanishing results (Theorem 3.4) to see that
 $C_G(H)$
is smooth affine, and use classical arguments over a field to show that
$C_G(H)$
is smooth affine, and use classical arguments over a field to show that
 $C_G(H)/C_G(H)^0$
is of order invertible on S.
$C_G(H)/C_G(H)^0$
is of order invertible on S. -
2. Reduce to the case
 $S = \operatorname {\mathrm {Spec}} A$
for a DVR A, and use Matsushima’s theorem (Theorem 2.1) to reduce to showing that the quotient
$S = \operatorname {\mathrm {Spec}} A$
for a DVR A, and use Matsushima’s theorem (Theorem 2.1) to reduce to showing that the quotient
 $G/C_G(H)$
is affine.
$G/C_G(H)$
is affine. -
3. Show that the natural monomorphism
 $i: G/C_G(H) \to \underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
, given as the orbit map through the inclusion
$i: G/C_G(H) \to \underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
, given as the orbit map through the inclusion
 $H \to G$
, is a closed embedding, and conclude using the above geometric property of
$H \to G$
, is a closed embedding, and conclude using the above geometric property of
 $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
.
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
.
The proof of Theorem 1.9(1) is similar, but when
![]() $H = C_G(\Lambda )$
, we cannot show that i is a closed embedding, so our argument is slightly longer.
$H = C_G(\Lambda )$
, we cannot show that i is a closed embedding, so our argument is slightly longer.
To prove Theorem 1.9(3), we first show that the automorphism functor
![]() $\underline {\operatorname {\mathrm {Aut}}}_{G/S}$
is representable by a smooth clopen subscheme
$\underline {\operatorname {\mathrm {Aut}}}_{G/S}$
is representable by a smooth clopen subscheme
![]() $\operatorname {\mathrm {Aut}}_{G/S}$
of
$\operatorname {\mathrm {Aut}}_{G/S}$
of
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(G, G)$
. Since
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(G, G)$
. Since
![]() $Z(G)$
is the kernel of the natural S-homomorphism
$Z(G)$
is the kernel of the natural S-homomorphism
![]() $\varphi : G \to \operatorname {\mathrm {Aut}}_{G/S}$
, this reduces us to understanding
$\varphi : G \to \operatorname {\mathrm {Aut}}_{G/S}$
, this reduces us to understanding
![]() $\operatorname {\mathrm {Aut}}_{G/S}$
and
$\operatorname {\mathrm {Aut}}_{G/S}$
and
![]() $\varphi $
. We prove Theorem 1.9(4) through a somewhat complicated reduction to the separate cases of reductive group schemes and finite étale group schemes, both of which are understood.
$\varphi $
. We prove Theorem 1.9(4) through a somewhat complicated reduction to the separate cases of reductive group schemes and finite étale group schemes, both of which are understood.
1.3 Outline of the paper
Sections 2 and 3 develop the theory of weakly reductive group schemes and establish a variety of results about centralizers. Section 4 introduces the notion of a decomposition type, and Sections 5 and 6 use this and the results about weakly reductive group schemes to construct lifts and the minimally ramified deformation condition. Depending on the reader’s interests, Sections 4–6 can be read first relying on the properties of weakly reductive group schemes summarized in Theorem 1.9.
1.4 Notation and terminology
Given a group scheme H defined over a ring R and an R-algebra A, we write
![]() $H_A$
for the base change of H to A, and write
$H_A$
for the base change of H to A, and write
![]() $H(A)$
for the A-points of H.
$H(A)$
for the A-points of H.
If S is a scheme and H is an S-group scheme acting on another S-group scheme G, then we denote by
![]() $C_G(H)$
the functor of fixed points for the action of H on G. If H is an S-subgroup scheme of G, then we denote by
$C_G(H)$
the functor of fixed points for the action of H on G. If H is an S-subgroup scheme of G, then we denote by
![]() $N_G(H)$
the functor of sections of G normalizing H. Note that if H is an S-subgroup scheme of G, then
$N_G(H)$
the functor of sections of G normalizing H. Note that if H is an S-subgroup scheme of G, then
![]() $C_G(H)$
is the centralizer of H in G. For representability results, see [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. XII, Proposition 9.2] and [Reference ConradCon14, Proposition 2.1.6]; when these functors are representable, we will use the same notation to denote their representing objects.
$C_G(H)$
is the centralizer of H in G. For representability results, see [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. XII, Proposition 9.2] and [Reference ConradCon14, Proposition 2.1.6]; when these functors are representable, we will use the same notation to denote their representing objects.
We follow the convention in [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11] and require that reductive group schemes have connected fibers. In Section 2, we introduce the notion of weakly reductive group schemes which allows disconnected fibers under some hypotheses. However, when working over a field, we do allow reductive groups to be disconnected, following general practice. We will require all groups of multiplicative type to be finitely presented, unlike the definition in [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. IX].
For a local field F, we use
![]() $\Gamma _F$
to denote the absolute Galois group of F,
$\Gamma _F$
to denote the absolute Galois group of F,
![]() $I_F$
to denote the inertia subgroup of
$I_F$
to denote the inertia subgroup of
![]() $\Gamma _F$
, and
$\Gamma _F$
, and
![]() $\Lambda _F \subset I_F$
to be the kernel of a homomorphism
$\Lambda _F \subset I_F$
to be the kernel of a homomorphism
![]() $I_F \to \mathbf Z_p$
as in Section 5.1.
$I_F \to \mathbf Z_p$
as in Section 5.1.
We also recall the definition of a good and pretty good primes for a root datum
![]() $(X,\Phi ,Y,\Phi ^\vee )$
.
$(X,\Phi ,Y,\Phi ^\vee )$
.
Definition 1.11. A prime p is good if for every closed subsystem
![]() $\Sigma \subset \Phi $
,
$\Sigma \subset \Phi $
,
![]() $\mathbf Z\Phi /\mathbf Z\Sigma $
is p-torsion free.
$\mathbf Z\Phi /\mathbf Z\Sigma $
is p-torsion free.
Definition 1.12. We say that p is pretty good if the groups
![]() $X/\mathbf Z \Phi '$
and
$X/\mathbf Z \Phi '$
and
![]() $Y/\mathbf Z {\Phi '}^\vee $
have no p-torsion for all subsets
$Y/\mathbf Z {\Phi '}^\vee $
have no p-torsion for all subsets
![]() $\Phi ' \subset \Phi $
.
$\Phi ' \subset \Phi $
.
A prime is good (resp. pretty good) for a weakly reductive group G if it is good (resp. pretty good) for the root datum associated to
![]() $G^0$
. By convention, we also say that
$G^0$
. By convention, we also say that
![]() $0$
is good (and pretty good).
$0$
is good (and pretty good).
Remark 1.13. By [Reference CotnerCot22a, Lemma 2.2], a prime p is pretty good for a connected reductive group G over a field of characteristic p if and only if all of the following conditions hold:
-
1. p is good for G,
-
2. p does not divide the order of
 $\pi _1({\mathscr D}(G))$
,
$\pi _1({\mathscr D}(G))$
, -
3.
 $Z(G)$
is smooth.
$Z(G)$
is smooth.
2 Weakly reductive group schemes
In this section, we study weakly reductive group schemes. Weak reductivity is slightly more stringent than the condition of geometric reductivity, as introduced in [Reference AlperAlp14, Definition 9.1.1]. We will not recall the definition in general, but we quote the following theorem, which will be used several times in the sequel, especially in Section 3.
Theorem 2.1 [Reference AlperAlp14, Theorems 9.4.1, 9.7.6].
Let S be a scheme, and let
![]() $H \subset G$
be flat, finitely presented, and separated S-group schemes, with H closed in G.
$H \subset G$
be flat, finitely presented, and separated S-group schemes, with H closed in G.
-
1. If G is smooth and affine, then it is geometrically reductive if and only if
 $G^0$
is reductive and
$G^0$
is reductive and
 $G/G^0$
is finite.
$G/G^0$
is finite. -
2. If G is affine and geometrically reductive, then H is geometrically reductive if and only if
 $G/H$
is affine.
$G/H$
is affine.
In light of Theorem 2.1, a weakly reductive group scheme is just a geometrically reductive smooth affine group scheme with tame component group in the sense of [Reference Abramovich, Olsson and VistoliAOV08]. We will extend some fundamental constructions for reductive group schemes to weakly reductive group schemes. These extensions do not generally work for more general geometrically reductive smooth affine group schemes (see Examples 2.16, 2.20 and 2.28). We note that, by [Reference Alper, Hall and RydhAHR23, Theorem 9.9], all smooth affine linearly reductive group schemes are weakly reductive; we omit the definition of linear reductivity (which may be found in [Reference Alper, Hall and RydhAHR23, Definition 2.1] because it is of a technical nature orthogonal to the goals of this paper.
We work throughout with arbitrary base schemes, but many proofs begin by reducing to simpler cases. For the most part, we do not spell out these reductions in detail, and we refer the reader to [Reference Dieudonne and GrothendieckDG67, IV3, Sections 8, 9, 11] for the techniques involved in such reduction steps.
2.1 Schemes of homomorphism
Let S be a scheme. If G and H are S-group schemes, then we define the set-valued functor
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
on S-schemes by
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
on S-schemes by
The goal of this section is to study this functor. The first aim is the following theorem.
Theorem 2.2. Let S be a scheme, let G be a smooth affine S-group scheme, and let H be a geometrically reductive smooth affine S-group scheme. The functor
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable by an ind-quasi-affine S-scheme locally of finite presentation. Moreover, suppose S is normal, quasi-compact and quasi-separated, and
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable by an ind-quasi-affine S-scheme locally of finite presentation. Moreover, suppose S is normal, quasi-compact and quasi-separated, and
![]() $H^0$
admits a maximal S-torus. Then
$H^0$
admits a maximal S-torus. Then
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable by a disjoint union of finitely presented S-affine S-schemes.
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable by a disjoint union of finitely presented S-affine S-schemes.
As a general rule, we like to use underlines to refer to functors, and we omit the underline when referring to a representing object. However, in this case, the notation without the underline has an independent meaning, so it would be confusing to omit it.
It is not clear a priori that
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is even representable; for this, we begin with the following fundamental result of Demazure.
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is even representable; for this, we begin with the following fundamental result of Demazure.
Lemma 2.3. Suppose that H is a reductive S-group scheme and that G is smooth and quasi-projective over S with affine fibers. Then
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable by a separated S-scheme locally of finite presentation.
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable by a separated S-scheme locally of finite presentation.
Proof. This is [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. XXIV, Corollaire 7.2.3].
Example 2.4 [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. XXIV, 7.4].
The scheme
![]() $\underline {\operatorname {\mathrm {Hom}}}_{\mathbf {Z}\textrm {-}\mathrm {gp}}(\operatorname {\mathrm {SL}}_{2, \mathbf {Z}}, \operatorname {\mathrm {SL}}_{2, \mathbf {Z}})$
is the disjoint union of the following
$\underline {\operatorname {\mathrm {Hom}}}_{\mathbf {Z}\textrm {-}\mathrm {gp}}(\operatorname {\mathrm {SL}}_{2, \mathbf {Z}}, \operatorname {\mathrm {SL}}_{2, \mathbf {Z}})$
is the disjoint union of the following
![]() $\mathbf {Z}$
-schemes:
$\mathbf {Z}$
-schemes:
-
1. a scheme isomorphic to
 $\operatorname {\mathrm {Spec}} \mathbf {Z}$
(corresponding to the trivial homomorphism
$\operatorname {\mathrm {Spec}} \mathbf {Z}$
(corresponding to the trivial homomorphism
 $\operatorname {\mathrm {SL}}_{2, \mathbf {Z}} \to \operatorname {\mathrm {SL}}_{2, \mathbf {Z}}$
),
$\operatorname {\mathrm {SL}}_{2, \mathbf {Z}} \to \operatorname {\mathrm {SL}}_{2, \mathbf {Z}}$
), -
2. a scheme isomorphic to
 $\operatorname {\mathrm {PGL}}_{2, \mathbf {Z}}$
(corresponding to conjugates of the identity homomorphism
$\operatorname {\mathrm {PGL}}_{2, \mathbf {Z}}$
(corresponding to conjugates of the identity homomorphism
 $\operatorname {\mathrm {SL}}_{2, \mathbf {Z}} \to \operatorname {\mathrm {SL}}_{2, \mathbf {Z}}$
),
$\operatorname {\mathrm {SL}}_{2, \mathbf {Z}} \to \operatorname {\mathrm {SL}}_{2, \mathbf {Z}}$
), -
3. for each prime number p and each positive integer n, a scheme isomorphic to
 $\operatorname {\mathrm {PGL}}_{2, \mathbf {F}_p}$
(corresponding to conjugates of the
$\operatorname {\mathrm {PGL}}_{2, \mathbf {F}_p}$
(corresponding to conjugates of the
 $p^n$
-Frobenius morphism
$p^n$
-Frobenius morphism
 $\operatorname {\mathrm {SL}}_{2, \mathbf {F}_p} \to \operatorname {\mathrm {SL}}_{2, \mathbf {F}_p}$
).
$\operatorname {\mathrm {SL}}_{2, \mathbf {F}_p} \to \operatorname {\mathrm {SL}}_{2, \mathbf {F}_p}$
).
In particular,
![]() $\underline {\operatorname {\mathrm {Hom}}}_{\mathbf {Z}\textrm {-}\mathrm {gp}}(\operatorname {\mathrm {SL}}_{2, \mathbf {Z}}, \operatorname {\mathrm {SL}}_{2, \mathbf {Z}})$
is neither flat nor quasi-compact.
$\underline {\operatorname {\mathrm {Hom}}}_{\mathbf {Z}\textrm {-}\mathrm {gp}}(\operatorname {\mathrm {SL}}_{2, \mathbf {Z}}, \operatorname {\mathrm {SL}}_{2, \mathbf {Z}})$
is neither flat nor quasi-compact.
To prove Theorem 2.2, we will use étale descent to pass further to the case that
![]() $H/H^0$
is constant and then realize
$H/H^0$
is constant and then realize
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
as a closed subscheme of
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
as a closed subscheme of
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H^0, G) \times G^n$
for some n. However, in order to make the descent argument, one needs to know effectivity of étale descent for closed subschemes of
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H^0, G) \times G^n$
for some n. However, in order to make the descent argument, one needs to know effectivity of étale descent for closed subschemes of
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H^0, G) \times G^n$
. Since
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H^0, G) \times G^n$
. Since
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H^0, G)$
is usually not quasi-compact over S, this descent argument is not trivial. Thus, before showing representability, we will show that
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H^0, G)$
is usually not quasi-compact over S, this descent argument is not trivial. Thus, before showing representability, we will show that
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H^0, G)$
is ind-quasi-affine over S [Sta21, Tag 0AP6] in order to apply effectivity of fpqc descent for ind-quasi-affine morphisms [Sta21, Tag 0APK]. We begin with a more detailed study of
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H^0, G)$
is ind-quasi-affine over S [Sta21, Tag 0AP6] in order to apply effectivity of fpqc descent for ind-quasi-affine morphisms [Sta21, Tag 0APK]. We begin with a more detailed study of
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
in the case that H is reductive.
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
in the case that H is reductive.
Lemma 2.5. Let X be a locally noetherian scheme, and let
![]() $\pi : Y \to X$
be a finite surjective morphism, where Y is a disjoint union of affine schemes. Then X is ind-quasi-affine. If
$\pi : Y \to X$
be a finite surjective morphism, where Y is a disjoint union of affine schemes. Then X is ind-quasi-affine. If
![]() $\pi $
is open (e.g., flat), then X is a disjoint union of affine schemes.
$\pi $
is open (e.g., flat), then X is a disjoint union of affine schemes.
Proof. Let
![]() $U \subset X$
be a quasi-compact open subscheme; to show that X is ind-quasi-affine, we must show that U is quasi-affine. Note that
$U \subset X$
be a quasi-compact open subscheme; to show that X is ind-quasi-affine, we must show that U is quasi-affine. Note that
![]() $\pi ^{-1}(U) \subset Y$
is quasi-compact, so it is contained in an affine clopen subscheme
$\pi ^{-1}(U) \subset Y$
is quasi-compact, so it is contained in an affine clopen subscheme
![]() $V \subset Y$
by assumption. By Chevalley’s theorem, that affineness can be checked after passing to a finite cover [Reference Dieudonne and GrothendieckDG67, II, Théorème 6.7.1], the closed subset
$V \subset Y$
by assumption. By Chevalley’s theorem, that affineness can be checked after passing to a finite cover [Reference Dieudonne and GrothendieckDG67, II, Théorème 6.7.1], the closed subset
![]() $\pi (V) \subset X$
is affine (when considered with its reduced subscheme structure). The schematic closure
$\pi (V) \subset X$
is affine (when considered with its reduced subscheme structure). The schematic closure
![]() $\overline {U}$
of U in X is a closed subset of
$\overline {U}$
of U in X is a closed subset of
![]() $\pi (V)$
, so
$\pi (V)$
, so
![]() $\overline {U}_{\mathrm {red}}$
is affine. Thus, by Chevalley’s theorem again,
$\overline {U}_{\mathrm {red}}$
is affine. Thus, by Chevalley’s theorem again,
![]() $\overline {U}$
is affine. Since U is open in
$\overline {U}$
is affine. Since U is open in
![]() $\overline {U}$
, it follows that U is quasi-affine.
$\overline {U}$
, it follows that U is quasi-affine.
If
![]() $\pi $
is open, then the closed subset
$\pi $
is open, then the closed subset
![]() $\pi (V) \subset X$
is also open, so it is affine when considered with the structure of an open subscheme of X.
$\pi (V) \subset X$
is also open, so it is affine when considered with the structure of an open subscheme of X.
Lemma 2.6. In the setting of Theorem 2.2, suppose that H is a torus. Then
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable by a smooth ind-quasi-affine S-scheme. If S is normal, quasi-compact and quasi-separated, then
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable by a smooth ind-quasi-affine S-scheme. If S is normal, quasi-compact and quasi-separated, then
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable by a disjoint union of smooth affine S-schemes.
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable by a disjoint union of smooth affine S-schemes.
Proof. First, smoothness of
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is proved in [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. XI, Corollaire 4.2]. If S is normal and locally noetherian, then the result follows from [Reference RaynaudRay70, Théorème IX 2.6]. For the remainder, we therefore assume that S is quasi-compact and quasi-separated. By spreading out (using [Reference Thomason and TrobaughTT90, Theorem C.9]), we may assume that S is of finite type over
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is proved in [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. XI, Corollaire 4.2]. If S is normal and locally noetherian, then the result follows from [Reference RaynaudRay70, Théorème IX 2.6]. For the remainder, we therefore assume that S is quasi-compact and quasi-separated. By spreading out (using [Reference Thomason and TrobaughTT90, Theorem C.9]), we may assume that S is of finite type over
![]() $\operatorname {\mathrm {Spec}} \mathbf {Z}$
. In particular, the normalization
$\operatorname {\mathrm {Spec}} \mathbf {Z}$
. In particular, the normalization
![]() $S' \to S$
is finite. Now
$S' \to S$
is finite. Now
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S'\textrm {-}\mathrm {gp}}(H_{S'}, G_{S'})$
is a disjoint union of affine S-schemes, and the morphism
$\underline {\operatorname {\mathrm {Hom}}}_{S'\textrm {-}\mathrm {gp}}(H_{S'}, G_{S'})$
is a disjoint union of affine S-schemes, and the morphism
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S'\textrm {-}\mathrm {gp}}(H_{S'}, G_{S'}) \to \underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is finite and surjective, so ind-quasi-affineness of
$\underline {\operatorname {\mathrm {Hom}}}_{S'\textrm {-}\mathrm {gp}}(H_{S'}, G_{S'}) \to \underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is finite and surjective, so ind-quasi-affineness of
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
follows from Lemma 2.5.
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
follows from Lemma 2.5.
Lemma 2.7. In the setting of Theorem 2.2, assume that H is reductive. Then
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable by an ind-quasi-affine S-scheme. If S is normal, quasi-compact, and quasi-separated, and H admits a maximal S-torus, then
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable by an ind-quasi-affine S-scheme. If S is normal, quasi-compact, and quasi-separated, and H admits a maximal S-torus, then
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable by a disjoint union of finitely presented affine S-schemes.
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable by a disjoint union of finitely presented affine S-schemes.
Proof. To show ind-quasi-affineness, we may work locally on S and spread out to assume that S is affine, noetherian and excellent. (For the second claim, we may use [Reference Thomason and TrobaughTT90, Theorem C.9] to make the same reduction.) Using Lemma 2.5, we may also pass from S to its normalization to assume that S is normal. Passing to a further étale cover, we may and do assume that H admits a maximal S-torus. By [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. XXIV, Corollaire 7.1.9], the natural restriction map
is finitely presented and affine, so the result follows from Lemma 2.6. (Note that a smooth affine S-scheme is automatically finitely presented.)
Proof of Theorem 2.2.
Recall that H is now assumed to be a geometrically reductive smooth affine S-group scheme. In particular,
![]() $H^0$
is a reductive group scheme and
$H^0$
is a reductive group scheme and
![]() $H/H^0$
is finite by Theorem 2.1 (and similarly for G). There are two issues: first, we need to show that
$H/H^0$
is finite by Theorem 2.1 (and similarly for G). There are two issues: first, we need to show that
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable, and then we need to show that if S is normal, quasi-compact and quasi-separated, and H admits a maximal S-torus, then
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable, and then we need to show that if S is normal, quasi-compact and quasi-separated, and H admits a maximal S-torus, then
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is a disjoint union of finitely presented S-affine S-schemes (at which point ind-quasi-affineness in general follows from Lemma 2.5). For both points, by working locally and spreading out, we may assume that S is noetherian and connected.
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is a disjoint union of finitely presented S-affine S-schemes (at which point ind-quasi-affineness in general follows from Lemma 2.5). For both points, by working locally and spreading out, we may assume that S is noetherian and connected.
To prove representability, first assume that
![]() $H/H^0$
is constant and that the natural map
$H/H^0$
is constant and that the natural map
![]() $H(S) \to (H/H^0)(S)$
is surjective. Let
$H(S) \to (H/H^0)(S)$
is surjective. Let
![]() $h_1, \dots , h_n \in H(S)$
be a system of representatives for
$h_1, \dots , h_n \in H(S)$
be a system of representatives for
![]() $(H/H^0)(S)$
. We may and do assume
$(H/H^0)(S)$
. We may and do assume
![]() $h_1 = 1$
. There is then a natural morphism of functors
$h_1 = 1$
. There is then a natural morphism of functors
given by
![]() $f \mapsto (f|_{H^0}, f(h_1), \dots , f(h_n))$
. We claim that
$f \mapsto (f|_{H^0}, f(h_1), \dots , f(h_n))$
. We claim that
![]() $\beta $
is a closed embedding. To this end, we need to understand when a tuple
$\beta $
is a closed embedding. To this end, we need to understand when a tuple
![]() $(f_0, g_1, \dots , g_n)$
in
$(f_0, g_1, \dots , g_n)$
in
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H^0, G)(S') \times G(S')^n$
lies in the image of
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H^0, G)(S') \times G(S')^n$
lies in the image of
![]() $\beta $
.
$\beta $
.
For indices
![]() $i, j$
, let
$i, j$
, let
![]() $h_i h_j = h_{\delta (i, j)} h_{i,j}$
, where
$h_i h_j = h_{\delta (i, j)} h_{i,j}$
, where
![]() $1 \leq \delta (i, j) \leq n$
and
$1 \leq \delta (i, j) \leq n$
and
![]() $h_{i,j} \in H^0(S)$
. In any case, there is a unique morphism of S-schemes
$h_{i,j} \in H^0(S)$
. In any case, there is a unique morphism of S-schemes
![]() $f: H \to G$
with
$f: H \to G$
with
![]() $f|_{H^0} = f_0$
and
$f|_{H^0} = f_0$
and
![]() $f(h_i) = g_i$
for all i: for this, note that for any S-scheme
$f(h_i) = g_i$
for all i: for this, note that for any S-scheme
![]() $S'$
and any
$S'$
and any
![]() $h \in H(S')$
, there is a unique open decomposition
$h \in H(S')$
, there is a unique open decomposition
![]() $S' = \bigsqcup _{i=1}^n S^{\prime }_i$
such that
$S' = \bigsqcup _{i=1}^n S^{\prime }_i$
such that
![]() $h|_{S^{\prime }_i} = h_i h^{\prime }_i$
for some
$h|_{S^{\prime }_i} = h_i h^{\prime }_i$
for some
![]() $h^{\prime }_i \in H^0(S^{\prime }_i)$
. Thus, f is defined uniquely by requiring
$h^{\prime }_i \in H^0(S^{\prime }_i)$
. Thus, f is defined uniquely by requiring
![]() $f(h_i h') = g_i f_0(h')$
for every S-scheme
$f(h_i h') = g_i f_0(h')$
for every S-scheme
![]() $S'$
and every
$S'$
and every
![]() $h' \in H^0(S')$
. Now
$h' \in H^0(S')$
. Now
![]() $(f_0, g_1, \dots , g_n)$
lies in the image of
$(f_0, g_1, \dots , g_n)$
lies in the image of
![]() $\beta $
if and only if the above-defined f is a homomorphism.
$\beta $
if and only if the above-defined f is a homomorphism.
Unraveling, we find that f is a homomorphism if and only if the following conditions are satisfied:
-
1.
 $g_1 = 1$
,
$g_1 = 1$
, -
2.
 $g_i^{-1} f_0(h) g_i = f_0(h_i^{-1} h h_i)$
for all i,
$g_i^{-1} f_0(h) g_i = f_0(h_i^{-1} h h_i)$
for all i, -
3.
 $g_i g_j = g_{\delta (i, j)} f_0(h_{i,j})$
.
$g_i g_j = g_{\delta (i, j)} f_0(h_{i,j})$
.
So indeed,
![]() $\beta $
is a finitely presented closed embedding, whence
$\beta $
is a finitely presented closed embedding, whence
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable, and in fact, it is ind-quasi-affine over S by Lemma 2.7. Moreover, if S is normal, then this shows that
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable, and in fact, it is ind-quasi-affine over S by Lemma 2.7. Moreover, if S is normal, then this shows that
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is a disjoint union of finitely presented S-affine S-schemes.
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is a disjoint union of finitely presented S-affine S-schemes.
Now pass to the general case (i.e., no longer assume that
![]() $H/H^0$
is constant and that
$H/H^0$
is constant and that
![]() $H(S) \to (H/H^0)(S)$
is surjective). In any case, there is a finite étale cover
$H(S) \to (H/H^0)(S)$
is surjective). In any case, there is a finite étale cover
![]() $S' \to S$
such that
$S' \to S$
such that
![]() $H_{S'}/H_{S'}^0$
is constant and
$H_{S'}/H_{S'}^0$
is constant and
![]() $H(S') \to (H/H^0)(S')$
is surjective (e.g., take
$H(S') \to (H/H^0)(S')$
is surjective (e.g., take
![]() $S'$
to be a Galois closure of the finite étale
$S'$
to be a Galois closure of the finite étale
![]() $H/H^0$
), and so
$H/H^0$
), and so
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S'\textrm {-}\mathrm {gp}}(H_{S'}, G_{S'})$
is ind-quasi-affine over
$\underline {\operatorname {\mathrm {Hom}}}_{S'\textrm {-}\mathrm {gp}}(H_{S'}, G_{S'})$
is ind-quasi-affine over
![]() $S'$
by the above. Thus, by effectivity of fpqc descent for ind-quasi-affine morphisms [Sta21, Tag 0APK], we see that
$S'$
by the above. Thus, by effectivity of fpqc descent for ind-quasi-affine morphisms [Sta21, Tag 0APK], we see that
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable and locally of finite presentation. Now that we have representability, we may assume that S is normal, quasi-compact and quasi-separated. As we have already seen,
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is representable and locally of finite presentation. Now that we have representability, we may assume that S is normal, quasi-compact and quasi-separated. As we have already seen,
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S'\textrm {-}\mathrm {gp}}(H_{S'}, G_{S'})$
is representable by a disjoint union of finitely presented
$\underline {\operatorname {\mathrm {Hom}}}_{S'\textrm {-}\mathrm {gp}}(H_{S'}, G_{S'})$
is representable by a disjoint union of finitely presented
![]() $S'$
-affine
$S'$
-affine
![]() $S'$
-schemes, so because the morphism
$S'$
-schemes, so because the morphism
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S'\textrm {-}\mathrm {gp}}(H_{S'}, G_{S'}) \to \underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is finite étale, the result follows from Lemma 2.5.
$\underline {\operatorname {\mathrm {Hom}}}_{S'\textrm {-}\mathrm {gp}}(H_{S'}, G_{S'}) \to \underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is finite étale, the result follows from Lemma 2.5.
Example 2.8. The schemes in Theorem 2.2 are usually not quasi-compact or flat, and they can fail to have smooth fibers. We saw examples of the first two phenomena in Example 2.4. For an example in which smoothness fails, let k be an algebraically closed field of characteristic
![]() $p> 0$
, and consider the component C of
$p> 0$
, and consider the component C of
![]() $\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(\operatorname {\mathrm {SL}}_2, \operatorname {\mathrm {GL}}_{p+1})$
containing the representation
$\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(\operatorname {\mathrm {SL}}_2, \operatorname {\mathrm {GL}}_{p+1})$
containing the representation
![]() $\operatorname {\mathrm {Sym}}^p V$
, where V is the standard representation of
$\operatorname {\mathrm {Sym}}^p V$
, where V is the standard representation of
![]() $\operatorname {\mathrm {SL}}_2$
. This representation is not semisimple: in the notation of [Reference JantzenJan03, II, Chapter 2], it has Jordan–Hölder factors
$\operatorname {\mathrm {SL}}_2$
. This representation is not semisimple: in the notation of [Reference JantzenJan03, II, Chapter 2], it has Jordan–Hölder factors
![]() $L(p)$
and
$L(p)$
and
![]() $L(p-2)$
. In fact, one can check that C consists of three orbits for the
$L(p-2)$
. In fact, one can check that C consists of three orbits for the
![]() $\operatorname {\mathrm {GL}}_{p+1}$
-action: the orbit of
$\operatorname {\mathrm {GL}}_{p+1}$
-action: the orbit of
![]() $\operatorname {\mathrm {Sym}}^p V$
, the orbit of
$\operatorname {\mathrm {Sym}}^p V$
, the orbit of
![]() $L(p) \oplus L(p-2)$
and the orbit of
$L(p) \oplus L(p-2)$
and the orbit of
![]() $(\operatorname {\mathrm {Sym}}^p V)^*$
. The first and last of these orbits are smooth and open, and their closures intersect in the second orbit.
$(\operatorname {\mathrm {Sym}}^p V)^*$
. The first and last of these orbits are smooth and open, and their closures intersect in the second orbit.
Even worse, components of
![]() $\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(\operatorname {\mathrm {SL}}_n, \operatorname {\mathrm {GL}}_N)$
can have infinitely many orbits for large n and N; one can deduce this using [Reference Scott and XiSX10, Theorem 5.2]. Consequently, it can be difficult to predict the dimensions of components of
$\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(\operatorname {\mathrm {SL}}_n, \operatorname {\mathrm {GL}}_N)$
can have infinitely many orbits for large n and N; one can deduce this using [Reference Scott and XiSX10, Theorem 5.2]. Consequently, it can be difficult to predict the dimensions of components of
![]() $\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
.
$\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
.
Question 2.9.
-
1. If k is a field of characteristic
 $p> 0$
and H and G are reductive, can
$p> 0$
and H and G are reductive, can
 $\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
be non-reduced? This cannot occur if
$\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
be non-reduced? This cannot occur if
 $p> \dim G/\operatorname {\mathrm {rank}} H$
, essentially by Theorem 3.4.
$p> \dim G/\operatorname {\mathrm {rank}} H$
, essentially by Theorem 3.4. -
2. More generally, if H and G are reductive group schemes over
 $\mathbf {Z}$
, can
$\mathbf {Z}$
, can
 $\underline {\operatorname {\mathrm {Hom}}}_{\mathbf {Z}\textrm {-}\mathrm {gp}}(H, G)$
be non-reduced?
$\underline {\operatorname {\mathrm {Hom}}}_{\mathbf {Z}\textrm {-}\mathrm {gp}}(H, G)$
be non-reduced? -
3. If A is a DVR and H and G are reductive, can
 $\underline {\operatorname {\mathrm {Hom}}}_{A\textrm {-}\mathrm {gp}}(H, G)$
have a non-flat component with an integral point? Again, this cannot happen if p is ‘large’.
$\underline {\operatorname {\mathrm {Hom}}}_{A\textrm {-}\mathrm {gp}}(H, G)$
have a non-flat component with an integral point? Again, this cannot happen if p is ‘large’.
The geometry of
![]() $\operatorname {\mathrm {Hom}}$
-schemes can be related to the theory of complete reducibility as in [Reference Bate, Martin and RöhrleBMR05]. Recall that if k is a field, G is a reductive k-group, and
$\operatorname {\mathrm {Hom}}$
-schemes can be related to the theory of complete reducibility as in [Reference Bate, Martin and RöhrleBMR05]. Recall that if k is a field, G is a reductive k-group, and
![]() $H \subset G$
is a closed k-subgroup scheme, then H is G-completely reducible (or G-cr) if, for any R-parabolic
$H \subset G$
is a closed k-subgroup scheme, then H is G-completely reducible (or G-cr) if, for any R-parabolic
![]() $\overline {k}$
-subgroup
$\overline {k}$
-subgroup
![]() $P \subset G_{\overline {k}}$
such that
$P \subset G_{\overline {k}}$
such that
![]() $H_{\overline {k}} \subset P$
, there exists an R-Levi
$H_{\overline {k}} \subset P$
, there exists an R-Levi
![]() $L \subset P$
such that
$L \subset P$
such that
![]() $H_{\overline {k}} \subset L$
. (The notions of R-parabolic and R-Levi subgroup are defined in [Reference Bate, Martin and RöhrleBMR05, Section 6]; they coincide with the usual notions of parabolic and Levi if G is connected.)
$H_{\overline {k}} \subset L$
. (The notions of R-parabolic and R-Levi subgroup are defined in [Reference Bate, Martin and RöhrleBMR05, Section 6]; they coincide with the usual notions of parabolic and Levi if G is connected.)
By [Reference Bate, Martin and RöhrleBMR05, Proposition 2.16, Theorem 3.1, Section 6], if H is topologically generated by
![]() $x_1, \dots , x_n \in H(k)$
(in the sense that the subgroup of
$x_1, \dots , x_n \in H(k)$
(in the sense that the subgroup of
![]() $H(k)$
generated by
$H(k)$
generated by
![]() $x_1, \dots , x_n$
is Zariski-dense in H), then H is G-cr if and only if the G-orbit of the n-tuple
$x_1, \dots , x_n$
is Zariski-dense in H), then H is G-cr if and only if the G-orbit of the n-tuple
![]() $(x_1, \dots , x_n)$
is closed in
$(x_1, \dots , x_n)$
is closed in
![]() $G^n$
. Moreover, [Reference SerreSer03, Property 4] shows that if H is smooth and G-cr, then
$G^n$
. Moreover, [Reference SerreSer03, Property 4] shows that if H is smooth and G-cr, then
![]() $H^0$
is reductive. With these two facts in mind, the following lemma relates G-complete reducibility to orbits in
$H^0$
is reductive. With these two facts in mind, the following lemma relates G-complete reducibility to orbits in
![]() $\operatorname {\mathrm {Hom}}$
-schemes.
$\operatorname {\mathrm {Hom}}$
-schemes.
Lemma 2.10. Let k be a field, and let G and H be (possibly disconnected) reductive k-groups. If H is topologically generated by
![]() $x_1, \dots , x_n \in H(k)$
, then the k-morphism
$x_1, \dots , x_n \in H(k)$
, then the k-morphism
![]() $\iota : \underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G) \to G^n$
sending f to
$\iota : \underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G) \to G^n$
sending f to
![]() $(f(x_1), \dots , f(x_n))$
is monic and satisfies the valuative criterion of properness. In particular,
$(f(x_1), \dots , f(x_n))$
is monic and satisfies the valuative criterion of properness. In particular,
![]() $\iota $
is a closed embedding when restricted to any connected component of
$\iota $
is a closed embedding when restricted to any connected component of
![]() $\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
.
$\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
.
Proof. It is clear that
![]() $\iota $
is monic, and the final claim follows from the others by [Reference Dieudonne and GrothendieckDG67, IV3, Proposition 8.11.5] and Theorem 2.2, which shows that every connected component of
$\iota $
is monic, and the final claim follows from the others by [Reference Dieudonne and GrothendieckDG67, IV3, Proposition 8.11.5] and Theorem 2.2, which shows that every connected component of
![]() $\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
is of finite type over k. We now verify that
$\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
is of finite type over k. We now verify that
![]() $\iota $
satisfies the valuative criterion of properness. Let A be a k-algebra which is a DVR with fraction field K, and let
$\iota $
satisfies the valuative criterion of properness. Let A be a k-algebra which is a DVR with fraction field K, and let
![]() $(g_1, \dots , g_n) \in G(A)^n$
be such that there exists a K-homomorphism
$(g_1, \dots , g_n) \in G(A)^n$
be such that there exists a K-homomorphism
![]() $f_1: H_K \to G_K$
satisfying
$f_1: H_K \to G_K$
satisfying
![]() $f_1(x_i) = g_i$
for all i. Let now
$f_1(x_i) = g_i$
for all i. Let now
![]() $\Gamma \subset H \times _{\operatorname {\mathrm {Spec}} A} G$
be the schematic closure of the graph of
$\Gamma \subset H \times _{\operatorname {\mathrm {Spec}} A} G$
be the schematic closure of the graph of
![]() $f_1$
, so that
$f_1$
, so that
![]() $\Gamma $
is a flat closed A-subgroup scheme of
$\Gamma $
is a flat closed A-subgroup scheme of
![]() $H \times _{\operatorname {\mathrm {Spec}} A} G$
whose projection map
$H \times _{\operatorname {\mathrm {Spec}} A} G$
whose projection map
![]() $\pi _1$
to H is an isomorphism on generic fibers over A. Moreover, since
$\pi _1$
to H is an isomorphism on generic fibers over A. Moreover, since
![]() $(x_i, g_i) \in H(A) \times G(A)$
for all i, it follows that
$(x_i, g_i) \in H(A) \times G(A)$
for all i, it follows that
![]() $(x_i, g_i) \in \Gamma (A)$
, and thus,
$(x_i, g_i) \in \Gamma (A)$
, and thus,
![]() $\pi _{1,s}: \Gamma _s \to H_s$
is surjective. Since
$\pi _{1,s}: \Gamma _s \to H_s$
is surjective. Since
![]() $H_s$
is smooth, we see that
$H_s$
is smooth, we see that
![]() $\pi _{1, s}$
is flat, and by fibral flatness, it follows that
$\pi _{1, s}$
is flat, and by fibral flatness, it follows that
![]() $\pi _1$
is flat. Since
$\pi _1$
is flat. Since
![]() $(\ker \pi _1)_K = \{1\}$
, it follows from flatness that
$(\ker \pi _1)_K = \{1\}$
, it follows from flatness that
![]() $\ker \pi _1 = \{1\}$
. Thus,
$\ker \pi _1 = \{1\}$
. Thus,
![]() $\pi _{1, s}$
is a closed embedding, and since
$\pi _{1, s}$
is a closed embedding, and since
![]() $\pi _{1, s}$
is surjective and
$\pi _{1, s}$
is surjective and
![]() $H_s$
is smooth, it follows that
$H_s$
is smooth, it follows that
![]() $\pi _{1, s}$
is an isomorphism. By the fibral isomorphism criterion,
$\pi _{1, s}$
is an isomorphism. By the fibral isomorphism criterion,
![]() $\pi _1$
is therefore an isomorphism, and it is the graph of an A-homomorphism
$\pi _1$
is therefore an isomorphism, and it is the graph of an A-homomorphism
![]() $f: H \to G$
whose generic fiber is
$f: H \to G$
whose generic fiber is
![]() $f_1$
. This verifies the valuative criterion.
$f_1$
. This verifies the valuative criterion.
Lemma 2.11. Let k be a field, and let G and H be reductive k-groups. If
![]() $f: H \to G$
is a k-homomorphism, then
$f: H \to G$
is a k-homomorphism, then
![]() $f(H) \subset G$
is G-cr if and only if the G-orbit through f in
$f(H) \subset G$
is G-cr if and only if the G-orbit through f in
![]() $\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
is closed.
$\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
is closed.
Proof. We may and do pass to a (possibly transcendental) field extension of k to assume that there exist
![]() $x_1, \dots , x_n \in H(k)$
which topologically generate H. If
$x_1, \dots , x_n \in H(k)$
which topologically generate H. If
![]() $f(H)$
is G-cr, then by [Reference Bate, Martin and RöhrleBMR05, Proposition 2.16, Theorem 3.1], the G-orbit of
$f(H)$
is G-cr, then by [Reference Bate, Martin and RöhrleBMR05, Proposition 2.16, Theorem 3.1], the G-orbit of
![]() $(f(x_1), \dots , f(x_n))$
in
$(f(x_1), \dots , f(x_n))$
in
![]() $G^n$
is closed. Thus, the G-orbit of f is closed in
$G^n$
is closed. Thus, the G-orbit of f is closed in
![]() $\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
since this orbit is simply the preimage of the G-orbit of
$\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
since this orbit is simply the preimage of the G-orbit of
![]() $(f(x_1), \dots , f(x_n))$
under the map
$(f(x_1), \dots , f(x_n))$
under the map
![]() $\iota $
of Lemma 2.10. Conversely, if the G-orbit of f is closed, then
$\iota $
of Lemma 2.10. Conversely, if the G-orbit of f is closed, then
![]() $\iota (G\cdot f)$
is closed in
$\iota (G\cdot f)$
is closed in
![]() $G^n$
by Lemma 2.10, and we conclude with the fact that
$G^n$
by Lemma 2.10, and we conclude with the fact that
![]() $\iota (G \cdot f)$
is simply the G-orbit of
$\iota (G \cdot f)$
is simply the G-orbit of
![]() $(f(x_1), \dots , f(x_n))$
.
$(f(x_1), \dots , f(x_n))$
.
Remark 2.12. Using [Reference MartinMar03, Proposition 3.2, Theorem 10.3] and Lemma 2.11, one can show that every component of
![]() $\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
contains only finitely many closed G-orbits. Consequently, [Reference SerreSer05, Théorème 4.4] shows that if G is simple and
$\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
contains only finitely many closed G-orbits. Consequently, [Reference SerreSer05, Théorème 4.4] shows that if G is simple and
![]() $p> 1 + \operatorname {\mathrm {rank}} G$
, then
$p> 1 + \operatorname {\mathrm {rank}} G$
, then
![]() $\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)_{\mathrm {red}}$
is a disjoint union of G-orbits. For classical groups G,
$\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)_{\mathrm {red}}$
is a disjoint union of G-orbits. For classical groups G,
![]() $\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
is reduced under these conditions, but we do not know what happens if G is exceptional.
$\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
is reduced under these conditions, but we do not know what happens if G is exceptional.
2.2 Automorphism schemes
Next, if G is an S-group scheme, we define the set-valued functor
![]() $\underline {\operatorname {\mathrm {Aut}}}_{G/S}$
by
$\underline {\operatorname {\mathrm {Aut}}}_{G/S}$
by
The following two lemmas are the crucial inputs needed to analyze this functor.
Lemma 2.13. Let G be a finitely presented S-group scheme. If
![]() $f: G \to G$
is an S-homomorphism, then f is an isomorphism if and only if
$f: G \to G$
is an S-homomorphism, then f is an isomorphism if and only if
![]() $\ker f_s = \{1\}$
for all
$\ker f_s = \{1\}$
for all
![]() $s \in S$
.
$s \in S$
.
Proof. If f is an isomorphism, then certainly
![]() $\ker f = \{1\}$
. If
$\ker f = \{1\}$
. If
![]() $\ker f_s = \{1\}$
for all
$\ker f_s = \{1\}$
for all
![]() $s \in S$
, then
$s \in S$
, then
![]() $\ker f = \{1\}$
: indeed, the identity section
$\ker f = \{1\}$
: indeed, the identity section
![]() $e: S \to \ker f$
is a morphism of S-schemes which is an isomorphism on fibers over S, so because S is S-flat, it follows from the fibral isomorphism criterion [Reference Dieudonne and GrothendieckDG67, IV4, Corollaire 17.9.5] that e is an isomorphism (i.e.,
$e: S \to \ker f$
is a morphism of S-schemes which is an isomorphism on fibers over S, so because S is S-flat, it follows from the fibral isomorphism criterion [Reference Dieudonne and GrothendieckDG67, IV4, Corollaire 17.9.5] that e is an isomorphism (i.e.,
![]() $\ker f = \{1\}$
). Thus, f is monic, and it follows from the Ax–Grothendieck theorem [Reference Dieudonne and GrothendieckDG67, IV4, Proposition 17.9.6] that f is an isomorphism.
$\ker f = \{1\}$
). Thus, f is monic, and it follows from the Ax–Grothendieck theorem [Reference Dieudonne and GrothendieckDG67, IV4, Proposition 17.9.6] that f is an isomorphism.
Lemma 2.14. Let A be a DVR, and let G and H be geometrically reductive smooth affine A-group schemes. If
![]() $f: G \to H$
is an A-homomorphism, then the following are equivalent.
$f: G \to H$
is an A-homomorphism, then the following are equivalent.
-
1.
 $f_s$
is an isomorphism,
$f_s$
is an isomorphism, -
2.
 $f_\eta $
is an isomorphism,
$f_\eta $
is an isomorphism, -
3. f is an isomorphism.
Proof. Clearly, (3) implies (1) and (2). Conversely, if
![]() $f_s$
and
$f_s$
and
![]() $f_\eta $
are both isomorphisms, then f is an isomorphism by the fibral isomorphism criterion [Reference Dieudonne and GrothendieckDG67, IV4, Corollaire 17.9.5]. Thus, it suffices to show that (1) and (2) are equivalent. We may and do further assume that A is complete with algebraically closed residue field.
$f_\eta $
are both isomorphisms, then f is an isomorphism by the fibral isomorphism criterion [Reference Dieudonne and GrothendieckDG67, IV4, Corollaire 17.9.5]. Thus, it suffices to show that (1) and (2) are equivalent. We may and do further assume that A is complete with algebraically closed residue field.
First, suppose that G (and hence also H under either (1) or (2), due to finiteness of
![]() $H/H^0$
) has connected fibers. Assume
$H/H^0$
) has connected fibers. Assume
![]() $f_s$
is an isomorphism. By the fibral isomorphism criterion,
$f_s$
is an isomorphism. By the fibral isomorphism criterion,
![]() $f_{A/\mathfrak {m}^n}$
is an isomorphism for all
$f_{A/\mathfrak {m}^n}$
is an isomorphism for all
![]() $n \geq 1$
. By the local flatness criterion [Reference MatsumuraMat89, Theorem 22.3], f is flat. In fact, f is étale near
$n \geq 1$
. By the local flatness criterion [Reference MatsumuraMat89, Theorem 22.3], f is flat. In fact, f is étale near
![]() $1$
because the étale locus is open, and since it is a homomorphism with G fppf over A, it follows that f is étale. In particular,
$1$
because the étale locus is open, and since it is a homomorphism with G fppf over A, it follows that f is étale. In particular,
![]() $\ker f$
is étale. One can check that an étale normal subgroup scheme of a connected group scheme over a field is automatically central, so
$\ker f$
is étale. One can check that an étale normal subgroup scheme of a connected group scheme over a field is automatically central, so
![]() $\ker f_\eta $
is central, and thus,
$\ker f_\eta $
is central, and thus,
![]() $\ker f$
is contained in
$\ker f$
is contained in
![]() $Z(G)$
. But
$Z(G)$
. But
![]() $Z(G)$
is of multiplicative type, and
$Z(G)$
is of multiplicative type, and
![]() $\ker f$
is a flat closed A-subgroup scheme of
$\ker f$
is a flat closed A-subgroup scheme of
![]() $Z(G)$
, so it is also of multiplicative type by [Reference ConradCon14, Corollary B.3.3]. Since
$Z(G)$
, so it is also of multiplicative type by [Reference ConradCon14, Corollary B.3.3]. Since
![]() $\ker f_s = \{1\}$
, we conclude that
$\ker f_s = \{1\}$
, we conclude that
![]() $\ker f_\eta = \{1\}$
, and hence,
$\ker f_\eta = \{1\}$
, and hence,
![]() $f_\eta $
is a closed embedding by [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. VIB, Corollaire 1.4.2]. For dimension reasons,
$f_\eta $
is a closed embedding by [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. VIB, Corollaire 1.4.2]. For dimension reasons,
![]() $f_\eta $
is dominant, so it is surjective by [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. VIB, Proposition 1.2], and hence, it is an isomorphism since
$f_\eta $
is dominant, so it is surjective by [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. VIB, Proposition 1.2], and hence, it is an isomorphism since
![]() $H_\eta $
is smooth.
$H_\eta $
is smooth.
Conversely, suppose that
![]() $f_\eta $
is an isomorphism. If
$f_\eta $
is an isomorphism. If
![]() $g \in G(k(s))$
is a nontrivial semisimple element, then there is a maximal
$g \in G(k(s))$
is a nontrivial semisimple element, then there is a maximal
![]() $k(s)$
-torus
$k(s)$
-torus
![]() $T_0 \subset G_s$
such that
$T_0 \subset G_s$
such that
![]() $g \in T_0(k(s))$
. By [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. IX, Théorème 3.6], since A is complete, we may find a maximal A-torus
$g \in T_0(k(s))$
. By [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. IX, Théorème 3.6], since A is complete, we may find a maximal A-torus
![]() $T \subset G$
with special fiber
$T \subset G$
with special fiber
![]() $T_0$
. Since
$T_0$
. Since
![]() $\ker f|_{T_\eta } = \{1\}$
, it follows from [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. IX, Théorème 6.8] that
$\ker f|_{T_\eta } = \{1\}$
, it follows from [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. IX, Théorème 6.8] that
![]() $\ker f|_T = \{1\}$
, so in particular,
$\ker f|_T = \{1\}$
, so in particular,
![]() $g \not \in (\ker f)(k(s))$
. Note that
$g \not \in (\ker f)(k(s))$
. Note that
![]() $(\ker f_s)^0_{\mathrm {{red}}}$
is a smooth connected closed normal subgroup of
$(\ker f_s)^0_{\mathrm {{red}}}$
is a smooth connected closed normal subgroup of
![]() $G_s$
, so it is reductive, and thus, its semisimple locus is dense. But the above argument shows that its semisimple locus is
$G_s$
, so it is reductive, and thus, its semisimple locus is dense. But the above argument shows that its semisimple locus is
![]() $\{1\}$
, so in fact,
$\{1\}$
, so in fact,
![]() $(\ker f_s)^0_{\mathrm {{red}}} = \{1\}$
, whence
$(\ker f_s)^0_{\mathrm {{red}}} = \{1\}$
, whence
![]() $\ker f_s$
is finite. Thus, for dimension reasons,
$\ker f_s$
is finite. Thus, for dimension reasons,
![]() $f_s$
is dominant, and since G is smooth, we find that
$f_s$
is dominant, and since G is smooth, we find that
![]() $f_s$
is flat: this follows from generic flatness and a simple translation argument. By the fibral flatness criterion [Reference Dieudonne and GrothendieckDG67, IV3, Théorème 11.3.10], f is flat, and so
$f_s$
is flat: this follows from generic flatness and a simple translation argument. By the fibral flatness criterion [Reference Dieudonne and GrothendieckDG67, IV3, Théorème 11.3.10], f is flat, and so
![]() $\ker f$
is flat. Since
$\ker f$
is flat. Since
![]() $\ker f_\eta = \{1\}$
, it follows that
$\ker f_\eta = \{1\}$
, it follows that
![]() $\ker f = \{1\}$
: as a flat closed subscheme of G,
$\ker f = \{1\}$
: as a flat closed subscheme of G,
![]() $\ker f$
is the closure of its generic fiber. So
$\ker f$
is the closure of its generic fiber. So
![]() $f_s$
is a surjective closed embedding, and hence an isomorphism.
$f_s$
is a surjective closed embedding, and hence an isomorphism.
Now consider the general case – namely, that
![]() $G/G^0$
is finite. Suppose that either
$G/G^0$
is finite. Suppose that either
![]() $f_s$
or
$f_s$
or
![]() $f_\eta $
is an isomorphism. By the reductive case settled above, we find that
$f_\eta $
is an isomorphism. By the reductive case settled above, we find that
![]() $f|_{G^0}: G^0 \to H^0$
is an isomorphism. Moreover, the homomorphism
$f|_{G^0}: G^0 \to H^0$
is an isomorphism. Moreover, the homomorphism
![]() $G/G^0 \to H/H^0$
between constant groups is an isomorphism, since this can be checked on either the special or generic fiber. Thus, a diagram chase shows that f is an isomorphism.
$G/G^0 \to H/H^0$
between constant groups is an isomorphism, since this can be checked on either the special or generic fiber. Thus, a diagram chase shows that f is an isomorphism.
Theorem 2.15. Let S be a scheme, and let G be a geometrically reductive smooth affine S-group scheme. The functor
![]() $\underline {\operatorname {\mathrm {Aut}}}_{G/S}$
is representable by an open and closed subscheme
$\underline {\operatorname {\mathrm {Aut}}}_{G/S}$
is representable by an open and closed subscheme
![]() $\operatorname {\mathrm {Aut}}_{G/S}$
of
$\operatorname {\mathrm {Aut}}_{G/S}$
of
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(G, G)$
.
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(G, G)$
.
Proof. By spreading out, we may and do assume that S is noetherian, so that ![]() is locally noetherian by Lemma 2.3. Note that there is a universal S-homomorphism
is locally noetherian by Lemma 2.3. Note that there is a universal S-homomorphism
whose fiber over a given section of
![]() $\mathscr {H}$
is the corresponding endomorphism of G. By Lemmas 2.13 and 2.14, since
$\mathscr {H}$
is the corresponding endomorphism of G. By Lemmas 2.13 and 2.14, since
![]() $\mathscr {H}$
is locally noetherian, the locus U of
$\mathscr {H}$
is locally noetherian, the locus U of
![]() $u \in \mathscr {H}$
such that
$u \in \mathscr {H}$
such that
![]() $\ker f_u = \{1\}$
is open and closed, and
$\ker f_u = \{1\}$
is open and closed, and
![]() $f_U: G \times _S U \to G \times _S U$
is an isomorphism. It follows from this reasoning that U represents
$f_U: G \times _S U \to G \times _S U$
is an isomorphism. It follows from this reasoning that U represents
![]() $\underline {\operatorname {\mathrm {Aut}}}_{G/S}$
.
$\underline {\operatorname {\mathrm {Aut}}}_{G/S}$
.
To use Theorem 2.15, it will be necessary to establish some more properties of the
![]() $\operatorname {\mathrm {Aut}}$
-scheme. If G is a weakly reductive group scheme over a scheme S, then we will see in Lemma 2.18 that
$\operatorname {\mathrm {Aut}}$
-scheme. If G is a weakly reductive group scheme over a scheme S, then we will see in Lemma 2.18 that
![]() $\operatorname {\mathrm {Aut}}_{G/S}$
is always smooth. However, the following example shows that
$\operatorname {\mathrm {Aut}}_{G/S}$
is always smooth. However, the following example shows that
![]() $\operatorname {\mathrm {Aut}}_{G/k}$
may fail to be smooth if k is a field of characteristic
$\operatorname {\mathrm {Aut}}_{G/k}$
may fail to be smooth if k is a field of characteristic
![]() $p> 0$
and G is a reductive k-group with component group of order divisible by p.
$p> 0$
and G is a reductive k-group with component group of order divisible by p.
Example 2.16. Let
![]() $G = \mathbf {G}_m \times \underline {\mathbf {Z}/p \mathbf {Z}}$
over a field k of characteristic
$G = \mathbf {G}_m \times \underline {\mathbf {Z}/p \mathbf {Z}}$
over a field k of characteristic
![]() $p> 0$
. If S is a k-scheme, then S-automorphisms of
$p> 0$
. If S is a k-scheme, then S-automorphisms of
![]() $G_S$
correspond to pairs
$G_S$
correspond to pairs
![]() $(\phi _0, g)$
, where
$(\phi _0, g)$
, where
![]() $\phi _0: \mathbf {G}_{m, S} \to \mathbf {G}_{m, S}$
is an S-automorphism and
$\phi _0: \mathbf {G}_{m, S} \to \mathbf {G}_{m, S}$
is an S-automorphism and
![]() $g \in G(S)$
is a section of order p such that for all
$g \in G(S)$
is a section of order p such that for all
![]() $s \in S$
,
$s \in S$
,
![]() $g_s$
does not lie in
$g_s$
does not lie in
![]() $G^0(k(s))$
; the correspondence is given by sending an S-automorphism
$G^0(k(s))$
; the correspondence is given by sending an S-automorphism
![]() $\phi $
of
$\phi $
of
![]() $G_S$
to
$G_S$
to
![]() $(\phi |_{G_S^0}, \phi (x))$
, where
$(\phi |_{G_S^0}, \phi (x))$
, where
![]() $x = (1, 1) \in \mathbf {G}_m(S) \times \underline {\mathbf {Z}/p \mathbf {Z}}(S)$
. Using this, one sees that
$x = (1, 1) \in \mathbf {G}_m(S) \times \underline {\mathbf {Z}/p \mathbf {Z}}(S)$
. Using this, one sees that
![]() $\operatorname {\mathrm {Aut}}_{G/k}^0 \cong \mu _p$
. In particular,
$\operatorname {\mathrm {Aut}}_{G/k}^0 \cong \mu _p$
. In particular,
![]() $\operatorname {\mathrm {Aut}}_{G/k}$
is not smooth.
$\operatorname {\mathrm {Aut}}_{G/k}$
is not smooth.
Lemma 2.17. Let G be a (possibly disconnected) reductive group over a field k. The natural map
![]() $G \to \operatorname {\mathrm {Aut}}_{G/k}$
is open. If k is perfect, then
$G \to \operatorname {\mathrm {Aut}}_{G/k}$
is open. If k is perfect, then
![]() $\phi : G \to (\operatorname {\mathrm {Aut}}_{G/k})_{\mathrm {{red}}}$
is flat.
$\phi : G \to (\operatorname {\mathrm {Aut}}_{G/k})_{\mathrm {{red}}}$
is flat.
Proof. Since formation of
![]() $(\operatorname {\mathrm {Aut}}_{G/k})_{\mathrm {{red}}}$
commutes with separable field extensions on k and purely inseparable extensions leave topological spaces unchanged, we may and do assume that k is algebraically closed. To show that
$(\operatorname {\mathrm {Aut}}_{G/k})_{\mathrm {{red}}}$
commutes with separable field extensions on k and purely inseparable extensions leave topological spaces unchanged, we may and do assume that k is algebraically closed. To show that
![]() $\phi $
is flat, it suffices to show that the map
$\phi $
is flat, it suffices to show that the map
![]() $G^0(k) \to (\operatorname {\mathrm {Aut}}_{G/k})^0(k)$
is surjective. Indeed, then
$G^0(k) \to (\operatorname {\mathrm {Aut}}_{G/k})^0(k)$
is surjective. Indeed, then
![]() $\phi $
is a dominant map from a smooth finite type k-scheme to a smooth k-scheme, so it is generically flat, and being a group homomorphism translation, arguments show that it is flat.
$\phi $
is a dominant map from a smooth finite type k-scheme to a smooth k-scheme, so it is generically flat, and being a group homomorphism translation, arguments show that it is flat.
Let
![]() $r: \operatorname {\mathrm {Aut}}_{G/k} \to \operatorname {\mathrm {Aut}}_{G^0/k} \times \operatorname {\mathrm {Aut}}_{(G/G^0)/k}$
denote the natural restriction homomorphism. The map
$r: \operatorname {\mathrm {Aut}}_{G/k} \to \operatorname {\mathrm {Aut}}_{G^0/k} \times \operatorname {\mathrm {Aut}}_{(G/G^0)/k}$
denote the natural restriction homomorphism. The map
![]() $G^0 \to \operatorname {\mathrm {Aut}}_{G/k}$
induces a map
$G^0 \to \operatorname {\mathrm {Aut}}_{G/k}$
induces a map
![]() $Z(G^0) \to \ker r$
. We claim that the image of
$Z(G^0) \to \ker r$
. We claim that the image of
![]() $Z(G^0)$
in
$Z(G^0)$
in
![]() $\ker r$
is of finite index. Once this is done, the lemma will follow: indeed, then
$\ker r$
is of finite index. Once this is done, the lemma will follow: indeed, then
Since the group scheme of outer automorphisms of
![]() $G^0$
is etale,
$G^0$
is etale,
![]() $\mathrm {pr}_1 \circ r: G^0 \to \operatorname {\mathrm {Aut}}_{G^0/k}^0$
is surjective. Since
$\mathrm {pr}_1 \circ r: G^0 \to \operatorname {\mathrm {Aut}}_{G^0/k}^0$
is surjective. Since
![]() $\operatorname {\mathrm {Aut}}_{(G/G^0)/k}$
is finite, we find in particular that
$\operatorname {\mathrm {Aut}}_{(G/G^0)/k}$
is finite, we find in particular that
![]() $\dim r(\phi (G)) = \dim r(\operatorname {\mathrm {Aut}}_{G/k})$
, so
$\dim r(\phi (G)) = \dim r(\operatorname {\mathrm {Aut}}_{G/k})$
, so
Therefore,
![]() $\phi (G^0)$
is an open subgroup scheme of the smooth k-group scheme
$\phi (G^0)$
is an open subgroup scheme of the smooth k-group scheme
![]() $(\operatorname {\mathrm {Aut}}_{G/k})_{\mathrm {{red}}}$
, so it contains
$(\operatorname {\mathrm {Aut}}_{G/k})_{\mathrm {{red}}}$
, so it contains
![]() $(\operatorname {\mathrm {Aut}}_{G/k})^0$
and hence is equal to it.
$(\operatorname {\mathrm {Aut}}_{G/k})^0$
and hence is equal to it.
So it remains to show that the image of
![]() $Z(G^0)$
of finite index in
$Z(G^0)$
of finite index in
![]() $(\ker r)(k)$
. First, we must understand some properties of
$(\ker r)(k)$
. First, we must understand some properties of
![]() $\operatorname {\mathrm {Aut}}_{G/k}$
. Suppose that
$\operatorname {\mathrm {Aut}}_{G/k}$
. Suppose that
![]() $f: G \to G$
is a k-homomorphism inducing the identity on
$f: G \to G$
is a k-homomorphism inducing the identity on
![]() $G^0$
and
$G^0$
and
![]() $G/G^0$
(i.e.,
$G/G^0$
(i.e.,
![]() $f \in (\ker r)(k)$
). We define a morphism
$f \in (\ker r)(k)$
). We define a morphism
![]() $\lambda : G \to G$
by
$\lambda : G \to G$
by
One checks that
![]() $\lambda $
is a
$\lambda $
is a
![]() $1$
-cocycle. Since
$1$
-cocycle. Since
![]() $f|_{G^0}$
is the identity, we have
$f|_{G^0}$
is the identity, we have
for all functorial points g and h of G and
![]() $G^0$
, respectively. Thus,
$G^0$
, respectively. Thus,
![]() $\lambda $
factors through a morphism
$\lambda $
factors through a morphism
![]() $G/G^0 \to G$
. Moreover, for such g and h, we have
$G/G^0 \to G$
. Moreover, for such g and h, we have
so in fact,
![]() $\lambda $
has image lying in
$\lambda $
has image lying in
![]() $Z(G^0)$
. Thus,
$Z(G^0)$
. Thus,
![]() $\lambda $
is a
$\lambda $
is a
![]() $1$
-cocycle
$1$
-cocycle
![]() $G/G^0 \to Z(G^0)$
. Note that any such
$G/G^0 \to Z(G^0)$
. Note that any such
![]() $\lambda $
determines f uniquely.
$\lambda $
determines f uniquely.
As in ordinary group cohomology, there is a short exact sequence
Notice that
![]() $\mathrm {B}^1(G/G^0, Z(G^0)) = \mathrm {B}^1((G/G^0)(k), Z(G^0)(k))$
(and so on) because
$\mathrm {B}^1(G/G^0, Z(G^0)) = \mathrm {B}^1((G/G^0)(k), Z(G^0)(k))$
(and so on) because
![]() $G/G^0$
is constant. Under the correspondence between f and
$G/G^0$
is constant. Under the correspondence between f and
![]() $\lambda $
as in the previous paragraph,
$\lambda $
as in the previous paragraph,
![]() $\mathrm {B}^1(G/G^0, Z(G^0))$
consists of those k-homomorphisms f induced by conjugation by an element of
$\mathrm {B}^1(G/G^0, Z(G^0))$
consists of those k-homomorphisms f induced by conjugation by an element of
![]() $Z(G^0)(k)$
. Moreover, if
$Z(G^0)(k)$
. Moreover, if
![]() $G/G^0$
is of order n, then
$G/G^0$
is of order n, then
![]() $\mathrm {H}^1(G/G^0, Z(G^0))$
is n-torsion, so
$\mathrm {H}^1(G/G^0, Z(G^0))$
is n-torsion, so
![]() $\mathrm {H}^1(G/G^0, Z(G^0))$
admits a surjection from
$\mathrm {H}^1(G/G^0, Z(G^0))$
admits a surjection from
![]() $\mathrm {H}^1(G/G^0, Z(G^0)[n])$
and hence is finite. So indeed, the map
$\mathrm {H}^1(G/G^0, Z(G^0)[n])$
and hence is finite. So indeed, the map
![]() $Z(G^0)(k) \to (\ker r)(k)$
has finite index image, and we are done.
$Z(G^0)(k) \to (\ker r)(k)$
has finite index image, and we are done.
Lemma 2.18. If G is a weakly reductive group scheme over S, then
![]() $\operatorname {\mathrm {Aut}}_{G/S}$
is smooth and the natural map
$\operatorname {\mathrm {Aut}}_{G/S}$
is smooth and the natural map
![]() $\phi : G \to \operatorname {\mathrm {Aut}}_{G/S}$
is flat. If
$\phi : G \to \operatorname {\mathrm {Aut}}_{G/S}$
is flat. If
![]() $Z(G^0)$
is smooth, then
$Z(G^0)$
is smooth, then
![]() $\phi $
is smooth.
$\phi $
is smooth.
Proof. Let
![]() $\mathfrak {g} = \operatorname {\mathrm {Lie}} G$
. We claim that
$\mathfrak {g} = \operatorname {\mathrm {Lie}} G$
. We claim that
![]() $\mathrm {H}^2(G_s, \mathfrak {g}_s) = 0$
for all
$\mathrm {H}^2(G_s, \mathfrak {g}_s) = 0$
for all
![]() $s \in S$
. There is a Hochschild–Serre spectral sequence
$s \in S$
. There is a Hochschild–Serre spectral sequence
and since
![]() $G_s/G_s^0$
has order prime to
$G_s/G_s^0$
has order prime to ![]() for all
for all
![]() $s \in S$
, we find
$s \in S$
, we find
for all n. By [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. XXIV, Corollaire 1.13(ii)] (in which reference reductive groups over fields are also required to be connected), we have
![]() $\mathrm {H}^2(G_s^0, \mathfrak {g}_s) = 0$
, so indeed,
$\mathrm {H}^2(G_s^0, \mathfrak {g}_s) = 0$
, so indeed,
![]() $\mathrm {H}^2(G_s, \mathfrak {g}_s) = 0$
for all
$\mathrm {H}^2(G_s, \mathfrak {g}_s) = 0$
for all
![]() $s \in S$
. The same argument, using [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. XXIV, Corollaire 1.15.1], shows that
$s \in S$
. The same argument, using [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. XXIV, Corollaire 1.15.1], shows that
![]() $\mathrm {H}^1(G_s, \mathfrak {g}_s) = 0$
for all
$\mathrm {H}^1(G_s, \mathfrak {g}_s) = 0$
for all
![]() $s \in S$
if
$s \in S$
if
![]() $Z(G^0)$
is smooth.
$Z(G^0)$
is smooth.
To show that
![]() $\underline {\operatorname {\mathrm {Aut}}}_{G/S}$
is smooth, it suffices to verify the infinitesimal criterion of smoothness, and for this [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. III, Corollaire 2.9(ii)] shows that it suffices to show
$\underline {\operatorname {\mathrm {Aut}}}_{G/S}$
is smooth, it suffices to verify the infinitesimal criterion of smoothness, and for this [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. III, Corollaire 2.9(ii)] shows that it suffices to show
![]() $\mathrm {H}^2(G_s, \mathfrak {g}_s) = 0$
for all
$\mathrm {H}^2(G_s, \mathfrak {g}_s) = 0$
for all
![]() $s \in S$
, which we showed above. Moreover, [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. III, Corollaire 2.9(i)] shows that if
$s \in S$
, which we showed above. Moreover, [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. III, Corollaire 2.9(i)] shows that if
![]() $\mathrm {H}^1(G_s, \mathfrak {g}_s) = 0$
for all
$\mathrm {H}^1(G_s, \mathfrak {g}_s) = 0$
for all
![]() $s \in S$
, then the morphism
$s \in S$
, then the morphism
![]() $\phi $
satisfies the infinitesimal criterion of smoothness, so it is smooth. In particular, the previous paragraph shows that if
$\phi $
satisfies the infinitesimal criterion of smoothness, so it is smooth. In particular, the previous paragraph shows that if
![]() $Z(G^0)$
is smooth, then
$Z(G^0)$
is smooth, then
![]() $\phi $
is smooth.
$\phi $
is smooth.
Finally, to show that
![]() $\phi $
is flat in general, we may use the fibral flatness criterion [Reference Dieudonne and GrothendieckDG67, IV3, Théorème 11.3.10] to assume that
$\phi $
is flat in general, we may use the fibral flatness criterion [Reference Dieudonne and GrothendieckDG67, IV3, Théorème 11.3.10] to assume that
![]() $S = \operatorname {\mathrm {Spec}} k$
for a field k. Thus, since
$S = \operatorname {\mathrm {Spec}} k$
for a field k. Thus, since
![]() $\operatorname {\mathrm {Aut}}_{G/k}$
is smooth, we may conclude using Lemma 2.17.
$\operatorname {\mathrm {Aut}}_{G/k}$
is smooth, we may conclude using Lemma 2.17.
Proposition 2.19. If G is a weakly reductive S-group scheme, the functorial center
![]() $Z(G)$
is an S-group scheme of multiplicative type. If
$Z(G)$
is an S-group scheme of multiplicative type. If
![]() $Z(G^0)$
is smooth, then
$Z(G^0)$
is smooth, then
![]() $Z(G)$
is smooth.
$Z(G)$
is smooth.
Example 2.20. Before proving the proposition, we offer the following example to show that geometric reductivity for a smooth affine G is not enough for flatness of
![]() $Z(G)$
. Let
$Z(G)$
. Let
![]() $A = \mathbf {Z}_p[\zeta _p]$
. There is a non-split central extension of constant A-group schemes
$A = \mathbf {Z}_p[\zeta _p]$
. There is a non-split central extension of constant A-group schemes
where U is isomorphic to the group of
![]() $\mathbf {F}_p$
-points of the unipotent radical of a Borel in
$\mathbf {F}_p$
-points of the unipotent radical of a Borel in
![]() $\operatorname {\mathrm {SL}}_3$
(i.e., U is the ‘Heisenberg group’ over
$\operatorname {\mathrm {SL}}_3$
(i.e., U is the ‘Heisenberg group’ over
![]() $\mathbf {F}_p$
). There is a homomorphism of A-group schemes
$\mathbf {F}_p$
). There is a homomorphism of A-group schemes
![]() $\mathbf {Z}/p \to \mu _p$
which is trivial on the special fiber and an isomorphism on the generic fiber, given by the choice of a primitive pth root of unity
$\mathbf {Z}/p \to \mu _p$
which is trivial on the special fiber and an isomorphism on the generic fiber, given by the choice of a primitive pth root of unity
![]() $\zeta _p$
. Pushing the above extension forward by the map
$\zeta _p$
. Pushing the above extension forward by the map
![]() $\mathbf {Z}/p \to \mu _p \to \mathbf {G}_m$
gives an extension
$\mathbf {Z}/p \to \mu _p \to \mathbf {G}_m$
gives an extension
where G has commutative special fiber and non-commutative generic fiber. In fact,
![]() $Z(G)$
has special fiber G and generic fiber
$Z(G)$
has special fiber G and generic fiber
![]() $G^0$
, so it is not flat.
$G^0$
, so it is not flat.
Proof. Working locally and spreading out, we may and do assume that S is locally noetherian. Consider the morphism
![]() $\phi : G \to \operatorname {\mathrm {Aut}}_{G/S}$
. By Lemma 2.18,
$\phi : G \to \operatorname {\mathrm {Aut}}_{G/S}$
. By Lemma 2.18,
![]() $\phi $
is flat, so
$\phi $
is flat, so
![]() $Z(G) = \ker \phi $
is a flat closed S-subgroup scheme of G, and it is smooth provided that
$Z(G) = \ker \phi $
is a flat closed S-subgroup scheme of G, and it is smooth provided that
![]() $Z(G^0)$
is smooth. So we need only show that
$Z(G^0)$
is smooth. So we need only show that
![]() $Z(G)$
is of multiplicative type.
$Z(G)$
is of multiplicative type.
We define ![]() ; note that
; note that
![]() $Z(G^0)$
is of multiplicative type. By [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. IX, Théorème 6.8], it follows that
$Z(G^0)$
is of multiplicative type. By [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. IX, Théorème 6.8], it follows that
![]() $C_{G^0}(G)$
is of multiplicative type. Moreover, there is a short exact sequence
$C_{G^0}(G)$
is of multiplicative type. Moreover, there is a short exact sequence
Since
![]() $Z(G)/C_{G^0}(G)$
is a closed commutative flat and finitely presented S-subgroup scheme of
$Z(G)/C_{G^0}(G)$
is a closed commutative flat and finitely presented S-subgroup scheme of
![]() $G/G^0$
, it is finite étale commutative of order invertible on S, and in particular, it is of multiplicative type. Thus,
$G/G^0$
, it is finite étale commutative of order invertible on S, and in particular, it is of multiplicative type. Thus,
![]() $Z(G)$
is a commutative extension of multiplicative type group schemes, so it is of multiplicative type by [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. XVII, Prop. 7.1.1].
$Z(G)$
is a commutative extension of multiplicative type group schemes, so it is of multiplicative type by [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. XVII, Prop. 7.1.1].
Remark 2.21. With more work, the kind of arguments used in the proof of Lemma 2.17 (expanded upon in the case of ‘abstract’ groups in [Reference WellsWel71]) can be used to proved that if G is weakly reductive over S, then there is a short exact sequence
in which
![]() $\operatorname {\mathrm {Out}}_{G/S}$
is an étale-locally constant S-group scheme, just as in the theory of reductive group schemes. Proving this would take us somewhat far afield, so we omit it.
$\operatorname {\mathrm {Out}}_{G/S}$
is an étale-locally constant S-group scheme, just as in the theory of reductive group schemes. Proving this would take us somewhat far afield, so we omit it.
We note that the above discussion gives a slight strengthening of [Reference MartinMar03, Lemma 6.8].
Corollary 2.22. Let k be a field, let G be a finite type k-group scheme, and let
![]() $H \subset G$
be a closed (not necessarily connected) reductive k-subgroup. The quotient
$H \subset G$
be a closed (not necessarily connected) reductive k-subgroup. The quotient
![]() $N_G(H)/HC_G(H)$
is finite. If
$N_G(H)/HC_G(H)$
is finite. If
![]() $H/H^0$
has order prime to
$H/H^0$
has order prime to ![]() , then
, then
![]() $N_G(H)/HC_G(H)$
is étale.
$N_G(H)/HC_G(H)$
is étale.
Proof. We may and do assume that k is algebraically closed. Let
![]() $\phi : H \to \operatorname {\mathrm {Aut}}_{H/k}$
be the natural map. By Lemma 2.17,
$\phi : H \to \operatorname {\mathrm {Aut}}_{H/k}$
be the natural map. By Lemma 2.17,
![]() $\phi (H)$
is an open subset of
$\phi (H)$
is an open subset of
![]() $\operatorname {\mathrm {Aut}}_{H/k}$
, so
$\operatorname {\mathrm {Aut}}_{H/k}$
, so
![]() $\phi (H)$
is an open subgroup scheme of
$\phi (H)$
is an open subgroup scheme of
![]() $(\operatorname {\mathrm {Aut}}_{H/k})_{\mathrm {{red}}}$
and the quotient
$(\operatorname {\mathrm {Aut}}_{H/k})_{\mathrm {{red}}}$
and the quotient ![]() (which exists as a scheme by [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. VIA, Théorème 3.2]) is locally of finite type. Moreover,
(which exists as a scheme by [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. VIA, Théorème 3.2]) is locally of finite type. Moreover,
![]() $A_{\mathrm {{red}}}$
is étale: since
$A_{\mathrm {{red}}}$
is étale: since
![]() $\phi (H)$
is (topologically) open in
$\phi (H)$
is (topologically) open in
![]() $\operatorname {\mathrm {Aut}}_{H/k}$
, A is discrete, and any reduced discrete scheme locally of finite type over an algebraically closed field is étale. The natural map
$\operatorname {\mathrm {Aut}}_{H/k}$
, A is discrete, and any reduced discrete scheme locally of finite type over an algebraically closed field is étale. The natural map
![]() $N_G(H) \to A$
has kernel
$N_G(H) \to A$
has kernel
![]() $HC_G(H)$
, so
$HC_G(H)$
, so
![]() $N_G(H)/HC_G(H)$
is a finite type closed subscheme of A. Since
$N_G(H)/HC_G(H)$
is a finite type closed subscheme of A. Since
![]() $A_{\mathrm {{red}}}$
is étale, it follows that
$A_{\mathrm {{red}}}$
is étale, it follows that
![]() $N_G(H)/HC_G(H)$
is finite. If
$N_G(H)/HC_G(H)$
is finite. If
![]() $H/H^0$
has order prime to
$H/H^0$
has order prime to ![]() , so H is weakly reductive, then already A is étale by Lemma 2.18, and thus,
, so H is weakly reductive, then already A is étale by Lemma 2.18, and thus,
![]() $N_G(H)/HC_G(H)$
is étale.
$N_G(H)/HC_G(H)$
is étale.
Definition 2.23. If G is a finite type k-group scheme and H is a reductive k-subgroup scheme of G, then we set ![]() , which we call the Weyl group of the pair
, which we call the Weyl group of the pair
![]() $(G, H)$
.
$(G, H)$
.
If H is a maximal torus of a smooth affine G, then this is the usual Weyl group W of G.
Proposition 2.24. Let G be a reductive group over a field k, and let H be a reductive k-subgroup scheme of G. For a prime p, if
![]() $p \nmid |W|$
and
$p \nmid |W|$
and
![]() $p \geq |H/H^0|$
, then
$p \geq |H/H^0|$
, then
![]() $p \nmid |W_H|$
.
$p \nmid |W_H|$
.
Proof. We may and do assume that k is algebraically closed. Let
![]() $g \in N_G(H)(k)$
; we need to show that under our hypotheses,
$g \in N_G(H)(k)$
; we need to show that under our hypotheses,
![]() $g^n$
acts by an inner automorphism on H for some integer n prime to p. Let T be a maximal torus of H, and note that conjugacy of maximal tori in
$g^n$
acts by an inner automorphism on H for some integer n prime to p. Let T be a maximal torus of H, and note that conjugacy of maximal tori in
![]() $H^0$
implies that after translation by
$H^0$
implies that after translation by
![]() $H^0(k)$
, we may assume
$H^0(k)$
, we may assume
![]() $g \in N_G(T)(k)$
. Since
$g \in N_G(T)(k)$
. Since
![]() $N_G(T)/C_G(T)$
is a subquotient of W, it follows that
$N_G(T)/C_G(T)$
is a subquotient of W, it follows that
![]() $g^{|W|} \in C_G(T)(k)$
. Thus, after replacing g by
$g^{|W|} \in C_G(T)(k)$
. Thus, after replacing g by
![]() $g^{|W|}$
, we may and do assume that g centralizes T. In particular, g acts trivially on the Dynkin diagram of
$g^{|W|}$
, we may and do assume that g centralizes T. In particular, g acts trivially on the Dynkin diagram of
![]() $(H^0, T)$
, so g acts on
$(H^0, T)$
, so g acts on
![]() $H^0$
by an inner automorphism. Thus, after further translation by
$H^0$
by an inner automorphism. Thus, after further translation by
![]() $H^0(k)$
, we may and do assume that g centralizes
$H^0(k)$
, we may and do assume that g centralizes
![]() $H^0$
. Since
$H^0$
. Since
![]() $p \geq |H/H^0|$
, we may pass to a further prime-to-p power of g to assume that g acts trivially on
$p \geq |H/H^0|$
, we may pass to a further prime-to-p power of g to assume that g acts trivially on
![]() $H/H^0$
. (It is a general fact, easily checked, that if
$H/H^0$
. (It is a general fact, easily checked, that if
![]() $p \mid |\operatorname {\mathrm {Aut}}(A)|$
for a finite group A, then
$p \mid |\operatorname {\mathrm {Aut}}(A)|$
for a finite group A, then
![]() $p < |A|$
.)
$p < |A|$
.)
Now that g acts trivially on
![]() $H^0$
and
$H^0$
and
![]() $H/H^0$
, the argument of Lemma 2.17 shows that
$H/H^0$
, the argument of Lemma 2.17 shows that
![]() $\operatorname {\mathrm {Ad}}(g)$
corresponds to a
$\operatorname {\mathrm {Ad}}(g)$
corresponds to a
![]() $1$
-cocycle
$1$
-cocycle
![]() $\eta : H/H^0 \to Z(H^0)$
(which lands in
$\eta : H/H^0 \to Z(H^0)$
(which lands in
![]() $Z(H^0)(k)$
since
$Z(H^0)(k)$
since
![]() $H/H^0$
is constant). The corresponding class in
$H/H^0$
is constant). The corresponding class in
![]() $\mathrm {H}^1(H/H^0, Z(H^0)(k))$
is killed by
$\mathrm {H}^1(H/H^0, Z(H^0)(k))$
is killed by
![]() $|H/H^0|$
, so further passing from g to
$|H/H^0|$
, so further passing from g to
![]() $g^{|H/H^0|}$
, we may and do assume that
$g^{|H/H^0|}$
, we may and do assume that
![]() $\operatorname {\mathrm {Ad}}(g)$
is cohomologically trivial, from which is follows that g acts on H by conjugation by an element of
$\operatorname {\mathrm {Ad}}(g)$
is cohomologically trivial, from which is follows that g acts on H by conjugation by an element of
![]() $h \in Z(H^0)(k)$
. Thus, g now acts on H by inner automorphisms, and we are done.
$h \in Z(H^0)(k)$
. Thus, g now acts on H by inner automorphisms, and we are done.
2.3 Abelianization
Our final goal in this section is to show the existence of the ‘abelianization’ of a weakly reductive group scheme G. We begin with the following folkloric lemma.
Lemma 2.25. Let S be a scheme, and let
![]() $f: G \to H$
be a homomorphism of finitely presented S-group schemes. The following are equivalent.
$f: G \to H$
be a homomorphism of finitely presented S-group schemes. The following are equivalent.
-
1. f is faithfully flat,
-
2. f is an epimorphism of fppf sheaves and
 $\ker f$
is flat.
$\ker f$
is flat.
Proof. Omitted.
Lemma 2.26. Let
![]() $1 \to M \to E \to H \to 1$
be a central extension, where M is an S-group scheme of multiplicative type and H is a finite étale group scheme of constant order n invertible on S. Letting
$1 \to M \to E \to H \to 1$
be a central extension, where M is an S-group scheme of multiplicative type and H is a finite étale group scheme of constant order n invertible on S. Letting
![]() $N = n^2$
, for every integer
$N = n^2$
, for every integer
![]() $d \geq 1$
, the S-morphism
$d \geq 1$
, the S-morphism
![]() $[Nd]: E \to E$
is a homomorphism. If M is moreover a torus, then
$[Nd]: E \to E$
is a homomorphism. If M is moreover a torus, then
![]() $E[N] \to H$
is faithfully flat, where
$E[N] \to H$
is faithfully flat, where ![]() .
.
Proof. By spreading out and étale-localizing around a point of S, we may and do assume that
![]() $S = \operatorname {\mathrm {Spec}} A$
for a strictly henselian noetherian local ring A. In particular, since H is finite étale, it is a constant group and there exists a scheme-theoretic section
$S = \operatorname {\mathrm {Spec}} A$
for a strictly henselian noetherian local ring A. In particular, since H is finite étale, it is a constant group and there exists a scheme-theoretic section
![]() $H \to E$
. We may moreover pushforward by an inclusion of M into a torus to assume that M is a torus. The existence of a section implies that for every S-scheme
$H \to E$
. We may moreover pushforward by an inclusion of M into a torus to assume that M is a torus. The existence of a section implies that for every S-scheme
![]() $S'$
, the sequence
$S'$
, the sequence
is exact.
First, note that as an extension of H by M which admits a section, E corresponds to a cohomology class in
![]() $\mathrm {H}^2(H, M)$
, the Hochschild cohomology group (see, for example, [Reference Demazure and GabrielDG70, II, §3, Prop. 2.3] or [Reference DemarcheDem15, Prop. 2.3.6]). Concretely, this is the space of
$\mathrm {H}^2(H, M)$
, the Hochschild cohomology group (see, for example, [Reference Demazure and GabrielDG70, II, §3, Prop. 2.3] or [Reference DemarcheDem15, Prop. 2.3.6]). Concretely, this is the space of
![]() $2$
-cocycles
$2$
-cocycles
![]() $H \times H \to M$
modulo coboundaries. Since H is a constant group scheme, we have
$H \times H \to M$
modulo coboundaries. Since H is a constant group scheme, we have
![]() $\mathrm {H}^2(H, M) = \mathrm {H}^2(H(S), M(S))$
. Since
$\mathrm {H}^2(H, M) = \mathrm {H}^2(H(S), M(S))$
. Since
![]() $H(S)$
is finite of order n,
$H(S)$
is finite of order n,
![]() $\mathrm {H}^2(H(S), M(S))$
is killed by n by the classical theory. Since n is invertible on the strictly henselian S, via the correspondence between extensions and classes in
$\mathrm {H}^2(H(S), M(S))$
is killed by n by the classical theory. Since n is invertible on the strictly henselian S, via the correspondence between extensions and classes in
![]() $\mathrm {H}^2$
, the image of the extension corresponding to multiplication by n on M is
$\mathrm {H}^2$
, the image of the extension corresponding to multiplication by n on M is
Thus, this extension is split (i.e., there is a section
![]() $\alpha _0: H(S) \to E(S)/M[n](S)$
which is a homomorphism). This is equivalent to a section
$\alpha _0: H(S) \to E(S)/M[n](S)$
which is a homomorphism). This is equivalent to a section
![]() $H \to E/M[n]$
, which we also denote by
$H \to E/M[n]$
, which we also denote by
![]() $\alpha _0$
.
$\alpha _0$
.
Since S is strictly henselian,
![]() $\alpha _0$
lifts to a section
$\alpha _0$
lifts to a section
![]() $\alpha : H \to E$
. Now
$\alpha : H \to E$
. Now
![]() $\alpha _0(x)^n = \alpha _0(x^n) = 1$
for all
$\alpha _0(x)^n = \alpha _0(x^n) = 1$
for all
![]() $x \in H(S)$
, so we have
$x \in H(S)$
, so we have
![]() $\alpha (x)^n \in M[n](S)$
, and thus,
$\alpha (x)^n \in M[n](S)$
, and thus,
Moreover, since
![]() $\alpha _0$
is a homomorphism, we have
$\alpha _0$
is a homomorphism, we have
![]() $\alpha (xx')^{-1}\alpha (x)\alpha (x') \in M[n](S)$
for all
$\alpha (xx')^{-1}\alpha (x)\alpha (x') \in M[n](S)$
for all
![]() $x, x' \in H(S)$
. In other words,
$x, x' \in H(S)$
. In other words,
for some
![]() $g_{x, x'} \in M[n](S)$
.
$g_{x, x'} \in M[n](S)$
.
Now we conclude the proof that
![]() $[Nd]: E \to E$
is a homomorphism. We shall check this on
$[Nd]: E \to E$
is a homomorphism. We shall check this on
![]() $S'$
-points for every S-scheme
$S'$
-points for every S-scheme
![]() $S'$
. Any element of
$S'$
. Any element of
![]() $G(S')$
is Zariski-locally of the form
$G(S')$
is Zariski-locally of the form
![]() $\alpha (x)g$
for some
$\alpha (x)g$
for some
![]() $x \in H(S')$
and
$x \in H(S')$
and
![]() $g \in M(S')$
, and using centrality of M, we compute, for
$g \in M(S')$
, and using centrality of M, we compute, for
![]() $x, x' \in H(S')$
and
$x, x' \in H(S')$
and
![]() $g, g' \in M(S')$
,
$g, g' \in M(S')$
,
so indeed
![]() $[Nd]: E \to E$
is a homomorphism.
$[Nd]: E \to E$
is a homomorphism.
Finally, we show that
![]() $E[N] \to H$
is faithfully flat when M is a torus. For this, let h be a local section of H. After fppf localization, we may lift h to a section e of E. Note that
$E[N] \to H$
is faithfully flat when M is a torus. For this, let h be a local section of H. After fppf localization, we may lift h to a section e of E. Note that
![]() $e^n$
is a local section of M, so because M is a divisible group scheme, we may pass to a further fppf localization to assume
$e^n$
is a local section of M, so because M is a divisible group scheme, we may pass to a further fppf localization to assume
![]() $e^n = m^n$
for some local section m of M. Because M is central in E, we see that
$e^n = m^n$
for some local section m of M. Because M is central in E, we see that
![]() $(em^{-1})^n = 1$
, and thus,
$(em^{-1})^n = 1$
, and thus,
![]() $em^{-1}$
is a local section of
$em^{-1}$
is a local section of
![]() $E[N]$
mapping to h. So faithful flatness follows from Lemma 2.25.
$E[N]$
mapping to h. So faithful flatness follows from Lemma 2.25.
Proposition 2.27. Suppose G is a weakly reductive S-group scheme. There exists a smooth S-group scheme
![]() $G^{\mathrm {ab}}$
of multiplicative type and a faithfully flat homomorphism
$G^{\mathrm {ab}}$
of multiplicative type and a faithfully flat homomorphism
![]() $\pi : G \to G^{\mathrm {ab}}$
with the universal property that for any fppf abelian sheaf H on the category of S-schemes and homomorphism of sheaves
$\pi : G \to G^{\mathrm {ab}}$
with the universal property that for any fppf abelian sheaf H on the category of S-schemes and homomorphism of sheaves
![]() $f: G \to H$
, there is a unique homomorphism
$f: G \to H$
, there is a unique homomorphism
![]() $G^{\mathrm {ab}} \to H$
through which f factors.
$G^{\mathrm {ab}} \to H$
through which f factors.
The kernel
![]() ${\mathscr D}(G)$
of
${\mathscr D}(G)$
of
![]() $\pi $
represents the fppf-sheafification of the functor
$\pi $
represents the fppf-sheafification of the functor
![]() $S' \mapsto [G(S'), G(S')]$
on S-schemes
$S' \mapsto [G(S'), G(S')]$
on S-schemes
![]() $S'$
, and in particular, the formation of
$S'$
, and in particular, the formation of
![]() $G^{\mathrm {ab}}$
commutes with any base change on S.
$G^{\mathrm {ab}}$
commutes with any base change on S.
Example 2.28. Before giving the proof, we illustrate again the relevance of weak reductivity (as opposed to geometric reductivity). For the G in Example 2.20, we claim that
![]() $G^{\mathrm {ab}}$
cannot exist as a scheme. Indeed, note that
$G^{\mathrm {ab}}$
cannot exist as a scheme. Indeed, note that
![]() $G_s$
is commutative, so on the special fiber, we have
$G_s$
is commutative, so on the special fiber, we have
![]() ${\mathscr D}(G_s) = 1$
. However, since
${\mathscr D}(G_s) = 1$
. However, since
![]() $\zeta _p$
does not lie in
$\zeta _p$
does not lie in
![]() $pA$
, it follows that
$pA$
, it follows that
![]() $G_{A/p}$
is not commutative, so
$G_{A/p}$
is not commutative, so
![]() ${\mathscr D}(G_{A/p}) \neq 1$
. Since every scheme over
${\mathscr D}(G_{A/p}) \neq 1$
. Since every scheme over
![]() $A/p$
with trivial special fiber is trivial (by ‘nilpotent Nakayama’), this is a contradiction.
$A/p$
with trivial special fiber is trivial (by ‘nilpotent Nakayama’), this is a contradiction.
Proof of Proposition 2.27.
The claims in the second paragraph of the proposition follow directly from the universal property of the first paragraph. First, note that if G has connected fibers, then [Reference ConradCon14, Thm. 5.3.1] shows that
![]() $G^{\mathrm {ab}}$
exists and is a torus. In general, any S-homomorphism
$G^{\mathrm {ab}}$
exists and is a torus. In general, any S-homomorphism
![]() $f: G \to H$
as in the statement of the proposition induces an S-homomorphism
$f: G \to H$
as in the statement of the proposition induces an S-homomorphism
![]() $G^0 \to H$
, so f kills
$G^0 \to H$
, so f kills
![]() ${\mathscr D}(G^0)$
and hence factors through an S-homomorphism
${\mathscr D}(G^0)$
and hence factors through an S-homomorphism
![]() $G/{\mathscr D}(G^0) \to H$
, where
$G/{\mathscr D}(G^0) \to H$
, where
![]() $G/{\mathscr D}(G^0)$
is a smooth affine S-group scheme with torus identity component. Thus, we may and do assume that
$G/{\mathscr D}(G^0)$
is a smooth affine S-group scheme with torus identity component. Thus, we may and do assume that
![]() $G^0$
is a torus.
$G^0$
is a torus.
Working étale-locally on S (using effectivity of étale descent for affine S-schemes), we may choose representatives
![]() $h_1, \dots , h_n \in G(S)$
for
$h_1, \dots , h_n \in G(S)$
for
![]() $G/G^0$
. Define the map
$G/G^0$
. Define the map
![]() $\phi : (G^0)^n \to G^0$
by
$\phi : (G^0)^n \to G^0$
by
![]() $\phi (g_1, \dots , g_n) = \prod _{i=1}^n h_ig_ih_i^{-1}g_i^{-1}$
. Note that
$\phi (g_1, \dots , g_n) = \prod _{i=1}^n h_ig_ih_i^{-1}g_i^{-1}$
. Note that
![]() $\phi $
is an S-homomorphism, so by [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. IX, Thm. 6.8], there is some S-subgroup scheme M of
$\phi $
is an S-homomorphism, so by [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. IX, Thm. 6.8], there is some S-subgroup scheme M of
![]() $G^0$
of multiplicative type through which
$G^0$
of multiplicative type through which
![]() $\phi $
factors and such that the factored map
$\phi $
factors and such that the factored map
![]() $\phi : (G^0)^n \to M$
is faithfully flat. Since f vanishes on all commutators, it annihilates M, and thus, f must factor through
$\phi : (G^0)^n \to M$
is faithfully flat. Since f vanishes on all commutators, it annihilates M, and thus, f must factor through
![]() $G/M$
. By definition, if
$G/M$
. By definition, if
![]() $g \in G^0(S')$
is a section, then
$g \in G^0(S')$
is a section, then
![]() $h_igh_i^{-1} \in gM$
, so since
$h_igh_i^{-1} \in gM$
, so since
![]() $G^0$
is commutative, it follows that
$G^0$
is commutative, it follows that
![]() $G^0/M$
is central in
$G^0/M$
is central in
![]() $G/M$
. Thus, replacing G by
$G/M$
. Thus, replacing G by
![]() $G/M$
, we may and do assume that
$G/M$
, we may and do assume that
![]() $G^0$
is central in G.
$G^0$
is central in G.
Working Zariski-locally on S, we may and do assume that the index of
![]() $G^0$
in G is constant, say equal to n. By Lemma 2.26,
$G^0$
in G is constant, say equal to n. By Lemma 2.26, ![]() is an S-subgroup scheme of G where
is an S-subgroup scheme of G where
![]() $N = n^2$
. By the same lemma, the map
$N = n^2$
. By the same lemma, the map
![]() $G[N] \to G/G^0$
is faithfully flat, so there is a short exact sequence
$G[N] \to G/G^0$
is faithfully flat, so there is a short exact sequence
Since
![]() $G^0[N]$
and
$G^0[N]$
and
![]() $G/G^0$
are both finite étale (the former because N is invertible on the base), it follows that
$G/G^0$
are both finite étale (the former because N is invertible on the base), it follows that
![]() $G[N]$
is also finite étale.
$G[N]$
is also finite étale.
By working étale locally on S, we may assume that
![]() $G[N]$
is a constant group scheme. In this case, the functor on S-schemes
$G[N]$
is a constant group scheme. In this case, the functor on S-schemes
![]() $S' \mapsto [G[N](S'), G[N](S')]$
is represented by the constant S-group scheme
$S' \mapsto [G[N](S'), G[N](S')]$
is represented by the constant S-group scheme
![]() ${\mathscr D}(G[N])$
. Moreover, if
${\mathscr D}(G[N])$
. Moreover, if
![]() ${\mathscr D}(G)$
denotes the sheafification of the functor
${\mathscr D}(G)$
denotes the sheafification of the functor
![]() $S' \mapsto [G(S'), G(S')]$
, then we have
$S' \mapsto [G(S'), G(S')]$
, then we have
![]() ${\mathscr D}(G) = {\mathscr D}(G[N])$
: indeed, for an S-scheme
${\mathscr D}(G) = {\mathscr D}(G[N])$
: indeed, for an S-scheme
![]() $S'$
and
$S'$
and
![]() $g, h \in G(S')$
, centrality of
$g, h \in G(S')$
, centrality of
![]() $G^0$
in G shows that the commutator
$G^0$
in G shows that the commutator
![]() $ghg^{-1}h^{-1}$
depends only on the images of g and h in
$ghg^{-1}h^{-1}$
depends only on the images of g and h in
![]() $(G/G^0)(S')$
. In particular, since the map
$(G/G^0)(S')$
. In particular, since the map
![]() $G[N] \to G/G^0$
is an epimorphism of fppf sheaves, we may pass to an fppf cover of
$G[N] \to G/G^0$
is an epimorphism of fppf sheaves, we may pass to an fppf cover of
![]() $S'$
to assume
$S'$
to assume
![]() $g, h \in G[N](S')$
. So indeed,
$g, h \in G[N](S')$
. So indeed,
![]() ${\mathscr D}(G) = {\mathscr D}(G[N])$
, which is a finite étale group scheme killed by N, so its order is invertible on S.
${\mathscr D}(G) = {\mathscr D}(G[N])$
, which is a finite étale group scheme killed by N, so its order is invertible on S.
Finally, note that ![]() is a smooth S-group scheme by [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. V, Thm. 4.1]. It is commutative by the previous paragraph. Moreover, since
is a smooth S-group scheme by [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. V, Thm. 4.1]. It is commutative by the previous paragraph. Moreover, since
![]() $G^0$
is a torus the image of
$G^0$
is a torus the image of
![]() $G^0$
in
$G^0$
in
![]() $G^{\mathrm {ab}}$
(which makes sense by [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. IX, Thm. 6.8]) is also a torus, which must be equal to the relative identity component
$G^{\mathrm {ab}}$
(which makes sense by [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. IX, Thm. 6.8]) is also a torus, which must be equal to the relative identity component
![]() $(G^{\mathrm {ab}})^0$
for dimension reasons. Moreover,
$(G^{\mathrm {ab}})^0$
for dimension reasons. Moreover,
![]() $G/G^0 \to G^{\mathrm {ab}}/(G^{\mathrm {ab}})^0$
is an epimorphism of sheaves, so the component group of
$G/G^0 \to G^{\mathrm {ab}}/(G^{\mathrm {ab}})^0$
is an epimorphism of sheaves, so the component group of
![]() $G^{\mathrm {ab}}$
is of order invertible on S. Thus, it follows from [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. XVII, Prop. 7.1.1] that
$G^{\mathrm {ab}}$
is of order invertible on S. Thus, it follows from [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. XVII, Prop. 7.1.1] that
![]() $G^{\mathrm {ab}}$
is a group scheme of multiplicative type, as desired.
$G^{\mathrm {ab}}$
is a group scheme of multiplicative type, as desired.
The center and abelianization of G are related. We begin with a useful lemma.
Lemma 2.29. Let
![]() $T_1$
and
$T_1$
and
![]() $T_2$
be S-group schemes of multiplicative type such that
$T_2$
be S-group schemes of multiplicative type such that
![]() $T_2$
is a torus, and let
$T_2$
is a torus, and let
![]() $f: T_1 \to T_2$
be an isogeny. Let
$f: T_1 \to T_2$
be an isogeny. Let
![]() $\Gamma $
be a finite group acting on
$\Gamma $
be a finite group acting on
![]() $T_1$
and
$T_1$
and
![]() $T_2$
compatibly with f, and define maps
$T_2$
compatibly with f, and define maps
 $$ \begin{align*} \phi: T_1 \to \prod_{\gamma \in \Gamma} T_1, \,\,\,\,\,\,\,\,\,\, &\phi(x) = ((\gamma \cdot x) x^{-1})_{\gamma \in \Gamma} \\ \psi: \prod_{\gamma \in \Gamma} T_2 \to T_2, \,\,\,\,\,\,\,\,\,\, &\psi((y_\gamma)_{\gamma \in \Gamma}) = \prod_{\gamma \in \Gamma} (\gamma \cdot y_\gamma) y_\gamma^{-1}. \end{align*} $$
$$ \begin{align*} \phi: T_1 \to \prod_{\gamma \in \Gamma} T_1, \,\,\,\,\,\,\,\,\,\, &\phi(x) = ((\gamma \cdot x) x^{-1})_{\gamma \in \Gamma} \\ \psi: \prod_{\gamma \in \Gamma} T_2 \to T_2, \,\,\,\,\,\,\,\,\,\, &\psi((y_\gamma)_{\gamma \in \Gamma}) = \prod_{\gamma \in \Gamma} (\gamma \cdot y_\gamma) y_\gamma^{-1}. \end{align*} $$
The natural map ![]() is an isogeny, and if
is an isogeny, and if
![]() $\Gamma $
is of order n, then
$\Gamma $
is of order n, then
![]() $\ker \overline {f}$
is contained in
$\ker \overline {f}$
is contained in
![]() $[n]^{-1}(\ker f)$
.
$[n]^{-1}(\ker f)$
.
Note that
![]() $\ker \phi $
and
$\ker \phi $
and ![]() are S-group schemes of multiplicative type and that
are S-group schemes of multiplicative type and that
![]() $\ker \overline {f}$
is of multiplicative type, and in particular flat, by [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. IX, Thm. 6.8].
$\ker \overline {f}$
is of multiplicative type, and in particular flat, by [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. IX, Thm. 6.8].
Proof. By Lemma 2.25, to show that
![]() $\overline {f}$
is faithfully flat, it suffices to show that
$\overline {f}$
is faithfully flat, it suffices to show that
![]() $\overline {f}$
is an epimorphism of fppf sheaves. To this end, let
$\overline {f}$
is an epimorphism of fppf sheaves. To this end, let
![]() $t_2$
be a local section of
$t_2$
be a local section of
![]() $T_2$
. Since
$T_2$
. Since
![]() $T_2$
is a torus, after localizing, we may assume there is some section
$T_2$
is a torus, after localizing, we may assume there is some section
![]() $t_2'$
such that
$t_2'$
such that
![]() $t_2^{\prime }n = t_2$
. Further localizing, there exists a section
$t_2^{\prime }n = t_2$
. Further localizing, there exists a section
![]() $t_1$
of
$t_1$
of
![]() $T_1$
such that
$T_1$
such that
![]() $f(t_1) = t_2'$
. We then have
$f(t_1) = t_2'$
. We then have
 $$\begin{align*}f\left(\prod_{\gamma \in \Gamma} (\gamma \cdot t_1)\right) = \prod_{\gamma \in \Gamma} (\gamma \cdot t_2') = t_2 \cdot \prod_{\gamma \in \Gamma} (\gamma \cdot t_2') t_2^{\prime}{-1}, \end{align*}$$
$$\begin{align*}f\left(\prod_{\gamma \in \Gamma} (\gamma \cdot t_1)\right) = \prod_{\gamma \in \Gamma} (\gamma \cdot t_2') = t_2 \cdot \prod_{\gamma \in \Gamma} (\gamma \cdot t_2') t_2^{\prime}{-1}, \end{align*}$$
which has the same image in ![]() as
as
![]() $t_2$
. Since
$t_2$
. Since
![]() $\prod _{\gamma \in \Gamma } (\gamma \cdot t_1)$
lies in
$\prod _{\gamma \in \Gamma } (\gamma \cdot t_1)$
lies in
![]() $\ker \phi $
, we see that indeed
$\ker \phi $
, we see that indeed
![]() $\overline {f}$
is an epimorphism of fppf sheaves.
$\overline {f}$
is an epimorphism of fppf sheaves.
Now suppose that
![]() $t_1$
is a local section of
$t_1$
is a local section of
![]() $\ker \phi $
such that
$\ker \phi $
such that
![]() $\overline {f}(t_1) = 1$
. We claim that then
$\overline {f}(t_1) = 1$
. We claim that then
![]() $f(t_1)^n = 1$
. We may write
$f(t_1)^n = 1$
. We may write
![]() $f(t_1) = \prod _{\gamma \in \Gamma } (\gamma \cdot t_{2, \gamma }) t_{2, \gamma }^{-1}$
locally. Using
$f(t_1) = \prod _{\gamma \in \Gamma } (\gamma \cdot t_{2, \gamma }) t_{2, \gamma }^{-1}$
locally. Using
![]() $\Gamma $
-equivariance of f and the fact that
$\Gamma $
-equivariance of f and the fact that
![]() $t_1$
is fixed by
$t_1$
is fixed by
![]() $\Gamma $
, we have
$\Gamma $
, we have
 $$\begin{align*}f(t_1)^n = \prod_{\gamma' \in \Gamma} (\gamma' \cdot f(t_1)) = \prod_{\gamma, \gamma' \in \Gamma} (\gamma' \gamma \cdot t_{2, \gamma})(\gamma' \cdot t_{2, \gamma}^{-1}) = \prod_{\gamma \in \Gamma} \left(\prod_{\gamma' \in \Gamma} (\gamma'\gamma \cdot t_{2, \gamma})(\gamma' \cdot t_{2, \gamma})^{-1}\right) = 1, \end{align*}$$
$$\begin{align*}f(t_1)^n = \prod_{\gamma' \in \Gamma} (\gamma' \cdot f(t_1)) = \prod_{\gamma, \gamma' \in \Gamma} (\gamma' \gamma \cdot t_{2, \gamma})(\gamma' \cdot t_{2, \gamma}^{-1}) = \prod_{\gamma \in \Gamma} \left(\prod_{\gamma' \in \Gamma} (\gamma'\gamma \cdot t_{2, \gamma})(\gamma' \cdot t_{2, \gamma})^{-1}\right) = 1, \end{align*}$$
where the final equality follows by reindexing. So indeed,
![]() $\ker \overline {f}$
lies in
$\ker \overline {f}$
lies in
![]() $[n]^{-1}(\ker f)$
, and in particular, it is quasi-finite. Since it is of multiplicative type, it is finite, and hence,
$[n]^{-1}(\ker f)$
, and in particular, it is quasi-finite. Since it is of multiplicative type, it is finite, and hence,
![]() $\overline {f}$
is an isogeny.
$\overline {f}$
is an isogeny.
Proposition 2.30. Let G be a weakly reductive S-group scheme. If
![]() $Z(G)$
is smooth, then the natural map
$Z(G)$
is smooth, then the natural map
![]() $f: Z(G)^0 \to G^{\mathrm {ab}, 0}$
is an isogeny of S-tori. If, moreover,
$f: Z(G)^0 \to G^{\mathrm {ab}, 0}$
is an isogeny of S-tori. If, moreover,
![]() $Z({\mathscr D}(G^0))$
is smooth, then f is smooth (equivalently, étale).
$Z({\mathscr D}(G^0))$
is smooth, then f is smooth (equivalently, étale).
Proof. Propositions 2.19 and 2.27 show that
![]() $Z(G)^0$
and
$Z(G)^0$
and
![]() $G^{\mathrm {ab}, 0}$
are S-tori under our assumptions, so it suffices to check the result on geometric fibers. In other words, we may and do assume that
$G^{\mathrm {ab}, 0}$
are S-tori under our assumptions, so it suffices to check the result on geometric fibers. In other words, we may and do assume that
![]() $S = \operatorname {\mathrm {Spec}} k$
for an algebraically closed field k. Note that the natural
$S = \operatorname {\mathrm {Spec}} k$
for an algebraically closed field k. Note that the natural
![]() $Z(G^0) \to G^{0, \mathrm {ab}}$
(whose target is not
$Z(G^0) \to G^{0, \mathrm {ab}}$
(whose target is not
![]() $G^{\mathrm {ab}, 0}$
) is an isogeny of multiplicative type groups with kernel
$G^{\mathrm {ab}, 0}$
) is an isogeny of multiplicative type groups with kernel
![]() $Z({\mathscr D}(G^0))$
(irrespective of whether
$Z({\mathscr D}(G^0))$
(irrespective of whether
![]() $Z(G^0)$
is smooth): a maximal central torus
$Z(G^0)$
is smooth): a maximal central torus
![]() $T_0$
of
$T_0$
of
![]() $G^0$
is of finite index in
$G^0$
is of finite index in
![]() $Z(G^0)$
, and there is the standard central isogeny
$Z(G^0)$
, and there is the standard central isogeny
![]() $T_0 \times {\mathscr D}(G^0) \to G^0$
.
$T_0 \times {\mathscr D}(G^0) \to G^0$
.
Now
![]() $G/G^0$
acts on
$G/G^0$
acts on
![]() $Z(G^0)$
and
$Z(G^0)$
and
![]() $G^0/{\mathscr D}(G^0)$
by conjugation, so we can apply Lemma 2.29 with
$G^0/{\mathscr D}(G^0)$
by conjugation, so we can apply Lemma 2.29 with
![]() $T_1 = Z(G^0)$
,
$T_1 = Z(G^0)$
,
![]() $T_2 = G^{0, \mathrm {ab}}$
,
$T_2 = G^{0, \mathrm {ab}}$
,
![]() $\Gamma = G/G^0$
, and
$\Gamma = G/G^0$
, and
![]() $f: T_1 \to T_2$
the natural map. We will also use the notation
$f: T_1 \to T_2$
the natural map. We will also use the notation
![]() $\phi $
,
$\phi $
,
![]() $\psi $
,
$\psi $
,
![]() $\overline {f}$
of Lemma 2.29. In this case,
$\overline {f}$
of Lemma 2.29. In this case,
![]() $\ker \phi = C_{G^0}(G)$
, which admits
$\ker \phi = C_{G^0}(G)$
, which admits
![]() $Z(G)^0$
as an open and closed S-subgroup scheme: indeed,
$Z(G)^0$
as an open and closed S-subgroup scheme: indeed,
![]() $C_{G^0}(G) = G^0 \cap Z(G)$
, and
$C_{G^0}(G) = G^0 \cap Z(G)$
, and
![]() $Z(G)^0$
(resp.
$Z(G)^0$
(resp.
![]() $G^0$
) is open and closed in
$G^0$
) is open and closed in
![]() $Z(G)$
(resp. G). Moreover,
$Z(G)$
(resp. G). Moreover, ![]() . Thus, to establish the proposition, it suffices to show that
. Thus, to establish the proposition, it suffices to show that
![]() $\overline {f}$
is an isogeny, which is smooth provided
$\overline {f}$
is an isogeny, which is smooth provided
![]() $Z({\mathscr D}(G^0))$
is smooth. The fact that
$Z({\mathscr D}(G^0))$
is smooth. The fact that
![]() $\overline {f}$
is an isogeny follows directly from Lemma 2.29. The last statement of Lemma 2.29 shows that
$\overline {f}$
is an isogeny follows directly from Lemma 2.29. The last statement of Lemma 2.29 shows that
![]() $\ker \overline {f}$
lies in
$\ker \overline {f}$
lies in
![]() $[n]^{-1}(Z({\mathscr D}(G^0)))$
, where n is the order of
$[n]^{-1}(Z({\mathscr D}(G^0)))$
, where n is the order of
![]() $G/G^0$
. Since n is invertible on S by hypothesis, smoothness of
$G/G^0$
. Since n is invertible on S by hypothesis, smoothness of
![]() $Z({\mathscr D}(G^0))$
implies smoothness of
$Z({\mathscr D}(G^0))$
implies smoothness of
![]() $[n]^{-1}(Z({\mathscr D}(G^0)))$
.
$[n]^{-1}(Z({\mathscr D}(G^0)))$
.
3 Centralizers
In this section, we study various kinds of centralizers in weakly reductive group schemes. Before diving into the results, we would like to summarize what is available in the literature for centralizers of weakly reductive subgroups of weakly reductive groups.
-
1. Over a field of pretty good characteristic (see Definition 1.12), [Reference HerpelHer13] shows that the centralizer of any subgroup scheme of any connected reductive group is smooth. In fact, this property characterizes pretty good characteristic.
-
2. Over a field of good characteristic
 $p> 0$
, the centralizer of any subgroup scheme of a connected reductive group has no p-torsion in its component group; this follows via a short argument with the Springer isomorphism. This general statement is false in every bad characteristic, as Springer showed in [Reference SpringerSpr66, Theorem 4.12] by considering centralizers of regular unipotent elements.
$p> 0$
, the centralizer of any subgroup scheme of a connected reductive group has no p-torsion in its component group; this follows via a short argument with the Springer isomorphism. This general statement is false in every bad characteristic, as Springer showed in [Reference SpringerSpr66, Theorem 4.12] by considering centralizers of regular unipotent elements. -
3. If G is a connected reductive group over a field k of characteristic
 $p \geq 0$
and H is a finite subgroup of
$p \geq 0$
and H is a finite subgroup of
 $G(k)$
of order prime to p, then
$G(k)$
of order prime to p, then
 $C_G(H)$
has reductive identity component by [Reference Prasad and YuPY02, Theorem 2.1], and its component group is of order prime to p (even in bad characteristic) by [Reference Fargues and ScholzeFS24, Proposition VIII.5.11].
$C_G(H)$
has reductive identity component by [Reference Prasad and YuPY02, Theorem 2.1], and its component group is of order prime to p (even in bad characteristic) by [Reference Fargues and ScholzeFS24, Proposition VIII.5.11]. -
4. If H is a connected reductive subgroup of a connected reductive group G over a field of characteristic
 $p> 0$
, then we are not aware of any general results concerning reductivity of
$p> 0$
, then we are not aware of any general results concerning reductivity of
 $C_G(H)$
apart from the ‘classical’ case that H is of multiplicative type [Reference ConradCon14, Lemma 2.2.4] or the upcoming Corollary 3.5.
$C_G(H)$
apart from the ‘classical’ case that H is of multiplicative type [Reference ConradCon14, Lemma 2.2.4] or the upcoming Corollary 3.5. -
5. If G is a weakly reductive group scheme over a base scheme S and H is a finite subgroup of
 $G(S)$
of order invertible on S, then
$G(S)$
of order invertible on S, then
 $C_G(H)$
is smooth and affine with reductive identity component; this follows from simple deformation theory and (3). If H is moreover solvable, then [Reference Dat, Helm, Kurinczuk and MossDHKM24, Theorem A.12] shows that
$C_G(H)$
is smooth and affine with reductive identity component; this follows from simple deformation theory and (3). If H is moreover solvable, then [Reference Dat, Helm, Kurinczuk and MossDHKM24, Theorem A.12] shows that
 $C_G(H)$
has finite component group. Apart from this, we are not aware of any results in the literature concerning smoothness, reductivity or finiteness of component groups for centralizers of weakly reductive subgroup schemes of G prior to Corollaries 3.5 and 3.7 below.
$C_G(H)$
has finite component group. Apart from this, we are not aware of any results in the literature concerning smoothness, reductivity or finiteness of component groups for centralizers of weakly reductive subgroup schemes of G prior to Corollaries 3.5 and 3.7 below.
3.1 Centralizers of weakly reductive subgroup schemes
We will now input the general results of Section 2 into concrete results on centralizers. We begin with the following lemma.
Lemma 3.1. Let A be a DVR, and let X be a locally noetherian A-scheme. If
![]() $X_0$
is an open and closed subscheme of the special fiber
$X_0$
is an open and closed subscheme of the special fiber
![]() $X_s$
, then the natural map
$X_s$
, then the natural map
![]() $X - X_0 \to X$
is affine. In particular, if X is affine, then
$X - X_0 \to X$
is affine. In particular, if X is affine, then
![]() $X - X_0$
is also affine.
$X - X_0$
is also affine.
Proof. Affineness of a morphism can be checked Zariski-locally on the target, so we may freely shrink X to assume that the special fiber of X is connected. In this case,
![]() $X_0$
is either empty or all of
$X_0$
is either empty or all of
![]() $X_s$
. If
$X_s$
. If
![]() $X_0$
is empty, then the lemma is obvious; otherwise,
$X_0$
is empty, then the lemma is obvious; otherwise,
![]() $X_0 = V(\pi )$
, where
$X_0 = V(\pi )$
, where
![]() $\pi $
is a uniformizer of A, and the lemma is again clear.
$\pi $
is a uniformizer of A, and the lemma is again clear.
The proof of the following theorem is similar in spirit to one of the proofs of [Reference Prasad and YuPY02, Theorem 2.1], which shows reductivity of the centralizer
![]() $C_G(\Lambda )$
of a finite group
$C_G(\Lambda )$
of a finite group
![]() $\Lambda $
over a field k by realizing it as the stabilizer of the conjugation action of G on
$\Lambda $
over a field k by realizing it as the stabilizer of the conjugation action of G on
![]() $\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(\Lambda , G)$
.
$\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(\Lambda , G)$
.
Theorem 3.2. Let S be a scheme, and let G and H be geometrically reductive smooth affine S-group schemes. Suppose
![]() $f: H \to G$
is an S-homomorphism such that
$f: H \to G$
is an S-homomorphism such that
-
1.
 $\mathrm {H}^1(H_s, \mathfrak {g}_s) = 0$
for all
$\mathrm {H}^1(H_s, \mathfrak {g}_s) = 0$
for all
 $s \in S$
,
$s \in S$
, -
2.
 $f_s(H_s)$
is
$f_s(H_s)$
is
 $G_s$
-cr for all
$G_s$
-cr for all
 $s \in S$
.
$s \in S$
.
Then
![]() $C_G(H)$
is geometrically reductive smooth affine S-scheme. If G is weakly reductive and
$C_G(H)$
is geometrically reductive smooth affine S-scheme. If G is weakly reductive and ![]() is good for
is good for
![]() $G_s$
for all
$G_s$
for all
![]() $s \in S$
, then
$s \in S$
, then
![]() $C_G(H)$
is also weakly reductive.
$C_G(H)$
is also weakly reductive.
Proof. By (1) and deformation theory [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. III, Corollaire 2.8], the orbit map
![]() $\phi : G \to \underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is smooth, and thus,
$\phi : G \to \underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is smooth, and thus,
![]() $C_G(H)$
is smooth and affine. To show that
$C_G(H)$
is smooth and affine. To show that
![]() $C_G(H)$
is geometrically reductive, it suffices by Theorem 2.1 to assume that
$C_G(H)$
is geometrically reductive, it suffices by Theorem 2.1 to assume that
![]() $S = \operatorname {\mathrm {Spec}} A$
for a complete DVR A with algebraically closed residue field. In this case, Theorem 2.2 shows that
$S = \operatorname {\mathrm {Spec}} A$
for a complete DVR A with algebraically closed residue field. In this case, Theorem 2.2 shows that
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is a disjoint union of finite type S-affine S-schemes.
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is a disjoint union of finite type S-affine S-schemes.
Let C be the schematic closure of the G-orbit of
![]() $f_\eta $
in
$f_\eta $
in
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
, so C is a G-stable closed subscheme of
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
, so C is a G-stable closed subscheme of
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
through which the orbit map of f factors. Let
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
through which the orbit map of f factors. Let
![]() $C_1$
be the G-stable open subscheme of C obtained by deleting all of the components of
$C_1$
be the G-stable open subscheme of C obtained by deleting all of the components of
![]() $C_s$
not containing a G-translate of
$C_s$
not containing a G-translate of
![]() $f_s$
, so
$f_s$
, so
![]() $C_1$
is affine by Lemma 3.1. Since
$C_1$
is affine by Lemma 3.1. Since
![]() $\phi $
is smooth,
$\phi $
is smooth,
![]() $\phi $
has open image; moreover, each fiber of
$\phi $
has open image; moreover, each fiber of
![]() $\phi $
has closed image by (2) and Lemma 2.10. Consequently, each fiber of
$\phi $
has closed image by (2) and Lemma 2.10. Consequently, each fiber of
![]() $C_1$
is the (open) orbit of f in that fiber, and the map
$C_1$
is the (open) orbit of f in that fiber, and the map
![]() $i: C_1 \to \underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is an open embedding on both fibers. Since
$i: C_1 \to \underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G)$
is an open embedding on both fibers. Since
![]() $C_1$
is flat, it follows that i is étale and radicial, and thus, [Reference Dieudonne and GrothendieckDG67, IV4, Théorème 17.9.1] shows that i is an open embedding.
$C_1$
is flat, it follows that i is étale and radicial, and thus, [Reference Dieudonne and GrothendieckDG67, IV4, Théorème 17.9.1] shows that i is an open embedding.
Now we show that
![]() $C_G(H)$
is geometrically reductive; for this, it is equivalent to show that
$C_G(H)$
is geometrically reductive; for this, it is equivalent to show that
![]() $G/C_G(H)$
is affine by Theorem 2.1. We will show, in fact, that the natural map
$G/C_G(H)$
is affine by Theorem 2.1. We will show, in fact, that the natural map
![]() $G/C_G(H) \to C_1$
is an isomorphism. By definition,
$G/C_G(H) \to C_1$
is an isomorphism. By definition,
![]() $\phi $
factors through
$\phi $
factors through
![]() $C_1$
, and the previous paragraph shows that this factored map is surjective. Note that the quotient
$C_1$
, and the previous paragraph shows that this factored map is surjective. Note that the quotient
![]() $G/C_G(H)$
exists as a smooth separated algebraic space of finite type by work of Artin [Reference ArtinArt74, Corollary 6.3]. Moreover, the induced morphism
$G/C_G(H)$
exists as a smooth separated algebraic space of finite type by work of Artin [Reference ArtinArt74, Corollary 6.3]. Moreover, the induced morphism
![]() $G/C_G(H) \to C_1$
is a monomorphism, so by [Reference KnutsonKnu71, II, 6.15], it follows that
$G/C_G(H) \to C_1$
is a monomorphism, so by [Reference KnutsonKnu71, II, 6.15], it follows that
![]() $G/C_G(H)$
is a scheme. We claim that the morphism
$G/C_G(H)$
is a scheme. We claim that the morphism
![]() $G/C_G(H) \to C_1$
is an isomorphism. Indeed, from the above, we see that it is a smooth surjective monomorphism. Thus, by [Reference Dieudonne and GrothendieckDG67, IV4, Théorème 17.9.1], it is a surjective open embedding and thus an isomorphism. As remarked above, this shows that
$G/C_G(H) \to C_1$
is an isomorphism. Indeed, from the above, we see that it is a smooth surjective monomorphism. Thus, by [Reference Dieudonne and GrothendieckDG67, IV4, Théorème 17.9.1], it is a surjective open embedding and thus an isomorphism. As remarked above, this shows that
![]() $C_G(H)$
is geometrically reductive.
$C_G(H)$
is geometrically reductive.
For the final claim, we may and do assume that
![]() $S = \operatorname {\mathrm {Spec}} k$
for an algebraically closed field k of characteristic
$S = \operatorname {\mathrm {Spec}} k$
for an algebraically closed field k of characteristic
![]() $p> 0$
. If
$p> 0$
. If
![]() $\pi _0 C_G(H)$
has any p-torsion, then a simple argument with the Jordan decomposition shows that
$\pi _0 C_G(H)$
has any p-torsion, then a simple argument with the Jordan decomposition shows that
![]() $C_G(H)(k)$
admits unipotent elements not lying in
$C_G(H)(k)$
admits unipotent elements not lying in
![]() $C_G(H)^0(k)$
. This does not happen in good characteristic by the argument of [Reference Springer and SteinbergSS70, III, 3.15].
$C_G(H)^0(k)$
. This does not happen in good characteristic by the argument of [Reference Springer and SteinbergSS70, III, 3.15].
In order to apply Theorem 3.2, we need the following simple lemma.
Lemma 3.3. Let k be an algebraically closed field, and let G and H be (possibly disconnected) reductive groups over k. Let T be a maximal k-torus of H. Suppose
![]() $f: H \to G$
is a k-homomorphism such that
$f: H \to G$
is a k-homomorphism such that
![]() $\mathrm {H}^1(H, V) = 0$
for all representations V isomorphic to
$\mathrm {H}^1(H, V) = 0$
for all representations V isomorphic to
![]() $\operatorname {\mathrm {Lie}} G$
under some k-homomorphism
$\operatorname {\mathrm {Lie}} G$
under some k-homomorphism
![]() $H \to G$
such that the multiset of weights for T on V is the same as the multiset of weights for T on
$H \to G$
such that the multiset of weights for T on V is the same as the multiset of weights for T on
![]() $\mathfrak {g}$
. Then
$\mathfrak {g}$
. Then
![]() $f(H)$
is G-cr.
$f(H)$
is G-cr.
Proof. Note that
![]() $\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
admits a disjoint union decomposition into pieces on which the multiset of weights for T on
$\underline {\operatorname {\mathrm {Hom}}}_{k\textrm {-}\mathrm {gp}}(H, G)$
admits a disjoint union decomposition into pieces on which the multiset of weights for T on
![]() $\mathfrak {g}$
is constant; let U be the piece containing f. By hypothesis and [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. III, Corollaire 2.8], every orbit map
$\mathfrak {g}$
is constant; let U be the piece containing f. By hypothesis and [Reference Gille, Polo, Demazure, Grothendieck, Artin, Bertin, Gabriel, Raynaud and SerreGP11, Exp. III, Corollaire 2.8], every orbit map
![]() $G \to U$
is smooth, and thus, every orbit is an open subscheme of U. Thus, every orbit is also closed. By Lemma 2.11, it follows that
$G \to U$
is smooth, and thus, every orbit is an open subscheme of U. Thus, every orbit is also closed. By Lemma 2.11, it follows that
![]() $f(H)$
is G-cr.
$f(H)$
is G-cr.
Now we recall the following fundamental result of McNinch [Reference McNinchMcN98], which builds on work of Jantzen [Reference JantzenJan97]. If H is a (possibly disconnected) reductive group and
![]() $H_1, \dots , H_n$
are the simple factors of
$H_1, \dots , H_n$
are the simple factors of
![]() ${\mathscr D}(H^0)$
, we let
${\mathscr D}(H^0)$
, we let
![]() $\ell _H = \inf _i(\operatorname {\mathrm {rank}} H_i)$
. Note that if
$\ell _H = \inf _i(\operatorname {\mathrm {rank}} H_i)$
. Note that if
![]() $H^0$
is a torus, then
$H^0$
is a torus, then
![]() $\ell _H = \infty $
.
$\ell _H = \infty $
.
Theorem 3.4 [Reference McNinchMcN98, Corollary 1.1.2].
Let k be a field of characteristic
![]() $p> 0$
, and let H be a connected reductive k-group. If V is an algebraic k-representation of H and
$p> 0$
, and let H be a connected reductive k-group. If V is an algebraic k-representation of H and
![]() $\dim V \leq p\ell _H$
, then V is semisimple. In particular, if
$\dim V \leq p\ell _H$
, then V is semisimple. In particular, if
![]() $\dim V < p\ell _H$
, then
$\dim V < p\ell _H$
, then
![]() $\mathrm {H}^1(H, V) = \operatorname {\mathrm {Ext}}_H^1(k, V) = 0$
.
$\mathrm {H}^1(H, V) = \operatorname {\mathrm {Ext}}_H^1(k, V) = 0$
.
Corollary 3.5. Let S be a scheme, and let G and H be geometrically reductive smooth affine S-group schemes. Suppose that H is weakly reductive and that for every
![]() $s \in S$
, either
$s \in S$
, either ![]() or
or ![]() . If H acts faithfully on G, then
. If H acts faithfully on G, then
![]() $C_G(H)$
is smooth, affine and geometrically reductive. If G is weakly reductive, then
$C_G(H)$
is smooth, affine and geometrically reductive. If G is weakly reductive, then
![]() $C_G(H)$
is also weakly reductive.
$C_G(H)$
is also weakly reductive.
Note that if
![]() $H^0$
is a torus (in particular if H is finite étale), then Corollary 3.5 involves no hypothesis on the residue characteristics of S.
$H^0$
is a torus (in particular if H is finite étale), then Corollary 3.5 involves no hypothesis on the residue characteristics of S.
Proof. By passing separately from H to
![]() ${\mathscr D}(H^0)$
,
${\mathscr D}(H^0)$
,
![]() $H^0/{\mathscr D}(H^0)$
, and
$H^0/{\mathscr D}(H^0)$
, and
![]() $H/H^0$
(and from G to centralizers of these), we can assume that H is either semisimple, a torus or finite étale of order invertible on S. Assume first that H is either a torus or finite étale. In this case, let
$H/H^0$
(and from G to centralizers of these), we can assume that H is either semisimple, a torus or finite étale of order invertible on S. Assume first that H is either a torus or finite étale. In this case, let
![]() $G_1 = G \ltimes H$
, a geometrically reductive smooth affine S-group scheme which is weakly reductive whenever G is. By Theorem 3.2 (whose hypotheses always hold in the current setting), the centralizer
$G_1 = G \ltimes H$
, a geometrically reductive smooth affine S-group scheme which is weakly reductive whenever G is. By Theorem 3.2 (whose hypotheses always hold in the current setting), the centralizer
![]() $C_{G_1}(H)$
is smooth, affine and geometrically reductive, and it is weakly reductive whenever G is. There is a natural projection map
$C_{G_1}(H)$
is smooth, affine and geometrically reductive, and it is weakly reductive whenever G is. There is a natural projection map
![]() $f: C_{G_1}(H) \to H$
, and
$f: C_{G_1}(H) \to H$
, and
![]() $C_G(H) = f^{-1}(1)$
. If H is a torus, then in particular, it is commutative, and so f is split by the natural inclusion
$C_G(H) = f^{-1}(1)$
. If H is a torus, then in particular, it is commutative, and so f is split by the natural inclusion
![]() $H \to G_1$
. Thus,
$H \to G_1$
. Thus,
![]() $C_{G_1}(H) = C_G(H) \times H$
and
$C_{G_1}(H) = C_G(H) \times H$
and
![]() $C_G(H)$
is geometrically reductive, smooth and affine. Moreover,
$C_G(H)$
is geometrically reductive, smooth and affine. Moreover,
![]() $C_{G^0}(H)$
has connected fibers by the classical theory, so
$C_{G^0}(H)$
has connected fibers by the classical theory, so
![]() $C_G(H)$
is weakly reductive if G is weakly reductive. Now assume that H is finite étale of order invertible on S. Note f factors through a constant map
$C_G(H)$
is weakly reductive if G is weakly reductive. Now assume that H is finite étale of order invertible on S. Note f factors through a constant map
![]() $C_{G_1}(H)/C_{G_1}(H)^0 \to H$
, so
$C_{G_1}(H)/C_{G_1}(H)^0 \to H$
, so
![]() $C_G(H)$
is an open and closed S-subgroup scheme of
$C_G(H)$
is an open and closed S-subgroup scheme of
![]() $C_{G_1}(H)$
, from which the result follows in this case. If G is weakly reductive, then to show that
$C_{G_1}(H)$
, from which the result follows in this case. If G is weakly reductive, then to show that
![]() $C_G(H)$
is weakly reductive, it suffices to show that
$C_G(H)$
is weakly reductive, it suffices to show that
![]() $C_{G^0}(H)$
is weakly reductive, which follows from the above and [Reference Fargues and ScholzeFS24, Proposition VIII 5.11] applied on S-fibers.
$C_{G^0}(H)$
is weakly reductive, which follows from the above and [Reference Fargues and ScholzeFS24, Proposition VIII 5.11] applied on S-fibers.
Now assume that H is semisimple. By Lemma 3.3, Theorem 3.4, [Reference Bate, Martin and RöhrleBMR05, Corollary 3.42], and our bounds on the residue characteristics,
![]() $H_s$
is
$H_s$
is
![]() $G_s$
-cr for all
$G_s$
-cr for all
![]() $s \in S$
. The action of H on
$s \in S$
. The action of H on
![]() $G^0$
is given by a map
$G^0$
is given by a map
![]() $f: H \to G^0/Z(G^0)$
, and Theorem 3.2 combines with Theorem 3.4 to show that
$f: H \to G^0/Z(G^0)$
, and Theorem 3.2 combines with Theorem 3.4 to show that
![]() $C_{G^0/Z(G^0)}(H)$
is geometrically reductive, smooth and affine. The assumption on residue characteristics implies (by considering the simple types) that
$C_{G^0/Z(G^0)}(H)$
is geometrically reductive, smooth and affine. The assumption on residue characteristics implies (by considering the simple types) that
![]() $Z(G^0)$
is smooth, so as H acts faithfully, we conclude that
$Z(G^0)$
is smooth, so as H acts faithfully, we conclude that
![]() $C_{G^0}(H)$
is geometrically reductive, smooth and affine. If X is the stabilizer of f in G, then
$C_{G^0}(H)$
is geometrically reductive, smooth and affine. If X is the stabilizer of f in G, then
![]() $C_{G^0}(H) = X \cap G^0$
is an open S-subgroup scheme of X, so X is smooth affine, and we claim that X is geometrically reductive. For this, we may and do assume
$C_{G^0}(H) = X \cap G^0$
is an open S-subgroup scheme of X, so X is smooth affine, and we claim that X is geometrically reductive. For this, we may and do assume
![]() $S = \operatorname {\mathrm {Spec}} A$
for a DVR A. Now the quotient
$S = \operatorname {\mathrm {Spec}} A$
for a DVR A. Now the quotient
![]() $G/X$
is affine: first,
$G/X$
is affine: first,
![]() $G^0/C_{G^0}(H)$
is isomorphic to an affine open subscheme U of
$G^0/C_{G^0}(H)$
is isomorphic to an affine open subscheme U of
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G^0/Z(G^0))$
which is also a closed subscheme on S-fibers, as follows from the proof of Theorem 3.2. The quotient
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G^0/Z(G^0))$
which is also a closed subscheme on S-fibers, as follows from the proof of Theorem 3.2. The quotient
![]() $G/X$
is a finite union of
$G/X$
is a finite union of
![]() $G/G^0$
-translates of U in
$G/G^0$
-translates of U in
![]() $\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G^0/Z(G^0))$
, so it is an open subscheme which is closed on fibers. By Theorem 2.2 and Lemma 3.1, it follows that
$\underline {\operatorname {\mathrm {Hom}}}_{S\textrm {-}\mathrm {gp}}(H, G^0/Z(G^0))$
, so it is an open subscheme which is closed on fibers. By Theorem 2.2 and Lemma 3.1, it follows that
![]() $G/X$
is affine and thus X is geometrically reductive by Theorem 2.1. We may now pass from G to X to assume that H acts trivially on
$G/X$
is affine and thus X is geometrically reductive by Theorem 2.1. We may now pass from G to X to assume that H acts trivially on
![]() $G^0$
.
$G^0$
.
Since H has connected fibers, it also acts trivially on the finite étale S-group scheme
![]() $G/G^0$
. It would now be enough to show that H acts trivially on G. Thus, there is a natural map
$G/G^0$
. It would now be enough to show that H acts trivially on G. Thus, there is a natural map
![]() $\varphi : H \times G \to G^0$
given by
$\varphi : H \times G \to G^0$
given by
![]() $\varphi (h, g) = (hgh^{-1})g^{-1}$
. Since H acts trivially on
$\varphi (h, g) = (hgh^{-1})g^{-1}$
. Since H acts trivially on
![]() $G^0$
, it follows that
$G^0$
, it follows that
![]() $\varphi $
factors through a map
$\varphi $
factors through a map
![]() $H \times G/G^0 \to Z(G^0)$
. For fixed
$H \times G/G^0 \to Z(G^0)$
. For fixed
![]() $g \in (G/G^0)(S)$
, the map
$g \in (G/G^0)(S)$
, the map
![]() $\varphi (-, g): H \to Z(G^0)$
is an S-homomorphism. Since
$\varphi (-, g): H \to Z(G^0)$
is an S-homomorphism. Since
![]() $Z(G^0)$
is of multiplicative type and H is semisimple,
$Z(G^0)$
is of multiplicative type and H is semisimple,
![]() $\varphi (-, g)$
is trivial, as desired. Finally, if G is weakly reductive, then to show that
$\varphi (-, g)$
is trivial, as desired. Finally, if G is weakly reductive, then to show that
![]() $C_G(H)$
is weakly reductive, it is easy to pass from G to
$C_G(H)$
is weakly reductive, it is easy to pass from G to
![]() $G^0/Z(G^0)$
and thus reduce to Theorem 3.2.
$G^0/Z(G^0)$
and thus reduce to Theorem 3.2.
Next, we obtain a similar result under better bounds when H is the centralizer of a finite group of order invertible on the base. For this, we will use recent fundamental results of Fargues–Scholze. First, we must recall the notion of good filtration. The following theorem is a basic consequence of [Reference Fargues and ScholzeFS24, Proposition VIII.5.12].
Theorem 3.6 [Reference Fargues and ScholzeFS24, Proposition VIII.5.12].
Let k be an algebraically closed field of characteristic
![]() $p> 0$
, and let G be a connected reductive k-group such that p is pretty good for G. If
$p> 0$
, and let G be a connected reductive k-group such that p is pretty good for G. If
![]() $\Lambda $
is a finite group of order prime to p acting on G, then
$\Lambda $
is a finite group of order prime to p acting on G, then
![]() $\mathrm {H}^i(C_G(\Lambda ), \mathfrak {g}) = 0$
for all
$\mathrm {H}^i(C_G(\Lambda ), \mathfrak {g}) = 0$
for all
![]() $i> 0$
.
$i> 0$
.
Proof. By [Reference Andersen and JantzenAJ84, 4.4], every symmetric power
![]() $\operatorname {\mathrm {Sym}}^n \mathfrak {g}^*$
admits a good filtration: in other words, there is a filtration of
$\operatorname {\mathrm {Sym}}^n \mathfrak {g}^*$
admits a good filtration: in other words, there is a filtration of
![]() $\operatorname {\mathrm {Sym}}^n \mathfrak {g}^*$
such that every subquotient is isomorphic to
$\operatorname {\mathrm {Sym}}^n \mathfrak {g}^*$
such that every subquotient is isomorphic to
![]() $\mathrm {H}^0(\lambda )$
for some dominant weight
$\mathrm {H}^0(\lambda )$
for some dominant weight
![]() $\lambda $
. Since p is pretty good for G, [Reference HerpelHer13, Theorem 5.2] shows that
$\lambda $
. Since p is pretty good for G, [Reference HerpelHer13, Theorem 5.2] shows that
![]() $\mathfrak {g} \cong \mathfrak {g}^*$
as G-representations and thus, in particular,
$\mathfrak {g} \cong \mathfrak {g}^*$
as G-representations and thus, in particular,
![]() $\mathfrak {g}$
admits a good filtration. Now if
$\mathfrak {g}$
admits a good filtration. Now if
![]() $H = C_G(\Lambda )$
, then the above discussion and [Reference Fargues and ScholzeFS24, Proposition VIII.5.12] show that
$H = C_G(\Lambda )$
, then the above discussion and [Reference Fargues and ScholzeFS24, Proposition VIII.5.12] show that
![]() $\mathcal {O}(G/H)$
also admits a good filtration. Using the equality
$\mathcal {O}(G/H)$
also admits a good filtration. Using the equality
![]() $\mathrm {H}^i(H, \mathfrak {g}) = \mathrm {H}^i(G, \mathfrak {g} \otimes _k \mathcal {O}(G/H))$
(which relies on the fact that
$\mathrm {H}^i(H, \mathfrak {g}) = \mathrm {H}^i(G, \mathfrak {g} \otimes _k \mathcal {O}(G/H))$
(which relies on the fact that
![]() $G/H$
is affine), it is enough to show that
$G/H$
is affine), it is enough to show that
![]() $\mathrm {H}^i(G, \mathrm {H}^0(\lambda ) \otimes _k \mathrm {H}^0(\mu )) = 0$
for all
$\mathrm {H}^i(G, \mathrm {H}^0(\lambda ) \otimes _k \mathrm {H}^0(\mu )) = 0$
for all
![]() $i> 0$
and all dominant weights
$i> 0$
and all dominant weights
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
. This is proved in [Reference JantzenJan03, II, 4.13].
$\mu $
. This is proved in [Reference JantzenJan03, II, 4.13].
Corollary 3.7. Let S be a scheme, and let G be a weakly reductive S-group scheme. Let
![]() $\Lambda $
be a finite étale S-group scheme of order invertible on S which acts on G. Then
$\Lambda $
be a finite étale S-group scheme of order invertible on S which acts on G. Then
![]() $C_G(\Lambda )$
is a weakly reductive S-group scheme. Moreover, suppose that for every
$C_G(\Lambda )$
is a weakly reductive S-group scheme. Moreover, suppose that for every
![]() $s \in S$
,
$s \in S$
, ![]() is pretty good for
is pretty good for
![]() $G_s$
. Then
$G_s$
. Then
![]() $C_G(C_G(\Lambda ))$
is a weakly reductive S-group scheme.
$C_G(C_G(\Lambda ))$
is a weakly reductive S-group scheme.
Proof. The first claim follows immediately from Corollary 3.5. Let
![]() $H = C_G(\Lambda )$
. By Theorem 3.2, it is enough to show that
$H = C_G(\Lambda )$
. By Theorem 3.2, it is enough to show that
![]() $\mathrm {H}^1(H_s, \mathfrak {g}_s) = 0$
and
$\mathrm {H}^1(H_s, \mathfrak {g}_s) = 0$
and
![]() $H_s$
is
$H_s$
is
![]() $G_s$
-cr for all
$G_s$
-cr for all
![]() $s \in S$
. The first condition holds by Theorem 3.6, and the second condition holds by [Reference Bate, Martin and RöhrleBMR05, Corollary 3.17].
$s \in S$
. The first condition holds by Theorem 3.6, and the second condition holds by [Reference Bate, Martin and RöhrleBMR05, Corollary 3.17].
Example 3.8. In general, some bound on the residue characteristics as in Corollary 3.5 is necessary, even in pretty good characteristic. For example, let p be any prime number, let
![]() $S = \operatorname {\mathrm {Spec}} \mathbf {F}_p[\![t]\!]$
, let
$S = \operatorname {\mathrm {Spec}} \mathbf {F}_p[\![t]\!]$
, let
![]() $H = \operatorname {\mathrm {SL}}_2$
, and let
$H = \operatorname {\mathrm {SL}}_2$
, and let
![]() $G = \operatorname {\mathrm {GL}}_{p+1}$
. With notation as in [Reference JantzenJan03, II, Chapter 2], there is an indecomposable
$G = \operatorname {\mathrm {GL}}_{p+1}$
. With notation as in [Reference JantzenJan03, II, Chapter 2], there is an indecomposable
![]() $p+1$
-dimensional representation
$p+1$
-dimensional representation
![]() $\mathrm {H}^0(p)$
of
$\mathrm {H}^0(p)$
of
![]() $\operatorname {\mathrm {SL}}_2$
equipped with a filtration
$\operatorname {\mathrm {SL}}_2$
equipped with a filtration
This gives an extension class in
![]() $\operatorname {\mathrm {Ext}}^1_H(\mathrm {L}(p-2), \mathrm {L}(p))$
. Multiplying this class by t gives a
$\operatorname {\mathrm {Ext}}^1_H(\mathrm {L}(p-2), \mathrm {L}(p))$
. Multiplying this class by t gives a
![]() $p+1$
-dimensional representation V of
$p+1$
-dimensional representation V of
![]() $\operatorname {\mathrm {SL}}_2$
over S with special fiber
$\operatorname {\mathrm {SL}}_2$
over S with special fiber
![]() $\mathrm {L}(p) \oplus \mathrm {L}(p-2)$
and generic fiber
$\mathrm {L}(p) \oplus \mathrm {L}(p-2)$
and generic fiber
![]() $\mathrm {H}^0(p)$
. Relative to the corresponding map
$\mathrm {H}^0(p)$
. Relative to the corresponding map
![]() $H \to G$
, we have
$H \to G$
, we have
![]() $C_G(H)_s \cong \mathbf {G}_m^2$
, while
$C_G(H)_s \cong \mathbf {G}_m^2$
, while
![]() $C_G(H)_\eta \cong \mathbf {G}_m$
[Reference JantzenJan03, Proposition II.2.8], so
$C_G(H)_\eta \cong \mathbf {G}_m$
[Reference JantzenJan03, Proposition II.2.8], so
![]() $C_G(H)$
is not flat.
$C_G(H)$
is not flat.
Moreover, the centralizer of a connected reductive subgroup of a reductive group need not be reductive if the characteristic is too small; this is related to the fact that representations of connected reductive groups can fail to be semisimple in positive characteristic. For explicit examples, see the MathOverflow answer [Reference McNinchhm], as well as the comments on that answer.
We do not know the optimal bound on the residue characteristics in Corollary 3.5; if
![]() $G = \operatorname {\mathrm {GL}}_n$
, then one can improve the bound from
$G = \operatorname {\mathrm {GL}}_n$
, then one can improve the bound from
![]() $n^2/\ell _H$
to
$n^2/\ell _H$
to
![]() $n/\ell _H$
. If
$n/\ell _H$
. If
![]() $G = \operatorname {\mathrm {Sp}}_n$
(resp.
$G = \operatorname {\mathrm {Sp}}_n$
(resp.
![]() $\operatorname {\mathrm {SO}}_n$
), then one can improve the bound from
$\operatorname {\mathrm {SO}}_n$
), then one can improve the bound from
![]() $n(2n+1)/\ell _H$
(resp.
$n(2n+1)/\ell _H$
(resp.
![]() $n(n-1)/2\ell _H$
) to
$n(n-1)/2\ell _H$
) to
![]() $n/\ell _H$
. In general, it seems reasonable to expect that something like
$n/\ell _H$
. In general, it seems reasonable to expect that something like
![]() $h_G/\ell _H$
is the correct bound, where
$h_G/\ell _H$
is the correct bound, where
![]() $h_G$
is the Coxeter number of G.
$h_G$
is the Coxeter number of G.
3.2 Centralizers of pure unipotent elements
Later arguments rely heavily on the smoothness of centralizers of pure fiberwise unipotent elements. The notion of purity will capture the idea that an element of G ‘looks similar’ across all fibers. For example, an element like  will not be pure.
will not be pure.
Definition 3.9. Let G a reductive group over a scheme S. A section
![]() $g \in G(S)$
is pure if
$g \in G(S)$
is pure if
![]() $s \mapsto C_{G_s}(g_s)$
is locally constant on s. There is an analogous definition for elements of the Lie algebra.
$s \mapsto C_{G_s}(g_s)$
is locally constant on s. There is an analogous definition for elements of the Lie algebra.
If S is the spectrum of a discrete valuation ring, this means that the special and generic fibers of the centralizer of g have the same dimension.
Using a Springer isomorphism, the smoothness for centralizers of unipotent elements is closely related to the smoothness for centralizers of nilpotent elements in the Lie algebra. This smoothness was claimed in [Reference McNinchMcN08], but the argument there has a gap. This has been fixed by Hardesty (for pure nilpotents) and by the second author (for pure unipotents and nilpotents) [Reference HardestyHar18, Reference CotnerCot22a]. Since our later arguments are naturally phrased in terms of unipotent elements, we will build on the latter.
Theorem 3.10. Let A be a DVR with residue characteristic p, and let G be a weakly reductive group scheme over
![]() $\operatorname {\mathrm {Spec}} A$
. If p is pretty good for G and
$\operatorname {\mathrm {Spec}} A$
. If p is pretty good for G and
![]() $u \in G(A)$
is a pure fiberwise unipotent element, then
$u \in G(A)$
is a pure fiberwise unipotent element, then
![]() $C_G(u)$
is A-smooth.
$C_G(u)$
is A-smooth.
Using Remark 1.13, it would be equivalent to suppose that p is good for
![]() $G^0$
, that
$G^0$
, that
![]() $\# \pi _1 ({\mathscr D}(G^{0}))$
is prime-to-p, and that
$\# \pi _1 ({\mathscr D}(G^{0}))$
is prime-to-p, and that
![]() $Z(G^0)$
is A-smooth.
$Z(G^0)$
is A-smooth.
Proof. If G is connected, flatness comes from [Reference CotnerCot22a, Theorem 1.1]. The smoothness of the fibers follows, for example, from [Reference HerpelHer13, Theorem 1.1].
In general, note that
![]() $\overline {u}$
has order a power of p, and hence, u lies in the identity component of G. It suffices to show that every component of G which contains a point in the special fiber centralizing u has an A-point centralizing u. For then, the centralizer
$\overline {u}$
has order a power of p, and hence, u lies in the identity component of G. It suffices to show that every component of G which contains a point in the special fiber centralizing u has an A-point centralizing u. For then, the centralizer
![]() $C_G(u)$
is a union of copies of the smooth
$C_G(u)$
is a union of copies of the smooth
![]() $C_{G^0}(u)$
.
$C_{G^0}(u)$
.
Given
![]() $g \in G(A)$
such that
$g \in G(A)$
such that
![]() $\overline {g}$
centralizes
$\overline {g}$
centralizes
![]() $u_s$
in the special fiber, as u is pure, [Reference CotnerCot22a, Theorem 5.11] shows that
$u_s$
in the special fiber, as u is pure, [Reference CotnerCot22a, Theorem 5.11] shows that
![]() $gu g^{-1}$
and u are
$gu g^{-1}$
and u are
![]() $G^0(A)$
-conjugate. Thus, there is
$G^0(A)$
-conjugate. Thus, there is
![]() $h \in G^0(A)$
such that
$h \in G^0(A)$
such that
![]() $h u h^{-1} = g u g^{-1}$
, and hence,
$h u h^{-1} = g u g^{-1}$
, and hence,
![]() $h^{-1} g \in G(A)$
centralizes u and lies in the desired component of G.
$h^{-1} g \in G(A)$
centralizes u and lies in the desired component of G.
3.3 Complements on pure unipotents
We conclude with some additional results about pure unipotents which elaborate the sense in which a pure unipotent ‘looks similar’ in the special and generic fibers.
We begin by reviewing the Bala-Carter method which classifies nilpotent orbits for a connected reductive group over an algebraically closed field k of good characteristic
![]() $p \geq 0$
. (More information can be found in [Reference JantzenJan04, §4], and a uniform proof without case-checking in small characteristic is due to Premet [Reference PremetPre03].) Using a Springer isomorphism, this equivalently gives a classification of conjugacy classes of unipotent elements. To state it, we need to define some terminology.
$p \geq 0$
. (More information can be found in [Reference JantzenJan04, §4], and a uniform proof without case-checking in small characteristic is due to Premet [Reference PremetPre03].) Using a Springer isomorphism, this equivalently gives a classification of conjugacy classes of unipotent elements. To state it, we need to define some terminology.
Let H be a connected reductive k-group with p good for H, and
![]() $\mathfrak {h} = \operatorname {\mathrm {Lie}} H$
.
$\mathfrak {h} = \operatorname {\mathrm {Lie}} H$
.
-
• A nilpotent
 $N \in \mathfrak {h}$
is a distinguished nilpotent if each torus contained in
$N \in \mathfrak {h}$
is a distinguished nilpotent if each torus contained in
 $C_{H}(N)$
is contained in the center of H.
$C_{H}(N)$
is contained in the center of H. -
• For a parabolic
 $P \subset H$
with unipotent radical U, the Richardson orbit associated to P is the unique nilpotent orbit of H with dense intersection with
$P \subset H$
with unipotent radical U, the Richardson orbit associated to P is the unique nilpotent orbit of H with dense intersection with
 $\operatorname {\mathrm {Lie}} U$
. Its intersection with
$\operatorname {\mathrm {Lie}} U$
. Its intersection with
 $\operatorname {\mathrm {Lie}} P$
is a single orbit under P.
$\operatorname {\mathrm {Lie}} P$
is a single orbit under P. -
• A parabolic subgroup
 $P \subset H$
with unipotent radical U is a distinguished parabolic if
$P \subset H$
with unipotent radical U is a distinguished parabolic if
 $\dim P/U = \dim U/ \mathscr {D}(U)$
.
$\dim P/U = \dim U/ \mathscr {D}(U)$
.
Bala and Carter classified nilpotent orbits when the characteristic is good. One can check that if p is good for H, it will also be good for any Levi factor of a parabolic subgroup of H. The following fact can be found in [Reference JantzenJan04, §4].
Fact 3.11. If p is a good prime for H, the nilpotent orbits for H are in bijection with
![]() $H(k)$
-conjugacy classes of pairs
$H(k)$
-conjugacy classes of pairs
![]() $(L,P)$
where L is a Levi factor of a parabolic subgroup of H and P is a distinguished parabolic of L. The nilpotent orbit for H associated to
$(L,P)$
where L is a Levi factor of a parabolic subgroup of H and P is a distinguished parabolic of L. The nilpotent orbit for H associated to
![]() $(L,P)$
is the unique one meeting
$(L,P)$
is the unique one meeting
![]() $\operatorname {\mathrm {Lie}}(P)$
in its Richardson orbit for L.
$\operatorname {\mathrm {Lie}}(P)$
in its Richardson orbit for L.
The Bala-Carter data for H is the set of
![]() $H(k)$
-conjugacy classes of pairs
$H(k)$
-conjugacy classes of pairs
![]() $(L,P)$
as above. It turns out it is independent of k in the sense that it can be described completely in terms of the root datum of H as follows. All Levi subgroups L of a parabolic k-subgroup Q of H are a single
$(L,P)$
as above. It turns out it is independent of k in the sense that it can be described completely in terms of the root datum of H as follows. All Levi subgroups L of a parabolic k-subgroup Q of H are a single
![]() $\mathcal {R}_{u,k}(Q)$
-orbit, so in Fact 3.11, we may restrict to one Q per
$\mathcal {R}_{u,k}(Q)$
-orbit, so in Fact 3.11, we may restrict to one Q per
![]() $H(k)$
-conjugacy class and one L per Q. We may pick L so that it contains a (split) maximal torus T. After conjugation by
$H(k)$
-conjugacy class and one L per Q. We may pick L so that it contains a (split) maximal torus T. After conjugation by
![]() $L(k)$
, the distinguished parabolic subgroup
$L(k)$
, the distinguished parabolic subgroup
![]() $P \subset L$
may be assumed to contain T as well. But we know that parabolic subgroups Q of H containing T are in bijection with parabolic subsets of
$P \subset L$
may be assumed to contain T as well. But we know that parabolic subgroups Q of H containing T are in bijection with parabolic subsets of
![]() $\Phi (H,T)$
via
$\Phi (H,T)$
via
![]() $Q \mapsto \Phi (Q,T)$
, so the possible Levi factors L of Q containing T are described just in terms of the root datum. Likewise, parabolic subgroups P of L containing T are in bijection with parabolic subsets of
$Q \mapsto \Phi (Q,T)$
, so the possible Levi factors L of Q containing T are described just in terms of the root datum. Likewise, parabolic subgroups P of L containing T are in bijection with parabolic subsets of
![]() $\Phi (L,T)$
. If we can characterize the condition that P is distinguished just in terms of the root data, this would mean that the Bala-Carter data can be described solely in terms of the root data and so is completely combinatorial.
$\Phi (L,T)$
. If we can characterize the condition that P is distinguished just in terms of the root data, this would mean that the Bala-Carter data can be described solely in terms of the root data and so is completely combinatorial.
We do so by constructing a grading on the Lie algebra of a parabolic P. Pick a Borel subgroup
![]() $B \subset H$
satisfying
$B \subset H$
satisfying
![]() $T \subset B \subset P$
. Let
$T \subset B \subset P$
. Let
![]() $\mathfrak {t} = \operatorname {\mathrm {Lie}}(T)$
and
$\mathfrak {t} = \operatorname {\mathrm {Lie}}(T)$
and
![]() $\Delta \subset \Phi = \Phi (L,T)$
be the set of positive simple roots determined by B. There is a unique subset
$\Delta \subset \Phi = \Phi (L,T)$
be the set of positive simple roots determined by B. There is a unique subset
![]() $I \subset \Delta $
such that
$I \subset \Delta $
such that
![]() $P = B W_I B$
where
$P = B W_I B$
where
![]() $W_I$
is the subset of the Weyl group generated by reflections with respect to roots in I. Define a group homomorphism
$W_I$
is the subset of the Weyl group generated by reflections with respect to roots in I. Define a group homomorphism
![]() $f: \mathbf Z \Phi \subset \mathbf Z^\Delta \to \mathbf Z$
by specifying that on the basis
$f: \mathbf Z \Phi \subset \mathbf Z^\Delta \to \mathbf Z$
by specifying that on the basis
![]() $\Delta $
, we have
$\Delta $
, we have
 $$\begin{align*}f(\alpha) = \begin{cases} 2 & \alpha \in \Delta - I, \\ 0 & \alpha \in I. \end{cases} \end{align*}$$
$$\begin{align*}f(\alpha) = \begin{cases} 2 & \alpha \in \Delta - I, \\ 0 & \alpha \in I. \end{cases} \end{align*}$$
This function gives a grading on
![]() $\mathfrak {l} = \operatorname {\mathrm {Lie}}(L)$
:
$\mathfrak {l} = \operatorname {\mathrm {Lie}}(L)$
:
 $$\begin{align*}\mathfrak{l}(i) = \bigoplus_{f(\alpha) = i} \mathfrak{l}_\alpha \quad \text{and} \quad \mathfrak{l}(0) = \left( \bigoplus_{f(\alpha) = 0} \mathfrak{l}_\alpha \right) \oplus \mathfrak{t} \end{align*}$$
$$\begin{align*}\mathfrak{l}(i) = \bigoplus_{f(\alpha) = i} \mathfrak{l}_\alpha \quad \text{and} \quad \mathfrak{l}(0) = \left( \bigoplus_{f(\alpha) = 0} \mathfrak{l}_\alpha \right) \oplus \mathfrak{t} \end{align*}$$
(sums indexed by
![]() $\alpha \in \Phi $
). With respect to this grading,
$\alpha \in \Phi $
). With respect to this grading,
The condition that P is distinguished is equivalent to the condition that
by [Reference CarterCar85, Corollary 5.8.3] as p is good for L. But this condition depends only on the root datum. Thus, the Bala-Carter data for H can be described in a manner independent of the choice of algebraically closed field. We call this combinatorial description the Bala-Carter label for the nilpotent (or unipotent) orbit.
Definition 3.12. If K is a field (not necessarily algebraically closed), then the Bala-Carter label label for a nilpotent (resp. unipotent) element of
![]() $\operatorname {\mathrm {Lie}} H$
(resp.
$\operatorname {\mathrm {Lie}} H$
(resp.
![]() $H(K)$
) is the Bala-Carter label for the corresponding nilpotent (resp. unipotent) orbit over the algebraic closure.
$H(K)$
) is the Bala-Carter label for the corresponding nilpotent (resp. unipotent) orbit over the algebraic closure.
Remark 3.13. From the classification of nilpotent orbits over algebraically closed fields, it is known that the corresponding nilpotent orbits in characteristic zero and characteristic p have the same dimension. Thus, the dimension of centralizers of elements in an orbit is also independent of the characteristic and depends only on the Bala-Carter label. There is a similar statement for conjugacy classes of unipotent elements and their centralizers.
We now return to the relative setting.
Lemma 3.14. Let G be a connected reductive group scheme over a DVR A with residue field k whose characteristic is good for G. Given a unipotent element
![]() $\overline {u} \in G(k)$
with Bala-Carter label
$\overline {u} \in G(k)$
with Bala-Carter label
![]() $\sigma $
, there exists a pure fiberwise unipotent element
$\sigma $
, there exists a pure fiberwise unipotent element
![]() $u \in G(A)$
lifting
$u \in G(A)$
lifting
![]() $\overline {u}$
with Bala-Carter label
$\overline {u}$
with Bala-Carter label
![]() $\sigma $
in the generic fiber, and a similar statement for nilpotent elements of the Lie algebra.
$\sigma $
in the generic fiber, and a similar statement for nilpotent elements of the Lie algebra.
Proof. We will prove this for a nilpotent element
![]() $\overline {X}$
; the unipotent case follows using an integral Springer isomorphism [Reference CotnerCot22b, Theorem 1.1]. Let
$\overline {X}$
; the unipotent case follows using an integral Springer isomorphism [Reference CotnerCot22b, Theorem 1.1]. Let
![]() $\tau _s : (\mathbf {G}_m)_s \to G_s$
be a cocharacter associated to
$\tau _s : (\mathbf {G}_m)_s \to G_s$
be a cocharacter associated to
![]() $\overline {X}$
, which exists since
$\overline {X}$
, which exists since
![]() $\textrm {char}(k)$
is good for G. This lifts to a cocharacter
$\textrm {char}(k)$
is good for G. This lifts to a cocharacter
![]() $\tau : \mathbf {G}_m \to G$
by smoothness of the scheme of maximal tori [Reference ConradCon14, Theorem 3.2.6]. This cocharacter defines
$\tau : \mathbf {G}_m \to G$
by smoothness of the scheme of maximal tori [Reference ConradCon14, Theorem 3.2.6]. This cocharacter defines
Over the special fiber,
![]() $\overline {X}$
is in
$\overline {X}$
is in
![]() $\mathfrak {g}_s(\tau ,2)$
, and the
$\mathfrak {g}_s(\tau ,2)$
, and the
![]() $\operatorname {\mathrm {Ad}}_{P(\tau _s)}$
-orbit of
$\operatorname {\mathrm {Ad}}_{P(\tau _s)}$
-orbit of
![]() $\overline {X}$
is open and dense. Pick a fiberwise nilpotent
$\overline {X}$
is open and dense. Pick a fiberwise nilpotent
![]() $X \in \mathfrak {g}(\tau ,2)$
lifting
$X \in \mathfrak {g}(\tau ,2)$
lifting
![]() $\overline {X}$
and consider the parabolic
$\overline {X}$
and consider the parabolic
![]() $P_G(\tau ) \subset G$
. It naturally acts on
$P_G(\tau ) \subset G$
. It naturally acts on
![]() $\bigoplus _{n \geq 2} \mathfrak {g}(\tau ,n) $
and the stabilizer of X is
$\bigoplus _{n \geq 2} \mathfrak {g}(\tau ,n) $
and the stabilizer of X is
![]() $C_G(X)$
. As we know,
$C_G(X)$
. As we know,
![]() $\dim C_G(X)_\eta \leq \dim C_G(X)_s$
, and since the orbit is open and dense in the special fiber, it follows that X is pure. Then argue as in [Reference CotnerCot22a, Lemma 5.2] to show that
$\dim C_G(X)_\eta \leq \dim C_G(X)_s$
, and since the orbit is open and dense in the special fiber, it follows that X is pure. Then argue as in [Reference CotnerCot22a, Lemma 5.2] to show that
![]() $P_G(\tau )$
gives the instability parabolic for X and
$P_G(\tau )$
gives the instability parabolic for X and
![]() $\tau $
is an associated cocharacter for X in the special and generic fibers. By [Reference CotnerCot22a, Proposition 2.13(6)], this information determines the Bala-Carter data in the special and generic fibers.
$\tau $
is an associated cocharacter for X in the special and generic fibers. By [Reference CotnerCot22a, Proposition 2.13(6)], this information determines the Bala-Carter data in the special and generic fibers.
Definition 3.15. Let K be a p-adic field and G be a connected reductive group over the ring of integers
![]() $\mathcal {O}_K$
. We say that
$\mathcal {O}_K$
. We say that
![]() $g_1,g_2 \in G(\mathcal {O}_K)$
are geometrically conjugate if there exists a finite extension L of K such that
$g_1,g_2 \in G(\mathcal {O}_K)$
are geometrically conjugate if there exists a finite extension L of K such that
![]() $g_1$
and
$g_1$
and
![]() $g_2$
are
$g_2$
are
![]() $G(\mathcal {O}_L)$
-conjugate.
$G(\mathcal {O}_L)$
-conjugate.
Proposition 3.16. Let K be a p-adic field with residue field k, and let G be a connected reductive group over
![]() $\mathcal {O}_K$
such that p is pretty good for G. Fix a Bala-Carter label
$\mathcal {O}_K$
such that p is pretty good for G. Fix a Bala-Carter label
![]() $\sigma $
and a pure unipotent
$\sigma $
and a pure unipotent
![]() $u_\sigma $
with Bala-Carter label
$u_\sigma $
with Bala-Carter label
![]() $\sigma $
in
$\sigma $
in
![]() $G(K)$
and
$G(K)$
and
![]() $G(k)$
using Lemma 3.14. The following are equivalent for a fiberwise unipotent
$G(k)$
using Lemma 3.14. The following are equivalent for a fiberwise unipotent
![]() $u \in G(\mathcal {O}_K)$
:
$u \in G(\mathcal {O}_K)$
:
-
1. u is geometrically conjugate to
 $u_{\sigma }$
;
$u_{\sigma }$
; -
2. the images of u in
 $G(K)$
and
$G(K)$
and
 $G(k)$
have Bala-Carter label
$G(k)$
have Bala-Carter label
 $\sigma $
;
$\sigma $
; -
3. u is pure, and it has Bala-Carter label
 $\sigma $
in
$\sigma $
in
 $G(K)$
;
$G(K)$
; -
4. u is pure, and it has Bala-Carter label
 $\sigma $
in
$\sigma $
in
 $G(k)$
;
$G(k)$
;
Proof. Note that (1) implies (2) as the images of
![]() $u_{\sigma }$
in
$u_{\sigma }$
in
![]() $G(K)$
and
$G(K)$
and
![]() $G(k)$
have the same Bala-Carter labels. Since the dimensions of the centralizer of a unipotent element over an algebraically closed field depend only on the Bala-Carter label and not the characteristic, (2) implies (3) and (4). If u is pure and generically has Bala-Carter label
$G(k)$
have the same Bala-Carter labels. Since the dimensions of the centralizer of a unipotent element over an algebraically closed field depend only on the Bala-Carter label and not the characteristic, (2) implies (3) and (4). If u is pure and generically has Bala-Carter label
![]() $\sigma $
, then u and
$\sigma $
, then u and
![]() $u_\sigma $
are
$u_\sigma $
are
![]() $G(K')$
-conjugate for some extension
$G(K')$
-conjugate for some extension
![]() $K'$
of K. By [Reference CotnerCot22a, Theorem 5.11], u and
$K'$
of K. By [Reference CotnerCot22a, Theorem 5.11], u and
![]() $u_\sigma $
are
$u_\sigma $
are
![]() $G(\mathcal {O}_{K'})$
-conjugate. Thus, (3) implies (1). Similarly, (4) implies (1).
$G(\mathcal {O}_{K'})$
-conjugate. Thus, (3) implies (1). Similarly, (4) implies (1).
Remark 3.17.
-
• When defining the minimally ramified deformation condition in [Reference BooherBoo19a] and this paper, a key step is to restrict to deformations where a particular inertial element
 $\sigma $
, whose mod-p image is unipotent, is sent to a conjugate of a particular pure unipotent lift. Proposition 3.16 shows that this condition is equivalent to controlling the conjugacy class of the lift in the generic fiber or to enforcing purity of the lift.
$\sigma $
, whose mod-p image is unipotent, is sent to a conjugate of a particular pure unipotent lift. Proposition 3.16 shows that this condition is equivalent to controlling the conjugacy class of the lift in the generic fiber or to enforcing purity of the lift. -
• There is, of course, an analogous statement for nilpotents. These can be cheaply deduced using an integral Springer isomorphism [Reference CotnerCot22b, Theorem 1.1] or proven directly using similar techniques.
We will also need the following lemma later.
Lemma 3.18. Let K be a p-adic field and G a connected reductive group defined over
![]() $\mathcal {O}_K$
such that p is good for G. Suppose u is a fiberwise unipotent element of
$\mathcal {O}_K$
such that p is good for G. Suppose u is a fiberwise unipotent element of
![]() $G(\mathcal {O}_K)$
satisfying any of the equivalent conditions of Proposition 3.16. Then for any integer n relatively prime to n, the elements u and
$G(\mathcal {O}_K)$
satisfying any of the equivalent conditions of Proposition 3.16. Then for any integer n relatively prime to n, the elements u and
![]() $u^n$
generically have the same Bala-Carter label, and
$u^n$
generically have the same Bala-Carter label, and
![]() $u^n$
is pure.
$u^n$
is pure.
Proof. Over an algebraically closed field, if X is nilpotent, then all nonzero multiples of X lie in the same nilpotent orbit [Reference JantzenJan04, 2.10 Lemma]. Thus, the same is true for powers of unipotents. In particular,
![]() $u^n$
is therefore pure, and
$u^n$
is therefore pure, and
![]() $u^n$
has the same Bala-Carter labels as u generically and in the special fiber.
$u^n$
has the same Bala-Carter labels as u generically and in the special fiber.
4 Decomposition types
Throughout this section, let G be a weakly reductive group scheme over a DVR
![]() $\mathcal {O}$
with residue field k of characteristic p.
$\mathcal {O}$
with residue field k of characteristic p.
4.1 Definitions and examples
Definition 4.1. A decomposition type for G over
![]() $\mathcal {O}$
is a pair
$\mathcal {O}$
is a pair
![]() $(\mathfrak {C}, \Delta )$
where
$(\mathfrak {C}, \Delta )$
where
![]() $\mathfrak {C}$
and
$\mathfrak {C}$
and
![]() $\Delta $
are closed subgroup schemes of G defined over
$\Delta $
are closed subgroup schemes of G defined over
![]() $\mathcal {O}$
such that
$\mathcal {O}$
such that
-
•
 $\mathfrak {C}$
and
$\mathfrak {C}$
and
 $\Delta $
are weakly reductive (i.e.,
$\Delta $
are weakly reductive (i.e.,
 $\mathcal {O}$
-smooth with (not necessarily connected) reductive fibers and finite étale component groups of order invertible on
$\mathcal {O}$
-smooth with (not necessarily connected) reductive fibers and finite étale component groups of order invertible on
 $\mathcal {O}$
).
$\mathcal {O}$
). -
•
 $\Delta $
(resp.
$\Delta $
(resp.
 $\mathfrak {C}$
) represents the scheme theoretic centralizer of
$\mathfrak {C}$
) represents the scheme theoretic centralizer of
 $\mathfrak {C}$
(resp.
$\mathfrak {C}$
(resp.
 $\Delta $
).
$\Delta $
).
Definition 4.2. Let
![]() $\overline {\Lambda } \subset G(k)$
be a finite subgroup with order prime to p. We say a decomposition type
$\overline {\Lambda } \subset G(k)$
be a finite subgroup with order prime to p. We say a decomposition type
![]() $(\mathfrak {C}, \Delta )$
over
$(\mathfrak {C}, \Delta )$
over
![]() $\mathcal {O}$
is adapted to
$\mathcal {O}$
is adapted to
![]() $\overline {\Lambda }$
if
$\overline {\Lambda }$
if
![]() $C_{G_k}(\overline {\Lambda })=\mathfrak {C}_k$
(hence, also
$C_{G_k}(\overline {\Lambda })=\mathfrak {C}_k$
(hence, also
![]() $C_{G_k}(C_{G_k}(\overline {\Lambda }))=\Delta _k$
).
$C_{G_k}(C_{G_k}(\overline {\Lambda }))=\Delta _k$
).
This definition is motivated by the goal of giving a group theoretic reformulation of the isotypic decomposition of a representation, which we now explain.
Example 4.3. This is an elaboration of the example of
![]() $\operatorname {\mathrm {GL}}_n$
discussed in the introduction. Let M be a free
$\operatorname {\mathrm {GL}}_n$
discussed in the introduction. Let M be a free
![]() $\mathcal {O}$
-module of rank n,
$\mathcal {O}$
-module of rank n,
![]() $G = \operatorname {\mathrm {Aut}}(M)$
, and
$G = \operatorname {\mathrm {Aut}}(M)$
, and
![]() $V = M_k$
. As
$V = M_k$
. As
![]() $\overline {\Lambda }$
has pro-order prime to p, V decomposes as a direct sum of irreducible
$\overline {\Lambda }$
has pro-order prime to p, V decomposes as a direct sum of irreducible
![]() $\overline {\Lambda }$
-representations
$\overline {\Lambda }$
-representations
where
![]() $V_i$
and
$V_i$
and
![]() $V_j$
are non-isomorphic for
$V_j$
are non-isomorphic for
![]() $i \neq j$
, and the
$i \neq j$
, and the
![]() $m_i$
’s are multiplicities of the irreducibles. Letting
$m_i$
’s are multiplicities of the irreducibles. Letting
![]() $W_i = \operatorname {\mathrm {Hom}}_{\overline {\Lambda }}(V_i,V)$
be the weight space associated to
$W_i = \operatorname {\mathrm {Hom}}_{\overline {\Lambda }}(V_i,V)$
be the weight space associated to
![]() $V_i$
, we have that
$V_i$
, we have that
![]() $\dim W_i = m_i$
and
$\dim W_i = m_i$
and
Enlarging k if necessary, we may and do assume that
![]() $V_i$
is absolutely irreducible for all i. Let
$V_i$
is absolutely irreducible for all i. Let
be the standard Levi associated to the decomposition of
![]() ${\overline {\tau }}$
, and let
${\overline {\tau }}$
, and let
![]() $d_i=\dim _k V_i$
. By Schur’s lemma,
$d_i=\dim _k V_i$
. By Schur’s lemma,

A direct computation then shows that

where the embedding into
![]() $\operatorname {\mathrm {GL}}(V)$
comes from acting on the first factors of the tensor products in (4.1). Note that
$\operatorname {\mathrm {GL}}(V)$
comes from acting on the first factors of the tensor products in (4.1). Note that
![]() $\Delta _k \subset L_k$
, with
$\Delta _k \subset L_k$
, with
![]() $\operatorname {\mathrm {GL}}(V_i)$
embedding in
$\operatorname {\mathrm {GL}}(V_i)$
embedding in
![]() $\operatorname {\mathrm {GL}}(V_i)^{m_i}$
diagonally. One checks that
$\operatorname {\mathrm {GL}}(V_i)^{m_i}$
diagonally. One checks that
![]() $(\mathfrak {C}_k,\Delta _k)$
is a decomposition type adapted to
$(\mathfrak {C}_k,\Delta _k)$
is a decomposition type adapted to
![]() $\overline {\Lambda }$
.
$\overline {\Lambda }$
.
A decomposition type for
![]() $\operatorname {\mathrm {GL}}_n$
over
$\operatorname {\mathrm {GL}}_n$
over
![]() $\mathcal {O}$
adapted to
$\mathcal {O}$
adapted to
![]() $\overline {\Lambda }$
is just a version of this decomposition for the
$\overline {\Lambda }$
is just a version of this decomposition for the
![]() $\mathcal {O}$
-module M phrased group-theoretically. We can specify a representation (of a group containing
$\mathcal {O}$
-module M phrased group-theoretically. We can specify a representation (of a group containing
![]() $\overline {\Lambda }$
) on M compatible with the isotypic decomposition using the groups
$\overline {\Lambda }$
) on M compatible with the isotypic decomposition using the groups
![]() $\mathfrak {C}$
and
$\mathfrak {C}$
and
![]() $\Delta $
, which are the automorphisms of the weight spaces and irreducible constituents.
$\Delta $
, which are the automorphisms of the weight spaces and irreducible constituents.
We also give some examples for the symplectic groups that are reminiscent of the ‘isotypic decomposition with pairings’ in [Reference BooherBoo19a, §6.1]. Fix the symmetric form so that
 $$ \begin{align*}\operatorname{\mathrm{Sp}}_{2n}= \left\{M \in \operatorname{\mathrm{GL}}_{2n} : M \begin{pmatrix} 0 & I_n \\ -I_n & 0 \end{pmatrix} M^t=\begin{pmatrix} 0 & I_n \\ -I_n & 0 \end{pmatrix} \right \}.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Sp}}_{2n}= \left\{M \in \operatorname{\mathrm{GL}}_{2n} : M \begin{pmatrix} 0 & I_n \\ -I_n & 0 \end{pmatrix} M^t=\begin{pmatrix} 0 & I_n \\ -I_n & 0 \end{pmatrix} \right \}.\end{align*} $$
For
![]() $A \in \operatorname {\mathrm {GL}}_n$
, we write
$A \in \operatorname {\mathrm {GL}}_n$
, we write
![]() $A^*$
for
$A^*$
for
![]() $(A^t)^{-1}$
. Notice that
$(A^t)^{-1}$
. Notice that
 $L=\left \{ \begin {pmatrix} A & 0 \\ 0 & A^* \end {pmatrix}: A \in \operatorname {\mathrm {GL}}_n \right \}$
is a Levi subgroup of
$L=\left \{ \begin {pmatrix} A & 0 \\ 0 & A^* \end {pmatrix}: A \in \operatorname {\mathrm {GL}}_n \right \}$
is a Levi subgroup of
![]() $\operatorname {\mathrm {Sp}}_{2n}$
. Let
$\operatorname {\mathrm {Sp}}_{2n}$
. Let
![]() $\overline {\Lambda } \subset L(k)$
be an L-irreducible subgroup. This gives a natural
$\overline {\Lambda } \subset L(k)$
be an L-irreducible subgroup. This gives a natural
![]() $2n$
-dimensional representation of the form
$2n$
-dimensional representation of the form
![]() $\tau \oplus \tau ^*$
where
$\tau \oplus \tau ^*$
where
![]() $\tau $
is irreducible representation of
$\tau $
is irreducible representation of
![]() $\overline {\Lambda }$
with dimension n.
$\overline {\Lambda }$
with dimension n.
Example 4.4. If
![]() $\tau $
and
$\tau $
and
![]() $\tau ^*$
are non-isomorphic
$\tau ^*$
are non-isomorphic
![]() $\overline {\Lambda }$
-representations, we have
$\overline {\Lambda }$
-representations, we have
 $$\begin{align*}\mathfrak{C}_k=\left\{ \begin{pmatrix} aI_n & 0 \\ 0 & a^{-1}I_n \end{pmatrix}: a \in \mathbf{G}_m \right \}=Z(L)_k, \quad \Delta_k=L_k. \end{align*}$$
$$\begin{align*}\mathfrak{C}_k=\left\{ \begin{pmatrix} aI_n & 0 \\ 0 & a^{-1}I_n \end{pmatrix}: a \in \mathbf{G}_m \right \}=Z(L)_k, \quad \Delta_k=L_k. \end{align*}$$
Example 4.5. Suppose
![]() $\tau \cong \tau ^*$
. In this case, it is easy to see that there exists
$\tau \cong \tau ^*$
. In this case, it is easy to see that there exists
![]() $J \in \operatorname {\mathrm {GL}}_n(k)$
, either symmetric or skew-symmetric, such that
$J \in \operatorname {\mathrm {GL}}_n(k)$
, either symmetric or skew-symmetric, such that
![]() $\tau J \tau ^t=J$
. Let us suppose that
$\tau J \tau ^t=J$
. Let us suppose that
![]() $p \neq 2$
and J is skew-symmetric (the other case is similar but occurs inside an orthogonal group). Conjugating
$p \neq 2$
and J is skew-symmetric (the other case is similar but occurs inside an orthogonal group). Conjugating
![]() $\tau $
if necessary, we may assume that
$\tau $
if necessary, we may assume that
 $J=\begin {pmatrix} 0 & I_{n/2} \\ -I_{n/2} & 0 \end {pmatrix}$
, so
$J=\begin {pmatrix} 0 & I_{n/2} \\ -I_{n/2} & 0 \end {pmatrix}$
, so
![]() $\tau $
takes values in
$\tau $
takes values in
![]() $\operatorname {\mathrm {Sp}}_n(k)$
. We then have
$\operatorname {\mathrm {Sp}}_n(k)$
. We then have
 $$\begin{align*}\mathfrak{C}_k=\left\{ \begin{pmatrix} aI_n & 0 \\ 0 & a^{-1}I_n \end{pmatrix} : a \in \mathbf{G}_m \right\} \cup \begin{pmatrix} 0 & J \\ -J & 0 \end{pmatrix} \left\{ \begin{pmatrix} aI_n & 0 \\ 0 & a^{-1}I_n \end{pmatrix} : a \in \mathbf{G}_m \right \}, \end{align*}$$
$$\begin{align*}\mathfrak{C}_k=\left\{ \begin{pmatrix} aI_n & 0 \\ 0 & a^{-1}I_n \end{pmatrix} : a \in \mathbf{G}_m \right\} \cup \begin{pmatrix} 0 & J \\ -J & 0 \end{pmatrix} \left\{ \begin{pmatrix} aI_n & 0 \\ 0 & a^{-1}I_n \end{pmatrix} : a \in \mathbf{G}_m \right \}, \end{align*}$$
 $$\begin{align*}\Delta_k=\left\{\begin{pmatrix} A & 0 \\ 0 & A^* \end{pmatrix}: A \in \operatorname{\mathrm{Sp}}_n \right \}. \end{align*}$$
$$\begin{align*}\Delta_k=\left\{\begin{pmatrix} A & 0 \\ 0 & A^* \end{pmatrix}: A \in \operatorname{\mathrm{Sp}}_n \right \}. \end{align*}$$
Definition 4.6. Let
![]() $(\mathfrak {C},\Delta )$
be a decomposition type over
$(\mathfrak {C},\Delta )$
be a decomposition type over
![]() $\mathcal {O}$
. We say p is good for
$\mathcal {O}$
. We say p is good for
![]() $(\mathfrak {C},\Delta )$
if
$(\mathfrak {C},\Delta )$
if
-
1. p is pretty good for G.
-
2.
 $Z({\mathscr D}(\Delta ^{0}))_k$
is smooth.
$Z({\mathscr D}(\Delta ^{0}))_k$
is smooth. -
3. p does not divide
 $\# N_{G_k}(\Delta _k)/\mathfrak {C}_k \Delta _k$
.
$\# N_{G_k}(\Delta _k)/\mathfrak {C}_k \Delta _k$
.
4.2 Basic properties
As the group schemes constituting a decomposition type are weakly reductive, we begin by recalling what we know about their centers and abelianizations.
Proposition 4.7. Let H be a weakly reductive group scheme over
![]() $\mathcal {O}$
.
$\mathcal {O}$
.
-
1. The center
 $Z(H)$
and abelianization
$Z(H)$
and abelianization
 $H^{\textrm {ab}}$
both exist as group schemes of multiplicative type over
$H^{\textrm {ab}}$
both exist as group schemes of multiplicative type over
 $\mathcal {O}$
.
$\mathcal {O}$
. -
2.
 $H^{\textrm {ab}}$
is smooth.
$H^{\textrm {ab}}$
is smooth. -
3. If
 $Z(H)$
is smooth, then the natural map
$Z(H)$
is smooth, then the natural map
 $Z(H)^0 \to H^{\textrm {ab},0}$
is an isogeny of tori. If
$Z(H)^0 \to H^{\textrm {ab},0}$
is an isogeny of tori. If
 $Z({\mathscr D}(H^{0}))$
is smooth, then this map is smooth.
$Z({\mathscr D}(H^{0}))$
is smooth, then this map is smooth.
Lemma 4.8. Let
![]() $(\mathfrak {C},\Delta )$
be a decomposition type over k. Then the quotient group scheme
$(\mathfrak {C},\Delta )$
be a decomposition type over k. Then the quotient group scheme
![]() $N_{G}(\mathfrak {C})/\mathfrak {C} \Delta = N_{G}(\Delta )/\mathfrak {C} \Delta $
is finite étale.
$N_{G}(\mathfrak {C})/\mathfrak {C} \Delta = N_{G}(\Delta )/\mathfrak {C} \Delta $
is finite étale.
Proof. Note that the quotient is well defined since
![]() $C_{G}(\Delta )=\mathfrak {C}$
and
$C_{G}(\Delta )=\mathfrak {C}$
and
![]() $C_{G}(\mathfrak {C})=\Delta $
. Since
$C_{G}(\mathfrak {C})=\Delta $
. Since
![]() $\mathfrak {C}$
and
$\mathfrak {C}$
and
![]() $\Delta $
are weakly reductive, the finiteness follows from Corollary 2.22.
$\Delta $
are weakly reductive, the finiteness follows from Corollary 2.22.
Lemma 4.9. Let
![]() $(\mathfrak {C}, \Delta )$
be a decomposition type for G over
$(\mathfrak {C}, \Delta )$
be a decomposition type for G over
![]() $\mathcal {O}$
. Then for any
$\mathcal {O}$
. Then for any
![]() $\mathcal {O}$
-algebra R,
$\mathcal {O}$
-algebra R,
![]() $N_{G(R)}(\mathfrak {C}(R))=N_{G(R)}(\Delta (R))$
. Moreover,
$N_{G(R)}(\mathfrak {C}(R))=N_{G(R)}(\Delta (R))$
. Moreover,
![]() $Z(\mathfrak {C})=Z(\Delta )$
.
$Z(\mathfrak {C})=Z(\Delta )$
.
Proof. This is basic group theory using Definition 4.1. For
![]() $\mathcal {O}$
-algebras R, if
$\mathcal {O}$
-algebras R, if
![]() $g \in G(R)$
normalizes
$g \in G(R)$
normalizes
![]() $\mathfrak {C}(R)$
, then it normalizes
$\mathfrak {C}(R)$
, then it normalizes
![]() $\Delta (R)=C_{G(R)}(\mathfrak {C}(R))$
, so
$\Delta (R)=C_{G(R)}(\mathfrak {C}(R))$
, so
![]() $N_{G(R)}(\mathfrak {C}(R)) \subset N_{G(R)}(\Delta (R))$
, and hence,
$N_{G(R)}(\mathfrak {C}(R)) \subset N_{G(R)}(\Delta (R))$
, and hence,
![]() $N_{G(R)}(\mathfrak {C}(R))=N_{G(R)}(\Delta (R))$
by symmetry. Note that for
$N_{G(R)}(\mathfrak {C}(R))=N_{G(R)}(\Delta (R))$
by symmetry. Note that for
![]() $\mathcal {O}$
-algebras R,
$\mathcal {O}$
-algebras R,
![]() $Z(\Delta )(R)=\Delta (R) \cap \mathfrak {C}(R)=Z(\mathfrak {C})(R)$
by Definition 4.1.
$Z(\Delta )(R)=\Delta (R) \cap \mathfrak {C}(R)=Z(\mathfrak {C})(R)$
by Definition 4.1.
Lemma 4.10. If
![]() $(\mathfrak {C},\Delta )$
is a decomposition type adapted to
$(\mathfrak {C},\Delta )$
is a decomposition type adapted to
![]() $\overline {\Lambda }$
, and
$\overline {\Lambda }$
, and
![]() $\Lambda $
is as in Proposition 4.12, then
$\Lambda $
is as in Proposition 4.12, then
![]() $C_{\Delta }(\Lambda )=Z(\Delta )$
.
$C_{\Delta }(\Lambda )=Z(\Delta )$
.
Proof. This is basic group theory using Definition 4.1: for
![]() $\mathcal {O}$
-algebras R, we see that
$\mathcal {O}$
-algebras R, we see that
![]() $C_{\Delta (R)}(\Lambda )=C_{G(R)}(\Lambda ) \cap \Delta (R)=\mathfrak {C}(R) \cap \Delta (R) \subset Z(\Delta (R)) = Z(\Delta )(R)$
.
$C_{\Delta (R)}(\Lambda )=C_{G(R)}(\Lambda ) \cap \Delta (R)=\mathfrak {C}(R) \cap \Delta (R) \subset Z(\Delta (R)) = Z(\Delta )(R)$
.
We also record a few useful properties about
![]() $C_G(\Lambda )$
for later use, where
$C_G(\Lambda )$
for later use, where
![]() $\Lambda $
is a constant group scheme whose order is invertible in
$\Lambda $
is a constant group scheme whose order is invertible in
![]() $\mathcal {O}$
(equivalently, the order of
$\mathcal {O}$
(equivalently, the order of
![]() $\Lambda $
is prime to p). We know it is
$\Lambda $
is prime to p). We know it is
![]() $\mathcal {O}$
-smooth and weakly reductive by Corollary 3.7.
$\mathcal {O}$
-smooth and weakly reductive by Corollary 3.7.
Lemma 4.11. If p is pretty good for G, then p is pretty good for
![]() $C_{G}(\Lambda )$
.
$C_{G}(\Lambda )$
.
Proof. It suffices to work over a field of characteristic p. By [Reference HerpelHer13, Theorem 3.3], p is pretty good if and only if the centralizer of every closed subgroup is smooth. Note
![]() $(G, C_G(\Lambda ))$
is a reductive pair in the sense of [Reference HerpelHer13, 2.7] since the
$(G, C_G(\Lambda ))$
is a reductive pair in the sense of [Reference HerpelHer13, 2.7] since the
![]() $\Lambda $
-isotypic decomposition of
$\Lambda $
-isotypic decomposition of
![]() $\operatorname {\mathrm {Lie}} G$
is stable under
$\operatorname {\mathrm {Lie}} G$
is stable under
![]() $C_G(\Lambda )$
. Using [Reference HerpelHer13, Lemma 3.6], if H is a closed subgroup of
$C_G(\Lambda )$
. Using [Reference HerpelHer13, Lemma 3.6], if H is a closed subgroup of
![]() $C_G(\Lambda )$
such that
$C_G(\Lambda )$
such that
![]() $C_G(H)$
is smooth, then
$C_G(H)$
is smooth, then
![]() $C_{C_G(\Lambda )}(H)$
is smooth as well. Since p is pretty good for G,
$C_{C_G(\Lambda )}(H)$
is smooth as well. Since p is pretty good for G,
![]() $C_G(H)$
is always smooth, and therefore,
$C_G(H)$
is always smooth, and therefore,
![]() $C_{C_G(\Lambda )}(H)$
is always smooth.
$C_{C_G(\Lambda )}(H)$
is always smooth.
Proposition 4.12. Let
![]() $(\mathfrak {C},\Delta )$
and
$(\mathfrak {C},\Delta )$
and
![]() $\overline {\Lambda }$
be as in Definition 4.2. Suppose that
$\overline {\Lambda }$
be as in Definition 4.2. Suppose that
![]() $\mathcal {O}$
is a complete DVR. Then there exists a subgroup
$\mathcal {O}$
is a complete DVR. Then there exists a subgroup
![]() $\Lambda \subset G(\mathcal {O})$
reducing to
$\Lambda \subset G(\mathcal {O})$
reducing to
![]() $\overline {\Lambda }$
such that
$\overline {\Lambda }$
such that
![]() $C_{G}(\Lambda )=\mathfrak {C}$
(hence, also
$C_{G}(\Lambda )=\mathfrak {C}$
(hence, also
![]() $C_{G}(C_{G}(\Lambda ))=\Delta $
).
$C_{G}(C_{G}(\Lambda ))=\Delta $
).
Proof. Note that
![]() $\overline {\Lambda } \subset \Delta (k)$
. Since
$\overline {\Lambda } \subset \Delta (k)$
. Since
![]() $\Delta $
is
$\Delta $
is
![]() $\mathcal {O}$
-smooth and
$\mathcal {O}$
-smooth and
![]() $\mathcal {O}$
is complete, there is a subgroup
$\mathcal {O}$
is complete, there is a subgroup
![]() $\Lambda \subset \Delta (\mathcal {O})$
lifting
$\Lambda \subset \Delta (\mathcal {O})$
lifting
![]() $\overline {\Lambda }$
. We have
$\overline {\Lambda }$
. We have
![]() $C_{G}(\Lambda ) \supset C_{G}(\Delta ) = \mathfrak {C}$
, which is an equality on special fibers. Since
$C_{G}(\Lambda ) \supset C_{G}(\Delta ) = \mathfrak {C}$
, which is an equality on special fibers. Since
![]() $\mathfrak {C}$
and
$\mathfrak {C}$
and
![]() $C_G(\Lambda )$
are smooth
$C_G(\Lambda )$
are smooth
![]() $\mathcal {O}$
-group schemes of the same dimension, it follows that
$\mathcal {O}$
-group schemes of the same dimension, it follows that
![]() $\mathfrak {C}^0 = C_G(\Lambda )^0$
: by the fibral isomorphism criterion, it is enough to show that if k is an algebraically closed field and
$\mathfrak {C}^0 = C_G(\Lambda )^0$
: by the fibral isomorphism criterion, it is enough to show that if k is an algebraically closed field and
![]() $H \subset H'$
is a closed embedding of reduced connected k-schemes of the same dimension, then
$H \subset H'$
is a closed embedding of reduced connected k-schemes of the same dimension, then
![]() $H = H'$
. For this, note that the natural map
$H = H'$
. For this, note that the natural map
![]() $H \to H'$
is dominant for dimension reasons, so it is surjective by closedness. Being a surjective closed embedding with reduced target, we find
$H \to H'$
is dominant for dimension reasons, so it is surjective by closedness. Being a surjective closed embedding with reduced target, we find
![]() $H = H'$
.
$H = H'$
.
In view of the previous paragraph, there is a monomorphism
![]() $\pi _0 \mathfrak {C} \hookrightarrow \pi _0 C_{G}(\Lambda )$
. Since
$\pi _0 \mathfrak {C} \hookrightarrow \pi _0 C_{G}(\Lambda )$
. Since
![]() $\pi _0 \mathfrak {C}_{k} = \pi _0 C_{G}(\Lambda )_{k}$
and both
$\pi _0 \mathfrak {C}_{k} = \pi _0 C_{G}(\Lambda )_{k}$
and both
![]() $\pi _0\mathfrak {C}$
and
$\pi _0\mathfrak {C}$
and
![]() $\pi _0C_{G}(\Lambda )$
are finite étale (by Corollary 3.7), it follows that
$\pi _0C_{G}(\Lambda )$
are finite étale (by Corollary 3.7), it follows that
![]() $\pi _0 \mathfrak {C} = \pi _0 C_{G}(\Lambda )$
, and hence,
$\pi _0 \mathfrak {C} = \pi _0 C_{G}(\Lambda )$
, and hence,
![]() $\mathfrak {C} = C_{G}(\Lambda )$
by the five lemma.
$\mathfrak {C} = C_{G}(\Lambda )$
by the five lemma.
Proposition 4.13. Let
![]() $(\mathfrak {C},\Delta )$
be a decomposition type adapted to
$(\mathfrak {C},\Delta )$
be a decomposition type adapted to
![]() $\overline {\Lambda }$
. Suppose that p is pretty good for G and
$\overline {\Lambda }$
. Suppose that p is pretty good for G and
![]() $Z({\mathscr D}(\Delta ^{0}))_k$
is smooth. Then
$Z({\mathscr D}(\Delta ^{0}))_k$
is smooth. Then
![]() $Z(\Delta )$
is smooth over
$Z(\Delta )$
is smooth over
![]() $\mathcal {O}$
, and the natural map
$\mathcal {O}$
, and the natural map
![]() $Z(\Delta )^0 \to \Delta ^{\textrm {ab},0}$
is a smooth isogeny of
$Z(\Delta )^0 \to \Delta ^{\textrm {ab},0}$
is a smooth isogeny of
![]() $\mathcal {O}$
-tori.
$\mathcal {O}$
-tori.
Proof. By hypothesis and Proposition 4.12, there is a group
![]() $\Lambda \subset G(\mathcal {O})$
such that
$\Lambda \subset G(\mathcal {O})$
such that
![]() $C_{G}(\Lambda )=\mathfrak {C}$
. To show the smoothness of
$C_{G}(\Lambda )=\mathfrak {C}$
. To show the smoothness of
![]() $Z(\Delta )$
, first note that
$Z(\Delta )$
, first note that
![]() $Z(\Delta )= Z(\mathfrak {C})=Z(C_{G}(\Lambda ))$
by Lemma 4.9. By Proposition 2.19, the smoothness of
$Z(\Delta )= Z(\mathfrak {C})=Z(C_{G}(\Lambda ))$
by Lemma 4.9. By Proposition 2.19, the smoothness of
![]() $Z(\Delta )$
would then follow from the smoothness of
$Z(\Delta )$
would then follow from the smoothness of
![]() $Z(C_{G}(\Lambda )^0)$
. As
$Z(C_{G}(\Lambda )^0)$
. As
![]() $Z(\Delta )$
is of multiplicative type and hence
$Z(\Delta )$
is of multiplicative type and hence
![]() $\mathcal {O}$
-flat, it suffices to check smoothness on fibers. But since p is pretty good for G, Lemma 4.11 and Remark 1.13 imply that
$\mathcal {O}$
-flat, it suffices to check smoothness on fibers. But since p is pretty good for G, Lemma 4.11 and Remark 1.13 imply that
![]() $Z(C_{G}(\Lambda )^0)$
is smooth. Thus,
$Z(C_{G}(\Lambda )^0)$
is smooth. Thus,
![]() $Z(\Delta )$
is smooth. By Proposition 4.7(3), it follows that the natural map
$Z(\Delta )$
is smooth. By Proposition 4.7(3), it follows that the natural map
![]() $Z(\Delta )^0 \to \Delta ^{\textrm {ab},0}$
is an isogeny of
$Z(\Delta )^0 \to \Delta ^{\textrm {ab},0}$
is an isogeny of
![]() $\mathcal {O}$
-tori. But
$\mathcal {O}$
-tori. But
![]() $Z({\mathscr D}(\Delta ^{0}))_k$
is smooth by assumption, so the isogeny is smooth by loc. cit.
$Z({\mathscr D}(\Delta ^{0}))_k$
is smooth by assumption, so the isogeny is smooth by loc. cit.
Proposition 4.14. Let
![]() $\overline {\Lambda }$
be as in Definition 4.2. Suppose that p is pretty good for G. Then there exists a decomposition type
$\overline {\Lambda }$
be as in Definition 4.2. Suppose that p is pretty good for G. Then there exists a decomposition type
![]() $(\mathfrak {C},\Delta )$
over
$(\mathfrak {C},\Delta )$
over
![]() $\mathcal {O}$
adapted to
$\mathcal {O}$
adapted to
![]() $\overline {\Lambda }$
.
$\overline {\Lambda }$
.
Proof. Fix a lift
![]() $\Lambda \subset G(\mathcal {O})$
of
$\Lambda \subset G(\mathcal {O})$
of
![]() $\overline {\Lambda }$
such that the natural map
$\overline {\Lambda }$
such that the natural map
![]() $\Lambda \to \overline {\Lambda }$
is an isomorphism. Let
$\Lambda \to \overline {\Lambda }$
is an isomorphism. Let
![]() $\mathfrak {C}=C_{G}(\Lambda )$
, and let
$\mathfrak {C}=C_{G}(\Lambda )$
, and let
![]() $\Delta =C_{G}(C_{G}(\Lambda ))$
. By Corollary 3.7,
$\Delta =C_{G}(C_{G}(\Lambda ))$
. By Corollary 3.7,
![]() $(\mathfrak {C},\Delta )$
is a decomposition type over
$(\mathfrak {C},\Delta )$
is a decomposition type over
![]() $\mathcal {O}$
adapted to
$\mathcal {O}$
adapted to
![]() $\overline {\Lambda }$
.
$\overline {\Lambda }$
.
5 Clifford theory
This section proves a result about lifting and extending representations that is the analog of Part 2 of the argument for
![]() $\operatorname {\mathrm {GL}}_n$
sketched in Section 1.2.
$\operatorname {\mathrm {GL}}_n$
sketched in Section 1.2.
5.1 Local Galois groups
Fix a local field F with residue characteristic
![]() $\ell \neq p$
. Let the residue field of F have size q, a power of
$\ell \neq p$
. Let the residue field of F have size q, a power of
![]() $\ell $
.
$\ell $
.
Lemma 5.1. The maximal tame extension of F has inertia group isomorphic to
![]() $\prod _{\ell ' \neq \ell } \mathbf Z_{\ell }$
. The Galois group of the maximal tame extension is a semi-direct product of the inertia group with
$\prod _{\ell ' \neq \ell } \mathbf Z_{\ell }$
. The Galois group of the maximal tame extension is a semi-direct product of the inertia group with
![]() $\widehat {\mathbf Z}$
, with
$\widehat {\mathbf Z}$
, with
![]() $\widehat {\mathbf Z}$
acting via the cyclotomic character. In particular, conjugation by the Frobenius is multiplication by q on
$\widehat {\mathbf Z}$
acting via the cyclotomic character. In particular, conjugation by the Frobenius is multiplication by q on
![]() $\prod _{\ell ' \neq \ell } \mathbf Z_{\ell }$
.
$\prod _{\ell ' \neq \ell } \mathbf Z_{\ell }$
.
Proof. This is standard.
Let
![]() $\Gamma _F$
be the absolute Galois group of F, and let
$\Gamma _F$
be the absolute Galois group of F, and let
![]() $I_F$
be the inertia group. Using Lemma 5.1, we may fix a surjection
$I_F$
be the inertia group. Using Lemma 5.1, we may fix a surjection
![]() $I_F \to \mathbf Z_p$
with kernel
$I_F \to \mathbf Z_p$
with kernel
![]() $\Lambda _F$
.
$\Lambda _F$
.
Lemma 5.2. The group
![]() $\Lambda _F$
is normal in
$\Lambda _F$
is normal in
![]() $\Gamma _F$
. The quotient
$\Gamma _F$
. The quotient
![]() $\Gamma _F / \Lambda _F$
is isomorphic to
$\Gamma _F / \Lambda _F$
is isomorphic to ![]() , where conjugating by
, where conjugating by
![]() $1 \in \widehat {\mathbf Z}$
is multiplication by q on
$1 \in \widehat {\mathbf Z}$
is multiplication by q on
![]() $\mathbf {Z}_p$
.
$\mathbf {Z}_p$
.
Proof. This is also well known.
Lemma 5.3. The exact sequence
is topologically split, so
![]() $\Gamma _F$
is a semi-direct product.
$\Gamma _F$
is a semi-direct product.
Proof. This is basically [Reference Clozel, Harris and TaylorCHT08, 2.4.10].
For the rest of this paper, fix a preimage
![]() $\sigma $
of a topological generator of
$\sigma $
of a topological generator of
![]() $\mathbf Z_p$
under the surjection
$\mathbf Z_p$
under the surjection
![]() $I_F \to \mathbf Z_p$
and a Frobenius
$I_F \to \mathbf Z_p$
and a Frobenius
![]() $\phi $
satisfying
$\phi $
satisfying
5.2
 $\nu $
-Tame extensions
$\nu $
-Tame extensions
Let
![]() $\mathcal {O}$
be the ring of integers in a p-adic field with residue field k and
$\mathcal {O}$
be the ring of integers in a p-adic field with residue field k and
![]() $\Delta $
be as in Definition 4.1. Recall Proposition 4.7. We write Z for
$\Delta $
be as in Definition 4.1. Recall Proposition 4.7. We write Z for
![]() $Z(\Delta )$
and write S for
$Z(\Delta )$
and write S for
![]() $\Delta ^{\textrm {ab}}$
, which are both multiplicative groups. The natural morphism
$\Delta ^{\textrm {ab}}$
, which are both multiplicative groups. The natural morphism
![]() $\nu : \Delta \to S$
restricts to an isogeny
$\nu : \Delta \to S$
restricts to an isogeny
![]() $Z \to S$
(also denoted by
$Z \to S$
(also denoted by
![]() $\nu $
). Let R be a complete local noetherian
$\nu $
). Let R be a complete local noetherian
![]() $\mathcal {O}$
-algebra with residue field k.
$\mathcal {O}$
-algebra with residue field k.
Definition 5.4. We say a homomorphism
![]() $\rho : I_F \to \Delta (R)$
is
$\rho : I_F \to \Delta (R)$
is
![]() $\nu $
-tame if for any
$\nu $
-tame if for any
![]() $\sigma \in I_F$
,
$\sigma \in I_F$
,
![]() $(\nu \circ \rho )(\sigma ) \in S(R)$
is of finite prime-to-p order.
$(\nu \circ \rho )(\sigma ) \in S(R)$
is of finite prime-to-p order.
We will prove the following:
Proposition 5.5. Given
![]() $\Delta $
as above. Assume that
$\Delta $
as above. Assume that
![]() $\nu \colon Z \to S$
is smooth. Given a continuous homomorphism
$\nu \colon Z \to S$
is smooth. Given a continuous homomorphism
![]() $\tau : \Lambda _F \to \Delta (R)$
such that
$\tau : \Lambda _F \to \Delta (R)$
such that
-
1.
 $\operatorname {\mathrm {ker}}\tau =\operatorname {\mathrm {ker}}{\overline {\tau }}$
(in particular, the image of
$\operatorname {\mathrm {ker}}\tau =\operatorname {\mathrm {ker}}{\overline {\tau }}$
(in particular, the image of
 $\tau $
is finite);
$\tau $
is finite); -
2.
 ${\overline {\tau }}^{\sigma } \cong {\overline {\tau }}$
for any
${\overline {\tau }}^{\sigma } \cong {\overline {\tau }}$
for any
 $\sigma \in I_F$
(i.e., the representations are conjugate by an element in
$\sigma \in I_F$
(i.e., the representations are conjugate by an element in
 $\Delta (k)$
);
$\Delta (k)$
); -
3.
 $C_{\Delta (R)}(\tau (\Lambda _F))=Z(R)$
;
$C_{\Delta (R)}(\tau (\Lambda _F))=Z(R)$
;
then
![]() $\tau $
admits a unique continuous,
$\tau $
admits a unique continuous,
![]() $\nu $
-tame extension to
$\nu $
-tame extension to
![]() $I_F$
.
$I_F$
.
We first establish some useful lemmas. Recall that for a group scheme H over
![]() $\mathcal {O}$
,
$\mathcal {O}$
,
![]() $\widehat {H}(R)$
is the kernel of the reduction map
$\widehat {H}(R)$
is the kernel of the reduction map
![]() $H(R) \to H(k)$
.
$H(R) \to H(k)$
.
Lemma 5.6. For any
![]() $\sigma \in I_F$
,
$\sigma \in I_F$
,
![]() $\tau ^{\sigma } \cong \tau $
(i.e., they are conjugate by an element in
$\tau ^{\sigma } \cong \tau $
(i.e., they are conjugate by an element in
![]() $\Delta (R)$
).
$\Delta (R)$
).
Proof. Note that
![]() $\mathrm {H}^1(\Lambda _F, \operatorname {\mathrm {ad}} {\overline {\tau }})=0$
since
$\mathrm {H}^1(\Lambda _F, \operatorname {\mathrm {ad}} {\overline {\tau }})=0$
since
![]() $\Lambda _F$
has pro-order prime to p and
$\Lambda _F$
has pro-order prime to p and
![]() $\operatorname {\mathrm {ad}} {\overline {\tau }}$
has order a power of p. Therefore, if
$\operatorname {\mathrm {ad}} {\overline {\tau }}$
has order a power of p. Therefore, if
![]() $\tau ': \Lambda _F \to \Delta (R)$
is another continuous lift of
$\tau ': \Lambda _F \to \Delta (R)$
is another continuous lift of
![]() ${\overline {\tau }}$
, then
${\overline {\tau }}$
, then
![]() $\tau '$
is
$\tau '$
is
![]() $\widehat {\Delta }(R)$
-conjugate to
$\widehat {\Delta }(R)$
-conjugate to
![]() $\tau $
. (See [Reference TilouineTil96, §3] for deformation theory in this level of generality.) By assumption for
$\tau $
. (See [Reference TilouineTil96, §3] for deformation theory in this level of generality.) By assumption for
![]() $\sigma \in I_F$
, we have
$\sigma \in I_F$
, we have
![]() ${\overline {\tau }}^{\sigma } \cong {\overline {\tau }}$
(i.e.,
${\overline {\tau }}^{\sigma } \cong {\overline {\tau }}$
(i.e.,
![]() ${\overline {\tau }}^{\sigma } = \bar g {\overline {\tau }} \bar g^{-1}$
for some
${\overline {\tau }}^{\sigma } = \bar g {\overline {\tau }} \bar g^{-1}$
for some
![]() $\bar g \in \Delta (k)$
). As
$\bar g \in \Delta (k)$
). As
![]() $\Delta $
is
$\Delta $
is
![]() $\mathcal {O}$
-smooth, there exists a lift
$\mathcal {O}$
-smooth, there exists a lift
![]() $g \in \Delta (R)$
of
$g \in \Delta (R)$
of
![]() $\bar g$
. Now both
$\bar g$
. Now both
![]() $\tau ^{\sigma }$
and
$\tau ^{\sigma }$
and
![]() $g \tau g^{-1}$
reduce to
$g \tau g^{-1}$
reduce to
![]() ${\overline {\tau }}^{\sigma }$
, and hence, they are
${\overline {\tau }}^{\sigma }$
, and hence, they are
![]() $\widehat \Delta (R)$
-conjugate. Thus,
$\widehat \Delta (R)$
-conjugate. Thus,
![]() $\tau ^\sigma \cong \tau $
.
$\tau ^\sigma \cong \tau $
.
Lemma 5.7. If H is a smooth group scheme over
![]() $\mathcal {O}$
, then
$\mathcal {O}$
, then
![]() $\widehat {H}(R)=\widehat {H^0}(R)$
for any
$\widehat {H}(R)=\widehat {H^0}(R)$
for any
![]() $\mathcal {O}$
-algebra R.
$\mathcal {O}$
-algebra R.
Proof. If an R-point reduces to the identity, it lies in the identity component of H.
Lemma 5.8. The group
![]() $S(R)$
is the product of
$S(R)$
is the product of
![]() $\widehat {S}(R)$
and a finite group whose order is prime to p.
$\widehat {S}(R)$
and a finite group whose order is prime to p.
Proof. Recall that S is smooth multiplicative by Proposition 4.7. In particular,
![]() $S(k)$
has order prime to p. Consider the exact sequence of groups
$S(k)$
has order prime to p. Consider the exact sequence of groups
Lemma 5.7 implies that
![]() $\widehat S(R)=\widehat {S^0}(R)$
, the latter is pro-p. Then since S is commutative,
$\widehat S(R)=\widehat {S^0}(R)$
, the latter is pro-p. Then since S is commutative,
![]() $S(R)$
is the product of the pro-p group
$S(R)$
is the product of the pro-p group
![]() $\widehat {S^0}(R)$
and the Teichmuller lifts of elements in
$\widehat {S^0}(R)$
and the Teichmuller lifts of elements in
![]() $S(k)$
.
$S(k)$
.
Lemma 5.9. The map
![]() $\nu \colon \widehat {Z}(R) \to \widehat {S}(R)$
is an isomorphism.
$\nu \colon \widehat {Z}(R) \to \widehat {S}(R)$
is an isomorphism.
Proof. By the completeness of R, it suffices to prove the following: suppose A is a local Artinian
![]() $\mathcal {O}$
-algebra and
$\mathcal {O}$
-algebra and
![]() $I \subset A$
is a nilpotent ideal. Let
$I \subset A$
is a nilpotent ideal. Let
![]() $z \in Z(A/I)$
and
$z \in Z(A/I)$
and
![]() $s \in S(A/I)$
be such that
$s \in S(A/I)$
be such that
![]() $\nu (z)=s$
. Then for any
$\nu (z)=s$
. Then for any
![]() $\tilde s \in S(A)$
mapping to
$\tilde s \in S(A)$
mapping to
![]() $s \in S(A/I)$
, there exists a unique element
$s \in S(A/I)$
, there exists a unique element
![]() $\tilde z \in Z(A)$
mapping to
$\tilde z \in Z(A)$
mapping to
![]() $z \in Z(A/I)$
such that
$z \in Z(A/I)$
such that
![]() $\nu (\tilde z)=\tilde s$
. By assumption,
$\nu (\tilde z)=\tilde s$
. By assumption,
![]() $\nu \colon Z \to S$
is a smooth isogeny of multiplicative groups; in particular, it is étale, so the above follows immediately from the infinitesimal criterion for étale morphisms.
$\nu \colon Z \to S$
is a smooth isogeny of multiplicative groups; in particular, it is étale, so the above follows immediately from the infinitesimal criterion for étale morphisms.
Proof of Proposition 5.5.
A continuous extension of
![]() $\tau $
to
$\tau $
to
![]() $I_F$
is determined by its value on
$I_F$
is determined by its value on
![]() $\sigma $
, a chosen topological generator of the
$\sigma $
, a chosen topological generator of the
![]() $\mathbf {Z}_p$
-part of the tame inertia. By Lemma 5.6, there is an
$\mathbf {Z}_p$
-part of the tame inertia. By Lemma 5.6, there is an
![]() $A \in \Delta (R)$
such that for
$A \in \Delta (R)$
such that for
![]() $g \in \Lambda _F$
,
$g \in \Lambda _F$
,
As
![]() ${\overline {\tau }}$
is continuous, it factors through a finite quotient, so there is a power
${\overline {\tau }}$
is continuous, it factors through a finite quotient, so there is a power
![]() $p^b$
such that
$p^b$
such that
![]() ${\overline {\tau }}^{\sigma ^{p^b}}={\overline {\tau }}$
as
${\overline {\tau }}^{\sigma ^{p^b}}={\overline {\tau }}$
as
![]() $\sigma $
has pro-p order.
$\sigma $
has pro-p order.
Since
![]() $\operatorname {\mathrm {ker}}\tau =\ker {\overline {\tau }}$
, we see that for all
$\operatorname {\mathrm {ker}}\tau =\ker {\overline {\tau }}$
, we see that for all
![]() $g \in \Lambda _F$
,
$g \in \Lambda _F$
,
It follows that
![]() $A^{p^b} \in C_{\Delta (R)}(\tau (\Lambda _F))$
, which equals
$A^{p^b} \in C_{\Delta (R)}(\tau (\Lambda _F))$
, which equals
![]() $Z(R)$
by assumption. As k is perfect and Z is multiplicative, the p-th power map is an automorphism of
$Z(R)$
by assumption. As k is perfect and Z is multiplicative, the p-th power map is an automorphism of
![]() $Z(k)$
. We can then modify A by a lift of an appropriate element of
$Z(k)$
. We can then modify A by a lift of an appropriate element of
![]() $Z(k)$
so that
$Z(k)$
so that
![]() $A^{p^b}$
reduces to the identity. By Lemma 5.8 and (the surjectivity part of) Lemma 5.9, we can further multiply A by an element in
$A^{p^b}$
reduces to the identity. By Lemma 5.8 and (the surjectivity part of) Lemma 5.9, we can further multiply A by an element in
![]() $\widehat {Z}(R)$
so that
$\widehat {Z}(R)$
so that
![]() $\nu (A)$
has finite prime-to-p order. We can now obtain a continuous,
$\nu (A)$
has finite prime-to-p order. We can now obtain a continuous,
![]() $\nu $
-tame extension
$\nu $
-tame extension
![]() $\tau : I_F \to \Delta (R)$
by sending
$\tau : I_F \to \Delta (R)$
by sending
![]() $\sigma $
to A.
$\sigma $
to A.
It remains to show this extension is unique. Suppose another (continuous and
![]() $\nu $
-tame) extension sends
$\nu $
-tame) extension sends
![]() $\sigma $
to
$\sigma $
to
![]() $B \in \Delta (R)$
. Note that
$B \in \Delta (R)$
. Note that
![]() $BA^{-1}$
commutes with
$BA^{-1}$
commutes with
![]() $\tau (\Lambda _F)$
so
$\tau (\Lambda _F)$
so ![]() . By continuity, there is a power
. By continuity, there is a power
![]() $p^b$
such that
$p^b$
such that
![]() $A^{p^b}$
and
$A^{p^b}$
and
![]() $B^{p^b}$
reduce to the identity in
$B^{p^b}$
reduce to the identity in
![]() $\Delta (k)$
, and hence,
$\Delta (k)$
, and hence,
![]() $z^{p^b}$
does as well. Hence, z reduces to the identity as the p-th power map is an automorphism of
$z^{p^b}$
does as well. Hence, z reduces to the identity as the p-th power map is an automorphism of
![]() $Z(k)$
. Since both extensions are
$Z(k)$
. Since both extensions are
![]() $\nu $
-tame, we see that
$\nu $
-tame, we see that
![]() $\nu (z)$
has finite order relatively prime to p. Since
$\nu (z)$
has finite order relatively prime to p. Since
![]() $\nu (z)$
also reduces to the identity, we see that
$\nu (z)$
also reduces to the identity, we see that
![]() $\nu (z)=1$
. By Lemma 5.9,
$\nu (z)=1$
. By Lemma 5.9,
![]() $\nu : \widehat {Z}(R) \to \widehat {S}(R)$
is injective. We conclude that
$\nu : \widehat {Z}(R) \to \widehat {S}(R)$
is injective. We conclude that
![]() $z=1$
, and hence, the extensions are the same.
$z=1$
, and hence, the extensions are the same.
Remark 5.10. We call this step in the argument ‘Clifford theory’ as the analogous step for
![]() $\operatorname {\mathrm {GL}}_n$
[Reference Clozel, Harris and TaylorCHT08, Lemma 2.4.11] makes use of ideas from Clifford theory (see [Reference Curtis and ReinerCR81, §11]).
$\operatorname {\mathrm {GL}}_n$
[Reference Clozel, Harris and TaylorCHT08, Lemma 2.4.11] makes use of ideas from Clifford theory (see [Reference Curtis and ReinerCR81, §11]).
6 Lifts and minimally ramified deformations
As before, let F be a local field of residue characteristic
![]() $\ell \neq p$
and G be a weakly reductive group scheme over a p-adic ring of integers
$\ell \neq p$
and G be a weakly reductive group scheme over a p-adic ring of integers
![]() $\mathcal {O}$
with residue field k.
$\mathcal {O}$
with residue field k.
6.1 Lifting residual representations
Recall the terminology for decomposition types from Definitions 4.1 and 4.2. We will prove the following theorem over the course of this subsection.
Theorem 6.1. Let
![]() ${\overline {\rho }} : \Gamma _F \to G(k)$
be a continuous homomorphism. Suppose there exists a decomposition type
${\overline {\rho }} : \Gamma _F \to G(k)$
be a continuous homomorphism. Suppose there exists a decomposition type
![]() $(\mathfrak {C},\Delta )$
over
$(\mathfrak {C},\Delta )$
over
![]() $\mathcal {O}$
adapted to
$\mathcal {O}$
adapted to
![]() ${\overline {\rho }}(\Lambda _F)$
. Suppose that p is good for the decomposition type
${\overline {\rho }}(\Lambda _F)$
. Suppose that p is good for the decomposition type
![]() $(\mathfrak {C},\Delta )$
. Then there exists a continuous homomorphism
$(\mathfrak {C},\Delta )$
. Then there exists a continuous homomorphism
![]() $\rho : \Gamma _F \to G(\mathcal {O})$
that lifts
$\rho : \Gamma _F \to G(\mathcal {O})$
that lifts
![]() ${\overline {\rho }}$
such that
${\overline {\rho }}$
such that
![]() $C_{G}(\rho (I_F))$
is
$C_{G}(\rho (I_F))$
is
![]() $\mathcal {O}$
-smooth.
$\mathcal {O}$
-smooth.
Remark 6.2. The proof will also show that
![]() $\rho (\Lambda _F) \subset \Delta (\mathcal {O})$
and give some control over the ‘inertial type’ of the lift. We remark that the
$\rho (\Lambda _F) \subset \Delta (\mathcal {O})$
and give some control over the ‘inertial type’ of the lift. We remark that the
![]() $\mathcal {O}$
-smoothness of
$\mathcal {O}$
-smoothness of
![]() $C_{G}(\rho (I_F))$
is crucial for identifying a formally smooth component of the deformation ring; see Theorem 6.16. In the course of the proof, we will construct ‘many’ lifts parameterized by an element
$C_{G}(\rho (I_F))$
is crucial for identifying a formally smooth component of the deformation ring; see Theorem 6.16. In the course of the proof, we will construct ‘many’ lifts parameterized by an element
![]() $z \in \mathfrak {C}^0(\mathcal {O})$
. This is not strictly necessary for the proof, and in fact, one can take z to be the identity element throughout this subsection. However, we use this z to build flexibility into our argument and allow inertial types that are not minimally ramified, which correspond to other components of the deformation ring.
$z \in \mathfrak {C}^0(\mathcal {O})$
. This is not strictly necessary for the proof, and in fact, one can take z to be the identity element throughout this subsection. However, we use this z to build flexibility into our argument and allow inertial types that are not minimally ramified, which correspond to other components of the deformation ring.
Set ![]() , and let
, and let ![]() . As the decomposition type is adapted to
. As the decomposition type is adapted to
![]() ${\overline {\rho }}(\Lambda _F)$
, by Proposition 4.12, there exists
${\overline {\rho }}(\Lambda _F)$
, by Proposition 4.12, there exists
![]() $\Lambda \subset \Delta (\mathcal {O})$
lifting
$\Lambda \subset \Delta (\mathcal {O})$
lifting
![]() $\overline {\Lambda }$
such that
$\overline {\Lambda }$
such that
![]() $C_G(\Lambda )= \mathfrak {C}$
and
$C_G(\Lambda )= \mathfrak {C}$
and
![]() $\Delta = C_G(\mathfrak {C})$
. As the pro-order of
$\Delta = C_G(\mathfrak {C})$
. As the pro-order of
![]() $\Lambda _F$
is prime to p, there is also a lift
$\Lambda _F$
is prime to p, there is also a lift
![]() $\tau : \Lambda _F \to \Delta (\mathcal {O})$
of
$\tau : \Lambda _F \to \Delta (\mathcal {O})$
of
![]() ${\overline {\rho }}|_{\Lambda _F}$
with
${\overline {\rho }}|_{\Lambda _F}$
with
![]() $\ker (\tau ) = \ker (\overline {\rho }|_{\Lambda _F})$
. Thus,
$\ker (\tau ) = \ker (\overline {\rho }|_{\Lambda _F})$
. Thus,
![]() $\Lambda = \tau (\Lambda _F)$
.
$\Lambda = \tau (\Lambda _F)$
.
Lemma 6.3. The order of
![]() $\pi _0C_{G}(\Lambda )$
is prime to p.
$\pi _0C_{G}(\Lambda )$
is prime to p.
Proof. This follows from Corollary 3.7.
Lemma 6.4. We have that
![]() $N_{G}(\Lambda ) \subset N_{G}(\Delta )$
.
$N_{G}(\Lambda ) \subset N_{G}(\Delta )$
.
Proof. Any point of
![]() $N_{G}({\Lambda })$
normalizes
$N_{G}({\Lambda })$
normalizes
![]() ${\Lambda }$
and hence normalizes
${\Lambda }$
and hence normalizes
![]() $C_{G}(\Lambda )$
and therefore normalizes
$C_{G}(\Lambda )$
and therefore normalizes
![]() $C_{G}(C_{G}(\Lambda ))=\Delta $
.
$C_{G}(C_{G}(\Lambda ))=\Delta $
.
As in Section 5.1, fix a preimage
![]() $\sigma $
of a topological generator of
$\sigma $
of a topological generator of
![]() $\mathbf Z_p$
under the surjection
$\mathbf Z_p$
under the surjection
![]() $I_F \to \mathbf Z_p$
and a Frobenius
$I_F \to \mathbf Z_p$
and a Frobenius
![]() $\phi $
satisfying
$\phi $
satisfying
where q is the size of the residue field of F (a power of
![]() $\ell $
). As
$\ell $
). As
![]() $\sigma $
and
$\sigma $
and
![]() $\phi $
normalize
$\phi $
normalize
![]() $\Lambda _F$
,
$\Lambda _F$
,
![]() ${\overline {\rho }}(\sigma )$
and
${\overline {\rho }}(\sigma )$
and
![]() ${\overline {\rho }}(\phi )$
belong to
${\overline {\rho }}(\phi )$
belong to
![]() $N_{G(k)}(\overline {\Lambda })$
. Then Lemma 6.4 shows that
$N_{G(k)}(\overline {\Lambda })$
. Then Lemma 6.4 shows that
![]() ${\overline {\rho }}(\sigma )$
and
${\overline {\rho }}(\sigma )$
and
![]() ${\overline {\rho }}(\phi )$
are contained in
${\overline {\rho }}(\phi )$
are contained in ![]() . As
. As
![]() $I_F/\Lambda _F$
is pro-p and p does not divide the index of
$I_F/\Lambda _F$
is pro-p and p does not divide the index of
![]() $\Delta (k) \mathfrak {C}(k)$
in
$\Delta (k) \mathfrak {C}(k)$
in
![]() $\mathcal {N}(k)$
as p is good for the decomposition type, it follows that
$\mathcal {N}(k)$
as p is good for the decomposition type, it follows that
![]() ${\overline {\rho }}(\sigma ) \in \Delta (k) \cdot \mathfrak {C}(k)$
.
${\overline {\rho }}(\sigma ) \in \Delta (k) \cdot \mathfrak {C}(k)$
.
Recall the morphism
![]() $\nu : \Delta \to \Delta ^{\textrm {ab}}$
and the notion of
$\nu : \Delta \to \Delta ^{\textrm {ab}}$
and the notion of
![]() $\nu $
-tameness from Definition 5.4.
$\nu $
-tameness from Definition 5.4.
Proposition 6.5. There is a continuous,
![]() $\nu $
-tame extension of
$\nu $
-tame extension of
![]() $\tau $
to a homomorphism
$\tau $
to a homomorphism
We use
![]() $\tau $
and
$\tau $
and
![]() ${\overline {\tau }}$
to denote the extensions as well as the functions originally defined on
${\overline {\tau }}$
to denote the extensions as well as the functions originally defined on
![]() $\Lambda _F$
.
$\Lambda _F$
.
Proof. We will apply Proposition 5.5 with
![]() $R=\mathcal {O}$
. First, since p is good for the decomposition type, Proposition 4.13 implies that
$R=\mathcal {O}$
. First, since p is good for the decomposition type, Proposition 4.13 implies that
![]() $\nu : Z(\Delta )^0 \to \Delta ^{\textrm {ab},0}$
is smooth. It remains to check the three hypotheses. The first is built into the construction of
$\nu : Z(\Delta )^0 \to \Delta ^{\textrm {ab},0}$
is smooth. It remains to check the three hypotheses. The first is built into the construction of
![]() $\tau $
. Since
$\tau $
. Since
![]() ${\overline {\rho }}(\sigma ) \in \Delta (k) \cdot \mathfrak {C}(k)$
and
${\overline {\rho }}(\sigma ) \in \Delta (k) \cdot \mathfrak {C}(k)$
and
![]() $\Delta $
and
$\Delta $
and
![]() $\mathfrak {C}$
commute, it follows that
$\mathfrak {C}$
commute, it follows that
![]() ${\overline {\tau }}^{\sigma }={\overline {\rho }}(\sigma ) {\overline {\tau }} \, {\overline {\rho }}(\sigma )^{-1}$
and
${\overline {\tau }}^{\sigma }={\overline {\rho }}(\sigma ) {\overline {\tau }} \, {\overline {\rho }}(\sigma )^{-1}$
and
![]() ${\overline {\tau }}$
are isomorphic as
${\overline {\tau }}$
are isomorphic as
![]() $\Delta (k)$
-valued representations, whence the second condition. Lemma 4.10 gives the third condition.
$\Delta (k)$
-valued representations, whence the second condition. Lemma 4.10 gives the third condition.
Corollary 6.6. We have
![]() ${\overline {\tau }}^{\phi }={\overline {\rho }}(\phi ) \cdot {\overline {\tau }} \cdot {\overline {\rho }}(\phi )^{-1}$
on
${\overline {\tau }}^{\phi }={\overline {\rho }}(\phi ) \cdot {\overline {\tau }} \cdot {\overline {\rho }}(\phi )^{-1}$
on
![]() $I_F$
.
$I_F$
.
Proof. Since
![]() ${\overline {\rho }}(\phi ) \in N_{G(k)}(\Delta (k))$
, this is a consequence of the uniqueness part of Proposition 5.5.
${\overline {\rho }}(\phi ) \in N_{G(k)}(\Delta (k))$
, this is a consequence of the uniqueness part of Proposition 5.5.
We next analyze
![]() ${\overline {\rho }}$
as a combination of
${\overline {\rho }}$
as a combination of
![]() ${\overline {\tau }}$
(valued in
${\overline {\tau }}$
(valued in
![]() $\Delta $
) and a representation valued in
$\Delta $
) and a representation valued in
![]() $\mathfrak {C}^0$
.
$\mathfrak {C}^0$
.
Proposition 6.7. Continuing the standing assumptions:
-
1. There is a continuous homomorphism
 ${\overline {\omega }}: I_F/\Lambda _F \to \mathfrak {C}^0(k)$
such that
${\overline {\omega }}: I_F/\Lambda _F \to \mathfrak {C}^0(k)$
such that  $$\begin{align*}{\overline{\rho}}|_{I_F}={\overline{\tau}} \cdot {\overline{\omega}} = {\overline{\omega}} \cdot {\overline{\tau}}. \end{align*}$$
$$\begin{align*}{\overline{\rho}}|_{I_F}={\overline{\tau}} \cdot {\overline{\omega}} = {\overline{\omega}} \cdot {\overline{\tau}}. \end{align*}$$
-
2. The element
 ${\overline {\omega }}(\sigma )$
is unipotent, and there exists a pure fiberwise unipotent
${\overline {\omega }}(\sigma )$
is unipotent, and there exists a pure fiberwise unipotent
 $u \in \mathfrak {C}^0(\mathcal {O})$
lifting
$u \in \mathfrak {C}^0(\mathcal {O})$
lifting
 ${\overline {\omega }}(\sigma )$
.
${\overline {\omega }}(\sigma )$
. -
3. For any element
 $z \in \mathfrak {C}^0(\mathcal {O})$
which reduces to the identity in
$z \in \mathfrak {C}^0(\mathcal {O})$
which reduces to the identity in
 $\mathfrak {C}^0(k)$
and commutes with u, define a homomorphism
$\mathfrak {C}^0(k)$
and commutes with u, define a homomorphism
 $\omega _z : I_F / \Lambda _F \to \mathfrak {C}^0(\mathcal {O})$
sending
$\omega _z : I_F / \Lambda _F \to \mathfrak {C}^0(\mathcal {O})$
sending
 $\sigma $
to
$\sigma $
to
 $z u$
. The function
$z u$
. The function
 $ \tau \cdot \omega _z : I_F \to \Delta (\mathcal {O}) \mathfrak {C}^0(\mathcal {O}) \subset G(\mathcal {O})$
is a continuous homomorphism lifting
$ \tau \cdot \omega _z : I_F \to \Delta (\mathcal {O}) \mathfrak {C}^0(\mathcal {O}) \subset G(\mathcal {O})$
is a continuous homomorphism lifting
 $\overline {\rho }|_{I_F}$
.
$\overline {\rho }|_{I_F}$
.
(At a first reading, it is fine to take z to be the identity.)
Proof. We define ![]() . For any
. For any
![]() $g \in I_F$
and for any
$g \in I_F$
and for any
![]() $h \in \Lambda _F$
,
$h \in \Lambda _F$
,
where the second equality holds because
![]() $ghg^{-1} \in \Lambda _F$
and
$ghg^{-1} \in \Lambda _F$
and
![]() ${\overline {\rho }}|_{\Lambda _F}={\overline {\tau }}|_{\Lambda _F}$
. Thus,
${\overline {\rho }}|_{\Lambda _F}={\overline {\tau }}|_{\Lambda _F}$
. Thus,
![]() ${\overline {\omega }}$
is valued in
${\overline {\omega }}$
is valued in
![]() $C_{G_{k}}(\overline {\Lambda })(k)$
. Since
$C_{G_{k}}(\overline {\Lambda })(k)$
. Since
![]() $I_F/\Lambda _F$
is pro-p and
$I_F/\Lambda _F$
is pro-p and
![]() $\pi _0C_{G_{k}}(\overline {\Lambda })$
has order prime to p by Lemma 6.3,
$\pi _0C_{G_{k}}(\overline {\Lambda })$
has order prime to p by Lemma 6.3,
![]() ${\overline {\omega }}$
is valued in
${\overline {\omega }}$
is valued in
![]() $C_{G}(\overline {\Lambda })^0(k)=\mathfrak {C}^0(k)$
, with the equality following from Definition 4.2.
$C_{G}(\overline {\Lambda })^0(k)=\mathfrak {C}^0(k)$
, with the equality following from Definition 4.2.
Moreover, for any
![]() $g,h \in I_F$
, we see that
$g,h \in I_F$
, we see that
where the third equality uses that
![]() ${\overline {\tau }}(g)^{-1}{\overline {\rho }}(g)={\overline {\omega }}(g) \in C_{G_{k}}(\overline {\Lambda })(k)=\mathfrak {C}(k)$
commutes with
${\overline {\tau }}(g)^{-1}{\overline {\rho }}(g)={\overline {\omega }}(g) \in C_{G_{k}}(\overline {\Lambda })(k)=\mathfrak {C}(k)$
commutes with
![]() ${\overline {\tau }}(h)^{-1} \in \Delta (k)$
(Definition 4.1). So
${\overline {\tau }}(h)^{-1} \in \Delta (k)$
(Definition 4.1). So
![]() ${\overline {\omega }}$
is a group homomorphism. It is continuous because both
${\overline {\omega }}$
is a group homomorphism. It is continuous because both
![]() ${\overline {\rho }}|_{I_F}$
and
${\overline {\rho }}|_{I_F}$
and
![]() ${\overline {\tau }}$
are continuous.
${\overline {\tau }}$
are continuous.
Second, we show that
![]() ${\overline {\omega }}(\sigma )$
is unipotent. This element decomposes as a commuting product of semisimple and unipotent elements of
${\overline {\omega }}(\sigma )$
is unipotent. This element decomposes as a commuting product of semisimple and unipotent elements of
![]() $\mathfrak {C}^0(k)$
. The order of a semisimple element in
$\mathfrak {C}^0(k)$
. The order of a semisimple element in
![]() $\mathfrak {C}^0(k)$
is prime to p, while by continuity, there is an
$\mathfrak {C}^0(k)$
is prime to p, while by continuity, there is an
![]() $r \geq 0$
such that
$r \geq 0$
such that
![]() $\sigma ^{p^r} \in \ker {\overline {\omega }}$
. Thus,
$\sigma ^{p^r} \in \ker {\overline {\omega }}$
. Thus,
![]() ${\overline {\omega }}(\sigma )$
is unipotent. By Lemma 3.14, there exists a pure unipotent in
${\overline {\omega }}(\sigma )$
is unipotent. By Lemma 3.14, there exists a pure unipotent in
![]() $\mathfrak {C}^0(\mathcal {O})$
lifting
$\mathfrak {C}^0(\mathcal {O})$
lifting
![]() ${\overline {\rho }}(\sigma )$
.
${\overline {\rho }}(\sigma )$
.
For the last statement, note that
![]() $\omega _z$
is continuous as the image of a topological generator of
$\omega _z$
is continuous as the image of a topological generator of
![]() ${I_F /\Lambda _F \simeq \mathbf Z_p}$
reduces to a unipotent element. The function
${I_F /\Lambda _F \simeq \mathbf Z_p}$
reduces to a unipotent element. The function
![]() $\tau \cdot \omega _z$
is a homomorphism as
$\tau \cdot \omega _z$
is a homomorphism as
![]() $\Delta $
and
$\Delta $
and
![]() $\mathfrak {C}^0$
commute.
$\mathfrak {C}^0$
commute.
Definition 6.8. For z as above, define
![]() $\theta _z : I_F \to \Delta (\mathcal {O}) \mathfrak {C}^0(\mathcal {O})$
to be the product
$\theta _z : I_F \to \Delta (\mathcal {O}) \mathfrak {C}^0(\mathcal {O})$
to be the product
![]() $\tau \cdot \omega _z$
.
$\tau \cdot \omega _z$
.
Note that
![]() $\bar \theta ^{\phi }_z= {\overline {\rho }}^{\phi } |_{I_F} = {\overline {\rho }}(\phi ) \cdot \bar \theta _z \cdot {\overline {\rho }}(\phi )^{-1}$
. Corollary 6.6 implies that
$\bar \theta ^{\phi }_z= {\overline {\rho }}^{\phi } |_{I_F} = {\overline {\rho }}(\phi ) \cdot \bar \theta _z \cdot {\overline {\rho }}(\phi )^{-1}$
. Corollary 6.6 implies that
![]() ${\overline {\omega }}^{\phi }={\overline {\rho }}(\phi ) \cdot {\overline {\omega }} \cdot {\overline {\rho }}(\phi )^{-1}$
, hence using the structure of
${\overline {\omega }}^{\phi }={\overline {\rho }}(\phi ) \cdot {\overline {\omega }} \cdot {\overline {\rho }}(\phi )^{-1}$
, hence using the structure of
![]() $\Gamma _F/\Lambda _F$
from Lemma 5.2 that
$\Gamma _F/\Lambda _F$
from Lemma 5.2 that
Lemma 6.9. Continuing the standing assumptions, there exists
![]() $n \in G(\mathcal {O})$
lifting
$n \in G(\mathcal {O})$
lifting
![]() ${\overline {\rho }}(\phi )$
such that
${\overline {\rho }}(\phi )$
such that
-
1.
 $\tau ^\phi = n \tau n^{-1}$
on
$\tau ^\phi = n \tau n^{-1}$
on
 $I_F$
and
$I_F$
and -
2.
 $u^q = n u n^{-1}$
.
$u^q = n u n^{-1}$
.
Proof. There exists an element
![]() $n \in G(\mathcal {O})$
lifting
$n \in G(\mathcal {O})$
lifting
![]() ${\overline {\rho }}(\phi )$
as G is
${\overline {\rho }}(\phi )$
as G is
![]() $\mathcal {O}$
-smooth. Since the mod-p reductions of
$\mathcal {O}$
-smooth. Since the mod-p reductions of
![]() $\tau ^{\phi }$
and
$\tau ^{\phi }$
and
![]() $n \tau n^{-1}$
agree on
$n \tau n^{-1}$
agree on
![]() $\Lambda _F$
and
$\Lambda _F$
and
![]() $\Lambda _F$
is prime to p, we may and do multiply n by an element in
$\Lambda _F$
is prime to p, we may and do multiply n by an element in
![]() $\widehat G(\mathcal {O})$
so that
$\widehat G(\mathcal {O})$
so that
![]() $\tau ^{\phi }=n \tau n^{-1}$
on
$\tau ^{\phi }=n \tau n^{-1}$
on
![]() $\Lambda _F$
. In particular, using Lemma 6.4, we see that
$\Lambda _F$
. In particular, using Lemma 6.4, we see that
![]() $n \in N_{G(\mathcal {O})}(\Lambda ) \subset N_{G(\mathcal {O})}(\Delta (\mathcal {O}))$
.
$n \in N_{G(\mathcal {O})}(\Lambda ) \subset N_{G(\mathcal {O})}(\Delta (\mathcal {O}))$
.
Since
![]() $\tau $
is
$\tau $
is
![]() $\nu $
-tame, so is
$\nu $
-tame, so is
![]() $\tau ^{\phi }$
. However,
$\tau ^{\phi }$
. However,
![]() $\operatorname {\mathrm {Ad}} n: \Delta _{\mathcal {O}} \to \Delta _{\mathcal {O}}$
induces an automorphism
$\operatorname {\mathrm {Ad}} n: \Delta _{\mathcal {O}} \to \Delta _{\mathcal {O}}$
induces an automorphism
![]() $A: \Delta ^{\textrm {ab}}_{\mathcal {O}} \to \Delta ^{\textrm {ab}}_{\mathcal {O}}$
with
$A: \Delta ^{\textrm {ab}}_{\mathcal {O}} \to \Delta ^{\textrm {ab}}_{\mathcal {O}}$
with
![]() $\nu \circ \operatorname {\mathrm {Ad}} n = A \circ \nu $
by natural properties of the abelianization map
$\nu \circ \operatorname {\mathrm {Ad}} n = A \circ \nu $
by natural properties of the abelianization map
![]() $\nu : \Delta \to \Delta ^{\textrm {ab}}$
. So for any
$\nu : \Delta \to \Delta ^{\textrm {ab}}$
. So for any
![]() $\sigma \in I_F$
,
$\sigma \in I_F$
,
![]() $\nu (n \cdot \tau (\sigma ) \cdot n^{-1})=A(\nu (\tau (\sigma )))$
has finite prime to p order. Therefore,
$\nu (n \cdot \tau (\sigma ) \cdot n^{-1})=A(\nu (\tau (\sigma )))$
has finite prime to p order. Therefore,
![]() $n \tau n^{-1}$
is
$n \tau n^{-1}$
is
![]() $\nu $
-tame, and the uniqueness part of Proposition 5.5 then implies that
$\nu $
-tame, and the uniqueness part of Proposition 5.5 then implies that
![]() $\tau ^{\phi }=n \tau n^{-1}$
on
$\tau ^{\phi }=n \tau n^{-1}$
on
![]() $I_F$
.
$I_F$
.
Note that u is pure by construction, and Lemma 3.18 implies that
![]() $u^q$
is pure. Furthermore,
$u^q$
is pure. Furthermore,
![]() $n u n^{-1} \in \mathfrak {C}^0(\mathcal {O})$
is also pure. Now (6.1) shows that
$n u n^{-1} \in \mathfrak {C}^0(\mathcal {O})$
is also pure. Now (6.1) shows that
![]() $u^q$
and
$u^q$
and
![]() $n u n^{-1}$
agree in the special fiber. Recall that p is pretty good for G, so Lemma 4.11 implies that p is pretty good for
$n u n^{-1}$
agree in the special fiber. Recall that p is pretty good for G, so Lemma 4.11 implies that p is pretty good for
![]() $\mathfrak {C}=C_{G}(\Lambda )$
. Hence, we can apply [Reference CotnerCot22a, Theorem 5.11] to conclude that
$\mathfrak {C}=C_{G}(\Lambda )$
. Hence, we can apply [Reference CotnerCot22a, Theorem 5.11] to conclude that
![]() $u^q$
and
$u^q$
and
![]() $n u n^{-1}$
are
$n u n^{-1}$
are
![]() $\mathfrak {C}^0(\mathcal {O})$
-conjugate (i.e.,
$\mathfrak {C}^0(\mathcal {O})$
-conjugate (i.e.,
![]() $c n u n^{-1} c^{-1} = u^q $
for some
$c n u n^{-1} c^{-1} = u^q $
for some
![]() $c \in \mathfrak {C}^0(\mathcal {O})$
).
$c \in \mathfrak {C}^0(\mathcal {O})$
).
We claim that we may choose c so that it reduces to the identity. We know that the reduction of c centralizes
![]() $\overline {u}^q = {\overline {\rho }}(\phi ) \overline {u} {\overline {\rho }}(\phi )^{-1}$
. As the centralizer
$\overline {u}^q = {\overline {\rho }}(\phi ) \overline {u} {\overline {\rho }}(\phi )^{-1}$
. As the centralizer
![]() $C_{\mathfrak {C}}(u^q)$
is smooth by Theorem 3.10 (recall that
$C_{\mathfrak {C}}(u^q)$
is smooth by Theorem 3.10 (recall that
![]() $\mathfrak {C}$
is weakly reductive and
$\mathfrak {C}$
is weakly reductive and
![]() $u^q$
is pure fiberwise unipotent), we may modify c so that it reduces to the identity. Making this choice, it is clear that
$u^q$
is pure fiberwise unipotent), we may modify c so that it reduces to the identity. Making this choice, it is clear that
![]() $cn$
reduces to
$cn$
reduces to
![]() ${\overline {\rho }}(\phi )$
and that
${\overline {\rho }}(\phi )$
and that
![]() $u^q = (cn) u (cn)^{-1}$
. As
$u^q = (cn) u (cn)^{-1}$
. As
![]() $\tau ^{\phi }=n \tau n^{-1}$
takes values in
$\tau ^{\phi }=n \tau n^{-1}$
takes values in
![]() $\Delta $
and the groups
$\Delta $
and the groups
![]() $\Delta $
and
$\Delta $
and
![]() $\mathfrak {C}$
commute, we have
$\mathfrak {C}$
commute, we have
![]() $\tau ^{\phi }=cn \tau n^{-1}c^{-1}$
on
$\tau ^{\phi }=cn \tau n^{-1}c^{-1}$
on
![]() $I_F$
, as desired.
$I_F$
, as desired.
We now have the necessary ingredients to complete the proof.
Proof of Theorem 6.1.
Given
![]() ${\overline {\rho }} : \Gamma _F \to G(k)$
, construct
${\overline {\rho }} : \Gamma _F \to G(k)$
, construct
![]() $\theta _z : I_F \to G(\mathcal {O})$
lifting
$\theta _z : I_F \to G(\mathcal {O})$
lifting
![]() ${\overline {\rho }}|_{I_F}$
as in Proposition 6.7, depending on the choice of pure fiberwise unipotent
${\overline {\rho }}|_{I_F}$
as in Proposition 6.7, depending on the choice of pure fiberwise unipotent
![]() $u \in \mathfrak {C}^0(\mathcal {O})$
lifting
$u \in \mathfrak {C}^0(\mathcal {O})$
lifting
![]() ${\overline {\omega }}(\sigma )$
and choice of z. Then Lemma 6.9 gives an element
${\overline {\omega }}(\sigma )$
and choice of z. Then Lemma 6.9 gives an element
![]() $n \in G(\mathcal {O})$
lifting
$n \in G(\mathcal {O})$
lifting
![]() ${\overline {\rho }}(\phi )$
such that
${\overline {\rho }}(\phi )$
such that
![]() $\tau ^{\phi } = n \tau n^{-1}$
on
$\tau ^{\phi } = n \tau n^{-1}$
on
![]() $I_F$
and such that
$I_F$
and such that
![]() $u^q = n u n^{-1}$
.
$u^q = n u n^{-1}$
.
We now fix a choice of
![]() $z \in \mathfrak {C}^0(\mathcal {O})$
so that
$z \in \mathfrak {C}^0(\mathcal {O})$
so that
-
• z reduces to the identity in
 $\mathfrak {C}^0(k)$
;
$\mathfrak {C}^0(k)$
; -
• z commutes with u;
-
•
 $n z n^{-1} = z^q$
.
$n z n^{-1} = z^q$
.
(For example, we may take
![]() $z=1$
.) We define the lift
$z=1$
.) We define the lift
![]() $\rho : \Gamma _F \to G(\mathcal {O})$
to be
$\rho : \Gamma _F \to G(\mathcal {O})$
to be
![]() $\theta _z$
on
$\theta _z$
on
![]() $I_F$
and by setting
$I_F$
and by setting
![]() $\rho (\phi ) = n$
. Note that
$\rho (\phi ) = n$
. Note that
Then
![]() $\rho $
is a homomorphism as
$\rho $
is a homomorphism as
where the penultimate step uses that
![]() $n u n^{-1} = u^q$
and that
$n u n^{-1} = u^q$
and that
![]() $n z n^{-1} = z^q$
. It is continuous as
$n z n^{-1} = z^q$
. It is continuous as
![]() $\theta _z$
is continuous, and
$\theta _z$
is continuous, and
![]() $\overline {\rho }(\phi ) = \bar {n}$
has finite order.
$\overline {\rho }(\phi ) = \bar {n}$
has finite order.
Finally, Lemma 6.11 implies that if, moreover,
![]() $z \in Z(\mathfrak {C})(\mathcal {O})$
, then the centralizer of the inertia is
$z \in Z(\mathfrak {C})(\mathcal {O})$
, then the centralizer of the inertia is
![]() $\mathcal {O}$
-smooth.
$\mathcal {O}$
-smooth.
Example 6.10. Taking
![]() $z=1$
is simplest and gives a minimally ramified lift. Other choices of z give lifts with different inertial types, which are of interest but are not the focus of the present work. We will just give an example.
$z=1$
is simplest and gives a minimally ramified lift. Other choices of z give lifts with different inertial types, which are of interest but are not the focus of the present work. We will just give an example.
After fixing the choice of
![]() $\tau $
, the restriction of
$\tau $
, the restriction of
![]() $\rho $
to
$\rho $
to
![]() $I_F$
depends on u and z. Let
$I_F$
depends on u and z. Let
![]() $V = \operatorname {span}_{\mathcal {O}}\{e_1,e_2,e_3,e_4\}$
and
$V = \operatorname {span}_{\mathcal {O}}\{e_1,e_2,e_3,e_4\}$
and
![]() $\mathfrak {C}$
be the Levi preserving the grading
$\mathfrak {C}$
be the Levi preserving the grading
![]() $V= \operatorname {span} \{e_1,e_2\} \oplus \operatorname {span} \{e_3,e_4\}$
; observe
$V= \operatorname {span} \{e_1,e_2\} \oplus \operatorname {span} \{e_3,e_4\}$
; observe
![]() $V \simeq \operatorname {\mathrm {GL}}_2 \times \operatorname {\mathrm {GL}}_2 \subset \operatorname {\mathrm {GL}}_4$
. Suppose u is the unipotent such that
$V \simeq \operatorname {\mathrm {GL}}_2 \times \operatorname {\mathrm {GL}}_2 \subset \operatorname {\mathrm {GL}}_4$
. Suppose u is the unipotent such that
One possible case is that
![]() ${\overline {\rho }}(\phi )$
, and hence n, swap
${\overline {\rho }}(\phi )$
, and hence n, swap
![]() $\operatorname {span} \{e_1,e_2\}$
and
$\operatorname {span} \{e_1,e_2\}$
and
![]() $\operatorname {span} \{e_3,e_4\}$
. In that case, for any
$\operatorname {span} \{e_3,e_4\}$
. In that case, for any
![]() $p^a$
-th root of unity
$p^a$
-th root of unity
![]() $\zeta \in \mathcal {O}$
where
$\zeta \in \mathcal {O}$
where
![]() $p^a | (q-1)$
, we can take the scalar matrix
$p^a | (q-1)$
, we can take the scalar matrix
![]() $z = \zeta I_4$
. It is clear that
$z = \zeta I_4$
. It is clear that
![]() $\zeta $
reduces to the identity in k, that n and u commute with z, and that
$\zeta $
reduces to the identity in k, that n and u commute with z, and that
![]() $z^q = z$
. In this case, the centralizer of
$z^q = z$
. In this case, the centralizer of
![]() $\rho (I_F)$
equals
$\rho (I_F)$
equals
![]() $C_{\mathfrak {C}}(u)$
and is
$C_{\mathfrak {C}}(u)$
and is
![]() $\mathcal {O}$
-smooth.
$\mathcal {O}$
-smooth.
Lemma 6.11. Under the standing assumptions, if
![]() $z \in Z(\mathfrak {C})(\mathcal {O})$
and satisfies the conditions on z in the proof of Theorem 6.1, then
$z \in Z(\mathfrak {C})(\mathcal {O})$
and satisfies the conditions on z in the proof of Theorem 6.1, then
![]() $C_{G}(\theta _z(I_F))=C_{\mathfrak {C}}(\omega _z(\sigma ))$
is
$C_{G}(\theta _z(I_F))=C_{\mathfrak {C}}(\omega _z(\sigma ))$
is
![]() $\mathcal {O}$
-smooth.
$\mathcal {O}$
-smooth.
Proof. Note that
![]() $\theta _z(I_F)$
is generated by
$\theta _z(I_F)$
is generated by
![]() $\theta _z(\Lambda _F)=\tau (\Lambda _F)$
and
$\theta _z(\Lambda _F)=\tau (\Lambda _F)$
and
![]() $\theta _z(\sigma )=\tau (\sigma )\omega _z(\sigma )$
. For any
$\theta _z(\sigma )=\tau (\sigma )\omega _z(\sigma )$
. For any
![]() $\mathcal {O}$
-algebra R, we have
$\mathcal {O}$
-algebra R, we have
Now an element of
![]() $\mathfrak {C}(R)$
commutes with
$\mathfrak {C}(R)$
commutes with
![]() $\theta _z(\sigma ) = \tau (\sigma ) \omega _z(\sigma )$
if and only if it commutes with
$\theta _z(\sigma ) = \tau (\sigma ) \omega _z(\sigma )$
if and only if it commutes with
![]() $\omega _z(\sigma )$
since
$\omega _z(\sigma )$
since
![]() $\tau (\sigma ) \in \Delta (\mathcal {O})$
and
$\tau (\sigma ) \in \Delta (\mathcal {O})$
and
![]() $\Delta $
commutes with
$\Delta $
commutes with
![]() $\mathfrak {C}$
, and hence,
$\mathfrak {C}$
, and hence,
![]() $C_{G(R)}(\theta _z(I_F))=C_{\mathfrak {C}(R)}(\omega _z(\sigma ))$
. When z is central in
$C_{G(R)}(\theta _z(I_F))=C_{\mathfrak {C}(R)}(\omega _z(\sigma ))$
. When z is central in
![]() $\mathfrak {C}$
, we see that
$\mathfrak {C}$
, we see that
![]() $C_{\mathfrak {C}(R)}(\omega _z(\sigma )) = C_{\mathfrak {C}(R)}(u)$
. Thus, the smoothness follows from Theorem 3.10 (recall that
$C_{\mathfrak {C}(R)}(\omega _z(\sigma )) = C_{\mathfrak {C}(R)}(u)$
. Thus, the smoothness follows from Theorem 3.10 (recall that
![]() $\mathfrak {C}$
is weakly reductive and u is pure fiberwise unipotent).
$\mathfrak {C}$
is weakly reductive and u is pure fiberwise unipotent).
Remark 6.12. If z is not central in
![]() $\mathfrak {C}$
, the centralizer need not be smooth. In particular, the dimension of the centralizer of the semisimple part of
$\mathfrak {C}$
, the centralizer need not be smooth. In particular, the dimension of the centralizer of the semisimple part of
![]() $\omega _z(\sigma ) = z u$
is not locally constant as would be needed to apply [Reference CotnerCot22a, Theorem 1.1] (since z reduces to the identity). See [Reference CotnerCot22a, Remark 5.5] for some examples of the failure of flatness for centralizers of pure sections.
$\omega _z(\sigma ) = z u$
is not locally constant as would be needed to apply [Reference CotnerCot22a, Theorem 1.1] (since z reduces to the identity). See [Reference CotnerCot22a, Remark 5.5] for some examples of the failure of flatness for centralizers of pure sections.
6.2 The minimally ramified deformation condition
We now fix a residual representation
![]() ${\overline {\rho }} : \Gamma _F \to G(k)$
. For a continuous homomorphism
${\overline {\rho }} : \Gamma _F \to G(k)$
. For a continuous homomorphism
![]() $\theta \colon I_F \to G(\mathcal {O})$
lifting
$\theta \colon I_F \to G(\mathcal {O})$
lifting
![]() ${\overline {\rho }}|_{I_F}$
, let
${\overline {\rho }}|_{I_F}$
, let
![]() $\theta _R$
denote the composition
$\theta _R$
denote the composition
![]() $I_F \to G(\mathcal {O}) \to G(R)$
for an
$I_F \to G(\mathcal {O}) \to G(R)$
for an
![]() $\mathcal {O}$
-algebra R. Recall that
$\mathcal {O}$
-algebra R. Recall that
![]() ${\widehat {\mathcal {C}}}_{\mathcal {O}}$
is the category of coefficient
${\widehat {\mathcal {C}}}_{\mathcal {O}}$
is the category of coefficient
![]() $\mathcal {O}$
-algebras (complete local Noetherian rings with residue field k, with morphisms local homomorphisms inducing the identity map on k and with the structure morphism a map of coefficient rings). For the rest of this subsection, we suppose there exists a decomposition type
$\mathcal {O}$
-algebras (complete local Noetherian rings with residue field k, with morphisms local homomorphisms inducing the identity map on k and with the structure morphism a map of coefficient rings). For the rest of this subsection, we suppose there exists a decomposition type
![]() $(\mathfrak {C}, \Delta )$
over
$(\mathfrak {C}, \Delta )$
over
![]() $\mathcal {O}$
adapted to
$\mathcal {O}$
adapted to
![]() ${\overline {\rho }}(\Lambda _F)$
and that p is good for
${\overline {\rho }}(\Lambda _F)$
and that p is good for
![]() $(\mathfrak {C}, \Delta )$
. By the paragraph below Remark 6.2, there is a lift
$(\mathfrak {C}, \Delta )$
. By the paragraph below Remark 6.2, there is a lift
![]() $\tau \colon \Lambda _F \to \Delta (\mathcal {O})$
of
$\tau \colon \Lambda _F \to \Delta (\mathcal {O})$
of
![]() ${\overline {\rho }}|_{\Lambda _F}$
such that
${\overline {\rho }}|_{\Lambda _F}$
such that
![]() $C_{G}(\tau (\Lambda _F))=\mathfrak {C}$
. Moreover,
$C_{G}(\tau (\Lambda _F))=\mathfrak {C}$
. Moreover,
![]() $\tau $
extends to a homomorphism
$\tau $
extends to a homomorphism
![]() $\tau \colon I_F \to \Delta (\mathcal {O})$
by Proposition 6.5. We fix this homomorphism throughout this subsection.
$\tau \colon I_F \to \Delta (\mathcal {O})$
by Proposition 6.5. We fix this homomorphism throughout this subsection.
Lemma 6.13. Let
![]() $\theta \colon I_F \to G(\mathcal {O})$
be a continuous homomorphism lifting
$\theta \colon I_F \to G(\mathcal {O})$
be a continuous homomorphism lifting
![]() ${\overline {\rho }}|_{I_F}$
. Then there exists
${\overline {\rho }}|_{I_F}$
. Then there exists
![]() $g \in \widehat G(\mathcal {O})$
and
$g \in \widehat G(\mathcal {O})$
and
![]() $\omega \colon I_F/\Lambda _F \to \mathfrak {C}(\mathcal {O})$
such that
$\omega \colon I_F/\Lambda _F \to \mathfrak {C}(\mathcal {O})$
such that
![]() $\theta ^g = \tau \cdot \omega $
. Moreover,
$\theta ^g = \tau \cdot \omega $
. Moreover,
![]() $\omega $
is unique up to
$\omega $
is unique up to
![]() $\mathfrak {C}(\mathcal {O})$
-conjugacy.
$\mathfrak {C}(\mathcal {O})$
-conjugacy.
Proof. Since both
![]() $\theta |_{\Lambda _F}$
and
$\theta |_{\Lambda _F}$
and
![]() $\tau |_{\Lambda _F}$
lift
$\tau |_{\Lambda _F}$
lift
![]() ${\overline {\rho }}|_{\Lambda _F}$
, they are
${\overline {\rho }}|_{\Lambda _F}$
, they are
![]() $\widehat G(\mathcal {O})$
-conjugate. So after conjugating, we may assume that
$\widehat G(\mathcal {O})$
-conjugate. So after conjugating, we may assume that
![]() $\theta |_{\Lambda _F}=\tau |_{\Lambda _F}$
. An argument similar to the first part of the proof of Proposition 6.7 then gives the first statement. For the second part, suppose
$\theta |_{\Lambda _F}=\tau |_{\Lambda _F}$
. An argument similar to the first part of the proof of Proposition 6.7 then gives the first statement. For the second part, suppose
![]() $\theta ^g=\tau \cdot \omega $
and
$\theta ^g=\tau \cdot \omega $
and
![]() $\theta ^{g'}=\tau \cdot \omega '$
for
$\theta ^{g'}=\tau \cdot \omega '$
for
![]() $\omega , \omega ' \colon I_F/\Lambda _F \to \mathfrak {C}(\mathcal {O})$
. Restricting to
$\omega , \omega ' \colon I_F/\Lambda _F \to \mathfrak {C}(\mathcal {O})$
. Restricting to
![]() $\Lambda _F$
, we see that
$\Lambda _F$
, we see that
![]() $g^{-1}g'$
centralizes
$g^{-1}g'$
centralizes
![]() $\tau (\Lambda _F)$
, and hence,
$\tau (\Lambda _F)$
, and hence, ![]() . So
. So
![]() $\theta ^{g'}=\theta ^{gc}=\tau ^c \cdot \omega ^c=\tau \cdot \omega ^c$
, and hence
$\theta ^{g'}=\theta ^{gc}=\tau ^c \cdot \omega ^c=\tau \cdot \omega ^c$
, and hence
![]() $\omega '=\omega ^c$
.
$\omega '=\omega ^c$
.
Corollary 6.14. There is a unique
![]() $\widehat G(\mathcal {O})$
-conjugacy class of lifts
$\widehat G(\mathcal {O})$
-conjugacy class of lifts
![]() $\theta \colon I_F \to G(\mathcal {O})$
of
$\theta \colon I_F \to G(\mathcal {O})$
of
![]() ${\overline {\rho }}|_{I_F}$
such that the associated homomorphism
${\overline {\rho }}|_{I_F}$
such that the associated homomorphism
![]() $\omega $
satisfies that
$\omega $
satisfies that
![]() $\omega (\sigma )$
is a pure unipotent element in
$\omega (\sigma )$
is a pure unipotent element in
![]() $\mathfrak {C}^0(\mathcal {O})$
. Moreover,
$\mathfrak {C}^0(\mathcal {O})$
. Moreover,
![]() $\theta $
extends to a continuous homomorphism
$\theta $
extends to a continuous homomorphism
![]() $\Gamma _{F} \to G(\mathcal {O})$
.
$\Gamma _{F} \to G(\mathcal {O})$
.
Proof. The existence follows from Section 6.1 (taking
![]() $z=1$
), which also shows that
$z=1$
), which also shows that
![]() $\theta $
extends to
$\theta $
extends to
![]() $\Gamma _{F}$
. For uniqueness, by Lemma 6.13, it suffices to show that if u and
$\Gamma _{F}$
. For uniqueness, by Lemma 6.13, it suffices to show that if u and
![]() $u'$
are pure unipotents in
$u'$
are pure unipotents in
![]() $\mathfrak {C}^0(\mathcal {O})$
lifting
$\mathfrak {C}^0(\mathcal {O})$
lifting
![]() ${\overline {\omega }}(\sigma ) \in \mathfrak {C}^0(k)$
, then they are
${\overline {\omega }}(\sigma ) \in \mathfrak {C}^0(k)$
, then they are
![]() $\mathfrak {C}^0(\mathcal {O})$
-conjugate. Recall that p is pretty good for G, so Lemma 4.11 implies that p is pretty good for
$\mathfrak {C}^0(\mathcal {O})$
-conjugate. Recall that p is pretty good for G, so Lemma 4.11 implies that p is pretty good for
![]() $\mathfrak {C}=C_{G}(\tau (\Lambda _F))$
. Since u and
$\mathfrak {C}=C_{G}(\tau (\Lambda _F))$
. Since u and
![]() $u'$
agree on the special fiber, [Reference CotnerCot22a, Theorem 5.11] implies that u and
$u'$
agree on the special fiber, [Reference CotnerCot22a, Theorem 5.11] implies that u and
![]() $u'$
are
$u'$
are
![]() $\mathfrak {C}^0(\mathcal {O})$
-conjugate.
$\mathfrak {C}^0(\mathcal {O})$
-conjugate.
Definition 6.15. Let
![]() $\theta \colon I_F \to G(\mathcal {O})$
be a continuous homomorphism lifting
$\theta \colon I_F \to G(\mathcal {O})$
be a continuous homomorphism lifting
![]() ${\overline {\rho }}|_{I_F}$
. Let
${\overline {\rho }}|_{I_F}$
. Let
![]() $\mathrm {Lift}_{{\overline {\rho }}}^{\theta } \colon \widehat {\mathcal {C}}_{\mathcal {O}} \to \textrm {Sets}$
be the functor whose set of R-points
$\mathrm {Lift}_{{\overline {\rho }}}^{\theta } \colon \widehat {\mathcal {C}}_{\mathcal {O}} \to \textrm {Sets}$
be the functor whose set of R-points
![]() $\mathrm {Lift}_{{\overline {\rho }}}^{\theta }(R)$
is given by lifts
$\mathrm {Lift}_{{\overline {\rho }}}^{\theta }(R)$
is given by lifts
![]() $\rho : \Gamma _{F} \to G(R)$
of
$\rho : \Gamma _{F} \to G(R)$
of
![]() ${\overline {\rho }}$
such that there exists
${\overline {\rho }}$
such that there exists
![]() $g \in \widehat {G}(R)$
such that
$g \in \widehat {G}(R)$
such that
![]() $\rho ^g|_{I_F}=\theta _R$
.
$\rho ^g|_{I_F}=\theta _R$
.
Let
![]() $\mathrm {Lift}_{{\overline {\rho }}}^{{m.r.}}$
be this functor when
$\mathrm {Lift}_{{\overline {\rho }}}^{{m.r.}}$
be this functor when
![]() $\theta $
is a homomorphism as in Corollary 6.14. We call this the minimally ramified lifting condition for
$\theta $
is a homomorphism as in Corollary 6.14. We call this the minimally ramified lifting condition for
![]() ${\overline {\rho }}$
.
${\overline {\rho }}$
.
We will use the notions of lifting conditions and deformation conditions for Galois representations which are reviewed in [Reference BooherBoo19a, Definition 2.3] – in particular, the notion of liftability and its connection with formal smoothness of the representing object.
Theorem 6.16. Let
![]() $\theta \colon I_F \to G(\mathcal {O})$
be a continuous homomorphism lifting
$\theta \colon I_F \to G(\mathcal {O})$
be a continuous homomorphism lifting
![]() ${\overline {\rho }}|_{I_F}$
. Suppose that
${\overline {\rho }}|_{I_F}$
. Suppose that
![]() $C_{G}(\theta (I_F))$
is
$C_{G}(\theta (I_F))$
is
![]() $\mathcal {O}$
-smooth and
$\mathcal {O}$
-smooth and
![]() $\theta $
extends to a continuous homomorphism
$\theta $
extends to a continuous homomorphism
![]() $\rho _0 \colon \Gamma _F \to G(\mathcal {O})$
. Then
$\rho _0 \colon \Gamma _F \to G(\mathcal {O})$
. Then
![]() $\mathrm {Lift}_{{\overline {\rho }}}^{\theta }$
is a well-defined lifting condition. Moreover, it is liftable, and the tangent space to the corresponding deformation functor
$\mathrm {Lift}_{{\overline {\rho }}}^{\theta }$
is a well-defined lifting condition. Moreover, it is liftable, and the tangent space to the corresponding deformation functor
![]() $\mathrm {Def}_{{\overline {\rho }}}^{\theta }$
has dimension
$\mathrm {Def}_{{\overline {\rho }}}^{\theta }$
has dimension
![]() $\dim _{k} \mathrm {H}^0(\Gamma _{F}, {\overline {\rho }}(\mathfrak {g}))$
.
$\dim _{k} \mathrm {H}^0(\Gamma _{F}, {\overline {\rho }}(\mathfrak {g}))$
.
Proof. The functor
![]() $\mathrm {Lift}_{{\overline {\rho }}}^{\theta }$
is obviously closed under strict equivalence. The key to checking the second condition of [Reference BooherBoo19a, Definition 2.3] is that
$\mathrm {Lift}_{{\overline {\rho }}}^{\theta }$
is obviously closed under strict equivalence. The key to checking the second condition of [Reference BooherBoo19a, Definition 2.3] is that
![]() $C_{G}(\theta (I_F))$
is
$C_{G}(\theta (I_F))$
is
![]() $\mathcal {O}$
-smooth. In particular, suppose we have a Cartesian diagram in
$\mathcal {O}$
-smooth. In particular, suppose we have a Cartesian diagram in
![]() ${\widehat {\mathcal {C}}}_{\mathcal {O}}$
${\widehat {\mathcal {C}}}_{\mathcal {O}}$

and
![]() $\rho _1 \in \mathrm {Lift}_{{\overline {\rho }}}^{\theta }(R_1) $
and
$\rho _1 \in \mathrm {Lift}_{{\overline {\rho }}}^{\theta }(R_1) $
and
![]() $\rho _2 \in \mathrm {Lift}_{{\overline {\rho }}}^{\theta }(R_2)$
with common image in
$\rho _2 \in \mathrm {Lift}_{{\overline {\rho }}}^{\theta }(R_2)$
with common image in
![]() $\mathrm {Lift}_{{\overline {\rho }}}^{\theta }(R_0)$
. There exists
$\mathrm {Lift}_{{\overline {\rho }}}^{\theta }(R_0)$
. There exists
![]() $g_1 \in \widehat {G}(R_1)$
and
$g_1 \in \widehat {G}(R_1)$
and
![]() $g_2 \in \widehat {G}(R_2)$
such that
$g_2 \in \widehat {G}(R_2)$
such that
![]() $g_1 \rho _1|_{I_F} g_1^{-1} = \theta _{R_1}$
and
$g_1 \rho _1|_{I_F} g_1^{-1} = \theta _{R_1}$
and
![]() $g_2 \rho _2 |_{I_F} g_2^{-1} = \theta _{R_2}$
. Looking at the images in
$g_2 \rho _2 |_{I_F} g_2^{-1} = \theta _{R_2}$
. Looking at the images in
![]() $R_0$
, we conclude that
$R_0$
, we conclude that
![]() $g_1 g_2^{-1} \in C_{G(R_0)}(\theta (I_F))$
. Since
$g_1 g_2^{-1} \in C_{G(R_0)}(\theta (I_F))$
. Since
![]() $C_{G}(\theta (I_F))$
is
$C_{G}(\theta (I_F))$
is
![]() $\mathcal {O}$
-smooth, there exists a lift
$\mathcal {O}$
-smooth, there exists a lift
![]() $x \in C_{G(R_1)}(\theta (I_F))$
. Then the element
$x \in C_{G(R_1)}(\theta (I_F))$
. Then the element
![]() $(x g_1, g_2) \in G(R_1 \times _{R_0} R_2)$
conjugates
$(x g_1, g_2) \in G(R_1 \times _{R_0} R_2)$
conjugates
![]() $(\rho _1,\rho _2)$
to
$(\rho _1,\rho _2)$
to
![]() $(\theta _{R_1},\theta _{R_2})$
, so
$(\theta _{R_1},\theta _{R_2})$
, so
![]() $(\rho _1,\rho _2) \in \mathrm {Lift}_{{\overline {\rho }}}^{\theta }(R_1 \times _{R_0} R_2)$
, as desired.
$(\rho _1,\rho _2) \in \mathrm {Lift}_{{\overline {\rho }}}^{\theta }(R_1 \times _{R_0} R_2)$
, as desired.
To check smoothness, let
![]() $R \to S$
be a small morphism in
$R \to S$
be a small morphism in
![]() ${\widehat {\mathcal {C}}}_{\mathcal {O}}$
, and let
${\widehat {\mathcal {C}}}_{\mathcal {O}}$
, and let
![]() $\rho _S \in \mathrm {Lift}_{{\overline {\rho }}}^{\theta }(S)$
. We need to show that there exists
$\rho _S \in \mathrm {Lift}_{{\overline {\rho }}}^{\theta }(S)$
. We need to show that there exists
![]() $\rho _R \in \mathrm {Lift}_{{\overline {\rho }}}^{\theta }(R)$
mapping to
$\rho _R \in \mathrm {Lift}_{{\overline {\rho }}}^{\theta }(R)$
mapping to
![]() $\rho _S$
under the morphism
$\rho _S$
under the morphism
![]() $R \to S$
. Since G is
$R \to S$
. Since G is
![]() $\mathcal {O}$
-smooth, we may assume that
$\mathcal {O}$
-smooth, we may assume that
![]() $\rho _S|_{I_F}=\theta _S$
by
$\rho _S|_{I_F}=\theta _S$
by
![]() $G(S)$
-conjugation. Since
$G(S)$
-conjugation. Since
![]() $\theta ^{\phi }= \rho _0(\phi ) \theta \rho _0(\phi )^{-1}$
and
$\theta ^{\phi }= \rho _0(\phi ) \theta \rho _0(\phi )^{-1}$
and
![]() $\theta ^{\phi }_S = \rho _S(\phi ) \theta _S \rho _S(\phi )^{-1}$
,
$\theta ^{\phi }_S = \rho _S(\phi ) \theta _S \rho _S(\phi )^{-1}$
,
![]() $\rho _0(\phi )^{-1} \rho _S(\phi )$
centralizes
$\rho _0(\phi )^{-1} \rho _S(\phi )$
centralizes
![]() $\theta _S(I_F)$
. Using the
$\theta _S(I_F)$
. Using the
![]() $\mathcal {O}$
-smoothness of
$\mathcal {O}$
-smoothness of
![]() $C_{G}(\theta (I_F))$
, we obtain an element
$C_{G}(\theta (I_F))$
, we obtain an element
![]() $c \in C_{G(R)}( \theta (I_F))$
lifting
$c \in C_{G(R)}( \theta (I_F))$
lifting
![]() $\rho _0(\phi )^{-1} \rho _S(\phi )$
. Then
$\rho _0(\phi )^{-1} \rho _S(\phi )$
. Then
![]() $\rho _0(\phi ) c$
lifts
$\rho _0(\phi ) c$
lifts
![]() $\rho _S(\phi )$
and on
$\rho _S(\phi )$
and on
![]() $I_F$
,
$I_F$
,
Define
![]() $\rho _R: \Gamma _{F} \to G(R)$
by
$\rho _R: \Gamma _{F} \to G(R)$
by
![]() $\rho _R|_{I_F}=\theta _R$
and
$\rho _R|_{I_F}=\theta _R$
and
![]() $\rho _R(\phi )=\rho _0(\phi ) c$
, and observe that
$\rho _R(\phi )=\rho _0(\phi ) c$
, and observe that
![]() $\rho _R \in \mathrm {Lift}_{{\overline {\rho }}}^{\theta }(R)$
and that it maps to
$\rho _R \in \mathrm {Lift}_{{\overline {\rho }}}^{\theta }(R)$
and that it maps to
![]() $\rho _S$
.
$\rho _S$
.
Notice that the tangent space to
![]() $\mathrm {Def}_{{\overline {\rho }}}^{\theta }$
equals
$\mathrm {Def}_{{\overline {\rho }}}^{\theta }$
equals
![]() $\operatorname {\mathrm {ker}} (\mathrm {H}^1(\Gamma _{F}, {\overline {\rho }}(\mathfrak {g})) \to \mathrm {H}^1(I_F, {\overline {\rho }}(\mathfrak {g}))$
. The last claim then follows from inflation-restriction and the fact that
$\operatorname {\mathrm {ker}} (\mathrm {H}^1(\Gamma _{F}, {\overline {\rho }}(\mathfrak {g})) \to \mathrm {H}^1(I_F, {\overline {\rho }}(\mathfrak {g}))$
. The last claim then follows from inflation-restriction and the fact that
![]() $\dim \mathrm {H}^1(\Gamma _{F}/I_F, {\overline {\rho }}(\mathfrak {g})^{I_F})=\dim \mathrm {H}^0(\Gamma _{F}, {\overline {\rho }}(\mathfrak {g}))$
[Reference WashingtonWas97, Lemma 1].
$\dim \mathrm {H}^1(\Gamma _{F}/I_F, {\overline {\rho }}(\mathfrak {g})^{I_F})=\dim \mathrm {H}^0(\Gamma _{F}, {\overline {\rho }}(\mathfrak {g}))$
[Reference WashingtonWas97, Lemma 1].
Corollary 6.17. Let
![]() ${\overline {\rho }} : \Gamma _F \to G(k)$
be a continuous homomorphism. Suppose there exists a decomposition type
${\overline {\rho }} : \Gamma _F \to G(k)$
be a continuous homomorphism. Suppose there exists a decomposition type
![]() $(\mathfrak {C},\Delta )$
over
$(\mathfrak {C},\Delta )$
over
![]() $\mathcal {O}$
adapted to
$\mathcal {O}$
adapted to
![]() ${\overline {\rho }}(\Lambda _F)$
, and that p is good for
${\overline {\rho }}(\Lambda _F)$
, and that p is good for
![]() $(\mathfrak {C},\Delta )$
. Then
$(\mathfrak {C},\Delta )$
. Then
![]() $\mathrm {Lift}_{{\overline {\rho }}}^{\operatorname {m.r.}}$
is a formally smooth lifting condition. Moreover, the corresponding deformation condition
$\mathrm {Lift}_{{\overline {\rho }}}^{\operatorname {m.r.}}$
is a formally smooth lifting condition. Moreover, the corresponding deformation condition
![]() $\mathrm {Def}_{{\overline {\rho }}}^{\operatorname {m.r.}}$
has dimension
$\mathrm {Def}_{{\overline {\rho }}}^{\operatorname {m.r.}}$
has dimension
![]() $\dim _{k} \mathrm {H}^0(\Gamma _{F}, {\overline {\rho }}(\mathfrak {g}))$
. Equivalently,
$\dim _{k} \mathrm {H}^0(\Gamma _{F}, {\overline {\rho }}(\mathfrak {g}))$
. Equivalently,
![]() $\operatorname {\mathrm {Spf}} R^{\operatorname {m.r.},\square }_{{\overline {\rho }}}$
is
$\operatorname {\mathrm {Spf}} R^{\operatorname {m.r.},\square }_{{\overline {\rho }}}$
is
![]() $\mathcal {O}$
-formally smooth of relative dimension
$\mathcal {O}$
-formally smooth of relative dimension
![]() $\dim _k G_k$
.
$\dim _k G_k$
.
Proof. Construct a lift
![]() $\rho $
as in Section 6.1 with
$\rho $
as in Section 6.1 with
![]() $z=1$
, and observe that
$z=1$
, and observe that
![]() $C_{G}(\theta (I_F))$
is
$C_{G}(\theta (I_F))$
is
![]() $\mathcal {O}$
-smooth by Lemma 6.11. Applying Theorem 6.16 with
$\mathcal {O}$
-smooth by Lemma 6.11. Applying Theorem 6.16 with
![]() $\theta =\rho |_{I_F}$
, we obtain that
$\theta =\rho |_{I_F}$
, we obtain that
![]() $\mathrm {Lift}_{{\overline {\rho }}}^{\theta }$
is formally smooth. Note that
$\mathrm {Lift}_{{\overline {\rho }}}^{\theta }$
is formally smooth. Note that
![]() $\theta $
satisfies Corollary 6.14 by construction (since
$\theta $
satisfies Corollary 6.14 by construction (since
![]() $z=1$
in Proposition 6.7), and so
$z=1$
in Proposition 6.7), and so
![]() $\mathrm {Lift}_{{\overline {\rho }}}^{\theta }=\mathrm {Lift}_{{\overline {\rho }}}^{\operatorname {m.r.}}$
. Finally, note that adding a framing increases the relative dimension by
$\mathrm {Lift}_{{\overline {\rho }}}^{\theta }=\mathrm {Lift}_{{\overline {\rho }}}^{\operatorname {m.r.}}$
. Finally, note that adding a framing increases the relative dimension by
![]() $\dim _k G_k$
minus the dimension of the automorphisms compatible with the
$\dim _k G_k$
minus the dimension of the automorphisms compatible with the
![]() $\Gamma _F$
-action,
$\Gamma _F$
-action,
![]() $\dim _k H^0(\Gamma _F,{\overline {\rho }}(\mathfrak {g}))$
.
$\dim _k H^0(\Gamma _F,{\overline {\rho }}(\mathfrak {g}))$
.
Remark 6.18. Let
![]() $\nu _R : G \to G^{\mathrm {ab}}=G/{\mathscr D}(G)$
be the quotient map (see Proposition 2.27). We could also formulate a variant of the deformation condition where the morphism
$\nu _R : G \to G^{\mathrm {ab}}=G/{\mathscr D}(G)$
be the quotient map (see Proposition 2.27). We could also formulate a variant of the deformation condition where the morphism
![]() $\nu _R \circ \rho _R : \Gamma _F \to G(R) \to G^{\mathrm {ab}}(R)$
is a fixed lift of
$\nu _R \circ \rho _R : \Gamma _F \to G(R) \to G^{\mathrm {ab}}(R)$
is a fixed lift of
![]() $\nu _k \circ {\overline {\rho }}$
. This generalizes adding the requirement that the determinant of the lift be fixed when
$\nu _k \circ {\overline {\rho }}$
. This generalizes adding the requirement that the determinant of the lift be fixed when
![]() $G = \operatorname {\mathrm {GL}}_n$
.
$G = \operatorname {\mathrm {GL}}_n$
.
Remark 6.19. The deformation conditions
![]() $\mathrm {Def}_{{\overline {\rho }}}^{\theta }$
where
$\mathrm {Def}_{{\overline {\rho }}}^{\theta }$
where
![]() $\theta $
has different inertial types should be of interest when investigating
$\theta $
has different inertial types should be of interest when investigating
![]() $\ell \neq p$
versions of the Breuil-Mézard conjecture. Lifts where
$\ell \neq p$
versions of the Breuil-Mézard conjecture. Lifts where
![]() $C_G(\theta (I_F))$
is
$C_G(\theta (I_F))$
is
![]() $\mathcal {O}$
-smooth give formally smooth components of the lifting ring
$\mathcal {O}$
-smooth give formally smooth components of the lifting ring
![]() $\operatorname {\mathrm {Spf}} R^{\square }_{{\overline {\rho }}}$
. For example, we may take
$\operatorname {\mathrm {Spf}} R^{\square }_{{\overline {\rho }}}$
. For example, we may take
![]() $\theta =\theta _z$
for
$\theta =\theta _z$
for
![]() $z \neq 1$
as in Lemma 6.11.
$z \neq 1$
as in Lemma 6.11.
We can now prove our main theorem from the introduction. Recall that G is a weakly reductive group defined over
![]() $\mathcal {O}$
.
$\mathcal {O}$
.
Theorem 6.20. Let
![]() ${\overline {\rho }} : \Gamma _F \to G(k)$
be a continuous homomorphism. Suppose that p is large enough relative to the root datum of G (the bound can be made effective). Then
${\overline {\rho }} : \Gamma _F \to G(k)$
be a continuous homomorphism. Suppose that p is large enough relative to the root datum of G (the bound can be made effective). Then
![]() $\mathrm {Lift}_{{\overline {\rho }}}^{\operatorname {m.r.}}$
is a formally smooth lifting condition. Moreover, the corresponding deformation condition
$\mathrm {Lift}_{{\overline {\rho }}}^{\operatorname {m.r.}}$
is a formally smooth lifting condition. Moreover, the corresponding deformation condition
![]() $\mathrm {Def}_{{\overline {\rho }}}^{\operatorname {m.r.}}$
has dimension
$\mathrm {Def}_{{\overline {\rho }}}^{\operatorname {m.r.}}$
has dimension
![]() $\dim _{k} \mathrm {H}^0(\Gamma _{F}, {\overline {\rho }}(\mathfrak {g}))$
. Equivalently,
$\dim _{k} \mathrm {H}^0(\Gamma _{F}, {\overline {\rho }}(\mathfrak {g}))$
. Equivalently,
![]() $\operatorname {\mathrm {Spf}} R^{\operatorname {m.r.},\square }_{{\overline {\rho }}}$
is
$\operatorname {\mathrm {Spf}} R^{\operatorname {m.r.},\square }_{{\overline {\rho }}}$
is
![]() $\mathcal {O}$
-formally smooth of relative dimension
$\mathcal {O}$
-formally smooth of relative dimension
![]() $\dim _k G_k$
.
$\dim _k G_k$
.
Proof. By Proposition 4.14, if p is pretty good for G, then there exists a decomposition type
![]() $(\mathfrak {C},\Delta )$
over
$(\mathfrak {C},\Delta )$
over
![]() $\mathcal {O}$
adapted to
$\mathcal {O}$
adapted to ![]() . We need to ensure that p is good for
. We need to ensure that p is good for
![]() $(\mathfrak {C},\Delta )$
in the sense of Definition 4.6. Condition (1) is trivially satisfied. If
$(\mathfrak {C},\Delta )$
in the sense of Definition 4.6. Condition (1) is trivially satisfied. If
![]() $p>\operatorname {\mathrm {rank}} {\mathscr D}(G^0) +1$
, condition (2) follows as well. In fact, for any connected semisimple group H and any prime p dividing the order of
$p>\operatorname {\mathrm {rank}} {\mathscr D}(G^0) +1$
, condition (2) follows as well. In fact, for any connected semisimple group H and any prime p dividing the order of
![]() $Z(H)$
,
$Z(H)$
,
![]() $p \leq \operatorname {\mathrm {rank}} H +1$
. To check this, we may assume that H is simply-connected, and hence, it is a direct product of simple, simply-connected groups, in which case the claim follows from a simple case-checking. It remains to consider Definition 4.6, (3). By Proposition 2.24, this will hold if
$p \leq \operatorname {\mathrm {rank}} H +1$
. To check this, we may assume that H is simply-connected, and hence, it is a direct product of simple, simply-connected groups, in which case the claim follows from a simple case-checking. It remains to consider Definition 4.6, (3). By Proposition 2.24, this will hold if
![]() $p \nmid |W_G|$
and
$p \nmid |W_G|$
and
![]() $p>|\pi _0 \mathfrak {C}_k|=|\pi _0 C_{G_k}(\overline {\Lambda })|$
. Theorem A.10 gives a bound for the last quantity which depends only on G. The theorem now follows from Corollary 6.17.
$p>|\pi _0 \mathfrak {C}_k|=|\pi _0 C_{G_k}(\overline {\Lambda })|$
. Theorem A.10 gives a bound for the last quantity which depends only on G. The theorem now follows from Corollary 6.17.
Remark 6.21. By the proof of the above theorem, the condition that p is large enough relative to the root datum of G is equivalent to the following:
-
• p is pretty good for G in the sense of Definition 1.12.
-
•
 $p>\operatorname {\mathrm {rank}} {\mathscr D}(G^0) +1$
.
$p>\operatorname {\mathrm {rank}} {\mathscr D}(G^0) +1$
. -
• p does not divide the order of
 $W_G$
.
$W_G$
. -
• p is larger than the constant in Theorem A.10.
The last condition is explicit but not always pleasant. To illustrate, notice that the constant in Theorem A.10 must be at least the number of components of the centralizer of any particular prime-to-p solvable subgroup of
![]() $G_k$
.
$G_k$
.
When
![]() $G = \operatorname {\mathrm {GL}}_n$
, Schur’s lemma shows that centralizer of a completely reducible subgroup is a product of general linear groups. Hence, the component group is always trivial.
$G = \operatorname {\mathrm {GL}}_n$
, Schur’s lemma shows that centralizer of a completely reducible subgroup is a product of general linear groups. Hence, the component group is always trivial.
For the exceptional group of type
![]() $G_2$
, the lower bound for p is 72; see Example A.5.
$G_2$
, the lower bound for p is 72; see Example A.5.
When
![]() $G = \operatorname {\mathrm {PGL}}_n$
, there is an example of a subgroup whose centralizer is finite of order
$G = \operatorname {\mathrm {PGL}}_n$
, there is an example of a subgroup whose centralizer is finite of order
![]() $n^2$
[Reference LiebeckLie23, Examples(3)]. Similarly, when
$n^2$
[Reference LiebeckLie23, Examples(3)]. Similarly, when
![]() $G = \operatorname {\mathrm {Sp}}_{2n}$
, there is an example of a subgroup whose centralizer is finite of order
$G = \operatorname {\mathrm {Sp}}_{2n}$
, there is an example of a subgroup whose centralizer is finite of order
![]() $2^n$
[Reference LiebeckLie23, Examples(2)].
$2^n$
[Reference LiebeckLie23, Examples(2)].
In particular, for
![]() $G = \operatorname {\mathrm {Sp}}_{2n}$
, the last example shows that we must require
$G = \operatorname {\mathrm {Sp}}_{2n}$
, the last example shows that we must require
![]() $p>2^n$
. This is far from optimal: the techniques from [Reference BooherBoo19a] work when
$p>2^n$
. This is far from optimal: the techniques from [Reference BooherBoo19a] work when
![]() $p>2n$
.
$p>2n$
.
Remark 6.22. Note that the last bulleted point in Remark 6.21 is needed to ensure Definition 4.6, (3) for the decomposition type
![]() $(\mathfrak {C}, \Delta )$
adapted to the residual representation
$(\mathfrak {C}, \Delta )$
adapted to the residual representation
![]() ${\overline {\rho }}$
. This in turn implies that
${\overline {\rho }}$
. This in turn implies that
![]() ${\overline {\rho }}(I_F) \subset \mathfrak {C}(k) \Delta (k)$
, which is the starting point of the argument in Section 6.1. Currently, we do not know how to construct lifts of
${\overline {\rho }}(I_F) \subset \mathfrak {C}(k) \Delta (k)$
, which is the starting point of the argument in Section 6.1. Currently, we do not know how to construct lifts of
![]() ${\overline {\rho }}$
without this condition.
${\overline {\rho }}$
without this condition.
Remark 6.23. A variant of the arguments in this section can be used to show the following mild strengthening of Theorem 6.20. Maintain all of the assumptions on F,
![]() $\mathcal {O}$
, G, and so on. Let W be the Weil group of F, and let
$\mathcal {O}$
, G, and so on. Let W be the Weil group of F, and let
![]() $W^0$
be the ‘discretized version’ from [Reference Dat, Helm, Kurinczuk and MossDHKM24], obtained by choosing a topological generator of tame intertia. Let
$W^0$
be the ‘discretized version’ from [Reference Dat, Helm, Kurinczuk and MossDHKM24], obtained by choosing a topological generator of tame intertia. Let
![]() ${\mathscr H}_W$
be the moduli space
${\mathscr H}_W$
be the moduli space
![]() $\underline {\operatorname {\mathrm {Hom}}}_{\mathcal {O}\textrm {-}\mathrm {gp}}(W^0, G)$
, which is representable by [Reference Dat, Helm, Kurinczuk and MossDHKM24]. Moreover, [Reference Dat, Helm, Kurinczuk and MossDHKM24, Theorem 1.5] shows that the p-adic formal completion of
$\underline {\operatorname {\mathrm {Hom}}}_{\mathcal {O}\textrm {-}\mathrm {gp}}(W^0, G)$
, which is representable by [Reference Dat, Helm, Kurinczuk and MossDHKM24]. Moreover, [Reference Dat, Helm, Kurinczuk and MossDHKM24, Theorem 1.5] shows that the p-adic formal completion of
![]() ${\mathscr H}_W$
represents the functor on p-adically complete (and separated)
${\mathscr H}_W$
represents the functor on p-adically complete (and separated)
![]() $\mathcal {O}$
-algebras given by
$\mathcal {O}$
-algebras given by
There is a similar functor
![]() ${\mathscr H}_{\Lambda }$
, obtained from
${\mathscr H}_{\Lambda }$
, obtained from
![]() ${\mathscr H}_W$
by replacing W by
${\mathscr H}_W$
by replacing W by
![]() $\Lambda _F$
. Attached to
$\Lambda _F$
. Attached to
![]() ${\mathscr H}_{\Lambda }$
are the universal centralizer
${\mathscr H}_{\Lambda }$
are the universal centralizer
![]() $\mathfrak {C}$
and the universal double centralizer
$\mathfrak {C}$
and the universal double centralizer
![]() $\Delta $
.
$\Delta $
.
For any continuous
![]() $f: W \to G(R)$
as above, the restriction
$f: W \to G(R)$
as above, the restriction
![]() $f|_{I_F}$
factors uniquely as
$f|_{I_F}$
factors uniquely as
![]() $f|_{I_F} = \tau \cdot \omega $
, where
$f|_{I_F} = \tau \cdot \omega $
, where
![]() $\tau : I_F \to \Delta (R)$
is the unique tame extension of
$\tau : I_F \to \Delta (R)$
is the unique tame extension of
![]() $f|_{\Lambda _F}$
(which exists by a variant of Proposition 5.5) and
$f|_{\Lambda _F}$
(which exists by a variant of Proposition 5.5) and
![]() $\omega : I_F/\Lambda _F \to \mathfrak {C}(R)$
is a homomorphism. Let
$\omega : I_F/\Lambda _F \to \mathfrak {C}(R)$
is a homomorphism. Let
![]() ${\mathscr H}_W^{\mathrm {{pure}}}$
be the subfunctor of
${\mathscr H}_W^{\mathrm {{pure}}}$
be the subfunctor of
![]() ${\mathscr H}_W$
with
${\mathscr H}_W$
with
![]() ${\mathscr H}_W^{\mathrm {{pure}}}(R)$
consisting of those f as above such that
${\mathscr H}_W^{\mathrm {{pure}}}(R)$
consisting of those f as above such that
![]() $\omega (\sigma )$
is pure fiberwise unipotent, where
$\omega (\sigma )$
is pure fiberwise unipotent, where
![]() $\sigma $
is a generator of the pro-p part of
$\sigma $
is a generator of the pro-p part of
![]() $I_F$
. (If R is not reduced, ‘pure fiberwise unipotent’ should be interpreted to mean that
$I_F$
. (If R is not reduced, ‘pure fiberwise unipotent’ should be interpreted to mean that
![]() $f(\sigma )$
is fppf-locally on R conjugate to a pure fiberwise unipotent section of
$f(\sigma )$
is fppf-locally on R conjugate to a pure fiberwise unipotent section of
![]() $G(\mathcal {O}')$
, for some finite extension
$G(\mathcal {O}')$
, for some finite extension
![]() $\mathcal {O}'$
of
$\mathcal {O}'$
of
![]() $\mathcal {O}$
.)
$\mathcal {O}$
.)
The arguments of this section can be used to show that
![]() ${\mathscr H}_W^{\mathrm {{pure}}}$
is formally smooth and the inclusion map
${\mathscr H}_W^{\mathrm {{pure}}}$
is formally smooth and the inclusion map
![]() ${\mathscr H}_W^{\mathrm {{pure}}} \to {\mathscr H}_W$
gives a stratification of
${\mathscr H}_W^{\mathrm {{pure}}} \to {\mathscr H}_W$
gives a stratification of
![]() ${\mathscr H}_W$
into smooth pieces, each of which is open in an irreducible component of
${\mathscr H}_W$
into smooth pieces, each of which is open in an irreducible component of
![]() ${\mathscr H}_W$
(for dimension reasons coming from Theorem 6.20). Because of this openness statement, it follows that every point f in the special fiber of
${\mathscr H}_W$
(for dimension reasons coming from Theorem 6.20). Because of this openness statement, it follows that every point f in the special fiber of
![]() ${\mathscr H}_W$
lies in an irreducible component X such that f is a smooth point of
${\mathscr H}_W$
lies in an irreducible component X such that f is a smooth point of
![]() $X_{\mathrm {{red}}}$
.
$X_{\mathrm {{red}}}$
.
A Some group theory
The following Theorem is due to Liebeck [Reference LiebeckLie23], which originated in an email correspondence between the third author (S.T.) and Martin Liebeck. S.T. would like to thank Martin Liebeck for his interest in our question and for answering it, which allows us to obtain an effective lower bound for p in Theorem 1.1.
Theorem A.1. Let G be a connected semisimple group over an algebraically closed field k, and let H be a G-irreducible subgroup. Then there is a constant
![]() $c \leq 197$
such that
$c \leq 197$
such that
![]() $\# C_{G}(H) \leq c^{\operatorname {\mathrm {rank}} G}\# Z(G)$
.
$\# C_{G}(H) \leq c^{\operatorname {\mathrm {rank}} G}\# Z(G)$
.
By [Reference LiebeckLie23], the constant c is at most 16 if all the simple factors of G are classical, and [Reference LiebeckLie23, Lemma 2.5] gives precise bounds for c when G is of exceptional type.
Corollary A.2. Let G be a connected reductive group over an algebraically closed field k, and let H be a G-irreducible subgroup. Then
![]() $\# \pi _0 C_{G}(H) \leq c^{\operatorname {\mathrm {rank}} G^{\operatorname {\mathrm {ad}}}} \# \pi _0 Z(G)$
.
$\# \pi _0 C_{G}(H) \leq c^{\operatorname {\mathrm {rank}} G^{\operatorname {\mathrm {ad}}}} \# \pi _0 Z(G)$
.
Proof. Consider the exact sequence
where
![]() $\overline {H} \subset G^{\operatorname {\mathrm {ad}}}$
is the image of H under the natural map
$\overline {H} \subset G^{\operatorname {\mathrm {ad}}}$
is the image of H under the natural map
![]() $G \to G^{\operatorname {\mathrm {ad}}}$
. Note that
$G \to G^{\operatorname {\mathrm {ad}}}$
. Note that
![]() $\overline {H}$
is
$\overline {H}$
is
![]() $G^{\operatorname {\mathrm {ad}}}$
-irreducible, so Theorem A.1 implies that
$G^{\operatorname {\mathrm {ad}}}$
-irreducible, so Theorem A.1 implies that
![]() $\# C_{G^{\operatorname {\mathrm {ad}}}}(\overline {H}) \leq c^{\operatorname {\mathrm {rank}} G^{\operatorname {\mathrm {ad}}}}$
. However, since H is G-irreducible,
$\# C_{G^{\operatorname {\mathrm {ad}}}}(\overline {H}) \leq c^{\operatorname {\mathrm {rank}} G^{\operatorname {\mathrm {ad}}}}$
. However, since H is G-irreducible,
![]() $C_{G}(H)^0 = Z(G)^0$
, so the above exact sequence implies that
$C_{G}(H)^0 = Z(G)^0$
, so the above exact sequence implies that
![]() $\pi _0 C_{G}(H)/\pi _0 Z(G)$
injects into
$\pi _0 C_{G}(H)/\pi _0 Z(G)$
injects into
![]() $C_{G^{\operatorname {\mathrm {ad}}}}(\overline {H})$
. Therefore,
$C_{G^{\operatorname {\mathrm {ad}}}}(\overline {H})$
. Therefore,
![]() $\# \pi _0 C_{G}(H) \leq \# \pi _0 Z(G) c^{\operatorname {\mathrm {rank}} G^{\operatorname {\mathrm {ad}}}}$
.
$\# \pi _0 C_{G}(H) \leq \# \pi _0 Z(G) c^{\operatorname {\mathrm {rank}} G^{\operatorname {\mathrm {ad}}}}$
.
Lemma A.3. Let H be a closed, completely reducible subgroup of G. Choose a maximal torus S of ![]() , and let
, and let
![]() $L=C_G(S)$
. Denote by
$L=C_G(S)$
. Denote by
![]() $W(G,L)$
(resp.
$W(G,L)$
(resp.
![]() $W(K,S)$
) the quotient
$W(K,S)$
) the quotient
![]() $N_G(L)/L$
(resp.
$N_G(L)/L$
(resp.
![]() $N_{K}(S)/S$
); the latter can be naturally identified as a subgroup of the former. Then there is a canonical injection
$N_{K}(S)/S$
); the latter can be naturally identified as a subgroup of the former. Then there is a canonical injection
Proof. Observe that
![]() $Z_L^0=S$
, which implies
$Z_L^0=S$
, which implies
![]() $N_G(L)=N_G(S)$
. So
$N_G(L)=N_G(S)$
. So
![]() $N_G(L)/L=N_{G}(S)/C_{G}(S)$
contains
$N_G(L)/L=N_{G}(S)/C_{G}(S)$
contains
![]() $N_{K}(S)/C_{K}(S)=N_{K}(S)/S$
as a subgroup. Any
$N_{K}(S)/C_{K}(S)=N_{K}(S)/S$
as a subgroup. Any
![]() $n \in N_G(H)$
normalizes
$n \in N_G(H)$
normalizes
![]() $K=C_G(H)^0$
, so
$K=C_G(H)^0$
, so
![]() $S^n$
is another maximal tori of K. By the conjugacy of maximal tori, there is an element
$S^n$
is another maximal tori of K. By the conjugacy of maximal tori, there is an element
![]() $c \in K$
such that
$c \in K$
such that
![]() $(S^n)^c=S$
(i.e.
$(S^n)^c=S$
(i.e.
![]() $nc \in N_G(S)=N_G(L)$
). For any element
$nc \in N_G(S)=N_G(L)$
). For any element
![]() $w \in N_G(L)$
, denote by
$w \in N_G(L)$
, denote by
![]() $\bar w$
its image in
$\bar w$
its image in
![]() $W(G,L)$
. Define a map
$W(G,L)$
. Define a map
by
![]() $\varphi (n)=\overline {nc}W(K,S)$
. First, note that
$\varphi (n)=\overline {nc}W(K,S)$
. First, note that
![]() $n \mapsto \overline {nc} W(K,S)$
is a well-defined map from
$n \mapsto \overline {nc} W(K,S)$
is a well-defined map from
![]() $N_{G}(H)$
to the quotient set
$N_{G}(H)$
to the quotient set
![]() $W(G,L)/W(K,S)$
, and that
$W(G,L)/W(K,S)$
, and that
![]() $nc$
normalizes
$nc$
normalizes
![]() $N_{K}(S)$
, which implies
$N_{K}(S)$
, which implies
![]() $\overline {nc}$
normalizes
$\overline {nc}$
normalizes
![]() $W(K,S)$
. It follows that
$W(K,S)$
. It follows that
![]() $\varphi $
defined above is a well-defined map. We check that
$\varphi $
defined above is a well-defined map. We check that
![]() $\varphi $
is a group homomorphism. Let
$\varphi $
is a group homomorphism. Let
![]() $n_1, n_2 \in N_{G}(H)$
with
$n_1, n_2 \in N_{G}(H)$
with
![]() $c_1, c_2 \in K$
such that
$c_1, c_2 \in K$
such that
![]() $n_1c_1, n_2c_2$
both normalize S. So
$n_1c_1, n_2c_2$
both normalize S. So
![]() $\varphi (n_i)=\overline {n_ic_i}W(K,S)$
for
$\varphi (n_i)=\overline {n_ic_i}W(K,S)$
for
![]() $i=1,2$
. However, the product
$i=1,2$
. However, the product
![]() $(n_1c_1)(n_2c_2)$
normalizes S, and we have
$(n_1c_1)(n_2c_2)$
normalizes S, and we have
![]() $(n_1c_1)(n_2c_2)=(n_1n_2)(n_2^{-1}c_1n_2)c_2$
with
$(n_1c_1)(n_2c_2)=(n_1n_2)(n_2^{-1}c_1n_2)c_2$
with
![]() $(n_2^{-1}c_1n_2)c_2 \in K$
, so
$(n_2^{-1}c_1n_2)c_2 \in K$
, so
 $\varphi (n_1n_2)=\overline {(n_1n_2)(n_2^{-1}c_1n_2)c_2} W(K,S)=\overline {(n_1c_1)(n_2c_2)}W(K,S)=\overline {n_1c_1}W(K,S)\overline {n_2c_2}W(K,S)=\varphi (n_1)\varphi (n_2)$
. We now compute
$\varphi (n_1n_2)=\overline {(n_1n_2)(n_2^{-1}c_1n_2)c_2} W(K,S)=\overline {(n_1c_1)(n_2c_2)}W(K,S)=\overline {n_1c_1}W(K,S)\overline {n_2c_2}W(K,S)=\varphi (n_1)\varphi (n_2)$
. We now compute
![]() $\operatorname {\mathrm {ker}} \varphi $
. It consists of
$\operatorname {\mathrm {ker}} \varphi $
. It consists of
![]() $n \in N_{G}(H)$
for which
$n \in N_{G}(H)$
for which
![]() $\overline {nc} \in W(K,S)=N_{K}(S)/S=N_{K}(S)/C_{K}(S)=N_{K}(S)/N_{K}(S) \cap C_{G}(S)=N_{K}(S) \cdot L/L$
for some
$\overline {nc} \in W(K,S)=N_{K}(S)/S=N_{K}(S)/C_{K}(S)=N_{K}(S)/N_{K}(S) \cap C_{G}(S)=N_{K}(S) \cdot L/L$
for some
![]() $c \in K$
. So
$c \in K$
. So
![]() $nc \in N_{K}(S) \cdot L$
, which implies
$nc \in N_{K}(S) \cdot L$
, which implies
![]() $n \in K \cdot L$
. As n normalizes H and K commutes with H, it follows that
$n \in K \cdot L$
. As n normalizes H and K commutes with H, it follows that
![]() $n \in K \cdot N_{L}(H)$
. However, if
$n \in K \cdot N_{L}(H)$
. However, if
![]() $n=b \cdot c \in N_{L}(H) \cdot K$
, then
$n=b \cdot c \in N_{L}(H) \cdot K$
, then
![]() $\varphi (n)=\overline {nc^{-1}}W(K,S)=\overline {b} W(K,S)=W(K,S)$
, where the first equality holds since
$\varphi (n)=\overline {nc^{-1}}W(K,S)=\overline {b} W(K,S)=W(K,S)$
, where the first equality holds since
![]() $S^{b}=S$
(
$S^{b}=S$
(
![]() $b \in L=C_{G}(S)$
), and the last equality holds since
$b \in L=C_{G}(S)$
), and the last equality holds since
![]() $b \in N_{L}(H) \subset L$
, and hence,
$b \in N_{L}(H) \subset L$
, and hence,
![]() $\overline b=\overline 1 \in W(G,L)$
. Thus,
$\overline b=\overline 1 \in W(G,L)$
. Thus,
![]() $\operatorname {\mathrm {ker}} \varphi = K \cdot N_{L}(H) = N_{L}(H) \cdot K$
(the last equality holds since
$\operatorname {\mathrm {ker}} \varphi = K \cdot N_{L}(H) = N_{L}(H) \cdot K$
(the last equality holds since
![]() $N_{L}(H)$
normalizes
$N_{L}(H)$
normalizes
![]() $K=C_{G}(H)^0$
).
$K=C_{G}(H)^0$
).
Theorem A.4. Let G be a connected reductive group over an algebraically closed field k, and let H be a G-completely reducible subgroup. Then the size of
![]() $\pi _0 C_{G}(H)$
is bounded by
$\pi _0 C_{G}(H)$
is bounded by
where L runs over the finitely many conjugacy classes of Levi subgroups of G.
Proof. Let L be as in Lemma A.3. Note that H is an irreducible subgroup of L. There is a natural surjection from
![]() $\pi _0(C_G(H))$
to
$\pi _0(C_G(H))$
to
![]() $C_G(H)/C_L(H)\cdot C_G(H)^0$
, the latter injects into the group on the left side of the inclusion in Lemma A.3, and the kernel is a quotient of
$C_G(H)/C_L(H)\cdot C_G(H)^0$
, the latter injects into the group on the left side of the inclusion in Lemma A.3, and the kernel is a quotient of
![]() $\pi _0 C_L(H)$
. The theorem now follows from Corollary A.2 and Lemma A.3.
$\pi _0 C_L(H)$
. The theorem now follows from Corollary A.2 and Lemma A.3.
Example A.5. The constant
![]() $c_G$
is a very crude bound, which can be made much smaller for specific G by going through the proof of Theorem A.4. For example, for G the exceptional group of type
$c_G$
is a very crude bound, which can be made much smaller for specific G by going through the proof of Theorem A.4. For example, for G the exceptional group of type
![]() $G_2$
, if H is not G-ir, then the minimal Levi containing H (unique up to conjugacy) is either a maximal torus or isomorphic to
$G_2$
, if H is not G-ir, then the minimal Levi containing H (unique up to conjugacy) is either a maximal torus or isomorphic to
![]() $\operatorname {\mathrm {GL}}_2$
, and
$\operatorname {\mathrm {GL}}_2$
, and
![]() $\pi _0 C_{G}(H)$
injects into the group on the left side of the inclusion in Lemma A.3, so
$\pi _0 C_{G}(H)$
injects into the group on the left side of the inclusion in Lemma A.3, so
![]() $\#\pi _0 C_{G}(H) \leq W_G=12$
. Now if H is G-ir, then
$\#\pi _0 C_{G}(H) \leq W_G=12$
. Now if H is G-ir, then
![]() $\pi _0 C_{G}(H) \leq 8.5^2=72.25$
by Theorem A.1 and [Reference LiebeckLie23, Lemma 2.5]. Thus, the bound
$\pi _0 C_{G}(H) \leq 8.5^2=72.25$
by Theorem A.1 and [Reference LiebeckLie23, Lemma 2.5]. Thus, the bound
![]() $c_G$
can be improved to
$c_G$
can be improved to
![]() $72$
in this case.
$72$
in this case.
For the remainder of this section, we will generalize Theorem A.4 to non-connected reductive groups in the case that H is solvable. In what follows, we make no attempt in optimizing the bounds for the component groups.
Lemma A.6. Let
![]() $f \colon G' \to G$
be a central isogeny of connected reductive groups over an algebraically closed field k, and let
$f \colon G' \to G$
be a central isogeny of connected reductive groups over an algebraically closed field k, and let
![]() $\lambda '$
and
$\lambda '$
and
![]() $\lambda $
be compatible automorphisms of
$\lambda $
be compatible automorphisms of
![]() $G'$
and G, respectively. Then
$G'$
and G, respectively. Then
![]() $\# \pi _0 C_{G}(\lambda ) \leq \# \pi _0 C_{G'}(\lambda ') \cdot \# \ker f$
.
$\# \pi _0 C_{G}(\lambda ) \leq \# \pi _0 C_{G'}(\lambda ') \cdot \# \ker f$
.
Proof. Note that there is an exact sequence
where the rightmost map is
![]() $x \mapsto \lambda '(x) x^{-1}$
. The component group of
$x \mapsto \lambda '(x) x^{-1}$
. The component group of
![]() $f^{-1}(C_{G}(\lambda ))$
is thus an extension of a subgroup of
$f^{-1}(C_{G}(\lambda ))$
is thus an extension of a subgroup of
![]() $(\ker f)_{\mathrm {red}}$
by a quotient of the component group of
$(\ker f)_{\mathrm {red}}$
by a quotient of the component group of
![]() $C_{G'}(\lambda ')$
.
$C_{G'}(\lambda ')$
.
Moreover, there is an obvious exact sequence
Thus, the component group of
![]() $C_{G}(\lambda )$
is a quotient of the component group of
$C_{G}(\lambda )$
is a quotient of the component group of
![]() $f^{-1}(C_{G}(\lambda ))$
. The lemma follows.
$f^{-1}(C_{G}(\lambda ))$
. The lemma follows.
Lemma A.7. Let T be a split torus, and let
![]() $\lambda $
be an automorphism of T of order n. Then
$\lambda $
be an automorphism of T of order n. Then
![]() $\# \pi _0 C_{T}(\lambda )$
divides
$\# \pi _0 C_{T}(\lambda )$
divides
![]() $n^{\dim T}$
.
$n^{\dim T}$
.
Proof. This follows immediately from [Reference Digne and MichelDM18, Lemma 1.2(1)].
Lemma A.8. Let G be a connected reductive group over an algebraically closed field k. Let
![]() $\lambda $
be a semisimple automorphism of G of order n. Then
$\lambda $
be a semisimple automorphism of G of order n. Then
![]() $\# \pi _0 C_{G}(\lambda ) \leq 4^{\operatorname {\mathrm {rank}} {\mathscr D}(G)} \cdot n^{\dim Z(G)}$
.
$\# \pi _0 C_{G}(\lambda ) \leq 4^{\operatorname {\mathrm {rank}} {\mathscr D}(G)} \cdot n^{\dim Z(G)}$
.
Proof. By a theorem of Steinberg, if G is semisimple, then
![]() $\pi _0 C_{G}(\lambda )$
can be identified with a subgroup of
$\pi _0 C_{G}(\lambda )$
can be identified with a subgroup of
![]() $\pi _1(G)$
. Moreover,
$\pi _1(G)$
. Moreover,
![]() $\# \pi _1(G) \leq 2^{\operatorname {\mathrm {rank}} G}$
(realized by
$\# \pi _1(G) \leq 2^{\operatorname {\mathrm {rank}} G}$
(realized by
![]() $G=(\operatorname {\mathrm {PGL}}_2)^{\operatorname {\mathrm {rank}} G}$
). Now we suppose that
$G=(\operatorname {\mathrm {PGL}}_2)^{\operatorname {\mathrm {rank}} G}$
). Now we suppose that
![]() $G = T \times H$
for a torus T and a semisimple group H. Then
$G = T \times H$
for a torus T and a semisimple group H. Then
![]() $\lambda $
induces acts on T and H. By the above,
$\lambda $
induces acts on T and H. By the above,
![]() $\# \pi _0 C_{H}(\lambda ) \leq 2^{\operatorname {\mathrm {rank}} H}=2^{\operatorname {\mathrm {rank}} {\mathscr D}(G)}$
. By Lemma A.7,
$\# \pi _0 C_{H}(\lambda ) \leq 2^{\operatorname {\mathrm {rank}} H}=2^{\operatorname {\mathrm {rank}} {\mathscr D}(G)}$
. By Lemma A.7,
![]() $\# \pi _0 C_{T}(\lambda ) \leq n^{\dim T} = n^{\dim Z(G)}$
. So
$\# \pi _0 C_{T}(\lambda ) \leq n^{\dim T} = n^{\dim Z(G)}$
. So
![]() $\# \pi _0 C_{G}(\lambda ) \leq 2^{\operatorname {\mathrm {rank}} {\mathscr D}(G)} \cdot n^{\dim Z(G)}$
.
$\# \pi _0 C_{G}(\lambda ) \leq 2^{\operatorname {\mathrm {rank}} {\mathscr D}(G)} \cdot n^{\dim Z(G)}$
.
For the general case, note the canonical isogeny
![]() $Z(G)^0 \times {\mathscr D}(G) \to G$
, whose kernel is contained in
$Z(G)^0 \times {\mathscr D}(G) \to G$
, whose kernel is contained in
![]() $Z({\mathscr D}(G))$
. By Lemma A.6 and the above, it follows that
$Z({\mathscr D}(G))$
. By Lemma A.6 and the above, it follows that
Finally, note that if H is semisimple, then
![]() $\#Z(H) \leq \#Z(H^{\mathrm {sc}})=\#\pi _1 H^{\mathrm {ad}} \leq 2^{\operatorname {\mathrm {rank}} H}$
. So
$\#Z(H) \leq \#Z(H^{\mathrm {sc}})=\#\pi _1 H^{\mathrm {ad}} \leq 2^{\operatorname {\mathrm {rank}} H}$
. So
![]() $\#Z({\mathscr D}(G)) \leq 2^{\operatorname {\mathrm {rank}} {\mathscr D}(G)}$
. The lemma follows.
$\#Z({\mathscr D}(G)) \leq 2^{\operatorname {\mathrm {rank}} {\mathscr D}(G)}$
. The lemma follows.
Lemma A.9. Let H be a (possibly nonconnected) reductive group over an algebraically closed field k. Let F be a solvable finite group with prime-to-p order acting on H. Then the size of
![]() $\pi _0 C_{H}(F)$
is bounded by a constant depending only on
$\pi _0 C_{H}(F)$
is bounded by a constant depending only on
![]() $\operatorname {\mathrm {rank}} H^0$
,
$\operatorname {\mathrm {rank}} H^0$
,
![]() $\#\pi _0 H$
and
$\#\pi _0 H$
and
![]() $\# F$
.
$\# F$
.
Proof. This will follow from the preceding lemma and induction. First, note the exact sequence
and that
![]() $C_{H^0}(F)^0=C_{H}(F)^0$
. It follows that
$C_{H^0}(F)^0=C_{H}(F)^0$
. It follows that
![]() $\# \pi _0 C_{H}(F) \leq \# \pi _0 H \cdot \# \pi _0 C_{H^0}(F)$
.
$\# \pi _0 C_{H}(F) \leq \# \pi _0 H \cdot \# \pi _0 C_{H^0}(F)$
.
Since F is solvable, there is a composition series
such that
![]() $F_{i+1}$
is normal in
$F_{i+1}$
is normal in
![]() $F_i$
and
$F_i$
and
![]() $F_i/F_{i+1}$
is cyclic. Since
$F_i/F_{i+1}$
is cyclic. Since
![]() $F_{i+1}$
is normal in
$F_{i+1}$
is normal in
![]() $F_i$
,
$F_i$
,
![]() $F_i$
acts on
$F_i$
acts on
![]() $C_{H}(F_{i+1})$
, and in fact,
$C_{H}(F_{i+1})$
, and in fact,
![]() $C_{H}(F_i)=C_{C_{H}(F_{i+1})}(F_i)=C_{C_{H}(F_{i+1})}(F_i/F_{i+1})$
. So
$C_{H}(F_i)=C_{C_{H}(F_{i+1})}(F_i)=C_{C_{H}(F_{i+1})}(F_i/F_{i+1})$
. So
and hence,
We now conclude by applying Lemma A.8 to the group
![]() $C_{C_{H}(F_{i+1})^0}(F_i/F_{i+1})$
.
$C_{C_{H}(F_{i+1})^0}(F_i/F_{i+1})$
.
Theorem A.10. Let G be a (possibly nonconnected) reductive group over an algebraically closed field k. Let
![]() $\Lambda \subset G(k)$
be a solvable finite group with prime-to-p order. Then the size of
$\Lambda \subset G(k)$
be a solvable finite group with prime-to-p order. Then the size of
![]() $\pi _0 C_{G}(\Lambda )$
is bounded by a constant depending only on
$\pi _0 C_{G}(\Lambda )$
is bounded by a constant depending only on
![]() $c_{G^0}$
,
$c_{G^0}$
,
![]() $\operatorname {\mathrm {rank}} G^0$
and
$\operatorname {\mathrm {rank}} G^0$
and
![]() $\# \pi _0 G$
. In the special case when G is connected,
$\# \pi _0 G$
. In the special case when G is connected,
![]() $\# \pi _0 C_{G}(\Lambda ) \leq c_G$
by Theorem A.4.
$\# \pi _0 C_{G}(\Lambda ) \leq c_G$
by Theorem A.4.
Proof. By the first part of the proof of Lemma A.9, we have
![]() $\# \pi _0 C_{G}(\Lambda ) \leq \# \pi _0 C_{G^0}(\Lambda ) \cdot \# \pi _0 G$
. Let
$\# \pi _0 C_{G}(\Lambda ) \leq \# \pi _0 C_{G^0}(\Lambda ) \cdot \# \pi _0 G$
. Let
![]() $\Lambda '$
be
$\Lambda '$
be
![]() $\Lambda \cap G^0(k)$
, so that
$\Lambda \cap G^0(k)$
, so that
![]() $\Lambda /\Lambda ' \hookrightarrow G/G^0$
. Note that
$\Lambda /\Lambda ' \hookrightarrow G/G^0$
. Note that
![]() $C_{G^0}(\Lambda )=C_{C_{G^0}(\Lambda ')}(\Lambda /\Lambda ')$
. By Theorem A.4 (recall
$C_{G^0}(\Lambda )=C_{C_{G^0}(\Lambda ')}(\Lambda /\Lambda ')$
. By Theorem A.4 (recall
![]() $\Lambda $
has prime-to-p order by assumption), the size of
$\Lambda $
has prime-to-p order by assumption), the size of
![]() $\pi _0 C_{G^0}(\Lambda ')$
is at most
$\pi _0 C_{G^0}(\Lambda ')$
is at most
![]() $c_{G^0}$
. Applying Lemma A.9 with
$c_{G^0}$
. Applying Lemma A.9 with
![]() $H=C_{G^0}(\Lambda ')$
and
$H=C_{G^0}(\Lambda ')$
and
![]() $F=\Lambda /\Lambda '$
yields a bound for
$F=\Lambda /\Lambda '$
yields a bound for
![]() $\# \pi _0 C_{G^0}(\Lambda )$
in terms of
$\# \pi _0 C_{G^0}(\Lambda )$
in terms of
![]() $c_{G^0}$
,
$c_{G^0}$
,
![]() $\operatorname {\mathrm {rank}} G^0$
and
$\operatorname {\mathrm {rank}} G^0$
and
![]() $\# \pi _0 G$
.
$\# \pi _0 G$
.
B A curious application
This section is not relevant to the main aims of this paper, but it follows from the methods developed here, so we will give a (terse) proof.
Theorem B.1. Let G be a connected reductive group over a field k, and let
![]() $\Lambda \subset G(k)$
be a finite subgroup of order n, prime to
$\Lambda \subset G(k)$
be a finite subgroup of order n, prime to ![]() . The only prime numbers dividing the order of
. The only prime numbers dividing the order of
![]() $\pi _0 C_G(\Lambda )$
also divide n.
$\pi _0 C_G(\Lambda )$
also divide n.
Proof. We may extend k to assume that G is split, and if k is of positive characteristic, we may then lift
![]() $\Lambda $
to characteristic
$\Lambda $
to characteristic
![]() $0$
. Using Corollary 3.7, it therefore suffices to assume that
$0$
. Using Corollary 3.7, it therefore suffices to assume that ![]() . By spreading out and specializing, we may and do assume that k is a number field. Let p be a prime number not dividing n, and let v be a place of k dividing p. The argument of [Reference Griess and RybaGR98, Lemma A.8] shows that after passing to a finite extension of k and conjugating, we may assume
. By spreading out and specializing, we may and do assume that k is a number field. Let p be a prime number not dividing n, and let v be a place of k dividing p. The argument of [Reference Griess and RybaGR98, Lemma A.8] shows that after passing to a finite extension of k and conjugating, we may assume
![]() $\Lambda \subset {\mathscr G}({\mathscr O}_v)$
, where
$\Lambda \subset {\mathscr G}({\mathscr O}_v)$
, where
![]() ${\mathscr G}$
is the split model of G over
${\mathscr G}$
is the split model of G over
![]() $\mathbf {Z}$
and
$\mathbf {Z}$
and
![]() ${\mathscr O}_v$
is the ring of integers of the completion of k at v. But now Corollary 3.5 shows that
${\mathscr O}_v$
is the ring of integers of the completion of k at v. But now Corollary 3.5 shows that
![]() $C_{{\mathscr G}}(\Lambda )$
is weakly reductive, so in particular, p does not divide the order of
$C_{{\mathscr G}}(\Lambda )$
is weakly reductive, so in particular, p does not divide the order of
![]() $\pi _0 C_G(\Lambda )$
, as desired.
$\pi _0 C_G(\Lambda )$
, as desired.
C A Proof of Corollary 1.2
Proof. It is enough to check the third bulleted point in [Reference Fakhruddin, Khare and PatrikisFKP21, Theorem A]. By Theorem 1.1, for
![]() $v \neq p$
,
$v \neq p$
,
![]() ${\overline {\rho }}|_{\Gamma _{\mathbf Q_v}}$
has a p-adic lift. However, by [Reference LinLin20b, Theorem C],
${\overline {\rho }}|_{\Gamma _{\mathbf Q_v}}$
has a p-adic lift. However, by [Reference LinLin20b, Theorem C], ![]() has a crystalline lift
has a crystalline lift
![]() $\rho _p \colon \Gamma _{\mathbf Q_p} \to G(\overline {\mathbf {Z}}_p)$
for
$\rho _p \colon \Gamma _{\mathbf Q_p} \to G(\overline {\mathbf {Z}}_p)$
for
![]() $p>3$
. We claim that the Hodge–Tate cocharacter of the lift can be chosen to be regular. If
$p>3$
. We claim that the Hodge–Tate cocharacter of the lift can be chosen to be regular. If
![]() ${\overline {\rho }}_p$
is irreducible, this follows from [Reference LinLin20a, Theorem 2]. Otherwise,
${\overline {\rho }}_p$
is irreducible, this follows from [Reference LinLin20a, Theorem 2]. Otherwise,
![]() ${\overline {\rho }}_p$
factors through a maximal parabolic subgroup P of G with Levi factor
${\overline {\rho }}_p$
factors through a maximal parabolic subgroup P of G with Levi factor
![]() $L \cong \operatorname {\mathrm {GL}}_2$
, and there is a corresponding representation
$L \cong \operatorname {\mathrm {GL}}_2$
, and there is a corresponding representation
![]() $\bar r_p \colon \Gamma _{\mathbf Q_p} \to L(\overline {\mathbf F}_p)$
. By [Reference LinLin20b, §7.2.1-7.2.2],
$\bar r_p \colon \Gamma _{\mathbf Q_p} \to L(\overline {\mathbf F}_p)$
. By [Reference LinLin20b, §7.2.1-7.2.2],
![]() $r_p$
has a crystalline lift
$r_p$
has a crystalline lift
![]() $r^o$
with regular Hodge–Tate cocharacter such that
$r^o$
with regular Hodge–Tate cocharacter such that
![]() $\phi ^{\operatorname {\mathrm {Lie}}}(r^o)$
has Hodge–Tate weights slightly less than
$\phi ^{\operatorname {\mathrm {Lie}}}(r^o)$
has Hodge–Tate weights slightly less than
![]() $\underline {0}$
(in the terminology of loc. cit.). Now the second half of [Reference LinLin20b, Theorem C] implies that
$\underline {0}$
(in the terminology of loc. cit.). Now the second half of [Reference LinLin20b, Theorem C] implies that
![]() $\rho _p$
can be chosen such that it factors through P, and its associated L-valued representation lies on the same irreducible component of the spectrum of the crystalline lifting ring that
$\rho _p$
can be chosen such that it factors through P, and its associated L-valued representation lies on the same irreducible component of the spectrum of the crystalline lifting ring that
![]() $r^o$
does; in particular, its Hodge–Tate cocharacter is the same as that of
$r^o$
does; in particular, its Hodge–Tate cocharacter is the same as that of
![]() $r^o$
. Thus, [Reference Fakhruddin, Khare and PatrikisFKP21, Theorem A] gives the desired lift of
$r^o$
. Thus, [Reference Fakhruddin, Khare and PatrikisFKP21, Theorem A] gives the desired lift of
![]() ${\overline {\rho }}$
.
${\overline {\rho }}$
.
Remark C.1. The lower bound for p in Corollary 1.2 has to do with the global lifting theorem [Reference Fakhruddin, Khare and PatrikisFKP21, Theorem A], the local lifting theorem in the
![]() $\ell =p$
case [Reference LinLin20b, Theorem C], and Theorem 1.1. The bound for [Reference Fakhruddin, Khare and PatrikisFKP21, Theorem A] can be made explicit; see [Reference Fakhruddin, Khare and PatrikisFKP21, Remark 6.17]. The bound for [Reference LinLin20b, Theorem C] is 3, and the bound for Theorem 1.1 in the
$\ell =p$
case [Reference LinLin20b, Theorem C], and Theorem 1.1. The bound for [Reference Fakhruddin, Khare and PatrikisFKP21, Theorem A] can be made explicit; see [Reference Fakhruddin, Khare and PatrikisFKP21, Remark 6.17]. The bound for [Reference LinLin20b, Theorem C] is 3, and the bound for Theorem 1.1 in the
![]() $G_2$
case is 72 (Remark 6.21).
$G_2$
case is 72 (Remark 6.21).
Acknowledgments
We thank Patrick Allen, Brian Conrad, Pol van Hoften, Mikko Korhonen, Daniel Le, Martin Liebeck, Ben Martin, Gil Moss, Stefan Patrikis, Jeroen Schillewaert, Jay Taylor and Felipe Voloch for helpful conversations. We thank the anonymous referees for their work.
Competing interests
The authors have no competing interest to declare.
Financial support
Booher was partially supported by the Marsden Fund Council administered by the Royal Society of New Zealand.