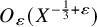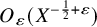1 Introduction
In [Reference Katz and SarnakKS1, Reference Katz and SarnakKS2], Katz and Sarnak made a series of fundamental conjectures about statistics of low-lying zeros in families of L-functions. Recently, these conjectures have been refined by Sarnak, Shin and Templier [Reference Sarnak, Shin and TemplierSaST] for families of parametric L-functions. There is a huge body of work on the confirmation of these conjectures for particular test functions in various families, many of which are harmonic (see, e.g. [Reference Iwaniec, Luo and SarnakILS, Reference RubinsteinRu, Reference Fouvry and IwaniecFI, Reference Hughes and RudnickHR, Reference Shin and TemplierST]). There are significantly fewer geometric families that have been studied. In this context, we mention the work of Miller [Reference MillerM1] and Young [Reference YoungYo] on families of elliptic curve L-functions and that of Yang [Reference YangYa], Cho and Kim [Reference Cho and KimCK1, Reference Cho and KimCK2] and Shankar, Södergren and Templier [Reference Shankar, Södergren and TemplierShST] on families of Artin L-functions.
In families of Artin L-functions, these results are strongly linked with counts of number fields. More precisely, the set of admissible test functions is determined by the quality of the error terms in such counting functions. In this paper we consider the sets
where for each cubic field
![]() $K/{\mathbb {Q}}$
of discriminant
$K/{\mathbb {Q}}$
of discriminant
![]() $D_K$
, we include only one of its three isomorphic copies. The first power-saving estimate for the cardinality
$D_K$
, we include only one of its three isomorphic copies. The first power-saving estimate for the cardinality
![]() $N^\pm (X):=|\mathcal {F}^\pm (X)|$
was obtained by Belabas, Bhargava and Pomerance [Reference Belabas, Bhargava and PomeranceBBP] and was later refined by Bhargava, Shankar and Tsimerman [Reference Bhargava, Shankar and TsimermanBST], Taniguchi and Thorne [Reference Taniguchi and ThorneTT] and Bhargava, Taniguchi and Thorne [Reference Bhargava, Taniguchi and ThorneBTT]. The last three of these estimates take the shape
$N^\pm (X):=|\mathcal {F}^\pm (X)|$
was obtained by Belabas, Bhargava and Pomerance [Reference Belabas, Bhargava and PomeranceBBP] and was later refined by Bhargava, Shankar and Tsimerman [Reference Bhargava, Shankar and TsimermanBST], Taniguchi and Thorne [Reference Taniguchi and ThorneTT] and Bhargava, Taniguchi and Thorne [Reference Bhargava, Taniguchi and ThorneBTT]. The last three of these estimates take the shape
for certain explicit values of
![]() $ \theta <\frac 56$
, implying, in particular, Roberts’s conjecture [Reference RobertsRo]. Here,
$ \theta <\frac 56$
, implying, in particular, Roberts’s conjecture [Reference RobertsRo]. Here,
 $$ \begin{align*}C_1^+:=\frac{1}{12\zeta(3)};\hspace{.5cm} C_2^+:=\frac{4\zeta(\frac 13)}{5\Gamma( \frac 23)^3\zeta(\frac 53)}; \hspace{.5cm} C_1^-:=\frac{1}{4\zeta(3)};\hspace{.5cm} C_2^-:=\frac{4\sqrt 3\zeta(\frac 13)}{5\Gamma( \frac 23)^3\zeta(\frac 53)}.\end{align*} $$
$$ \begin{align*}C_1^+:=\frac{1}{12\zeta(3)};\hspace{.5cm} C_2^+:=\frac{4\zeta(\frac 13)}{5\Gamma( \frac 23)^3\zeta(\frac 53)}; \hspace{.5cm} C_1^-:=\frac{1}{4\zeta(3)};\hspace{.5cm} C_2^-:=\frac{4\sqrt 3\zeta(\frac 13)}{5\Gamma( \frac 23)^3\zeta(\frac 53)}.\end{align*} $$
The presence of this secondary term is a striking feature of this family, and we are interested in studying its consequences for the distribution of low-lying zeros. More precisely, the estimate (1.1) suggests that one should be able to extract a corresponding lower-order term in various statistics on those zeros.
In addition to (1.1), we will consider precise estimates involving local conditions, which are of the form
 $$ \begin{align} N^\pm_{p} (X,T) : &= \#\{ K \in \mathcal F^\pm(X) : p \text{ has splitting type }T \text{ in } K\} \notag \\& = A^\pm_p (T ) X +B^\pm_p(T) X^{\frac 56} + O_{\varepsilon}(p^{ \omega}X^{\theta+\varepsilon}), \end{align} $$
$$ \begin{align} N^\pm_{p} (X,T) : &= \#\{ K \in \mathcal F^\pm(X) : p \text{ has splitting type }T \text{ in } K\} \notag \\& = A^\pm_p (T ) X +B^\pm_p(T) X^{\frac 56} + O_{\varepsilon}(p^{ \omega}X^{\theta+\varepsilon}), \end{align} $$
where p is a given prime, T is a splitting type and the constants
![]() $A^\pm _p (T )$
and
$A^\pm _p (T )$
and
![]() $B^\pm _p (T )$
are defined in Section 2. Here,
$B^\pm _p (T )$
are defined in Section 2. Here,
![]() $\theta $
is the same constant as that in (1.1) and
$\theta $
is the same constant as that in (1.1) and
![]() $\omega \geq 0$
. Note, in particular, that (1.2) implies (1.1) (take
$\omega \geq 0$
. Note, in particular, that (1.2) implies (1.1) (take
![]() $p=2$
in (1.2) and sum over all splitting types T).
$p=2$
in (1.2) and sum over all splitting types T).
Perhaps surprisingly, it turns out that the study of low-lying zeros has an application to cubic field counts. More precisely, we were able to obtain the following conditional omega result for
![]() $N^\pm _{p} (X,T)$
.
$N^\pm _{p} (X,T)$
.
Theorem 1.1. Assume the Generalised Riemann Hypothesis for
![]() $\zeta _K(s)$
for each
$\zeta _K(s)$
for each
![]() $K\in \mathcal F^{\pm }(X)$
. If
$K\in \mathcal F^{\pm }(X)$
. If
![]() $\theta ,\omega \geq 0$
are admissible values in (1.2), then
$\theta ,\omega \geq 0$
are admissible values in (1.2), then
![]() $\theta +\omega \geq \frac 12$
.
$\theta +\omega \geq \frac 12$
.
As part of this project, we have produced numerical data which suggest that
![]() $\theta =\frac 12$
and any
$\theta =\frac 12$
and any
![]() $\omega>0$
are admissible values in (1.2) (indicating, in particular, that the bound
$\omega>0$
are admissible values in (1.2) (indicating, in particular, that the bound
![]() $\omega +\theta \geq \frac 12$
in Theorem 1.1 could be the best possible). We have made several graphs to support this conjecture in Appendix A. As a first example of these results, in Figure 1, we display a graph of
$\omega +\theta \geq \frac 12$
in Theorem 1.1 could be the best possible). We have made several graphs to support this conjecture in Appendix A. As a first example of these results, in Figure 1, we display a graph of
![]() $X^{-\frac 12}(N^+_{5} (X,T)-A^+_5 (T ) X -B^+_5(T) X^{\frac 56} ) $
for the various splitting types T, which suggests that
$X^{-\frac 12}(N^+_{5} (X,T)-A^+_5 (T ) X -B^+_5(T) X^{\frac 56} ) $
for the various splitting types T, which suggests that
![]() $\theta =\frac 12$
is admissible and the best possible.
$\theta =\frac 12$
is admissible and the best possible.

Figure 1 The normalised error terms
![]() $X^{-\frac 12}(N^+_{5} (X,T)-A^+_5 (T ) X -B^+_5(T) X^{\frac 56} ) $
for the splitting types
$X^{-\frac 12}(N^+_{5} (X,T)-A^+_5 (T ) X -B^+_5(T) X^{\frac 56} ) $
for the splitting types
![]() $T= T_1,\dots ,T_5$
as described in Section 2.
$T= T_1,\dots ,T_5$
as described in Section 2.
Let us now describe our unconditional result on low-lying zeros. For a cubic field K, we will focus on the Dedekind zeta function
![]() $\zeta _K(s)$
, whose one-level density is defined by
$\zeta _K(s)$
, whose one-level density is defined by
 $$ \begin{align*}\mathfrak{D}_{\phi}(K) := \sum_{\gamma_{K}} \phi\left( \frac{\log (X/(2 \pi e)^2)}{2\pi} \gamma_K\right).\end{align*} $$
$$ \begin{align*}\mathfrak{D}_{\phi}(K) := \sum_{\gamma_{K}} \phi\left( \frac{\log (X/(2 \pi e)^2)}{2\pi} \gamma_K\right).\end{align*} $$
Here,
![]() $\phi $
is an even, smooth and rapidly decaying real function for which the Fourier transform
$\phi $
is an even, smooth and rapidly decaying real function for which the Fourier transform
is compactly supported. Note that
![]() $\phi $
can be extended to an entire function through the inverse Fourier transform. Moreover, X is a parameter (approximately equal to
$\phi $
can be extended to an entire function through the inverse Fourier transform. Moreover, X is a parameter (approximately equal to
![]() $|D_K|$
) and
$|D_K|$
) and
![]() $\rho _K=\frac 12+i\gamma _K$
runs through the nontrivial zerosFootnote 1 of
$\rho _K=\frac 12+i\gamma _K$
runs through the nontrivial zerosFootnote 1 of
![]() $\zeta _K(s)/\zeta (s)$
. In order to understand the distribution of the
$\zeta _K(s)/\zeta (s)$
. In order to understand the distribution of the
![]() $\gamma _K$
, we will average
$\gamma _K$
, we will average
![]() $\mathfrak {D}_{\phi }(K)$
over the family
$\mathfrak {D}_{\phi }(K)$
over the family
![]() $\mathcal F^\pm (X)$
. Our main technical result is a precise estimation of this average.
$\mathcal F^\pm (X)$
. Our main technical result is a precise estimation of this average.
Theorem 1.2. Assume that the cubic field count (1.2) holds for some fixed parameters
![]() $\frac 12\leq \theta <\frac 56$
and
$\frac 12\leq \theta <\frac 56$
and
![]() $ \omega \geq 0$
. Then, for any real even Schwartz function
$ \omega \geq 0$
. Then, for any real even Schwartz function
![]() $\phi $
for which
$\phi $
for which
![]() $\sigma :=\sup (\mathrm {supp}(\widehat \phi ))< \frac {1-\theta }{\omega + \frac 12}$
, we have the estimate
$\sigma :=\sup (\mathrm {supp}(\widehat \phi ))< \frac {1-\theta }{\omega + \frac 12}$
, we have the estimate
 $$ \begin{align} &\frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \mathfrak{D}_{\phi}(K)=\widehat \phi(0)\Big(1 + \frac{ \log (4 \pi^2 e) }{L} -\frac{C_2^\pm}{5C_1^\pm} \frac{X^{-\frac 16}}{L} + \frac{(C_2^\pm)^2 }{5(C_1^\pm)^2 } \frac{X^{-\frac 13}}{L} \Big)\nonumber \\ &\qquad\qquad+ \frac1{\pi}\int_{-\infty}^{\infty}\phi\Big(\frac{Lr}{2\pi}\Big)\operatorname{Re}\Big(\frac{\Gamma'_{\pm}}{\Gamma_{\pm}}(\tfrac12+ir)\Big)dr -\frac{2}{L}\sum_{p,e}\frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p)\nonumber\\ &\qquad\qquad-\frac{2C_2^\pm X^{-\frac 16}}{C_1^\pm L}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e}\frac{\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) \beta_e(p) +O_{\varepsilon}(X^{\theta - 1 + \sigma(\omega + \frac12 ) +\varepsilon}) , \end{align} $$
$$ \begin{align} &\frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \mathfrak{D}_{\phi}(K)=\widehat \phi(0)\Big(1 + \frac{ \log (4 \pi^2 e) }{L} -\frac{C_2^\pm}{5C_1^\pm} \frac{X^{-\frac 16}}{L} + \frac{(C_2^\pm)^2 }{5(C_1^\pm)^2 } \frac{X^{-\frac 13}}{L} \Big)\nonumber \\ &\qquad\qquad+ \frac1{\pi}\int_{-\infty}^{\infty}\phi\Big(\frac{Lr}{2\pi}\Big)\operatorname{Re}\Big(\frac{\Gamma'_{\pm}}{\Gamma_{\pm}}(\tfrac12+ir)\Big)dr -\frac{2}{L}\sum_{p,e}\frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p)\nonumber\\ &\qquad\qquad-\frac{2C_2^\pm X^{-\frac 16}}{C_1^\pm L}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e}\frac{\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) \beta_e(p) +O_{\varepsilon}(X^{\theta - 1 + \sigma(\omega + \frac12 ) +\varepsilon}) , \end{align} $$
where
![]() $\Gamma _+(s):= \pi ^{-s}\Gamma (\frac s2)^2$
,
$\Gamma _+(s):= \pi ^{-s}\Gamma (\frac s2)^2$
,
![]() $\Gamma _-(s):= \pi ^{-s}\Gamma (\frac s2)\Gamma (\frac {s+1}2)$
,
$\Gamma _-(s):= \pi ^{-s}\Gamma (\frac s2)\Gamma (\frac {s+1}2)$
,
![]() $x_p:=(1+\frac 1p+\frac 1{p^2})^{-1}$
,
$x_p:=(1+\frac 1p+\frac 1{p^2})^{-1}$
,
![]() $\theta _e$
and
$\theta _e$
and
![]() $\beta _e(p)$
are defined in (3.4) and (3.6), respectively, and
$\beta _e(p)$
are defined in (3.4) and (3.6), respectively, and
![]() $L:=\log \big ( \frac {X}{(2 \pi e)^2}\big )$
.
$L:=\log \big ( \frac {X}{(2 \pi e)^2}\big )$
.
Remark 1.3. In the language of the Katz–Sarnak heuristics, the first and third terms on the right-hand side of (1.3) are a manifestation of the symplectic symmetry type of the family
![]() $\mathcal {F}^\pm (X)$
. More precisely, one can turn (1.3) into an expansion in descending powers of L using Lemma 3.4 as well as [Reference Montgomery and VaughanMV, Lemma 12.14]. The first result in this direction is due to Yang [Reference YangYa], who showed that under the condition
$\mathcal {F}^\pm (X)$
. More precisely, one can turn (1.3) into an expansion in descending powers of L using Lemma 3.4 as well as [Reference Montgomery and VaughanMV, Lemma 12.14]. The first result in this direction is due to Yang [Reference YangYa], who showed that under the condition
![]() $\sigma <\frac 1{50}$
, we have that
$\sigma <\frac 1{50}$
, we have that
 $$ \begin{align} \frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \mathfrak{D}_{\phi}(K) =\widehat \phi(0)-\frac{\phi(0)}2+o_{X\rightarrow \infty}(1). \end{align} $$
$$ \begin{align} \frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \mathfrak{D}_{\phi}(K) =\widehat \phi(0)-\frac{\phi(0)}2+o_{X\rightarrow \infty}(1). \end{align} $$
This last condition was relaxed to
![]() $\sigma <\frac 4{41}$
by Cho–Kim [Reference Cho and KimCK1, Reference Cho and KimCK2]Footnote 2 and Shankar–Södergren–Templier [Reference Shankar, Södergren and TemplierShST], independently, and corresponds to the admissible values
$\sigma <\frac 4{41}$
by Cho–Kim [Reference Cho and KimCK1, Reference Cho and KimCK2]Footnote 2 and Shankar–Södergren–Templier [Reference Shankar, Södergren and TemplierShST], independently, and corresponds to the admissible values
![]() $\theta =\frac 79$
and
$\theta =\frac 79$
and
![]() $\omega =\frac {16}9$
in (1.1) and (1.2) (see [Reference Taniguchi and ThorneTT]). In the recent paper [Reference Bhargava, Taniguchi and ThorneBTT], Bhargava, Taniguchi and Thorne show that
$\omega =\frac {16}9$
in (1.1) and (1.2) (see [Reference Taniguchi and ThorneTT]). In the recent paper [Reference Bhargava, Taniguchi and ThorneBTT], Bhargava, Taniguchi and Thorne show that
![]() $\theta =\frac 23$
and
$\theta =\frac 23$
and
![]() $\omega =\frac 23$
are admissible and deduce that (1.4) holds as soon as
$\omega =\frac 23$
are admissible and deduce that (1.4) holds as soon as
![]() $\sigma <\frac 2{7}$
. Theorem 1.2 refines these results by obtaining a power saving estimate containing lower-order terms for the left-hand side of (1.4). Note, in particular, that the fourth term on the right-hand side of (1.3) is of order
$\sigma <\frac 2{7}$
. Theorem 1.2 refines these results by obtaining a power saving estimate containing lower-order terms for the left-hand side of (1.4). Note, in particular, that the fourth term on the right-hand side of (1.3) is of order
![]() $ X^{\frac {\sigma -1}6+o(1)}$
(see once more, Lemma 3.4).
$ X^{\frac {\sigma -1}6+o(1)}$
(see once more, Lemma 3.4).
The Katz–Sarnak heuristics are strongly linked with statistics of eigenvalues of random matrices and have been successful in predicting the main term in many families. However, this connection does not encompass lower-order terms. The major tool for making predictions in this direction is the L-functions Ratios Conjecture of Conrey, Farmer and Zirnbauer [Reference Conrey, Farmer and ZirnbauerCFZ]. In particular, these predictions are believed to hold down to an error term of size roughly the inverse of the square root of the size of the family. As an example, consider the unitary family of Dirichlet L-functions modulo q, in which the Ratios Conjecture’s prediction is particularly simple. It is shown in [Reference Goes, Jackson, Miller, Montague, Ninsuwan, Peckner and PhamG+] that if
![]() $ \eta $
is a real even Schwartz function for which
$ \eta $
is a real even Schwartz function for which
![]() $\widehat \eta $
has compact (but arbitrarily large) support, then this conjecture implies the estimate
$\widehat \eta $
has compact (but arbitrarily large) support, then this conjecture implies the estimate
 $$ \begin{align} \frac 1{\phi(q)}\sum_{\chi \bmod q}\sum_{\gamma_{\chi}} \eta\Big( \frac{\log q}{2\pi} \gamma_\chi\Big) = \widehat{\eta}(0) \Big( 1-\frac { \log(8\pi e^{\gamma})}{\log q}-\frac{\sum_{p\mid q}\frac{\log p}{p-1}}{\log q}\Big) +\int_0^{\infty}\frac{\widehat{\eta}(0)-\widehat{\eta}(t)}{q^{\frac t2}-q^{-\frac t2}} dt + E(q), \end{align} $$
$$ \begin{align} \frac 1{\phi(q)}\sum_{\chi \bmod q}\sum_{\gamma_{\chi}} \eta\Big( \frac{\log q}{2\pi} \gamma_\chi\Big) = \widehat{\eta}(0) \Big( 1-\frac { \log(8\pi e^{\gamma})}{\log q}-\frac{\sum_{p\mid q}\frac{\log p}{p-1}}{\log q}\Big) +\int_0^{\infty}\frac{\widehat{\eta}(0)-\widehat{\eta}(t)}{q^{\frac t2}-q^{-\frac t2}} dt + E(q), \end{align} $$
where
![]() $\rho _\chi =\frac 12+i\gamma _\chi $
is running through the nontrivial zeros of
$\rho _\chi =\frac 12+i\gamma _\chi $
is running through the nontrivial zeros of
![]() $L(s,\chi )$
and
$L(s,\chi )$
and
![]() $E(q) \ll _{\varepsilon } q^{-\frac 1 2+\varepsilon }$
. In [Reference Fiorilli and MillerFM], it was shown that this bound on
$E(q) \ll _{\varepsilon } q^{-\frac 1 2+\varepsilon }$
. In [Reference Fiorilli and MillerFM], it was shown that this bound on
![]() $E(q)$
is essentially the best possible, in general, but can be improved when the support of
$E(q)$
is essentially the best possible, in general, but can be improved when the support of
![]() $\widehat \eta $
is small. This last condition also results in improved error terms in various other families (see, e.g. [Reference MillerM2, Reference MillerM3, Reference Fiorilli, Parks and SödergrenFPS1, Reference Fiorilli, Parks and SödergrenFPS2, Reference Devin, Fiorilli and SödergrenDFS]).
$\widehat \eta $
is small. This last condition also results in improved error terms in various other families (see, e.g. [Reference MillerM2, Reference MillerM3, Reference Fiorilli, Parks and SödergrenFPS1, Reference Fiorilli, Parks and SödergrenFPS2, Reference Devin, Fiorilli and SödergrenDFS]).
Following the Ratios Conjecture recipe, we can obtain a prediction for the average of
![]() $\mathfrak {D}_\phi (K)$
over the family
$\mathfrak {D}_\phi (K)$
over the family
![]() $\mathcal {F}^\pm (X)$
. The resulting conjecture, however, differs from Theorem 1.2 by a term of order
$\mathcal {F}^\pm (X)$
. The resulting conjecture, however, differs from Theorem 1.2 by a term of order
![]() $X^{\frac {\sigma -1}6+o(1)} $
, which is considerably larger than the expected error term
$X^{\frac {\sigma -1}6+o(1)} $
, which is considerably larger than the expected error term
![]() $O_{\varepsilon }(X^{-\frac 12 +\varepsilon })$
. We were able to isolate a specific step in the argument which could be improved in order to include this additional contribution. More precisely, modifying Step 4 in [Reference Conrey, Farmer and ZirnbauerCFZ, Section 5.1], we recover a refined Ratios Conjecture which predicts a term of order
$O_{\varepsilon }(X^{-\frac 12 +\varepsilon })$
. We were able to isolate a specific step in the argument which could be improved in order to include this additional contribution. More precisely, modifying Step 4 in [Reference Conrey, Farmer and ZirnbauerCFZ, Section 5.1], we recover a refined Ratios Conjecture which predicts a term of order
![]() $X^{\frac {\sigma -1}6+o(1)}$
, in agreement with Theorem 1.2.
$X^{\frac {\sigma -1}6+o(1)}$
, in agreement with Theorem 1.2.
Theorem 1.4. Let
![]() $\frac 12\leq \theta <\frac 56$
and
$\frac 12\leq \theta <\frac 56$
and
![]() $\omega \geq 0 $
be, such that (1.2) holds. Assume Conjecture 4.3 on the average of shifts of the logarithmic derivative of
$\omega \geq 0 $
be, such that (1.2) holds. Assume Conjecture 4.3 on the average of shifts of the logarithmic derivative of
![]() $\zeta _K(s)/\zeta (s)$
, as well as the Riemann Hypothesis for
$\zeta _K(s)/\zeta (s)$
, as well as the Riemann Hypothesis for
![]() $\zeta _K(s)$
, for all
$\zeta _K(s)$
, for all
![]() $K\in \mathcal {F}^{\pm }(X)$
. Let
$K\in \mathcal {F}^{\pm }(X)$
. Let
![]() $\phi $
be a real even Schwartz function, such that
$\phi $
be a real even Schwartz function, such that
![]() $ \widehat \phi $
is compactly supported. Then we have the estimate
$ \widehat \phi $
is compactly supported. Then we have the estimate
 $$ \begin{align*} &\frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \sum_{\gamma_K}\phi \Big(\frac{L\gamma_K}{2\pi }\Big)=\widehat \phi(0)\Big(1 + \frac{ \log (4 \pi^2 e) }{L} -\frac{C_2^\pm}{5C_1^\pm} \frac{X^{-\frac 16}}{L} + \frac{(C_2^\pm)^2 }{5(C_1^\pm)^2 } \frac{X^{-\frac 13}}{L} \Big) \\ &\qquad + \frac1{\pi}\int_{-\infty}^{\infty}\phi\Big(\frac{Lr}{2\pi}\Big)\operatorname{Re}\Big(\frac{\Gamma'_{\pm}}{\Gamma_{\pm}}(\tfrac12+ir)\Big)dr -\frac{2}{L}\sum_{p,e}\frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p) \\ &\qquad -\frac{2C_2^\pm X^{-\frac 16}}{C_1^\pm L}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e}\frac{\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) \beta_e(p)+J^\pm(X) + O_\varepsilon(X^{\theta-1+\varepsilon}), \end{align*} $$
$$ \begin{align*} &\frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \sum_{\gamma_K}\phi \Big(\frac{L\gamma_K}{2\pi }\Big)=\widehat \phi(0)\Big(1 + \frac{ \log (4 \pi^2 e) }{L} -\frac{C_2^\pm}{5C_1^\pm} \frac{X^{-\frac 16}}{L} + \frac{(C_2^\pm)^2 }{5(C_1^\pm)^2 } \frac{X^{-\frac 13}}{L} \Big) \\ &\qquad + \frac1{\pi}\int_{-\infty}^{\infty}\phi\Big(\frac{Lr}{2\pi}\Big)\operatorname{Re}\Big(\frac{\Gamma'_{\pm}}{\Gamma_{\pm}}(\tfrac12+ir)\Big)dr -\frac{2}{L}\sum_{p,e}\frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p) \\ &\qquad -\frac{2C_2^\pm X^{-\frac 16}}{C_1^\pm L}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e}\frac{\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) \beta_e(p)+J^\pm(X) + O_\varepsilon(X^{\theta-1+\varepsilon}), \end{align*} $$
where
![]() $J^\pm (X)$
is defined in (5.1). If
$J^\pm (X)$
is defined in (5.1). If
![]() $\sigma =\sup ( \mathrm {supp}(\widehat \phi )) <1$
, then we have the estimate
$\sigma =\sup ( \mathrm {supp}(\widehat \phi )) <1$
, then we have the estimate
 $$ \begin{align} J^\pm(X) = C^{\pm} X^{-\frac 13} \int_{\mathbb R} \Big( \frac{X}{(2\pi e)^2 }\Big)^{\frac{\xi}6} \widehat \phi(\xi) d\xi +O_\varepsilon( X^{\frac{\sigma-1}2+\varepsilon}), \end{align} $$
$$ \begin{align} J^\pm(X) = C^{\pm} X^{-\frac 13} \int_{\mathbb R} \Big( \frac{X}{(2\pi e)^2 }\Big)^{\frac{\xi}6} \widehat \phi(\xi) d\xi +O_\varepsilon( X^{\frac{\sigma-1}2+\varepsilon}), \end{align} $$
where
![]() $C^{\pm } $
is a nonzero absolute constant which is defined in (5.7). Otherwise, we have the identity
$C^{\pm } $
is a nonzero absolute constant which is defined in (5.7). Otherwise, we have the identity
 $$ \begin{align} J^\pm(X)&=-\frac{1}{\pi i} \int_{(\frac 15)} \phi \Big(\frac{Ls}{2\pi i}\Big) \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) X^{-s} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \frac{ A_3( -s, s) }{1-s} ds \nonumber\\ &\quad-\frac{1}{\pi i} \int_{(\frac 1{20})} \phi \Big(\frac{Ls}{2\pi i}\Big)\frac{C_2^\pm }{C_1^\pm} X^{-s-\frac 16} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \Bigg\{ \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\zeta(\tfrac 56-s)}{\zeta(\tfrac 56+s)}\frac{ A_4(-s,s)}{ 1- \frac{ 6s}5}\nonumber \\ &\quad +\frac{C_2^\pm}{C_1^\pm}X^{-\frac 16} \frac{A_3( -s, s) }{1-s} \Bigg\}ds, \end{align} $$
$$ \begin{align} J^\pm(X)&=-\frac{1}{\pi i} \int_{(\frac 15)} \phi \Big(\frac{Ls}{2\pi i}\Big) \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) X^{-s} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \frac{ A_3( -s, s) }{1-s} ds \nonumber\\ &\quad-\frac{1}{\pi i} \int_{(\frac 1{20})} \phi \Big(\frac{Ls}{2\pi i}\Big)\frac{C_2^\pm }{C_1^\pm} X^{-s-\frac 16} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \Bigg\{ \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\zeta(\tfrac 56-s)}{\zeta(\tfrac 56+s)}\frac{ A_4(-s,s)}{ 1- \frac{ 6s}5}\nonumber \\ &\quad +\frac{C_2^\pm}{C_1^\pm}X^{-\frac 16} \frac{A_3( -s, s) }{1-s} \Bigg\}ds, \end{align} $$
where
![]() $A_3(-s,s)$
and
$A_3(-s,s)$
and
![]() $A_4(-s,s)$
are defined in (5.2) and (4.9), respectively.
$A_4(-s,s)$
are defined in (5.2) and (4.9), respectively.
Remark 1.5. It is interesting to compare Theorem 1.4 with Theorem 1.2, especially when
![]() $\sigma $
is small. Indeed, for
$\sigma $
is small. Indeed, for
![]() $\sigma <1$
, the difference between those two evaluations of the one-level density is given by
$\sigma <1$
, the difference between those two evaluations of the one-level density is given by
 $$ \begin{align*}C^\pm X^{-\frac 13}\int_{\mathbb R} \Big( \frac{X}{(2\pi e)^2 }\Big)^{\frac{\xi}6} \widehat \phi(\xi) d\xi+O_\varepsilon\big(X^{\frac{\sigma-1}{2}+\varepsilon}+X^{\theta - 1 + \sigma(\omega + \frac12 ) +\varepsilon}\big).\end{align*} $$
$$ \begin{align*}C^\pm X^{-\frac 13}\int_{\mathbb R} \Big( \frac{X}{(2\pi e)^2 }\Big)^{\frac{\xi}6} \widehat \phi(\xi) d\xi+O_\varepsilon\big(X^{\frac{\sigma-1}{2}+\varepsilon}+X^{\theta - 1 + \sigma(\omega + \frac12 ) +\varepsilon}\big).\end{align*} $$
Selecting test functions
![]() $\phi $
for which
$\phi $
for which
![]() $\widehat \phi \geq 0$
and
$\widehat \phi \geq 0$
and
![]() $\sigma $
is positive but arbitrarily small, this shows that no matter how large
$\sigma $
is positive but arbitrarily small, this shows that no matter how large
![]() $\omega $
is, any admissible
$\omega $
is, any admissible
![]() $\theta <\frac 23$
in (1.1) and (1.2) would imply that this difference is asymptotic to
$\theta <\frac 23$
in (1.1) and (1.2) would imply that this difference is asymptotic to
![]() $C^\pm X^{-\frac 13}\int _{\mathbb R} ( \frac {X}{(2\pi e)^2 })^{\frac {\xi }6} \widehat \phi (\xi ) d\xi \gg X^{-\frac 13}$
. In fact, Roberts’s numerics [Reference RobertsRo] (see also [Reference BelabasB]), as well as our numerical investigations described in Appendix A, indicate that
$C^\pm X^{-\frac 13}\int _{\mathbb R} ( \frac {X}{(2\pi e)^2 })^{\frac {\xi }6} \widehat \phi (\xi ) d\xi \gg X^{-\frac 13}$
. In fact, Roberts’s numerics [Reference RobertsRo] (see also [Reference BelabasB]), as well as our numerical investigations described in Appendix A, indicate that
![]() $\theta = \frac 12$
could be admissible in (1.1) and (1.2). In other words, in this family, the Ratios Conjecture, as well as our refinement (combined with the assumption of (1.1) and (1.2) for some
$\theta = \frac 12$
could be admissible in (1.1) and (1.2). In other words, in this family, the Ratios Conjecture, as well as our refinement (combined with the assumption of (1.1) and (1.2) for some
![]() $\theta <\frac 23$
and
$\theta <\frac 23$
and
![]() $\omega \geq 0$
), are not sufficient to obtain a prediction with precision
$\omega \geq 0$
), are not sufficient to obtain a prediction with precision
![]() $o(X^{-\frac 13})$
. This is surprising, since Conrey, Farmer and Zirnbauer have conjectured this error term to be of size
$o(X^{-\frac 13})$
. This is surprising, since Conrey, Farmer and Zirnbauer have conjectured this error term to be of size
![]() $O_\varepsilon (X^{-\frac 12+\varepsilon })$
, and this has been confirmed in several important families [Reference MillerM2, Reference MillerM3, Reference Fiorilli, Parks and SödergrenFPS1, Reference Fiorilli, Parks and SödergrenFPS2, Reference Devin, Fiorilli and SödergrenDFS] (for a restricted set of test functions).
$O_\varepsilon (X^{-\frac 12+\varepsilon })$
, and this has been confirmed in several important families [Reference MillerM2, Reference MillerM3, Reference Fiorilli, Parks and SödergrenFPS1, Reference Fiorilli, Parks and SödergrenFPS2, Reference Devin, Fiorilli and SödergrenDFS] (for a restricted set of test functions).
2 Background
Let
![]() $K/{\mathbb {Q}}$
be a non-Galois cubic field, and let
$K/{\mathbb {Q}}$
be a non-Galois cubic field, and let
![]() $\widehat {K}$
be the Galois closure of K over
$\widehat {K}$
be the Galois closure of K over
![]() $\mathbb {Q}$
. Then, the Dedekind zeta function of the field K has the decomposition
$\mathbb {Q}$
. Then, the Dedekind zeta function of the field K has the decomposition
where
![]() $L(s,\rho ,\widehat {K}/\mathbb {Q})$
is the Artin L-function associated to the two-dimensional representation
$L(s,\rho ,\widehat {K}/\mathbb {Q})$
is the Artin L-function associated to the two-dimensional representation
![]() $\rho $
of
$\rho $
of
![]() $\mathrm {Gal}(\widehat K/{\mathbb {Q}}) \simeq S_3$
. The strong Artin conjecture is known for such representations; in this particular case, we have an explicit underlying cuspidal representation
$\mathrm {Gal}(\widehat K/{\mathbb {Q}}) \simeq S_3$
. The strong Artin conjecture is known for such representations; in this particular case, we have an explicit underlying cuspidal representation
![]() $\tau $
of
$\tau $
of
![]() $GL_2/\mathbb {Q}$
, such that
$GL_2/\mathbb {Q}$
, such that
![]() $L(s,\rho ,\widehat {K}/\mathbb {Q})=L(s,\tau )$
. For the sake of completeness, let us describe
$L(s,\rho ,\widehat {K}/\mathbb {Q})=L(s,\tau )$
. For the sake of completeness, let us describe
![]() $\tau $
in more detail. Let
$\tau $
in more detail. Let
![]() $F=\mathbb {Q}[\sqrt {D_K}]$
, and let
$F=\mathbb {Q}[\sqrt {D_K}]$
, and let
![]() $\chi $
be a nontrivial character of Gal
$\chi $
be a nontrivial character of Gal
![]() $(\widehat {K}/F)\simeq C_3$
, considered as a Hecke character of F. Then
$(\widehat {K}/F)\simeq C_3$
, considered as a Hecke character of F. Then
![]() $\tau =\text {Ind}^{\mathbb Q}_{F} \chi $
is a dihedral representation of central character
$\tau =\text {Ind}^{\mathbb Q}_{F} \chi $
is a dihedral representation of central character
![]() $\chi _{D_K}=\big (\frac {D_K}\cdot \big )$
. When
$\chi _{D_K}=\big (\frac {D_K}\cdot \big )$
. When
![]() $D_K <0$
,
$D_K <0$
,
![]() $\tau $
corresponds to a weight one newform of level
$\tau $
corresponds to a weight one newform of level
![]() $\left | D_K \right |$
and nebentypus
$\left | D_K \right |$
and nebentypus
![]() $\chi _{D_K}$
, and when
$\chi _{D_K}$
, and when
![]() $D_K>0$
, it corresponds to a weight zero Maass form (see [Reference Duke, Friedlander and IwaniecDFI, Introduction]). In both cases, we will denote the corresponding automorphic form by
$D_K>0$
, it corresponds to a weight zero Maass form (see [Reference Duke, Friedlander and IwaniecDFI, Introduction]). In both cases, we will denote the corresponding automorphic form by
![]() $f_K$
, and, in particular, we have the equality
$f_K$
, and, in particular, we have the equality
We are interested in the analytic properties of
![]() $\zeta _K(s)/\zeta (s)=L(s,f_K)$
. We have the functional equation
$\zeta _K(s)/\zeta (s)=L(s,f_K)$
. We have the functional equation
Here,
![]() $\Lambda (s,f_K):= |D_K|^{\frac s2} \Gamma _{f_K}(s) L(s,f_K)$
is the completed L-function, with the gamma factor
$\Lambda (s,f_K):= |D_K|^{\frac s2} \Gamma _{f_K}(s) L(s,f_K)$
is the completed L-function, with the gamma factor
 $$ \begin{align*}\Gamma_{f_K}(s)=\begin{cases} \Gamma_+(s) & \text{ if } D_K>0 \text{ } (\text{that is } K \text{ has signature } (3,0) ); \\ \Gamma_-(s) & \text{ if } D_K < 0 \text{ } (\text{that is } K \text{ has signature } (1,1) ) , \end{cases}\end{align*} $$
$$ \begin{align*}\Gamma_{f_K}(s)=\begin{cases} \Gamma_+(s) & \text{ if } D_K>0 \text{ } (\text{that is } K \text{ has signature } (3,0) ); \\ \Gamma_-(s) & \text{ if } D_K < 0 \text{ } (\text{that is } K \text{ has signature } (1,1) ) , \end{cases}\end{align*} $$
where
![]() $\Gamma _+(s):= \pi ^{-s}\Gamma (\frac s2)^2$
and
$\Gamma _+(s):= \pi ^{-s}\Gamma (\frac s2)^2$
and
![]() $\Gamma _-(s):= \pi ^{-s}\Gamma (\frac s2)\Gamma (\frac {s+1}2)$
.
$\Gamma _-(s):= \pi ^{-s}\Gamma (\frac s2)\Gamma (\frac {s+1}2)$
.
The coefficients of
![]() $L(s,f_K)$
have an explicit description in terms of the splitting type of the prime ideal
$L(s,f_K)$
have an explicit description in terms of the splitting type of the prime ideal
![]() $(p)\mathcal O_{K}$
. Writing
$(p)\mathcal O_{K}$
. Writing
 $$ \begin{align*}L(s,f_K) = \sum_{n =1}^\infty \frac{\lambda_K (n)}{n^s},\end{align*} $$
$$ \begin{align*}L(s,f_K) = \sum_{n =1}^\infty \frac{\lambda_K (n)}{n^s},\end{align*} $$
we have that

where
 $$ \begin{align*}\tau_e:= \begin{cases} 1 &\text{ if } e\equiv 0 \bmod 3; \\ -1 &\text{ if } e\equiv 1 \bmod 3; \\ 0 &\text{ if } e\equiv 2 \bmod 3. \end{cases}\end{align*} $$
$$ \begin{align*}\tau_e:= \begin{cases} 1 &\text{ if } e\equiv 0 \bmod 3; \\ -1 &\text{ if } e\equiv 1 \bmod 3; \\ 0 &\text{ if } e\equiv 2 \bmod 3. \end{cases}\end{align*} $$
Furthermore, we find that the coefficients of the reciprocal
 $$ \begin{align} \frac{1}{L(s,f_K)} = \sum_{n=1}^\infty \frac{ \mu_K (n)}{n^s} \end{align} $$
$$ \begin{align} \frac{1}{L(s,f_K)} = \sum_{n=1}^\infty \frac{ \mu_K (n)}{n^s} \end{align} $$
are given by
 $$ \begin{align*} \mu_{K}(p^k) = \begin{cases} -\lambda_K(p) & \mbox{ if } k = 1;\\ \Big( \frac{D_K} p\Big) & \mbox{ if } k = 2;\\ 0 & \mbox{ if } k> 2. \end{cases} \end{align*} $$
$$ \begin{align*} \mu_{K}(p^k) = \begin{cases} -\lambda_K(p) & \mbox{ if } k = 1;\\ \Big( \frac{D_K} p\Big) & \mbox{ if } k = 2;\\ 0 & \mbox{ if } k> 2. \end{cases} \end{align*} $$
The remaining values of
![]() $\lambda _K(n)$
and
$\lambda _K(n)$
and
![]() $\mu _K(n)$
are determined by multiplicativity. Finally, the coefficients of the logarithmic derivative
$\mu _K(n)$
are determined by multiplicativity. Finally, the coefficients of the logarithmic derivative
 $$ \begin{align*}-\frac{L'}{L}(s,f_K)=\sum_{n\geq 1} \frac{\Lambda(n)a_K(n)}{n^s}\end{align*} $$
$$ \begin{align*}-\frac{L'}{L}(s,f_K)=\sum_{n\geq 1} \frac{\Lambda(n)a_K(n)}{n^s}\end{align*} $$
are given by

where
 $$ \begin{align*}\eta_e:= \begin{cases} 2 &\text{ if } e \equiv 0 \bmod 3; \\ -1 &\text{ if } e \equiv \pm 1 \bmod 3. \end{cases}\end{align*} $$
$$ \begin{align*}\eta_e:= \begin{cases} 2 &\text{ if } e \equiv 0 \bmod 3; \\ -1 &\text{ if } e \equiv \pm 1 \bmod 3. \end{cases}\end{align*} $$
We now describe explicitly the constants
![]() $A_p^\pm (T)$
and
$A_p^\pm (T)$
and
![]() $B_p^\pm (T)$
that appear in (1.2). More generally, let
$B_p^\pm (T)$
that appear in (1.2). More generally, let
![]() $\mathbf {p} = ( p_1 , \ldots , p_J)$
be a vector of primes and let
$\mathbf {p} = ( p_1 , \ldots , p_J)$
be a vector of primes and let
![]() $\mathbf {k} = ( k_1 ,\ldots , k_J )\in \{1,2,3,4,5\}^J $
(when
$\mathbf {k} = ( k_1 ,\ldots , k_J )\in \{1,2,3,4,5\}^J $
(when
![]() $J=1$
,
$J=1$
,
![]() $\mathbf {p}=(p)$
is a scalar, and we will abbreviate by writing
$\mathbf {p}=(p)$
is a scalar, and we will abbreviate by writing
![]() $\mathbf {p}=p$
and similarly for
$\mathbf {p}=p$
and similarly for
![]() $\mathbf {k}$
). We expect that
$\mathbf {k}$
). We expect that
 $$ \begin{align} N^\pm_{\mathbf{p}} (X,T_{\mathbf{k}}) : &= \#\{ K \in \mathcal F^\pm(X) : p_j \text{ has splitting type }T_{k_j} \text{ in }K \; (1\leq j\leq J)\} \notag \\& = A^\pm_{\mathbf{p}} (T_{\mathbf{k}} ) X +B^\pm_{\mathbf{p}}(T_{\mathbf{k}}) X^{\frac 56} + O_{\varepsilon}((p_1 \cdots p_J )^{ \omega}X^{\theta+\varepsilon}), \end{align} $$
$$ \begin{align} N^\pm_{\mathbf{p}} (X,T_{\mathbf{k}}) : &= \#\{ K \in \mathcal F^\pm(X) : p_j \text{ has splitting type }T_{k_j} \text{ in }K \; (1\leq j\leq J)\} \notag \\& = A^\pm_{\mathbf{p}} (T_{\mathbf{k}} ) X +B^\pm_{\mathbf{p}}(T_{\mathbf{k}}) X^{\frac 56} + O_{\varepsilon}((p_1 \cdots p_J )^{ \omega}X^{\theta+\varepsilon}), \end{align} $$
for some
![]() $\omega \geq 0$
and with the same
$\omega \geq 0$
and with the same
![]() $\theta $
as in (1.1). Here,
$\theta $
as in (1.1). Here,
 $$ \begin{align*}A^\pm_{\mathbf{p}} ( T_{\mathbf{k}} ) = C_1^\pm \prod_{j = 1}^J ( x_{p_j} c_{k_j} (p_j ) ),\hspace{1cm} B^\pm_{\mathbf{p}} ( T_{\mathbf{k}} ) = C_2^\pm \prod_{j = 1}^J ( y_{p_j} d_{k_j} (p_j ) ) ,\end{align*} $$
$$ \begin{align*}A^\pm_{\mathbf{p}} ( T_{\mathbf{k}} ) = C_1^\pm \prod_{j = 1}^J ( x_{p_j} c_{k_j} (p_j ) ),\hspace{1cm} B^\pm_{\mathbf{p}} ( T_{\mathbf{k}} ) = C_2^\pm \prod_{j = 1}^J ( y_{p_j} d_{k_j} (p_j ) ) ,\end{align*} $$
 $$ \begin{align*}x_p:=\Big(1+\frac 1p+\frac 1{p^2}\Big)^{-1}, \hspace{2cm} y_p:=\frac{1-p^{-\frac 13}}{(1-p^{-\frac 53})(1+p^{-1})},\end{align*} $$
$$ \begin{align*}x_p:=\Big(1+\frac 1p+\frac 1{p^2}\Big)^{-1}, \hspace{2cm} y_p:=\frac{1-p^{-\frac 13}}{(1-p^{-\frac 53})(1+p^{-1})},\end{align*} $$
and
![]() $c_k(p)$
and
$c_k(p)$
and
![]() $d_k(p)$
are defined in the following table:
$d_k(p)$
are defined in the following table:

Recently, Bhargava, Taniguchi and Thorne [Reference Bhargava, Taniguchi and ThorneBTT] have shown that the values
![]() $\theta =\omega =\frac {2}3$
are admissible in (2.3).
$\theta =\omega =\frac {2}3$
are admissible in (2.3).
3 New lower-order terms in the one-level density
In this section, we shall estimate the one-level density
 $$ \begin{align*}\frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \mathfrak{D}_{\phi}(K)\end{align*} $$
$$ \begin{align*}\frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \mathfrak{D}_{\phi}(K)\end{align*} $$
assuming the cubic field count (1.2) for some fixed parameters
![]() $\frac 12\leq \theta <\frac 56$
and
$\frac 12\leq \theta <\frac 56$
and
![]() $ \omega \geq 0$
. Throughout the paper, we will use the shorthand
$ \omega \geq 0$
. Throughout the paper, we will use the shorthand
The starting point of this section is the explicit formula.
Lemma 3.1. Let
![]() $\phi $
be a real even Schwartz function whose Fourier transform is compactly supported, and let
$\phi $
be a real even Schwartz function whose Fourier transform is compactly supported, and let
![]() $K\in \mathcal {F}^\pm (X)$
. We have the formula
$K\in \mathcal {F}^\pm (X)$
. We have the formula
 $$ \begin{align} \mathfrak{D}_\phi(K) = \sum_{\gamma_K}\phi\Big(\frac{L\gamma_K}{2\pi}\Big)=& \frac{\widehat\phi(0)}{L } \log{|D_K|} + \frac1{\pi}\int_{-\infty}^{\infty}\phi\Big(\frac{Lr}{2\pi}\Big)\operatorname{Re}\Big(\frac{\Gamma'_{\pm}}{\Gamma_{\pm}}(\tfrac12+ir)\Big)dr \nonumber\\ & -\frac2{L }\sum_{n=1}^{\infty}\frac{\Lambda(n)}{\sqrt n}\widehat\phi\Big(\frac{\log n}{L}\Big) a_K(n), \end{align} $$
$$ \begin{align} \mathfrak{D}_\phi(K) = \sum_{\gamma_K}\phi\Big(\frac{L\gamma_K}{2\pi}\Big)=& \frac{\widehat\phi(0)}{L } \log{|D_K|} + \frac1{\pi}\int_{-\infty}^{\infty}\phi\Big(\frac{Lr}{2\pi}\Big)\operatorname{Re}\Big(\frac{\Gamma'_{\pm}}{\Gamma_{\pm}}(\tfrac12+ir)\Big)dr \nonumber\\ & -\frac2{L }\sum_{n=1}^{\infty}\frac{\Lambda(n)}{\sqrt n}\widehat\phi\Big(\frac{\log n}{L}\Big) a_K(n), \end{align} $$
where
![]() $\rho _K=\frac 12+i\gamma _K$
runs over the nontrivial zeros of
$\rho _K=\frac 12+i\gamma _K$
runs over the nontrivial zeros of
![]() $L(s,f_K)$
.
$L(s,f_K)$
.
Proof. This follows from, for example, [Reference Rudnick and SarnakRS, Proposition 2.1], but for the sake of completeness, we reproduce the proof here. By Cauchy’s integral formula, we have the identity
 $$ \begin{align*} \sum_{\gamma_K}\phi\Big(\frac{L\gamma_K}{2\pi}\Big) &=\frac{1}{2\pi i} \int_{(\frac 32)}\phi\left( \frac{L}{2\pi i} \left( s - \frac{1}{2} \right)\right) \frac{\Lambda'}{\Lambda}(s,f_K)ds \\ &\quad-\frac{1}{2\pi i} \int_{(-\frac 12)}\phi\left( \frac{L}{2\pi i} \left( s - \frac{1}{2} \right)\right) \frac{\Lambda'}{\Lambda}(s,f_K) ds. \end{align*} $$
$$ \begin{align*} \sum_{\gamma_K}\phi\Big(\frac{L\gamma_K}{2\pi}\Big) &=\frac{1}{2\pi i} \int_{(\frac 32)}\phi\left( \frac{L}{2\pi i} \left( s - \frac{1}{2} \right)\right) \frac{\Lambda'}{\Lambda}(s,f_K)ds \\ &\quad-\frac{1}{2\pi i} \int_{(-\frac 12)}\phi\left( \frac{L}{2\pi i} \left( s - \frac{1}{2} \right)\right) \frac{\Lambda'}{\Lambda}(s,f_K) ds. \end{align*} $$
These integrals converge since
![]() $\phi \left (\frac {L}{2 \pi i}\left ( s-\frac {1}{2} \right ) \right )$
is rapidly decreasing in vertical strips. For the second integral, we apply the change of variables
$\phi \left (\frac {L}{2 \pi i}\left ( s-\frac {1}{2} \right ) \right )$
is rapidly decreasing in vertical strips. For the second integral, we apply the change of variables
![]() $s \rightarrow 1-s$
. Then, by the functional equation in the form
$s \rightarrow 1-s$
. Then, by the functional equation in the form
![]() $ \frac {\Lambda '}{\Lambda }(1-s,f_K)=-\frac {\Lambda '}{\Lambda }(s,f_K)$
and since
$ \frac {\Lambda '}{\Lambda }(1-s,f_K)=-\frac {\Lambda '}{\Lambda }(s,f_K)$
and since
![]() $\phi (-s)=\phi (s)$
, we deduce that
$\phi (-s)=\phi (s)$
, we deduce that
 $$ \begin{align*} \sum_{\gamma_K}\phi\Big(\frac{L\gamma_K}{2\pi}\Big)=\frac{1}{\pi i} \int_{(\frac 32)} \phi\left( \frac{L}{2\pi i} \left( s - \frac{1}{2} \right)\right) \frac{\Lambda'}{\Lambda}(s,f_K)ds. \end{align*} $$
$$ \begin{align*} \sum_{\gamma_K}\phi\Big(\frac{L\gamma_K}{2\pi}\Big)=\frac{1}{\pi i} \int_{(\frac 32)} \phi\left( \frac{L}{2\pi i} \left( s - \frac{1}{2} \right)\right) \frac{\Lambda'}{\Lambda}(s,f_K)ds. \end{align*} $$
Next, we insert the identity
 $$ \begin{align*}\frac{\Lambda'}{\Lambda}(s,f_K)=\frac{1}{2}\log |D_K| + \frac{\Gamma_{f_K}'}{\Gamma_{f_K}}(s) - \sum_{n\geq 1}\frac{\Lambda(n)a_K(n)}{n^s}\end{align*} $$
$$ \begin{align*}\frac{\Lambda'}{\Lambda}(s,f_K)=\frac{1}{2}\log |D_K| + \frac{\Gamma_{f_K}'}{\Gamma_{f_K}}(s) - \sum_{n\geq 1}\frac{\Lambda(n)a_K(n)}{n^s}\end{align*} $$
and separate into three integrals. By shifting the contour of integration to
![]() $\operatorname {Re}(s)=\frac 12$
in the first two integrals, we obtain the first two terms on the right-hand side of (3.1). The third integral is equal to
$\operatorname {Re}(s)=\frac 12$
in the first two integrals, we obtain the first two terms on the right-hand side of (3.1). The third integral is equal to
 $$ \begin{align*} -2\sum_{n\geq 1} \frac{\Lambda(n)a_K(n)}{\sqrt{n}}\frac{1}{2\pi i} \int_{(\frac 32)} \phi\left( \frac{L}{2\pi i} \left( s - \frac{1}{2} \right)\right)n^{-(s-\frac 12)}ds. \end{align*} $$
$$ \begin{align*} -2\sum_{n\geq 1} \frac{\Lambda(n)a_K(n)}{\sqrt{n}}\frac{1}{2\pi i} \int_{(\frac 32)} \phi\left( \frac{L}{2\pi i} \left( s - \frac{1}{2} \right)\right)n^{-(s-\frac 12)}ds. \end{align*} $$
By moving the contour to
![]() $\operatorname {Re}(s)=\frac 12$
and applying Fourier inversion, we find the third term on the right-hand side of (3.1) and the claim follows.
$\operatorname {Re}(s)=\frac 12$
and applying Fourier inversion, we find the third term on the right-hand side of (3.1) and the claim follows.
Our goal is to average (3.1) over
![]() $K \in \mathcal {F}^\pm (X)$
. We begin with the first term.
$K \in \mathcal {F}^\pm (X)$
. We begin with the first term.
Lemma 3.2. Assume that (1.1) holds for some
![]() $0\leq \theta <\frac 56$
. Then, we have the estimate
$0\leq \theta <\frac 56$
. Then, we have the estimate
 $$ \begin{align*}\frac{1}{ N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \log{|D_K|} = \log X - 1 -\frac{C_2^\pm}{5C_1^\pm} X^{-\frac 16} + \frac{(C_2^\pm)^2}{ 5 (C_1^\pm)^2 } X^{- \frac13} +O_{\varepsilon}(X^{\theta-1+\varepsilon}+X^{-\frac 12}).\end{align*} $$
$$ \begin{align*}\frac{1}{ N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \log{|D_K|} = \log X - 1 -\frac{C_2^\pm}{5C_1^\pm} X^{-\frac 16} + \frac{(C_2^\pm)^2}{ 5 (C_1^\pm)^2 } X^{- \frac13} +O_{\varepsilon}(X^{\theta-1+\varepsilon}+X^{-\frac 12}).\end{align*} $$
Proof. Applying partial summation, we find that
 $$ \begin{align*} \sum_{K \in \mathcal{F}^\pm(X)} \log |D_K| = \int_1^X (\log t) dN^\pm(t) = N^\pm(X)\log X-N^\pm(X)-\frac 15 C_2^\pm X^{\frac 56} +O_{\varepsilon}(X^{\theta+\varepsilon}). \end{align*} $$
$$ \begin{align*} \sum_{K \in \mathcal{F}^\pm(X)} \log |D_K| = \int_1^X (\log t) dN^\pm(t) = N^\pm(X)\log X-N^\pm(X)-\frac 15 C_2^\pm X^{\frac 56} +O_{\varepsilon}(X^{\theta+\varepsilon}). \end{align*} $$
The claimed estimate follows from applying (1.1).
For the second term of (3.1), we note that it is constant on
![]() $\mathcal {F}^\pm (X)$
. We can now concentrate our efforts on the average of the third (and most crucial) term
$\mathcal {F}^\pm (X)$
. We can now concentrate our efforts on the average of the third (and most crucial) term
 $$ \begin{align} I^{\pm}(X;\phi) := -\frac2{LN^\pm(X) }\sum_{p} \sum_{e=1}^\infty \frac{\log p }{p^{e/2}} \widehat\phi\Big(\frac{e \log p}{L}\Big) \sum_{K \in \mathcal{F}^\pm(X)} a_K(p^e ). \end{align} $$
$$ \begin{align} I^{\pm}(X;\phi) := -\frac2{LN^\pm(X) }\sum_{p} \sum_{e=1}^\infty \frac{\log p }{p^{e/2}} \widehat\phi\Big(\frac{e \log p}{L}\Big) \sum_{K \in \mathcal{F}^\pm(X)} a_K(p^e ). \end{align} $$
It follows from (1.2) that
 $$ \begin{align} \notag \sum_{K \in \mathcal{F}^\pm(X)} a_K(p^e)&=2N^\pm_p(X,T_1)+(1+(-1)^e)N^\pm_p(X,T_2)+ \eta_e N^\pm_p(X,T_3)+N^\pm_p(X,T_4)\\ &= C_1^\pm X (\theta_e+\tfrac 1p)x_p+ C_2^\pm X^{\frac 56} (1+p^{-\frac 13})(\kappa_e(p)+p^{-1}+p^{-\frac 43})y_p +O_{\varepsilon}(p^{\omega }X^{\theta +\varepsilon}), \end{align} $$
$$ \begin{align} \notag \sum_{K \in \mathcal{F}^\pm(X)} a_K(p^e)&=2N^\pm_p(X,T_1)+(1+(-1)^e)N^\pm_p(X,T_2)+ \eta_e N^\pm_p(X,T_3)+N^\pm_p(X,T_4)\\ &= C_1^\pm X (\theta_e+\tfrac 1p)x_p+ C_2^\pm X^{\frac 56} (1+p^{-\frac 13})(\kappa_e(p)+p^{-1}+p^{-\frac 43})y_p +O_{\varepsilon}(p^{\omega }X^{\theta +\varepsilon}), \end{align} $$
where
 $$ \begin{align} \theta_e:=\delta_{2\mid e}+\delta_{3\mid e}=\begin{cases} 2 &\text{ if } e\equiv 0 \bmod 6 \\ 0 &\text{ if } e\equiv 1 \bmod 6 \\ 1 &\text{ if } e\equiv 2 \bmod 6 \\ 1 &\text{ if } e\equiv 3 \bmod 6 \\ 1 &\text{ if } e\equiv 4 \bmod 6 \\ 0 &\text{ if } e\equiv 5 \bmod 6, \end{cases} \end{align} $$
$$ \begin{align} \theta_e:=\delta_{2\mid e}+\delta_{3\mid e}=\begin{cases} 2 &\text{ if } e\equiv 0 \bmod 6 \\ 0 &\text{ if } e\equiv 1 \bmod 6 \\ 1 &\text{ if } e\equiv 2 \bmod 6 \\ 1 &\text{ if } e\equiv 3 \bmod 6 \\ 1 &\text{ if } e\equiv 4 \bmod 6 \\ 0 &\text{ if } e\equiv 5 \bmod 6, \end{cases} \end{align} $$
and
 $$ \begin{align} \kappa_e(p):=(\delta_{2\mid e}+\delta_{3\mid e})(1+p^{-\frac 23}) + (1-\delta_{3\mid e})p^{-\frac 13}=\begin{cases} 2+2p^{-\frac 23} &\text{ if } e\equiv 0 \bmod 6 \\ p^{-\frac 13} &\text{ if } e\equiv 1 \bmod 6 \\ 1+p^{-\frac 13}+p^{-\frac 23} &\text{ if } e\equiv 2 \bmod 6 \\ 1+p^{-\frac 23} &\text{ if } e\equiv 3 \bmod 6 \\ 1+p^{-\frac 13}+p^{-\frac 23} &\text{ if } e\equiv 4 \bmod 6 \\ p^{-\frac 13} &\text{ if } e\equiv 5 \bmod 6. \end{cases} \end{align} $$
$$ \begin{align} \kappa_e(p):=(\delta_{2\mid e}+\delta_{3\mid e})(1+p^{-\frac 23}) + (1-\delta_{3\mid e})p^{-\frac 13}=\begin{cases} 2+2p^{-\frac 23} &\text{ if } e\equiv 0 \bmod 6 \\ p^{-\frac 13} &\text{ if } e\equiv 1 \bmod 6 \\ 1+p^{-\frac 13}+p^{-\frac 23} &\text{ if } e\equiv 2 \bmod 6 \\ 1+p^{-\frac 23} &\text{ if } e\equiv 3 \bmod 6 \\ 1+p^{-\frac 13}+p^{-\frac 23} &\text{ if } e\equiv 4 \bmod 6 \\ p^{-\frac 13} &\text{ if } e\equiv 5 \bmod 6. \end{cases} \end{align} $$
Here,
![]() $ \delta _{\mathcal P} $
is equal to
$ \delta _{\mathcal P} $
is equal to
![]() $1$
if
$1$
if
![]() $ \mathcal P$
is true and is equal to
$ \mathcal P$
is true and is equal to
![]() $0$
otherwise. Note that we have the symmetries
$0$
otherwise. Note that we have the symmetries
![]() $\theta _{-e} = \theta _e$
and
$\theta _{-e} = \theta _e$
and
![]() $\kappa _{-e}(p) = \kappa _e(p)$
. With this notation, we prove the following proposition.
$\kappa _{-e}(p) = \kappa _e(p)$
. With this notation, we prove the following proposition.
Proposition 3.3. Let
![]() $\phi $
be a real even Schwartz function for which
$\phi $
be a real even Schwartz function for which
![]() $\widehat \phi $
has compact support, and let
$\widehat \phi $
has compact support, and let
![]() $\sigma :=\sup (\mathrm {supp}(\widehat \phi ))$
. Assume that (1.2) holds for some fixed parameters
$\sigma :=\sup (\mathrm {supp}(\widehat \phi ))$
. Assume that (1.2) holds for some fixed parameters
![]() $0\leq \theta <\frac 56$
and
$0\leq \theta <\frac 56$
and
![]() $\omega \geq 0$
. Then we have the estimate
$\omega \geq 0$
. Then we have the estimate
 $$ \begin{align*} &I^{\pm}(X;\phi)= -\frac{2}{L}\sum_{p,e}\frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p) \\ &\quad + \frac{2}{L}\bigg( - \frac{ C_2^\pm }{C_1^\pm }X^{-\frac 16} + \frac{ ( C_2^\pm )^2 }{(C_1^\pm )^2 }X^{-\frac 13} \bigg) \sum_{p,e}\frac{\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) \beta_e(p) +O_{\varepsilon}(X^{\theta - 1 + \sigma(\omega + \frac12 ) +\varepsilon}+X^{-\frac 12+\frac{\sigma}6}), \end{align*} $$
$$ \begin{align*} &I^{\pm}(X;\phi)= -\frac{2}{L}\sum_{p,e}\frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p) \\ &\quad + \frac{2}{L}\bigg( - \frac{ C_2^\pm }{C_1^\pm }X^{-\frac 16} + \frac{ ( C_2^\pm )^2 }{(C_1^\pm )^2 }X^{-\frac 13} \bigg) \sum_{p,e}\frac{\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) \beta_e(p) +O_{\varepsilon}(X^{\theta - 1 + \sigma(\omega + \frac12 ) +\varepsilon}+X^{-\frac 12+\frac{\sigma}6}), \end{align*} $$
where
Proof. Applying (3.3), we see that
 $$ \begin{align*} I^{\pm}(X;\phi) &= -\frac{2C_1^\pm X}{LN^\pm(X)}\sum_p \sum_{e=1}^\infty \frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p)\\ &\quad- \frac{2C_2^\pm X^{\frac 56}}{LN^\pm(X)} \sum_p \sum_{e=1}^\infty \frac{y_p(1+p^{-\frac 13})\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\kappa_e(p) +p^{-1}+p^{-\frac 43}) \\ &\quad+O_{\varepsilon}\Big(X^{\theta - 1 +\varepsilon}\sum_{\substack{p^e \leq X^\sigma \\ e\geq 1}}p^{\omega -\frac e2}\log p \Big)\\ & = -\frac{2 }{L }\bigg( 1 - \frac{ C_2^\pm}{C_1^\pm} X^{- \frac16} + \frac{ (C_2^\pm)^2 }{(C_1^\pm)^2 } X^{- \frac13} \bigg) \sum_p \sum_{e=1}^\infty \frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p)\\ &\quad - \frac{2}{L} \bigg( \frac{C_2^\pm }{C_1^\pm}X^{-\frac 16} - \frac{ (C_2^\pm)^2 }{(C_1^\pm)^2 } X^{- \frac13} \bigg) \sum_p \sum_{e=1}^\infty \frac{y_p(1+p^{-\frac 13})\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\kappa_e(p) +p^{-1}+p^{-\frac 43}) \\ &\quad +O_{\varepsilon}\big(X^{\theta - 1 + \sigma(\omega + \frac12 ) +\varepsilon} +X^{-\frac 12+\frac{\sigma}6}\big). \end{align*} $$
$$ \begin{align*} I^{\pm}(X;\phi) &= -\frac{2C_1^\pm X}{LN^\pm(X)}\sum_p \sum_{e=1}^\infty \frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p)\\ &\quad- \frac{2C_2^\pm X^{\frac 56}}{LN^\pm(X)} \sum_p \sum_{e=1}^\infty \frac{y_p(1+p^{-\frac 13})\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\kappa_e(p) +p^{-1}+p^{-\frac 43}) \\ &\quad+O_{\varepsilon}\Big(X^{\theta - 1 +\varepsilon}\sum_{\substack{p^e \leq X^\sigma \\ e\geq 1}}p^{\omega -\frac e2}\log p \Big)\\ & = -\frac{2 }{L }\bigg( 1 - \frac{ C_2^\pm}{C_1^\pm} X^{- \frac16} + \frac{ (C_2^\pm)^2 }{(C_1^\pm)^2 } X^{- \frac13} \bigg) \sum_p \sum_{e=1}^\infty \frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p)\\ &\quad - \frac{2}{L} \bigg( \frac{C_2^\pm }{C_1^\pm}X^{-\frac 16} - \frac{ (C_2^\pm)^2 }{(C_1^\pm)^2 } X^{- \frac13} \bigg) \sum_p \sum_{e=1}^\infty \frac{y_p(1+p^{-\frac 13})\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\kappa_e(p) +p^{-1}+p^{-\frac 43}) \\ &\quad +O_{\varepsilon}\big(X^{\theta - 1 + \sigma(\omega + \frac12 ) +\varepsilon} +X^{-\frac 12+\frac{\sigma}6}\big). \end{align*} $$
Note, in particular, that the error term
![]() $O(X^{-\frac 12+\frac {\sigma }6})$
bounds the size of the contribution of the first omitted term in the expansion of
$O(X^{-\frac 12+\frac {\sigma }6})$
bounds the size of the contribution of the first omitted term in the expansion of
![]() $X^{\frac 56}/N^{\pm }(X)$
appearing in the second double sum above. Indeed, this follows since
$X^{\frac 56}/N^{\pm }(X)$
appearing in the second double sum above. Indeed, this follows since
![]() $\kappa _1(p)=p^{-\frac 13}$
and
$\kappa _1(p)=p^{-\frac 13}$
and
 $$ \begin{align*} X^{-\frac12}\sum_{p\leq X^{\sigma}}\frac{\log p}{p^{\frac56}}=O\big(X^{-\frac 12+\frac{\sigma}6}\big). \end{align*} $$
$$ \begin{align*} X^{-\frac12}\sum_{p\leq X^{\sigma}}\frac{\log p}{p^{\frac56}}=O\big(X^{-\frac 12+\frac{\sigma}6}\big). \end{align*} $$
The claimed estimate follows.
We shall estimate
![]() $ I^{\pm }(X;\phi )$
further and find asymptotic expansions for the double sums in Proposition 3.3.
$ I^{\pm }(X;\phi )$
further and find asymptotic expansions for the double sums in Proposition 3.3.
Lemma 3.4. Let
![]() $\phi $
be a real even Schwartz function whose Fourier transform is compactly supported, define
$\phi $
be a real even Schwartz function whose Fourier transform is compactly supported, define
![]() $\sigma :=\sup (\mathrm {supp}(\widehat \phi ))$
, and let
$\sigma :=\sup (\mathrm {supp}(\widehat \phi ))$
, and let
![]() $\ell $
be a positive integer. Define
$\ell $
be a positive integer. Define
 $$ \begin{align*}I_1(X;\phi) := \sum_{p}\sum_{e=1}^\infty \frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p) , \qquad I_2(X;\phi) := \sum_{p}\sum_{e=1}^\infty \frac{\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) \beta_e(p) .\end{align*} $$
$$ \begin{align*}I_1(X;\phi) := \sum_{p}\sum_{e=1}^\infty \frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p) , \qquad I_2(X;\phi) := \sum_{p}\sum_{e=1}^\infty \frac{\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) \beta_e(p) .\end{align*} $$
Then, we have the asymptotic expansion
 $$ \begin{align*}I_1(X;\phi) = \frac{\phi (0)}{4} L + \sum_{n=0 }^\ell \frac{ \widehat{\phi}^{(n)} (0) \nu_1 (n) }{ n!} \frac{ 1 }{L^n } + O_{\ell} \Big( \frac{1 }{L^{\ell+1} } \Big), \end{align*} $$
$$ \begin{align*}I_1(X;\phi) = \frac{\phi (0)}{4} L + \sum_{n=0 }^\ell \frac{ \widehat{\phi}^{(n)} (0) \nu_1 (n) }{ n!} \frac{ 1 }{L^n } + O_{\ell} \Big( \frac{1 }{L^{\ell+1} } \Big), \end{align*} $$
where
 $$ \begin{align*} \nu_1 (n ) &:= \delta_{n=0} + \sum_{p}\sum_{ e \neq 2 } \frac{x_p e^n ( \log p)^{n+1} }{p^{\frac e2}} (\theta_e+\tfrac 1p) + \sum_p \frac{ 2^n ( \log p)^{n+1} }{p} \Big( x_p\Big( 1 + \frac1p\Big) -1 \Big) \\ &\quad + \int_1^\infty \frac{2^n ( \log u)^{n-1} ( \log u - n ) }{u^2} \mathcal{R} (u) du \end{align*} $$
$$ \begin{align*} \nu_1 (n ) &:= \delta_{n=0} + \sum_{p}\sum_{ e \neq 2 } \frac{x_p e^n ( \log p)^{n+1} }{p^{\frac e2}} (\theta_e+\tfrac 1p) + \sum_p \frac{ 2^n ( \log p)^{n+1} }{p} \Big( x_p\Big( 1 + \frac1p\Big) -1 \Big) \\ &\quad + \int_1^\infty \frac{2^n ( \log u)^{n-1} ( \log u - n ) }{u^2} \mathcal{R} (u) du \end{align*} $$
with
![]() $ \mathcal {R}(u) := \sum _{ p \leq u } \log p - u $
. Moreover, we have the estimate
$ \mathcal {R}(u) := \sum _{ p \leq u } \log p - u $
. Moreover, we have the estimate
where
![]() $c_0(\sigma )>0$
is a constant. Under the Riemann Hypothesis, we have the more precise expansion
$c_0(\sigma )>0$
is a constant. Under the Riemann Hypothesis, we have the more precise expansion
 $$ \begin{align*}I_2(X;\phi) = L \int_0^\infty \widehat{\phi} ( u) e^{\frac{Lu}{6}} du + \sum_{n=0}^\ell \frac{ \widehat{\phi}^{(n)} (0) \nu_2 (n) }{ n!} \frac{ 1 }{L^n } + O_{\ell} \Big( \frac{1 }{L^{\ell+1} } \Big),\end{align*} $$
$$ \begin{align*}I_2(X;\phi) = L \int_0^\infty \widehat{\phi} ( u) e^{\frac{Lu}{6}} du + \sum_{n=0}^\ell \frac{ \widehat{\phi}^{(n)} (0) \nu_2 (n) }{ n!} \frac{ 1 }{L^n } + O_{\ell} \Big( \frac{1 }{L^{\ell+1} } \Big),\end{align*} $$
where
 $$ \begin{align*} \nu_2 (n ) &:= \delta_{n=0} + \sum_{p}\sum_{e=2}^\infty \frac{e^n (\log p )^{n+1} \beta_e(p) }{p^{\frac e2}} + \sum_{p} \frac{(\log p)^{n+1}}{p^{\frac 12}} \Big( \beta_1 (p) - \frac{1}{p^{\frac13}} \Big)\\ &\quad + \int_1^{\infty} \frac{( \log u)^{n-1} ( 5 \log u - 6n) }{6 u^{\frac{11}{6} }} \mathcal{R} (u) du. \end{align*} $$
$$ \begin{align*} \nu_2 (n ) &:= \delta_{n=0} + \sum_{p}\sum_{e=2}^\infty \frac{e^n (\log p )^{n+1} \beta_e(p) }{p^{\frac e2}} + \sum_{p} \frac{(\log p)^{n+1}}{p^{\frac 12}} \Big( \beta_1 (p) - \frac{1}{p^{\frac13}} \Big)\\ &\quad + \int_1^{\infty} \frac{( \log u)^{n-1} ( 5 \log u - 6n) }{6 u^{\frac{11}{6} }} \mathcal{R} (u) du. \end{align*} $$
Proof. We first split the sums as
 $$ \begin{align} I_1(X;\phi) = \sum_p \frac{\log p }{p} \widehat{\phi} \Big( \frac{ 2 \log p }{L} \Big) + I'_1(X;\phi), \qquad I_2(X;\phi) =\sum_p \frac{ \log p }{ p^{\frac56}}\widehat\phi\Big(\frac{\log p }{L}\Big) +I'_2(X;\phi) , \end{align} $$
$$ \begin{align} I_1(X;\phi) = \sum_p \frac{\log p }{p} \widehat{\phi} \Big( \frac{ 2 \log p }{L} \Big) + I'_1(X;\phi), \qquad I_2(X;\phi) =\sum_p \frac{ \log p }{ p^{\frac56}}\widehat\phi\Big(\frac{\log p }{L}\Big) +I'_2(X;\phi) , \end{align} $$
where
 $$ \begin{align} I'_1(X;\phi) & := \sum_{p}\sum_{e \neq 2 } \frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p) + \sum_p \frac{ \log p }{p} \Big( x_p\Big( 1 + \frac1p\Big) -1 \Big) \widehat{\phi} \Big( \frac{ 2 \log p }{L} \Big), \nonumber\\ I'_2(X;\phi) & := \sum_{p}\sum_{e=2}^\infty \frac{\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) \beta_e(p) + \sum_{p} \frac{\log p}{p^{\frac 12}}\widehat\phi\Big(\frac{\log p }{L}\Big) \Big( \beta_1 (p) - \frac{1}{p^{\frac13}} \Big). \end{align} $$
$$ \begin{align} I'_1(X;\phi) & := \sum_{p}\sum_{e \neq 2 } \frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p) + \sum_p \frac{ \log p }{p} \Big( x_p\Big( 1 + \frac1p\Big) -1 \Big) \widehat{\phi} \Big( \frac{ 2 \log p }{L} \Big), \nonumber\\ I'_2(X;\phi) & := \sum_{p}\sum_{e=2}^\infty \frac{\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) \beta_e(p) + \sum_{p} \frac{\log p}{p^{\frac 12}}\widehat\phi\Big(\frac{\log p }{L}\Big) \Big( \beta_1 (p) - \frac{1}{p^{\frac13}} \Big). \end{align} $$
We may also rewrite the sums in (3.7) using partial summation as follows:
 $$ \begin{align} \sum_p \frac{\log p }{p} \widehat{\phi} \Big( \frac{ 2 \log p }{L} \Big) & = \int_1^\infty \frac{1 }{u} \widehat{\phi} \Big( \frac{ 2 \log u }{L} \Big)d( u+ \mathcal{R}(u)) \nonumber\\ & = \frac{ \phi(0) }{4} L + \widehat{\phi}(0) - \int_1^\infty \Big(\frac{-1}{u^2} \widehat{\phi} \Big( \frac{2 \log u }{L} \Big) + \frac{2}{u^2L} \widehat{\phi}' \Big( \frac{2 \log u }{L} \Big) \Big) \mathcal{R} (u) du , \nonumber\\ \sum_p \frac{\log p }{p^{\frac56} } \widehat{\phi} \Big( \frac{ \log p }{L} \Big) & = L \int_0^\infty \widehat{\phi} ( u) e^{Lu/6} du + \widehat{\phi}(0) \nonumber\\ & \quad - \int_1^{X^{\sigma}} \Big(\frac{-5}{6 u^2} \widehat{\phi} \Big( \frac{ \log u }{L} \Big) + \frac{ 1 }{u^2L} \widehat{\phi}' \Big( \frac{ \log u }{L} \Big) \Big) u^{\frac16} \mathcal{R} (u) du. \end{align} $$
$$ \begin{align} \sum_p \frac{\log p }{p} \widehat{\phi} \Big( \frac{ 2 \log p }{L} \Big) & = \int_1^\infty \frac{1 }{u} \widehat{\phi} \Big( \frac{ 2 \log u }{L} \Big)d( u+ \mathcal{R}(u)) \nonumber\\ & = \frac{ \phi(0) }{4} L + \widehat{\phi}(0) - \int_1^\infty \Big(\frac{-1}{u^2} \widehat{\phi} \Big( \frac{2 \log u }{L} \Big) + \frac{2}{u^2L} \widehat{\phi}' \Big( \frac{2 \log u }{L} \Big) \Big) \mathcal{R} (u) du , \nonumber\\ \sum_p \frac{\log p }{p^{\frac56} } \widehat{\phi} \Big( \frac{ \log p }{L} \Big) & = L \int_0^\infty \widehat{\phi} ( u) e^{Lu/6} du + \widehat{\phi}(0) \nonumber\\ & \quad - \int_1^{X^{\sigma}} \Big(\frac{-5}{6 u^2} \widehat{\phi} \Big( \frac{ \log u }{L} \Big) + \frac{ 1 }{u^2L} \widehat{\phi}' \Big( \frac{ \log u }{L} \Big) \Big) u^{\frac16} \mathcal{R} (u) du. \end{align} $$
Next, for any
![]() $\ell \geq 1$
and
$\ell \geq 1$
and
![]() $ |t| \leq \sigma $
, Taylor’s theorem reads
$ |t| \leq \sigma $
, Taylor’s theorem reads
 $$ \begin{align} \widehat{\phi} ( t ) = \sum_{n=0}^\ell \frac{ \widehat{\phi}^{(n)} (0) }{ n!} t^n + O_{\ell} ( |t|^{\ell+1}), \end{align} $$
$$ \begin{align} \widehat{\phi} ( t ) = \sum_{n=0}^\ell \frac{ \widehat{\phi}^{(n)} (0) }{ n!} t^n + O_{\ell} ( |t|^{\ell+1}), \end{align} $$
and one has a similar expansion for
![]() $\widehat \phi '$
. The claimed estimates follow from substituting this expression into (3.8) and (3.9) and evaluating the error term using the prime number theorem
$\widehat \phi '$
. The claimed estimates follow from substituting this expression into (3.8) and (3.9) and evaluating the error term using the prime number theorem
![]() $ \mathcal {R}(u)\ll u e^{-c \sqrt { \log u }} $
.
$ \mathcal {R}(u)\ll u e^{-c \sqrt { \log u }} $
.
We end this section by proving Theorem 1.1.
Proof of Theorem 1.1
Assume that
![]() $\theta ,\omega \geq 0$
are admissible values in (1.2) and are such that
$\theta ,\omega \geq 0$
are admissible values in (1.2) and are such that
![]() $\theta +\omega <\frac 12$
. Let
$\theta +\omega <\frac 12$
. Let
![]() $\phi $
be any real even Schwartz function, such that
$\phi $
be any real even Schwartz function, such that
![]() $\widehat \phi \geq 0$
and
$\widehat \phi \geq 0$
and
![]() $1< \sup (\mathrm {supp}(\widehat \phi )) < (\frac 56-\theta )/(\frac 13+\omega )$
; this is possible thanks to the restriction
$1< \sup (\mathrm {supp}(\widehat \phi )) < (\frac 56-\theta )/(\frac 13+\omega )$
; this is possible thanks to the restriction
![]() $\theta +\omega <\frac 12$
. Combining Lemmas 3.1 and 3.2 with Proposition 3.3, we obtain the estimateFootnote 3
$\theta +\omega <\frac 12$
. Combining Lemmas 3.1 and 3.2 with Proposition 3.3, we obtain the estimateFootnote 3
 $$ \begin{align} &\frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \mathfrak{D}_{\phi}(K)=\widehat \phi(0)\Big(1 + \frac{ \log (4 \pi^2 e) }{L} -\frac{C_2^\pm}{5C_1^\pm} \frac{X^{-\frac 16}}{L} + \frac{(C_2^\pm)^2 }{5(C_1^\pm)^2 } \frac{X^{-\frac 13}}{L} \Big) \nonumber\\ &\qquad\quad+ \frac1{\pi}\int_{-\infty}^{\infty}\phi\Big(\frac{Lr}{2\pi}\Big)\operatorname{Re}\Big(\frac{\Gamma'_{\pm}}{\Gamma_{\pm}}(\tfrac12+ir)\Big)dr -\frac{2}{L}\sum_{p,e}\frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p)\nonumber\\ & -\frac{2C_2^\pm X^{-\frac 16}}{C_1^\pm L}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e}\frac{\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) \beta_e(p) +O_{\varepsilon}(X^{\theta - 1 + \sigma(\omega + \frac12 ) +\varepsilon}+X^{-\frac 12+\frac \sigma 6}), \end{align} $$
$$ \begin{align} &\frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \mathfrak{D}_{\phi}(K)=\widehat \phi(0)\Big(1 + \frac{ \log (4 \pi^2 e) }{L} -\frac{C_2^\pm}{5C_1^\pm} \frac{X^{-\frac 16}}{L} + \frac{(C_2^\pm)^2 }{5(C_1^\pm)^2 } \frac{X^{-\frac 13}}{L} \Big) \nonumber\\ &\qquad\quad+ \frac1{\pi}\int_{-\infty}^{\infty}\phi\Big(\frac{Lr}{2\pi}\Big)\operatorname{Re}\Big(\frac{\Gamma'_{\pm}}{\Gamma_{\pm}}(\tfrac12+ir)\Big)dr -\frac{2}{L}\sum_{p,e}\frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p)\nonumber\\ & -\frac{2C_2^\pm X^{-\frac 16}}{C_1^\pm L}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e}\frac{\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) \beta_e(p) +O_{\varepsilon}(X^{\theta - 1 + \sigma(\omega + \frac12 ) +\varepsilon}+X^{-\frac 12+\frac \sigma 6}), \end{align} $$
where
![]() $\sigma =\sup (\mathrm {supp}(\widehat \phi ))$
.
$\sigma =\sup (\mathrm {supp}(\widehat \phi ))$
.
To bound the integral involving the gamma function in (3.11), we note that Stirling’s formula implies that for s in any fixed vertical strip minus discs centred at the poles of
![]() $\Gamma _\pm (s)$
, we have the estimate
$\Gamma _\pm (s)$
, we have the estimate
 $$ \begin{align*}\operatorname{Re} \left( \frac{ \Gamma'_{\pm} }{ \Gamma_{\pm}} ( s) \right) = \log | s | + O(1).\end{align*} $$
$$ \begin{align*}\operatorname{Re} \left( \frac{ \Gamma'_{\pm} }{ \Gamma_{\pm}} ( s) \right) = \log | s | + O(1).\end{align*} $$
Now,
![]() $ \phi (x) \ll |x|^{-2}$
, and thus,
$ \phi (x) \ll |x|^{-2}$
, and thus,
 $$ \begin{align*}\frac{1 }{ \pi} \int_{-\infty}^\infty \phi \Big( \frac{ Lr}{ 2 \pi} \Big) \operatorname{Re} \Big( \frac{ \Gamma'_{\pm} }{ \Gamma_{\pm}} ( \tfrac12 + ir ) \Big) dr \ll \int_{-1}^1 \left| \phi \Big( \frac{ Lr}{ 2 \pi} \Big) \right| dr + \int_{ |r|\geq 1 } \frac{ \log (1+|r|)}{ (Lr)^2} dr \ll \frac1L.\end{align*} $$
$$ \begin{align*}\frac{1 }{ \pi} \int_{-\infty}^\infty \phi \Big( \frac{ Lr}{ 2 \pi} \Big) \operatorname{Re} \Big( \frac{ \Gamma'_{\pm} }{ \Gamma_{\pm}} ( \tfrac12 + ir ) \Big) dr \ll \int_{-1}^1 \left| \phi \Big( \frac{ Lr}{ 2 \pi} \Big) \right| dr + \int_{ |r|\geq 1 } \frac{ \log (1+|r|)}{ (Lr)^2} dr \ll \frac1L.\end{align*} $$
Moreover, Lemma 3.4 implies the estimates
 $$ \begin{align*}- \frac{2}{L}\sum_{p,e}\frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p) \ll 1\end{align*} $$
$$ \begin{align*}- \frac{2}{L}\sum_{p,e}\frac{x_p\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) (\theta_e+\tfrac 1p) \ll 1\end{align*} $$
and
 $$ \begin{align*} &-\frac{2C_2^\pm X^{-\frac 16}}{C_1^\pm L}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e}\frac{\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) \beta_e(p) \\ &\qquad = -\frac{2C_2^\pm X^{-\frac 16}}{C_1^\pm } \int_0^\infty \widehat \phi(u) e^{\frac{Lu}{6}} du +O\big( X^{-\frac { 1}6}+X^{\frac{\sigma -2}{6}} \big), \end{align*} $$
$$ \begin{align*} &-\frac{2C_2^\pm X^{-\frac 16}}{C_1^\pm L}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e}\frac{\log p}{p^{\frac e2}}\widehat\phi\Big(\frac{\log p^e}{L}\Big) \beta_e(p) \\ &\qquad = -\frac{2C_2^\pm X^{-\frac 16}}{C_1^\pm } \int_0^\infty \widehat \phi(u) e^{\frac{Lu}{6}} du +O\big( X^{-\frac { 1}6}+X^{\frac{\sigma -2}{6}} \big), \end{align*} $$
since the Riemann Hypothesis for
![]() $\zeta _K(s)$
implies the Riemann Hypothesis for
$\zeta _K(s)$
implies the Riemann Hypothesis for
![]() $\zeta (s)$
. Combining these estimates, we deduce that the right-hand side of (3.11) is
$\zeta (s)$
. Combining these estimates, we deduce that the right-hand side of (3.11) is
where
![]() $\varepsilon>0$
is arbitrary,
$\varepsilon>0$
is arbitrary,
![]() $C_\varepsilon $
is a positive constant and
$C_\varepsilon $
is a positive constant and
![]() $\delta :=\frac {\sigma -1}6 -( \theta - 1 + \sigma (\omega + \frac 12 ))>0 $
. However, for small enough
$\delta :=\frac {\sigma -1}6 -( \theta - 1 + \sigma (\omega + \frac 12 ))>0 $
. However, for small enough
![]() $\varepsilon $
, this contradicts the bound
$\varepsilon $
, this contradicts the bound
 $$ \begin{align*}\frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \mathfrak{D}_{\phi}(K) = O( \log X),\end{align*} $$
$$ \begin{align*}\frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \mathfrak{D}_{\phi}(K) = O( \log X),\end{align*} $$
which is a direct consequence of the Riemann Hypothesis for
![]() $\zeta _K(s)$
and the Riemann-von Mangoldt formula [Reference Iwaniec and KowalskiIK, Theorem 5.31].
$\zeta _K(s)$
and the Riemann-von Mangoldt formula [Reference Iwaniec and KowalskiIK, Theorem 5.31].
4 A refined Ratios Conjecture
The celebrated L-functions Ratios Conjecture [Reference Conrey, Farmer and ZirnbauerCFZ] predicts precise formulas for estimates of averages of ratios of (products of) L-functions evaluated at points close to the critical line. The conjecture is presented in the form of a recipe with instructions on how to produce predictions of a certain type in any family of L-functions. In order to follow the recipe, it is of fundamental importance to have control of counting functions of the type (1.1) and (2.3) related to the family. The connections between counting functions, low-lying zeros and the Ratios Conjecture are central in the present investigation.
The Ratios Conjecture has a large variety of applications. Applications to problems about low-lying zeros first appeared in the work of Conrey and Snaith [Reference Conrey and SnaithCS], where they study the one-level density of families of quadratic Dirichlet L-functions and quadratic twists of a holomorphic modular form. The investigation in [Reference Conrey and SnaithCS] has inspired a large amount of work on low-lying zeros in different families (see, e.g. [Reference MillerM2, Reference MillerM3, Reference Huynh, Keating and SnaithHKS, Reference Fiorilli and MillerFM, Reference David, Huynh and ParksDHP, Reference Fiorilli, Parks and SödergrenFPS1, Reference Fiorilli, Parks and SödergrenFPS3, Reference Mason and SnaithMS, Reference Cho and ParkCP, Reference WaxmanW]).
As part of this project, we went through the steps of the Ratios Conjecture recipe with the goal of estimating the one-level density. We noticed that the resulting estimate does not predict certain terms in Theorem 1.2. To fix this, we modified [Reference Conrey, Farmer and ZirnbauerCFZ, Step 4], which is the evaluation of the average of the coefficients appearing in the approximation of the expression
 $$ \begin{align} R(\alpha,\gamma;X):=\frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \frac{L\left(\frac{1}{2}+\alpha,f_K\right)}{L\left(\frac{1}{2}+\gamma,f_K\right)}. \end{align} $$
$$ \begin{align} R(\alpha,\gamma;X):=\frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \frac{L\left(\frac{1}{2}+\alpha,f_K\right)}{L\left(\frac{1}{2}+\gamma,f_K\right)}. \end{align} $$
More precisely, instead of only considering the main term, we kept track of the secondary term in Lemma 4.1.
We now describe more precisely the steps in the Ratios Conjecture recipe. The first step involves the approximate functional equation for
![]() $L(s,f_K)$
, which reads
$L(s,f_K)$
, which reads
 $$ \begin{align} L\left(s, f_K\right) = \sum_{n<x} \frac{\lambda_K(n)}{n^s}+|D_K|^{\frac 12-s}\frac{\Gamma_{\pm}(1-s)}{\Gamma_{\pm}(s)} \sum_{n<y} \frac{\lambda_K(n)}{n^{1-s}}+\:\mathrm{Error}, \end{align} $$
$$ \begin{align} L\left(s, f_K\right) = \sum_{n<x} \frac{\lambda_K(n)}{n^s}+|D_K|^{\frac 12-s}\frac{\Gamma_{\pm}(1-s)}{\Gamma_{\pm}(s)} \sum_{n<y} \frac{\lambda_K(n)}{n^{1-s}}+\:\mathrm{Error}, \end{align} $$
where
![]() $x,y$
are such that
$x,y$
are such that
![]() $xy\asymp |D_K| (1+|t|)^2 $
(this is in analogy with [Reference Conrey and SnaithCS]; see [Reference Iwaniec and KowalskiIK, Theorem 5.3] for a description of the approximate functional equation of a general L-function). The analysis will be carried out assuming that the error term can be neglected and that the sums can be completed.
$xy\asymp |D_K| (1+|t|)^2 $
(this is in analogy with [Reference Conrey and SnaithCS]; see [Reference Iwaniec and KowalskiIK, Theorem 5.3] for a description of the approximate functional equation of a general L-function). The analysis will be carried out assuming that the error term can be neglected and that the sums can be completed.
Following [Reference Conrey, Farmer and ZirnbauerCFZ], we replace the numerator of (4.1) with the approximate functional equation (4.2) and the denominator of (4.1) with (2.2). We will need to estimate the first sum in (4.2) evaluated at
![]() $s=\frac {1}{2}+\alpha $
, where
$s=\frac {1}{2}+\alpha $
, where
![]() $|\operatorname {Re}(\alpha )|$
is sufficiently small. This gives the contribution
$|\operatorname {Re}(\alpha )|$
is sufficiently small. This gives the contribution
 $$ \begin{align} R_1(\alpha, \gamma;X):=\frac1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \sum_{h,m} \frac{\lambda_K(m)\mu_{K}(h)}{m^{\frac{1}{2} + \alpha}h^{\frac{1}{2}+\gamma}} \end{align} $$
$$ \begin{align} R_1(\alpha, \gamma;X):=\frac1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \sum_{h,m} \frac{\lambda_K(m)\mu_{K}(h)}{m^{\frac{1}{2} + \alpha}h^{\frac{1}{2}+\gamma}} \end{align} $$
to (4.1). This infinite sum converges absolutely in the region
![]() $\operatorname {Re}(\alpha )>\frac 12$
and
$\operatorname {Re}(\alpha )>\frac 12$
and
![]() $\operatorname {Re}(\gamma )>\frac 12$
, however, later in this section, we will provide an analytic continuation to a wider domain. We will also need to evaluate the contribution of the second sum in (4.2), which is given by
$\operatorname {Re}(\gamma )>\frac 12$
, however, later in this section, we will provide an analytic continuation to a wider domain. We will also need to evaluate the contribution of the second sum in (4.2), which is given by
 $$ \begin{align} R_2(\alpha, \gamma;X):=\frac1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} |D_K|^{-\alpha}\frac{\Gamma_{\pm}\left(\frac 12-\alpha \right)}{\Gamma_{\pm}\left(\frac 12+\alpha\right)}\sum_{h,m} \frac{\lambda_K(m)\mu_{K}(h)}{m^{\frac{1}{2}-\alpha}h^{\frac{1}{2}+\gamma}} \end{align} $$
$$ \begin{align} R_2(\alpha, \gamma;X):=\frac1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} |D_K|^{-\alpha}\frac{\Gamma_{\pm}\left(\frac 12-\alpha \right)}{\Gamma_{\pm}\left(\frac 12+\alpha\right)}\sum_{h,m} \frac{\lambda_K(m)\mu_{K}(h)}{m^{\frac{1}{2}-\alpha}h^{\frac{1}{2}+\gamma}} \end{align} $$
(Once more, the series converges absolutely for
![]() $\operatorname {Re}(\alpha )<-\frac 12$
and
$\operatorname {Re}(\alpha )<-\frac 12$
and
![]() $\operatorname {Re}(\gamma )>\frac 12$
, but we will later provide an analytic continuation to a wider domain).
$\operatorname {Re}(\gamma )>\frac 12$
, but we will later provide an analytic continuation to a wider domain).
A first step in the understanding of the
![]() $R_j(\alpha , \gamma ;X)$
will be achieved using the following precise evaluation of the expected value of
$R_j(\alpha , \gamma ;X)$
will be achieved using the following precise evaluation of the expected value of
![]() $\lambda _K(m)\mu _K(h) $
.
$\lambda _K(m)\mu _K(h) $
.
Lemma 4.1. Let
![]() $m,h\in \mathbb N$
, and let
$m,h\in \mathbb N$
, and let
![]() $\frac 12 \leq \theta <\frac 56$
and
$\frac 12 \leq \theta <\frac 56$
and
![]() $\omega \geq 0$
be, such that (2.3) holds. Assume that h is cubefree. We have the estimate
$\omega \geq 0$
be, such that (2.3) holds. Assume that h is cubefree. We have the estimate
 $$ \begin{align*} &\frac{1}{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)}\lambda_K(m)\mu_K(h) \\ &\quad\!\! = \prod_{p^e\parallel m, p^s \parallel h}f(e,s,p)x_p + \Bigg( \prod_{p^e\parallel m, p^s \parallel h}g(e,s,p)y_p- \prod_{p^e\parallel m, p^s \parallel h}f(e,s,p)x_p\Bigg) \frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \\ &\qquad +O_\varepsilon\bigg( \prod_{ p \mid hm , p^e \parallel m } \big( (2 e + 5)p^{\omega}\big) X^{\theta-1 +\varepsilon}\bigg), \end{align*} $$
$$ \begin{align*} &\frac{1}{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)}\lambda_K(m)\mu_K(h) \\ &\quad\!\! = \prod_{p^e\parallel m, p^s \parallel h}f(e,s,p)x_p + \Bigg( \prod_{p^e\parallel m, p^s \parallel h}g(e,s,p)y_p- \prod_{p^e\parallel m, p^s \parallel h}f(e,s,p)x_p\Bigg) \frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \\ &\qquad +O_\varepsilon\bigg( \prod_{ p \mid hm , p^e \parallel m } \big( (2 e + 5)p^{\omega}\big) X^{\theta-1 +\varepsilon}\bigg), \end{align*} $$
where
 $$ \begin{align*} f(e,0,p)&:= \frac{e+1}{6}+\frac{1+(-1)^e}{4}+\frac{\tau_e}{3}+\frac{1}{p}; \\ f(e,1,p)&:= - \frac{e+1}{3}+\frac{\tau_e}{3}- \frac{1}{p}; \\ f(e,2,p)&:=\frac{e+1}{6}-\frac{1+(-1)^e}{4}+\frac{\tau_e}{3}; \\ g(e,0,p)&:= \frac{(e+1)(1+p^{-\frac 13})^3}{6} +\frac{(1+(-1)^e)(1+p^{-\frac 13})(1+p^{-\frac 23})}{4} \\ & \quad + \frac{\tau_e(1+p^{-1})}{3} + \frac{(1+p^{-\frac 13})^2}{p}; \\ g(e,1,p)&:= -\frac{(e+1)(1+p^{-\frac 13})^3}{3}+ \frac{\tau_e(1+p^{-1})}{3}-\frac{(1+p^{-\frac 13})^2}{p}; \\ g(e,2,p)&:= \frac{(e+1)(1+p^{-\frac 13})^3}{6} -\frac{(1+(-1)^e)(1+p^{-\frac 13})(1+p^{-\frac 23})}{4} + \frac{\tau_e(1+p^{-1})}{3}. \end{align*} $$
$$ \begin{align*} f(e,0,p)&:= \frac{e+1}{6}+\frac{1+(-1)^e}{4}+\frac{\tau_e}{3}+\frac{1}{p}; \\ f(e,1,p)&:= - \frac{e+1}{3}+\frac{\tau_e}{3}- \frac{1}{p}; \\ f(e,2,p)&:=\frac{e+1}{6}-\frac{1+(-1)^e}{4}+\frac{\tau_e}{3}; \\ g(e,0,p)&:= \frac{(e+1)(1+p^{-\frac 13})^3}{6} +\frac{(1+(-1)^e)(1+p^{-\frac 13})(1+p^{-\frac 23})}{4} \\ & \quad + \frac{\tau_e(1+p^{-1})}{3} + \frac{(1+p^{-\frac 13})^2}{p}; \\ g(e,1,p)&:= -\frac{(e+1)(1+p^{-\frac 13})^3}{3}+ \frac{\tau_e(1+p^{-1})}{3}-\frac{(1+p^{-\frac 13})^2}{p}; \\ g(e,2,p)&:= \frac{(e+1)(1+p^{-\frac 13})^3}{6} -\frac{(1+(-1)^e)(1+p^{-\frac 13})(1+p^{-\frac 23})}{4} + \frac{\tau_e(1+p^{-1})}{3}. \end{align*} $$
Proof. We may write
![]() $ m = \prod _{j=1}^J p_j^{e_j}$
and
$ m = \prod _{j=1}^J p_j^{e_j}$
and
![]() $ h = \prod _{j=1}^J p_j^{s_j }$
, where
$ h = \prod _{j=1}^J p_j^{s_j }$
, where
![]() $ p_1 , \ldots , p_J$
are distinct primes and for each
$ p_1 , \ldots , p_J$
are distinct primes and for each
![]() $ j $
,
$ j $
,
![]() $ e_j $
and
$ e_j $
and
![]() $ s_j $
are nonnegative integers but not both zero. Then we see that
$ s_j $
are nonnegative integers but not both zero. Then we see that
 $$ \begin{align*} \sum_{K \in \mathcal{F}^\pm(X)} \lambda_K (m) \mu_K (h) = & \sum_{K \in \mathcal{F}^\pm(X)} \prod_{j=1}^J \bigg( \lambda_K \big( p_j ^{e_j} \big) \mu_K \big( p_j^{s_j} \big) \bigg) = \sum_{\mathbf{k}} \sum_{ \substack{ K \in \mathcal{F}^{\pm}(X) \\ \mathbf{p} : ~type ~T_{\mathbf{k}} }} \prod_{j=1}^J \bigg( \lambda_K \big( p_j ^{e_j} \big) \mu_K \big( p_j^{s_j} \big) \bigg) , \end{align*} $$
$$ \begin{align*} \sum_{K \in \mathcal{F}^\pm(X)} \lambda_K (m) \mu_K (h) = & \sum_{K \in \mathcal{F}^\pm(X)} \prod_{j=1}^J \bigg( \lambda_K \big( p_j ^{e_j} \big) \mu_K \big( p_j^{s_j} \big) \bigg) = \sum_{\mathbf{k}} \sum_{ \substack{ K \in \mathcal{F}^{\pm}(X) \\ \mathbf{p} : ~type ~T_{\mathbf{k}} }} \prod_{j=1}^J \bigg( \lambda_K \big( p_j ^{e_j} \big) \mu_K \big( p_j^{s_j} \big) \bigg) , \end{align*} $$
where
![]() $\mathbf {k} = (k_1 , \ldots , k_J ) $
runs over
$\mathbf {k} = (k_1 , \ldots , k_J ) $
runs over
![]() $\{ 1, 2, 3, 4, 5 \}^J $
and
$\{ 1, 2, 3, 4, 5 \}^J $
and
![]() $\mathbf {p} = ( p_1 , \ldots , p_J)$
. When each
$\mathbf {p} = ( p_1 , \ldots , p_J)$
. When each
![]() $p_j$
has splitting type
$p_j$
has splitting type
![]() $T_{k_j}$
in K, the values
$T_{k_j}$
in K, the values
![]() $\lambda _K (p_j^{e_j})$
and
$\lambda _K (p_j^{e_j})$
and
![]() $ \mu _K ( p_j^{s_j})$
depend on
$ \mu _K ( p_j^{s_j})$
depend on
![]() $p_j$
,
$p_j$
,
![]() $k_j $
,
$k_j $
,
![]() $e_j$
and
$e_j$
and
![]() $ s_j$
. Define
$ s_j$
. Define
for each
![]() $ j \leq J$
with
$ j \leq J$
with
![]() $p_j $
of splitting type
$p_j $
of splitting type
![]() $T_{k_j}$
in K, as well as
$T_{k_j}$
in K, as well as
 $$ \begin{align} \eta_{1, \mathbf{p}} ( \mathbf{k}, \mathbf{e}) := \prod_{j=1}^J \eta_{1, p_j} (k_j, e_j ), \qquad \eta_{2, \mathbf{p}} ( \mathbf{k}, \mathbf{s}) := \prod_{j=1}^J \eta_{2, p_j} (k_j, s_j ). \end{align} $$
$$ \begin{align} \eta_{1, \mathbf{p}} ( \mathbf{k}, \mathbf{e}) := \prod_{j=1}^J \eta_{1, p_j} (k_j, e_j ), \qquad \eta_{2, \mathbf{p}} ( \mathbf{k}, \mathbf{s}) := \prod_{j=1}^J \eta_{2, p_j} (k_j, s_j ). \end{align} $$
We see that
 $$ \begin{align*} \sum_{K \in \mathcal{F}^\pm(X)} \lambda_K (m) \mu_K (h) & = \sum_{\mathbf{k}} \eta_{1, \mathbf{p}} ( \mathbf{k}, \mathbf{e}) \eta_{2,\mathbf{p}} ( \mathbf{k}, \mathbf{s}) \sum_{ \substack{ K \in \mathcal{F}^{\pm}(X) \\ \mathbf{p} : ~type ~T_{\mathbf{k}} }} 1 \\ & = \sum_{\mathbf{k}} \eta_{1, \mathbf{p}} ( \mathbf{k}, \mathbf{e}) \eta_{2,\mathbf{p}} ( \mathbf{k}, \mathbf{s}) N^{\pm}_{\mathbf{p}} ( X , T_{\mathbf{k}}), \end{align*} $$
$$ \begin{align*} \sum_{K \in \mathcal{F}^\pm(X)} \lambda_K (m) \mu_K (h) & = \sum_{\mathbf{k}} \eta_{1, \mathbf{p}} ( \mathbf{k}, \mathbf{e}) \eta_{2,\mathbf{p}} ( \mathbf{k}, \mathbf{s}) \sum_{ \substack{ K \in \mathcal{F}^{\pm}(X) \\ \mathbf{p} : ~type ~T_{\mathbf{k}} }} 1 \\ & = \sum_{\mathbf{k}} \eta_{1, \mathbf{p}} ( \mathbf{k}, \mathbf{e}) \eta_{2,\mathbf{p}} ( \mathbf{k}, \mathbf{s}) N^{\pm}_{\mathbf{p}} ( X , T_{\mathbf{k}}), \end{align*} $$
which by (2.3) is equal to
 $$ \begin{align*} & \sum_{\mathbf{k}} \eta_{1, \mathbf{p}} ( \mathbf{k}, \mathbf{e}) \eta_{2,\mathbf{p}} ( \mathbf{k}, \mathbf{s}) \bigg(C_1^\pm \prod_{j = 1}^J ( x_{p_j} c_{k_j} (p_j ) ) X + C_2^\pm \prod_{j = 1}^J ( y_{p_j} d_{k_j} (p_j ) ) X^{\frac 56} + O_{\varepsilon} \bigg(\prod_{j =1}^J p_j^{\omega}X^{\theta+\varepsilon} \bigg) \bigg) \\ &= C_1^\pm X \bigg( \sum_{\mathbf{k}} \eta_{1, \mathbf{p}} ( \mathbf{k}, \mathbf{e}) \eta_{2,\mathbf{p}} ( \mathbf{k}, \mathbf{s}) \prod_{j = 1}^J ( x_{p_j} c_{k_j} (p_j )) \bigg) + C_2^\pm X^{\frac 56} \bigg( \sum_{\mathbf{k}} \eta_{1, \mathbf{p}} ( \mathbf{k}, \mathbf{e}) \eta_{2,\mathbf{p}} ( \mathbf{k}, \mathbf{s}) \prod_{j = 1}^J ( y_{p_j} d_{k_j} (p_j )) \bigg) \\ &\quad + O_{\varepsilon} \bigg( \sum_{\mathbf{k}} | \eta_{1, \mathbf{p}} ( \mathbf{k}, \mathbf{e}) \eta_{2,\mathbf{p}} ( \mathbf{k}, \mathbf{s}) | \prod_{j =1}^J p_j^{\omega}X^{\theta+\varepsilon} \bigg). \end{align*} $$
$$ \begin{align*} & \sum_{\mathbf{k}} \eta_{1, \mathbf{p}} ( \mathbf{k}, \mathbf{e}) \eta_{2,\mathbf{p}} ( \mathbf{k}, \mathbf{s}) \bigg(C_1^\pm \prod_{j = 1}^J ( x_{p_j} c_{k_j} (p_j ) ) X + C_2^\pm \prod_{j = 1}^J ( y_{p_j} d_{k_j} (p_j ) ) X^{\frac 56} + O_{\varepsilon} \bigg(\prod_{j =1}^J p_j^{\omega}X^{\theta+\varepsilon} \bigg) \bigg) \\ &= C_1^\pm X \bigg( \sum_{\mathbf{k}} \eta_{1, \mathbf{p}} ( \mathbf{k}, \mathbf{e}) \eta_{2,\mathbf{p}} ( \mathbf{k}, \mathbf{s}) \prod_{j = 1}^J ( x_{p_j} c_{k_j} (p_j )) \bigg) + C_2^\pm X^{\frac 56} \bigg( \sum_{\mathbf{k}} \eta_{1, \mathbf{p}} ( \mathbf{k}, \mathbf{e}) \eta_{2,\mathbf{p}} ( \mathbf{k}, \mathbf{s}) \prod_{j = 1}^J ( y_{p_j} d_{k_j} (p_j )) \bigg) \\ &\quad + O_{\varepsilon} \bigg( \sum_{\mathbf{k}} | \eta_{1, \mathbf{p}} ( \mathbf{k}, \mathbf{e}) \eta_{2,\mathbf{p}} ( \mathbf{k}, \mathbf{s}) | \prod_{j =1}^J p_j^{\omega}X^{\theta+\varepsilon} \bigg). \end{align*} $$
We can change the last three
![]() $\mathbf {k}$
-sums into products by (4.5). Doing so, we obtain that the above is equal to
$\mathbf {k}$
-sums into products by (4.5). Doing so, we obtain that the above is equal to
 $$ \begin{align*} &C_1^\pm X \prod_{j =1}^J \bigg( x_{p_j} \widetilde f(e_j, s_j, p_j ) \bigg) + C_2^\pm X^{\frac 56} \prod_{j =1}^J \bigg( y_{p_j} \widetilde g(e_j, s_j, p_j ) \bigg) + O_{\varepsilon} \bigg( \prod_{j =1}^J \bigg( p_j^{\omega} (2e_j +5 ) \bigg) X^{\theta+\varepsilon} \bigg) \\ &\quad = C_1^\pm X \prod_{p^e\parallel m, p^s \parallel h}\widetilde f(e,s,p)x_p + C_2^\pm X^{\frac 56} \prod_{p^e\parallel m, p^s \parallel h}\widetilde g(e,s,p)y_p + O_{\varepsilon} \bigg( \prod_{j =1}^J \bigg( p_j^{\omega} ( 2 e_j + 5 ) \bigg) X^{\theta+\varepsilon} \bigg) , \end{align*} $$
$$ \begin{align*} &C_1^\pm X \prod_{j =1}^J \bigg( x_{p_j} \widetilde f(e_j, s_j, p_j ) \bigg) + C_2^\pm X^{\frac 56} \prod_{j =1}^J \bigg( y_{p_j} \widetilde g(e_j, s_j, p_j ) \bigg) + O_{\varepsilon} \bigg( \prod_{j =1}^J \bigg( p_j^{\omega} (2e_j +5 ) \bigg) X^{\theta+\varepsilon} \bigg) \\ &\quad = C_1^\pm X \prod_{p^e\parallel m, p^s \parallel h}\widetilde f(e,s,p)x_p + C_2^\pm X^{\frac 56} \prod_{p^e\parallel m, p^s \parallel h}\widetilde g(e,s,p)y_p + O_{\varepsilon} \bigg( \prod_{j =1}^J \bigg( p_j^{\omega} ( 2 e_j + 5 ) \bigg) X^{\theta+\varepsilon} \bigg) , \end{align*} $$
where
 $$ \begin{align*}\widetilde f( e, s, p) := \sum_{k=1}^5 \eta_{1, p } (k , e ) \eta_{2,p } (k , s ) c_{k } (p ) , \qquad \widetilde g(e,s,p) := \sum_{k =1}^5 \eta_{1, p } ( k , e ) \eta_{2,p } ( k , s ) d_{k } (p ) .\end{align*} $$
$$ \begin{align*}\widetilde f( e, s, p) := \sum_{k=1}^5 \eta_{1, p } (k , e ) \eta_{2,p } (k , s ) c_{k } (p ) , \qquad \widetilde g(e,s,p) := \sum_{k =1}^5 \eta_{1, p } ( k , e ) \eta_{2,p } ( k , s ) d_{k } (p ) .\end{align*} $$
A straightforward calculation shows that
![]() $\widetilde f( e, s, p) = f( e, s, p) $
and
$\widetilde f( e, s, p) = f( e, s, p) $
and
![]() $\widetilde g( e, s, p)=g( e, s, p) $
(see the explicit description of the coefficients in Section 2; note that
$\widetilde g( e, s, p)=g( e, s, p) $
(see the explicit description of the coefficients in Section 2; note that
![]() $ \eta _{2,p}(k,0) = 1 $
) and the lemma follows.
$ \eta _{2,p}(k,0) = 1 $
) and the lemma follows.
We now proceed with the estimation of
![]() $R_1(\alpha , \gamma; X )$
. Taking into account the two main terms in Lemma 4.1, we expect that
$R_1(\alpha , \gamma; X )$
. Taking into account the two main terms in Lemma 4.1, we expect that
 $$ \begin{align} R_1(\alpha, \gamma;X)=R_1^M(\alpha, \gamma)+\frac{C_2^\pm}{C_1^\pm}X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) (R_1^S(\alpha, \gamma)-R_1^M(\alpha, \gamma))+\text{Error}, \end{align} $$
$$ \begin{align} R_1(\alpha, \gamma;X)=R_1^M(\alpha, \gamma)+\frac{C_2^\pm}{C_1^\pm}X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) (R_1^S(\alpha, \gamma)-R_1^M(\alpha, \gamma))+\text{Error}, \end{align} $$
where
 $$ \begin{align} R_1^M(\alpha, \gamma):=&\prod_p \Big( 1 + \sum_{ e\geq 1} \frac{x_p f(e,0,p)}{p^{e(\frac 12+\alpha)}} + \sum_{ e\geq 0} \frac{x_p f(e,1,p)}{p^{e(\frac 12+\alpha) +(\frac 12+\gamma) }} + \sum_{ e\geq 0} \frac{x_p f(e,2,p)}{p^{e(\frac 12+\alpha) + 2(\frac 12+\gamma) }}\Big),\nonumber\\ R_1^S(\alpha, \gamma):=&\prod_p \Big( 1 + \sum_{ e\geq 1} \frac{y_p g(e,0,p)}{p^{e(\frac 12+\alpha)}} + \sum_{ e\geq 0} \frac{y_p g(e,1,p)}{p^{e(\frac 12+\alpha) +(\frac 12+\gamma) }} + \sum_{ e\geq 0} \frac{y_p g(e,2,p)}{p^{e(\frac 12+\alpha) + 2(\frac 12+\gamma) }}\Big) \end{align} $$
$$ \begin{align} R_1^M(\alpha, \gamma):=&\prod_p \Big( 1 + \sum_{ e\geq 1} \frac{x_p f(e,0,p)}{p^{e(\frac 12+\alpha)}} + \sum_{ e\geq 0} \frac{x_p f(e,1,p)}{p^{e(\frac 12+\alpha) +(\frac 12+\gamma) }} + \sum_{ e\geq 0} \frac{x_p f(e,2,p)}{p^{e(\frac 12+\alpha) + 2(\frac 12+\gamma) }}\Big),\nonumber\\ R_1^S(\alpha, \gamma):=&\prod_p \Big( 1 + \sum_{ e\geq 1} \frac{y_p g(e,0,p)}{p^{e(\frac 12+\alpha)}} + \sum_{ e\geq 0} \frac{y_p g(e,1,p)}{p^{e(\frac 12+\alpha) +(\frac 12+\gamma) }} + \sum_{ e\geq 0} \frac{y_p g(e,2,p)}{p^{e(\frac 12+\alpha) + 2(\frac 12+\gamma) }}\Big) \end{align} $$
for
![]() $ \operatorname {Re} ( \alpha ) , \operatorname {Re} ( \gamma )> \frac 12$
. Since
$ \operatorname {Re} ( \alpha ) , \operatorname {Re} ( \gamma )> \frac 12$
. Since
 $$ \begin{align*} R_1^M(\alpha, \gamma) &= \prod_p \Bigg( 1 + \frac{1}{p^{1+2\alpha}} - \frac{1}{p^{1+\alpha+\gamma}}\\ &\quad+ O \Big(\frac{1}{p^{\frac 32 +\operatorname{Re}(\alpha)}}+\frac{1}{p^{\frac 32 +3\operatorname{Re}(\alpha)}}+\frac{1}{p^{\frac 32 +\operatorname{Re}(\gamma)}} + \frac{1}{p^{\frac 32+ \operatorname{Re} ( 2 \alpha + \gamma) }} + \frac{1}{p^{\frac 52 + \operatorname{Re} (3 \alpha+ 2 \gamma) }} \Big) \Bigg), \end{align*} $$
$$ \begin{align*} R_1^M(\alpha, \gamma) &= \prod_p \Bigg( 1 + \frac{1}{p^{1+2\alpha}} - \frac{1}{p^{1+\alpha+\gamma}}\\ &\quad+ O \Big(\frac{1}{p^{\frac 32 +\operatorname{Re}(\alpha)}}+\frac{1}{p^{\frac 32 +3\operatorname{Re}(\alpha)}}+\frac{1}{p^{\frac 32 +\operatorname{Re}(\gamma)}} + \frac{1}{p^{\frac 32+ \operatorname{Re} ( 2 \alpha + \gamma) }} + \frac{1}{p^{\frac 52 + \operatorname{Re} (3 \alpha+ 2 \gamma) }} \Big) \Bigg), \end{align*} $$
we see that
is analytically continued to the regionFootnote 4
![]() $ \operatorname {Re} (\alpha ), \operatorname {Re} (\gamma )> - \frac 16 $
. Similarly, from the estimates
$ \operatorname {Re} (\alpha ), \operatorname {Re} (\gamma )> - \frac 16 $
. Similarly, from the estimates
 $$ \begin{align*} & \sum_{ e\geq 1} \frac{y_p g(e,0,p)}{p^{e(\frac 12+\alpha)}} = \frac 1{p^{\frac 56+\alpha}}+\frac 1{p^{1+2\alpha}} +O\Big( \frac 1{p^{\operatorname{Re}(\alpha) + \frac 32}}+\frac 1{p^{2\operatorname{Re}(\alpha) + \frac 43}}+ \frac 1{p^{3\operatorname{Re}(\alpha) + \frac 32}}\Big),\\ &\sum_{ e\geq 0} \frac{y_p g(e,1,p)}{p^{e(\frac 12+\alpha) +(\frac 12+\gamma) }}=-\frac 1{p^{\frac 56+\gamma}} - \frac 1{p^{1+\alpha+\gamma}}+O\Big(\frac 1{p^{\frac 43+\operatorname{Re}(\alpha+\gamma)}} \Big),\\ &\sum_{ e\geq 0} \frac{y_p g(e,2,p)}{p^{e(\frac 12+\alpha) + 2(\frac 12+\gamma) }} = O \Big( \frac 1{p^{\frac 32+\operatorname{Re}(\alpha+2\gamma)}} \Big) , \end{align*} $$
$$ \begin{align*} & \sum_{ e\geq 1} \frac{y_p g(e,0,p)}{p^{e(\frac 12+\alpha)}} = \frac 1{p^{\frac 56+\alpha}}+\frac 1{p^{1+2\alpha}} +O\Big( \frac 1{p^{\operatorname{Re}(\alpha) + \frac 32}}+\frac 1{p^{2\operatorname{Re}(\alpha) + \frac 43}}+ \frac 1{p^{3\operatorname{Re}(\alpha) + \frac 32}}\Big),\\ &\sum_{ e\geq 0} \frac{y_p g(e,1,p)}{p^{e(\frac 12+\alpha) +(\frac 12+\gamma) }}=-\frac 1{p^{\frac 56+\gamma}} - \frac 1{p^{1+\alpha+\gamma}}+O\Big(\frac 1{p^{\frac 43+\operatorname{Re}(\alpha+\gamma)}} \Big),\\ &\sum_{ e\geq 0} \frac{y_p g(e,2,p)}{p^{e(\frac 12+\alpha) + 2(\frac 12+\gamma) }} = O \Big( \frac 1{p^{\frac 32+\operatorname{Re}(\alpha+2\gamma)}} \Big) , \end{align*} $$
we deduce that
 $$ \begin{align} A_4(\alpha,\gamma):= \frac{ \zeta(\tfrac 56+\gamma) \zeta(1+\alpha+\gamma)}{\zeta(\tfrac 56+\alpha) \zeta(1+2\alpha) }R_1^S(\alpha, \gamma) \end{align} $$
$$ \begin{align} A_4(\alpha,\gamma):= \frac{ \zeta(\tfrac 56+\gamma) \zeta(1+\alpha+\gamma)}{\zeta(\tfrac 56+\alpha) \zeta(1+2\alpha) }R_1^S(\alpha, \gamma) \end{align} $$
is analytic in the region
![]() $\operatorname {Re}(\alpha ),\operatorname {Re}(\gamma )>-\frac 16$
. Note that by their defining product formulas, we have the bounds
$\operatorname {Re}(\alpha ),\operatorname {Re}(\gamma )>-\frac 16$
. Note that by their defining product formulas, we have the bounds
for
![]() $ \operatorname {Re} ( \alpha ) , \operatorname {Re} ( \gamma ) \geq - \frac 16 + \varepsilon> - \frac 16$
. Using this notation, (4.6) takes the form
$ \operatorname {Re} ( \alpha ) , \operatorname {Re} ( \gamma ) \geq - \frac 16 + \varepsilon> - \frac 16$
. Using this notation, (4.6) takes the form
 $$ \begin{align*} & R_1(\alpha,\gamma;X) = \frac{\zeta(1+2\alpha)}{\zeta(1+\alpha+\gamma)} \Big( A_3(\alpha,\gamma)+\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \Big( \frac{\zeta(\tfrac 56+\alpha)}{\zeta(\tfrac 56+\gamma)} A_4(\alpha,\gamma) - A_3(\alpha,\gamma) \Big)\Big)\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad +\text{Error}. \end{align*} $$
$$ \begin{align*} & R_1(\alpha,\gamma;X) = \frac{\zeta(1+2\alpha)}{\zeta(1+\alpha+\gamma)} \Big( A_3(\alpha,\gamma)+\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \Big( \frac{\zeta(\tfrac 56+\alpha)}{\zeta(\tfrac 56+\gamma)} A_4(\alpha,\gamma) - A_3(\alpha,\gamma) \Big)\Big)\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad +\text{Error}. \end{align*} $$
The above computation is sufficient in order to obtain a conjectural evaluation of the average (4.3). However, our goal is to evaluate the one-level density through the average of
![]() $\frac {L'}{L} (\frac 12+r ,f_K ) $
; therefore, it is necessary to also compute the partial derivative
$\frac {L'}{L} (\frac 12+r ,f_K ) $
; therefore, it is necessary to also compute the partial derivative
![]() $\frac {\partial }{ \partial \alpha }R_1(\alpha , \gamma ;X)|_{\alpha =\gamma =r} $
. To do so, we need to make sure that the error term stays small after a differentiation. This is achieved by applying Cauchy’s integral formula for the derivative
$\frac {\partial }{ \partial \alpha }R_1(\alpha , \gamma ;X)|_{\alpha =\gamma =r} $
. To do so, we need to make sure that the error term stays small after a differentiation. This is achieved by applying Cauchy’s integral formula for the derivative
 $$ \begin{align*}f'(a)=\frac{1}{2\pi i}\int_{|z-a|=\kappa} \frac{f(z)}{(z-a)^2}dz\end{align*} $$
$$ \begin{align*}f'(a)=\frac{1}{2\pi i}\int_{|z-a|=\kappa} \frac{f(z)}{(z-a)^2}dz\end{align*} $$
(valid for all small enough
![]() $\kappa>0$
) and bounding the integrand using the approximation for
$\kappa>0$
) and bounding the integrand using the approximation for
![]() $R_1(\alpha ,\gamma ;X) $
above. As for the main terms, one can differentiate them term by term and obtain the expected approximation
$R_1(\alpha ,\gamma ;X) $
above. As for the main terms, one can differentiate them term by term and obtain the expected approximation
 $$ \begin{align} & \frac{\partial }{ \partial \alpha}R_1(\alpha, \gamma;X)\Big|_{\alpha=\gamma=r}=A_{3,\alpha}(r,r)+ \frac{\zeta'}{\zeta}(1+2r) A_3(r,r) + \frac{C_2^\pm}{C_1^\pm} X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big)\nonumber\\ & \quad \times \Big( A_{4,\alpha}(r,r) +\frac{\zeta'}{\zeta} (\tfrac 56+r) A_4 (r,r) - A_{3,\alpha}(r,r) +\frac{\zeta'}{\zeta}(1+2r) ( A_4(r,r)-A_3(r,r)) \Big) \nonumber\\ &\quad +\text{Error}, \end{align} $$
$$ \begin{align} & \frac{\partial }{ \partial \alpha}R_1(\alpha, \gamma;X)\Big|_{\alpha=\gamma=r}=A_{3,\alpha}(r,r)+ \frac{\zeta'}{\zeta}(1+2r) A_3(r,r) + \frac{C_2^\pm}{C_1^\pm} X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big)\nonumber\\ & \quad \times \Big( A_{4,\alpha}(r,r) +\frac{\zeta'}{\zeta} (\tfrac 56+r) A_4 (r,r) - A_{3,\alpha}(r,r) +\frac{\zeta'}{\zeta}(1+2r) ( A_4(r,r)-A_3(r,r)) \Big) \nonumber\\ &\quad +\text{Error}, \end{align} $$
where
![]() $A_{3,\alpha }(r,r)=\frac {\partial }{ \partial \alpha }A_3(\alpha ,\gamma )\Big |_{\alpha =\gamma =r}$
and
$A_{3,\alpha }(r,r)=\frac {\partial }{ \partial \alpha }A_3(\alpha ,\gamma )\Big |_{\alpha =\gamma =r}$
and
![]() $A_{4,\alpha }(r,r)=\frac {\partial }{ \partial \alpha }A_4(\alpha ,\gamma )\Big |_{\alpha =\gamma =r}.$
$A_{4,\alpha }(r,r)=\frac {\partial }{ \partial \alpha }A_4(\alpha ,\gamma )\Big |_{\alpha =\gamma =r}.$
Now, from the definition of
![]() $f(e,j,p) $
and
$f(e,j,p) $
and
![]() $g(e,j,p)$
(see Lemma 4.1) as well as (3.4) and (3.5), we have
$g(e,j,p)$
(see Lemma 4.1) as well as (3.4) and (3.5), we have
 $$ \begin{align*} f(1,0,p)+f(0,1,p) & =g(1,0,p)+g(0,1,p)=0,\\ f(e,0,p)+f(e-1,1,p) +f(e-2,2,p) & =g(e,0,p)+g(e-1,1,p) +g(e-2,2,p)=0, \\ f(e, 0 , p ) - f(e-2 , 2, p ) & = \theta_e + p^{-1} , \\ g(e, 0 , p ) - g(e-2 , 2, p ) & = ( 1 + p^{- \frac13} ) ( \kappa_e ( p ) + p^{-1} + p^{- \frac43} ). \end{align*} $$
$$ \begin{align*} f(1,0,p)+f(0,1,p) & =g(1,0,p)+g(0,1,p)=0,\\ f(e,0,p)+f(e-1,1,p) +f(e-2,2,p) & =g(e,0,p)+g(e-1,1,p) +g(e-2,2,p)=0, \\ f(e, 0 , p ) - f(e-2 , 2, p ) & = \theta_e + p^{-1} , \\ g(e, 0 , p ) - g(e-2 , 2, p ) & = ( 1 + p^{- \frac13} ) ( \kappa_e ( p ) + p^{-1} + p^{- \frac43} ). \end{align*} $$
By the above identities and the definition (4.7), we deduce that
It follows that for
![]() $\operatorname {Re}(r)>\frac 12$
,
$\operatorname {Re}(r)>\frac 12$
,
 $$ \begin{align*} R^M_{1,\alpha}(r,r) &= \frac{R^M_{1,\alpha}(r,r)}{R^M_1(r,r)} = \frac{ \partial}{\partial \alpha} \log R^M_{1} ( \alpha, \gamma) \bigg|_{ \alpha=\gamma = r}\\ &= \sum_p \left( - \frac{ x_p \log p }{p^{\frac12 + r}}f(1,0,p) - \sum_{ e \geq 2} \frac{ x_p \log p }{ p^{ e( \frac12 + r ) } } \big( f(e,0,p ) - f(e-2,2,p)\big) \right)\\ &\quad + \sum_p \left( - \sum_{ e \geq 2} \frac{ x_p \log p }{ p^{ e( \frac12 + r ) } } (e-1) \big( f( e,0,p) + f(e-1,1,p) + f( e-2,2,p) \big) \right) \\ & =- \sum_p \sum_{ e \geq 1} \frac{ x_p \log p }{ p^{ e( \frac12 + r ) } } \Big( \theta_e + \frac1p \Big) \end{align*} $$
$$ \begin{align*} R^M_{1,\alpha}(r,r) &= \frac{R^M_{1,\alpha}(r,r)}{R^M_1(r,r)} = \frac{ \partial}{\partial \alpha} \log R^M_{1} ( \alpha, \gamma) \bigg|_{ \alpha=\gamma = r}\\ &= \sum_p \left( - \frac{ x_p \log p }{p^{\frac12 + r}}f(1,0,p) - \sum_{ e \geq 2} \frac{ x_p \log p }{ p^{ e( \frac12 + r ) } } \big( f(e,0,p ) - f(e-2,2,p)\big) \right)\\ &\quad + \sum_p \left( - \sum_{ e \geq 2} \frac{ x_p \log p }{ p^{ e( \frac12 + r ) } } (e-1) \big( f( e,0,p) + f(e-1,1,p) + f( e-2,2,p) \big) \right) \\ & =- \sum_p \sum_{ e \geq 1} \frac{ x_p \log p }{ p^{ e( \frac12 + r ) } } \Big( \theta_e + \frac1p \Big) \end{align*} $$
and
 $$ \begin{align*} R^S_{1,\alpha}(r,r) &= \sum_p \left( - \frac{ y_p \log p }{p^{\frac12 + r}}g(1,0,p) - \sum_{ e \geq 2} \frac{ y_p \log p }{ p^{ e( \frac12 + r ) } } \big( g(e,0,p ) - g(e-2,2,p)\big) \right)\\ &\quad + \sum_p \left( - \sum_{ e \geq 2} \frac{ y_p \log p }{ p^{ e( \frac12 + r ) } } (e-1) \big( g( e,0,p) + g(e-1,1,p) + g( e-2,2,p) \big) \right) \\ & =- \sum_p \sum_{ e \geq 1} \frac{y_p \log p }{ p^{ e( \frac12 + r ) } } \big( 1 + p^{- \frac13} \big) \big( \kappa_e ( p ) + p^{-1} + p^{- \frac43} \big) \\ & =- \sum_p \sum_{ e \geq 1} \frac{ \log p }{ p^{ e( \frac12 + r ) } } \Big( \beta_e (p)+ x_p \Big( \theta_e+ \frac1p \Big)\Big) , \end{align*} $$
$$ \begin{align*} R^S_{1,\alpha}(r,r) &= \sum_p \left( - \frac{ y_p \log p }{p^{\frac12 + r}}g(1,0,p) - \sum_{ e \geq 2} \frac{ y_p \log p }{ p^{ e( \frac12 + r ) } } \big( g(e,0,p ) - g(e-2,2,p)\big) \right)\\ &\quad + \sum_p \left( - \sum_{ e \geq 2} \frac{ y_p \log p }{ p^{ e( \frac12 + r ) } } (e-1) \big( g( e,0,p) + g(e-1,1,p) + g( e-2,2,p) \big) \right) \\ & =- \sum_p \sum_{ e \geq 1} \frac{y_p \log p }{ p^{ e( \frac12 + r ) } } \big( 1 + p^{- \frac13} \big) \big( \kappa_e ( p ) + p^{-1} + p^{- \frac43} \big) \\ & =- \sum_p \sum_{ e \geq 1} \frac{ \log p }{ p^{ e( \frac12 + r ) } } \Big( \beta_e (p)+ x_p \Big( \theta_e+ \frac1p \Big)\Big) , \end{align*} $$
by (3.6). Thus, we have
 $$ \begin{align*} A_{3,\alpha}(r,r)&=R^M_{1,\alpha}(r,r) - \frac{\zeta'}{\zeta}(1+2r) = -\sum_{p,e\geq 1} \Big(\theta_e+\frac 1p\Big) \frac{x_p\log p }{p^{e(\frac 12+r)}}- \frac{\zeta'}{\zeta}(1+2r) \end{align*} $$
$$ \begin{align*} A_{3,\alpha}(r,r)&=R^M_{1,\alpha}(r,r) - \frac{\zeta'}{\zeta}(1+2r) = -\sum_{p,e\geq 1} \Big(\theta_e+\frac 1p\Big) \frac{x_p\log p }{p^{e(\frac 12+r)}}- \frac{\zeta'}{\zeta}(1+2r) \end{align*} $$
and
 $$ \begin{align} A_{4,\alpha}(r,r)-A_{3,\alpha}(r,r) = -\sum_{p,e\geq 1} \frac{(\beta_e(p)-p^{-\frac e3}) \log p }{p^{e(\frac 12+r)}}, \end{align} $$
$$ \begin{align} A_{4,\alpha}(r,r)-A_{3,\alpha}(r,r) = -\sum_{p,e\geq 1} \frac{(\beta_e(p)-p^{-\frac e3}) \log p }{p^{e(\frac 12+r)}}, \end{align} $$
which are now valid in the extended region
![]() $ \operatorname {Re}(r)>0 $
. Coming back to (4.11), we deduce that
$ \operatorname {Re}(r)>0 $
. Coming back to (4.11), we deduce that
 $$ \begin{align*}\notag \frac{\partial }{ \partial \alpha}R_1(\alpha, \gamma;X)\Big|_{\alpha=\gamma=r} & =A_{3,\alpha}(r,r)+ \frac{\zeta'}{\zeta}(1+2r) \\&\notag\quad + \frac{C_2^\pm}{C_1^\pm} X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \Big( A_{4,\alpha}(r,r) - A_{3,\alpha}(r,r) +\frac{\zeta'}{\zeta} (\tfrac 56+r) \Big) +\text{Error}\\ \notag &=-\sum_{p,e\geq 1} \Big(\theta_e+\frac 1p\Big) \frac{x_p\log p }{p^{e(\frac 12+r)}} -\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e\geq 1} \frac{(\beta_e(p)-p^{-\frac e3} )\log p }{p^{e(\frac 12+r)}}\\ &\quad +\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big)\frac{\zeta'}{\zeta} (\tfrac 56+r) +\text{Error}, \end{align*} $$
$$ \begin{align*}\notag \frac{\partial }{ \partial \alpha}R_1(\alpha, \gamma;X)\Big|_{\alpha=\gamma=r} & =A_{3,\alpha}(r,r)+ \frac{\zeta'}{\zeta}(1+2r) \\&\notag\quad + \frac{C_2^\pm}{C_1^\pm} X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \Big( A_{4,\alpha}(r,r) - A_{3,\alpha}(r,r) +\frac{\zeta'}{\zeta} (\tfrac 56+r) \Big) +\text{Error}\\ \notag &=-\sum_{p,e\geq 1} \Big(\theta_e+\frac 1p\Big) \frac{x_p\log p }{p^{e(\frac 12+r)}} -\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e\geq 1} \frac{(\beta_e(p)-p^{-\frac e3} )\log p }{p^{e(\frac 12+r)}}\\ &\quad +\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big)\frac{\zeta'}{\zeta} (\tfrac 56+r) +\text{Error}, \end{align*} $$
where the second equality is valid in the region
![]() $\operatorname {Re}(r)>0$
.
$\operatorname {Re}(r)>0$
.
We now move to
![]() $R_2(\alpha , \gamma ;X).$
We recall that
$R_2(\alpha , \gamma ;X).$
We recall that
 $$ \begin{align} R_2(\alpha, \gamma;X)=\frac1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} |D_K|^{-\alpha}\frac{\Gamma_{\pm}(\frac 12-\alpha)}{\Gamma_{\pm}(\frac 12+\alpha)} \sum_{h,m} \frac{\lambda_K(m)\mu_{K}(h)}{m^{\frac{1}{2}-\alpha}h^{\frac{1}{2}+\gamma}}, \end{align} $$
$$ \begin{align} R_2(\alpha, \gamma;X)=\frac1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} |D_K|^{-\alpha}\frac{\Gamma_{\pm}(\frac 12-\alpha)}{\Gamma_{\pm}(\frac 12+\alpha)} \sum_{h,m} \frac{\lambda_K(m)\mu_{K}(h)}{m^{\frac{1}{2}-\alpha}h^{\frac{1}{2}+\gamma}}, \end{align} $$
and the Ratios Conjecture recipe tells us that we should replace
![]() $\lambda _K(m)\mu _K(h)$
with its average. However, a calculation involving Lemma 4.1 suggests that the terms
$\lambda _K(m)\mu _K(h)$
with its average. However, a calculation involving Lemma 4.1 suggests that the terms
![]() $ |D_K|^{-\alpha }$
and
$ |D_K|^{-\alpha }$
and
![]() $\lambda _K(m)\mu _{K}(h)$
have nonnegligible covariance. To take this into account, we substitute this step with the use of the following corollary of Lemma 4.1.
$\lambda _K(m)\mu _{K}(h)$
have nonnegligible covariance. To take this into account, we substitute this step with the use of the following corollary of Lemma 4.1.
Corollary 4.2. Let
![]() $m,h\in \mathbb N$
, and let
$m,h\in \mathbb N$
, and let
![]() $\frac 12 \leq \theta <\frac 56$
and
$\frac 12 \leq \theta <\frac 56$
and
![]() $\omega \geq 0$
be, such that (2.3) holds. For
$\omega \geq 0$
be, such that (2.3) holds. For
![]() $\alpha \in \mathbb {C}$
with
$\alpha \in \mathbb {C}$
with
![]() $0<\operatorname {Re}(\alpha ) < \frac 12$
, we have the estimate
$0<\operatorname {Re}(\alpha ) < \frac 12$
, we have the estimate
 $$ \begin{align*} &\frac{1}{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} |D_K|^{-\alpha} \lambda_K(m)\mu_K(h) = \frac{X^{-\alpha}}{1-\alpha} \prod_{p^e\parallel m, p^s \parallel h}f(e,s,p)x_p \\ &\quad + X^{-\frac16-\alpha} \Bigg( \frac{1}{1- \frac{6\alpha}5} \prod_{p^e\parallel m, p^s \parallel h}g(e,s,p)y_p- \frac{1}{1-\alpha} \prod_{p^e\parallel m, p^s \parallel h}f(e,s,p)x_p\Bigg) \frac{C_2^\pm}{C_1^\pm} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \\ &\quad +O_{\varepsilon}\bigg((1+|\alpha|)\prod_{ p \mid hm, p^e \parallel m } \big( (2 e + 5)p^{\omega}\big)X^{\theta-1-\operatorname{Re}(\alpha)+\varepsilon}\bigg). \end{align*} $$
$$ \begin{align*} &\frac{1}{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} |D_K|^{-\alpha} \lambda_K(m)\mu_K(h) = \frac{X^{-\alpha}}{1-\alpha} \prod_{p^e\parallel m, p^s \parallel h}f(e,s,p)x_p \\ &\quad + X^{-\frac16-\alpha} \Bigg( \frac{1}{1- \frac{6\alpha}5} \prod_{p^e\parallel m, p^s \parallel h}g(e,s,p)y_p- \frac{1}{1-\alpha} \prod_{p^e\parallel m, p^s \parallel h}f(e,s,p)x_p\Bigg) \frac{C_2^\pm}{C_1^\pm} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \\ &\quad +O_{\varepsilon}\bigg((1+|\alpha|)\prod_{ p \mid hm, p^e \parallel m } \big( (2 e + 5)p^{\omega}\big)X^{\theta-1-\operatorname{Re}(\alpha)+\varepsilon}\bigg). \end{align*} $$
Proof. This follows from applying Lemma 4.1 and (1.1) to the identity
 $$ \begin{align*} & \sum_{K \in \mathcal{F}^\pm(X)} |D_K|^{-\alpha} \lambda_K(m)\mu_K(h) = \int_1^X u^{-\alpha} d\bigg( \sum_{K \in \mathcal{F}^\pm(u)} \lambda_K(m)\mu_K(h) \bigg) \\ &\qquad\qquad\qquad\qquad= X^{-\alpha} \sum_{K \in \mathcal{F}^\pm(X)} \lambda_K(m)\mu_K(h) + \alpha \int_1^X u^{-\alpha -1 } \bigg( \sum_{K \in \mathcal{F}^\pm(u)} \lambda_K(m)\mu_K(h)\bigg) du. \end{align*} $$
$$ \begin{align*} & \sum_{K \in \mathcal{F}^\pm(X)} |D_K|^{-\alpha} \lambda_K(m)\mu_K(h) = \int_1^X u^{-\alpha} d\bigg( \sum_{K \in \mathcal{F}^\pm(u)} \lambda_K(m)\mu_K(h) \bigg) \\ &\qquad\qquad\qquad\qquad= X^{-\alpha} \sum_{K \in \mathcal{F}^\pm(X)} \lambda_K(m)\mu_K(h) + \alpha \int_1^X u^{-\alpha -1 } \bigg( \sum_{K \in \mathcal{F}^\pm(u)} \lambda_K(m)\mu_K(h)\bigg) du. \end{align*} $$
Applying this lemma, we deduce the following heuristic approximation of
![]() $R_2 ( \alpha , \gamma; X)$
:
$R_2 ( \alpha , \gamma; X)$
:
 $$ \begin{align*} & \frac{\Gamma_{\pm}(\frac 12-\alpha)}{\Gamma_{\pm}(\frac 12+\alpha)} \sum_{h,m} \frac{1}{m^{\frac{1}{2}-\alpha}h^{\frac{1}{2}+\gamma}} \bigg\{ \frac{X^{-\alpha}}{1-\alpha} \prod_{p^e\parallel m, p^s \parallel h}f(e,s,p)x_p\\ & + X^{-\frac 16-\alpha} \frac{C_2^\pm}{C_1^\pm} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \Big( \frac{1}{1-\frac{6\alpha}5} \prod_{p^e\parallel m, p^s \parallel h}g(e,s,p)y_p- \frac{1}{1-\alpha} \prod_{p^e\parallel m, p^s \parallel h}f(e,s,p)x_p\Big) \bigg\} \\ = & \frac{\Gamma_{\pm}(\frac 12-\alpha)}{\Gamma_{\pm}(\frac 12+\alpha)} \bigg\{ X^{-\alpha} \frac{ R_1^M ( - \alpha, \gamma)}{1-\alpha} + X^{-\frac 16-\alpha}\frac{C_2^\pm}{C_1^\pm} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \Big( \frac{R_1^S ( - \alpha, \gamma) }{1-\frac{6\alpha}5} - \frac{R_1^M ( - \alpha, \gamma)}{1-\alpha} \Big) \bigg\} \\ = & \frac{\Gamma_{\pm}(\frac 12-\alpha)}{\Gamma_{\pm}(\frac 12+\alpha)} \frac{\zeta(1-2\alpha)}{ \zeta( 1 - \alpha + \gamma) } \bigg\{ X^{-\alpha} \frac{A_3 ( - \alpha, \gamma)}{1-\alpha} \\ & + X^{-\frac 16-\alpha}\frac{C_2^\pm}{C_1^\pm} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \Big( \frac{A_4 ( - \alpha, \gamma)}{1- \frac{6\alpha}5} \frac{ \zeta(\frac 56-\alpha)}{ \zeta( \frac 56+\gamma)} - \frac{A_3 ( - \alpha, \gamma) }{1-\alpha} \Big) \bigg\}. \end{align*} $$
$$ \begin{align*} & \frac{\Gamma_{\pm}(\frac 12-\alpha)}{\Gamma_{\pm}(\frac 12+\alpha)} \sum_{h,m} \frac{1}{m^{\frac{1}{2}-\alpha}h^{\frac{1}{2}+\gamma}} \bigg\{ \frac{X^{-\alpha}}{1-\alpha} \prod_{p^e\parallel m, p^s \parallel h}f(e,s,p)x_p\\ & + X^{-\frac 16-\alpha} \frac{C_2^\pm}{C_1^\pm} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \Big( \frac{1}{1-\frac{6\alpha}5} \prod_{p^e\parallel m, p^s \parallel h}g(e,s,p)y_p- \frac{1}{1-\alpha} \prod_{p^e\parallel m, p^s \parallel h}f(e,s,p)x_p\Big) \bigg\} \\ = & \frac{\Gamma_{\pm}(\frac 12-\alpha)}{\Gamma_{\pm}(\frac 12+\alpha)} \bigg\{ X^{-\alpha} \frac{ R_1^M ( - \alpha, \gamma)}{1-\alpha} + X^{-\frac 16-\alpha}\frac{C_2^\pm}{C_1^\pm} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \Big( \frac{R_1^S ( - \alpha, \gamma) }{1-\frac{6\alpha}5} - \frac{R_1^M ( - \alpha, \gamma)}{1-\alpha} \Big) \bigg\} \\ = & \frac{\Gamma_{\pm}(\frac 12-\alpha)}{\Gamma_{\pm}(\frac 12+\alpha)} \frac{\zeta(1-2\alpha)}{ \zeta( 1 - \alpha + \gamma) } \bigg\{ X^{-\alpha} \frac{A_3 ( - \alpha, \gamma)}{1-\alpha} \\ & + X^{-\frac 16-\alpha}\frac{C_2^\pm}{C_1^\pm} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \Big( \frac{A_4 ( - \alpha, \gamma)}{1- \frac{6\alpha}5} \frac{ \zeta(\frac 56-\alpha)}{ \zeta( \frac 56+\gamma)} - \frac{A_3 ( - \alpha, \gamma) }{1-\alpha} \Big) \bigg\}. \end{align*} $$
If
![]() $\operatorname {Re}( r) $
is positive and small enough, then we expect that
$\operatorname {Re}( r) $
is positive and small enough, then we expect that
 $$ \begin{align*} \frac{\partial }{ \partial \alpha}R_2(\alpha, \gamma;X)\Big|_{\alpha=\gamma=r} = & - \frac{\Gamma_{\pm}(\frac 12-r)}{\Gamma_{\pm}(\frac 12+r)} \zeta(1-2r) \bigg\{ X^{-r} \frac{A_3 ( - r,r)}{1-r} \\ & + X^{-\frac 16-r} \frac{C_2^\pm}{C_1^\pm} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \Big( \frac{\zeta(\tfrac 56-r)}{\zeta(\tfrac 56+r)} \frac{A_4(-r,r)}{ 1- \frac{6r}5} - \frac{ A_3( -r, r)}{1-r} \Big) \bigg\}+\text{Error}. \end{align*} $$
$$ \begin{align*} \frac{\partial }{ \partial \alpha}R_2(\alpha, \gamma;X)\Big|_{\alpha=\gamma=r} = & - \frac{\Gamma_{\pm}(\frac 12-r)}{\Gamma_{\pm}(\frac 12+r)} \zeta(1-2r) \bigg\{ X^{-r} \frac{A_3 ( - r,r)}{1-r} \\ & + X^{-\frac 16-r} \frac{C_2^\pm}{C_1^\pm} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \Big( \frac{\zeta(\tfrac 56-r)}{\zeta(\tfrac 56+r)} \frac{A_4(-r,r)}{ 1- \frac{6r}5} - \frac{ A_3( -r, r)}{1-r} \Big) \bigg\}+\text{Error}. \end{align*} $$
We arrive at the following conjecture.
Conjecture 4.3. Let
![]() $\frac 12 \leq \theta <\frac 56$
and
$\frac 12 \leq \theta <\frac 56$
and
![]() $\omega \geq 0$
be, such that (2.3) holds. There exists
$\omega \geq 0$
be, such that (2.3) holds. There exists
![]() $0<\delta <\frac 1{6}$
, such that for any fixed
$0<\delta <\frac 1{6}$
, such that for any fixed
![]() $\varepsilon>0$
and for
$\varepsilon>0$
and for
![]() $r\in \mathbb C$
with
$r\in \mathbb C$
with
![]() $ \frac 1{L} \ll \operatorname {Re}(r) <\delta $
and
$ \frac 1{L} \ll \operatorname {Re}(r) <\delta $
and
![]() $|r|\leq X^{\frac \varepsilon 2}$
,
$|r|\leq X^{\frac \varepsilon 2}$
,
 $$ \begin{align} &\frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \frac{L'(\frac 12+r,f_K)}{L(\frac 12+r,f_K)}\nonumber\\ &\quad = -\sum_{p,e\geq 1} \Big(\theta_e+\frac 1p\Big) \frac{x_p\log p }{p^{e(\frac 12+r)}} -\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e\geq 1} \frac{(\beta_e(p)-p^{-\frac e3}) \log p }{p^{e(\frac 12+r)}} \nonumber\\ &\qquad +\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\zeta'}{\zeta}(\tfrac 56+r) - X^{-r} \frac{\Gamma_{\pm}(\frac 12-r)}{\Gamma_{\pm}(\frac 12+r)}\zeta(1-2r) \frac{A_3( -r, r)}{1-r} \nonumber\\ &\qquad - \frac{C_2^\pm }{C_1^\pm } X^{-r-\frac 16} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\Gamma_{\pm}(\frac 12-r)}{\Gamma_{\pm}(\frac 12+r)}\zeta(1-2r) \Big( \frac{\zeta(\tfrac 56-r)}{\zeta(\tfrac 56+r)} \frac{A_4(-r,r)}{ 1- \frac{6r}5} - \frac{ A_3( -r, r)}{1-r} \Big) +O_\varepsilon(X^{\theta-1+\varepsilon}). \end{align} $$
$$ \begin{align} &\frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \frac{L'(\frac 12+r,f_K)}{L(\frac 12+r,f_K)}\nonumber\\ &\quad = -\sum_{p,e\geq 1} \Big(\theta_e+\frac 1p\Big) \frac{x_p\log p }{p^{e(\frac 12+r)}} -\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e\geq 1} \frac{(\beta_e(p)-p^{-\frac e3}) \log p }{p^{e(\frac 12+r)}} \nonumber\\ &\qquad +\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\zeta'}{\zeta}(\tfrac 56+r) - X^{-r} \frac{\Gamma_{\pm}(\frac 12-r)}{\Gamma_{\pm}(\frac 12+r)}\zeta(1-2r) \frac{A_3( -r, r)}{1-r} \nonumber\\ &\qquad - \frac{C_2^\pm }{C_1^\pm } X^{-r-\frac 16} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\Gamma_{\pm}(\frac 12-r)}{\Gamma_{\pm}(\frac 12+r)}\zeta(1-2r) \Big( \frac{\zeta(\tfrac 56-r)}{\zeta(\tfrac 56+r)} \frac{A_4(-r,r)}{ 1- \frac{6r}5} - \frac{ A_3( -r, r)}{1-r} \Big) +O_\varepsilon(X^{\theta-1+\varepsilon}). \end{align} $$
Note that the two sums on the right-hand side are absolutely convergent.
Traditionally, when applying the Ratios Conjecture recipe, one has to restrict the real part of the variable r to small enough positive values. For example, in the family of quadratic Dirichlet L-functions [Reference Conrey and SnaithCS, Reference Fiorilli, Parks and SödergrenFPS3], one requires that
![]() $\frac 1{\log X}\ll \operatorname {Re}(r)<\frac 14$
. This ensures that one is far enough from a pole for the expression in the right-hand side. In the current situation, we will see that the term involving
$\frac 1{\log X}\ll \operatorname {Re}(r)<\frac 14$
. This ensures that one is far enough from a pole for the expression in the right-hand side. In the current situation, we will see that the term involving
![]() $X^{-r-\frac 16}$
has a pole at
$X^{-r-\frac 16}$
has a pole at
![]() $s=\frac 16$
.
$s=\frac 16$
.
Proposition 4.4. Assume Conjecture 4.3 and the Riemann Hypothesis for
![]() $\zeta _K(s)$
for all
$\zeta _K(s)$
for all
![]() $K\in \mathcal {F}^{\pm }(X)$
, and let
$K\in \mathcal {F}^{\pm }(X)$
, and let
![]() $\phi $
be a real even Schwartz function, such that
$\phi $
be a real even Schwartz function, such that
![]() $ \widehat \phi $
is compactly supported. For any constant
$ \widehat \phi $
is compactly supported. For any constant
![]() $ 0< c < \frac 16$
, we have that
$ 0< c < \frac 16$
, we have that
 $$ \begin{align} &\frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \sum_{\gamma_K}\phi \Big(\frac{L\gamma_K}{2\pi }\Big)=\widehat \phi(0)\Big(1+ \frac{\log(4 \pi^2 e)}{L} -\frac{C_2^\pm}{5C_1^\pm} \frac{X^{-\frac 16}}{L} + \frac{(C_2^\pm)^2 }{5(C_1^\pm)^2 } \frac{X^{-\frac 13}}{L} \Big)\nonumber\\ &\qquad + \frac1{\pi}\int_{-\infty}^{\infty}\phi\left(\frac{Lr}{2\pi}\right)\operatorname{Re}\Big(\frac{\Gamma'_{\pm}}{\Gamma_{\pm}}(\tfrac12+ir)\Big)dr -\frac{2}{L}\sum_{p,e}\frac{x_p\log p}{p^{\frac e2}}\widehat\phi\left(\frac{\log p^e}{L}\right) (\theta_e+\tfrac 1p)\nonumber\\ &\qquad -\frac{2C_2^\pm X^{-\frac 16}}{C_1^\pm L}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e}\frac{\log p}{p^{\frac e2}}\widehat\phi\left(\frac{\log p^e}{L}\right) (\beta_e(p)-p^{-\frac e3})\nonumber\\ &\qquad -\frac{1}{\pi i} \int_{(c )} \phi \Big(\frac{Ls}{2\pi i}\Big) \Big\{ -\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\zeta'}{\zeta}(\tfrac 56+s) + X^{-s} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \frac{A_3( -s, s) }{1-s} \nonumber\\ &\qquad +\frac{C_2^\pm }{C_1^\pm} X^{-s-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \Big( \frac{\zeta(\tfrac 56-s)}{\zeta(\tfrac 56+s)} \frac{A_4(-s,s)}{ 1- \frac{6s}5} - \frac{ A_3( -s, s)}{1-s} \Big) \Big\}ds \nonumber\\ &\qquad + O_\varepsilon(X^{\theta-1+\varepsilon}). \end{align} $$
$$ \begin{align} &\frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \sum_{\gamma_K}\phi \Big(\frac{L\gamma_K}{2\pi }\Big)=\widehat \phi(0)\Big(1+ \frac{\log(4 \pi^2 e)}{L} -\frac{C_2^\pm}{5C_1^\pm} \frac{X^{-\frac 16}}{L} + \frac{(C_2^\pm)^2 }{5(C_1^\pm)^2 } \frac{X^{-\frac 13}}{L} \Big)\nonumber\\ &\qquad + \frac1{\pi}\int_{-\infty}^{\infty}\phi\left(\frac{Lr}{2\pi}\right)\operatorname{Re}\Big(\frac{\Gamma'_{\pm}}{\Gamma_{\pm}}(\tfrac12+ir)\Big)dr -\frac{2}{L}\sum_{p,e}\frac{x_p\log p}{p^{\frac e2}}\widehat\phi\left(\frac{\log p^e}{L}\right) (\theta_e+\tfrac 1p)\nonumber\\ &\qquad -\frac{2C_2^\pm X^{-\frac 16}}{C_1^\pm L}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e}\frac{\log p}{p^{\frac e2}}\widehat\phi\left(\frac{\log p^e}{L}\right) (\beta_e(p)-p^{-\frac e3})\nonumber\\ &\qquad -\frac{1}{\pi i} \int_{(c )} \phi \Big(\frac{Ls}{2\pi i}\Big) \Big\{ -\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\zeta'}{\zeta}(\tfrac 56+s) + X^{-s} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \frac{A_3( -s, s) }{1-s} \nonumber\\ &\qquad +\frac{C_2^\pm }{C_1^\pm} X^{-s-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \Big( \frac{\zeta(\tfrac 56-s)}{\zeta(\tfrac 56+s)} \frac{A_4(-s,s)}{ 1- \frac{6s}5} - \frac{ A_3( -s, s)}{1-s} \Big) \Big\}ds \nonumber\\ &\qquad + O_\varepsilon(X^{\theta-1+\varepsilon}). \end{align} $$
Proof. By the residue theorem, we have the identity
 $$ \begin{align} \frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \mathfrak{D}_\phi(K)= \frac{1}{2 \pi i} \left( \int_{(\frac1L)} - \int_{(-\frac1L)} \right) \frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \frac{L'(s+\frac 12,f_K)}{L(s+\frac 12,f_K)}\phi \Big(\frac{Ls}{2\pi i}\Big)ds. \end{align} $$
$$ \begin{align} \frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \mathfrak{D}_\phi(K)= \frac{1}{2 \pi i} \left( \int_{(\frac1L)} - \int_{(-\frac1L)} \right) \frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \frac{L'(s+\frac 12,f_K)}{L(s+\frac 12,f_K)}\phi \Big(\frac{Ls}{2\pi i}\Big)ds. \end{align} $$
Under Conjecture 4.3 and well-known arguments (see, e.g. [Reference Fiorilli, Parks and SödergrenFPS3, Section 3.2]), the part of this sum involving the first integral is equal to
 $$ \begin{align*} &-\frac{1}{2\pi i} \int_{(\frac1L)} \phi \Big(\frac{Ls}{2\pi i}\Big) \bigg\{\sum_{p,e\geq 1} \Big(\theta_e+\frac 1p\Big) \frac{x_p\log p }{p^{e(\frac 12+s)}} +\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e\geq 1} \frac{(\beta_e(p)-p^{-\frac e3}) \log p }{p^{e(\frac 12+s)}} \\ &\qquad -\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\zeta'}{\zeta}(\tfrac 56+s) + X^{-s} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \frac{A_3( -s, s) }{1-s} \\ &\qquad +\frac{C_2^\pm }{C_1^\pm}X^{-s-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \Big( \frac{\zeta(\tfrac 56-s)}{\zeta(\tfrac 56+s)} \frac{A_4(-s,s)}{ 1- \frac{6s}5} - \frac{ A_3( -s, s)}{1-s} \Big) \bigg\} ds \\ &\qquad +O_\varepsilon(X^{\theta-1+\varepsilon}), \end{align*} $$
$$ \begin{align*} &-\frac{1}{2\pi i} \int_{(\frac1L)} \phi \Big(\frac{Ls}{2\pi i}\Big) \bigg\{\sum_{p,e\geq 1} \Big(\theta_e+\frac 1p\Big) \frac{x_p\log p }{p^{e(\frac 12+s)}} +\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e\geq 1} \frac{(\beta_e(p)-p^{-\frac e3}) \log p }{p^{e(\frac 12+s)}} \\ &\qquad -\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\zeta'}{\zeta}(\tfrac 56+s) + X^{-s} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \frac{A_3( -s, s) }{1-s} \\ &\qquad +\frac{C_2^\pm }{C_1^\pm}X^{-s-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \Big( \frac{\zeta(\tfrac 56-s)}{\zeta(\tfrac 56+s)} \frac{A_4(-s,s)}{ 1- \frac{6s}5} - \frac{ A_3( -s, s)}{1-s} \Big) \bigg\} ds \\ &\qquad +O_\varepsilon(X^{\theta-1+\varepsilon}), \end{align*} $$
where we used the bounds (4.10) and
 $$ \begin{align} \phi\Big(\frac{Ls}{2\pi i}\Big) = \frac { (-1)^\ell} {L^\ell s^\ell }\int_{\mathbb R} e^{ L \operatorname{Re}(s) x} e^{ i L \operatorname{Im}(s) x} \widehat \phi^{(\ell)}(x) dx \ll_\ell \frac{e^{L|\operatorname{Re}(s)| \sup(\mathrm{supp}(\widehat \phi)) } }{L^\ell |s|^\ell } \end{align} $$
$$ \begin{align} \phi\Big(\frac{Ls}{2\pi i}\Big) = \frac { (-1)^\ell} {L^\ell s^\ell }\int_{\mathbb R} e^{ L \operatorname{Re}(s) x} e^{ i L \operatorname{Im}(s) x} \widehat \phi^{(\ell)}(x) dx \ll_\ell \frac{e^{L|\operatorname{Re}(s)| \sup(\mathrm{supp}(\widehat \phi)) } }{L^\ell |s|^\ell } \end{align} $$
for every integer
![]() $\ell>0 $
, which is decaying on the line
$\ell>0 $
, which is decaying on the line
![]() $\operatorname {Re}(s) = \frac 1L$
. We may also shift the contour of integration to the line
$\operatorname {Re}(s) = \frac 1L$
. We may also shift the contour of integration to the line
![]() $\operatorname {Re}(s)=c$
with
$\operatorname {Re}(s)=c$
with
![]() $ 0 < c < \frac 16$
.
$ 0 < c < \frac 16$
.
For the second integral in (4.16) (over the line
![]() $\operatorname {Re}(s)=-\frac {1}{L}$
), we treat it as follows. By the functional equation (2.1), we have
$\operatorname {Re}(s)=-\frac {1}{L}$
), we treat it as follows. By the functional equation (2.1), we have
 $$ \begin{align*} - \frac{1}{2 \pi i} & \int_{(-\frac1L)} \frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \frac{L'(s+\frac 12,f_K)}{L(s+\frac 12,f_K)}\phi \Big(\frac{Ls}{2\pi i}\Big)ds \\ = & \frac{1}{2 \pi i} \int_{(\frac1L)} \frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \frac{L'(s+\frac 12,f_K)}{L(s+\frac 12,f_K)}\phi \Big(\frac{Ls}{2\pi i}\Big)ds \\ & + \frac{1}{2 \pi i} \int_{(-\frac1L)} \frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \left( \log |D_K| + \frac{ \Gamma'_{\pm}}{\Gamma_\pm} ( \tfrac12 + s )+ \frac{ \Gamma'_{\pm}}{\Gamma_\pm} ( \tfrac12 - s ) \right)\phi \Big(\frac{Ls}{2\pi i}\Big)ds. \end{align*} $$
$$ \begin{align*} - \frac{1}{2 \pi i} & \int_{(-\frac1L)} \frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \frac{L'(s+\frac 12,f_K)}{L(s+\frac 12,f_K)}\phi \Big(\frac{Ls}{2\pi i}\Big)ds \\ = & \frac{1}{2 \pi i} \int_{(\frac1L)} \frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \frac{L'(s+\frac 12,f_K)}{L(s+\frac 12,f_K)}\phi \Big(\frac{Ls}{2\pi i}\Big)ds \\ & + \frac{1}{2 \pi i} \int_{(-\frac1L)} \frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \left( \log |D_K| + \frac{ \Gamma'_{\pm}}{\Gamma_\pm} ( \tfrac12 + s )+ \frac{ \Gamma'_{\pm}}{\Gamma_\pm} ( \tfrac12 - s ) \right)\phi \Big(\frac{Ls}{2\pi i}\Big)ds. \end{align*} $$
The first integral on the right-hand side is identically equal to the integral that was just evaluated in the first part of this proof. As for the second, by shifting the contour to the line
![]() $\operatorname {Re} (s)=0$
, we find that it equals
$\operatorname {Re} (s)=0$
, we find that it equals
 $$ \begin{align*} & \left( \frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \log |D_K| \right) \frac{1}{2 \pi i} \int_{(0)} \phi \Big(\frac{Ls}{2\pi i}\Big)ds + \frac{1}{2 \pi i} \int_{(0)} \left( \frac{ \Gamma'_{\pm}}{\Gamma_\pm} ( \tfrac12 + s )+ \frac{ \Gamma'_{\pm}}{\Gamma_\pm} ( \tfrac12 - s ) \right) \phi \Big(\frac{Ls}{2\pi i}\Big)ds \\ & = \left( \frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \log |D_K| \right) \frac{ \widehat{\phi} (0)}{L} + \frac{1}{ \pi} \int_{- \infty}^\infty \phi \Big(\frac{Lr}{2\pi }\Big) \operatorname{Re} \left( \frac{ \Gamma'_{\pm}}{\Gamma_\pm} ( \tfrac12 + ir ) \right)dr. \end{align*} $$
$$ \begin{align*} & \left( \frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \log |D_K| \right) \frac{1}{2 \pi i} \int_{(0)} \phi \Big(\frac{Ls}{2\pi i}\Big)ds + \frac{1}{2 \pi i} \int_{(0)} \left( \frac{ \Gamma'_{\pm}}{\Gamma_\pm} ( \tfrac12 + s )+ \frac{ \Gamma'_{\pm}}{\Gamma_\pm} ( \tfrac12 - s ) \right) \phi \Big(\frac{Ls}{2\pi i}\Big)ds \\ & = \left( \frac 1{N^\pm(X)} \sum_{K \in \mathcal{F}^\pm(X)} \log |D_K| \right) \frac{ \widehat{\phi} (0)}{L} + \frac{1}{ \pi} \int_{- \infty}^\infty \phi \Big(\frac{Lr}{2\pi }\Big) \operatorname{Re} \left( \frac{ \Gamma'_{\pm}}{\Gamma_\pm} ( \tfrac12 + ir ) \right)dr. \end{align*} $$
By applying Lemma 3.2 to the first term, we find the leading terms on the right-hand side of (4.15).
Finally, by absolute convergence, we have the identity
 $$ \begin{align*} \frac{1}{2\pi i} \int_{(c)}\phi \Big(\frac{Ls}{2\pi i}\Big)\sum_{p,e\geq 1} \Big(\theta_e+\frac 1p\Big) \frac{x_p\log p }{p^{e(\frac 12+s)}} ds &= \sum_{p,e\geq 1} \Big(\theta_e+\frac 1p\Big) \frac{x_p\log p } {p^{\frac e2}} \frac 1{2\pi i} \int_{(c)}\phi \Big(\frac{Ls}{2\pi i}\Big) p^{-es}ds\\ &=\frac{1}{L}\sum_{p,e\geq 1} \Big(\theta_e+\frac 1p\Big) \frac{x_p\log p }{p^{\frac e2}}\widehat \phi\Big( \frac{e\log p}{L} \Big), \end{align*} $$
$$ \begin{align*} \frac{1}{2\pi i} \int_{(c)}\phi \Big(\frac{Ls}{2\pi i}\Big)\sum_{p,e\geq 1} \Big(\theta_e+\frac 1p\Big) \frac{x_p\log p }{p^{e(\frac 12+s)}} ds &= \sum_{p,e\geq 1} \Big(\theta_e+\frac 1p\Big) \frac{x_p\log p } {p^{\frac e2}} \frac 1{2\pi i} \int_{(c)}\phi \Big(\frac{Ls}{2\pi i}\Big) p^{-es}ds\\ &=\frac{1}{L}\sum_{p,e\geq 1} \Big(\theta_e+\frac 1p\Big) \frac{x_p\log p }{p^{\frac e2}}\widehat \phi\Big( \frac{e\log p}{L} \Big), \end{align*} $$
since the contour of the inner integral can be shifted to the line
![]() $\operatorname {Re}(s)=0$
. The same argument works for the term involving
$\operatorname {Re}(s)=0$
. The same argument works for the term involving
![]() $\beta _e(p)-p^{-\frac e3}$
. Hence, the proposition follows.
$\beta _e(p)-p^{-\frac e3}$
. Hence, the proposition follows.
5 Analytic continuation of
 $A_3 ( -s, s ) $
and
$A_3 ( -s, s ) $
and
 $A_4 ( -s , s )$
$A_4 ( -s , s )$
The goal of this section is to prove Theorem 1.4. To do so, we will need to estimate some of the terms in (4.15), namely,
 $$ \begin{align} J^\pm & (X) := \frac{2C_2^\pm X^{-\frac 16}}{C_1^\pm L}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e}\frac{\log p}{p^{\frac {5e}{6}}}\widehat\phi\left(\frac{\log p^e}{L}\right) \nonumber\\ & -\frac{1}{\pi i} \int_{(c )} \phi \Big(\frac{Ls}{2\pi i}\Big) \Big\{ -\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\zeta'}{\zeta}(\tfrac 56+s) + X^{-s} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \frac{ A_3( -s, s) }{1-s}\nonumber\\ & +\frac{C_2^\pm }{C_1^\pm} X^{-s-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \Big( \frac{\zeta(\tfrac 56-s)}{\zeta(\tfrac 56+s)} \frac{A_4(-s,s)}{ 1- \frac{6s}5} - \frac{ A_3( -s, s)}{1-s} \Big) \Big\}ds, \end{align} $$
$$ \begin{align} J^\pm & (X) := \frac{2C_2^\pm X^{-\frac 16}}{C_1^\pm L}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e}\frac{\log p}{p^{\frac {5e}{6}}}\widehat\phi\left(\frac{\log p^e}{L}\right) \nonumber\\ & -\frac{1}{\pi i} \int_{(c )} \phi \Big(\frac{Ls}{2\pi i}\Big) \Big\{ -\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\zeta'}{\zeta}(\tfrac 56+s) + X^{-s} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \frac{ A_3( -s, s) }{1-s}\nonumber\\ & +\frac{C_2^\pm }{C_1^\pm} X^{-s-\frac 16}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \Big( \frac{\zeta(\tfrac 56-s)}{\zeta(\tfrac 56+s)} \frac{A_4(-s,s)}{ 1- \frac{6s}5} - \frac{ A_3( -s, s)}{1-s} \Big) \Big\}ds, \end{align} $$
for
![]() $ 0 < c < \frac 16 $
. The idea is to provide an analytic continuation to the Dirichlet series
$ 0 < c < \frac 16 $
. The idea is to provide an analytic continuation to the Dirichlet series
![]() $A_3(-s,s)$
and
$A_3(-s,s)$
and
![]() $A_4(-s,s)$
in the strip
$A_4(-s,s)$
in the strip
![]() $ 0<\operatorname {Re}(s) < \frac 12$
and to shift the contour of integration to the right.
$ 0<\operatorname {Re}(s) < \frac 12$
and to shift the contour of integration to the right.
Lemma 5.1. The product formula
 $$ \begin{align} A_3 ( -s, s) = \zeta(3) \zeta( \tfrac32 - 3s ) \prod_p \bigg( 1 - \frac{1}{ p^{\frac32 +s}} + \frac{1}{p^{\frac52 - s}} - \frac{1}{p^{\frac52 -3s}} - \frac{1}{p^{3-4s}} + \frac{1}{p^{\frac92 - 5s}} \bigg) \end{align} $$
$$ \begin{align} A_3 ( -s, s) = \zeta(3) \zeta( \tfrac32 - 3s ) \prod_p \bigg( 1 - \frac{1}{ p^{\frac32 +s}} + \frac{1}{p^{\frac52 - s}} - \frac{1}{p^{\frac52 -3s}} - \frac{1}{p^{3-4s}} + \frac{1}{p^{\frac92 - 5s}} \bigg) \end{align} $$
provides an analytic continuation of
![]() $A_3 (-s, s)$
to
$A_3 (-s, s)$
to
![]() $|\operatorname {Re} ( s )| < \frac 12$
except for a simple pole at
$|\operatorname {Re} ( s )| < \frac 12$
except for a simple pole at
![]() $s= \frac 16$
with residue
$s= \frac 16$
with residue
 $$ \begin{align*}-\frac{\zeta(3)}{3\zeta(\frac53)\zeta(2)}.\end{align*} $$
$$ \begin{align*}-\frac{\zeta(3)}{3\zeta(\frac53)\zeta(2)}.\end{align*} $$
Proof. From (4.7) and (4.8), we see that in the region
![]() $ | \operatorname {Re} (s) | < \frac 16$
,
$ | \operatorname {Re} (s) | < \frac 16$
,
 $$ \begin{align} \notag A_3 ( -s, s) & = \prod_p \bigg( 1 - \frac1{p^3} \bigg)^{-1} \bigg( 1 - \frac1{p^{1-2s}}\bigg) \\ &\quad \times\bigg( 1+ \frac1p + \frac1{p^2} + \sum_{e \geq 1 } \frac{ f(e,0,p)}{p^{e(\frac 12-s)}} + \sum_{ e \geq 0 } \frac{f(e,1,p)}{p^{e(\frac 12-s)+\frac12+s}} + \sum_{e \geq 0 } \frac{f(e,2,p)}{ p^{e(\frac 12-s)+1+2s }} \bigg) \notag \\ & = \zeta(3) \prod_p \bigg( 1 - \frac1{p^{1-2s}}\bigg) \bigg( \frac1{p^2} + \sum_{e \geq 0 } \frac{1}{p^{e(\frac 12-s)}} \bigg( f(e,0,p) + \frac{f(e,1,p)}{p^{\frac 12+s}} + \frac{f(e,2,p)}{ p^{1+2s }}\bigg) \bigg). \end{align} $$
$$ \begin{align} \notag A_3 ( -s, s) & = \prod_p \bigg( 1 - \frac1{p^3} \bigg)^{-1} \bigg( 1 - \frac1{p^{1-2s}}\bigg) \\ &\quad \times\bigg( 1+ \frac1p + \frac1{p^2} + \sum_{e \geq 1 } \frac{ f(e,0,p)}{p^{e(\frac 12-s)}} + \sum_{ e \geq 0 } \frac{f(e,1,p)}{p^{e(\frac 12-s)+\frac12+s}} + \sum_{e \geq 0 } \frac{f(e,2,p)}{ p^{e(\frac 12-s)+1+2s }} \bigg) \notag \\ & = \zeta(3) \prod_p \bigg( 1 - \frac1{p^{1-2s}}\bigg) \bigg( \frac1{p^2} + \sum_{e \geq 0 } \frac{1}{p^{e(\frac 12-s)}} \bigg( f(e,0,p) + \frac{f(e,1,p)}{p^{\frac 12+s}} + \frac{f(e,2,p)}{ p^{1+2s }}\bigg) \bigg). \end{align} $$
The sum over
![]() $e\geq 0$
on the right-hand side is equal to
$e\geq 0$
on the right-hand side is equal to
 $$ \begin{align} & \frac16 \bigg( 1 - \frac{1}{ p^{\frac 12+s}} \bigg)^2 \sum_{e \geq 0 } (e+1) \frac{1}{p^{e(\frac 12-s)}} + \frac12 \bigg( 1 - \frac{1}{p^{1+2s}} \bigg) \sum_{e \geq 0 } \frac{ 1+(-1)^e}{2} \frac{1}{p^{e(\frac 12-s)}} \nonumber\\ &\qquad + \frac13 \bigg( 1 + \frac{1}{p^{\frac 12+s}}+ \frac{1}{p^{1+2s}} \bigg) \sum_{e \geq 0 }\tau_e \frac{1}{p^{e(\frac 12-s)}} + \frac1p \bigg( 1- \frac{1}{p^{\frac 12+s}}\bigg) \sum_{e \geq 0 } \frac{1}{p^{e(\frac 12-s)}}\nonumber\\ &\quad = \frac16 \cdot \frac{ \Big(1 - \frac{1}{ p^{\frac 12+s}} \Big)^2}{ \Big(1 - \frac{1}{ p^{\frac 12-s}}\Big)^2} + \frac12 \cdot \frac{ 1 - \frac{1}{p^{1+2s}} }{ 1 - \frac{1}{p^{1-2s}} } + \frac13 \cdot \frac{ 1 + \frac{1}{p^{\frac 12+s}}+ \frac{1}{p^{1+2s}}}{ 1 + \frac{1}{p^{\frac 12-s}}+ \frac{1}{p^{1-2s}} } + \frac1p \cdot \frac{ 1- \frac{1}{p^{\frac 12+s}}}{ 1- \frac{1}{p^{\frac 12-s}} }. \end{align} $$
$$ \begin{align} & \frac16 \bigg( 1 - \frac{1}{ p^{\frac 12+s}} \bigg)^2 \sum_{e \geq 0 } (e+1) \frac{1}{p^{e(\frac 12-s)}} + \frac12 \bigg( 1 - \frac{1}{p^{1+2s}} \bigg) \sum_{e \geq 0 } \frac{ 1+(-1)^e}{2} \frac{1}{p^{e(\frac 12-s)}} \nonumber\\ &\qquad + \frac13 \bigg( 1 + \frac{1}{p^{\frac 12+s}}+ \frac{1}{p^{1+2s}} \bigg) \sum_{e \geq 0 }\tau_e \frac{1}{p^{e(\frac 12-s)}} + \frac1p \bigg( 1- \frac{1}{p^{\frac 12+s}}\bigg) \sum_{e \geq 0 } \frac{1}{p^{e(\frac 12-s)}}\nonumber\\ &\quad = \frac16 \cdot \frac{ \Big(1 - \frac{1}{ p^{\frac 12+s}} \Big)^2}{ \Big(1 - \frac{1}{ p^{\frac 12-s}}\Big)^2} + \frac12 \cdot \frac{ 1 - \frac{1}{p^{1+2s}} }{ 1 - \frac{1}{p^{1-2s}} } + \frac13 \cdot \frac{ 1 + \frac{1}{p^{\frac 12+s}}+ \frac{1}{p^{1+2s}}}{ 1 + \frac{1}{p^{\frac 12-s}}+ \frac{1}{p^{1-2s}} } + \frac1p \cdot \frac{ 1- \frac{1}{p^{\frac 12+s}}}{ 1- \frac{1}{p^{\frac 12-s}} }. \end{align} $$
Here, we have used geometric sum identities, for example,
 $$ \begin{align*} \sum_{k=0}^\infty \tau_k x^k & = \sum_{k=0}^\infty x^{3k} - \sum_{k=0}^\infty x^{3k+1} = \frac{1-x}{1-x^3 } = \frac{1}{1+x+x^2 } \qquad (|x| < 1). \end{align*} $$
$$ \begin{align*} \sum_{k=0}^\infty \tau_k x^k & = \sum_{k=0}^\infty x^{3k} - \sum_{k=0}^\infty x^{3k+1} = \frac{1-x}{1-x^3 } = \frac{1}{1+x+x^2 } \qquad (|x| < 1). \end{align*} $$
Inserting the expression (5.4) in (5.3) and simplifying, we obtain the identity
 $$ \begin{align*} A_3 ( -s, s) = \zeta(3) \zeta( \tfrac32 - 3s ) \prod_p \bigg( 1 - \frac{1}{ p^{\frac 32+s}} + \frac{1}{p^{\frac 52 - s}} - \frac{1}{p^{\frac 52-3s}} - \frac{1}{p^{3-4s}} + \frac{1}{p^{\frac 92 - 5s}} \bigg) \end{align*} $$
$$ \begin{align*} A_3 ( -s, s) = \zeta(3) \zeta( \tfrac32 - 3s ) \prod_p \bigg( 1 - \frac{1}{ p^{\frac 32+s}} + \frac{1}{p^{\frac 52 - s}} - \frac{1}{p^{\frac 52-3s}} - \frac{1}{p^{3-4s}} + \frac{1}{p^{\frac 92 - 5s}} \bigg) \end{align*} $$
in the region
![]() $|\operatorname {Re}(s)|<1/6$
. Now, this clearly extends to
$|\operatorname {Re}(s)|<1/6$
. Now, this clearly extends to
![]() $ | \operatorname {Re} ( s ) | < 1/2$
except for a simple pole at
$ | \operatorname {Re} ( s ) | < 1/2$
except for a simple pole at
![]() $ s= 1/6 $
with residue equal to
$ s= 1/6 $
with residue equal to
 $$ \begin{align*}-\frac{\zeta(3)}{3} \prod_p \big( 1 - p^{-\frac53} - p^{-2} + p^{-\frac{11}{3}}\big) = - \frac{ \zeta(3)}{3} \frac{ 1}{ \zeta(\frac53) \zeta(2)} ,\end{align*} $$
$$ \begin{align*}-\frac{\zeta(3)}{3} \prod_p \big( 1 - p^{-\frac53} - p^{-2} + p^{-\frac{11}{3}}\big) = - \frac{ \zeta(3)}{3} \frac{ 1}{ \zeta(\frac53) \zeta(2)} ,\end{align*} $$
as desired.
Lemma 5.2. Assuming the Riemann Hypothesis, the function
![]() $A_4(-s,s)$
admits an analytic continuation to the region
$A_4(-s,s)$
admits an analytic continuation to the region
![]() $|\operatorname {Re}(s)|< \frac 12$
, except for a double pole at
$|\operatorname {Re}(s)|< \frac 12$
, except for a double pole at
![]() $s=\frac 16$
. Furthermore, for any
$s=\frac 16$
. Furthermore, for any
![]() $0<\varepsilon <\frac 14$
and in the region
$0<\varepsilon <\frac 14$
and in the region
![]() $|\operatorname {Re}(s)|< \frac 12-\varepsilon $
, we have the bound
$|\operatorname {Re}(s)|< \frac 12-\varepsilon $
, we have the bound
Proof. By (4.7) and (4.9), for
![]() $ | \operatorname {Re} (s) | < \frac 16$
, we have that
$ | \operatorname {Re} (s) | < \frac 16$
, we have that
 $$ \begin{align*} A_4 ( -s, s) = & \prod_p \frac{ \Big(1- \frac1{p^{1-2s}}\Big)\Big( 1- \frac1{p^{\frac56-s}}\Big)\Big( 1 - \frac1{p^{\frac13}} \Big) }{ \Big(1- \frac1{p^2}\Big)\Big( 1- \frac1{p^{\frac56+s}}\Big) \Big(1- \frac1{p^{\frac53}}\Big) } \Bigg( \frac1{p^2} \Big( 1+ \frac1{p^{\frac13}}\Big) + \sum_{e \geq 0 } \frac{ g(e,0,p) + \frac{g(e,1,p)}{p^{\frac12+s}} + \frac{g(e,2,p)}{ p^{1+2s }} }{p^{e(\frac 12-s)}} \Bigg), \end{align*} $$
$$ \begin{align*} A_4 ( -s, s) = & \prod_p \frac{ \Big(1- \frac1{p^{1-2s}}\Big)\Big( 1- \frac1{p^{\frac56-s}}\Big)\Big( 1 - \frac1{p^{\frac13}} \Big) }{ \Big(1- \frac1{p^2}\Big)\Big( 1- \frac1{p^{\frac56+s}}\Big) \Big(1- \frac1{p^{\frac53}}\Big) } \Bigg( \frac1{p^2} \Big( 1+ \frac1{p^{\frac13}}\Big) + \sum_{e \geq 0 } \frac{ g(e,0,p) + \frac{g(e,1,p)}{p^{\frac12+s}} + \frac{g(e,2,p)}{ p^{1+2s }} }{p^{e(\frac 12-s)}} \Bigg), \end{align*} $$
since
![]() $ y_p^{-1} - g(0,0,p) = \frac 1{p^2} \Big ( 1+ \frac 1{p^{\frac 13}}\Big ) $
. Recalling the definition of
$ y_p^{-1} - g(0,0,p) = \frac 1{p^2} \Big ( 1+ \frac 1{p^{\frac 13}}\Big ) $
. Recalling the definition of
![]() $g(e,j,p)$
(see Lemma 4.1), a straightforward evaluation of the infinite sum over
$g(e,j,p)$
(see Lemma 4.1), a straightforward evaluation of the infinite sum over
![]() $e\geq 0$
yields the expression
$e\geq 0$
yields the expression
 $$ \begin{align*} & A_4 ( -s, s) = \zeta(2) \zeta(\tfrac53) \prod_p \frac{ \Big(1- \frac1{p^{1-2s}}\Big)\Big( 1- \frac1{p^{\frac56 -s}}\Big)\Big( 1 - \frac1{p^{\frac13}}\Big) }{ \Big( 1- \frac1{p^{\frac56 +s}}\Big) } \Bigg( \frac{ \Big(1+\frac{1}{p^{ \frac13}} \Big)^3\Big( 1 - \frac{1}{ p^{\frac12+s}} \Big)^2 }{ 6 \Big( 1 - \frac{1}{ p^{\frac12-s}} \Big)^2} \\ & + \frac{ \Big(1+\frac{1}{p^{ \frac13}} \Big)\Big(1+\frac{1}{p^{ \frac23}} \Big) \Big( 1 - \frac{1}{p^{1+2s}}\Big) }{2 \Big( 1 - \frac{1}{p^{1-2s}}\Big)} + \frac{ \Big( 1+\frac1p \Big) \Big( 1 + \frac{1}{p^{\frac12 +s}}+ \frac{1}{p^{1+2s}}\Big) }{ 3 \Big( 1 + \frac{1}{p^{\frac12-s}} + \frac{1}{p^{1-2s}} \Big) } + \frac{\Big(1+\frac{1}{p^{ \frac13}} \Big)^2 \Big( 1- \frac{1}{p^{\frac12+s}}\Big) }{ p\Big( 1- \frac{1}{p^{\frac12-s}}\Big) } + \frac{ 1+\frac{1}{p^{ \frac13}} }{p^2} \Bigg). \end{align*} $$
$$ \begin{align*} & A_4 ( -s, s) = \zeta(2) \zeta(\tfrac53) \prod_p \frac{ \Big(1- \frac1{p^{1-2s}}\Big)\Big( 1- \frac1{p^{\frac56 -s}}\Big)\Big( 1 - \frac1{p^{\frac13}}\Big) }{ \Big( 1- \frac1{p^{\frac56 +s}}\Big) } \Bigg( \frac{ \Big(1+\frac{1}{p^{ \frac13}} \Big)^3\Big( 1 - \frac{1}{ p^{\frac12+s}} \Big)^2 }{ 6 \Big( 1 - \frac{1}{ p^{\frac12-s}} \Big)^2} \\ & + \frac{ \Big(1+\frac{1}{p^{ \frac13}} \Big)\Big(1+\frac{1}{p^{ \frac23}} \Big) \Big( 1 - \frac{1}{p^{1+2s}}\Big) }{2 \Big( 1 - \frac{1}{p^{1-2s}}\Big)} + \frac{ \Big( 1+\frac1p \Big) \Big( 1 + \frac{1}{p^{\frac12 +s}}+ \frac{1}{p^{1+2s}}\Big) }{ 3 \Big( 1 + \frac{1}{p^{\frac12-s}} + \frac{1}{p^{1-2s}} \Big) } + \frac{\Big(1+\frac{1}{p^{ \frac13}} \Big)^2 \Big( 1- \frac{1}{p^{\frac12+s}}\Big) }{ p\Big( 1- \frac{1}{p^{\frac12-s}}\Big) } + \frac{ 1+\frac{1}{p^{ \frac13}} }{p^2} \Bigg). \end{align*} $$
Isolating the ‘divergent terms’ leads us to the identity
where
 $$ \begin{align*} D_{4,p,1}(s) & := \frac{ 1- \frac1{p^{\frac56-s}} }{ 1- \frac1{p^{\frac56+s}} } \Bigg( \frac{ \Big(1+ \frac2{p^{\frac13}} - \frac2p \Big) \Big(1 - \frac{1}{ p^{\frac12+s}} \Big)^2 \Big(1 + \frac1{p^{\frac12-s}}\Big) }{ 6\Big( 1 - \frac{1}{ p^{\frac12-s}}\Big)} \\ &\quad + \frac{ 1 - \frac{1}{p^{1+2s}} }{2} + \frac{\Big(1 - \frac1{p^{\frac13}} +\frac1p \Big)\Big( 1 + \frac{1}{p^{\frac12+s}}+ \frac{1}{p^{1+2s}} \Big) \Big(1- \frac1{p^{1-2s}}\Big) }{3\Big( 1 + \frac{1}{p^{\frac12-s}} + \frac{1}{p^{1-2s}} \Big) } + \frac1p \Bigg) \end{align*} $$
$$ \begin{align*} D_{4,p,1}(s) & := \frac{ 1- \frac1{p^{\frac56-s}} }{ 1- \frac1{p^{\frac56+s}} } \Bigg( \frac{ \Big(1+ \frac2{p^{\frac13}} - \frac2p \Big) \Big(1 - \frac{1}{ p^{\frac12+s}} \Big)^2 \Big(1 + \frac1{p^{\frac12-s}}\Big) }{ 6\Big( 1 - \frac{1}{ p^{\frac12-s}}\Big)} \\ &\quad + \frac{ 1 - \frac{1}{p^{1+2s}} }{2} + \frac{\Big(1 - \frac1{p^{\frac13}} +\frac1p \Big)\Big( 1 + \frac{1}{p^{\frac12+s}}+ \frac{1}{p^{1+2s}} \Big) \Big(1- \frac1{p^{1-2s}}\Big) }{3\Big( 1 + \frac{1}{p^{\frac12-s}} + \frac{1}{p^{1-2s}} \Big) } + \frac1p \Bigg) \end{align*} $$
and
 $$ \begin{align*} A_{4,p,1}(s) &:= \frac{ 1- \frac1{p^{\frac56-s}} }{ 1- \frac1{p^{\frac56+s}} } \Bigg( - \frac{ \Big(1 - \frac{1}{ p^{\frac12+s}} \Big)^2 \Big(1 + \frac1{p^{\frac12-s}}\Big) }{ 6 p^{\frac43} \Big( 1 - \frac{1}{ p^{\frac12-s}}\Big)} - \frac{ 1 - \frac{1}{p^{1+2s}} }{2p^{\frac43}} - \frac{ \Big( 1 + \frac{1}{p^{\frac12+s}}+\frac{1}{p^{1+2s}} \Big) \Big(1- \frac1{p^{1-2s}}\Big) }{3 p^{\frac43} \Big( 1 + \frac{1}{p^{\frac12-s}} + \frac{1}{p^{1-2s}} \Big) } \\ & \quad + \frac{\Big(1+ \frac1{p^{\frac13}} - \frac1{p^{\frac23}}- \frac1p \Big) \Big( 1- \frac{1}{p^{\frac12+s}}\Big)\Big( 1+ \frac{1}{p^{\frac12-s}} \Big) -1 }{p} + \frac1{p^2} \Big( 1- \frac1{p^{\frac23}}\Big) \Big(1- \frac1{p^{1-2s}}\Big) \Bigg). \end{align*} $$
$$ \begin{align*} A_{4,p,1}(s) &:= \frac{ 1- \frac1{p^{\frac56-s}} }{ 1- \frac1{p^{\frac56+s}} } \Bigg( - \frac{ \Big(1 - \frac{1}{ p^{\frac12+s}} \Big)^2 \Big(1 + \frac1{p^{\frac12-s}}\Big) }{ 6 p^{\frac43} \Big( 1 - \frac{1}{ p^{\frac12-s}}\Big)} - \frac{ 1 - \frac{1}{p^{1+2s}} }{2p^{\frac43}} - \frac{ \Big( 1 + \frac{1}{p^{\frac12+s}}+\frac{1}{p^{1+2s}} \Big) \Big(1- \frac1{p^{1-2s}}\Big) }{3 p^{\frac43} \Big( 1 + \frac{1}{p^{\frac12-s}} + \frac{1}{p^{1-2s}} \Big) } \\ & \quad + \frac{\Big(1+ \frac1{p^{\frac13}} - \frac1{p^{\frac23}}- \frac1p \Big) \Big( 1- \frac{1}{p^{\frac12+s}}\Big)\Big( 1+ \frac{1}{p^{\frac12-s}} \Big) -1 }{p} + \frac1{p^2} \Big( 1- \frac1{p^{\frac23}}\Big) \Big(1- \frac1{p^{1-2s}}\Big) \Bigg). \end{align*} $$
The term
![]() $A_{4,p,1}(s)$
is ‘small’ for
$A_{4,p,1}(s)$
is ‘small’ for
![]() $ | \operatorname {Re} (s)|< \frac 12$
, hence, we will concentrate our attention on
$ | \operatorname {Re} (s)|< \frac 12$
, hence, we will concentrate our attention on
![]() $D_{4,p,1}(s)$
. We see that
$D_{4,p,1}(s)$
. We see that
 $$ \begin{align*}D_{4,p,1}(s) = \frac{ 1- \frac1{p^{\frac56-s}} }{ 1- \frac1{p^{\frac56+s}} } D_{4,p,2}(s) + \frac1p + A_{4,p,2}(s) , \end{align*} $$
$$ \begin{align*}D_{4,p,1}(s) = \frac{ 1- \frac1{p^{\frac56-s}} }{ 1- \frac1{p^{\frac56+s}} } D_{4,p,2}(s) + \frac1p + A_{4,p,2}(s) , \end{align*} $$
where
 $$ \begin{align*}D_{4,p,2}(s) & := \frac{ \Big(1+ \frac2{p^{\frac13}} \Big) \Big(1 - \frac{1}{ p^{\frac12+s}} \Big)^2 \Big(1 + \frac1{p^{\frac12-s}}\Big) }{ 6\Big( 1 - \frac{1}{ p^{\frac12-s}}\Big)} + \frac{ 1 - \frac{1}{p^{1+2s}} }{2} \\ &\quad + \frac{\Big(1 - \frac1{p^{\frac13}} \Big)\Big( 1 + \frac{1}{p^{\frac12+s}}+ \frac{1}{p^{1+2s}} \Big) \Big(1- \frac1{p^{1-2s}}\Big) }{3\Big( 1 + \frac{1}{p^{\frac12-s}} + \frac{1}{p^{1-2s}} \Big) }\end{align*} $$
$$ \begin{align*}D_{4,p,2}(s) & := \frac{ \Big(1+ \frac2{p^{\frac13}} \Big) \Big(1 - \frac{1}{ p^{\frac12+s}} \Big)^2 \Big(1 + \frac1{p^{\frac12-s}}\Big) }{ 6\Big( 1 - \frac{1}{ p^{\frac12-s}}\Big)} + \frac{ 1 - \frac{1}{p^{1+2s}} }{2} \\ &\quad + \frac{\Big(1 - \frac1{p^{\frac13}} \Big)\Big( 1 + \frac{1}{p^{\frac12+s}}+ \frac{1}{p^{1+2s}} \Big) \Big(1- \frac1{p^{1-2s}}\Big) }{3\Big( 1 + \frac{1}{p^{\frac12-s}} + \frac{1}{p^{1-2s}} \Big) }\end{align*} $$
and
 $$ \begin{align*} A_{4,p,2}(s):= \frac{ \Big( 1- \frac1{p^{\frac56-s}} \Big) }{ p \Big( 1- \frac1{p^{\frac56+s}} \Big) } \Bigg( & - \frac{ \Big(1 - \frac{1}{ p^{\frac12+s}} \Big)^2 \Big(1 + \frac1{p^{\frac12-s}}\Big) }{ 3\Big( 1 - \frac{1}{ p^{\frac12 -s}}\Big)} + \frac{ \Big( 1 + \frac{1}{p^{\frac12+s}}+ \frac{1}{p^{1+2s}} \Big) \Big(1- \frac1{p^{1-2s}}\Big) }{3\Big( 1 + \frac{1}{p^{\frac12-s}} + \frac{1}{p^{1-2s}} \Big) } +1 \Bigg) - \frac1p, \end{align*} $$
$$ \begin{align*} A_{4,p,2}(s):= \frac{ \Big( 1- \frac1{p^{\frac56-s}} \Big) }{ p \Big( 1- \frac1{p^{\frac56+s}} \Big) } \Bigg( & - \frac{ \Big(1 - \frac{1}{ p^{\frac12+s}} \Big)^2 \Big(1 + \frac1{p^{\frac12-s}}\Big) }{ 3\Big( 1 - \frac{1}{ p^{\frac12 -s}}\Big)} + \frac{ \Big( 1 + \frac{1}{p^{\frac12+s}}+ \frac{1}{p^{1+2s}} \Big) \Big(1- \frac1{p^{1-2s}}\Big) }{3\Big( 1 + \frac{1}{p^{\frac12-s}} + \frac{1}{p^{1-2s}} \Big) } +1 \Bigg) - \frac1p, \end{align*} $$
which is also ‘small’. Taking common denominators and expanding out shows that
 $$ \begin{align*}D_{4,p,2}(s)=\frac{1}{ 1- \frac{1}{p^{\frac32 -3s}} } \bigg( 1 - \frac1p - \frac{1}{p^{\frac56+s}} + \frac{1}{p^{\frac56-s}} + \frac1{p^{\frac43-2s}} + A_{4,p,3}(s) \bigg),\end{align*} $$
$$ \begin{align*}D_{4,p,2}(s)=\frac{1}{ 1- \frac{1}{p^{\frac32 -3s}} } \bigg( 1 - \frac1p - \frac{1}{p^{\frac56+s}} + \frac{1}{p^{\frac56-s}} + \frac1{p^{\frac43-2s}} + A_{4,p,3}(s) \bigg),\end{align*} $$
where
 $$ \begin{align*}A_{4,p,3}(s) := - \frac{1}{p^{\frac32-s}} + \frac{1}{ p^{\frac52-s}} - \frac1{p^{\frac43}} + \frac{1}{p^{\frac{11}6+s}} - \frac1{p^{\frac{11}6 -s}} + \frac1{p^{\frac73} } - \frac{1}{p^{\frac73-2s}}\end{align*} $$
$$ \begin{align*}A_{4,p,3}(s) := - \frac{1}{p^{\frac32-s}} + \frac{1}{ p^{\frac52-s}} - \frac1{p^{\frac43}} + \frac{1}{p^{\frac{11}6+s}} - \frac1{p^{\frac{11}6 -s}} + \frac1{p^{\frac73} } - \frac{1}{p^{\frac73-2s}}\end{align*} $$
is ‘small’. More precisely, for
![]() $ | \operatorname {Re} (s) |\leq \frac 12 - \varepsilon < \frac 12 $
and
$ | \operatorname {Re} (s) |\leq \frac 12 - \varepsilon < \frac 12 $
and
![]() $ j = 1,2,3$
, we have the bound
$ j = 1,2,3$
, we have the bound
![]() $ A_{4,p,j } (s) = O_\varepsilon \Big ( \frac {1}{p^{1+\varepsilon }}\Big ) $
. Therefore,
$ A_{4,p,j } (s) = O_\varepsilon \Big ( \frac {1}{p^{1+\varepsilon }}\Big ) $
. Therefore,
 $$ \begin{align} A_4 ( -s, s) = \zeta(2) \zeta(\tfrac53) \zeta( \tfrac32-3s) \widetilde{A}_4 (s) \prod_p \Bigg( \frac{\Big( 1- \frac1{p^{\frac56-s}}\Big) }{ \Big( 1- \frac1{p^{\frac56+s}}\Big) } \bigg( 1 - \frac{1}{p^{\frac56+s}} + \frac{1}{p^{\frac56-s}} + \frac1{p^{\frac43-2s}} \bigg) \Bigg) , \end{align} $$
$$ \begin{align} A_4 ( -s, s) = \zeta(2) \zeta(\tfrac53) \zeta( \tfrac32-3s) \widetilde{A}_4 (s) \prod_p \Bigg( \frac{\Big( 1- \frac1{p^{\frac56-s}}\Big) }{ \Big( 1- \frac1{p^{\frac56+s}}\Big) } \bigg( 1 - \frac{1}{p^{\frac56+s}} + \frac{1}{p^{\frac56-s}} + \frac1{p^{\frac43-2s}} \bigg) \Bigg) , \end{align} $$
where
 $$ \begin{align*} \widetilde{A}_4 (s) := & \prod_p \left( 1 + \frac{ \frac1p \bigg( 1- \frac{1}{p^{\frac32 -3s}} - \frac{ 1- p^{-\frac56+s} }{ 1- p^{- \frac56-s} } \bigg) + \frac{ 1- p^{-\frac56+s} }{ 1- p^{- \frac56-s} } A_{4,p,3}(s) + \Big( 1- \frac{1}{p^{\frac32-3s}}\Big)(A_{4,p,2}(s) + A_{4,p,1}(s)) }{ \frac{ 1- p^{-\frac56+s} }{ 1- p^{- \frac56-s} } \Big( 1 - \frac{1}{p^{\frac56+s}} + \frac{1}{p^{\frac56-s}} + \frac1{p^{\frac43-2s}} \Big) } \right) \end{align*} $$
$$ \begin{align*} \widetilde{A}_4 (s) := & \prod_p \left( 1 + \frac{ \frac1p \bigg( 1- \frac{1}{p^{\frac32 -3s}} - \frac{ 1- p^{-\frac56+s} }{ 1- p^{- \frac56-s} } \bigg) + \frac{ 1- p^{-\frac56+s} }{ 1- p^{- \frac56-s} } A_{4,p,3}(s) + \Big( 1- \frac{1}{p^{\frac32-3s}}\Big)(A_{4,p,2}(s) + A_{4,p,1}(s)) }{ \frac{ 1- p^{-\frac56+s} }{ 1- p^{- \frac56-s} } \Big( 1 - \frac{1}{p^{\frac56+s}} + \frac{1}{p^{\frac56-s}} + \frac1{p^{\frac43-2s}} \Big) } \right) \end{align*} $$
is absolutely convergent for
![]() $|\operatorname {Re} (s) | < \frac 12 $
. Hence, the final step is to find a meromorphic continuation for the infinite product on the right-hand side of (5.5), which we will denote by
$|\operatorname {Re} (s) | < \frac 12 $
. Hence, the final step is to find a meromorphic continuation for the infinite product on the right-hand side of (5.5), which we will denote by
![]() $D_3(s)$
. However, it is straightforward to show that
$D_3(s)$
. However, it is straightforward to show that
 $$ \begin{align} A_{4,4}(s):= D_3(s) \frac{ \zeta(\tfrac83-4s) \zeta(\tfrac53-2s) \zeta(\tfrac{13}6-3s) } { \zeta(\tfrac43-2s)} \end{align} $$
$$ \begin{align} A_{4,4}(s):= D_3(s) \frac{ \zeta(\tfrac83-4s) \zeta(\tfrac53-2s) \zeta(\tfrac{13}6-3s) } { \zeta(\tfrac43-2s)} \end{align} $$
converges absolutely for
![]() $|\operatorname {Re}(s)|<\frac 12$
. This finishes the proof of the first claim in the lemma.
$|\operatorname {Re}(s)|<\frac 12$
. This finishes the proof of the first claim in the lemma.
Finally, the growth estimate
follows from (5.5), (5.6), as well as [Reference Montgomery and VaughanMV, Theorems 13.18 and 13.23] and the functional equation for
![]() $\zeta (s)$
.
$\zeta (s)$
.
Now that we have a meromorphic continuation of
![]() $A_4(-s,s)$
, we will calculate the leading Laurent coefficient at
$A_4(-s,s)$
, we will calculate the leading Laurent coefficient at
![]() $s=\frac 16$
.
$s=\frac 16$
.
Lemma 5.3. We have the formula
 $$ \begin{align*}\lim_{s\rightarrow \frac 16} (s-\tfrac 16)^2 A_4(-s,s) = \frac16 \frac{ \zeta(2)\zeta(\tfrac 53)}{\zeta( \tfrac43)} \prod_p \Big(1-\frac 1{p^{\frac 23}}\Big)^2 \Big(1- \frac1p \Big)\Big(1+\frac 2{p^{\frac 23}}+\frac 1p+\frac 1{p^{\frac 43}}\Big) .\end{align*} $$
$$ \begin{align*}\lim_{s\rightarrow \frac 16} (s-\tfrac 16)^2 A_4(-s,s) = \frac16 \frac{ \zeta(2)\zeta(\tfrac 53)}{\zeta( \tfrac43)} \prod_p \Big(1-\frac 1{p^{\frac 23}}\Big)^2 \Big(1- \frac1p \Big)\Big(1+\frac 2{p^{\frac 23}}+\frac 1p+\frac 1{p^{\frac 43}}\Big) .\end{align*} $$
Proof. By Lemma 5.2,
![]() $A_4 ( -s, s ) $
has a double pole at
$A_4 ( -s, s ) $
has a double pole at
![]() $ s= \frac 16 $
. Moreover, by (5.5) and (5.6), we find that
$ s= \frac 16 $
. Moreover, by (5.5) and (5.6), we find that
![]() $ \frac { A_4 ( -s, s)}{ \zeta ( \frac 32 - 3s ) \zeta ( \frac 43 - 2s ) } $
has a convergent Euler product in the region
$ \frac { A_4 ( -s, s)}{ \zeta ( \frac 32 - 3s ) \zeta ( \frac 43 - 2s ) } $
has a convergent Euler product in the region
![]() $|\operatorname {Re}(s)| < \frac 13$
(this allows us to interchange the order of the limit and the product in the calculation below), so that
$|\operatorname {Re}(s)| < \frac 13$
(this allows us to interchange the order of the limit and the product in the calculation below), so that
 $$ \begin{align*} \lim_{s \to \frac16 } & (s-\tfrac16 )^2 A_4 ( -s , s) = \frac{1}{6} \lim_{s \to \frac16} \frac{ A_4 ( -s, s)}{ \zeta( \frac32 - 3s ) \zeta ( \frac43 - 2s ) } \\ = & \frac{ \zeta(2)\zeta(\tfrac 53) }{6} \prod_p \Big(1-\frac1p \Big) \Big(1-\frac 1{p^{\frac 23}}\Big)^2 \Big(1-\frac 1{p^{\frac 13}}\Big) \Bigg\{ \frac{ \Big(1+\frac 1{p^{\frac 13}}\Big)^3 \Big(1 - \frac{1}{ p^{\frac23}}\Big)^2 }{ 6 \Big( 1 - \frac{1}{ p^{\frac13}}\Big)^2 } \\ & + \frac{ \Big(1+ \frac1{p^{ \frac13}} \Big) \Big( 1+ \frac1{p^{ \frac23}} \Big) \Big( 1 - \frac{1}{p^{\frac43}}\Big) }{2\Big( 1 - \frac{1}{p^{\frac23}}\Big) } + \frac{ \Big(1+ \frac1p \Big)\Big(1 + \frac{1}{p^{\frac23}}+ \frac{1}{p^{\frac43}}\Big) }{3 \Big( 1 + \frac{1}{p^{\frac13}} + \frac{1}{p^{\frac23}} \Big) } + \frac{ \Big( 1 + \frac1{p^{ \frac13}} \Big)^2 \Big( 1- \frac{1}{p^{\frac23}} \Big) }{p\Big( 1- \frac{1}{p^{\frac13}} \Big) } + \frac{ 1+ \frac1{p^{\frac13}} }{p^2} \Bigg\}. \end{align*} $$
$$ \begin{align*} \lim_{s \to \frac16 } & (s-\tfrac16 )^2 A_4 ( -s , s) = \frac{1}{6} \lim_{s \to \frac16} \frac{ A_4 ( -s, s)}{ \zeta( \frac32 - 3s ) \zeta ( \frac43 - 2s ) } \\ = & \frac{ \zeta(2)\zeta(\tfrac 53) }{6} \prod_p \Big(1-\frac1p \Big) \Big(1-\frac 1{p^{\frac 23}}\Big)^2 \Big(1-\frac 1{p^{\frac 13}}\Big) \Bigg\{ \frac{ \Big(1+\frac 1{p^{\frac 13}}\Big)^3 \Big(1 - \frac{1}{ p^{\frac23}}\Big)^2 }{ 6 \Big( 1 - \frac{1}{ p^{\frac13}}\Big)^2 } \\ & + \frac{ \Big(1+ \frac1{p^{ \frac13}} \Big) \Big( 1+ \frac1{p^{ \frac23}} \Big) \Big( 1 - \frac{1}{p^{\frac43}}\Big) }{2\Big( 1 - \frac{1}{p^{\frac23}}\Big) } + \frac{ \Big(1+ \frac1p \Big)\Big(1 + \frac{1}{p^{\frac23}}+ \frac{1}{p^{\frac43}}\Big) }{3 \Big( 1 + \frac{1}{p^{\frac13}} + \frac{1}{p^{\frac23}} \Big) } + \frac{ \Big( 1 + \frac1{p^{ \frac13}} \Big)^2 \Big( 1- \frac{1}{p^{\frac23}} \Big) }{p\Big( 1- \frac{1}{p^{\frac13}} \Big) } + \frac{ 1+ \frac1{p^{\frac13}} }{p^2} \Bigg\}. \end{align*} $$
The claim follows.
We are now ready to estimate
![]() $J^\pm (X)$
when the support of
$J^\pm (X)$
when the support of
![]() $\widehat \phi $
is small.
$\widehat \phi $
is small.
Lemma 5.4. Let
![]() $\phi $
be a real even Schwartz function, such that
$\phi $
be a real even Schwartz function, such that
![]() $\sigma =\sup (\mathrm {supp} (\widehat \phi )) <1$
. Let
$\sigma =\sup (\mathrm {supp} (\widehat \phi )) <1$
. Let
![]() $J^\pm (X)$
be defined by (5.1). Then we have the estimate
$J^\pm (X)$
be defined by (5.1). Then we have the estimate
where
 $$ \begin{align} C^\pm := \frac{5}{12} \frac{C_2^\pm }{C_1^\pm} \frac{\Gamma_{\pm}(\frac 13)}{\Gamma_{\pm}(\frac 23)} \frac{ \zeta(\tfrac 23)^2 \zeta(\tfrac 53) \zeta(2) }{ \zeta( \tfrac43)} \prod_p \Big(1-\frac 1{p^{\frac 23}}\Big)^2 \Big(1- \frac1p \Big)\Big(1+\frac 2{p^{\frac 23}}+\frac 1p+\frac 1{p^{\frac 43}}\Big). \end{align} $$
$$ \begin{align} C^\pm := \frac{5}{12} \frac{C_2^\pm }{C_1^\pm} \frac{\Gamma_{\pm}(\frac 13)}{\Gamma_{\pm}(\frac 23)} \frac{ \zeta(\tfrac 23)^2 \zeta(\tfrac 53) \zeta(2) }{ \zeta( \tfrac43)} \prod_p \Big(1-\frac 1{p^{\frac 23}}\Big)^2 \Big(1- \frac1p \Big)\Big(1+\frac 2{p^{\frac 23}}+\frac 1p+\frac 1{p^{\frac 43}}\Big). \end{align} $$
Proof. We rewrite the integral in
![]() $J^\pm (X)$
as
$J^\pm (X)$
as
 $$ \begin{align} &\frac{1}{2 \pi i} \int_{(c)} (-2) \phi \Big(\frac{Ls}{2\pi i}\Big)\Big\{ \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big)\Big(-\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16} \frac{\zeta'}{\zeta}(\tfrac 56+s)+ X^{-s} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \frac{A_3( -s, s)}{1-s} \Big)\nonumber\\ &\qquad +\frac{C_2^\pm }{C_1^\pm} X^{-s-\frac 16} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)} \zeta(1-2s) \frac{\zeta(\tfrac 56-s)}{\zeta(\tfrac 56+s)} \frac{A_4(-s,s)}{ 1- \frac{6s}5} \nonumber\\ &\qquad +\Big(\frac{C_2^\pm}{C_1^\pm}\Big)^2 X^{-s-\frac 13} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \frac{ A_3( -s, s)}{1-s} \Big\}ds \end{align} $$
$$ \begin{align} &\frac{1}{2 \pi i} \int_{(c)} (-2) \phi \Big(\frac{Ls}{2\pi i}\Big)\Big\{ \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big)\Big(-\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16} \frac{\zeta'}{\zeta}(\tfrac 56+s)+ X^{-s} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \frac{A_3( -s, s)}{1-s} \Big)\nonumber\\ &\qquad +\frac{C_2^\pm }{C_1^\pm} X^{-s-\frac 16} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)} \zeta(1-2s) \frac{\zeta(\tfrac 56-s)}{\zeta(\tfrac 56+s)} \frac{A_4(-s,s)}{ 1- \frac{6s}5} \nonumber\\ &\qquad +\Big(\frac{C_2^\pm}{C_1^\pm}\Big)^2 X^{-s-\frac 13} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \frac{ A_3( -s, s)}{1-s} \Big\}ds \end{align} $$
for
![]() $ 0 < c < \frac 16$
. The integrand has a simple pole at
$ 0 < c < \frac 16$
. The integrand has a simple pole at
![]() $s=\frac 16$
with residue
$s=\frac 16$
with residue
 $$ \begin{align} & -2\phi \Big( \frac{L }{12 \pi i}\Big) \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) X^{-\frac 16} \Big(\frac{C_2^\pm}{C_1^\pm} - \frac25 \frac{\Gamma_{\pm}(\frac 13)}{\Gamma_{\pm}(\frac 23)} \frac{ \zeta(\tfrac23 ) \zeta(3)}{ \zeta( \tfrac53 ) \zeta(2)} \Big) \notag \\ & -2 \phi \Big( \frac{L }{12 \pi i}\Big) \frac{C_2^\pm }{C_1^\pm} X^{-\frac 13} \frac{\Gamma_{\pm}(\frac 13)}{\Gamma_{\pm}(\frac 23)} \frac{5\zeta(\tfrac 23)^2}{4} \lim_{s\rightarrow \frac 16} (s-\tfrac 16)^2A_4(-s,s) +O\Big(\phi\Big( \frac{L}{12 \pi i}\Big) X^{-\frac 12} \Big) \\ &\qquad = -{C^\pm} \phi \Big( \frac{L }{12 \pi i}\Big) X^{- \frac13} + O( X^{\frac{\sigma}{6}- \frac12}) \notag \end{align} $$
$$ \begin{align} & -2\phi \Big( \frac{L }{12 \pi i}\Big) \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) X^{-\frac 16} \Big(\frac{C_2^\pm}{C_1^\pm} - \frac25 \frac{\Gamma_{\pm}(\frac 13)}{\Gamma_{\pm}(\frac 23)} \frac{ \zeta(\tfrac23 ) \zeta(3)}{ \zeta( \tfrac53 ) \zeta(2)} \Big) \notag \\ & -2 \phi \Big( \frac{L }{12 \pi i}\Big) \frac{C_2^\pm }{C_1^\pm} X^{-\frac 13} \frac{\Gamma_{\pm}(\frac 13)}{\Gamma_{\pm}(\frac 23)} \frac{5\zeta(\tfrac 23)^2}{4} \lim_{s\rightarrow \frac 16} (s-\tfrac 16)^2A_4(-s,s) +O\Big(\phi\Big( \frac{L}{12 \pi i}\Big) X^{-\frac 12} \Big) \\ &\qquad = -{C^\pm} \phi \Big( \frac{L }{12 \pi i}\Big) X^{- \frac13} + O( X^{\frac{\sigma}{6}- \frac12}) \notag \end{align} $$
by Lemma 5.3, as well as the fact that the first line vanishes. Due to Lemmas 5.1 and 5.2, we can shift the contour of integration to the line
![]() $\operatorname {Re}(s)=\frac 12 - \frac {\varepsilon }{2}$
, at the cost of
$\operatorname {Re}(s)=\frac 12 - \frac {\varepsilon }{2}$
, at the cost of
![]() $-1$
times the residue (5.9).
$-1$
times the residue (5.9).
We now estimate the shifted integral. The term involving
![]() $\frac {\zeta '}{\zeta }(\tfrac 56+s)$
can be evaluated by interchanging sum and integral; we obtain the identity
$\frac {\zeta '}{\zeta }(\tfrac 56+s)$
can be evaluated by interchanging sum and integral; we obtain the identity
 $$ \begin{align} \frac{1}{\pi i} \int_{(\frac 12-\frac \varepsilon 2)} \phi \Big(\frac{Ls}{2\pi i}\Big) \frac{\zeta'}{\zeta}(\tfrac 56+s)ds = - \frac 2 L\sum_{p,e}\frac{\log p}{p^{\frac {5e}6}}\widehat\phi\Big(\frac{\log p^e}{L}\Big). \end{align} $$
$$ \begin{align} \frac{1}{\pi i} \int_{(\frac 12-\frac \varepsilon 2)} \phi \Big(\frac{Ls}{2\pi i}\Big) \frac{\zeta'}{\zeta}(\tfrac 56+s)ds = - \frac 2 L\sum_{p,e}\frac{\log p}{p^{\frac {5e}6}}\widehat\phi\Big(\frac{\log p^e}{L}\Big). \end{align} $$
The last step is to bound the remaining terms, which is carried out by combining (4.17) with Lemmas 5.1 and 5.2.
Finally, we complete the Proof of Theorem 1.4.
Proof of Theorem 1.4
Given Proposition 4.4 and Lemma 5.4, the only thing remaining to prove is (1.7). Applying (5.8) with
![]() $c=\frac 1{20}$
and splitting the integral into two parts, we obtain the identity
$c=\frac 1{20}$
and splitting the integral into two parts, we obtain the identity
 $$ \begin{align*} &J^\pm (X) = \frac{2C_2^\pm X^{-\frac 16}}{C_1^\pm L}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e}\frac{\log p}{p^{\frac {5e}{6}}}\widehat\phi\left(\frac{\log p^e}{L}\right) \\ &\quad -\frac{1}{\pi i} \int_{(\frac{1}{20})} \phi \Big(\frac{Ls}{2\pi i}\Big)\Big\{ \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big)\Big(-\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16} \frac{\zeta'}{\zeta}(\tfrac 56+s)+ X^{-s} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \frac{ A_3( -s, s)}{1-s} \Big) \Big\} ds\\ &\quad-\frac{1}{\pi i} \int_{(\frac{1}{20})} \phi \Big(\frac{Ls}{2\pi i}\Big)\Big\{ \frac{C_2^\pm }{C_1^\pm} X^{-s-\frac 16} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)} \zeta(1-2s) \frac{\zeta(\tfrac 56-s)}{\zeta(\tfrac 56+s)} \frac{A_4(-s,s)}{ 1- \frac{6s}5} \\ &\quad +\Big(\frac{C_2^\pm}{C_1^\pm}\Big)^2X^{-s-\frac 13} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \frac{ A_3( -s, s) }{1-s} \Big\}ds. \end{align*} $$
$$ \begin{align*} &J^\pm (X) = \frac{2C_2^\pm X^{-\frac 16}}{C_1^\pm L}\Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \sum_{p,e}\frac{\log p}{p^{\frac {5e}{6}}}\widehat\phi\left(\frac{\log p^e}{L}\right) \\ &\quad -\frac{1}{\pi i} \int_{(\frac{1}{20})} \phi \Big(\frac{Ls}{2\pi i}\Big)\Big\{ \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big)\Big(-\frac{C_2^\pm}{C_1^\pm} X^{-\frac 16} \frac{\zeta'}{\zeta}(\tfrac 56+s)+ X^{-s} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \frac{ A_3( -s, s)}{1-s} \Big) \Big\} ds\\ &\quad-\frac{1}{\pi i} \int_{(\frac{1}{20})} \phi \Big(\frac{Ls}{2\pi i}\Big)\Big\{ \frac{C_2^\pm }{C_1^\pm} X^{-s-\frac 16} \Big( 1-\frac{C_2^\pm}{C_1^\pm}X^{-\frac{1}{6}}\Big) \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)} \zeta(1-2s) \frac{\zeta(\tfrac 56-s)}{\zeta(\tfrac 56+s)} \frac{A_4(-s,s)}{ 1- \frac{6s}5} \\ &\quad +\Big(\frac{C_2^\pm}{C_1^\pm}\Big)^2X^{-s-\frac 13} \frac{\Gamma_{\pm}(\frac 12-s)}{\Gamma_{\pm}(\frac 12+s)}\zeta(1-2s) \frac{ A_3( -s, s) }{1-s} \Big\}ds. \end{align*} $$
By shifting the first integral to the line
![]() $\operatorname {Re}(s) = \frac 15$
and applying (5.10), we derive (1.7). Note that the residue at
$\operatorname {Re}(s) = \frac 15$
and applying (5.10), we derive (1.7). Note that the residue at
![]() $s=\frac 16$
is the first line of (5.9), which is equal to zero.
$s=\frac 16$
is the first line of (5.9), which is equal to zero.

Figure 2 A plot of
![]() $(p,f_{p}(10^4,T_j))$
for
$(p,f_{p}(10^4,T_j))$
for
![]() $p<10^4$
and
$p<10^4$
and
![]() $j=1,2,3$
.
$j=1,2,3$
.
A Numerical investigations
In this section, we present several graphsFootnote 5 associated to the error term
We recall that we expect a bound of the form
![]() $ E^+_{p} (X,T) \ll _{\varepsilon } p^{ \omega }X^{\theta +\varepsilon } $
(see (1.2)). Moreover, from the graphs shown in Figure 1, it seems likely that
$ E^+_{p} (X,T) \ll _{\varepsilon } p^{ \omega }X^{\theta +\varepsilon } $
(see (1.2)). Moreover, from the graphs shown in Figure 1, it seems likely that
![]() $\theta =\frac 12$
is admissible and the best possible. Now, to test the uniformity in p, we consider the function
$\theta =\frac 12$
is admissible and the best possible. Now, to test the uniformity in p, we consider the function
we then expect a bound of the form
![]() $f_p(X,T) \ll _\varepsilon p^{\omega }X^{\theta -\frac 12+\varepsilon }$
with
$f_p(X,T) \ll _\varepsilon p^{\omega }X^{\theta -\frac 12+\varepsilon }$
with
![]() $\theta $
possibly equal to
$\theta $
possibly equal to
![]() $\frac 12$
. To predict the smallest admissible value of
$\frac 12$
. To predict the smallest admissible value of
![]() $\omega $
, in Figure 2, we plot
$\omega $
, in Figure 2, we plot
![]() $f_{p}(10^4,T_j)$
for
$f_{p}(10^4,T_j)$
for
![]() $j=1,2,3,$
as a function of
$j=1,2,3,$
as a function of
![]() $p<10^4$
. From this data, it seems likely that any
$p<10^4$
. From this data, it seems likely that any
![]() $\omega>0$
is admissible. Now, one might wonder whether this is still valid in the range
$\omega>0$
is admissible. Now, one might wonder whether this is still valid in the range
![]() $p>X$
. To investigate this, in Figure 3, we plot the function
$p>X$
. To investigate this, in Figure 3, we plot the function
![]() $f_{p}(10^4,T_3)$
for every
$f_{p}(10^4,T_3)$
for every
![]() $10^4$
-th prime up to
$10^4$
-th prime up to
![]() $10^8$
, revealing similar behaviour. Finally, we have also produced similar data associated to the quantity
$10^8$
, revealing similar behaviour. Finally, we have also produced similar data associated to the quantity
![]() $N^-_{p}(X,T_j)$
with
$N^-_{p}(X,T_j)$
with
![]() $j=1,2,3$
, and the result was comparable to Figure 2.
$j=1,2,3$
, and the result was comparable to Figure 2.

Figure 3 A plot of some of the values of
![]() $(p,f_{p}(10^4,T_3))$
for
$(p,f_{p}(10^4,T_3))$
for
![]() $p<10^8$
.
$p<10^8$
.

Figure 4 A plot of
![]() $(p,pf_{p}(10^4,T_4))$
for
$(p,pf_{p}(10^4,T_4))$
for
![]() $p<10^5$
.
$p<10^5$
.

Figure 5 A plot of
![]() $(p,p^{\frac 12}f_{p}(10^5,T_4))$
for
$(p,p^{\frac 12}f_{p}(10^5,T_4))$
for
![]() $p<10^4$
.
$p<10^4$
.
However, it seems like the splitting type
![]() $T_4$
behaves differently (see Figure 4 for a plot of
$T_4$
behaves differently (see Figure 4 for a plot of
![]() $p\cdot f_p(10^4,T_4)$
for every
$p\cdot f_p(10^4,T_4)$
for every
![]() $p<10^5$
). One can see that this graph is eventually essentially constant. This is readily explained by the fact that in the range
$p<10^5$
). One can see that this graph is eventually essentially constant. This is readily explained by the fact that in the range
![]() $p>X$
, we have
$p>X$
, we have
![]() $N^{\pm }_{p} (X,T_4) =0$
. Indeed, if p has splitting type
$N^{\pm }_{p} (X,T_4) =0$
. Indeed, if p has splitting type
![]() $T_4$
in a cubic field K of discriminant at most X, then p must divide
$T_4$
in a cubic field K of discriminant at most X, then p must divide
![]() $D_K$
, which implies that
$D_K$
, which implies that
![]() $p\leq X$
. As a consequence,
$p\leq X$
. As a consequence,
![]() $pf_p(X,T_4)\asymp X^{\frac 12} $
, which is constant as a function of p. As for the more interesting range
$pf_p(X,T_4)\asymp X^{\frac 12} $
, which is constant as a function of p. As for the more interesting range
![]() $p\leq X$
, it seems like
$p\leq X$
, it seems like
![]() $f_p(X,T_4)\ll _\varepsilon p^{-\frac 12+\varepsilon }X^\varepsilon $
(i.e. for
$f_p(X,T_4)\ll _\varepsilon p^{-\frac 12+\varepsilon }X^\varepsilon $
(i.e. for
![]() $T=T_4$
, the values
$T=T_4$
, the values
![]() $\theta =\frac 12$
and any
$\theta =\frac 12$
and any
![]() $\omega>-\frac 12$
are admissible in (1.2)). In Figure 5, we test this hypothesis with larger values of X by plotting
$\omega>-\frac 12$
are admissible in (1.2)). In Figure 5, we test this hypothesis with larger values of X by plotting
![]() $p^{\frac 12} \cdot f_p(10^5,T_4)$
for all
$p^{\frac 12} \cdot f_p(10^5,T_4)$
for all
![]() $p< 10^4$
. This seems to confirm that for
$p< 10^4$
. This seems to confirm that for
![]() $T=T_4$
, the values
$T=T_4$
, the values
![]() $\theta =\frac 12$
and any
$\theta =\frac 12$
and any
![]() $\omega>-\frac 12$
are admissible in (1.2). In other words, it seems like we have
$\omega>-\frac 12$
are admissible in (1.2). In other words, it seems like we have
![]() $E_p^+(X,T_4)\ll _\varepsilon p^{-\frac 12+\varepsilon } X^{\frac 12+\varepsilon }$
, and the sum of the two exponents here is
$E_p^+(X,T_4)\ll _\varepsilon p^{-\frac 12+\varepsilon } X^{\frac 12+\varepsilon }$
, and the sum of the two exponents here is
![]() $2\varepsilon $
, which is significantly smaller than the sum of exponents in Theorem 1.1, which is
$2\varepsilon $
, which is significantly smaller than the sum of exponents in Theorem 1.1, which is
![]() $\omega +\theta \geq \frac 12$
. Note that this is not contradictory, since in that theorem we are assuming such a bound uniformly for all splitting types and, from the discussion above, we expect that
$\omega +\theta \geq \frac 12$
. Note that this is not contradictory, since in that theorem we are assuming such a bound uniformly for all splitting types and, from the discussion above, we expect that
![]() $E_p^+(X,T_1)\ll _\varepsilon p^{\varepsilon } X^{\frac 12+\varepsilon }$
is essentially the best possible. Finally, we have also produced data for the quantity
$E_p^+(X,T_1)\ll _\varepsilon p^{\varepsilon } X^{\frac 12+\varepsilon }$
is essentially the best possible. Finally, we have also produced data for the quantity
![]() $N_p^-(X,T_4)$
. The result was somewhat similar but far from identical. We would require more data to make a guess as strong as the one we made for
$N_p^-(X,T_4)$
. The result was somewhat similar but far from identical. We would require more data to make a guess as strong as the one we made for
![]() $E_p^+(X,T_4)$
.
$E_p^+(X,T_4)$
.

Figure 6 A plot of
![]() $(p,p^{2}f_{p}(10^6,T_5))$
for
$(p,p^{2}f_{p}(10^6,T_5))$
for
![]() $p<10^3$
.
$p<10^3$
.
For the splitting type
![]() $T_5$
, it seems like the error term is even smaller (probably owing to the fact that these fields are very rare). Indeed, this is what the graph of
$T_5$
, it seems like the error term is even smaller (probably owing to the fact that these fields are very rare). Indeed, this is what the graph of
![]() $p^2\cdot f_p(10^6,T_5)$
for all
$p^2\cdot f_p(10^6,T_5)$
for all
![]() $p< 10^3$
in Figure 6 indicates. Again, there are two regimes. Firstly, by [Reference BelabasB, p. 1216],
$p< 10^3$
in Figure 6 indicates. Again, there are two regimes. Firstly, by [Reference BelabasB, p. 1216],
![]() $p>2$
has splitting type
$p>2$
has splitting type
![]() $T_5$
in the cubic field K if and only if
$T_5$
in the cubic field K if and only if
![]() $p^2\mid D_K$
, hence,
$p^2\mid D_K$
, hence,
![]() $N^{\pm }_p(X,T_5)=0$
for
$N^{\pm }_p(X,T_5)=0$
for
![]() $p>X^{\frac 12}$
(that is
$p>X^{\frac 12}$
(that is
![]() $p^2\cdot f_p(X,T_5) \asymp X^{\frac 12}$
). As for
$p^2\cdot f_p(X,T_5) \asymp X^{\frac 12}$
). As for
![]() $p\leq X^{\frac 12}$
, Figure 6 indicates that
$p\leq X^{\frac 12}$
, Figure 6 indicates that
![]() $f_p(X,T_5) \ll _\varepsilon p^{-1 +\varepsilon }X^{\varepsilon } $
(e.g. for
$f_p(X,T_5) \ll _\varepsilon p^{-1 +\varepsilon }X^{\varepsilon } $
(e.g. for
![]() $T=T_5$
, the values
$T=T_5$
, the values
![]() $\theta =\frac 12$
and any
$\theta =\frac 12$
and any
![]() $\omega>-1$
are admissible in (1.2)). Once more, it is interesting to compare this with Theorem 1.1, since it seems like
$\omega>-1$
are admissible in (1.2)). Once more, it is interesting to compare this with Theorem 1.1, since it seems like
![]() $ E^+_p(X,T_5) \ll _\varepsilon p^{-1+\varepsilon } X^{\frac 12+\varepsilon } $
, and the sum of the two exponents is now
$ E^+_p(X,T_5) \ll _\varepsilon p^{-1+\varepsilon } X^{\frac 12+\varepsilon } $
, and the sum of the two exponents is now
![]() $-\frac 12+2\epsilon $
. We have also produced analogous data associated to the quantity
$-\frac 12+2\epsilon $
. We have also produced analogous data associated to the quantity
![]() $N_p^-(X,T_5)$
. The result was somewhat similar.
$N_p^-(X,T_5)$
. The result was somewhat similar.
Finally, we end this section with a graph (see Figure 7) of
for
![]() $X< 10^{11}$
(which is the limit of Belabas’ programFootnote 6 used for this computation). Here,
$X< 10^{11}$
(which is the limit of Belabas’ programFootnote 6 used for this computation). Here,
![]() $N_{\mathrm { all}}^+(X)$
counts all cubic fields of discriminant up to X, including Galois fields (by Cohn’s work [Reference CohnC],
$N_{\mathrm { all}}^+(X)$
counts all cubic fields of discriminant up to X, including Galois fields (by Cohn’s work [Reference CohnC],
![]() $N^+_{\mathrm {all}}(X) -N^+(X)\sim c X^{\frac 12}$
, with
$N^+_{\mathrm {all}}(X) -N^+(X)\sim c X^{\frac 12}$
, with
![]() $c=0.1585\ldots $
). This strongly supports the conjecture that
$c=0.1585\ldots $
). This strongly supports the conjecture that
![]() $E^+(X)\ll _\varepsilon X^{\frac 12+\varepsilon }$
and that the exponent
$E^+(X)\ll _\varepsilon X^{\frac 12+\varepsilon }$
and that the exponent
![]() $\frac 12$
is the best possible. It is also interesting that the graph is always positive, which is not without reminding us of Chebyshev’s bias (see, for instance, the graphs in the survey paper [Reference Granville and MartinGM]) in the distribution of primes.
$\frac 12$
is the best possible. It is also interesting that the graph is always positive, which is not without reminding us of Chebyshev’s bias (see, for instance, the graphs in the survey paper [Reference Granville and MartinGM]) in the distribution of primes.

Figure 7 A plot of
![]() $E^+(X) $
for
$E^+(X) $
for
![]() $X<10^{11}$
.
$X<10^{11}$
.
Given this numerical evidence, one may summarise this section by stating that in all cases, it seems like we have square-root cancellation. More precisely, the data indicate that the bound
could hold, at least for almost all p and X. This is reminiscent of Montgomery’s conjecture [Reference MontgomeryMo] for primes in arithmetic progressions, which states that
 $$ \begin{align*}\sum_{\substack{n\leq x \\ n\equiv a \bmod q} }\Lambda(n)- \frac{x}{\phi(q)} \ll_\varepsilon x^{\varepsilon} \Big(\frac{x}{\phi(q)}\Big)^{\frac 12} \qquad (q\leq x,\qquad (a,q)=1).\end{align*} $$
$$ \begin{align*}\sum_{\substack{n\leq x \\ n\equiv a \bmod q} }\Lambda(n)- \frac{x}{\phi(q)} \ll_\varepsilon x^{\varepsilon} \Big(\frac{x}{\phi(q)}\Big)^{\frac 12} \qquad (q\leq x,\qquad (a,q)=1).\end{align*} $$
Precise bounds such as (A.1) seem to be far from reach with the current methods, however, we hope to return to such questions in future work.
Acknowledgements
We would like to thank Frank Thorne for inspiring conversations and for sharing the preprint [Reference Bhargava, Taniguchi and ThorneBTT] with us. We also thank Keunyoung Jeong for providing us with preliminary computational results. The computations in this paper were carried out on a personal computer using pari/gp as well as Belabas’s CUBIC program. We thank Bill Allombert for his help regarding the latest development version of pari/gp. Peter J. Cho is supported by an National Research Foundation (NRF) grant funded by the Korea government (Ministry of Science and ICT (MSIT)) (No. 2019R1F1A1062599) and the Basic Science Research Program (2020R1A4A1016649). Yoonbok Lee is supported by an NRF grant funded by the Korea government (MSIT) (No.2019R1F1A1050795). Daniel Fiorilli was supported at the University of Ottawa by an Natural Sciences and Engineering Research Council of Canada (NSERC) discovery grant. Anders Södergren was supported by a grant from the Swedish Research Council (grant 2016-03759).
Conflict of Interest
The authors have no conflicts of interest to declare.