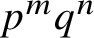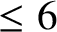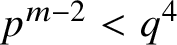On the structure of spectral and tiling subsets of cyclic groups

Abstract

The purpose of this paper is to investigate the properties of spectral and tiling subsets of cyclic groups, with an eye towards the spectral set conjecture [9] in one dimension, which states that a bounded measurable subset of $\mathbb {R}$ accepts an orthogonal basis of exponentials if and only if it tiles $\mathbb {R}$ by translations. This conjecture is strongly connected to its discrete counterpart, namely that, in every finite cyclic group, a subset is spectral if and only if it is a tile. The tools presented herein are refinements of recent ones used in the setting of cyclic groups; the structure of vanishing sums of roots of unity [20] is a prevalent notion throughout the text, as well as the structure of tiling subsets of integers [1]. We manage to prove the conjecture for cyclic groups of order $p^{m}q^{n}$ , when one of the exponents is $\leq 6$ or when $p^{m-2}<q^{4}$ , and also prove that a tiling subset of a cyclic group of order $p_{1}^{m}p_{2}\dotsm p_{n}$ is spectral.

1 Introduction

A basic fact in Fourier analysis is the decomposition of a periodic function into a series of orthogonal exponential functions. A natural question that arises is whether this concept can be generalized for functions defined not necessarily on intervals $[0,T]$ , where T is the period, but on more general domains with some weaker conditions (for example, measurability or boundedness). This is the definition of a spectral set. This, of course, can be generalized to higher dimensions as well, where periodic functions have a similar decomposition.

Definition 1.1. Let $\mu $ denote the Lebesgue measure on $\mathbb {R}$ . A bounded, measurable set $\Omega \subseteq \mathbb {R}^{d}$ with $\mu (\Omega )>0$ is called spectral if there is a discrete set $\Lambda \subseteq \mathbb {R}^{d}$ such that the set of exponential functions ${\left \{{e_{\lambda }(x)}\right \}}_{\lambda \in \Lambda }$ , where $e_{\lambda }(x)=e^{2\pi i \lambda \cdot x}$ , is a complete orthogonal set, that is,

$$ \begin{align*}{\left\langle{e_{\lambda},e_{\lambda^{\prime}}}\right\rangle}_{\Omega}=\int_{\Omega}e_{\lambda-\lambda^{\prime}}(x)dx=\delta_{\lambda\lambda^{\prime}}\mu(\Omega),\end{align*} $$

and every $f\in L^{2}(\Omega )$ can be expressed as a Fourier series,

$$ \begin{align*}f(x)=\sum_{\lambda\in\Lambda}a_{\lambda}e_{\lambda}(x),\end{align*} $$

for some $a_{\lambda }\in \mathbb {C}$ (Fourier coefficients).

Usually, we restrict periodic functions on a fundamental domain with respect to the period lattice, so $[0,1]^{d}$ is the standard case, when the period lattice is $\mathbb {Z}^{d}$ . In general, functions defined on fundamental parallelepipeds of a lattice $\Lambda \subseteq \mathbb {R}^{d}$ have the same property; the exponentials then correspond to $e_{\lambda }(x)$ , where $\lambda $ ranges through the dual lattice $\Lambda ^{\star }$ . We note that fundamental parallelepipeds are tiles of $\mathbb {R}^{d}$ with respect to the period lattice, say $\Lambda $ .

Definition 1.2. A subset $A\subseteq \mathbb {R}^{d}$ tiles $\mathbb {R}^{d}$ by translations if there is a translation set $T\subseteq \mathbb {R}^{d}$ such that almost all elements of $\mathbb {R}^{d}$ have a unique representation as a sum $a+t$ , where $a\in A$ , $t\in T$ . We will denote this by $A\oplus T=\mathbb {R}^{d}$ . T is called the tiling complement of A, and $(A,T)$ is called a tiling pair.

Given the premise in the standard periodic case, i.e., functions defined on $[0,1]^{d}$ , it might be tempting to generalize this situation. This was first attempted in 1974 when Fuglede [9] stated the following conjecture, connecting spectral subsets and tiles of $\mathbb {R}^{d}$ .

Conjecture 1.3. Let $\Omega \subseteq \mathbb {R}^{d}$ be a bounded measurable set. $\Omega $ accepts a complete orthonormal basis of exponentials if and only if $\Omega $ tiles $\mathbb {R}^{d}$ by translations.

Fuglede proved this conjecture when either a spectrum or a tiling complement of $\Omega $ is a lattice. All results proven in the next 30 years were in the positive direction until Tao [35] disproved this conjecture by constructing spectral subsets of $\mathbb {R}^{5}$ that do not tile the space. Shortly thereafter, tiles with no spectra in $\mathbb {R}^{5}$ were found by Kolountzakis and Matolcsi [15]. The current state of art on Euclidean spaces is the failure of Fuglede’s conjecture on dimensions 3 and above in both directions [6, 7, 14, 24]. The noteworthy aspect of the construction of counterexamples is the passage to the setting of finite abelian groups, which is also the setting of the present article. To be more precise, an example of a spectral subset of $\mathbb {Z}_{8}^{3}$ that does not tile is lifted to a counterexample in $\mathbb {R}^{3}$ [14], and similarly, an example of a tile with no spectra in $\mathbb {Z}_{24}^{3}$ is lifted to a counterexample in $\mathbb {R}^{3}$ [6]. The conjecture is still open in $\mathbb {R}$ and $\mathbb {R}^{2}$ . In the one-dimensional case, this is best summarized as follows ([3] and the references therein):

$$ \begin{align*}\textbf{T-S}(\mathbb{R})\Longleftrightarrow\textbf{T-S}(\mathbb{Z})\Longleftrightarrow\forall N\textbf{T-S}(\mathbb{Z}_{N})\end{align*} $$

and

$$ \begin{align*}\textbf{S-T}(\mathbb{R})\Longrightarrow\textbf{S-T}(\mathbb{Z})\Longrightarrow\forall N\textbf{S-T}(\mathbb{Z}_{N}),\end{align*} $$

where $\textbf {S-T}(G)$ denotes the fact that the Spectral $\Rightarrow $ Tiling direction holds in G, while $\textbf {T-S}(G)$ denotes that fact that the reverse implication is true.

We emphasize that the equivalence of the Spectral $\Rightarrow $ Tiling direction between the ‘continuous’ and the ‘discrete’ settings depends on rationality of spectrum: the claim that every spectral subset of $\mathbb {R}$ of measure $1$ has a spectrum in $\mathbb {Q}$ , which is a difficult problem in its own right. Another important ingredient for this yet unproved equivalence is the periodicity of spectrum [10].

This conjecture has a renewed interest in the setting of finite abelian groups during the last few years, mostly due to the counterexamples mentioned above. In the cyclic case, Łaba first connected [17] the work of Coven and Meyerowitz [1] on tiling subsets of integers to Fuglede’s conjecture and proved subsequently that tiles of $\mathbb {Z}$ of cardinality $p^{m}$ or $p^{m}q^{n}$ , where $p,q$ primes, are also spectral; the reverse direction holds when the cardinality is $p^{m}$ . These arguments can be adapted to the finite cyclic group setting, proving that the Tiling $\Rightarrow $ Spectral direction is true for finite cyclic groups of order $p^{m}q^{n}$ . For a self-contained account, we refer the reader to [23]. Moreover, both directions of Fuglede’s conjecture hold for cyclic groups of order $p^{m}$ ; again, self-contained proofs can be found in [5] and [23].

We mention in passing two another recent breakthroughs in Fuglede’s conjecture. This conjecture has also been confirmed for the field of p-adic rational numbers $\mathbb {Q}_{p}$ [4, 5] and for convex bodies in $\mathbb {R}^{d}$ [21]. We return to the setting of this paper, namely finite abelian groups. For finite abelian groups with two generators, it has been shown that Fuglede’s conjecture holds in $\mathbb {Z}_{p}\times \mathbb {Z}_{p}$ [11], a result later extended to $\mathbb {Z}_{p}\times \mathbb {Z}_{p^{2}}$ [32] and very recently to $\mathbb {Z}_{p}\times \mathbb {Z}_{p^{n}}$ [37]. When the generators are at least four, the Spectral $\Rightarrow $ Tiling direction fails when the cardinality of the group is odd [8].

The goal of the present article is to develop tools and prove facts about spectral subsets of $\mathbb {Z}_{N}$ , especially when N has at most two distinct prime factors. We note that the conjecture is known to be true when $N=p^{n}q$ [23] or $N=p^{n}q^{2}$ [13], i.e., when one of the exponents is $\leq 2$ . The methods and techniques developed herein extend these results, thus ‘raising’ the exponent of q:

Theorem 1.4. Let $A\subseteq \mathbb {Z}_{N}$ be a spectral set, where $N=p^{m}q^{n}$ , with $p,q$ distinct primes. Then A tiles $\mathbb {Z}_{N}$ if one of the following holds:

1. 1. $p<q$ and $m\leq 9$ or $n\leq 6$ .

2. 2. $p^{m-2}<q^{4}$ .

Fuglede’s conjecture in $\mathbb {Z}_{N}$ when $N=p^{m}q^{n}$ seems within reach. It is the hope of the author that the methods developed here to ‘raise’ the exponent, combined with the recent proofs of Fuglede’s conjecture in the groups $\mathbb {Z}_{pqr}$ [31], $\mathbb {Z}_{p^{2}qr}$ [33], and $\mathbb {Z}_{pqrs}$ [12], where the number of primes dividing N is increased, will provide the groundwork towards a more effective attack on the one-dimensional Fuglede conjecture.

Regarding the Tiling $\Rightarrow $ Spectral direction, we will provide a proof in cyclic groups of order $p_{1}^{n}p_{2}\dotsb p_{k}$ ; this direction was previously known for groups of order $p^{m}q^{n}$ [17] (see also [23]) or of square-free order (proven in Terence Tao’s blog ¹ by Łaba and Meyerowitz; see also [31]). Very recently, it was also proved for groups of order $(pqr)^{2}$ [18, 19].

Theorem 1.5. Let $N=p_{1}^{n}p_{2}\dotsb p_{k}$ , where $p_{1},\dotsc ,p_{k}$ are distinct primes. If $A\subseteq \mathbb {Z}_{N}$ tiles, then A is spectral.

Even if Fuglede’s conjecture is proven for $\mathbb {Z}_{p^{m}q^{n}}$ , one should be cautious before conjecturing further that this might be true in all cyclic groups. For example, several strengthened versions of the Tiling $\Rightarrow $ Spectral directions, such as the conjectures of Sands [28] and Tijdeman [36], are known to hold when N has the form $p^{m}q^{n}$ , but they break down when N has at least three distinct prime factors due to counterexamples given by Szabo [34]. Furthermore, the main tools used here, such as the structure of vanishing sums of Nth roots of unity [20] and primitive subsets of $\mathbb {Z}_{N}$ , are much stronger when N has at most two distinct prime factors.

The different tools needed for the proofs of the above theorems are laid out in Sections 2 and 3. In Section 4, we prove 1.5, which is based on an inductive approach and is relatively easy to follow. The remaining sections are exclusively devoted to the two-prime case, $N=p^{m}q^{n}$ , and they are much more technical and demanding. Theorem 1.4 is eventually proven in Section 11.

2 Multisets and mask polynomials

We denote by $\mathbb {Z}_{N}$ the cyclic additive group of N elements. A multiset A in $\mathbb {Z}_{N}$ is a collection of elements of $\mathbb {Z}_{N}$ along with some multiplicities: Any element $a\in A$ appears $m_{a}\in \mathbb {N}$ times in A. The characteristic function of A is denoted by $\mathbf {1}_{A}$ , and is defined by $\mathbf {1}_{A}(a)=m_{a}$ . It is understood that, if A is a proper set, this function takes only the values $0$ and $1$ . The support of the multiset A, denoted by $\operatorname {supp} A$ , is simply the subset of $\mathbb {Z}_{N}$ of elements that appear at least once in A; in other words, $\operatorname {supp} A=\operatorname {supp}(\mathbf {1}_{A})$ .

Definition 2.1. Let A be a multiset of elements in $\mathbb {Z}_{N}$ . The mask polynomial of A is defined by $A(X)=\sum _{a\in A}m_{a} X^{a}$ and is considered as an element in $\mathbb {Z}[X]/(X^{N}-1)$ . As such, the values of $A(X)$ on the Nth roots of unity $\zeta _{N}^{d}$ , $1\leq d\leq N$ , (here $\zeta _{N}=e^{2\pi i/N}$ ) are well-defined, i.e., independent of the representative of their class $\ \bmod\ (X^{N}-1)$ . Also, for every $d\in \mathbb {Z}$ define the multiset $d\cdot A$ whose characteristic function is

$$ \begin{align*}\mathbf{1}_{d\cdot A}(x)=\sum_{a\in\mathbb{Z}_{N}, da=x}\mathbf{1}_{A}(a).\end{align*} $$

The support of $d\cdot A$ will simply be denoted by $dA$ . Finally, the multiset of elements of A that are congruent to $j\ \bmod\ m$ for $m\mid N$ will be denoted as $A_{j\ \bmod\ m}$ .

Example. If $A={\left \{{0,3}\right \}}\subseteq \mathbb {Z}_{6}$ , then $2A={\left \{{0}\right \}}$ , while $2\cdot A={\left \{{0,0}\right \}}$ ; moreover, $A(X)\equiv 1+X^{3} \ \bmod\ (X^{6}-1)$ , $(2A)(X)\equiv 1$ , $(2\cdot A)(X)\equiv 2$ . Also, $A_{0\ \bmod\ 3}=A$ , while $A_{1\ \bmod\ 3}=A_{2\ \bmod\ 3}=\varnothing $ .

In general, the following holds for the mask polynomial of $m\cdot A$ :

Proposition 2.2. Let A be a multiset with elements from $\mathbb {Z}_{N}$ . Then $A(X^{m})\equiv (m\cdot A)(X)\ \bmod\ (X^{N}-1)$ for every $m\in \mathbb {N}$ . If $m\mid N$ , then

$$ \begin{align*}A(X^{m})\equiv\sum_{j=0}^{N/m-1}\lvert A_{j\ \bmod\ N/m} \rvert X^{jm}\ \bmod\ (X^{N}-1).\end{align*} $$

Proof. We have

$$ \begin{align*}A(X^{m})\equiv \sum_{j\in A}X^{jm}\equiv \sum_{\substack{j\in A\\ jm\equiv g\ \bmod\ N}} X^{g}\ \bmod\ (X^{N}-1),\end{align*} $$

and the last one is precisely the definition of the mask polynomial of the multiset $m\cdot A$ . If $m\mid N$ , then

$$ \begin{align*}\sum_{\substack{j\in A\\ jm\equiv g\ \bmod\ N}} X^{g}\equiv\sum_{\substack{j\in A\\ j\equiv gm^{-1}\ \bmod\ N/m}}X^{g}\equiv \sum_{j=0}^{N/m-1}\lvert A_{j\ \bmod\ N/m} \rvert X^{jm}\ \bmod\ (X^{N}-1),\end{align*} $$

as desired.

The Fourier transform of functions on $\mathbb {Z}_{N}$ is defined as

$$ \begin{align*}\hat{f}(x)=\sum_{d\in\mathbb{Z}_{N}} f(d)\zeta_{N}^{-dx}.\end{align*} $$

The values of mask polynomials $A(X)$ on Nth roots of unity have the following relation with those of the Fourier transform of $\mathbf {1}_{A}$ :

$$ \begin{align*}\widehat{\mathbf{1}}_{A}(d)=A(\zeta_{N}^{-d}).\end{align*} $$

The reduced residues $\ \bmod\ N$ will be denoted as usual by $\mathbb {Z}_{N}^{\star }$ . The group $\mathbb {Z}_{N}$ is partitioned into the subsets

(2.1) $$ \begin{align} d\mathbb{Z}_{N}^{\star}={\left\{{x\in\mathbb{Z}_{N}:\gcd(x,N)=d}\right\}}={\left\{{x\in\mathbb{Z}_{N}:\operatorname{\mathrm{ord}}(x)=N/d}\right\}}, \end{align} $$

called divisor classes, where d runs through the divisors of N. Since we will evaluate polynomials on Nth roots of unity, we unavoidably have to use the cyclotomic polynomials $\Phi _{d}(X)$ for $d\mid N$ , which is the irreducible polynomial of $\zeta _{d}$ over $\mathbb {Q}$ , and is factored as

$$ \begin{align*}\Phi_{d}(X)=\prod_{g\in\mathbb{Z}_{d}^{\star}}(X-\zeta_{d}^{g}).\end{align*} $$

Therefore, divisibility of $A(X)\ \bmod\ (X^{N}-1)$ by cyclotomic polynomials of degree $d\mid N$ , denoted by $\Phi _{d}(X)$ , also makes sense as $X^{N}-1=\prod _{d\mid N}\Phi _{d}(X)$ . $\Phi _{d}(X)\mid A(X)$ would then hold precisely when $A(\zeta _{d})=0$ , which would also imply that $A(\zeta _{d}^{g})=0$ for every $g\in \mathbb {Z}_{N}$ with $\gcd (d,g)=1$ . From this, we readily deduce that the zero set

$$ \begin{align*}Z(A):=Z(\widehat{\mathbf{1}}_{A})={\left\{{x\in\mathbb{Z}_{N}:A(\zeta_{N}^{-x})=0}\right\}}\end{align*} $$

is a union of divisor classes.

3 Tiles and spectral subsets

These notions are similarly defined when we work on a finite cyclic group.

Definition 3.1. Let $A\subseteq \mathbb {Z}_{N}$ . We say that A tiles $\mathbb {Z}_{N}$ by translations if there is some $T\subseteq \mathbb {Z}_{N}$ such that any element of $\mathbb {Z}_{N}$ can be written uniquely as a sum of an element of A and an element of T. T is called the tiling complement of A, and we write $A\oplus T=\mathbb {Z}_{N}$ ; we will also call $(A,T)$ a tiling pair. We call A spectral if there is some $B\subseteq \mathbb {Z}_{N}$ with $\lvert A \rvert =\lvert B \rvert $ and the exponential functions

$$ \begin{align*}e_{b}(x)=\zeta_{N}^{bx}\end{align*} $$

are pairwise orthogonal on A, that is,

(3.1) $$ \begin{align} {\left\langle{e_{b},e_{b^{\prime}}}\right\rangle}_{A}=\sum_{a\in A}\zeta_{N}^{a(b-b^{\prime})}=0, \end{align} $$

for every $b,b^{\prime }\in B$ , $b\neq b^{\prime }$ , or equivalently, the matrix

$$ \begin{align*}\frac{1}{\sqrt{\lvert A \rvert}}{\left({\zeta_{N}^{ab}}\right)}_{a\in A, b\in B}\end{align*} $$

is unitary. In this case, B is called a spectrum of A, and $(A,B)$ a spectral pair of $\mathbb {Z}_{N}$ .

Using mask polynomials is very useful when describing tiling properties. The following was proven in [1] (Lemmata 1.3 and 3.1).

Lemma 3.2. Let $A,T$ be multisets in $\mathbb {Z}_{N}$ . Then A and T are proper sets and form a tiling pair if and only if

$$ \begin{align*}A(X)T(X)\equiv 1+X+\dotsb+X^{N-1}\ \bmod\ (X^{N}-1).\end{align*} $$

Furthermore, if m is prime to $\lvert A \rvert $ , the above equation also implies

$$ \begin{align*}A(X^{m})T(X)\equiv 1+X+\dotsb+X^{N-1}\ \bmod\ (X^{N}-1),\end{align*} $$

i.e., $m\cdot A$ is also a tiling complement of T.

Remark. Lemma 3.1 in [1] actually proves the second part when $m=p$ a prime; however, one could use this repetitively for all primes dividing m and obtain the above result.

Spectrality and the tiling property impose some structural properties on the difference set $A-A$ .

Theorem 3.3. Let $A\subseteq \mathbb {Z}_{N}$ .

1. (i) $B\subseteq \mathbb {Z}_{N}$ is a spectrum of A if and only if $\lvert A \rvert =\lvert B \rvert $ and $B-B\subseteq {\left \{{0}\right \}}\cup Z(A)$ .

2. (ii) A tiles $\mathbb {Z}_{N}$ by $T\subseteq \mathbb {Z}_{N}$ , if and only if $N=\lvert A \rvert \lvert T \rvert $ and $(A-A)\cap (T-T)={\left \{{0}\right \}}$ .

3. (iii) If $(A,B)$ is a spectral pair of $\mathbb {Z}_{N}$ and $m\in \mathbb {Z}_{N}^{\star }$ , then $(A,mB)$ is also a spectral pair.

Proof.

1. (i) This almost follows by definition. The space of functions $f:A\to \mathbb {C}$ has dimension $\lvert A \rvert $ ; therefore, a spectrum must have the same cardinality. Furthermore, by equation (3.1), we get that any $b,b^{\prime }\in B$ with $b\neq b^{\prime }$ must satisfy $b-b^{\prime }\in Z(A)$ .

2. (ii) Since every element of $\mathbb {Z}_{N}$ can be expressed uniquely as $a+t$ with $a\in A$ , $t\in T$ , we get a bijection between $\mathbb {Z}_{N}$ and $A\times T$ , proving $N=\lvert A \rvert \lvert T \rvert $ . Furthermore, suppose that $a,a^{\prime }\in A$ and $t,t^{\prime }\in T$ satisfy $a-a^{\prime }=t-t^{\prime }$ . Then $a+t^{\prime }=a^{\prime }+t$ , so by uniqueness of representation of $a+t^{\prime }$ as an element of A and an element of T, we must have $a=a^{\prime }$ and $t=t^{\prime }$ , proving the desired fact.

3. (iii) We will show that $m(b-b^{\prime })\in Z(A)$ for every $m\in \mathbb {Z}_{N}^{\star }$ and $b,b^{\prime }\in B$ with $b\neq b^{\prime }$ . Assume that $b-b^{\prime }\in d\mathbb {Z}_{N}^{\star }$ ; hence, by equation (3.1), we get $A(\zeta _{N}^{dg})=0$ , where $b-b^{\prime }\equiv dg\ \bmod\ N$ , with $g\in \mathbb {Z}_{N}^{\star }$ . Then $\Phi _{N/d}(X)\mid A(X)$ ; thus,

   $$ \begin{align*}0=A(\zeta_{N}^{dgm})=A(\zeta_{N}^{m(b-b^{\prime})}),\end{align*} $$
   completing the proof.

Another way to express Theorem 3.3(i) is the following.

Corollary 3.4. Let $(A,B)$ be a spectral pair in $\mathbb {Z}_{N}$ . Then $A(\zeta _{\operatorname {\mathrm {ord}}(b-b^{\prime })})=0$ , for all $b,b^{\prime }\in B$ with $b\neq b^{\prime }$ .

Proof. This follows from Theorem 3.3(i) as $Z(A)$ contains all divisor classes $d\mathbb {Z}_{N}^{\star }$ for which there are $b,b^{\prime }\in B$ satisfying $b-b^{\prime }\in d\mathbb {Z}_{N}^{\star }$ , so by equation (2.1) $\operatorname {\mathrm {ord}}(b-b^{\prime })=N/d$ , or equivalently, $\zeta _{N}^{b-b^{\prime }}$ is a primitive $N/d$ -th root of unity, yielding

$$ \begin{align*}A(\zeta_{N/d})=A(\zeta_{\operatorname{\mathrm{ord}}(b-b^{\prime})})=0,\end{align*} $$

as desired.

Denote by $S^{N}$ be the set of prime powers dividing N, and let $S_{A}^{N}={\left \{{s\in S^{N}: A(\zeta _{s})=0}\right \}}$ . We define the following properties:

• (T1) $A(1)=\prod _{s\in S_{A}^{N}} \Phi _{s}(1)$

• (T2) Let $s_{1},s_{2},\dotsc ,s_{k}\in S_{A}^{N}$ be powers of different primes. Then $\Phi _{s}(X)\mid A(X)$ , where $s=s_{1}\dotsm s_{k}$ .

These properties implicitly assume that the cyclic group under question has order N (see also [16]). Sometimes, a set $A\subseteq \mathbb {Z}_{N}$ might be reduced $\ \bmod\ M$ , for some $M\mid N$ , $M<N$ , when no two elements of A are congruent $\ \bmod\ M$ . In this case, we will explicitly mention the underlying group and say, for example, that ‘A satisfies (T1) and (T2) in $\mathbb {Z}_{M}$ ’. For subsets of $\mathbb {Z}$ , these properties were first defined by Coven and Meyerowitz [1] to study tiling subsets of integers. They proved that (T1) and (T2) (for integers) imply that A tiles $\mathbb {Z}$ ; furthermore, if $\lvert A \rvert $ is divided by at most two distinct primes, then (T1) and (T2) are equivalent to tiling. On the other hand, Łaba [17] proved that it also implies that A is spectral. Here, we will show that the same situation carries to the finite cyclic case. ²

Theorem 3.5. Let $A\subseteq \mathbb {Z}_{N}$ .

1. (I) If A satisfies (T1) and (T2), then it tiles $\mathbb {Z}_{N}$ .

2. (II) If A satisfies (T1) and (T2), then it has a spectrum.

3. (III) If N is divisible by at most two distinct primes, then A tiles $\mathbb {Z}_{N}$ if and only if it satisfies (T1) and (T2).

Proof. Suppose that $A\subseteq \mathbb {Z}_{N}$ satisfies (T1) and (T2). Denote by $N_{s}$ the maximal divisor of N that is prime to s. For example, if

$$ \begin{align*}N=p_{1}^{\alpha_{1}}p_{2}^{\alpha_{2}}\dotsm p_{k}^{\alpha_{k}},\end{align*} $$

then

$$ \begin{align*}N_{p_{1}^{m}}=p_{2}^{\alpha_{2}}\dotsm p_{k}^{\alpha_{k}}, \;\;\;\; \forall m \text{ with } 1\leq m\leq \alpha_{1}.\end{align*} $$

Consider the polynomial

$$ \begin{align*}T(X)=\prod_{s\in S^{N}\setminus S_{A}^{N}}\Phi_{s}(X^{N_{s}}).\end{align*} $$

By construction, $S_{T}^{N}=S^{N}\setminus S_{A}^{N}$ and $\lvert A \rvert \lvert T \rvert =N$ . Next, we will show that $A(X)T(X)$ vanishes on any Nth root of unity. Let $X=\zeta _{d}$ , $d\mid N$ . We write

$$ \begin{align*}d=p_{1}^{\beta_{1}}\dotsm p_{k}^{\beta_{k}},\end{align*} $$

with $0\leq \beta _{j}\leq \alpha _{j}$ , $1\leq j\leq k$ . If $s=p_{j}^{\beta _{j}}\in S_{T}^{N}$ for some j so that $d=s\cdot d_{s}$ , then $\Phi _{s}(X^{N_{s}})$ divides $T(X)$ and $d_{s}$ divides $N_{s}$ ; therefore,

$$ \begin{align*}\Phi_{s}(\zeta_{d}^{N_{s}})=\Phi_{s}(\zeta_{s}^{g})=0,\end{align*} $$

for $g=N_{s}/d_{s}$ , which is prime to s, yielding $T(\zeta _{d})=0$ . Otherwise, every $p_{j}^{\beta _{j}}\in S_{A}^{N}$ , and since A satisfies (T2), we get $\Phi _{d}(X)\mid A(X)$ or, equivalently $A(\zeta _{d})=0$ . Combined with $\lvert A \rvert \lvert T \rvert =N$ , this implies

$$ \begin{align*}A(X)T(X)\equiv1+X+\dotsb+X^{N-1}\ \bmod\ (X^{N}-1);\end{align*} $$

thus, $T(X)$ is the mask polynomial of a set $T\subseteq \mathbb {Z}_{N}$ , which is a tiling complement of A, proving (I).

For (II), we define the set $B\subseteq \mathbb {Z}_{N}$ consisting of all elements of the form

(3.2) $$ \begin{align} \sum_{s\in S_{A}^{N}}k_{s}\frac{N}{s}, \end{align} $$

where for each $s\in S_{A}^{N}$ , $k_{s}$ ranges through the set ${\left \{{0,1,\dotsc ,p-1}\right \}}$ , where $p=\Phi _{s}(1)$ is the prime dividing s. Different choices of $k_{s}$ , $s\in S_{A}^{N}$ give different elements, yielding $\lvert A \rvert =\lvert B \rvert $ since A satisfies (T1). Moreover, an element in $B-B$ has the form (3.2), with the difference that $\lvert k_{s} \rvert <\Phi _{s}(1)$ holds instead of $0\leq k_{s}\leq \Phi _{s}(1)-1$ . The order of $k_{s}\frac {N}{s}$ with $\lvert k_{s} \rvert <\Phi _{s}(1)$ is exactly s. Based on this simple fact, the order of a nonzero element of $B-B$ is $s_{1}s_{2}\dotsm s_{\ell }$ , where $s_{1},\dotsc ,s_{\ell }\in S_{A}^{N}$ powers of distinct primes. Since A satisfies (T2), we will then have $A(\zeta _{\operatorname {\mathrm {ord}}(b-b^{\prime })})=0$ for every $b,b^{\prime }\in B$ , $b\neq b^{\prime }$ , so B is the spectrum of A by Theorem 3.3(i) and Corollary 3.4.

A proof for part (III) is in [23].

Using (II) and (III) we can easily deduce:

Theorem 3.6. If A tiles $\mathbb {Z}_{N}$ , where N is divisible by at most two distinct primes, then A has a spectrum.

4 Proof of Theorem 1.5

Here, we will test the tools of the previous section to prove the Tiling $\Rightarrow $ Spectral direction in $\mathbb {Z}_{N}$ , where $N=p_{1}^{m}p_{2}p_{3}\dotsm p_{n}$ , where $p_{1},\dotsc ,p_{n}$ are distinct primes and $m,n\geq 2$ are integers. We will do so by proving that (T1) and (T2) always hold for a tiling subset of $\mathbb {Z}_{N}$ .

Suppose that $A\subseteq \mathbb {Z}_{N}$ tiles $\mathbb {Z}_{N}$ by translations so that $A\oplus T=\mathbb {Z}_{N}$ . If $\gcd (\lvert A \rvert ,\lvert T \rvert )=1$ , then Lemma 3.2 implies that

(4.1) $$ \begin{align} A(X)T(X^{M})\equiv 1+X+\dotsb+X^{N-1}\ \bmod\ (X^{N}-1), \end{align} $$

where $M=\lvert A \rvert $ . Therefore, $M\cdot T$ is a proper set; moreover, $\lvert M\cdot T \rvert =\lvert T \rvert =N/M$ and $M\cdot T\subseteq M\mathbb {Z}_{N}$ , which yield $M\cdot T=M\mathbb {Z}_{N}$ , i.e., A tiles by the subgroup $M\mathbb {Z}_{N}$ or, equivalently,

$$ \begin{align*}A(X)\equiv 1+X+\dotsb+X^{M-1}=\prod_{1<d\mid M}\Phi_{d}(X)\ \bmod\ (X^{M}-1).\end{align*} $$

From the last representation of $A(X)$ as a product of cyclotomic polynomials $\ \bmod\ (X^{M}-1)$ , it is evident that A satisfies (T1) and (T2) in $\mathbb {Z}_{N}$ and hence is a spectral subset of $\mathbb {Z}_{N}$ . We remark that the direction Tiling $\Rightarrow $ Spectral holds for every tiling subset $A\subseteq \mathbb {Z}_{N}$ satisfying $\gcd (\lvert A \rvert ,N/\lvert A \rvert )=1$ , regardless of the primes dividing N, using the same argument.

We proceed to the difficult case, where $\gcd (\lvert A \rvert ,\lvert T \rvert )>1$ , and hence, $\gcd (\lvert A \rvert ,\lvert T \rvert )$ is a power of $p_{1}$ . Let M be the maximal divisor of $\lvert A \rvert $ that is prime to $p_{1}$ ; in particular, $\gcd (M,\lvert T \rvert )=1$ . Hence, as before, $M\cdot T$ is a proper set and also a tiling complement of A by Lemma 3.2 so that equation (4.1) holds. Next, suppose that

$$ \begin{align*}S_{A}^{N}={\left\{{p_{1}^{\ell_{1}},\dotsc,p_{1}^{\ell_{r}},p_{2},\dotsc,p_{k}}\right\}}\end{align*} $$

so that

$$ \begin{align*}S_{M\cdot T}^{N}=S^{N}\setminus S_{A}^{N}={\left\{{p^{m_{1}},\dotsc,p^{m_{s}},p_{k+1},\dotsc}\right\}},\end{align*} $$

where the sets of exponents ${\left \{{\ell _{1},\dotsc \ell _{r}}\right \}}$ and ${\left \{{m_{1},\dotsc ,m_{s}}\right \}}$ form a partition of ${\left \{{1,2,\dotsc ,m}\right \}}$ by equation (4.1). It is clear that A satisfies (T1) as

$$ \begin{align*}\lvert A \rvert\cdot\lvert T \rvert=N, \;\;\;\; p_{1}^{r}p_{2}\dotsm p_{k}\mid\lvert A \rvert, \;\;\;\; p_{1}^{s}p_{k+1}\dotsm p_{n}\mid\lvert T \rvert\end{align*} $$

imply that $\lvert A \rvert =p_{1}^{r}p_{2}\dotsm p_{k}$ (besides, it is already known that tiling always implies (T1) in every $\mathbb {Z}_{N}$ or in $\mathbb {Z}$ [1]). For the property (T2), consider first d to be a composite divisor of $p_{2}\dotsm p_{k}=M$ . Then $T(\zeta _{d}^{M})=T(1)\neq 0$ ; hence, $A(\zeta _{d})=0$ by (4.1), verifying (T2) when we consider primes among $p_{2},\dotsc ,p_{k}$ . Next, consider a root of unity of order $p_{1}^{\ell _{j}}d$ ( $d\mid M$ as before); we get

$$ \begin{align*}T(\zeta_{p_{1}^{\ell_{j}}d}^{M})=T(\zeta_{p_{1}^{\ell_{j}}}^{M/d})=\sigma(T(\zeta_{p^{\ell_{j}}_{1}}))\neq0,\end{align*} $$

for some $\sigma \in \text{Gal}(\mathbb {Q}(\zeta _{p_{1}^{\ell _{j}}})/\mathbb {Q})$ , since $p_{1}\nmid \frac {M}{d}$ , whence

$$ \begin{align*}\Phi_{p^{\ell_{j}}_{1}d}(X)\mid A(X),\end{align*} $$

confirming (T2) completely for A. By Theorem 3.5(II), A is spectral, completing the proof of Theorem 1.5.

5 Vanishing sums of roots of unity

Let $G={\left \langle {\zeta _{N}}\right \rangle }$ , the cyclic group generated by the standard Nth root of unity. Consider the group ring $\mathbb {Z}[G]$ , the ring of all formal integer linear combinations of Nth roots of unity. It is known that $\mathbb {Z}[G]\cong \mathbb {Z}[X]/(X^{N}-1)$ , so we may represent an element of $\mathbb {Z}[G]$ by a polynomial with integer coefficients modulo $X^{N}-1$ . $\mathbb {Z}[G]$ is equipped with a natural evaluation map, say v, which simply evaluates the given sum. Considered as an element of $\mathbb {Z}[X]/(X^{N}-1)$ , say $F(X)$ , the effect of the evaluation map is $v(F)=F(\zeta _{N})$ , as expected.

When this sum vanishes, we obtain some information on the structure of $F(X)$ . We note that $\Phi _{p}(\zeta _{p})=0$ for p prime implies that

$$ \begin{align*}1+\zeta_{p}+\dotsb+\zeta_{p}^{p-1}\end{align*} $$

is a vanishing sum of roots of unity. The same holds true for any integer linear combination of sums of this form, multiplied by roots of unity. The following theorem, attributed to Rédei [26, 27], de Bruijn [2] and Schoenberg [30], shows that the converse is true as well. We will express it in polynomial notation.

Theorem 5.1. Let $F(X)\in \mathbb {Z}[X]$ with $F(\zeta _{N})=0$ . Then

$$ \begin{align*}F(X)\equiv \sum_{p\mid N, \; p \text{ prime}}F_{p}(X)\Phi_{p}(X^{N/p})\ \bmod\ (X^{N}-1),\end{align*} $$

where $F_{p}(X)\in \mathbb {Z}[X]$ .

When N is divisible by at most two primes and $F(X)$ has nonnegative coefficients, we obtain something stronger. This is due to Lam and Leung [20].

Theorem 5.2. Let $F(X)\in \mathbb {Z}_{\geq 0}[X]$ . Then $F(\zeta _{N})=0$ , where $N=p^{m}q^{n}$ and $p, q$ primes if and only if

$$ \begin{align*}F(X)\equiv P(X)\Phi_{p}(X^{N/p})+Q(X)\Phi_{q}(X^{N/q})\ \bmod\ (X^{N}-1)\end{align*} $$

for some $P(X),Q(X)\in \mathbb {Z}_{\geq 0}[X]$ . If $F(\zeta _{N}^{p^{k}})\neq 0$ (respectively, $F(\zeta _{N}^{q^{\ell }})\neq 0$ ) for some $1\leq k\leq m$ (resp., $1\leq \ell \leq n$ ), then we cannot have $P(X)\equiv 0\ \bmod\ (X^{N}-1)$ (resp., $Q(X)\equiv 0\ \bmod\ (X^{N}-1)$ ).

This is no longer true if N has at least three distinct prime factors, say $p,q,r$ , as the polynomial

$$ \begin{align*}F(X)=(\Phi_{p}(X^{N/p})-1)(\Phi_{q}(X^{N/q})-1)+(\Phi_{r}(X^{N/r})-1)\end{align*} $$

satisfies $F(\zeta _{N})=0$ but has no such representation.

We observe that

$$ \begin{align*}\Phi_{p}(X^{N/p})=1+X^{N/p}+X^{2N/p}+\dotsb+X^{(p-1)N/p}\end{align*} $$

is the mask polynomial of the subgroup of $\mathbb {Z}_{N}$ of order p. In general, for $d\mid N$ , the cosets of the subgroup of order d, $\frac {N}{d}\mathbb {Z}_{N}$ , will be called d-cycles. So, Theorem 5.2 asserts that a vanishing sum of roots of unity of order $N=p^{m}q^{n}$ can be expressed as a disjoint union (i.e., as multisets, counting multiplicities) of p- and q-cycles. This is very important when we consider the difference set $A-A$ of a spectral set $A\subseteq \mathbb {Z}_{N}$ with $A(\zeta _{N})=0$ as it yields both $\frac {N}{p}\mathbb {Z}_{N}$ , $\frac {N}{q}\mathbb {Z}_{N}\subseteq A-A$ under certain mild conditions, which in turn gives roots for the mask polynomial of the spectrum B due to Theorem 3.3(i).

The condition $A(\zeta _{N})=0$ is satisfied when a spectrum B is primitive. We will subsequently focus on spectral pairs $(A,B)$ of primitive sets. Otherwise, we may consider A and B (after an appropriate translation) as subsets of a proper subgroup.

Definition 5.3. Let G be a finite abelian group and T a subset. We call T primitive if it is not contained in a coset of a proper subgroup of G.

Lemma 5.4. Let $G=\mathbb {Z}_{N}$ with $N=p^{m} q^{n}$ . A subset $T\subseteq G$ is primitive if and only if $(T-T)\cap \mathbb {Z}_{N}^{\star }\neq \varnothing $ .

Proof. Since T is primitive, for a given $t\in T$ it would hold $t-T\nsubseteq p\mathbb {Z}_{N}$ and $t-T\nsubseteq q\mathbb {Z}_{N}$ , yielding $t^{\prime },t^{\prime \prime }\in T$ such that $t-t^{\prime }\notin p\mathbb {Z}_{N}$ , $t-t^{\prime \prime }\notin q\mathbb {Z}_{N}$ . If either $t-t^{\prime }\notin q\mathbb {Z}_{N}$ or $t-t^{\prime \prime }\notin p\mathbb {Z}_{N}$ , then we get $t-t^{\prime }\in \mathbb {Z}_{N}^{\star }$ or $t-t^{\prime \prime }\in \mathbb {Z}_{N}^{\star }$ , respectively. Otherwise, $t-t^{\prime }\in q\mathbb {Z}_{N}$ and $t-t^{\prime \prime }\in p\mathbb {Z}_{N}$ ; therefore, $t^{\prime }-t^{\prime \prime }\notin p\mathbb {Z}_{N}\cup q\mathbb {Z}_{N}$ , giving $t^{\prime }-t^{\prime \prime }\in \mathbb {Z}_{N}^{\star }$ , thus $(T-T)\cap \mathbb {Z}_{N}^{\star }\neq \varnothing $ . The converse is trivial.

Proposition 5.5. Let $A\subseteq \mathbb {Z}_{N}$ . Suppose that there is j such that $A\cap (j+\frac {N}{pq}\mathbb {Z}_{N})=A_{j\ \bmod\ \frac {N}{pq}}$ is not supported on a p- or q-cycle. Then $(A-A)\cap \frac {N}{pq}\mathbb {Z}_{N}^{\star }\neq \varnothing $ .

Proof. Let j be as in the hypothesis, and without loss of generality assume that $A\subseteq j+\frac {N}{pq}\mathbb {Z}_{N}$ or, equivalently, $A=A_{j\ \bmod\ \frac {N}{pq}}$ . Translating A does not affect the conclusion, so we may further assume that $j=0$ . This confines A in the subgroup of order $pq$ . Dividing every element by $\frac {N}{pq}$ , we can assume that $N=pq$ . The problem has thus been reduced to the following: Assume that $A\subseteq \mathbb {Z}_{pq}$ is not a subset of a p- or a q-cycle, then $(A-A)\cap \mathbb {Z}_{pq}^{\star }\neq \varnothing $ . Indeed, this is the case, since A is primitive, so the conlcusion of the reduced problem follows from Lemma 5.4 with $m=n=1$ .

Lemma 5.6. Let $A\subseteq \mathbb {Z}_{N}$ with $N=p^{m}q^{n}$ . Suppose that there is $d\mid \frac {N}{q}$ such that $(qd)\cdot A$ is a union of p-cycles, but $A(\zeta _{N}^{d})\neq 0$ . Then

$$ \begin{align*}(A-A)\cap\frac{N}{pqd}\mathbb{Z}_{N}^{\star}\neq\varnothing.\end{align*} $$

If, in addition, A is spectral, then $B(\zeta _{pqd})=0$ for any spectrum B of A.

Proof. By hypothesis and Proposition 2.2, we have

$$ \begin{align*}A(X^{qd})\equiv P(X)\Phi_{p}(X^{N/p})\ \bmod\ (X^{N}-1).\end{align*} $$

Consider the intersections of $dA$ with the cosets of the subgroup of index $pq$ , namely

$$ \begin{align*}dA\cap(j+\frac{N}{pq}\mathbb{Z}_{N})={\left({dA}\right)}_{j\ \bmod\ \frac{N}{pq}},\end{align*} $$

where $0\leq j\leq \frac {N}{pq}-1$ . If ${\left ({dA}\right )}_{j\ \bmod\ \frac {N}{pq}}\neq \varnothing $ , then it intersects every coset of the subgroup $\frac {N}{q}\mathbb {Z}_{N}$ contained in $j+\frac {N}{pq}\mathbb {Z}_{N}$ . Indeed, if $da\in {\left ({dA}\right )}_{j\ \bmod\ \frac {N}{pq}}$ , then

$$ \begin{align*}qda+i\frac{N}{p}\in qdA\end{align*} $$

for $0\leq i\leq p-1$ by hypothesis, so, for each i, there is $a^{\prime }\in A$ such that $qda^{\prime }\equiv qda+i\frac {N}{p}\ \bmod\ N$ ; therefore,

$$ \begin{align*}da^{\prime}\equiv da+i\frac{N}{pq}+k\frac{N}{q}\ \bmod\ N\end{align*} $$

for some k. Each element of the form $da+i\frac {N}{pq}+k\frac {N}{q}$ belongs to a different q-cycle of $j+\frac {N}{pq}\mathbb {Z}_{N}$ , and since there are exactly p of them, $dA$ intersects them all. If every pair of elements $da,da^{\prime }\in {\left ({dA}\right )}_{j\ \bmod\ \frac {N}{pq}}$ lying on two different q-cycles belongs to the same p-cycle, then it is evident that ${\left ({dA}\right )}_{j\ \bmod\ \frac {N}{pq}}$ is a single p-cycle. By hypothesis, the multiset $(qd)\cdot A$ contains the entire p-cycle $qj+\frac {N}{p}\mathbb {Z}_{N}$ with some multiplicity (i.e., every element in this p-cycle appears with the same positive multiplicity in $(qd)\cdot A$ ), since ${\left ({dA}\right )}_{j\ \bmod\ \frac {N}{pq}}\neq \varnothing $ . We have proven that the elements $d\cdot A$ restricted to $j+\frac {N}{pq}\mathbb {Z}_{N}$ (i.e. the inverse image of $qj+\frac {N}{p}\mathbb {Z}_{N}$ under the multiplication by q map) are supported on a single p-cycle; therefore, this p-cycle must appear with the same multiplicity in $d\cdot A$ as $qj+\frac {N}{p}\mathbb {Z}_{N}$ appears in $(qd)\cdot A$ . Thus, if every ${\left ({dA}\right )}_{j\ \bmod\ \frac {N}{pq}}$ is supported on a p-cycle, we conlcude that $d\cdot A$ is also a union of p-cycles as a multiset, giving $A(\zeta _{N}^{d})=0$ , a contradiction.

This proves the existence of $da,da^{\prime }\in {\left ({dA}\right )}_{j\ \bmod\ \frac {N}{pq}}$ , lying on two different q-cycles, and two different p-cycles as well, for some j. Then ${\left ({dA}\right )}_{j\ \bmod\ \frac {N}{pq}}$ is not supported on a p- or q-cycle, so by Proposition 5.5

$$ \begin{align*}(dA-dA)\cap\frac{N}{pq}\mathbb{Z}_{N}^{\star}\neq\varnothing,\end{align*} $$

or equivalently, there are $a,a^{\prime }\in A$ such that $d(a-a^{\prime })\in \frac {N}{pq}\mathbb {Z}_{N}^{\star }$ , which shows that $\operatorname {\mathrm {ord}}(a-a^{\prime })=pqd$ ; indeed, as $pqd(a-a^{\prime })\equiv 0\ \bmod\ N$ , while $pd(a-a^{\prime })\in \frac {N}{q}\mathbb {Z}_{N}^{\star }$ and $qd(a-a^{\prime })\in \frac {N}{p}\mathbb {Z}_{N}^{\star }$ . This implies that $(A-A)\cap \frac {N}{pqd}\mathbb {Z}_{N}^{\star }\neq \varnothing $ , hence $B(\zeta _{pqd})=0$ for any spectrum B of A by Corollary 3.4, completing the proof.

6 Some special cases

For the rest of this article, we restrict to $N=p^{m}q^{n}$ , where $p,q$ are distinct primes. There are some special cases that yield somewhat easily the Spectral $\Rightarrow $ Tile direction and serve as building blocks in more general cases.

Consider the natural map $\mathbb {Z}[X]\twoheadrightarrow \mathbb {F}_{q}[X]$ , which is just reduction of the coefficients $\ \bmod\ q$ . The image of a polynomial $P(X)\in \mathbb {Z}[X]$ will be denoted simply by $\overline {P}(X)$ . Reducing the coefficients modulo a prime dividing N seems very advantageous when a small power of said prime appears in the prime decomposition of N.

Theorem 6.1. Let p, q be distinct primes and $N=p^{m}q^{n}$ , where m, n are positive integers. Suppose that $A\subseteq \mathbb {Z}_{N}$ is spectral such that $pq\nmid \lvert A \rvert $ . Then A tiles $\mathbb {Z}_{N}$ by translations.

Proof. Without loss of generality, we may assume that $q\nmid \lvert A \rvert $ . It holds $A(\zeta )\neq 0$ when $\zeta ^{q^{n}}=1$ ; otherwise, $A(X)$ would be divided by some cyclotomic polynomial $\Phi _{q^{k}}(X)$ for some $1\leq k\leq n$ , and as a consequence, $q=\Phi _{q^{k}}(1)$ would divide $A(1)=\lvert A \rvert $ , a contradiction. Next, consider the set

$$ \begin{align*}R={\left\{{r\in[1,m]:A(\zeta_{p^{r}}\zeta_{q^{k}})=0,\text{ for some }k, 0\leq k\leq n}\right\}}.\end{align*} $$

Define the following polynomial

(6.1) $$ \begin{align} F(X)=A(X)\prod_{\substack{1\leq r\leq m\\ r\notin R}}\Phi_{p^{r}}(X), \end{align} $$

which has nonnegative integer coefficients. We will show that $F(1)\leq p^{m}$ or, equivalently, $A(1)\leq p^{\lvert R \rvert }$ . To this end, consider the spectrum B of A, which satisfies $\lvert A \rvert =\lvert B \rvert $ and $B-B\subseteq {\left \{{0}\right \}}\cup Z(A)$ by Theorem 3.3(i). Since $A(\zeta )\neq 0$ when $\zeta ^{q^{n}}=1$ , we obtain $(B-B)\cap p^{m}\mathbb {Z}_{N}={\left \{{0}\right \}}$ ; therefore, any two distinct elements of B are not congruent modulo $p^{m}$ (giving a first estimate of $\lvert A \rvert \leq p^{m}$ ). So, we may write for every $b\in B$

$$ \begin{align*}b\equiv b_{0}+b_{1}p+\dotsb+b_{m-1}p^{m-1}\ \bmod\ p^{m},\ 0\leq b_{j}\leq p-1,\ 0\leq j\leq m-1\end{align*} $$

and observe that no two elements of B correspond to the same m-tuple $(b_{0},\dotsc ,b_{m-1})$ . Moreover, no two elements of B can agree on all p-adic digits $b_{r}$ for $m-r\in R$ . If such elements existed, say $b\neq b^{\prime }$ , then $p^{r}\mid \!\mid b-b^{\prime }$ for some $m-r\notin R$ , and since $(A,B)$ is a spectral pair, we should have $A(\zeta _{p^{m-r}}\zeta _{q^{k}})=0$ for some k by Corollary 3.4, contradicting the fact $m-r\notin R$ . This clearly shows that $\lvert A \rvert \leq p^{\lvert R \rvert }$ , and thus $F(1)\leq p^{m}$ .

Next, we will show that $\overline {\Phi }_{p^{r}}(X)\mid \overline {F}(X)$ in $\mathbb {F}_{q}[X]$ for $1\leq r\leq m$ . If $r\notin R$ , this follows immediately from equation (6.1). If $r\in R$ , then by definition $\Phi _{p^{r}q^{k}}(X)\mid A(X)$ for some k, hence $\Phi _{p^{r}q^{k}}(X)\mid F(X)$ , where $p^{r}q^{k}\mid N$ . Using standard properties of cyclotomic polynomials, we get

$$ \begin{align*}\Phi_{p^{r}q^{k}}(X)=\Phi_{pq}(X^{p^{r-1}q^{k-1}})=\frac{\Phi_{p}(X^{p^{r-1}q^{k}})}{\Phi_{p}(X^{p^{r-1}q^{k-1}})}.\end{align*} $$

Reducing coefficients $\ \bmod\ q$ , we obtain

$$ \begin{align*}\frac{\overline{\Phi}_{p}(X^{p^{r-1}})^{q^{k}}}{\overline{\Phi}_{p}(X^{p^{r-1}})^{q^{k-1}}}=\overline{\Phi}_{p}(X^{p^{r-1}})^{q^{k-1}(q-1)}=\overline{\Phi}_{p^{r}}(X)^{q^{k-1}(q-1)}.\end{align*} $$

Therefore,

$$ \begin{align*}\prod_{r=1}^{m}\overline{\Phi}_{p^{r}}(X)=X^{p^{m}-1}+\dotsb+1\mid \overline{F}(X)\end{align*} $$

in $\mathbb {F}_{q}[X]$ , say

$$ \begin{align*}\overline{F}(X)=(X^{p^{m}-1}+\dotsb+1)G(X).\end{align*} $$

Now, we reduce $\ \bmod\ (X^{p^{m}}-1)$ . Since

$$ \begin{align*}X^{\ell}(X^{p^{m}-1}+\dotsb+1)\equiv X^{p^{m}-1}+\dotsb+1\ \bmod\ (X^{p^{m}}-1)\end{align*} $$

for every $\ell $ , we get

(6.2) $$ \begin{align} \overline{F}(X)\equiv G(1)(X^{p^{m}-1}+\dotsb+1)\ \bmod\ (X^{p^{m}}-1), \end{align} $$

where $G(1)\neq 0$ (in $\mathbb {F}_{q}$ ) by assumption. Consider the remainder of the Euclidean division $F(X):X^{p^{m}}-1$ in $\mathbb {Z}[X]$ , say $R(X)$ . It is not hard to show that R has also nonnegative coefficients; indeed, if $F(X)=\sum _{k=0}^{\deg F}f_{k}X^{k}\in \mathbb {Z}_{\geq 0}[X]$ , then

$$ \begin{align*}R(X)=\sum_{k=0}^{p^{m}-1}{\left({\sum_{\ell\equiv k\ \bmod\ (p^{m}-1)}f_{\ell}}\right)}X^{k}\in\mathbb{Z}_{\geq0}[X].\end{align*} $$

All coefficients of $R(X)$ must be congruent to $c\equiv G(1)\ \bmod\ q$ due to equation (6.2). Without loss of generality, we may assume $0<c<q$ ; hence, positivity of the coefficients of R implies

$$ \begin{align*}R(X)=c(X^{p^{m}-1}+\dotsb+1)+qQ(X),\end{align*} $$

where $Q(X)\in \mathbb {Z}_{\geq 0}[X]$ . Therefore,

$$ \begin{align*}F(1)=R(1)=cp^{m}+qQ(1)\geq p^{m},\end{align*} $$

implying $F(1)=p^{m}$ and $Q(X)\equiv 0$ . From this we obtain

$$ \begin{align*}F(X)\equiv X^{p^{m}-1}+\dotsb+1\ \bmod\ (X^{p^{m}}-1)\end{align*} $$

in $\mathbb {Z}[X]$ . Clearly,

$$ \begin{align*}F(X)\sum_{s=0}^{q^{n}-1}X^{p^{m}s}\equiv X^{N-1}+\dotsb+1\ \bmod\ (X^{N}-1),\end{align*} $$

so, for the polynomial $C(X)\in \mathbb {Z}[X]$ with nonnegative coefficients defined by

$$ \begin{align*}C(X)={\left({\sum_{s=0}^{q^{n}-1}X^{p^{m}s}}\right)}\prod_{\substack{1\leq r\leq m\\ r\notin R}}\Phi_{p^{r}}(X),\end{align*} $$

we have

$$ \begin{align*}A(X)C(X)\equiv X^{N-1}+\dotsb+1\ \bmod\ (X^{N}-1),\end{align*} $$

implying that $C(X)$ is the mask polynomial of a set C which is the tiling complement of A. This completes the proof.

Theorem 6.1 proves the Spectral $\Rightarrow $ Tiling direction for sets A whose cardinality is prime to either p or q. On the other extreme, the same holds when the cardinality is divisible by the maximal power of either p or q, dividing N.

Proposition 6.2. Let $N=p^{m}q^{n}$ and $A\subseteq \mathbb {Z}_{N}$ spectral such that $p^{m}\mid \lvert A \rvert $ or $q^{n}\mid \lvert A \rvert $ . Then A tiles $\mathbb {Z}_{N}$ .

Proof. Without loss of generality, $p^{m}\mid \lvert A \rvert $ , and let B be a spectrum of A. Suppose that

$$ \begin{align*}S_{B}^{N}={\left\{{p^{m_{1}},\dotsc,p^{m_{\ell}},q^{n_{1}},\dotsc,q^{n_{k}}}\right\}},\end{align*} $$

where $1\leq m_{1}<\dotsb <m_{\ell }\leq m$ and $1\leq n_{1}<\dotsb <n_{k}\leq n$ . Since

$$ \begin{align*}\Phi_{q^{n_{1}}}(X)\dotsm\Phi_{q^{n_{k}}}(X)\mid B(X),\end{align*} $$

we obtain

$$ \begin{align*}p^{m} q^{k}\mid \lvert B \rvert=\lvert A \rvert\end{align*} $$

by putting $X=1$ , and using the hypothesis. For every j, consider $A_{j\ \bmod\ p^{m}}$ . Since $A_{j\ \bmod\ p^{m}}-A_{j\ \bmod\ p^{m}}\subseteq p^{m}\mathbb {Z}_{N}$ , we must have

(6.3) $$ \begin{align} A_{j\ \bmod\ p^{m}}-A_{j\ \bmod\ p^{m}}\subseteq{\left\{{0}\right\}}\cup p^{m}q^{n-n_{1}}\mathbb{Z}_{N}^{\star}\cup\dotsb\cup p^{m}q^{n-n_{k}}\mathbb{Z}_{N}^{\star} \end{align} $$

by Theorem 3.3(i). As usual, we consider the (finite) q-adic expansion of each $a\in \mathbb {Z}_{N}$ as

$$ \begin{align*}a\equiv a_{0}+a_{1}q+a_{2}q^{2}+\dotsb+a_{n-1}q^{n-1}\ \bmod\ q^{n}, \;\;\;\; 0\leq a_{i}\leq q-1, 0\leq i\leq n-1.\end{align*} $$

Suppose that $\lvert A_{j\ \bmod\ p^{m}} \rvert>q^{k}$ for some j. This would imply the existence of $a,a^{\prime }\in A_{j\ \bmod\ p^{m}}$ that would have the same q-adic digits at positions $n-n_{1},\dotsc ,n-n_{k}$ ; hence, $a-a^{\prime }$ would not belong to the above union, contradiction. Thus, $\lvert A_{j\ \bmod\ p^{m}} \rvert \leq q^{k}$ for all j, and in light of $p^{m}q^{k}\mid \lvert A \rvert $ , we must have

$$ \begin{align*}\lvert A_{j\ \bmod\ p^{m}} \rvert=q^{k},\ \forall j.\end{align*} $$

This further implies $A(\zeta _{p^{\ell }})=0$ , $1\leq \ell \leq m$ . Using the same argument as above, where we reverse the roles of A and B, we also obtain $B(\zeta _{p^{\ell }})=0$ , for $1\leq \ell \leq m$ , whence

$$ \begin{align*}\lvert B_{j\ \bmod\ p^{m}} \rvert=q^{k},\ \forall j.\end{align*} $$

Next, consider

$$ \begin{align*}S_{A}^{N}={\left\{{p,p^{2},\dotsc,p^{m},q^{s_{1}},\dotsc,q^{s_{t}}}\right\}},\end{align*} $$

where $1\leq s_{1}<\dotsb <s_{t}\leq n$ so that

$$ \begin{align*}\Phi_{q^{s_{1}}}(X)\dotsm\Phi_{q^{s_{t}}}(X)\mid A(X),\end{align*} $$

and putting $X=1$ , we get $q^{t}\mid \lvert A \rvert $ , which yields $t\leq k$ . We actually have $t=k$ since

(6.4) $$ \begin{align} B_{j\ \bmod\ p^{m}}-B_{j\ \bmod\ p^{m}}={\left\{{0}\right\}}\cup p^{m}q^{n-s_{1}}\mathbb{Z}_{N}^{\star}\cup\dotsb\cup p^{m}q^{n-s_{t}}\mathbb{Z}_{N}^{\star}, \end{align} $$

for every j, and $\lvert B_{j\ \bmod\ p^{m}} \rvert =q^{k}$ . If $t<k$ , then there would exist $b,b^{\prime }\in B_{j\ \bmod\ p^{m}}$ , $b\neq b^{\prime }$ whose q-adic expansions $\ \bmod\ q^{n}$ agree on all q-adic digits corresponding to $q^{n-s_{i}}$ , $1\leq i\leq t$ . But then

$$ \begin{align*}b-b^{\prime}\notin {\left\{{0}\right\}}\cup p^{m}q^{n-s_{1}}\mathbb{Z}_{N}^{\star}\cup\dotsb\cup p^{m}q^{n-s_{t}}\mathbb{Z}_{N}^{\star},\end{align*} $$

contradiction. Thus, $t=k$ and in particular, A satisfies (T1).

Next, consider the polynomial

$$ \begin{align*}\Lambda(X)=\prod_{i=1}^{k}\Phi_{q^{n_{i}}}(X^{p^{m}}).\end{align*} $$

As the coefficients of $\Lambda (X)$ are $0$ or $1$ , it is the mask polynomial of a set $\Lambda \subseteq \mathbb {Z}_{N}$ with cardinality $\lvert \Lambda \rvert =\Lambda (1)=q^{k}$ . By equation (6.3), $\Lambda $ is then the common spectrum of the sets $A_{j\ \bmod\ p^{m}}$ . It holds

$$ \begin{align*}\bigcup_{i=1}^{k} p^{m}q^{n_{i}-1}\mathbb{Z}_{N}^{\star}\subseteq \Lambda-\Lambda \subseteq{\left\{{0}\right\}}\cup Z(A_{j\ \bmod\ p^{m}})\end{align*} $$

for every j by Theorem 3.3(i); therefore,

$$ \begin{align*}A_{j\ \bmod\ p^{m}}(\zeta_{q^{n-n_{i}+1}})=0,\ 1\leq i\leq k,\ \forall j.\end{align*} $$

Thus, $A(\zeta _{q^{n-n_{i}+1}})=0$ , $1\leq i\leq k$ , proving eventually that $n_{i}+s_{i}=n+1$ , and

$$ \begin{align*}S_{A}^{N}={\left\{{p,p^{2},\dotsc,p^{m},q^{n-n_{1}+1},\dotsc,q^{n-n_{k}+1}}\right\}}.\end{align*} $$

Next, we fix j and consider the polynomial $F(X)$ satisfying

$$ \begin{align*}A_{j\ \bmod\ p^{m}}(X)\equiv X^{j} F(X^{p^{m}})\ \bmod\ (X^{N}-1).\end{align*} $$

Since $\Phi _{q^{n-n_{i}+1}}(X)\mid F(X^{p^{m}})$ for $1\leq i\leq k$ and $p^{m}$ is prime to $q^{n-n_{i}+1}$ , we also have $\Phi _{q^{n-n_{i}+1}}(X)\mid F(X)$ . Therefore, for $1\leq \ell \leq m$ , we have

$$ \begin{align*}A_{j\ \bmod\ p^{m}}(\zeta_{p^{\ell}q^{n-n_{i}+1}})=\zeta_{p^{\ell}q^{n-n_{i}+1}}^{j}F(\zeta_{p^{\ell}q^{n-n_{i}+1}}^{p^{m}})=\zeta_{p^{\ell}q^{n-n_{i}+1}}^{j}F(\zeta_{q^{n-n_{i}+1}}^{p^{m-\ell}})=0,\end{align*} $$

proving

$$ \begin{align*}A(\zeta_{p^{\ell}q^{n-n_{i}+1}})=0,\ 1\leq i\leq k,\ 1\leq \ell\leq m;\end{align*} $$

thus, A satisfies (T2) as well, hence tiles $\mathbb {Z}_{N}$ by virtue of Theorem 3.5(I), as desired.

The techniques developed so far cover the result proven [23].

Corollary 6.3. Let $N=p^{n}q$ . Then $A\subseteq \mathbb {Z}_{N}$ is spectral if and only if it is a tile.

Proof. If A tiles, then it is spectral by Theorem 3.6. Suppose that A is spectral. If $q\nmid \lvert A \rvert $ , then A tiles by Theorem 6.1; if $q\mid \lvert A \rvert $ , then A tiles by Proposition 6.2.

7 Sketch of the proof of Theorem 1.4

Before proceeding to the most technical part of the proof of Theorem 1.4, we will describe the main ideas. First of all, the proof is inductive in nature. So far, there are some positive results involving products of two prime powers (for example, Corollary 6.3), so we may work in a group $\mathbb {Z}_{N}$ with $N=p^{m}q^{n}$ such that Fuglede’s conjecture holds in all proper subgroups of $\mathbb {Z}_{N}$ . In other words, it holds in all groups of the form $\mathbb {Z}_{M}$ with $M\mid N$ , $M<N$ .

If $(A,B)$ is a spectral pair in such a group, we may easily make some reductions for both A and B. If either A or B is a subset of a coset of a proper subgroup, we reduce to a spectral pair in a subgroup of $\mathbb {Z}_{N}$ . Hence, we obtain the tiling property in the smaller group, which in turn implies that A tiles $\mathbb {Z}_{N}$ (Proposition 8.2). Therefore, we reduce to the case where A and every spectrum B are primitive. Primitivity implies that both difference sets $A-A$ and $B-B$ intersect $\mathbb {Z}_{N}^{\star }$ by Lemma 5.4. Then Theorem 3.3(i) yields that $\zeta _{N}$ is a root of both $A(X)$ and $B(X)$ (Corollary 8.3). Hence, each of them is a disjoint union of p- and q-cycles by Theorem 5.2. We obtain thus a first strong information about the structure of both A and B, which in turn shows that $A-A$ and $B-B$ intersect other divisor classes, which provide more roots for $A(X)$ and $B(X)$ , hence more information about A and B, and so on.

Further reductions are possible. If A is a union only of p-cycles (or only of q-cycles), then we can again reduce the problem to a smaller subgroup where Fuglede’s conjecture holds, which yields that A tiles $\mathbb {Z}_{N}$ . We can thus reduce to the case where A is not a union only of p-cycles or only of q-cycles (Proposition 8.4). The same fact applies for every spectrum B of A; however, it is more difficult to prove (Corollary 10.8).

Next, we consider subsets of a spectral set $A\subseteq \mathbb {Z}_{N}$ , of the form $A_{j\ \bmod\ d}=A\cap (j+d\mathbb {Z}_{N})$ , where $d\mid N$ . If, say, $pd\mid N$ , we have the obvious partition of $A_{j\ \bmod\ d}$

$$ \begin{align*}A_{j\ \bmod\ d}=\bigsqcup_{k=0}^{p-1}A_{j+kd\ \bmod\ pd},\end{align*} $$

and a same partition holds when $qd\mid N$ . If all sets in the above disjoint union have equal cardinalities, then we say that $A_{j\ \bmod\ d}$ is equidistributed $\ \bmod\ pd$ , and on the other extreme, if only one of the above sets is nonempty, we say that $A_{j\ \bmod\ d}$ is absorbed $\ \bmod\ pd$ . One or the other property holds when a certain combination of roots of $A(X)$ and $B(X)$ appears (Lemma 9.2). Taking into account how $A_{j\ \bmod\ d}$ distributes $\ \bmod\ pd$ or $\ \bmod\ qd$ and then taking the difference between sets in the union above, we obtain information not only about the roots of $B(X)$ (using Theorem 3.3(i)) but also of $A(X)$ . This is the content of Section 9.

If there is some $d=p^{k}$ (respectively, $d=q^{\ell }$ ) such that either $A_{j\ \bmod\ d}$ or $B_{j\ \bmod\ d}$ is absorbed $\ \bmod\ pd$ (respectively, $\ \bmod\ qd$ ) for every j, then we can extend both sets so that we obtain a new spectral pair $(A^{\prime },B^{\prime })$ (Lemma 9.3, Corollary 9.4, Lemma 9.6). Both $A^{\prime }$ and $B^{\prime }$ are absorption-free, and $A^{\prime }=A\oplus S$ , for some $S\subseteq \mathbb {Z}_{N}$ for which $0\in S$ . In particular, if $A^{\prime }$ tiles, then so does A. With this argument, we may further reduce the problem to those spectral sets A that are absorption-free as well. This certainly holds true when $A\in \mathscr {F}(N)$ has maximal size; we denote the set of all such spectral sets by $\mathscr {F}_{\max }(N)$ .

The failure of Fuglede’s conjecture in $\mathbb {Z}_{N}$ , especially when it holds for all proper groups $\mathbb {Z}_{N}$ , imposes some symmetry on the roots of the mask polynomials of the spectral pair $(A,B)$ when $A\in \mathscr {F}(N)$ (Lemma 10.3 and Proposition 10.4). This result, along with subsequent ones, is obtained by checking how sets of the form $B_{j\ \bmod\ d}$ or $A_{j\ \bmod\ d}$ distribute $\ \bmod\ pd$ and $\ \bmod\ qd$ (i.e., especially when we have absorption or equidistribution) when d ranges through the powers $p, p^{2},\dots $ or $q, q^{2}\dotsc $ . Arguments of this type are used in the proofs of Lemma 10.5 and the more technical Lemmata 11.4 and 11.8 (in Lemma 11.4 we also examine the distribution of sets of the form $A_{j\ \bmod\ p^{m-r-1}q^{n-1}}$ ).

Lemma 10.5 is the first indication that, if $A\in \mathscr {F}_{\max }(N)$ , then (T1) fails for every spectrum B so that $B\in \mathscr {F}_{\max }(N)$ (Corollary 10.7). We recall that every root of the form $\zeta _{p^{x}}$ contributes a factor of p in the cardinality of B; Lemma 10.5 states also that we get a contribution of a factor of p even when $B(\zeta _{p^{x}})\neq 0=B(\zeta _{p^{x}q})$ . Lemma 11.4 estimates the number of such x, and then Lemma 11.8 estimates the number of x for which the symmetry of root patterns fails, called herein the root deficit. These estimates eventually lead to the desired result when one of the exponents m or n is small enough or when $p^{m-2}<q^{4}$ .

8 Primitive subsets and an inductive approach

The existence of a spectral subset $A\subseteq \mathbb {Z}_{N}$ that does not tile imposes a very rigid structure on A that is impossible to appear in a subset of $\mathbb {Z}_{N}$ under certain conditions. This is the main argument for proving Fuglede’s conjecture in certain cyclic groups of order $N=p^{m}q^{n}$ . We will usually consider groups such that Fuglede’s conjecture holds in all proper subgroups.

Definition 8.1. For two distinct primes p, q, define the following set:

$$ \begin{align*}\mathscr{S}_{p,q}={\left\{{N=p^{m}q^{n}:\mathbb{Z}_{N}\text{ has spectral subsets that do not tile}}\right\}}.\end{align*} $$

We distinguish also the minimal elements in terms of division by defining the following subset of $\mathscr {S}_{p,q}$ :

$$ \begin{align*}\mathscr{S}^{\prime}_{p,q}={\left\{{N\in\mathscr{S}_{p,q}:\forall M\mid N\text{ satisfying }M\neq N, \text{ it holds } M\notin \mathscr{S}_{p,q}}\right\}}\end{align*} $$

or, equivalently, $N\in \mathscr {S}^{\prime }_{p,q}$ if Fuglede’s conjecture is not true in $\mathbb {Z}_{N}$ but holds in every subgroup of $\mathbb {Z}_{N}$ . Finally, for each $N\in \mathscr {S}_{p,q}$ , we define

$$ \begin{align*}\mathscr{F}(N)={\left\{{A\subseteq\mathbb{Z}_{N}:A\text{ is spectral but does not tile}}\right\}}.\end{align*} $$

Remark. Fuglede’s conjecture holds in $\mathbb {Z}_{p^{m}q^{n}}$ for every $m,n\geq 1$ if and only if $\mathscr {S}_{p,q}=\varnothing $ . Throughout this paper, we will usually show that Fuglede’s conjecture holds for a specific $\mathbb {Z}_{N}$ (or a family of cyclic groups) by showing that N cannot belong to $\mathscr {S}_{p,q}$ or, equivalently, that $\mathscr {F}(N)=\varnothing $ . We will do so by proving some properties of the sets belonging to $\mathscr {F}(N)$ , which will be impossible to hold under some conditions, for example, if one of the exponents $m,n$ is relatively small.

Now, we start proving properties for the sets defined above. We recall that a subset of $\mathbb {Z}_{N}$ is called primitive if it is not contained in a coset of a proper subgroup of $\mathbb {Z}_{N}$ .

Proposition 8.2. Let $A\subseteq \mathbb {Z}_{N}$ be a spectral set, $N\in \mathscr {S}^{\prime }_{p,q}$ , such that A is not primitive or possesses a nonprimitive spectrum, B. Then A satisfies (T1) and (T2) or, equivalently, $A\notin \mathscr {F}(N)$ .

Proof. Suppose that A has a spectrum B that is not primitive. Then a translate of B must be contained in a maximal subgroup of $\mathbb {Z}_{N}$ , i.e., either $p\mathbb {Z}_{N}$ or $q\mathbb {Z}_{N}$ . This translate is also a spectrum of A, so without loss of generality, we may assume $B\subseteq p\mathbb {Z}_{N}$ . This shows the existence of $B^{\prime }\subseteq \mathbb {Z}_{N}$ with $\lvert B \rvert =\lvert B^{\prime } \rvert $ and $B=pB^{\prime }$ . The matrix

$$ \begin{align*}\tfrac{1}{\sqrt{\lvert A \rvert}}{\left({\zeta_{N}^{ab}}\right)}_{a\in A, b\in B}=\tfrac{1}{\sqrt{\lvert A \rvert}}{\left({\zeta_{N/p}^{ab^{\prime}}}\right)}_{a\in A, b^{\prime}\in B^{\prime}}\end{align*} $$

is unitary by definition; hence, no two elements of A leave the same residue $\ \bmod\ N/p$ (as well as of $B^{\prime }$ ). Hence, $(A,B^{\prime })$ can be considered as a spectral in $\mathbb {Z}_{N/p}$ , so $A(X)\ \bmod\ (X^{N/p}-1)$ satisfies (T1) and (T2) by definition of $\mathscr {S}^{\prime }_{p,q}$ . This in particular shows that $A(\zeta _{p^{m}})\neq 0$ . Otherwise, (T1) would fail $\ \bmod\ N/p$ . Therefore, (T1) and (T2) are satisfied by $A(X)\ \bmod\ (X^{N}-1)$ as well.

Next, suppose that A is not primitive so that $A\subseteq p\mathbb {Z}_{N}$ without loss of generality. As before, $(A^{\prime },B)$ would be a spectral pair in $\mathbb {Z}_{N/p}$ , where $A=pA^{\prime }$ , so $A^{\prime }(X)$ satisfies (T1) and (T2) by definition of $\mathscr {S}^{\prime }_{p,q}$ . We have $A(X)\equiv A^{\prime }(X^{p})\ \bmod\ (X^{N}-1)$ , hence $A(\zeta _{p})\neq 0$ . The following show that A also satisfies (T1) and (T2):

$$ \begin{align*}A^{\prime}(\zeta_{p^{k}q^{\ell}})=0\Longrightarrow A(\zeta_{p^{k+1}q^{\ell}})=0,\end{align*} $$

and

$$ \begin{align*}A^{\prime}(\zeta_{q^{k}})=0\Longrightarrow A(\zeta_{pq^{k}})=A(\zeta_{q^{k}})=0.\end{align*} $$

For the latter, consider t such that $pt\equiv 1\ \bmod\ q^{k}$ . Then

$$ \begin{align*}A(\zeta_{q^{k}}^{t})=A^{\prime}(\zeta_{q^{k}}^{pt})=A^{\prime}(\zeta_{q^{k}})=0,\end{align*} $$

and by a Galois action, we get $A(\zeta _{q^{k}})=0$ as well. This completes the proof.

Corollary 8.3. If $A\in \mathscr {F}(N)$ , $N\in \mathscr {S}_{p,q}^{\prime }$ , then

$$ \begin{align*}A(\zeta_{N})=B(\zeta_{N})=0\end{align*} $$

for any spectrum $B\subseteq \mathbb {Z}_{N}$ of A.

Proof. By Proposition 8.2, A and every spectrum B are primitive. By Lemma 5.4, we get $(A-A)\cap \mathbb {Z}_{N}^{\star }\neq \varnothing \neq (B-B)\cap \mathbb {Z}_{N}^{\star }$ , so by Theorem 3.3(i), we obtain $A(\zeta _{N})=B(\zeta _{N})=0$ .

Consider $A\in \mathscr {F}(N)$ , $N\in \mathscr {S}_{p,q}^{\prime }$ , and B a spectrum of A. By Corollary 8.3 and Theorem 5.2, we may write

(8.1) $$ \begin{align} A(X)\equiv P(X)\Phi_{p}(X^{N/p})+Q(X)\Phi_{q}(X^{N/q})\ \bmod\ (X^{N}-1), \end{align} $$

for $P(X),Q(X)\in \mathbb {Z}_{\geq 0}[X]$ , and

(8.2) $$ \begin{align} B(X)\equiv R(X)\Phi_{p}(X^{N/p})+S(X)\Phi_{q}(X^{N/q})\ \bmod\ (X^{N}-1) \end{align} $$

for $R(X),S(X)\in \mathbb {Z}_{\geq 0}[X]/(X^{N}-1)$ . Next, we will show that Fuglede’s conjecture is satisfied if P or Q is identically zero.

Proposition 8.4. Suppose that $A\in \mathscr {F}(N)$ , $N\in \mathscr {S}_{p,q}^{\prime }$ . Then A cannot be expressed as a union of p- or q-cycles exclusively (i.e., $Q\equiv 0$ or $P\equiv 0$ , respectively).

Proof. Let B be a spectrum of A, and suppose that A is a union of p- or q-cycles exclusively. Without loss of generality, we may assume $Q\equiv 0$ so that

(8.3) $$ \begin{align} A(X)\equiv P(X)\Phi_{p}(X^{N/p})\ \bmod\ (X^{N}-1). \end{align} $$

For every $a\in A$ , we have $a+\frac {N}{p}\mathbb {Z}_{N}\subseteq A$ , hence $(A-A)\cap \frac {N}{p}\mathbb {Z}_{N}^{\star }\neq \varnothing $ , implying $B(\zeta _{p})=0$ and

$$ \begin{align*}\lvert B_{j\ \bmod\ p} \rvert=\frac{1}{p}\lvert B \rvert,\ \forall j.\end{align*} $$

Since $P(X)\in \mathbb {Z}_{\geq 0}[X]$ , the coefficients must be either $0$ or $1$ ; therefore, $P(X)$ is the mask polynomial of a set $P\subseteq \mathbb {Z}_{N}$ . Furthermore, equation (8.3) shows that any element of P is unique $\ \bmod\ N/p$ , so we may consider this as a subset in $\mathbb {Z}_{N/p}$ .

Next, we will show that each $B_{j\ \bmod\ p}$ is a spectrum for P. Since

$$ \begin{align*}B_{j\ \bmod\ p}-B_{j\ \bmod\ p}\subseteq p\mathbb{Z}_{N}\cap (Z(A)\cup{\left\{{0}\right\}}),\end{align*} $$

by Theorem 3.3(i), it suffices to show that $A(\zeta _{N}^{d})=0$ implies $P(\zeta _{N}^{d})=0$ whenever $p\mid d$ and $d\mid N$ , i.e., $A(X)$ and $P(X)$ have the same roots when we restrict to the $\frac {N}{p}$ -roots of unity. But this is true since (8.3) implies

$$ \begin{align*}A(X)\equiv pP(X)\ \bmod\ (X^{N/p}-1),\end{align*} $$

therefore, $A(\zeta _{N/p}^{d})=pP(\zeta _{N/p}^{d})$ for all d. We observe that each spectrum $-j+B_{j\ \bmod\ p}$ is a subset of the subgroup of $\mathbb {Z}_{N}$ of order $N/p$ , which shows that $P\subseteq \mathbb {Z}_{N/p}$ is spectral since $\lvert P \rvert =\lvert B_{j\ \bmod\ p} \rvert $ for all j.

By definition of $\mathscr {S}_{p,q}^{\prime }$ , P satisfies (T1) and (T2). We remind that $A(X)$ and $P(X)$ have precisely the same roots when we restrict to the $\frac {N}{p}$ -roots of unity. In addition, $A(X)$ vanishes for all other Nth roots of unity as $\Phi _{p}(X^{N/p})\mid A(X)$ , clearly showing that $A(X)$ satisfies (T1) and (T2) as well.

One might expect that a similar proof applies when B is a union of p- or q-cycles exclusively. However, we didn’t manage to find such a straightforward proof but rather a complicated one. The crucial ideas needed for this are examined in the next sections.

9 The absorption-equidistribution property

Definition 9.1. Let $A\subseteq \mathbb {Z}_{N}$ , and let $pd\mid N$ , where p is a prime. We call the set $A_{i\ \bmod\ d}$ absorbed $\ \bmod\ pd$ if there is k with $0\leq k\leq p-1$ such that $A_{i\ \bmod\ d}=A_{i+kd\ \bmod\ pd}$ . We call it equidistributed $\ \bmod\ pd$ if $\lvert A_{i+kd\ \bmod\ pd} \rvert =\frac {1}{p}\lvert A_{i\ \bmod\ d} \rvert $ for every k with $0\leq k\leq p-1$ .

A fundamental observation coming from the structure of the vanishing sums of roots of unity, i.e., Theorem 5.2, is the fact that $A(\zeta _{p^{k+1}})=0$ implies that each $A_{i\ \bmod\ p^{k}}$ is equidistributed $\ \bmod\ p^{k+1}$ .

Lemma 9.2. Let $(A,B)$ be a spectral pair in $\mathbb {Z}_{N}$ , $N=p^{m}q^{n}$ and d a divisor of $\frac {N}{pq}$ such that

$$ \begin{align*}A(\zeta_{N}^{d})B(\zeta_{pd})\neq0=B(\zeta_{pqd}).\end{align*} $$

Then each subset $B_{i\ \bmod\ d}$ is either absorbed or equidistributed $\ \bmod\ pd$ . Absorption occurs for at least one i.

Proof. By Theorem 5.2, the multiset $\frac {N}{pqd}\cdot B$ is a disjoint union of p- and q-cycles. Each such cycle is a subset of a unique $pq$ -cycle (i.e., a coset of the subgroup $\frac {N}{pq}\mathbb {Z}_{N}$ ) as $j+\frac {N}{p}\mathbb {Z}_{N}\subseteq j+\frac {N}{pq}\mathbb {Z}_{N}$ , for example. Therefore, the same conclusion holds for the elements of $\frac {N}{pqd}\cdot B$ (counting multiplicities) in an arbitrary $pq$ -cycle. If $\frac {N}{pqd}\cdot B\cap (j+\frac {N}{pq}\mathbb {Z}_{N})$ is not supported on a single p- or q-cycle, then there are $b,b^{\prime }\in B$ such that $\frac {N}{pqd}(b-b^{\prime })\in \frac {N}{pq}\mathbb {Z}_{N}^{\star }$ by virtue of Proposition 5.5. This yields $b-b^{\prime }\in d\mathbb {Z}_{N}^{\star }$ , contradicting the fact that $A(\zeta _{N}^{d})\neq 0$ , using Theorem 3.3(i). Now, every element of $\frac {N}{pqd}\cdot B_{i\ \bmod\ d}$ belongs to the $pq$ -cycle $\frac {iN}{pqd}+\frac {N}{pq}\mathbb {Z}_{N}$ ; therefore, it must also be a disjoint union of p- and q-cycles. In our case, it must be a single p- or q-cycle with a certain multiplicity. If $\frac {N}{pqd}\cdot B_{i\ \bmod\ d}$ is a p-cycle with a multiplicity, then this p-cycle must be

$$ \begin{align*}\frac{iN}{pqd}+k\frac{N}{q}+\frac{N}{p}\mathbb{Z}_{N}=\frac{N}{pqd} B_{i\ \bmod\ d}\end{align*} $$

for some k, which clearly shows that $\lvert B_{i+kpd+jqd\ \bmod\ pqd} \rvert $ is constant in j, and

$$ \begin{align*}B_{i+k^{\prime}pd+jqd\ \bmod\ pqd}=\varnothing,\end{align*} $$

for $k^{\prime }\not \equiv k\ \bmod\ q$ . This yields the absorption

$$ \begin{align*}B_{i+jqd\ \bmod\ pd}=B_{i+kpd+jqd\ \bmod\ pqd}\end{align*} $$

for all j, which shows that $B_{i\ \bmod\ d}$ is equidistributed $\ \bmod\ pd$ . If on the other hand, $\frac {N}{pqd}\cdot B_{i\ \bmod\ d}$ is a q-cycle with a multiplicity, then this q-cycle must be

$$ \begin{align*}\frac{iN}{pqd}+j\frac{N}{p}+\frac{N}{q}\mathbb{Z}_{N}=\frac{N}{pqd} B_{i\ \bmod\ d}\end{align*} $$

for some j, which shows that $\lvert B_{i+jqd+kpd\ \bmod\ pqd} \rvert $ is constant in k, and

$$ \begin{align*}B_{i+j^{\prime}qd+kpd\ \bmod\ pqd}=\varnothing,\end{align*} $$

for $j^{\prime }\not \equiv j\ \bmod\ p$ . This yields

$$ \begin{align*}\lvert B_{i\ \bmod\ d} \rvert=\lvert B_{i+jqd\ \bmod\ pd} \rvert=p\lvert B_{i+jqd+kpd\ \bmod\ pqd} \rvert\end{align*} $$

for this value of j and every k, which shows that $B_{i\ \bmod\ d}$ is absorbed $\ \bmod\ pd$ . Absorption $\ \bmod\ pd$ must occur for at least one i. Otherwise, we would have $B(\zeta _{pd})=0$ , contradiction.

Lemma 9.3. Let $(A,B)$ be a spectral pair in $\mathbb {Z}_{N}$ , $N=p^{m}q^{n}$ such that $B_{i\ \bmod\ p^{k}}$ is absorbed $\ \bmod\ p^{k+1}$ for every i, where $0\leq k<m$ . Then

$$ \begin{align*}\overline{A}(X)\equiv A(X)\Phi_{p^{m-k}}(X^{q^{n}})\ \bmod\ (X^{N}-1)\end{align*} $$

is the mask polynomial of a spectral set whose spectrum has the following mask polynomial:

$$ \begin{align*}\overline{B}(X)\equiv B(X)\Phi_{p^{k+1}}(X^{q^{n}})\ \bmod\ (X^{N}-1).\end{align*} $$

Moreover, $\overline {B}_{i\ \bmod\ p^{k}}$ is equidistributed $\ \bmod\ p^{k+1}$ for every i.

Proof. Denote by T the set whose mask polynomial is $\Phi _{p^{m-k}}(X^{q^{n}})$ so that

$$ \begin{align*}T={\left\{{0,p^{m-k-1}q^{n},2p^{m-k-1}q^{n},\dotsc,(p-1)p^{m-k-1}q^{n}}\right\}}.\end{align*} $$

Since $B_{i\ \bmod\ p^{k}}$ is absorbed $\ \bmod\ p^{k+1}$ for every i, we have $B(\zeta _{p^{k+1}})\neq 0$ . Therefore, by Theorem 3.3(i), we get

$$ \begin{align*}(A-A)\cap\frac{N}{p^{k+1}}\mathbb{Z}_{N}^{\star}=\varnothing.\end{align*} $$

Moreover,

$$ \begin{align*}T-T={\left\{{\ell p^{m-k-1}q^{n}:\lvert \ell \rvert<p}\right\}}\subseteq {\left\{{0}\right\}}\cup\frac{N}{p^{k+1}}\mathbb{Z}_{N}^{\star};\end{align*} $$

therefore, $(A-A)\cap (T-T)={\left \{{0}\right \}}$ . Hence, every element in $A+T$ has a unique representation as $a+t$ with $a\in A$ , $t\in T$ (proof is similar to that of Theorem 3.3(ii)). This shows that $\overline {A}(X)$ is a mask polynomial of the set $\overline {A}=A\oplus T$ . Furthermore, since each $B_{i\ \bmod\ p^{k}}$ is absorbed $\ \bmod\ p^{k+1}$ , if $p^{k}\mid b-b^{\prime }$ for some $b,b^{\prime }\in B$ , then $p^{k+1}\mid b-b^{\prime }$ (definition of absorption). In other words,

(9.1) $$ \begin{align} (B-B)\cap (p^{k}\mathbb{Z}_{N}^{\star}\cup p^{k}q\mathbb{Z}_{N}^{\star}\cup\dotsb\cup p^{k}q^{n}\mathbb{Z}_{N}^{\star})=\varnothing. \end{align} $$

The set

(9.2) $$ \begin{align} S={\left\{{0,p^{k}q^{n},2p^{k}q^{n},\dotsc,(p-1)p^{k}q^{n}}\right\}} \end{align} $$

has mask polynomial $\Phi _{p^{k+1}}(X^{q^{n}})$ and satisfies

(9.3) $$ \begin{align} S-S={\left\{{\ell p^{k}q^{n}:\lvert \ell \rvert<p}\right\}}\subseteq {\left\{{0}\right\}}\cup p^{k}q^{n}\mathbb{Z}_{N}^{\star}; \end{align} $$

therefore, $(B-B)\cap (S-S)={\left \{{0}\right \}}$ and, similarly as before, we deduce that $\overline {B}(X)$ is the mask polynomial of the set $\overline {B}=B\oplus S$ . We observe that $\lvert \overline {A} \rvert =\lvert \overline {B} \rvert $ .

Next, we will show that $\overline {A}(\zeta _{\operatorname {\mathrm {ord}}(\beta -\beta ^{\prime })})=0$ for every $\beta ,\beta ^{\prime }\in \overline {B}$ , $\beta \neq \beta ^{\prime }$ . Every $\beta \in \overline {B}$ has a unique representation as $b+s$ , where $b\in B$ and $s\in S$ ; we write also $\beta ^{\prime }=b^{\prime }+s^{\prime }$ , $b^{\prime }\in B$ , $s^{\prime }\in S$ . By equation (9.3), $s-s^{\prime }\in {\left \{{0}\right \}}\cup p^{k}q^{n}\mathbb {Z}_{N}^{\star }$ , while $v_{p}(b-b^{\prime })\neq k$ by (9.1). If $s=s^{\prime }$ , then $\beta -\beta ^{\prime }=b-b^{\prime }$ and

$$ \begin{align*}\overline{A}(\zeta_{\operatorname{\mathrm{ord}}(b-b^{\prime})})=A(\zeta_{\operatorname{\mathrm{ord}}(b-b^{\prime})})\Phi_{p^{m-k}}(\zeta_{\operatorname{\mathrm{ord}}(b-b^{\prime})}^{q^{n}})=0\end{align*} $$

by Corollary 3.4 since B is a spectrum of A. So, assume $s\neq s^{\prime }$ so that $s-s^{\prime }\in p^{k}q^{n}\mathbb {Z}_{N}^{\star }$ . Since $v_{p}(b-b^{\prime })\neq k$ , we will either have $p^{k+1}\mid b-b^{\prime }$ or $p^{k}\nmid b-b^{\prime }$ . In the former case, $v_{p}(\beta -\beta ^{\prime })=k$ , yielding $\operatorname {\mathrm {ord}}(\beta -\beta ^{\prime })=p^{m-k}q^{r}$ , where $0\leq r\leq n$ . Hence,

$$ \begin{align*}\overline{A}(\zeta_{\operatorname{\mathrm{ord}}(\beta-\beta^{\prime})})=A(\zeta_{\operatorname{\mathrm{ord}}(\beta-\beta^{\prime})})\Phi_{p^{m-k}}(\zeta_{p^{m-k}q^{r}}^{q^{n}})=A(\zeta_{\operatorname{\mathrm{ord}}(\beta-\beta^{\prime})})\Phi_{p^{m-k}}(\zeta_{p^{m-k}}^{q^{n-r}})=0.\end{align*} $$

In the latter case, $\operatorname {\mathrm {ord}}(s-s^{\prime })=p^{m-k}\mid \operatorname {\mathrm {ord}}(b-b^{\prime })$ ; therefore, $\operatorname {\mathrm {ord}}(b-b^{\prime })=\operatorname {\mathrm {ord}}(b-b^{\prime }+s-s^{\prime })=\operatorname {\mathrm {ord}}(\beta -\beta ^{\prime })$ . Hence, again, Corollary 3.4 gives $\overline {A}(\zeta _{\operatorname {\mathrm {ord}}(\beta -\beta ^{\prime })})=0$ . One more application of Corollary 3.4 gives the desired conclusion as $\overline {A}(\zeta _{\operatorname {\mathrm {ord}}(\beta -\beta ^{\prime })})=0$ for every $\beta ,\beta ^{\prime }\in \overline {B}$ , $\beta \neq \beta ^{\prime }$ . The second part of the lemma follows from the fact that $\overline {B}(\zeta _{p^{k+1}})=0$ .

Corollary 9.4. Let $(A,B)$ be a spectral pair in $\mathbb {Z}_{N}$ , $N=p^{m}q^{n}$ . Let $K_{p}(B)\subseteq [0,m-1]$ be the set of all k such that $B_{i\ \bmod\ p^{k}}$ is absorbed $\ \bmod\ p^{k+1}$ for all i. Then

$$ \begin{align*}\overline{A}(X)\equiv A(X)\prod_{k\in K_{p}(B)}\Phi_{p^{m-k}}(X^{q^{n}})\ \bmod\ (X^{N}-1)\end{align*} $$

is the mask polynomial of a spectral set whose spectrum has the following mask polynomial:

$$ \begin{align*}\overline{B}(X)\equiv B(X)\prod_{k\in K_{p}(B)}\Phi_{p^{k+1}}(X^{q^{n}})\ \bmod\ (X^{N}-1).\end{align*} $$

Moreover, for every k with $p^{k+1}\mid N$ , there is i such that $\overline {B}_{i\ \bmod\ p^{k}}$ is not absorbed $\ \bmod\ p^{k+1}$ (i.e., the set $K_{p}(\overline {B})$ is empty).

Proof. Induction on $\lvert K_{p}(B) \rvert $ ; the case $\lvert K_{p}(B) \rvert =1$ is Lemma 9.3, and the proof for the induction step is almost identical. For the second part, we proceed by contradiction; suppose that $K_{p}(\overline {B})\neq \varnothing $ . By the second part of Lemma 9.3, we definitely have $K_{p}(B)\cap K_{p}(\overline {B})=\varnothing $ as, for every $k\in K_{p}(B)$ , it holds $\overline {B}(\zeta _{p^{k+1}})=0$ ; hence, each $\overline {B}_{i\ \bmod\ p^{k}}$ is equidistributed $\ \bmod\ p^{k+1}$ (and not absorbed).

Consider next some arbitrary $\ell \notin K_{p}(B)$ , $0\leq \ell \leq m$ . By definition, there is i such that $B_{i\ \bmod\ p^{\ell }}$ is not absorbed $\ \bmod\ p^{\ell +1}$ . Then, as $B\subseteq \overline {B}$ , it is obvious that $\overline {B}_{i\ \bmod\ p^{k}}$ is not absorbed $\ \bmod\ p^{k+1}$ .

Definition 9.5. We call a set $A\subseteq \mathbb {Z}_{N}$ absorption-free at $p^{k}$ if, for a prime p and $k\in \mathbb {N}$ with $p^{k+1}\mid N$ , there is a class $A_{i\ \bmod\ p^{k}}$ that is not absorbed $\ \bmod\ p^{k+1}$ (i.e., $k\notin K_{p}(A)$ ). We call A absorption-free if it is absorption-free at every prime power $p^{k}$ such that $p^{k+1}\mid N$ (i.e., $K_{p}(A)=\varnothing $ for every prime $p\mid N$ ).

Lemma 9.6. Let $(A,B)$ be a spectral pair in $\mathbb {Z}_{N}$ , $N=p^{m}q^{n}$ . Then, there are $S,T\subseteq \mathbb {Z}_{N}$ such that $(A\oplus S,B\oplus T)$ is a spectral pair in $\mathbb {Z}_{N}$ , with the additional property that $A\oplus S$ and $B\oplus T$ are absorption-free.

Proof. If both A and B are absorption-free, there is nothing to prove as we can just take $S=T={\left \{{0}\right \}}$ . So, suppose first that B is not absorption-free. The process described in Lemma 9.3 and subsequently in Corollary 9.4 ‘kills’ all absorption in the following sense: If $B_{i\ \bmod\ p^{k}}$ is absorbed $\ \bmod\ p^{k+1}$ for all i, then $\overline {B}_{i\ \bmod\ p^{k}}$ is equidistributed $\ \bmod\ p^{k+1}$ for all i since $\overline {B}(\zeta _{p^{k+1}})=0$ , and thus, $\overline {B}$ is absorption-free at $p^{k}$ . Moreover, for every $k\in [0,m-1]$ , there is i such that $\overline {B}_{i\ \bmod\ p^{k}}$ is not absorbed $\ \bmod\ p^{k+1}$ . With the goal to eliminate all absorption from A and B, we successively multiply $B(X)$ by polynomials of the form $\Phi _{p^{k+1}}(X^{q^{n}})$ or $\Phi _{q^{\ell +1}}(X^{p^{m}})$ , whose product is a mask polynomial of a set S, and, respectively, $A(X)$ by polynomials of the form $\Phi _{p^{m-k}}(X^{q^{n}})$ or $\Phi _{q^{n-\ell }}(X^{p^{m}})$ , whose product is a mask polynomial of a set T. We thus obtain a pair of absorption-free sets $(A\oplus S,B\oplus T)$ , which is also spectral, by virtue of Lemma 9.3 or Corollary 9.4.

Corollary 9.7. Suppose that every absorption-free spectral subset of $\mathbb {Z}_{N}$ tiles $\mathbb {Z}_{N}$ . Then, every spectral subset of $\mathbb {Z}_{N}$ tiles $\mathbb {Z}_{N}$ .

Proof. Let $(A,B)$ be a spectral pair in $\mathbb {Z}_{N}$ . If A is absorption-free, then it tiles $\mathbb {Z}_{N}$ by hypothesis. If not, there are $S,T\subseteq \mathbb {Z}_{N}$ by Lemma 9.6 such that $(A\oplus T, B\oplus S)$ is an absorption-free spectral pair. By hypothesis, this shows the existence of $R\subseteq \mathbb {Z}_{N}$ such that $(A\oplus T)\oplus R=\mathbb {Z}_{N}$ or, alternatively, $A\oplus (T\oplus R)=\mathbb {Z}_{N}$ , that is, A tiles $\mathbb {Z}_{N}$ .

All the above motivate the following definition.

Definition 9.8. Let $N\in \mathbb {N}$ . Define the following subset of $\mathscr {F}(N)$

$$ \begin{align*}\mathscr{F}_{\max} (N)={\left\{{A\subseteq\mathbb{Z}_{N}:A\in \mathscr{F}(N), \text{ and }A\text{ has maximal size}}\right\}}.\end{align*} $$

Lemma 9.6 and Corollary 9.7 imply that every $A\in \mathscr {F}_{\max }(N)$ is absorption-free, as well as every spectrum B of A. Hence, Corollary 9.7 implies

(9.4) $$ \begin{align} N\in\mathscr{S}_{p,q} \Longleftrightarrow \mathscr{F}_{\max}(N)\neq\varnothing. \end{align} $$

10 Symmetry of root patterns

We consider again $N\in \mathscr {S}_{p,q}^{\prime }$ , $A\in \mathscr {F}(N)$ and B a spectrum of A. We recall Propositions 8.2, 8.4 and Corollary 8.3, which imply that A and B are both primitive; they satisfy equations (8.1) and (8.2) such that the polynomials $P,Q$ in (8.1) are nonzero. Therefore, A contains a coset from each of the subgroups $\frac {N}{p}\mathbb {Z}_{N}$ and $\frac {N}{q}\mathbb {Z}_{N}$ , so using Theorem 3.3(i) we obtain

$$ \begin{align*}\frac{N}{p}\mathbb{Z}_{N}\cup\frac{N}{q}\mathbb{Z}_{N}\subseteq A-A\subseteq{\left\{{0}\right\}}\cup Z(B),\end{align*} $$

and then Corollary 3.4 gives

(10.1) $$ \begin{align} B(\zeta_{p})=B(\zeta_{q})=0 \end{align} $$

for any spectrum B of A. If in addition $A\in \mathscr {F}_{\max }(N)$ holds, then A and every spectrum B are absorption-free by Lemma 9.6.

Definition 10.1. For $A\subseteq \mathbb {Z}_{N}$ , we define

$$ \begin{align*}S_{A}^{N}(p):={\left\{{\log_{p} s:s\in S_{A}^{N}, p\mid s}\right\}}={\left\{{x\in[1,m]:A(\zeta_{p^{x}})=0}\right\}},\end{align*} $$

and the definition of $S_{A}^{N}(q)$ is similar. Also, denote by $m_{p}(A)$ the maximal exponent $x\leq m$ such that $A(\zeta _{N}^{p^{x}})\neq 0$ , and similarly define $m_{q}(A)$ to be the maximal exponent $y\leq n$ such that $A(\zeta _{N}^{q^{y}})\neq 0$ . If such exponents do not exist, we put $m_{p}(A)=-1$ , $m_{q}(A)=-1$ , respectively. Lastly, define the following set

$$ \begin{align*} R_{A}^{N}(p):={\left\{{x\in[0,m]:A(\zeta_{N}^{p^{x}})=0}\right\}} \end{align*} $$

and, similarly, $R_{A}^{N}(q)$ . The sets thus defined will be called root patterns of A.

We remark that, if the sets below are nonempty, then

$$ \begin{align*}m_{p}(A)=\max{\left({[0,m]\setminus R_{A}^{N}(p)}\right)}, \;\;\;\; m_{q}(A)=\max{\left({[0,m]\setminus R_{A}^{N}(q)}\right)}.\end{align*} $$

For $A\in \mathscr {F}(N)$ , the above sets are always nonempty, i.e., $m_{p}(A),n_{p}(A)\geq 0$ . This is a consequence of Ma’s lemma for the cyclic case [22] (see also Lemma 1.5.1 [29], or Corollary 1.2.14 [25]), using the polynomial notation.

Lemma 10.2. Suppose that $A(X)\in \mathbb {Z}[X]$ , and let $\mathbb {Z}_{N}$ be a cyclic group such that $p^{m}\mid \!\mid N$ for p prime. If $A(\zeta _{d})=0$ , for every $p^{m}\mid d\mid N$ , then

$$ \begin{align*}A(X)\equiv P(X)\Phi_{p}(X^{N/p})\ \bmod\ (x^{N}-1).\end{align*} $$

If the coefficients of A are nonnegative, then P can be taken with nonnegative coefficients as well. In particular, if $A\subseteq \mathbb {Z}_{N}$ satisfies $A(\zeta _{d})=0$ for every $p^{m}\mid d\mid N$ , then A is a union of p-cycles.

Therefore, if $A\subseteq \mathbb {Z}_{N}$ satisfies $m_{p}(A)=-1$ (resp., $m_{q}(A)=-1$ ), then it is a union of q-cycles (resp., p-cycles), so if $N\in \mathscr {S}_{p,q}^{\prime }$ and A are spectral, then A is also a tile by Proposition 8.4.

Lemma 10.3. Let $N\in \mathscr {S}_{p,q}^{\prime }$ , $A\in \mathscr {F}(N)$ and B any spectrum of A. Then, we have the following relation between the root patterns of A and B:

(10.2) $$ \begin{align} (S_{B}^{N}(p)-1)\cap[0,m_{p}(A)] &= R_{A}^{N}(p)\cap[0,m_{p}(A)] \end{align} $$

(10.3) $$ \begin{align} (S_{B}^{N}(q)-1)\cap[0,m_{q}(A)] &= R_{A}^{N}(q)\cap[0,m_{q}(A)]. \end{align} $$

Equations (10.2) and (10.3) are also equivalent to the statements

(10.4) $$ \begin{align} \text{If }x\leq m_{p}(A), \text{ then it holds } A(\zeta_{N}^{p^{x}})=0\Longleftrightarrow B(\zeta_{p^{x+1}})=0 \end{align} $$

(10.5) $$ \begin{align} \text{If }x\leq m_{q}(A), \text{ then it holds } A(\zeta_{N}^{q^{x}})=0\Longleftrightarrow B(\zeta_{q^{x+1}})=0. \end{align} $$

Proof. Since $A\in \mathscr {F}(N)$ and $N\in \mathscr {S}_{p,q}^{\prime }$ , we obtain that A cannot be expressed as a union of p- or q-cycles exclusively by virtue of Theorem 5.2, Corollary 8.3 and Proposition 8.4. Thus, $m_{p}(A), m_{q}(A)\geq 0$ . Let $x< m_{p}(A)$ and $A(\zeta _{N}^{p^{x}})=0$ . Then $p^{x}\cdot A$ is a union of p- and q-cycles, not exclusively of q-cycles by Theorem 5.2 (second part) because $A(\zeta _{N}^{p^{m_{p}(A)}})\neq 0$ . So, there are $a,a^{\prime }\in A$ such that

$$ \begin{align*}p^{x}(a-a^{\prime})\equiv\frac{N}{p}\ \bmod\ N\end{align*} $$

or, equivalently,

$$ \begin{align*}a-a^{\prime}\equiv\frac{N}{p^{x+1}}\ \bmod\ \frac{N}{p^{x}},\end{align*} $$

which in turn implies $a-a^{\prime }\in \frac {N}{p^{x+1}}\mathbb {Z}_{N}^{\star }$ , whence $B(\zeta _{p^{x+1}})=0$ by Theorem 3.3. This proves one direction of equation (10.4).

Next, suppose that the reverse implication of equation (10.4) does not hold, and let y be the smallest exponent such that $A(\zeta _{N}^{p^{y}})\neq 0=B(\zeta _{p^{y+1}})$ . For every $x\leq y$ and every i, we have the obvious partition

$$ \begin{align*}B_{i\ \bmod\ p^{x}}=\bigcup_{k=1}^{p} B_{i+kp^{x}\ \bmod\ p^{x+1}}.\end{align*} $$

If $A(\zeta _{N}^{p^{x}})=0$ so that $B(\zeta _{p^{x+1}})=0$ , the above partition is an equidistribution $\ \bmod\ p^{x+1}$ , that is,

$$ \begin{align*}\lvert B_{i\ \bmod\ p^{x}} \rvert=p\lvert B_{i+kp^{x}\ \bmod\ p^{x+1}} \rvert\end{align*} $$

for every k. If $A(\zeta _{N}^{p^{x}})\neq 0\neq B(\zeta _{p^{x+1}})$ , we certainly do not have equidistribution for at least one choice of j; if we do not have absorption $\ \bmod\ p^{x+1}$ , i.e., $B_{i\ \bmod\ p^{x}}=B_{i+kp^{x}\ \bmod\ p^{x+1}}$ , then there are $k,k^{\prime }$ with $k\not \equiv k^{\prime }\ \bmod\ p$ such that $B_{i+kp^{x}\ \bmod\ p^{x+1}}$ and $B_{i+k^{\prime }p^{x}\ \bmod\ p^{x+1}}$ are nonempty. Let

$$ \begin{align*}b\in B_{i+kp^{x}\ \bmod\ p^{x+1}}, b^{\prime}\in B_{i+k^{\prime}p^{x}\ \bmod\ p^{x+1}}\end{align*} $$

be arbitrary. It holds $p^{x}\mid \!\mid b-b^{\prime }$ by assumption, and $b-b^{\prime }\notin p^{x}\mathbb {Z}_{N}^{\star }$ due to $A(\zeta _{N}^{p^{x}})\neq 0$ . This shows $q\mid b-b^{\prime }$ ; therefore, all elements of $B_{i+kp^{x}\ \bmod\ p^{x+1}}$ and $B_{i+k^{\prime }p^{x}\ \bmod\ p^{x+1}}$ have the same residue $\ \bmod\ q$ . The same holds for all other elements of $B_{i\ \bmod\ p^{x}}$ , establishing

$$ \begin{align*}B_{i\ \bmod\ p^{x}}\subseteq B_{j\ \bmod\ q}\end{align*} $$

for some j. Now, for each $i\in [0,p^{y}-1]$ , define $x(i)$ to be the smallest exponent x such that $B_{i\ \bmod\ p^{x}}$ is neither absorbed nor equidistributed $\ \bmod\ p^{x+1}$ , and then define $j(i)$ such that

(10.6) $$ \begin{align} B_{i\ \bmod\ p^{x(i)}}\subseteq B_{j(i)\ \bmod\ q}. \end{align} $$

If for every $x\leq y$ , $B_{i\ \bmod\ p^{x}}$ is either absorbed or equidistributed $\ \bmod\ p^{x+1}$ , define $x(i)=y$ ; since $B_{i\ \bmod\ p^{y}}$ is equidistributed $\ \bmod\ p^{y+1}$ and $A(\zeta _{N}^{p^{y}})\neq 0$ , we conclude that there is again some $j(i)$ such that equation (10.6) still holds. On $[0,p^{y}-1]$ , we define an equivalence relation: It holds $i\sim i^{\prime }$ if and only if $i\equiv i^{\prime }\ \bmod\ p^{x(i)}$ (it is not hard to show that this satisfies the properties of an equivalence relation as $i\equiv i^{\prime }\ \bmod\ p^{x(i)}$ implies $x(i)=x(i^{\prime })$ ). Let $I\subseteq [0,p^{y}-1]$ be a complete system of representatives; it holds

$$ \begin{align*}B=\bigsqcup_{i\in I}B_{i\ \bmod\ p^{x(i)}}.\end{align*} $$

The important fact about the above partition is that each $B_{i\ \bmod\ p^{x(i)}}$ has cardinality $\frac {\lvert B \rvert }{p^{k(i)}}$ for some positive integer $k(i)$ . Indeed, as for every $x<x(i)$ , we have either $\lvert B_{i\ \bmod\ p^{x}} \rvert =\lvert B_{i\ \bmod\ p^{x+1}} \rvert $ (absorption) or $\lvert B_{i\ \bmod\ p^{x}} \rvert =p\lvert B_{i\ \bmod\ p^{x+1}} \rvert $ (equidistribution). Then, by equation (10.6), we have

$$ \begin{align*}B_{0\ \bmod\ q}=\bigsqcup_{i\in I, j(i)=0}B_{i\ \bmod\ p^{x(i)}},\end{align*} $$

and taking cardinalities on both sides, we obtain

$$ \begin{align*}\frac{\lvert B \rvert}{q}=\sum_{i\in I, j(i)=0}\frac{\lvert B \rvert}{p^{k(i)}},\end{align*} $$

which then leads to an equation of the form $1/q=s/p^{t}$ , which has no solutions in integers, contradicting the fact that $A(\zeta _{N}^{p^{y}})\neq 0=B(\zeta _{p^{y+1}})$ . This completes the proof.

Proposition 10.4. Let $N\in \mathscr {S}_{p,q}^{\prime }$ , $A\in \mathscr {F}(N)$ and B be any spectrum of A. Then

$$ \begin{align*}A(\zeta_{q^{n}})=A(\zeta_{p^{m}})=0\end{align*} $$

and

$$ \begin{align*}B(\zeta_{p^{m_{p}(A)+1}q})=B(\zeta_{pq^{m_{q}(A)+1}})=0.\end{align*} $$

Proof. We will show first that $A(\zeta _{q^{n}})=A(\zeta _{p^{m}})=0$ . Suppose that it doesn’t hold, say $A(\zeta _{q^{n}})\neq 0$ , so that $m_{p}(A)=m$ . By equation (10.2), we get

$$ \begin{align*}S_{B}^{N}(p)-1 = R_{A}^{N}(p).\end{align*} $$

Using the same argument as in the proof of Lemma 10.3, replacing y by m, we get

$$ \begin{align*}B=\bigsqcup_{i\in I}B_{i\ \bmod\ p^{x(i)}},\end{align*} $$

where each $B_{i\ \bmod\ p^{x(i)}}$ has cardinality $\frac {\lvert B \rvert }{p^{k(i)}}$ and is contained in $B_{j(i)\ \bmod\ q}$ ; this is also true if $x(i)=m$ as $A(\zeta _{N}^{p^{m}})\neq 0$ . We establish a contradiction in the same way.

This shows $m_{p}(A)<m$ and $m_{q}(A)<n$ . Since $B(\zeta _{p^{m_{p}(A)+1}})\neq 0$ by (10.4), the polynomial

$$ \begin{align*}\overline{A}(X)\equiv A(X)\Phi_{p}(X^{p^{m-m_{p}(A)-1}q^{n}})\ \bmod\ (X^{N}-1)\end{align*} $$

is the mask polynomial of a set, say $\overline {A}$ ; this follows from the fact that $(A-A)\cap \frac {N}{p^{m_{p}(A)+1}}\mathbb {Z}_{N}^{\star }=\varnothing $ , which implies that $A-A$ and the difference set whose mask polynomial is $\Phi _{p}(X^{p^{m-m_{p}(A)-1}q^{n}})$ intersect trivially. Consider now the multiset $p^{m_{p}(A)}\cdot A$ . By definition, its mask polynomial does not vanish on $\zeta _{N}$ , while on the other hand, $p^{m_{p}(A)+1}\cdot A$ is a disjoint union of q-cycles by Lemma 10.2. By Lemma 5.6 and Theorem 3.3(i), we obtain $B(\zeta _{p^{m_{p}(A)+1}q})=0$ and, similarly, $B(\zeta _{pq^{m_{q}(A)+1}})=0$ , as desired.

Using the above notation, condition (T1) can be rewritten as

$$ \begin{align*}\lvert A \rvert=p^{\lvert S_{A}^{N}(p) \rvert}q^{\lvert S_{A}^{N}(q) \rvert}.\end{align*} $$

At any rate, regardless whether A is spectral or not, it holds

$$ \begin{align*}p^{\lvert S_{A}^{N}(p) \rvert}q^{\lvert S_{A}^{N}(q) \rvert}\mid \lvert A \rvert.\end{align*} $$

We restrict now to $A\in \mathscr {F}_{\max }(N)$ , $N\in \mathscr {S}_{p,q}^{\prime }$ due to equation (9.4). In this case, we will show that (T1) fails for B when the multiset $\frac {N}{p^{m_{p}(A)+1}q}\cdot B$ is not a union of q-cycles only; in particular, the power of p is higher than it is supposed to be.

Lemma 10.5. Let $N\in \mathscr {S}_{p,q}^{\prime }$ , $A\in \mathscr {F}_{\max }(N)$ , and B any spectrum of A so that $m_{p}(A), m_{q}(A)\geq 0$ . Consider the set

$$ \begin{align*}U_{B}^{N}(p)={\left\{{x: B(\zeta_{p^{x}})\neq0=B(\zeta_{p^{x}q})}\right\}}.\end{align*} $$

Then

$$ \begin{align*}p^{\lvert S_{B}^{N}(p) \rvert+\lvert U_{B}^{N}(p) \rvert}\mid \lvert B \rvert.\end{align*} $$

Moreover, for every j, every $x\in [1,m_{p}(A)+1]\setminus S_{B}^{N}(p)$ and every $y\in [1,m_{q}(A)+1]\setminus S_{B}^{N}(q)$ , each of the sets

$$ \begin{align*}{\left({\frac{N}{p^{x}q}B}\right)}_{j\ \bmod\ \frac{N}{pq}}=\frac{N}{p^{x}q}B\cap\left(j+\frac{N}{pq}\mathbb{Z}_{N}\right), \;\;\;\; {\left({\frac{N}{pq^{y}}B}\right)}_{j\ \bmod\ \frac{N}{pq}}=\frac{N}{pq^{y}}B\cap\left(j+\frac{N}{pq}\mathbb{Z}_{N}\right),\end{align*} $$

is supported either on a p- or a q-cycle.

Proof. We first note, that $x=m_{p}(A)+1$ satisfies $B(\zeta _{p^{x}})\neq 0=B(\zeta _{p^{x}q})$ by Lemma 10.3 and Proposition 10.4, therefore $U_{B}^{N}(p)\neq \varnothing $ . By (10.1), we have $B(\zeta _{p})=0$ or, equivalently, $\lvert B_{i\ \bmod\ p} \rvert =\frac {1}{p}\lvert B \rvert $ for all i. At every step, we will estimate

$$ \begin{align*}\min{\left\{{i:v_{p}(\lvert B_{i\ \bmod\ p^{x}} \rvert)}\right\}}\end{align*} $$

or, in other words, how much the power of p drops from $\lvert B \rvert $ down to one of the subsets $\lvert B_{i\ \bmod\ p^{x}} \rvert $ . If $x\in S_{B}^{N}(p)$ , then each $B_{i\ \bmod\ p^{x-1}}$ is equidistributed $\ \bmod\ p^{x}$ , therefore

$$ \begin{align*}v_{p}(\lvert B_{i\ \bmod\ p^{x-1}} \rvert)-1=v_{p}(\lvert B_{i\ \bmod\ p^{x}} \rvert),\end{align*} $$

for all i. If $x\notin S_{B}^{N}(p)$ , we have in general

$$ \begin{align*}v_{p}(\lvert B_{i\ \bmod\ p^{x-1}} \rvert)\geq \min{\left\{{v_{p}(\lvert B_{i+kp^{x-1}\ \bmod\ p^{x}} \rvert):0\leq k\leq p-1}\right\}}.\end{align*} $$

Next, consider the minimum element of $U_{B}^{N}(p)$ , say x, and suppose that $B_{i\ \bmod\ p^{x-1}}$ is not absorbed $\ \bmod\ p^{x}$ ; such an i exists due to hypothesis and equation (9.4) since B is absorption-free. Each nonempty class $B_{i+kp^{x-1}\ \bmod\ p^{x}}$ would then be absorbed $\ \bmod\ p^{x}q$ . Otherwise, $\frac {N}{p^{x}q}B\cap (j+\frac {N}{pq}\mathbb {Z}_{N})$ would neither be supported on a p-cycle nor on a q-cycle for some j. For the same reason, each element in $B_{i+kp^{x-1}\ \bmod\ p^{x}}$ must have the same residue $\ \bmod\ q$ for all k, showing that $B_{i\ \bmod\ p^{x-1}}$ is absorbed $\ \bmod\ p^{x-1}q$ ; furthermore, since $B(\zeta _{p^{x}q})=0$ , $B_{i\ \bmod\ p^{x-1}}$ and $B_{i\ \bmod\ p^{x-1}q}$ are equidistributed $\ \bmod\ p^{x}$ and $\ \bmod\ p^{x}q$ , respectively. Therefore,

$$ \begin{align*}v_{p}(\lvert B_{i\ \bmod\ p^{x-1}} \rvert)-1=v_{p}(\lvert B_{i\ \bmod\ p^{x}} \rvert).\end{align*} $$

Next, let x be the minimum element not belonging to $S_{B}^{N}(p)$ , that is,

$$ \begin{align*}B(\zeta_{p})=\dotsb=B(\zeta_{p^{x-1}})=0\neq B(\zeta_{p^{x}}).\end{align*} $$

Suppose that $B_{i\ \bmod\ p^{x-1}}$ is not absorbed $\ \bmod\ p^{x}$ ; such an i exists due to hypothesis and equation (9.4). Let then $B_{i+kp^{x-1}\ \bmod\ p^{x}}$ and $B_{i+k^{\prime }p^{x-1}\ \bmod\ p^{x}}$ be nonempty with $p\nmid k-k^{\prime }$ . If there are $b\in B_{i+kp^{x-1}\ \bmod\ p^{x}}$ and $b^{\prime }\in B_{i+k^{\prime }p^{x-1}\ \bmod\ p^{x}}$ with $q\nmid b-b^{\prime }$ , then $b-b^{\prime }\in p^{x-1}\mathbb {Z}_{N}^{\star }$ , yielding $A(\zeta _{N}^{p^{x-1}})=0$ by Theorem 3.3(i), and then $B(\zeta _{p^{x}})=0$ by Lemma 10.3, contradicting the definition of x. Thus, we must have $q\mid b-b^{\prime }$ for every such selection of $b,b^{\prime }$ , implying eventually that every element of $B_{i\ \bmod\ p^{x-1}}$ has the same residue $\ \bmod\ q$ .

For every $y\geq x$ , we choose an integer $i_{y}\equiv i\ \bmod\ p^{x-1}$ as follows (we denote $i_{j}=i$ for $1\leq j\leq x-1$ ):

• • If $y\notin S_{B}^{N}(p)\cup U_{B}^{N}(p)$ , choose $i_{y}$ satisfying

  $$ \begin{align*}v_{p}(\lvert B_{i_{y-1}\ \bmod\ p^{y-1}} \rvert)\geq v_{p}(\lvert B_{i_{y}\ \bmod\ p^{y}} \rvert).\end{align*} $$

• • If $y\in S_{B}^{N}(p)\cup U_{B}^{N}(p)$ , then $i_{y}=i_{y-1}$ .

We have $\lvert B_{i\ \bmod\ p^{x-1}} \rvert =\frac {1}{p^{x-1}}\lvert B \rvert $ . If $y\in S_{B}^{N}(p)$ , then $B_{i_{y-1}\ \bmod\ p^{y-1}}$ is equidistributed $\ \bmod\ p^{y}$ , so

(10.7) $$ \begin{align} \lvert B_{i_{y}\ \bmod\ p^{y}} \rvert=\frac{1}{p}\lvert B_{i_{y-1}\ \bmod\ p^{y-1}} \rvert. \end{align} $$

If $y\in U_{B}^{N}(p)$ , we have $B(\zeta _{p^{y}q})=0$ . Therefore, the multiset $\frac {N}{p^{y}q}\cdot B$ is a disjoint union of p- and q-cycles by Theorem 5.2. Every such cycle consists of elements $p^{y}qb$ for $b\in B$ that have the same residue $\ \bmod\ p^{y-1}$ ; indeed, if $\frac {N}{p^{y}q}(b-b^{\prime })\in \frac {N}{p}\mathbb {Z}_{N}$ , then $b-b^{\prime }\equiv kp^{y-1}q\ \bmod\ p^{y}q$ for some k, and if $\frac {N}{p^{y}q}(b-b^{\prime })\in \frac {N}{q}\mathbb {Z}_{N}$ , then $b-b^{\prime }\equiv kp^{y}\ \bmod\ p^{y}q$ for some k, proving our claim. This shows that $\frac {N}{p^{y}q}\cdot B_{i_{y-1}\ \bmod\ p^{y-1}}$ is a disjoint union of p- and q-cycles; however, a q-cycle in $\frac {N}{p^{y}q}\cdot B_{i_{y-1}\ \bmod\ p^{y-1}}\subseteq \frac {N}{p^{y}q}B$ consists of elements having all possible residues $\ \bmod\ q$ , a contradiction, since every element of $B_{i\ \bmod\ p^{x-1}}$ has the same residue $\ \bmod\ q$ . This shows that $\frac {N}{p^{y}q}\cdot B_{i_{y-1}\ \bmod\ p^{y-1}}$ is a union of p-cycles, yielding the equidistribution of $B_{i_{y-1}\ \bmod\ p^{y-1}}$ modulo $p^{y}$ . Thus, (10.7) holds in this case as well.

Summarizing, we obtain the following: If $y\in S_{B}^{N}(p)\cup U_{B}^{N}(p)$ , then (10.7) is valid; otherwise,

$$ \begin{align*}v_{p}(\lvert B_{i_{y-1}\ \bmod\ p^{y-1}} \rvert)\geq v_{p}(\lvert B_{i_{y}\ \bmod\ p^{y}} \rvert)\end{align*} $$

holds. This obviously yields that

$$ \begin{align*}0\leq v_p(\lvert B_{i_m\ \bmod\ p^m} \rvert)\leq v_p(\lvert B \rvert)-\lvert S_B^N(p) \rvert-\lvert U_B^N(p) \rvert,\end{align*} $$

proving the first part.

For the second part of the lemma, we proceed by contradiction. If there is some j and $x\in U_{B}^{N}(p)$ with $x\leq m_{p}(A)+1$ such that $\frac {N}{p^{x}q}B\cap (j+\frac {N}{pq}\mathbb {Z}_{N})$ is supported neither on a p- nor on a q-cycle, then by Proposition 5.5 we get that

$$ \begin{align*}{\left({\frac{N}{p^{x}q}B-\frac{N}{p^{x}q}B}\right)}\cap\frac{N}{pq}\mathbb{Z}_{N}^{\star}\neq\varnothing.\end{align*} $$

This shows the existence of $b,b^{\prime }\in B$ such that

$$ \begin{align*}\frac{N}{p^{x}q}(b-b^{\prime})\in\frac{N}{pq}\mathbb{Z}_{N}^{\star}\end{align*} $$

or, equivalently,

$$ \begin{align*}\operatorname{\mathrm{ord}}(b-b^{\prime})=pq\frac{N}{p^{x}q}=\frac{N}{p^{x-1}}.\end{align*} $$

Hence, by Theorem 3.3(i), we obtain

$$ \begin{align*}A(\zeta_{N/p^{x-1}})=A(\zeta_{N}^{p^{x-1}})=0,\end{align*} $$

contradicting the definition of x. This completes the proof.

Definition 10.6. Let $A\subseteq \mathbb {Z}_{N}$ . We define

• (wT1) $p^{\lvert S_{A}^{N}(p) \rvert }\mid \!\mid \lvert A \rvert $ , for some $p\mid \lvert A \rvert $ .

Obviously, when (T1) holds for A, then (wT1) holds for every $p\mid A$ . An immediate consequence of this definition and Lemma 10.5 is the following.

Corollary 10.7. Let $N\in \mathscr {S}_{p,q}^{\prime }$ , $A\in \mathscr {F}_{\max }(N)$ . Then, no spectrum B of A satisfies (wT1) . In particular, every spectrum B of A satisfies $B\in \mathscr {F}_{\max }(N)$ .

Proof. This is obvious by Lemma 10.5 since the sets $U_{B}^{N}(p)$ and $U_{B}^{N}(q)$ are nonempty.

Corollary 10.8. Let $N\in \mathscr {S}_{p,q}^{\prime }$ , $A\in \mathscr {F}_{\max }(N)$ . Then no spectrum B of A is a disjoint union either of p- or q-cycles exclusively.

Proof. If B was a union of (say) p-cycles only, then by Proposition 8.4, B satisfies (T1) and (T2). On the other hand, Corollary 10.7 gives us that (wT1) fails for B, a contradiction, as (T1) implies (wT1) .

This corollary complements Proposition 8.4. We summarize below all the reductions made so far:

Theorem 10.9. Let $N\in \mathscr {S}_{p,q}^{\prime }$ , $A\in \mathscr {F}_{\max }(N)$ . Then the following hold:

1. 1. A and any spectrum B are primitive.

2. 2. A, as well as any spectrum B, can be expressed as disjoint unions of p- and q-cycles; not exclusively of p- or q-cycles (i.e., none of the polynomials $P,Q,R,S$ in both equation (8.1) and equation (8.2) can be identically zero).

3. 3. If $N=p^{m}q^{n}$ , it holds

   (10.8) $$ \begin{align} A(\zeta_{N})=A(\zeta_{p})=A(\zeta_{q})=A(\zeta_{p^{m}})=A(\zeta_{q^{n}})=& \nonumber\\ =B(\zeta_{N})=B(\zeta_{p})=B(\zeta_{q})=B(\zeta_{p^{m}})=B(\zeta_{q^{n}})=& 0 \end{align} $$
   for any spectrum B of A. This also implies that both A and B are equidistributed both $\ \bmod\ p$ and $\ \bmod\ q$ .

4. 4. A as well as any spectrum B are absorption-free.

5. 5. Every spectrum B of A satisfies $B\in \mathscr {F}_{\max }(N)$ .

We have established enough tools to extend the results of [13] related to Fuglede’s conjecture.

Corollary 10.10. Let $N=p^{m}q^{n}$ , $n\leq 3$ and $(A,B)$ be a spectral pair in $\mathbb {Z}_{N}$ . Then A tiles $\mathbb {Z}_{N}$ .

Proof. Suppose on the contrary that there is such an N with $\mathscr {F}(N)\neq \varnothing $ , $A\in \mathscr {F}_{\max }(N)$ and B a spectrum. Corollary 6.3 implies that $n\geq 2$ . By Theorem 10.9, we obtain $A(\zeta _{q})=A(\zeta _{q^{n}})=0$ , so if $n=2$ we have $q^{n}\mid \lvert A \rvert $ , and so by Proposition 6.2 we get that A tiles, contradiction. If $n=3$ , we have $B(\zeta _{q})=B(\zeta _{q^{3}})=0$ again by Theorem 10.9 so that $\lvert S_{B}^{N}(q) \rvert \geq 2$ . Since $U_{B}^{N}(q)$ is nonempty, by Lemma 10.5 we obtain $q^{3}\mid \lvert B \rvert $ , and then Proposition 6.2 gives us again that A tiles $\mathbb {Z}_{N}$ , a contradiction. Thus, $\mathscr {S}_{p,q}$ cannot have elements of the form $p^{m}q^{n}$ with $n\leq 3$ , proving the desired result.

Proposition 10.11. Let $N=p^{m}q^{n}\in \mathscr {S}_{p,q}^{\prime }$ , $A\in \mathscr {F}_{\max }(N)$ and B any spectrum of A. Then

$$ \begin{align*}A(\zeta_{p^{m}q})=A(\zeta_{pq^{n}})=B(\zeta_{p^{m}q})=B(\zeta_{pq^{n}})=A(\zeta_{pq})=B(\zeta_{pq})=0.\end{align*} $$

Proof. By Theorem 10.9, we also have $B\in \mathscr {F}_{\max }(N)$ , so we may use Lemma 10.3 with the roles of A and B reversed. If $A(\zeta _{pq^{n}})=A(\zeta _{N}^{p^{m-1}})\neq 0=A(\zeta _{N}^{p^{m}})=A(\zeta _{q^{n}})$ , we would have $m_{p}(A)=m-1$ , so by virtue of Lemma 10.3 we would have $B(\zeta _{p^{m}})\neq 0$ , contradicting equations 10.2. Reversing the roles of p, q, and A, B, we obtain with the same reasoning

$$ \begin{align*}A(\zeta_{p^{m}q})=A(\zeta_{pq^{n}})=B(\zeta_{p^{m}q})=B(\zeta_{pq^{n}})=0.\end{align*} $$

Next, consider the minimal element of $U_{B}^{N}(p)$ , say x so that $B(\zeta _{p^{x}})\neq 0=B(\zeta _{p^{x}q})$ . By Proposition 10.4, we have $x\leq m_{p}(A)+1$ ; hence, by Lemma 10.3 we get $A(\zeta _{N}^{p^{x-1}})\neq 0$ . Applying Lemma 9.2 for $d=p^{x-1}$ , we get that each $B_{i\ \bmod\ p^{x-1}}$ is either absorbed or equidistributed $\ \bmod\ p^{x}$ . Since $B(\zeta _{p^{x}})\neq 0$ , there is some i such that $B_{i\ \bmod\ p^{x-1}}$ is absorbed $\ \bmod\ p^{x}$ ; without loss of generality we put $B_{i\ \bmod\ p^{x-1}}= B_{i\ \bmod\ p^{x}}$ . This also shows that $B_{i\ \bmod\ p^{x}q}$ is supported on a q-cycle. In fact, $B_{i\ \bmod\ p^{x}}$ must be equidistributed $\ \bmod\ p^{x}q$ , hence

(10.9) $$ \begin{align} \lvert B_{i+kp^{x}\ \bmod\ p^{x}q} \rvert=\frac{1}{q}\lvert B_{i\ \bmod\ p^{x}} \rvert, \;\;\;\; 0\leq k\leq q-1. \end{align} $$

For $y\leq x-1$ , we then claim the following: $B_{i\ \bmod\ p^{y}}$ is either absorbed or equidistributed $\ \bmod\ p^{y+1}$ . Indeed, if $y+1\in S_{B}^{N}(p)$ , then $B(\zeta _{p^{y+1}})=0$ and $B_{i\ \bmod\ p^{y}}$ is equidistributed $\ \bmod\ p^{y+1}$ . If $B(\zeta _{p^{y+1}})\neq 0$ , then $A(\zeta _{N}^{p^{y}})\neq 0$ by Lemma 10.3. If $B_{i\ \bmod\ p^{y}}$ is not absorbed $\ \bmod\ p^{y+1}$ , then there are $k\not \equiv k^{\prime }\ \bmod\ p$ such that

$$ \begin{align*}B_{i+kp^{y}\ \bmod\ p^{y+1}}\neq\varnothing, B_{i+k^{\prime}p^{y}\ \bmod\ p^{y+1}}\neq\varnothing.\end{align*} $$

This means that the multiset $\frac {N}{p^{y+1}q}\cdot B_{i\ \bmod\ p^{y}}$ (which is supported in a $pq$ -cycle) intersects nontrivially at least two q-cycles, namely

$$ \begin{align*}\frac{iN}{p^{y+1}q}+k\frac{N}{pq}+\frac{N}{q}\mathbb{Z}_{N}, \;\;\;\; \frac{iN}{p^{y+1}q}+k^{\prime}\frac{N}{pq}+\frac{N}{q}\mathbb{Z}_{N}.\end{align*} $$

By the second part of Lemma 10.5, $\frac {N}{p^{y+1}q}\cdot B_{i\ \bmod\ p^{y}}$ must be supported on a p-cycle, in particular,

$$ \begin{align*}\frac{iN}{p^{y+1}q}+\ell\frac{N}{q}+\frac{N}{p}\mathbb{Z}_{N},\end{align*} $$

for some $\ell $ . But the latter implies that $B_{i\ \bmod\ p^{y}}$ is absorbed $\ \bmod\ p^{y}q$ :

$$ \begin{align*}B_{i\ \bmod\ p^{y}}=B_{i+\ell^{\prime}p^{y}\ \bmod\ p^{y}q},\end{align*} $$

where

$$ \begin{align*}\ell^{\prime}\equiv p\ell\ \bmod\ q.\end{align*} $$

But this leads to a contradiction since (10.9) implies that $B_{i+kp^{x}\ \bmod\ p^{x}q}\neq \varnothing $ for every k, while

$$ \begin{align*}B_{i+kp^{x}\ \bmod\ p^{x}q}\subseteq B_{i+(kp^{x-y})p^{y}\ \bmod\ p^{y}q}=\varnothing\end{align*} $$

when $kp^{x-y}\not \equiv \ell ^{\prime }\ \bmod\ q$ , contradiction.

Therefore, if $B_{i\ \bmod\ p^{x-1}}$ is absorbed $\ \bmod\ p^{x}$ , then $B_{i\ \bmod\ p^{y}}$ is either absorbed of equidistributed $\ \bmod\ p^{y+1}$ for every $y<x$ ; this implies

$$ \begin{align*}\lvert B_{i+kp^{x}\ \bmod\ p^{x}q} \rvert=\frac{1}{q}\lvert B_{i\ \bmod\ p^{x}} \rvert=\frac{\lvert B \rvert}{p^{t}q}\end{align*} $$

for some $t\in \mathbb {N}$ . With the same arguments as above, if $B_{i\ \bmod\ p^{x-1}}$ is equidistributed $\ \bmod\ p^{x}$ , we deduce that if $y\leq x-1$ is the smallest exponent such that $B_{i\ \bmod\ p^{y}}$ is neither absorbed nor equidistributed $\ \bmod\ p^{y+1}$ (assuming there exists one), then $B_{i\ \bmod\ p^{y}}$ is absorbed $\ \bmod\ p^{y}q$ , which means that every element in $B_{i\ \bmod\ p^{y}}$ has the same residue $\ \bmod\ q$ , again by the second part of Lemma 10.5. In this case, there is some k such that

$$ \begin{align*}\lvert B_{i+kp^{y}\ \bmod\ p^{y}q} \rvert=\lvert B_{i\ \bmod\ p^{y}} \rvert=\frac{\lvert B \rvert}{p^{s}}\end{align*} $$

for some $s\in \mathbb {N}$ . We write

$$ \begin{align*}B_{i\ \bmod\ pq}=\bigsqcup_{k=1}^{p^{x-1}}B_{i+kpq\ \bmod\ p^{x}q},\end{align*} $$

and we define $y(k)\leq x-1$ to be the smallest exponent such that $B_{i+kpq\ \bmod\ p^{y(k)}}$ is neither absorbed nor equidistributed $\ \bmod\ p^{y(k)+1}$ ; if such an exponent does not exist, define $y(k)=x-1$ . We define the relation $k\sim k^{\prime }$ to denote $y(k)=y(k^{\prime })$ and $k\equiv k^{\prime }\ \bmod\ p^{y(k)-1}$ . It is not hard to see that this is an equivalence relation and

$$ \begin{align*}B_{i\ \bmod\ pq}=\bigsqcup_{k\in K}B_{i+kpq\ \bmod\ p^{y(k)-1}q}.\end{align*} $$

As we have seen, though, the cardinality of each set in the union above is divisible by $\frac {\lvert B \rvert }{p^{r}q}$ for some $r\in \mathbb {N}$ . Reversing the roles of p and q, we obtain that

(10.10) $$ \begin{align} \frac{\lvert B \rvert}{pq}\mid \lvert B_{i\ \bmod\ pq} \rvert \end{align} $$

for every i. If B were not equidistributed $\ \bmod\ pq$ , there would exist some i such that

$$ \begin{align*}\lvert B_{i\ \bmod\ pq} \rvert\geq \frac{2\lvert B \rvert}{pq}.\end{align*} $$

By equation (10.10) and the trivial partition

$$ \begin{align*}B_{i\ \bmod\ q}=\bigsqcup_{j=1}^{p}B_{i+jq\ \bmod\ pq},\end{align*} $$

we obtain the existence of a j such that $B_{i+jq\ \bmod\ pq}=\varnothing $ . Similarly, there is some $\ell $ such that $B_{i+\ell p\ \bmod\ pq}=\varnothing $ . If $B_{i+kpq\ \bmod\ p^{x-1}}$ is absorbed $\ \bmod\ p^{x}$ , then it is equidistributed $\ \bmod\ p^{x-1}q$ , as we’ve shown above. But then, $B_{i+kpq+up^{x-1}\ \bmod\ p^{x-1}q}$ is nonempty for every u, however,

$$ \begin{align*}B_{i+kpq+up^{x-1}\ \bmod\ p^{x-1}q}\subseteq B_{i+\ell p\ \bmod\ pq}=\varnothing\end{align*} $$

for $up^{x-1}\equiv \ell p\ \bmod\ pq$ , contradiction. This shows that $B_{i+kpq\ \bmod\ p^{x-1}}$ is equidistributed $\ \bmod\ p^{x}$ for every k, showing that $\frac {\lvert B \rvert }{p^{t}}$ divides $\lvert B_{i\ \bmod\ pq} \rvert $ . Similarly, we obtain that $\frac {\lvert B \rvert }{q^{s}}$ divides $\lvert B_{i\ \bmod\ pq} \rvert $ , showing thus $\lvert B \rvert \mid \lvert B_{i\ \bmod\ pq} \rvert $ , contradiction. Thus, B is equidistributed $\ \bmod\ pq$ , and the same holds for A by reversing the roles of A and B. This eventually shows

$$ \begin{align*}A(\zeta_{pq})=B(\zeta_{pq})=0,\end{align*} $$

as desired.

Remark. The above verifies property (T2) for the pairs of prime powers $(p^{m},q)$ , $(p,q^{n})$ and $(p,q)$ .

11 Root deficit

We continue to assume that $N\in \mathscr {S}_{p,q}^{\prime }$ and $(A,B)$ is a spectral pair with $A\in \mathscr {F}_{\max }(N)$ so that $B\in \mathscr {F}_{\max }(N)$ as well.

Definition 11.1. Let $A\subseteq \mathbb {Z}_{N}$ satisfy $A(\zeta _{q})=A(\zeta _{p})=\dotsb =A(\zeta _{p^{k}})=0\neq A(\zeta _{p^{k+1}})$ . We define the following property:

• (wT2) It holds $A(\zeta _{pq})=\dotsb =A(\zeta _{p^{k}q})=0$ .

It should be emphasized that, when (wT2) holds, then A is equidistributed $\ \bmod\ p^{k}q$ (and in particular, every $A_{j\ \bmod\ p^{k}}$ is equidistributed $\ \bmod\ p^{k}q$ ). Indeed, the hypothesis of the definition and (wT2) imply that $\Phi _{d}(X)\mid A(X)$ for every $d\mid p^{k}q$ , $d\neq 1$ . Therefore,

$$ \begin{align*}X^{p^{k}q-1}+\dotsb+1\mid A(X)\end{align*} $$

or, equivalently, $A(X)=G(X)(X^{p^{k}q-1}+\dotsb +1)$ for some $G(X)\in \mathbb {Z}[X]$ . When we reduce $\ \bmod\ (X^{p^{k}q}-1)$ , we obtain

$$ \begin{align*} A(X) &\equiv G(X)(X^{p^{k}q-1}+\dotsb+1)\ \bmod\ (X^{p^{k}q}-1)\\ &\equiv G(1)(X^{p^{k}q-1}+\dotsb+1)\ \bmod\ (X^{p^{k}q}-1), \end{align*} $$

which clearly shows that

(11.1) $$ \begin{align} \lvert A_{j\ \bmod\ p^{k}} \rvert=\frac{\lvert A \rvert}{p^{k}}, \;\;\;\; \lvert A_{j\ \bmod\ p^{k}q} \rvert=\frac{\lvert A \rvert}{p^{k}q}, \;\;\;\; \forall j. \end{align} $$

Proposition 11.2. Let $N\in \mathscr {S}_{p,q}^{\prime }$ , $A\in \mathscr {F}_{\max }(N)$ , satisfying

$$ \begin{align*}A(\zeta_{q})=A(\zeta_{p})=\dotsb=A(\zeta_{p^{k}})=0\neq A(\zeta_{p^{k+1}}).\end{align*} $$

Then there is some j such that $A_{j\ \bmod\ p^{k}}$ is absorbed $\ \bmod\ p^{k}q$ . In particular, (wT2) fails for A.

Proof. By definition, A is absorption-free; therefore, there is some j such that $A_{j\ \bmod\ p^{k}}$ is not absorbed $\ \bmod\ p^{k+1}$ . Hence,

$$ \begin{align*}A_{j\ \bmod\ p^{k}}=\bigcup_{i=1}^{r} A_{j+(\ell_{i}q) p^{k}\ \bmod\ p^{k+1}},\end{align*} $$

where $r\geq 2$ , the $\ell _{i}$ are pairwise distinct $\ \bmod\ p$ and all sets in the above union are nonempty. This shows that the multiset $\frac {N}{p^{k+1}q}\cdot A_{j\ \bmod\ p^{k}}$ has elements on r distinct q-cycles, namely

$$ \begin{align*}\frac{jN}{p^{k+1}q}+\ell_{i}\frac{N}{p}+\frac{N}{q}\mathbb{Z}_{N}, \;\;\;\; 1\leq i\leq r.\end{align*} $$

Consider two arbitrary elements from two different q-cycles (relabeling the $\ell _{i}$ if necessary), say

$$ \begin{align*}\frac{a_{1}N}{p^{k+1}q}=\frac{jN}{p^{k+1}q}+\ell_{1}\frac{N}{p}+m_{1}\frac{N}{q} \;\;\;\; \text{ and } \;\;\;\; \frac{a_{2}N}{p^{k+1}q}=\frac{jN}{p^{k+1}q}+\ell_{2}\frac{N}{p}+m_{2}\frac{N}{q},\end{align*} $$

where $a_{1}, a_{2}\in A_{j\ \bmod\ p^{k}}$ . We will show that $m_{1}\equiv m_{2}\ \bmod\ q$ ; if not, then

$$ \begin{align*}\frac{N}{p^{k+1}q}(a_{2}-a_{1})=(\ell_{2}-\ell_{1})\frac{N}{p}+(m_{2}-m_{1})\frac{N}{q}\in\frac{N}{pq}\mathbb{Z}_{N}^{\star}\end{align*} $$

or, equivalently $a_{2}-a_{1}\in p^{k}\mathbb {Z}_{N}^{\star }$ or $\operatorname {\mathrm {ord}}(a_{2}-a_{1})=\frac {N}{p^{k}}$ , which by Corollary 3.4 gives $B(\zeta _{N}^{p^{k}})=0$ , contradicting the hypothesis $A(\zeta _{p^{k+1}})\neq 0$ due to Lemma 10.3 (especially equation (10.4), with the roles of A and B reversed). Thus, $m_{1}\equiv m_{2}\ \bmod\ q$ , and considering any other pair of elements of $\frac {N}{p^{k+1}q}\cdot A_{j\ \bmod\ p^{k}}$ on two different q-cycles, where one element is either $\frac {a_{1}N}{p^{k+1}q}$ or $\frac {a_{2}N}{p^{k+1}q}$ , we obtain

$$ \begin{align*}\frac{N}{p^{k+1}q} A_{j\ \bmod\ p^{k}}\subseteq \frac{jN}{p^{k+1}q}+\frac{N}{p}\mathbb{Z}_{N}+m_{1}\frac{N}{q},\end{align*} $$

by repeating the above argument. This shows that $\frac {N}{p^{k+1}q}\cdot A_{j\ \bmod\ p^{k}}$ is supported on a p-cycle; thus, $A_{j\ \bmod\ p^{k}}$ is absorbed $\ \bmod\ p^{k}q$ , as desired. The fact that (wT2) fails follows easily from equation (11.1).

Corollary 11.3. Let $N\in \mathscr {S}_{p,q}^{\prime }$ , $(A,B)$ a spectral pair in $\mathbb {Z}_{N}$ with $A\in \mathscr {F}_{\max }(N)$ . It holds

$$ \begin{align*}A(\zeta_{q^{2}})=B(\zeta_{q^{2}})=A(\zeta_{p^{2}})=B(\zeta_{p^{2}})=0.\end{align*} $$

If $p<q$ , then

$$ \begin{align*}A(\zeta_{p^{3}})=\dotsb=A(\zeta_{p^{{\lceil{\log_{p}q}\rceil}+1}})=B(\zeta_{p^{3}})=\dotsb=B(\zeta_{p^{{\lceil{\log_{p}q}\rceil}+1}})=0,\end{align*} $$

as well. Moreover,

$$ \begin{align*}A(\zeta_{N}^{q})=B(\zeta_{N}^{q})=A(\zeta_{N}^{p})=\dotsb=A(\zeta_{N}^{p^{{\lceil{\log_{p}q}\rceil}}})=B(\zeta_{N}^{p})=\dotsb=B(\zeta_{N}^{p^{{\lceil{\log_{p}q}\rceil}}})=0.\end{align*} $$

Proof. By Proposition 11.2, property (wT2) fails for both A and B. Combined with Proposition 10.11, this shows that

$$ \begin{align*}A(\zeta_{p^{2}})=B(\zeta_{p^{2}})=A(\zeta_{q^{2}})=B(\zeta_{q^{2}})=0,\end{align*} $$

and then Lemma 10.3 implies

$$ \begin{align*}A(\zeta_{N}^{p})=B(\zeta_{N}^{p})=A(\zeta_{N}^{q})=B(\zeta_{N}^{q})=0.\end{align*} $$

Next, assume $p<q$ , and suppose

$$ \begin{align*}A(\zeta_{p})=\dotsb=A(\zeta_{p^{k}})=0\neq A(\zeta_{p^{k+1}}).\end{align*} $$

By Proposition 11.2, there is some j such that $A_{j\ \bmod\ p^{k}}$ is absorbed $\ \bmod\ p^{k}q$ , that is,

$$ \begin{align*}A_{j\ \bmod\ p^{k}}=A_{j+\ell p^{k}\ \bmod\ p^{k}q}\end{align*} $$

for some $\ell $ . But then,

$$ \begin{align*}A_{j\ \bmod\ p^{k}}\subseteq A_{j+\ell p^{k}\ \bmod\ pq};\end{align*} $$

therefore,

$$ \begin{align*}\frac{\lvert A \rvert}{p^{k}}=\lvert A_{j\ \bmod\ p^{k}} \rvert\leq \lvert A_{j+\ell p^{k}\ \bmod\ pq} \rvert=\frac{\lvert A \rvert}{pq},\end{align*} $$

which yields $p^{k-1}> q$ or, equivalently, $k>\log _{p}q+1$ , so finally

$$ \begin{align*}k\geq{\lceil{\log_{p}q}\rceil}+1.\end{align*} $$

Reversing the roles of A and B, we obtain the same result for B. The final part then follows directly from Lemma 10.3.

Lemma 11.4. Let $(A,B)$ be a spectral pair in $\mathbb {Z}_{N}$ , where $N\in \mathscr {S}_{p,q}^{\prime }$ and $A\in \mathscr {F}_{\max }(N)$ . Then neither A nor B satisfy (wT1) as

$$ \begin{align*}\lvert U_{A}^{N}(p) \rvert, \lvert U_{B}^{N}(p) \rvert\geq {\lceil{\log_{p}q}\rceil}\end{align*} $$

and

$$ \begin{align*}\lvert U_{A}^{N}(q) \rvert, \lvert U_{B}^{N}(q) \rvert\geq {\lceil{\log_{q}p}\rceil}.\end{align*} $$

Proof. Without loss of generality, we may assume $p<q$ so that the second inequality becomes $\lvert U_{A}^{N}(q) \rvert , \lvert U_{B}^{N}(q) \rvert \geq 1$ , which easily follows from Proposition 10.4. We remind that $m_{p}(A)$ denotes as usual the maximal exponent x such that $A(\zeta _{N}^{p^{x}})\neq 0$ . We will show

$$ \begin{align*}\lvert U_{B}^{N}(p) \rvert\geq{\lceil{\log_{p}q}\rceil},\end{align*} $$

and the inequality $\lvert U_{A}^{N}(p) \rvert \geq {\lceil {\log _{p}q}\rceil }$ has similar proof. Denote

$$ \begin{align*}s=\lvert [0,m_{p}(A)]\cap R_{A}^{N}(p) \rvert.\end{align*} $$

We will show the existence of j satisfying

$$ \begin{align*}\lvert A_{j\ \bmod\ p^{m-m_{p}(A)-1}q^{n-1}} \rvert=p^{s}q\end{align*} $$

and $A_{j\ \bmod\ p^{m-m_{p}(A)-1}q^{n-1}}$ is not absorbed $\ \bmod\ p^{m-m_{p}(A)}q^{n-1}$ . For convenience, we will put $d=p^{m-m_{p}(A)-1}q^{n-1}$ . Suppose that

$$ \begin{align*}A(\zeta_{N})=A(\zeta_{N}^{p})=\dotsb=A(\zeta_{N}^{p^{k}})=0\neq A(\zeta_{N}^{p^{k+1}})\end{align*} $$

so that

$$ \begin{align*}B(\zeta_{p})=B(\zeta_{p^{2}})=\dotsb=B(\zeta_{p^{k+1}})=0\neq B(\zeta_{p^{k+2}})\end{align*} $$

by Lemma 10.3. It holds

$$ \begin{align*}A(X)\equiv P(X)\Phi_{p}(X^{N/p})+Q(X)\Phi_{q}(X^{N/q})\ \bmod\ (X^{N}-1)\end{align*} $$

for some $P(X),Q(X)\in \mathbb {Z}_{\geq 0}[X]$ by Theorem 5.2, and $P\not \equiv 0$ by Theorem 10.9(2). Replacing X by $X^{p}$ and observing that $\Phi _{q}(X^{N/q})\equiv \Phi _{q}(X^{pN/q})\ \bmod\ (X^{N}-1)$ , we obtain

$$ \begin{align*}A(X^{p})\equiv pP(X^{p})+Q(X^{p})\Phi_{q}(X^{N/q})\ \bmod\ (X^{N}-1).\end{align*} $$

Since $A(\zeta _{N}^{p})=0$ , we must have

$$ \begin{align*}pP(\zeta_{N}^{p})=A(\zeta_{N}^{p})-Q(\zeta_{N}^{p})\Phi_{q}(\zeta_{q}^{p})=0,\end{align*} $$

therefore

$$ \begin{align*}P(X^{p})\equiv \widetilde{P}(X^{p})\Phi_{p}(X^{N/p})+\widetilde{Q}(X^{p})\Phi_{q}(X^{N/q})\ \bmod\ (X^{N}-1),\end{align*} $$

where $\widetilde {P}(X),\widetilde {Q}(X)\in \mathbb {Z}_{\geq 0}[X]$ , hence

$$ \begin{align*}A(X^{p})\equiv pP_{1}(X^{p})\Phi_{p}(X^{N/p})+Q_{1}(X^{p})\Phi_{q}(X^{N/q})\ \bmod\ (X^{N}-1),\end{align*} $$

where $P_{1}(X^{p})=\widetilde {P}(X^{p})$ and $Q_{1}(X^{p})=Q(X^{p})+p\widetilde {Q}(X^{p})$ . The polynomial $P_{1}$ is not identically zero since $A(\zeta _{N}^{p^{k+1}})\neq 0$ (see Theorem 5.2). Repeating this process for the roots

$$ \begin{align*}\zeta_{N}^{p^{2}},\dotsc,\zeta_{N}^{p^{k}},\end{align*} $$

we obtain

(11.2) $$ \begin{align} A(X^{p^{k}})\equiv p^{k}P_{k}(X^{p^{k}})\Phi_{p}(X^{N/p})+Q_{k}(X^{p^{k}})\Phi_{q}(X^{N/q})\ \bmod\ (X^{N}-1), \end{align} $$

where $P_{k}(X),Q_{k}(X)\in \mathbb {Z}_{\geq 0}[X]$ , and $P_{k}$ is not identically zero since $A(\zeta _{N}^{p^{k+1}})\neq 0$ . As

(11.3) $$ \begin{align} A(X^{p^{k+1}})\equiv p^{k+1}P_{k}(X^{p^{k+1}})+Q_{k}(X^{p^{k+1}})\Phi_{q}(X^{N/q})\ \bmod\ (X^{N}-1) \end{align} $$

is the mask polynomial of the mutliset $p^{k+1}\cdot A$ , we deduce that there are elements in $p^{k+1}\cdot A$ whose multiplicity is exactly $p^{k+1}$ (in general, since A is a proper set, the multiplicity of any element in $d\cdot A$ cannot exceed d). The element $p^{k+1}a$ can only have multiplicity $p^{k+1}$ in A if

$$ \begin{align*}a+\frac{N}{p^{k+1}}\mathbb{Z}_{N}\subseteq A,\end{align*} $$

i.e., a is an element of a $p^{k+1}$ -cycle contained in A or, equivalently, $\lvert A_{a\ \bmod\ p^{m-k-1}q^{n}} \rvert =p^{k+1}$ . A cannot have two $p^{k+1}$ -cycles of the form

$$ \begin{align*}a+\frac{N}{p^{k+1}}\mathbb{Z}_{N}, \;\;\;\; a+\ell\frac{N}{p^{k+1}q}+\frac{N}{p^{k+1}}\mathbb{Z}_{N},\end{align*} $$

for $\ell \not \equiv 0\ \bmod\ q$ because, in that case, we would have

$$ \begin{align*}\ell p^{m-k-1}q^{n-1}+p^{m-k-1}q^{n}\mathbb{Z}_{N}\subseteq A-A,\end{align*} $$

which implies that

$$ \begin{align*}(A-A)\cap d\mathbb{Z}_{N}^{\star}\neq0, \;\;\;\; \forall d\in{\left\{{p^{m-k-1}q^{n-1},p^{m-k}q^{n-1},\dotsc,p^{m-2}q^{n-1},p^{m-1}q^{n-1}}\right\}},\end{align*} $$

whence

$$ \begin{align*}B(\zeta_{pq})=B(\zeta_{p^{2}q})=\dotsb=B(\zeta_{p^{k+1}q})=0\end{align*} $$

by Theorem 3.3(i), which means that B satisfies (wT2) , contradicting Proposition 11.2. The above show that

(11.4) $$ \begin{align} \lvert A_{a\ \bmod\ p^{m-k-1}q^{n}} \rvert=p^{k+1}\Longrightarrow A_{a\ \bmod\ p^{m-k-1}q^{n-1}}\text{ is absorbed }\ \bmod\ p^{m-k-1}q^{n}. \end{align} $$

Now let

$$ \begin{align*}R_{A}^{N}(p)\cap[0,m_{p}(A)]={\left\{{r_{0},r_{1},\dotsc,r_{s-1}}\right\}},\end{align*} $$

where the $r_{i}$ are in increasing order. We know already that $r_{i}=i$ for $0\leq i\leq k$ . Continuing from equation (11.2), we obtain

$$ \begin{align*}A(X^{p^{r_{k+1}}})\equiv p^{k+1}P_{k}(X^{p^{r_{k+1}}})+Q_{k}(X^{p^{r_{k+1}}})\Phi_{q}(X^{N/q})\ \bmod\ (X^{N}-1).\end{align*} $$

Since $A(\zeta _{N}^{p^{r_{k+1}}})=0\neq A(\zeta _{N}^{p^{m_{p}(A)}})$ , we get that $P_{k}(\zeta _{N}^{p^{r_{k+1}}})=0\neq P_{k}(\zeta _{N}^{p^{m_{p}(A)}})$ , whence by Theorem 3.3(i) we obtain

$$ \begin{align*}P_{k}(X^{p^{r_{k+1}}})\equiv\widetilde{P}_{k}(X^{p^{r_{k+1}}})\Phi_{p}(X^{N/p})+\widetilde{Q}_{k}(X^{p^{r_{k+1}}})\Phi_{q}(X^{N/q})\ \bmod\ (X^{N}-1)\end{align*} $$

for some $\widetilde {P}_{k}(X), \widetilde {Q}_{k}(X)\in \mathbb {Z}_{\geq 0}[X]$ , with $\widetilde {P}_{k}$ not identically zero. This gives

$$ \begin{align*}A(X^{p^{r_{k+1}}})\equiv p^{k+1}P_{k+1}(X^{p^{r_{k+1}}})\Phi_{p}(X^{N/p})+Q_{k+1}(X^{p^{r_{k+1}}})\Phi_{q}(X^{N/q})\ \bmod\ (X^{N}-1),\end{align*} $$

where $P_{k+1}(X)=\widetilde {P}_{k}(X)$ and $Q_{k+1}(X)=Q_{k}(X)+p^{k+1}\widetilde {Q}_{k}(X)$ . Repeating this process for the roots

$$ \begin{align*}\zeta_{N}^{p^{r_{k+2}}},\dotsc,\zeta_{N}^{p^{r_{s-1}}},\end{align*} $$

we obtain

$$ \begin{align*}A(X^{p^{r_{s-1}}})\equiv p^{s-1}P_{s-1}(X^{p^{r_{s-1}}})\Phi_{p}(X^{N/p})+Q_{s-1}(X^{p^{r_{s-1}}})\Phi_{q}(X^{N/q})\ \bmod\ (X^{N}-1)\end{align*} $$

for some $P_{s-1}(X),Q_{s-1}(X)\in \mathbb {Z}_{\geq 0}[X]$ , where $P_{s-1}$ is not identically zero since $r_{s-1}<m_{p}(A)$ and $A(\zeta _{N}^{p^{m_{p}(A)}})\neq 0$ ; this is achieved by repeated use of Theorem 5.2. Therefore, it holds

$$ \begin{align*}A(X^{p^{m_{p}(A)+1}})\equiv p^{s}P_{s-1}(X^{p^{m_{p}(A)+1}})+Q_{s-1}(X^{p^{m_{p}(A)+1}})\Phi_{q}(X^{N/q})\ \bmod\ (X^{N}-1).\end{align*} $$

By definition of $m_{p}(A)$ , we have

$$ \begin{align*}A(\zeta_{N}^{p^{m_{p}(A)+1}})=A(\zeta_{N}^{p^{m_{p}(A)+2}})=\dotsb=A(\zeta_{N}^{p^{m}})=0,\end{align*} $$

hence

$$ \begin{align*}P_{s-1}(\zeta_{N}^{p^{m_{p}(A)+1}})=P_{s-1}(\zeta_{N}^{p^{m_{p}(A)+2}})=\dotsb=P_{s-1}(\zeta_{N}^{p^{m}})=0,\end{align*} $$

so by Lemma 10.2 we get

$$ \begin{align*}P_{s-1}(X^{p^{m_{p}(A)+1}})\equiv P_{s}(X^{p^{m_{p}(A)+1}})\Phi_{q}(X^{N/q})\ \bmod\ (X^{N}-1),\end{align*} $$

where $P_{s}(X)\in \mathbb {Z}_{\geq 0}[X]$ , hence

(11.5) $$ \begin{align} A(X^{p^{m_{p}(A)+1}})\equiv(p^{s}P_{s}(X^{p^{m_{p}(A)+1}})+Q_{s-1}(X^{p^{m_{p}(A)+1}}))\Phi_{q}(X^{N/q})\ \bmod\ (X^{N}-1) \end{align} $$

so that the multiset $p^{m_{p}(A)+1}\cdot A$ is a disjoint union of q-cycles. It is clear from equation (11.5) that there is some j with $\lvert A_{j\ \bmod\ p^{m-m_{p}(A)-1}q^{n}} \rvert \geq p^{s}$ . However, we will show that

$$ \begin{align*}\lvert A_{j\ \bmod\ p^{m-m_{p}(A)-1}q^{n}} \rvert\leq p^{s}\end{align*} $$

for every j. For this purpose, consider the p-adic expansion of $a-j$ , where a is an arbitrary element of $A_{j\ \bmod\ p^{m-m_{p}(A)-1}q^{n}}$

$$ \begin{align*}a-j\equiv a_{m-m_{p}(A)-1}p^{m-m_{p}(A)-1}+\dotsb+a_{m-1}p^{m-1}\ \bmod\ p^{m},\end{align*} $$

where, as usual, $0\leq a_{i}\leq p-1$ , $m-m_{p}(A)-1\leq i\leq m-1$ . Now, if $\lvert A_{j\ \bmod\ p^{m-m_{p}(A)-1}q^{n}} \rvert> p^{s}$ , then there would exist two elements $a,a^{\prime }\in A_{j\ \bmod\ p^{m-m_{p}(A)-1}q^{n}}$ such that the p-adic expansions of $a-j$ and $a^{\prime }-j$ would have the same digits at all places $m-r$ for $r-1\in R_{A}^{N}(p)$ . Therefore, $a-a^{\prime }=(a-j)-(a^{\prime }-j)\in d\mathbb {Z}_{N}^{\star }$ , where $d=p^{m-r}q^{n}$ , with $r-1\leq m_{p}(A)$ and $r-1\notin R_{A}^{N}(p)$ . By Lemma 10.3, we would have $r\notin S_{B}^{N}(p)$ , whence $B(\zeta _{p^{r}})\neq 0$ , contradicting Theorem 3.3(i) or Corollary 3.4, which yield $B(\zeta _{p^{r}})=0$ due to $a-a^{\prime }\in p^{m-r}q^{n}\mathbb {Z}_{N}^{\star }$ .

To summarize, we have $\lvert A_{j\ \bmod\ p^{m-m_{p}(A)-1}q^{n}} \rvert \leq p^{s}$ for every j, and equality occurs for some j. Using the same arguments as above, we deduce that, if $\lvert A_{j\ \bmod\ p^{m-m_{p}(A)-1}q^{n}} \rvert =p^{s}$ , then the elements of $A_{j\ \bmod\ p^{m-m_{p}(A)-1}q^{n}}-j$ obtain all possible arrangements of p-adic digits at the places $m-r$ , where $r-1\in R_{A}^{N}(p)$ ; in particular, $A_{j\ \bmod\ p^{m-m_{p}(A)-1}q^{n}}$ must be a disjoint union of $p^{k+1}$ -cycles. So, let $\lvert A_{j\ \bmod\ p^{m-m_{p}(A)-1}q^{n}} \rvert = p^{s}$ . By equations (11.4) and (11.5), we obtain

$$ \begin{align*}\lvert A_{j\ \bmod\ p^{m-k-1}q^{n-1}} \rvert=p^{k+1}, \;\;\;\; \lvert A_{j\ \bmod\ p^{m-m_{p}(A)-1}q^{n-1}} \rvert=p^{s}q.\end{align*} $$

We observe that $A_{j\ \bmod\ p^{m-m_{p}(A)-1}q^{n-1}}$ is equidistributed $\ \bmod\ p^{m-m_{p}(A)-1}q^{n}$ , while $A_{j\ \bmod\ p^{m-k-1}q^{n-1}}$ is absorbed $\ \bmod\ p^{m-k-1}q^{n}$ . For every $r\in [k,m_{p}(A)]$ , we will take into account the number of nonempty sets in the partition

$$ \begin{align*}A_{j\ \bmod\ p^{m-r-1}q^{n-1}}=\bigsqcup_{u=0}^{q-1}A_{j+u p^{m-r-1}q^{n-1}\ \bmod\ p^{m-r-1}q^{n}},\end{align*} $$

denoted by $f_{j}(r)$ , so that $1\leq f_{j}(r)\leq q$ for all $r\in [k,m_{p}(A)]$ and $f_{j}(m_{p}(A))=q$ , $f_{j}(k)=1$ . Now, pick $j^{\prime }$ such that $j^{\prime }\equiv j\ \bmod\ p^{m-m_{p}(A)-1}q^{n}$ and

$$ \begin{align*}f_{j^{\prime}}(r-1)=\max_{0\leq\ell\leq p-1}f_{j^{\prime}+\ell p^{m-r-1}q^{n-1}}(r-1).\end{align*} $$

Without loss of generality, we may simply have $j^{\prime }=j$ , and it holds

$$ \begin{align*}f_{j}(r-1)\geq\frac{1}{p} f_{j}(r), \;\;\;\; r\in[k+1,m_{p}(A)].\end{align*} $$

We observe that, if $f_{j}(r-1)<f_{j}(r)$ , then $r+1\in U_{B}^{N}(p)$ . Indeed, consider the multiset $p^{r}\cdot A_{j\ \bmod\ p^{m-r-1}q^{n-1}}$ , which is supported at the $pq$ -cycle $p^{r}j+\frac {N}{pq}\mathbb {Z}_{N}$ . We will show that $A(\zeta _{N}^{p^{r}})\neq 0$ , which implies $B(\zeta _{p^{r+1}})\neq 0$ by Lemma 10.3. Assume otherwise, that $A(\zeta _{N}^{p^{r}})=0$ ; hence, $p^{r}\cdot A_{j\ \bmod\ p^{m-r-1}q^{n-1}}$ must be a disjoint union of p- and q-cycles. Since $f_{j}(r-1)<f_{j}(r)$ , we cannot have any q-cycles because

$$ \begin{align*}f_{j+\ell p^{m-r-1}q^{n-1}}(r-1)\leq f_{j}(r-1)<f_{j}(r)\leq f_{j}(m_{p}(A))=q, \;\;\;\; 0\leq\ell\leq p-1,\end{align*} $$

which means that, for every $0\leq \ell \leq p-1$ , there is $0\leq u\leq q-1$ such that

$$ \begin{align*}A_{j+\ell p^{m-r-1}q^{n-1}+u p^{m-r}q^{n-1}\ \bmod\ p^{m-r}q^{n}}=\varnothing.\end{align*} $$

But $p^{r}\cdot A_{j\ \bmod\ p^{m-r-1}q^{n-1}}$ cannot be a disjoint union of p-cycles either because in this case $A_{j\ \bmod\ p^{m-r-1}q^{n-1}}$ would be equidistributed $\ \bmod\ p^{m-r}q^{n-1}$ , whence $f_{j}(r-1)=f_{j}(r)$ , contradiction. Hence, $A(\zeta _{N}^{p^{r}})B(\zeta _{p^{r+1}})\neq 0$ . Moreover, $p^{r}\cdot A_{j\ \bmod\ p^{m-r-1}q^{n-1}}$ can be supported neither on a q-cycle, because in this case $f_{j}(r-1)=f_{j}(r)$ and

$$ \begin{align*}f_{j+\ell p^{m-r-1}q^{n-1}}(r-1)=0, \;\;\;\; 1\leq \ell \leq p-1,\end{align*} $$

nor on a p-cycle because it would hold

$$ \begin{align*}f_{j+\ell p^{m-r-1}q^{n-1}}(r-1)=f_{j}(r)=1, \;\;\;\; 0\leq \ell\leq p-1,\end{align*} $$

contradiction. Hence, by Proposition 5.5, we obtain

$$ \begin{align*}(p^{r}A-p^{r}A)\cap\frac{N}{pq}\mathbb{Z}_{N}^{\star}\neq\varnothing,\end{align*} $$

so there are $a,a^{\prime }\in A$ such that $a-a^{\prime }\in \frac {N}{p^{r+1}q}$ , whence $B(\zeta _{p^{r+1}q})=0$ by Theorem 3.3(i), and $r+1\in U_{B}^{N}(p)$ , as desired.

For the last part of our proof, we will just show that we have $f_{j}(r-1)<f_{j}(r)$ for at least ${\lceil {\log _{p}q}\rceil }$ values of r. Indeed, let

$$ \begin{align*}{\left\{{r_{1},\dotsc,r_{t}}\right\}}={\left\{{r\in[k,m_{p}(A)]:f_{j}(r-1)<f_{j}(r)}\right\}}.\end{align*} $$

By definition and the property $f_{j}(r-1)\geq \frac {1}{p}f_{j}(r)$ for all r, we obtain

$$ \begin{align*} q=f_{j}(r_{t})\leq pf_{j}(r_{t}-1)=pf_{j}(r_{t-1})\leq p^{2} f_{j}(r_{t-1}-1)=p^{2} f_{j}(r_{t-2})\leq \dotsb\\ \dotsb\leq p^{t-1}f_{j}(r_{1})\leq p^{t}f_{j}(r_{1}-1)=p^{t}f_{j}(k)=p^{t}, \end{align*} $$

which clearly implies $t\geq {\lceil {\log _{p}q}\rceil }$ , finally showing

$$ \begin{align*}\lvert U_{B}^{N}(p)\cap[1,m_{p}(A)+1] \rvert\geq {\lceil{\log_{p}q}\rceil},\end{align*} $$

as desired.

Corollary 11.5. Let $(A,B)$ be a spectral pair in $\mathbb {Z}_{N}$ , where $N\in \mathscr {S}_{p,q}^{\prime }$ and $A\in \mathscr {F}_{\max }(N)$ . Then

$$ \begin{align*}p^{\lvert S_{B}^{N}(p) \rvert+{\lceil{\log_{p}q}\rceil}}q^{\lvert S_{B}^{N}(q) \rvert+{\lceil{\log_{q}p}\rceil}}\mid \lvert B \rvert\end{align*} $$

and

$$ \begin{align*}p^{\lvert S_{A}^{N}(p) \rvert+{\lceil{\log_{p}q}\rceil}}q^{\lvert S_{A}^{N}(q) \rvert+{\lceil{\log_{q}p}\rceil}}\mid \lvert A \rvert.\end{align*} $$

Proof. By Lemmata 10.5 and 11.4 we obtain

$$ \begin{align*}p^{\lvert S_{B}^{N}(p) \rvert+{\lceil{\log_{p}q}\rceil}}\mid \lvert B \rvert.\end{align*} $$

Reversing the roles of A and B and of p and q, we obtain the desired result.

If $p<q$ , we observe that the power of p dividing $\lvert A \rvert $ with $A\in \mathscr {F}_{\max }(N)$ is at least

$$ \begin{align*}\lvert S_{A}^{N}(p) \rvert+{\lceil{\log_{p}q}\rceil}\geq 2{\lceil{\log_{p}q}\rceil}+2\geq6,\end{align*} $$

which can be seen by Theorem 10.9 and Corollary 11.3. Moreover, the power of q dividing $\lvert A \rvert $ is at least

$$ \begin{align*}\lvert S_{A}^{N}(q) \rvert+1\geq 4,\end{align*} $$

again by Theorem 10.9 and Corollary 11.3. We have thus proven:

Corollary 11.6. Let $N=p^{m}q^{n}$ , with $p<q$ , and let $A\subseteq \mathbb {Z}_{N}$ be spectral. If either $m\leq 6$ or $n\leq 4$ , then A tiles. The same conclusion holds if $p^{m-4}<q^{2}$ .

Proof. Assume otherwise, that $N\in \mathscr {S}_{p,q}$ ; without loss of generality, we may assume $N\in \mathscr {S}_{p,q}^{\prime }$ . Let $A\in \mathscr {F}_{\max }(N)$ so that $p^{6}q^{4}\mid \lvert A \rvert $ , as shown above. By Proposition 6.2, this would mean that A tiles if either $m\leq 6$ or $n\leq 4$ , contradiction. For the second part, we observe that $p^{m-4}<q^{2}$ is equivalent to $p^{\frac {m}{2}-2}<q$ or, equivalently,

$$ \begin{align*}\frac{m}{2}-1\leq{\lceil{\log_{p}q}\rceil}\Leftrightarrow m\leq 2{\lceil{\log_{p}q}\rceil}+2\leq \lvert S_{A}^{N}(p) \rvert+{\lceil{\log_{p}q}\rceil},\end{align*} $$

which again implies that $p^{m}\mid \lvert A \rvert $ ; hence, A tiles by Proposition 6.2, contradiction. This completes the proof.

We may assume henceforth that both exponents are at least $5$ , and that of the smallest prime is at least $7$ . We will refine the above bound by introducing a new concept.

Definition 11.7. Let $(A,B)$ be a primitive spectral pair in $\mathbb {Z}_{N}$ . Define the p-root deficit of A as

$$ \begin{align*}\operatorname{def}_{p}(A)=\left| {{\left\{{x:A(\zeta_{p^{x+1}})\neq0=B(\zeta_{N}^{p^{x}})}\right\}}}\right | ,\end{align*} $$

and similarly define $\operatorname {def}_{q}(A)$ , $\operatorname {def}_{p}(B)$ , $\operatorname {def}_{q}(B)$ .

Remark. We should note that the root deficits of a spectral set A always depend on the choice of the spectrum B.

Lemma 11.8. Let $(A,B)$ be a primitive spectral pair in $\mathbb {Z}_{N}$ , $N\in \mathscr {S}_{p,q}^{\prime }$ , $A\in \mathscr {F}_{\max }(N)$ . Then, the following inequalities hold:

$$ \begin{align*} \lvert A \rvert=\lvert B \rvert\leq\min\{p^{\lvert S_{B}^{N}(p) \rvert+\operatorname{def}_{p}(B)}q^{\lvert S_{A}^{N}(q) \rvert},p^{\lvert S_{A}^{N}(p) \rvert+\operatorname{def}_{p}(A)}q^{\lvert S_{B}^{N}(q) \rvert},\\ p^{\lvert S_{B}^{N}(p) \rvert}q^{\lvert S_{A}^{N}(q) \rvert+\operatorname{def}_{q}(A)}, p^{\lvert S_{A}^{N}(p) \rvert}q^{\lvert S_{B}^{N}(q) \rvert+\operatorname{def}_{q}(B)}\} \end{align*} $$

Proof. We will show that

$$ \begin{align*}\lvert A \rvert\leq p^{\lvert S_{B}^{N}(p) \rvert}q^{\lvert S_{A}^{N}(q) \rvert+\operatorname{def}_{q}(A)}.\end{align*} $$

All the other inequalities are obtained by reversing the roles of p, q and of A, B. First, we will prove that

(11.6) $$ \begin{align} \lvert A_{j\ \bmod\ q^{n}} \rvert\leq p^{\lvert S_{B}^{N}(p) \rvert} \end{align} $$

for all j. Let

$$ \begin{align*}S_{B}^{N}(p)={\left\{{x_{1},\dotsc,x_{t}}\right\}}\subseteq{\left\{{1,2,\dotsc,m}\right\}},\end{align*} $$

where $t=\lvert S_{B}^{N}(p) \rvert $ and the $x_{i}$ are in increasing order. We will write every element of $a\in A_{j\ \bmod\ q^{n}}$ in p-adic representation, that is,

$$ \begin{align*}a\equiv a_{0}+a_{1}p+\dotsb+a_{m-1}p^{m-1}\ \bmod\ p^{m},\end{align*} $$

where, as usual, $0\leq a_{i}\leq p-1$ , $0\leq i\leq m-1$ . No two elements of $A_{j\ \bmod\ q^{n}}$ have the same p-adic digits; otherwise, $N=p^{m}q^{n}$ would divide their difference, i.e., they would be equal. Moreover, two distinct elements $a,a^{\prime }\in A_{j\ \bmod\ q^{n}}$ cannot have the same p-adic digits at the places

$$ \begin{align*}m-x_{t},\dotsc,m-x_{1},\end{align*} $$

otherwise, $a-a^{\prime }\in p^{m-x}q^{n}\mathbb {Z}_{N}^{\star }$ where $x\notin S_{B}^{N}(p)$ , and as a consequence,

$$ \begin{align*}B(\zeta_{\operatorname{\mathrm{ord}}(a-a^{\prime})})=B(\zeta_{p^{x}})\neq0,\end{align*} $$

contradicting Corollary 3.4. Thus, the elements of $A_{j\ \bmod\ q^{n}}$ have distinct digits at one of the places $m-x_{i}$ . This clearly shows that

$$ \begin{align*}\lvert A_{j\ \bmod\ q^{n}} \rvert\leq p^{t}=p^{\lvert S_{B}^{N}(p) \rvert},\end{align*} $$

proving our claim. Next, we will show that there is some j such that

$$ \begin{align*}\lvert A_{j\ \bmod\ q^{n}} \rvert\geq \frac{\lvert A \rvert}{q^{\lvert S_{A}^{N}(q) \rvert+\operatorname{def}_{q}(A)}}.\end{align*} $$

Recall that $m_{q}(B)$ is the maximal integer $x\in [0,n-1]$ for which

$$ \begin{align*}B(\zeta_{N}^{q^{x}})\neq0.\end{align*} $$

Since $B\in \mathscr {F}_{\max }(N)$ , such an exponent exists, as we have already seen. Furthermore, Lemma 10.3 and Proposition 10.4 imply that

$$ \begin{align*}A(\zeta_{q^{m_{q}(B)+1}})\neq0=A(\zeta_{pq^{m_{q}(B)+1}}).\end{align*} $$

Applying Lemma 9.2 for $d=q^{m_{q}(B)}$ , with the roles of $p,q$ and $A,B$ reversed, we obtain that $A_{j\ \bmod\ q^{m_{q}(B)}}$ is either absorbed or equidistributed $\ \bmod\ q^{m_{q}(B)+1}$ for every j. Since $A(\zeta _{q^{m_{q}(B)+1}})\neq 0$ , there must exist some j such that $A_{j\ \bmod\ q^{m_{q}(B)}}$ is absorbed $\ \bmod\ q^{m_{q}(B)+1}$ . Without loss of generality, we put

$$ \begin{align*}A_{j\ \bmod\ q^{m_{q}(B)}}=A_{j\ \bmod\ q^{m_{q}(B)+1}}.\end{align*} $$

The set $A_{j\ \bmod\ q^{m_{q}(B)+1}}$ is in turn equidistributed $\ \bmod\ pq^{m_{q}(B)+1}$ since the multiset $\frac {N}{pq^{m_{q}(B)+1}}\cdot A_{j\ \bmod\ q^{m_{q}(B)}}$ is contained in a $pq$ -cycle for every j, and for this specific value of j, it is supported on a p-cycle. In particular,

$$ \begin{align*}\lvert A_{j+\ell q^{m_{q}(B)+1}\ \bmod\ pq^{m_{q}(B)+1}} \rvert=\frac{1}{p}\lvert A_{j\ \bmod\ q^{m_{q}(B)+1}} \rvert\end{align*} $$

for every $\ell $ . For any $y\leq m_{q}(B)$ with $y+1\in S_{A}^{N}(q)$ , it holds

(11.7) $$ \begin{align} \lvert A_{j\ \bmod\ q^{y+1}} \rvert=\frac{1}{q}\lvert A_{j\ \bmod\ q^{y}} \rvert, \end{align} $$

while if $y\leq m_{q}(B)$ and $y+1\notin S_{A}^{N}(q)$ , it holds

(11.8) $$ \begin{align} \lvert A_{j\ \bmod\ q^{y+1}} \rvert=\lvert A_{j\ \bmod\ q^{y}} \rvert. \end{align} $$

Indeed, since $B(\zeta _{N}^{q^{y}})\neq 0$ by Lemma 10.3, we must have $a-a^{\prime }\notin q^{y}\mathbb {Z}_{N}^{\star }$ for every $a,a^{\prime }\in A$ , $a\neq a^{\prime }$ due to Theorem 3.3(i) (or Corollary 3.4). If $A_{j\ \bmod\ q^{y}}$ were not absorbed $\ \bmod\ q^{y+1}$ , there would exist some $u\not \equiv 0\ \bmod\ q$ such that $A_{j+u q^{y}\ \bmod\ q^{y+1}}\neq \varnothing $ ; hence, for some $0\leq \ell \leq p-1$ satisfying

$$ \begin{align*}\ell q^{m_{q}(B)+1-y}\not\equiv u\ \bmod\ p,\end{align*} $$

and $a\in A_{j+\ell q^{m_{q}(B)+1}\ \bmod\ pq^{m_{q}(B)+1}}$ , $a^{\prime }\in A_{j+uq^{y}\ \bmod\ q^{y+1}}$ , we obtain

$$ \begin{align*}a-a^{\prime}\equiv q^{y}(\ell q^{m_{q}(B)+1-y}-u)\ \bmod\ pq^{m_{q}(B)+1},\end{align*} $$

hence $a-a^{\prime }\in q^{y}\mathbb {Z}_{N}^{\star }$ , contradiction. Thus, combining equations (11.7) and (11.8), we get

$$ \begin{align*}\lvert A_{j\ \bmod\ q^{m_{q}(B)+1}} \rvert=\frac{\lvert A \rvert}{q^{\lvert S_{A}^{N}(q)\cap[1,m_{q}(B)+1] \rvert}}.\end{align*} $$

Next, we recall

$$ \begin{align*}\operatorname{def}_{q}(A)= \left| {{\left\{{y\in[1,n]:A(\zeta_{p^{y}})\neq0=B(\zeta_{N}^{p^{y-1}})}\right\}}} \right | ,\end{align*} $$

where the set of y in the description above must satisfy $y>m_{q}(B)+1$ . In other words, every $y\in [m_{q}(B)+2,n]$ either satisfies $A(\zeta _{q^{y}})=0$ or $A(\zeta _{p^{y}})\neq 0=B(\zeta _{N}^{p^{y-1}})$ , hence

$$ \begin{align*}n-m_{q}(B)-1=\lvert S_{A}^{N}(q)\cap[m_{q}(B)+2,n] \rvert+\operatorname{def}_{q}(A).\end{align*} $$

Therefore, by equation (11.6), we get

$$ \begin{align*} p^{\lvert S_{B}^{N}(p) \rvert} &\geq\max_{\ell}\lvert A_{j+\ell q^{m_{q}(B)+1}\ \bmod\ q^{n}} \rvert\\ &\geq\frac{1}{q^{n-m_{q}(B)-1}}\lvert A_{j\ \bmod\ q^{n}} \rvert\\ &= \frac{\lvert A \rvert}{q^{\lvert S_{A}^{N}(q)\cap[m_{q}(B)+2,n] \rvert+\operatorname{def}_{q}(A)}q^{\lvert S_{A}^{N}(q)\cap[1,m_{q}(B)+1] \rvert}}, \end{align*} $$

whence we finally obtain

$$ \begin{align*}\lvert A \rvert\leq p^{\lvert S_{B}^{N}(p) \rvert}q^{\lvert S_{A}^{N}(q) \rvert+\operatorname{def}_{q}(A)},\end{align*} $$

as desired.

Corollary 11.9. Let $(A,B)$ be a spectral pair in $\mathbb {Z}_{N}$ , where $N\in \mathscr {S}_{p,q}^{\prime }$ , $A\in \mathscr {F}_{\max }(N)$ . Then

$$ \begin{align*}p^{{\lceil{\log_{p}q}\rceil}}q^{{\lceil{\log_{q}p}\rceil}}<\min{\left\{{p^{\operatorname{def}_{p}(A)},p^{\operatorname{def}_{p}(B)},q^{\operatorname{def}_{q}(A)},q^{\operatorname{def}_{q}(B)}}\right\}}.\end{align*} $$

If in addition $p<q$ , we get

$$ \begin{align*}\operatorname{def}_{q}(A),\operatorname{def}_{q}(B)\geq3,\end{align*} $$

and

$$ \begin{align*}\operatorname{def}_{p}(A), \operatorname{def}_{p}(B)\geq 2{\lceil{\log_{p}q}\rceil}\geq4.\end{align*} $$

Proof. Denote

$$ \begin{align*}s_{p}=\max{\left\{{\lvert S_{A}^{N}(p) \rvert,\lvert S_{B}^{N}(p) \rvert}\right\}}, \;\;\;\; s_{q}=\max{\left\{{\lvert S_{A}^{N}(q) \rvert,\lvert S_{B}^{N}(q) \rvert}\right\}}.\end{align*} $$

By Corollary 11.5, we obtain

$$ \begin{align*}p^{s_{p}+{\lceil{\log_{p}q}\rceil}}q^{s_{q}+{\lceil{\log_{q}p}\rceil}}\mid\lvert A \rvert,\end{align*} $$

whence by Lemma 11.8 it follows

$$ \begin{align*} p^{s_{p}+{\lceil{\log_{p}q}\rceil}}q^{s_{q}+{\lceil{\log_{q}p}\rceil}}\leq \min\{p^{\lvert S_{B}^{N}(p) \rvert+\operatorname{def}_{p}(B)}q^{\lvert S_{A}^{N}(q) \rvert},p^{\lvert S_{A}^{N}(p) \rvert+\operatorname{def}_{p}(A)}q^{\lvert S_{B}^{N}(q) \rvert},\\ p^{\lvert S_{B}^{N}(p) \rvert}q^{\lvert S_{A}^{N}(q) \rvert+\operatorname{def}_{q}(A)}, p^{\lvert S_{A}^{N}(p) \rvert}q^{\lvert S_{B}^{N}(q) \rvert+\operatorname{def}_{q}(B)}\}, \end{align*} $$

which easily yields the inequality

$$ \begin{align*}p^{{\lceil{\log_{p}q}\rceil}}q^{{\lceil{\log_{q}p}\rceil}}<\min{\left\{{p^{\operatorname{def}_{p}(A)},p^{\operatorname{def}_{p}(B)},q^{\operatorname{def}_{q}(A)},q^{\operatorname{def}_{q}(B)}}\right\}}.\end{align*} $$

Next, suppose $p<q$ so that the above inequality becomes

$$ \begin{align*}p^{{\lceil{\log_{p}q}\rceil}}q<\min{\left\{{p^{\operatorname{def}_{p}(A)},p^{\operatorname{def}_{p}(B)},q^{\operatorname{def}_{q}(A)},q^{\operatorname{def}_{q}(B)}}\right\}}.\end{align*} $$

Since $q^{2}<p^{{\lceil {\log _{p}q}\rceil }}q$ , the above yields

$$ \begin{align*}\operatorname{def}_{q}(A),\operatorname{def}_{q}(B)\geq3\end{align*} $$

and

$$ \begin{align*}p^{2{\lceil{\log_{p}q}\rceil}}\leq\min{\left\{{p^{\operatorname{def}_{p}(A)},p^{\operatorname{def}_{p}(B)}}\right\}}\end{align*} $$

or, equivalently,

$$ \begin{align*}\operatorname{def}_{p}(A), \operatorname{def}_{p}(B)\geq 2{\lceil{\log_{p}q}\rceil}\geq4,\end{align*} $$

as desired.

Proposition 11.10. Let $(A,B)$ be a spectral pair in $\mathbb {Z}_{N}$ such that $N\in \mathscr {S}_{p,q}^{\prime }$ , $A\in \mathscr {F}_{\max }(N)$ and $p<q$ . Then

$$ \begin{align*}\operatorname{def}_{p}(A),\operatorname{def}_{p}(B)\leq m-2-2{\lceil{\log_{p}q}\rceil}\end{align*} $$

and

$$ \begin{align*}\operatorname{def}_{q}(A),\operatorname{def}_{q}(B)\leq n-4.\end{align*} $$

Proof. We remind that $\lvert S_{A}^{N}(p)-1 \rvert $ , $\lvert U_{A}^{N}(p)-1 \rvert $ and $\operatorname {def}_{p}(A)$ are cardinalities of pairwise disjoint subsets of ${\left \{{0,1,\dotsc ,m-1}\right \}}$ by definition. The bounds given by Proposition 10.11, Corollary 11.3, Lemma 11.4 and Corollary 11.9 yield

$$ \begin{align*}m\geq\lvert S_{A}^{N}(p) \rvert+\lvert U_{A}^{N}(p) \rvert+\operatorname{def}_{p}(A)\geq 2{\lceil{\log_{p}q}\rceil}+2+\operatorname{def}_{p}(A),\end{align*} $$

which easily gives the first estimate (the same holds for $\operatorname {def}_{p}(B)$ ). For the second inequality, we obtain similarly

$$ \begin{align*}n\geq\lvert S_{A}^{N}(q) \rvert+\lvert U_{A}^{N}(q) \rvert+\operatorname{def}_{q}(A)\geq 4+\operatorname{def}_{q}(A),\end{align*} $$

which gives the second inequality (the same inequality also holds for $\operatorname {def}_{q}(B)$ ).

12 Proof of Theorem 1.4

From Corollary 11.9 and Proposition 11.10, we obtain that $\mathscr {F}(N)$ , and hence, $\mathscr {F}_{\max }(N)$ is nonempty with $N\in \mathscr {S}_{p,q}^{\prime }$ only if

$$ \begin{align*}4\leq2{\lceil{\log_pq}\rceil}\leq m-2-2{\lceil{\log_pq}\rceil}\leq m-6,\end{align*} $$

and $3\leq n-4$ . This proves that, if $N=p^{m}q^{n}$ with $p<q$ , and either $m\leq 9$ or $n\leq 6$ holds, then every spectral subset of $\mathbb {Z}_{N}$ tiles, i.e., Fuglede’s conjecture holds for cyclic groups of order N with the given conditions. For the second part of the theorem, we invoke the inequalities involving $\operatorname {def}_{p}(A)$ and $\operatorname {def}_{p}(B)$ in Corollary 11.9 and Proposition 11.10 to obtain

$$ \begin{align*}4{\lceil{\log_{p}q}\rceil}+2\leq m,\end{align*} $$

which implies

$$ \begin{align*}q^{4}<p^{4{\lceil{\log_{p}q}\rceil}}\leq p^{m-2}.\end{align*} $$

Thus, if $p^{m-2}<q^{4}$ holds, then $\mathscr {F}_{\max }(N)$ must be necessarily empty, or in other words, $N\notin \mathscr {S}_{p,q}$ , which by definition means that Fuglede’s conjecture holds for cyclic groups of order $p^{m}q^{n}$ , where $p^{m-2}<q^{4}$ .