Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T09:31:46.139Z Has data issue: false hasContentIssue false
  • English
  • Français

RELATIVE COMPLETE REDUCIBILITY AND NORMALIZED SUBGROUPS

Part of: Linear algebraic groups and related topics Algebraic groups

Published online by Cambridge University Press:  26 May 2020

MAIKE GRUCHOT ,
ALASTAIR LITTERICK Open the ORCID record for ALASTAIR LITTERICK [Opens in a new window]  and
GERHARD RÖHRLE
MAIKE GRUCHOT
Affiliation:
Lehrstuhl für Algebra und Zahlentheorie, RWTH Aachen University, D-52062Aachen, Germany; maike.gruchot@rwth-aachen.de
ALASTAIR LITTERICK
Affiliation:
Department of Mathematical Sciences, University of Essex, Wivenhoe Park, Colchester, EssexCO4 3SQ, UK; a.litterick@essex.ac.uk
GERHARD RÖHRLE
Affiliation:
Fakultät für Mathematik, Ruhr-Universität Bochum, Universitätsstraße 150, D-44780Bochum, Germany; gerhard.roehrle@rub.de

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study a relative variant of Serre’s notion of 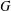$G$-complete reducibility for a reductive algebraic group 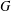$G$. We let 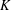$K$ be a reductive subgroup of 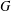$G$, and consider subgroups of 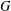$G$ that normalize the identity component 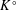$K^{\circ }$. We show that such a subgroup is relatively 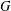$G$-completely reducible with respect to 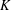$K$ if and only if its image in the automorphism group of $K^{\circ }$ is completely reducible. This allows us to generalize a number of fundamental results from the absolute to the relative setting. We also derive analogous results for Lie subalgebras of the Lie algebra of $G$, as well as ‘rational’ versions over nonalgebraically closed fields.

MSC classification

Primary: 20G15: Linear algebraic groups over arbitrary fields
Secondary: 14L24: Geometric invariant theory
Type
Algebra
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e30
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Attenborough, C., Bate, M., Gruchot, M., Litterick, A. and Röhrle, G., ‘On relative complete reducibility’, Q. J. Math. 71 (2020), 321–334.CrossRefGoogle Scholar
Bate, M., Herpel, S., Martin, B. and Röhrle, G., ‘G-complete reducibility and semisimple modules’, Bull. Lond. Math. Soc. 43(6) (2011), 1069–1078.CrossRefGoogle Scholar
Bate, M., Herpel, S., Martin, B. and Röhrle, G., ‘Cocharacter-closure and the rational Hilbert–Mumford theorem’, Math. Z. 287(1–2) (2017), 39–72.CrossRefGoogle Scholar
Bate, M., Martin, B. and Röhrle, G., ‘A geometric approach to complete reducibility’, Invent. Math. 161(1) (2005), 177–218.CrossRefGoogle Scholar
Bate, M., Martin, B. and Röhrle, G., ‘Complete reducibility and commuting subgroups’, J Teine Angew. Math. (Crelles J.) 2008(621) (2008), 213–235.Google Scholar
Bate, M., Martin, B., Röhrle, G. and Tange, R., ‘Complete reducibility and separability’, Trans. Amer. Math. Soc. 362(08) (2010), 4283–4311.CrossRefGoogle Scholar
Bate, M., Martin, B., Röhrle, G. and Tange, R., ‘Complete reducibility and conjugacy classes of tuples in algebraic groups and Lie algebras’, Math. Z. 269(3–4) (2011), 809–832.CrossRefGoogle Scholar
Bate, M., Martin, B., Röhrle, G. and Tange, R., ‘Closed orbits and uniform S-instability in geometric invariant theory’, Trans. Amer. Math. Soc. 365(7) (2013), 3643–3673.CrossRefGoogle Scholar
Borel, A., Linear Algebraic Groups, 2nd edn, Graduate Texts in Mathematics, 126 (Springer, New York, 1991).CrossRefGoogle Scholar
Brion, M., ‘On extensions of algebraic groups with finite quotient’, Pacific J. Math. 279(1–2) (2015), 135–153.CrossRefGoogle Scholar
Jantzen, J. C., Low Dimensional Representations of Reductive Groups are Semisimple, Algebraic Groups and Lie Groups (Cambridge University Press, Cambridge, England, 1997).Google Scholar
Liebeck, M. W. and Seitz, G. M., ‘Reductive subgroups of exceptional algebraic groups’, Mem. Amer. Math. Soc. 121(580) (1996), pp. vi+111.Google Scholar
Litterick, A. J. and Thomas, A. R., ‘Complete reducibility in good characteristic’, Trans. Amer. Math. Soc. 370(8) (2018), 5279–5340.CrossRefGoogle Scholar
McNinch, G., ‘Dimensional criteria for semisimplicity of representations’, Proc. Lond. Math. Soc. 76 (1998), 95–149.CrossRefGoogle Scholar
McNinch, G., ‘Completely reducible Lie subalgebras’, Transform. Groups 12(1) (2007), 127–135.CrossRefGoogle Scholar
Richardson, R. W., ‘On orbits of algebraic groups and Lie groups’, Bull. Austr. Math. Soc. 25 (1982), 1–28.CrossRefGoogle Scholar
Serre, J.-P., Moursund lectures, University of Oregon, arXiv:math/0305257, 1998.Google Scholar
Serre, J.-P., ‘Complète réductibilité’, Séminaire Bourbaki 46(2003–2004) 195–218; (in French).Google Scholar
Springer, T. A., Linear Algebraic Groups, 2nd edn, Modern Birkhäuser Classics (Birkhäuser Boston, Inc., Boston, MA, 2009).Google Scholar
Stewart, D. I., ‘Non-G-completely reducible subgroups of the exceptional algebraic groups’, Int. Math. Res. Not. IMRN 2014(22) (2013), 6053–6078.CrossRefGoogle Scholar
Uchiyama, T., ‘Non-separability and complete reducibility: E n examples with an application to a question of Külshammer’, J. Group Theory 20(5) (2017).CrossRefGoogle Scholar