Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T13:47:34.475Z Has data issue: false hasContentIssue false
  • English
  • Français

SECOND MOMENTS IN THE GENERALIZED GAUSS CIRCLE PROBLEM

Part of: Multiplicative number theory Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  19 December 2018

THOMAS A. HULSE ,
CHAN IEONG KUAN ,
DAVID LOWRY-DUDA  and
ALEXANDER WALKER
THOMAS A. HULSE
Affiliation:
Mathematics Department, Boston College, Chestnut Hill, MA 02467, USA; thomas.hulse@bc.edu
CHAN IEONG KUAN
Affiliation:
School of Mathematics (Zhuhai), Sun Yat-Sen University, Zhuhai, Guangdong Province, 519082, China; kuanchi3@mail.sysu.edu.cn
DAVID LOWRY-DUDA
Affiliation:
Warwick Mathematics Institute, Zeeman Building, University of Warwick, Coventry CV4 7AL, UK; d.lowry@warwick.ac.uk
ALEXANDER WALKER
Affiliation:
Department of Mathematics, Rutgers University Hill Center for the Mathematical Sciences, 110 Frelinghuysen Rd., Piscataway, NJ 08854, USA; alexander.walker@rutgers.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The generalized Gauss circle problem concerns the lattice point discrepancy of large spheres. We study the Dirichlet series associated to 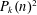$P_{k}(n)^{2}$, where 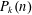$P_{k}(n)$ is the discrepancy between the volume of the 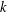$k$-dimensional sphere of radius 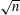$\sqrt{n}$ and the number of integer lattice points contained in that sphere. We prove asymptotics with improved power-saving error terms for smoothed sums, including 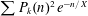$\sum P_{k}(n)^{2}e^{-n/X}$ and the Laplace transform 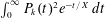$\int _{0}^{\infty }P_{k}(t)^{2}e^{-t/X}\,dt$, in dimensions 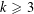$k\geqslant 3$. We also obtain main terms and power-saving error terms for the sharp sums 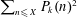$\sum _{n\leqslant X}P_{k}(n)^{2}$, along with similar results for the sharp integral 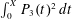$\int _{0}^{X}P_{3}(t)^{2}\,dt$. This includes producing the first power-saving error term in mean square for the dimension-3 Gauss circle problem.

MSC classification

Primary: 11N37: Asymptotic results on arithmetic functions
Secondary: 11F30: Fourier coefficients of automorphic forms
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 6 , 2018 , e24
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2018

References

Bourgain, J. and Watt, N., ‘Mean square of zeta function, circle problem and divisor problem revisited’. arXiv preprint, arXiv:1709.04340 (2017).Google Scholar
Choi, S. K. K., Kumchev, A. V. and Osburn, R., ‘On sums of three squares’, Int. J. Number Theory 1(2) (2005), 161–173.Google Scholar
Deshouillers, J.-M. and Iwaniec, H., ‘Kloosterman sums and Fourier coefficients of cusp forms’, Invent. Math. 70(2) (1982/83), 219–288.Google Scholar
Goldfeld, D., Automorphic Forms and L-functions for the Group GL(n, R), Cambridge Studies in Advanced Mathematics, 99 (Cambridge University Press, Cambridge, 2015), With an appendix by Kevin A. Broughan, Paperback edition of the 2006 original.Google Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Table of Integrals, Series, and Products, 8th edn (Elsevier/Academic Press, Amsterdam, 2015), Translated from the Russian, Translation edited and with a preface by Daniel Zwillinger and Victor Moll, Revised from the seventh edition.Google Scholar
Gupta, S. D., ‘Corrigendum to my paper ‘The Rankin–Selberg method on congruence subgroups’’, Illinois J. Math. 44(4) (2000), 924–926.Google Scholar
Gupta, S. D., ‘The Rankin–Selberg method on congruence subgroups’, Illinois J. Math. 44(1) (2000), 95–103.Google Scholar
Heath-Brown, D. R., ‘Lattice points in the sphere’, inNumber Theory in Progress, Vol. 2 (Zakopane-Kościelisko 1997) (de Gruyter, Berlin, 1999), 883–892.Google Scholar
Hoffstein, J. and Hulse, T. A., ‘Multiple Dirichlet series and shifted convolutions’, J. Number Theory 161 (2016), 457–533. With an appendix by Andre Reznikov.Google Scholar
Hulse, T. A., Kuan, C. I., Lowry-Duda, D. and Walker, A., ‘The Laplace transform of the second moment in the Gauss circle problem’. arXiv preprint, arXiv:1705.04771 (2017).Google Scholar
Hulse, T. A., Kuan, C. I., Lowry-Duda, D. and Walker, A., ‘The second moment of sums of coefficients of cusp forms’, J. Number Theory 173 (2017), 304–331.Google Scholar
Hulse, T. A., Kuan, C. I., Lowry-Duda, D. and Walker, A., ‘Short-interval averages of sums of Fourier coefficients of cusp forms’, J. Number Theory 173 (2017), 394–415.Google Scholar
Huxley, M. N., ‘Introduction to Kloostermania’, inElementary and Analytic Theory of Numbers (Warsaw, 1982), Banach Center Publ., 17 (PWN, Warsaw, 1985), 217–306.Google Scholar
Huxley, M. N., ‘Exponential sums and lattice points. III’, Proc. Lond. Math. Soc. (3) 87(3) (2003), 591–609.Google Scholar
Ivić, A., ‘A note on the Laplace transform of the square in the circle problem’, Studia Sci. Math. Hungar. 37(3–4) (2001), 391–399.Google Scholar
Ivić, A., Krätzel, E., Kühleitner, M. and Nowak, W. G., ‘Lattice points in large regions and related arithmetic functions: recent developments in a very classic topic’, inElementare und analytische Zahlentheorie, Publications of the Scientific Society at the Johann Wolfgang Goethe University, Frankfurt am Main. Franz Steiner Verlag Stuttgart, Postfach 10 10 61, 70009 Stuttgard, Germany, 20 (Franz Steiner Verlag Stuttgart, Stuttgart, 2006), 89–128.Google Scholar
Iwaniec, H., Spectral Methods of Automorphic Forms, Graduate Studies in Mathematics, 53 (American Mathematical Society, Providence, RI, 2002), Revista Matemática Iberoamericana, Madrid, second edition.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, American Mathematical Society Colloquium Publications, 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Jarník, V., ‘Über die Mittelwertsätze der Gitterpunktlehre. V’, Časopis Pěst. Mat. Fys. 69 (1940), 148–174.Google Scholar
Kıral, E. M., ‘Subconvexity for half integral weight L-functions’, Math. Z. 281(3–4) (2015), 689–722.Google Scholar
Krätzel, E., Analytische Funktionen in der Zahlentheorie, Teubner-Texte zur Mathematik [Teubner Texts in Mathematics], 139 (B. G. Teubner, Stuttgart, 2000).Google Scholar
Kubota, T., Elementary Theory of Eisenstein Series (Kodansha Ltd., Tokyo; Halsted Press [John Wiley & Sons], New York–London–Sydney, 1973).Google Scholar
Landau, E., ‘Über die Gitterpunkte in einem Kreise’, Math. Z. 5(3–4) (1919), 319–320.Google Scholar
Landau, E., Vorlesungen über Zahlentheorie. zweiter Band (Chelsea Publishing Co., New York, 1969).Google Scholar
Lau, Y.-K., ‘On the mean square formula of the error term for a class of arithmetical functions’, Monatsh. Math. 128(2) (1999), 111–129.Google Scholar
Lau, Y.-K. and Tsang, K.-M., ‘On the mean square formula of the error term in the Dirichlet divisor problem’, Math. Proc. Cambridge Philos. Soc. 146(2) (2009), 277–287.Google Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative Number Theory I: Classical Theory, Vol. 97 (Cambridge University Press, Cambridge, 2006).Google Scholar
Müller, W., ‘The mean square of Dirichlet series associated with automorphic forms’, Monatsh. Math. 113(2) (1992), 121–159.Google Scholar
Sierpiński, W., ‘O pewnem zagadnieniu z rachunku funckcyi asymptotycnych’, Prace mat.-fiz (1906), 77–118.Google Scholar
Vinogradov, I. M., ‘On the number of integer points in a sphere’, Izv. Akad. Nauk SSSR Ser. Mat. 27 (1963), 957–968.Google Scholar
Zagier, D., ‘The Rankin–Selberg method for automorphic functions which are not of rapid decay’, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 28(3) (1982), 415–437. 1981.Google Scholar