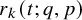1 Introduction
Let
![]() $K_n^{(k)}$
denote the complete k-uniform hypergraph on n vertices. We define
$K_n^{(k)}$
denote the complete k-uniform hypergraph on n vertices. We define
![]() $r_k(G; q)$
for
$r_k(G; q)$
for
![]() $k, q \in \mathbb N$
as the smallest integer n such that in every q-colouring of
$k, q \in \mathbb N$
as the smallest integer n such that in every q-colouring of
![]() $K_n^{(k)}$
, there is a monochromatic copy of the hypergraph G. For simplicity, when G is
$K_n^{(k)}$
, there is a monochromatic copy of the hypergraph G. For simplicity, when G is
![]() $K_{t}^{(k)}$
, we write
$K_{t}^{(k)}$
, we write
![]() $r_k(G;q) = r_k(t;q)$
. Observe that when
$r_k(G;q) = r_k(t;q)$
. Observe that when
![]() $q = 2$
,
$q = 2$
,
![]() $r_k(G;2)$
and
$r_k(G;2)$
and
![]() $r_k(t;2)$
coincide with the classical Ramsey numbers
$r_k(t;2)$
coincide with the classical Ramsey numbers
![]() $r_k(G)$
and
$r_k(G)$
and
![]() $r_k(t)$
, and we will denote them as such. One of the most central open problems in Ramsey theory is determining the growth rate of the 3-uniform Ramsey number
$r_k(t)$
, and we will denote them as such. One of the most central open problems in Ramsey theory is determining the growth rate of the 3-uniform Ramsey number
![]() $r_3(t)$
.
$r_3(t)$
.
A famous result of Erdős, Hajnal and Rado [Reference Erdős, Hajnal and Rado9] from the 60s shows that there exist constants c and
![]() $c'$
such that
$c'$
such that
Note that the upper bound is essentially exponential in the lower bound. Despite much attention, this remains the state of the art. Perhaps surprisingly, if we allow four colours instead of two, Erdős and Hajnal (see, for example, [Reference Graham, Rothschild and Spencer12]) showed that the double-exponential upper bound is essentially correct (i.e., there is a
![]() $c>0$
such that
$c>0$
such that
![]() $r_3(t;4)\geq 2^{2^{ct}}$
). More recently, Conlon, Fox and Sudakov [Reference Conlon, Fox and Sudakov6] proved a super-exponential bound with three colours – that is, that there exists
$r_3(t;4)\geq 2^{2^{ct}}$
). More recently, Conlon, Fox and Sudakov [Reference Conlon, Fox and Sudakov6] proved a super-exponential bound with three colours – that is, that there exists
![]() $c>0$
such that
$c>0$
such that
![]() $r_3(t;3) \geq 2^{t^{c\log t}}$
. Erdős conjectured that the double-exponential bound should hold without using extra colours, offering $500 dollars for a proof that
$r_3(t;3) \geq 2^{t^{c\log t}}$
. Erdős conjectured that the double-exponential bound should hold without using extra colours, offering $500 dollars for a proof that
![]() $r_3(t) \geq 2^{2^{ct}}$
for some constant
$r_3(t) \geq 2^{2^{ct}}$
for some constant
![]() $c>0$
. Raising the stakes for this conjecture is the ingenious stepping-up construction of Erdős and Hajnal (see, for example, [Reference Graham, Rothschild and Spencer12]), which shows that for all q and
$c>0$
. Raising the stakes for this conjecture is the ingenious stepping-up construction of Erdős and Hajnal (see, for example, [Reference Graham, Rothschild and Spencer12]), which shows that for all q and
![]() $k\geq 3$
,
$k\geq 3$
,
For the past 60 years, we have used (1.1) to stack our lower bounds for
![]() $r_k(t;q)$
upon that of
$r_k(t;q)$
upon that of
![]() $r_3(t;q)$
, yielding that
$r_3(t;q)$
, yielding that
![]() $r_k(t) \geq T_{k-1}(ct^2)$
, where
$r_k(t) \geq T_{k-1}(ct^2)$
, where
![]() $T_k(x)$
, the tower of height k in x, is defined by
$T_k(x)$
, the tower of height k in x, is defined by
![]() $T_1(x) = x,\, T_{i+1}(x) = 2^{T_i(x)}$
. The corresponding upper bounds of
$T_1(x) = x,\, T_{i+1}(x) = 2^{T_i(x)}$
. The corresponding upper bounds of
![]() $r_k(t) \leq T_k(O(t))$
(see [Reference Erdős and Hajnal7; Reference Erdős and Rado8; Reference Erdős, Hajnal and Rado9]) are once again exponential in the lower bounds, and thus a positive resolution of Erdős’s conjecture would be the decisive step in showing that
$r_k(t) \leq T_k(O(t))$
(see [Reference Erdős and Hajnal7; Reference Erdős and Rado8; Reference Erdős, Hajnal and Rado9]) are once again exponential in the lower bounds, and thus a positive resolution of Erdős’s conjecture would be the decisive step in showing that
![]() $r_k(t) = T_k(\Theta (t))$
for all
$r_k(t) = T_k(\Theta (t))$
for all
![]() $k\geq 3$
.
$k\geq 3$
.
Due to the lack of progress on this central conjecture, it is natural to try to understand just how significant a role the number of colours can play in hypergraph Ramsey numbers and whether or not there could really be such a large difference between
![]() $r_3(t)$
and
$r_3(t)$
and
![]() $r_3(t;4)$
. One argument in favour of the conjecture is that the reliance on extra colours to prove a double-exponential lower bound may be a technical limitation of the stepping-up construction. This is challenged by a stunning discovery of Conlon, Fox and Rödl [Reference Conlon, Fox and Rödl5] who exhibited an infinite family of
$r_3(t;4)$
. One argument in favour of the conjecture is that the reliance on extra colours to prove a double-exponential lower bound may be a technical limitation of the stepping-up construction. This is challenged by a stunning discovery of Conlon, Fox and Rödl [Reference Conlon, Fox and Rödl5] who exhibited an infinite family of
![]() $3$
-uniform hypergraphs called hedgehogs, whose Ramsey numbers display a strong dependence on the number of colours. Namely, they showed that the
$3$
-uniform hypergraphs called hedgehogs, whose Ramsey numbers display a strong dependence on the number of colours. Namely, they showed that the
![]() $2$
-colour Ramsey number of hedgehogs is polynomial in their order, whereas the
$2$
-colour Ramsey number of hedgehogs is polynomial in their order, whereas the
![]() $4$
-colour Ramsey number is at least exponential. To understand just how significant a role the number of colours could play they asked the following:
$4$
-colour Ramsey number is at least exponential. To understand just how significant a role the number of colours could play they asked the following:
Question 1.1. For any integer
![]() $h \geq 3$
, do there exist integers k and q and a family of k-uniform hypergraphs for which the
$h \geq 3$
, do there exist integers k and q and a family of k-uniform hypergraphs for which the
![]() $2$
-colour Ramsey number grows as a polynomial in the number of vertices, while the q-colour Ramsey number grows as a tower of height h?
$2$
-colour Ramsey number grows as a polynomial in the number of vertices, while the q-colour Ramsey number grows as a tower of height h?
Our main contribution is to answer this in the affirmative. Define the k-uniform balanced hedgehog
![]() $\hat H^{(k)}_{t}$
with body of order t to be the graph constructed as follows: take a set S of t vertices, called the body, and for each subset
$\hat H^{(k)}_{t}$
with body of order t to be the graph constructed as follows: take a set S of t vertices, called the body, and for each subset
![]() $X\subset S$
of order
$X\subset S$
of order
![]() $\lceil \frac k2 \rceil $
, add a k-edge e with
$\lceil \frac k2 \rceil $
, add a k-edge e with
![]() $e\cap S = X$
such that for all
$e\cap S = X$
such that for all
![]() $e,f \in E(\hat H^{(k)}_{t})$
, we have
$e,f \in E(\hat H^{(k)}_{t})$
, we have
![]() $e\cap f\subset S$
. The hedgehog
$e\cap f\subset S$
. The hedgehog
![]() $H_t^{(k)}$
as defined by Conlon, Fox and Rödl differs only in that they consider every
$H_t^{(k)}$
as defined by Conlon, Fox and Rödl differs only in that they consider every
![]() $X\subset S$
of order
$X\subset S$
of order
![]() $k-1$
rather than
$k-1$
rather than
![]() $\lceil \frac k2 \rceil $
. We observe that for
$\lceil \frac k2 \rceil $
. We observe that for
![]() $k=3$
, the two definitions coincide. When the uniformity is clear from the context, we shall drop the superscript.
$k=3$
, the two definitions coincide. When the uniformity is clear from the context, we shall drop the superscript.
Theorem 1.2. There exist
![]() $c>0$
and
$c>0$
and
![]() $q:{\mathbb {N}} \rightarrow {\mathbb {N}}$
such that for all
$q:{\mathbb {N}} \rightarrow {\mathbb {N}}$
such that for all
![]() $k\in {\mathbb {N}}$
and sufficiently large t, we have
$k\in {\mathbb {N}}$
and sufficiently large t, we have
-
(a)
 $ r_{2k+1}(\hat H_{t}) \leq t^{k+3}$
, and
$ r_{2k+1}(\hat H_{t}) \leq t^{k+3}$
, and -
(b)
 $r_{2k+1}(\hat H_{t};q(k)) \geq T_{\lfloor c\log _2\log _2 k\rfloor }(t)$
.
$r_{2k+1}(\hat H_{t};q(k)) \geq T_{\lfloor c\log _2\log _2 k\rfloor }(t)$
.
To prove this, we provide new stepping-up lemmas for a more general type of hypergraph Ramsey numbers. Let
![]() $r_k(G;q,p)$
for
$r_k(G;q,p)$
for
![]() $q \geq p$
be the smallest integer n such that in every q-colouring of
$q \geq p$
be the smallest integer n such that in every q-colouring of
![]() $K_n^{(k)}$
, there is a copy of the hypergraph G whose edges span fewer than p colours. As before, we use
$K_n^{(k)}$
, there is a copy of the hypergraph G whose edges span fewer than p colours. As before, we use
![]() $r_k(t; q, p)$
when
$r_k(t; q, p)$
when
![]() $G = K_{t}^{(k)}$
and suppress p when
$G = K_{t}^{(k)}$
and suppress p when
![]() $p = 2$
.
$p = 2$
.
A standard application of the first moment method (see, for example, [Reference Alon and Spencer1]) shows that for any
![]() $k,q\in {\mathbb {N}}$
, there exists
$k,q\in {\mathbb {N}}$
, there exists
![]() $c>0$
such that
$c>0$
such that
![]() $r_k(t;q,q) \geq 2^{ct^{k-1}}$
for all
$r_k(t;q,q) \geq 2^{ct^{k-1}}$
for all
![]() $t\in {\mathbb {N}}$
. We note that in the graph case (
$t\in {\mathbb {N}}$
. We note that in the graph case (
![]() $k=2$
), the special case of
$k=2$
), the special case of
![]() $q = p$
was already investigated by Erdős and Szemerédi [Reference Erdős and Szemerédi10] in the 70s; in fact, the more general case when
$q = p$
was already investigated by Erdős and Szemerédi [Reference Erdős and Szemerédi10] in the 70s; in fact, the more general case when
![]() $p<q$
is also indirectly discussed. They showed the following rather precise bounds: for all
$p<q$
is also indirectly discussed. They showed the following rather precise bounds: for all
![]() $q\ll t$
,
$q\ll t$
,
![]() $2^{\Omega (t/q)} \leq r_2(t; q, q) \leq q^{O(t/q)}$
.
$2^{\Omega (t/q)} \leq r_2(t; q, q) \leq q^{O(t/q)}$
.
These generalized hypergraph Ramsey numbers were also considered in a special case by Conlon, Fox and Rödl [Reference Conlon, Fox and Rödl5] who asked if there exist an integer q and number
![]() $c>0$
such that
$c>0$
such that
![]() $r_3(t;q,3)\geq 2^{2^{ct}}$
. To date, the only nontrivial improvement on the first moment bound has been made by Mubayi and Suk [Reference Mubayi and Suk16], who proved there exists
$r_3(t;q,3)\geq 2^{2^{ct}}$
. To date, the only nontrivial improvement on the first moment bound has been made by Mubayi and Suk [Reference Mubayi and Suk16], who proved there exists
![]() $c>0$
such that for
$c>0$
such that for
![]() $q \geq 9$
, we have
$q \geq 9$
, we have
![]() $r_3(t;q,3)\geq 2^{t^{2+cq}}$
for
$r_3(t;q,3)\geq 2^{t^{2+cq}}$
for
![]() $t\in {\mathbb {N}}$
sufficiently large; for all other values of
$t\in {\mathbb {N}}$
sufficiently large; for all other values of
![]() $k,q,p \geq 3$
, the random construction is essentially the state of the art. Our knowledge (or lack thereof) is thus summarised by the following bounds for
$k,q,p \geq 3$
, the random construction is essentially the state of the art. Our knowledge (or lack thereof) is thus summarised by the following bounds for
![]() $k,q,p \geq 3$
and sufficiently large
$k,q,p \geq 3$
and sufficiently large
![]() $t\in {\mathbb {N}}$
:
$t\in {\mathbb {N}}$
:
where
![]() $c\geq 1$
is allowed to depend on
$c\geq 1$
is allowed to depend on
![]() $k,q$
and p. Note that in this case, our upper bounds are a staggering tower of height
$k,q$
and p. Note that in this case, our upper bounds are a staggering tower of height
![]() $k-2$
in the lower bounds.
$k-2$
in the lower bounds.
A related notion called the set-colouring Ramsey number was introduced by Erdős, Hajnal and Rado in [Reference Erdős, Hajnal and Rado9] and subsequently studied in [Reference Xu, Shao, Su and Li19] and much more recently in [Reference Conlon, Fox, He, Mubayi, Suk and Verstraëte4] and [Reference Aragão, Collares, Marciano, Martins and Morris2]. Borrowing notation from [Reference Conlon, Fox, He, Mubayi, Suk and Verstraëte4], let
![]() $R_k(t;q,s)$
denote the minimum number of vertices such that every
$R_k(t;q,s)$
denote the minimum number of vertices such that every
![]() $(q,s)$
-set colouring of
$(q,s)$
-set colouring of
![]() $K_n^{(k)}$
– that is, a colouring in which each k-set is assigned an element of
$K_n^{(k)}$
– that is, a colouring in which each k-set is assigned an element of
![]() ${[q] \choose s}$
– contains a monochromatic
${[q] \choose s}$
– contains a monochromatic
![]() $K_{t}^{(k)}$
. Here, monochromatic means the intersection of the colour sets assigned to the edges is nonempty. Observe that certain cases of
$K_{t}^{(k)}$
. Here, monochromatic means the intersection of the colour sets assigned to the edges is nonempty. Observe that certain cases of
![]() $R_k$
and
$R_k$
and
![]() $r_k$
coincide. For example,
$r_k$
coincide. For example,
![]() $R_k(t;q,q-1) = r_k(t;q,q)$
and in general, we have the bound
$R_k(t;q,q-1) = r_k(t;q,q)$
and in general, we have the bound
 $$\begin{align*}r_{k}(t ; q, p) \leq R_k \bigg(t ;{q \choose p-1}, {q-1 \choose p-2}\bigg). \end{align*}$$
$$\begin{align*}r_{k}(t ; q, p) \leq R_k \bigg(t ;{q \choose p-1}, {q-1 \choose p-2}\bigg). \end{align*}$$
We prove lower bounds on
![]() $r_k(t; q, p)$
, thus giving lower bounds on certain set-colouring Ramsey numbers. However, we are not able to definitively resolve any questions from [Reference Conlon, Fox, He, Mubayi, Suk and Verstraëte4] due to central gaps in our understanding of hypergraph Ramsey numbers. See Section 5 for more on this.
$r_k(t; q, p)$
, thus giving lower bounds on certain set-colouring Ramsey numbers. However, we are not able to definitively resolve any questions from [Reference Conlon, Fox, He, Mubayi, Suk and Verstraëte4] due to central gaps in our understanding of hypergraph Ramsey numbers. See Section 5 for more on this.
Our main tool in the proof of Theorem 1.2 is the development of two new stepping-up constructions which yield the first tower-type results of their kind. We show the following three stepping-up statements, listed in order of decreasing strength, with
![]() ${C_k = \frac{1}{k+1}{2k \choose k}}$
denoting the k-th Catalan number.
${C_k = \frac{1}{k+1}{2k \choose k}}$
denoting the k-th Catalan number.
Theorem 1.3. Let
![]() $k, q, p \geq 3$
. There exist
$k, q, p \geq 3$
. There exist
![]() $c \geq 1$
and
$c \geq 1$
and
![]() $t_0$
such that for all
$t_0$
such that for all
![]() $t> t_0$
,
$t> t_0$
,
-
(a) if
 $p \leq C_k-2$
, then
$p \leq C_k-2$
, then
 $r_{k+1}(t^c; q,p)> 2^{r_k(t;q,p)-1}$
,
$r_{k+1}(t^c; q,p)> 2^{r_k(t;q,p)-1}$
, -
(b) if
 $p \leq C_k$
, then
$p \leq C_k$
, then
 $r_{k+1}(t^c; 2q+p,p)> 2^{r_k(t;q,p)-1}$
and
$r_{k+1}(t^c; 2q+p,p)> 2^{r_k(t;q,p)-1}$
and -
(c) if
 $p \leq k!$
, then
$p \leq k!$
, then
 $r_{2k}(t^c;qp,p)> 2^{r_k(t;q,p)-1}$
.
$r_{2k}(t^c;qp,p)> 2^{r_k(t;q,p)-1}$
.
Note that the growth rate in k which is implied by Part (c) (approximately a tower of height
![]() $\log _2 k$
) of Theorem 1.3 is much smaller than that of Parts (a) and (b) because we can only step up at the cost of doubling the uniformity size. Unfortunately, this does not allow us to answer the question of Conlon, Fox and Rödl on
$\log _2 k$
) of Theorem 1.3 is much smaller than that of Parts (a) and (b) because we can only step up at the cost of doubling the uniformity size. Unfortunately, this does not allow us to answer the question of Conlon, Fox and Rödl on
![]() $r_3(t;q,3)$
since
$r_3(t;q,3)$
since
![]() $C_2 = 2$
, but already for
$C_2 = 2$
, but already for
![]() $k\geq 4$
, we have the following two corollaries:
$k\geq 4$
, we have the following two corollaries:
Corollary 1.4. For all
![]() $k\geq 4$
, there is
$k\geq 4$
, there is
![]() $q\in {\mathbb {N}}$
and
$q\in {\mathbb {N}}$
and
![]() $c>0$
such that
$c>0$
such that
![]() $ r_k(t;q,5) \geq T_{k-1}(t^{c})$
.
$ r_k(t;q,5) \geq T_{k-1}(t^{c})$
.
Corollary 1.5. For all
![]() $k\geq 4$
, there is
$k\geq 4$
, there is
![]() $c>0$
such that
$c>0$
such that
![]() $ r_k(t;3,3) \geq T_{k-1}(t^{c})$
.
$ r_k(t;3,3) \geq T_{k-1}(t^{c})$
.
Observe that by the second corollary, the growth rate of
![]() $r_k(t;3,3)$
matches the current best lower bounds for
$r_k(t;3,3)$
matches the current best lower bounds for
![]() $r_k(t)$
up to a polynomial in t. The reason we have an absolute constant c in the exponent is due to the use of an Erdős-Hajnal type result on sequences (see Section 2).
$r_k(t)$
up to a polynomial in t. The reason we have an absolute constant c in the exponent is due to the use of an Erdős-Hajnal type result on sequences (see Section 2).
The second main element of our proof connects the problem of avoiding monochromatic balanced hedgehogs to that of avoiding cliques that span few colours. It is a straightforward adaptation of ideas from Conlon, Fox and Rödl [Reference Conlon, Fox and Rödl5].
Lemma 1.6. Given
![]() $k,q,t \in {\mathbb {N}}$
, let
$k,q,t \in {\mathbb {N}}$
, let
![]() $p={2k+1 \choose k+1}$
and
$p={2k+1 \choose k+1}$
and
![]() $q' = {q \choose p}$
. Then
$q' = {q \choose p}$
. Then
 $$\begin{align*}r_{2k+1}(\hat H_{t};q',2) > r_{k+1}\bigg(t; q, p+1\bigg) - 1.\end{align*}$$
$$\begin{align*}r_{2k+1}(\hat H_{t};q',2) > r_{k+1}\bigg(t; q, p+1\bigg) - 1.\end{align*}$$
Using this result along with Part (c) of Theorem 1.3 yields the lower bound in Theorem 1.2(b). It is natural to ask whether one can combine the growth rate in k given by Part (a) of Theorem 1.3 with the ability to impose as many colours as in Part (c). Unfortunately, the condition
![]() $p \leq C_k$
prevents us from using Part (a) as the right-hand side because
$p \leq C_k$
prevents us from using Part (a) as the right-hand side because
![]() $C_k = \frac {1}{k+1}{2k\choose k} < {2k+1 \choose k+1}$
. This is tantalisingly close, if not a little curious, as the dependence on
$C_k = \frac {1}{k+1}{2k\choose k} < {2k+1 \choose k+1}$
. This is tantalisingly close, if not a little curious, as the dependence on
![]() $C_k$
comes from our exact solution to a subsequence avoidance problem (Corollary 2.4). We show that
$C_k$
comes from our exact solution to a subsequence avoidance problem (Corollary 2.4). We show that
![]() $C_k$
presents a natural barrier in this endeavour. This barrier is made concrete by some new and tight results on the Ramsey theory of sequences, including an Erdős-Hajnal-type result in Section 2.
$C_k$
presents a natural barrier in this endeavour. This barrier is made concrete by some new and tight results on the Ramsey theory of sequences, including an Erdős-Hajnal-type result in Section 2.
1.1 Outline
The outline of the paper is as follows. In Section 2, we introduce and prove results on the Ramsey theory of sequences. In Section 3, we use these to prove our stepping up constructions – namely, Theorem 1.3, and in Section 4, we prove our hedgehog-related results, including Theorem 1.2 and Lemma 1.6, and provide a construction of a degenerate hypergraph that relates to the Burr-Erdős Conjecture. To finish, we pose some questions and problems highlighted by our results.
2 Ramsey theory of sequences
Let
![]() $V=\{0,1\}^m$
and given vectors
$V=\{0,1\}^m$
and given vectors
![]() $v,w \in V$
, define
$v,w \in V$
, define
We say
![]() $v<w$
if
$v<w$
if
![]() $v_\delta < w_\delta $
. For every set of vertices
$v_\delta < w_\delta $
. For every set of vertices
![]() $v_1< v_2 < \dots < v_{k+1}$
in V, there is a corresponding sequence
$v_1< v_2 < \dots < v_{k+1}$
in V, there is a corresponding sequence
![]() $(\delta _1,\delta _2,\ldots ,\delta _{k})$
given by
$(\delta _1,\delta _2,\ldots ,\delta _{k})$
given by
![]() $\delta _i = \delta (v_i,v_{i+1})$
. In this section, we introduce some definitions that will be useful in order to analyse the structure of these
$\delta _i = \delta (v_i,v_{i+1})$
. In this section, we introduce some definitions that will be useful in order to analyse the structure of these
![]() $\delta $
-sequences.
$\delta $
-sequences.
We say a sequence
![]() $S = (a_1, a_2, \dots , a_m)$
is monotonic if
$S = (a_1, a_2, \dots , a_m)$
is monotonic if
![]() $a_1 \leq a_2\leq \dots \leq a_m$
or
$a_1 \leq a_2\leq \dots \leq a_m$
or
![]() $a_1\geq a_2\geq \dots \geq a_m$
. Two sequences
$a_1\geq a_2\geq \dots \geq a_m$
. Two sequences
![]() $(a_1, a_2, \ldots ,a_t)$
and
$(a_1, a_2, \ldots ,a_t)$
and
![]() $(b_1, b_2, \ldots , b_t)$
have the same pattern if the relative ordering of every pair of elements is the same; that is,
$(b_1, b_2, \ldots , b_t)$
have the same pattern if the relative ordering of every pair of elements is the same; that is,
![]() $a_i>a_j$
,
$a_i>a_j$
,
![]() $a_i = a_j$
, or
$a_i = a_j$
, or
![]() $a_i < a_j$
if and only if
$a_i < a_j$
if and only if
![]() $b_i>b_j$
,
$b_i>b_j$
,
![]() $b_i = b_j$
, or
$b_i = b_j$
, or
![]() $b_i < b_j$
respectively for all
$b_i < b_j$
respectively for all
![]() $1 \le i < j \le t$
. A pattern is then the equivalence class of sequences with respect to this relative ordering. Given sequences S and P, we say S contains the pattern P if we can find a subsequence of S which has the same pattern as P; otherwise, we say S avoids P. A pattern is a permutation pattern if there is a permutation in the equivalence class, and we often use this permutation as a representative for the pattern. In what follows, we will mainly be concerned with permutations that avoid the patterns
$1 \le i < j \le t$
. A pattern is then the equivalence class of sequences with respect to this relative ordering. Given sequences S and P, we say S contains the pattern P if we can find a subsequence of S which has the same pattern as P; otherwise, we say S avoids P. A pattern is a permutation pattern if there is a permutation in the equivalence class, and we often use this permutation as a representative for the pattern. In what follows, we will mainly be concerned with permutations that avoid the patterns
![]() $132$
or
$132$
or
![]() $231$
.
$231$
.
2.1 Max-induced subsequences
With the aforementioned applications to hypergraph Ramsey theory in mind, we introduce ‘max-induced’ subsequences. We say
![]() $(a_{i_1},a_{i_2},\ldots ,a_{i_t})$
with
$(a_{i_1},a_{i_2},\ldots ,a_{i_t})$
with
![]() $i_1<i_2<\dots <i_t$
is a max-induced subsequence of
$i_1<i_2<\dots <i_t$
is a max-induced subsequence of
![]() $(a_1,a_2,\ldots , a_m)$
if the maximum of
$(a_1,a_2,\ldots , a_m)$
if the maximum of
![]() $(a_{i_j},a_{i_j+1},\ldots , a_{i_{j+1}})$
is attained at
$(a_{i_j},a_{i_j+1},\ldots , a_{i_{j+1}})$
is attained at
![]() $a_{i_j}$
or
$a_{i_j}$
or
![]() $a_{i_{j+1}}$
(i.e., at the left or right extreme) for all
$a_{i_{j+1}}$
(i.e., at the left or right extreme) for all
![]() $1 \leq j < t$
. We say a sequence S contains a max-induced pattern P if there is a max-induced subsequence of S which has pattern P, and a family of sequences
$1 \leq j < t$
. We say a sequence S contains a max-induced pattern P if there is a max-induced subsequence of S which has pattern P, and a family of sequences
![]() $\mathcal {F} $
has the max-induced Erdős-Hajnal property with exponent
$\mathcal {F} $
has the max-induced Erdős-Hajnal property with exponent
![]() $c(\mathcal {F} )$
if any sequence S that avoids every member of
$c(\mathcal {F} )$
if any sequence S that avoids every member of
![]() $\mathcal {F} $
as a max-induced subsequence has a monotonic max-induced subsequence of order
$\mathcal {F} $
as a max-induced subsequence has a monotonic max-induced subsequence of order
![]() $|S|^{c(\mathcal {F} )}$
, where
$|S|^{c(\mathcal {F} )}$
, where
![]() $|S|$
denotes the length of the sequence. We are able to characterize the families with this property.
$|S|$
denotes the length of the sequence. We are able to characterize the families with this property.
The following fact, whose short proof can be found in Section 3, relates the max-induced property to our original motivation:
Claim 2.1. Suppose
![]() $v_1 < v_2 < \dots < v_{\ell +1}$
are vectors in
$v_1 < v_2 < \dots < v_{\ell +1}$
are vectors in
![]() $\{0,1\}^m$
and let
$\{0,1\}^m$
and let
![]() $\delta _i = \delta (v_i, v_{i+1})$
. If
$\delta _i = \delta (v_i, v_{i+1})$
. If
![]() $(\delta _{i_1},\ldots , \delta _{i_k})$
is a max-induced subsequence of
$(\delta _{i_1},\ldots , \delta _{i_k})$
is a max-induced subsequence of
![]() $(\delta _1,\ldots ,\delta _\ell )$
, then there are
$(\delta _1,\ldots ,\delta _\ell )$
, then there are
![]() $v_{j_1},\ldots , v_{j_{k+1}}$
such that
$v_{j_1},\ldots , v_{j_{k+1}}$
such that
![]() $\delta (v_{j_s}, v_{j_{s+1}}) = \delta _{i_s}$
for each
$\delta (v_{j_s}, v_{j_{s+1}}) = \delta _{i_s}$
for each
![]() $s\in [k]$
.
$s\in [k]$
.
Define an interval in a sequence to be a subsequence of consecutive elements. The following theorem is our core result on max-induced patterns:
Theorem 2.2. A finite family of patterns
![]() $\mathcal {F}$
has the max-induced Erdős-Hajnal property if and only if
$\mathcal {F}$
has the max-induced Erdős-Hajnal property if and only if
![]() $\mathcal F$
contains a
$\mathcal F$
contains a
![]() $132$
-avoiding permutation pattern and a
$132$
-avoiding permutation pattern and a
![]() $231$
-avoiding permutation pattern.
$231$
-avoiding permutation pattern.
Observe that if a single permutation is
![]() $\{132, 231\}$
-avoiding, it must be decreasing up to some element and increasing for the rest of the permutation. We say such a permutation has a unique local minimum, and we immediately get the following corollary of Theorem 2.2:
$\{132, 231\}$
-avoiding, it must be decreasing up to some element and increasing for the rest of the permutation. We say such a permutation has a unique local minimum, and we immediately get the following corollary of Theorem 2.2:
Corollary 2.3. A permutation P has the max-induced Erdős-Hajnal property (with exponent
![]() $c(P) = 16^{-|P|}$
) if and only if it has a unique local minimum (in other words, it is
$c(P) = 16^{-|P|}$
) if and only if it has a unique local minimum (in other words, it is
![]() $\{132, 231\}$
-avoiding).
$\{132, 231\}$
-avoiding).
An old result of Shelah [Reference Shelah17] states that any graph which does not have large cliques or large independent sets must contain exponentially many non-isomorphic induced subgraphs. Taking inspiration from this, we may ask: given
![]() $k \in \mathbb N$
, what is the largest integer
$k \in \mathbb N$
, what is the largest integer
![]() $f(k)$
for which there is
$f(k)$
for which there is
![]() $\varepsilon>0$
such that every sequence of length n either contains at least
$\varepsilon>0$
such that every sequence of length n either contains at least
![]() $f(k)$
distinct max-induced patterns on k elements or a max-induced monotonic subsequence of length
$f(k)$
distinct max-induced patterns on k elements or a max-induced monotonic subsequence of length
![]() $n^{\varepsilon }$
? It is well-known that the number of 132-avoiding permutations on
$n^{\varepsilon }$
? It is well-known that the number of 132-avoiding permutations on
![]() $[k]$
is exactly the Catalan number,
$[k]$
is exactly the Catalan number,
![]() $C_k$
(see, for example, [Reference Stanley18, Section 1.5]). Thus, Theorem 2.2 allows us to answer the above question exactly and is the origin of the Catalan number that appears in Theorem 1.3.
$C_k$
(see, for example, [Reference Stanley18, Section 1.5]). Thus, Theorem 2.2 allows us to answer the above question exactly and is the origin of the Catalan number that appears in Theorem 1.3.
Corollary 2.4. The value of
![]() $f(k)$
is the number of
$f(k)$
is the number of
![]() $132$
-avoiding permutations (equivalently
$132$
-avoiding permutations (equivalently
![]() $231$
-avoiding), which is equal to the Catalan number
$231$
-avoiding), which is equal to the Catalan number
![]() $C_k$
.
$C_k$
.
To prove Theorem 2.2, we require the following lemma:
Lemma 2.5. For every
![]() $k \geq 1$
, there is a
$k \geq 1$
, there is a
![]() $231$
-avoiding permutation
$231$
-avoiding permutation
![]() $S_k$
of length
$S_k$
of length
![]() $2^{k+1}-1$
that does not contain a max-induced monotonic subsequence of length greater than
$2^{k+1}-1$
that does not contain a max-induced monotonic subsequence of length greater than
![]() $k+1$
.
$k+1$
.
Proof. We proceed by induction on k. Note that for
![]() $k=1$
, the permutation
$k=1$
, the permutation
![]() $(1,3,2)$
works. Let
$(1,3,2)$
works. Let
![]() $S_{k-1} = (a_1, a_2, \dots , a_{m_{k-1}})$
be a
$S_{k-1} = (a_1, a_2, \dots , a_{m_{k-1}})$
be a
![]() $231$
-avoiding permutation of length
$231$
-avoiding permutation of length
![]() $2^{k}-1$
with no max-induced monotonic subsequence of length greater than k. Define the sequence
$2^{k}-1$
with no max-induced monotonic subsequence of length greater than k. Define the sequence
![]() $S_k = (b_1, \dots , b_{2^{k+1}-1})$
by
$S_k = (b_1, \dots , b_{2^{k+1}-1})$
by
 $$ \begin{align*} b_i = \begin{cases}a_i &\text{if } i < 2^k; \\2^{k+1}-1 &\text{if } i = 2^k;\\a_{i-2^k} + 2^{k}-1 &\text{if } i > 2^k.\\\end{cases}\end{align*} $$
$$ \begin{align*} b_i = \begin{cases}a_i &\text{if } i < 2^k; \\2^{k+1}-1 &\text{if } i = 2^k;\\a_{i-2^k} + 2^{k}-1 &\text{if } i > 2^k.\\\end{cases}\end{align*} $$
If
![]() $(b_{i_1},\ldots , b_{i_\ell })$
is a max-induced monotonic subsequence of
$(b_{i_1},\ldots , b_{i_\ell })$
is a max-induced monotonic subsequence of
![]() $S_k$
, then either
$S_k$
, then either
![]() $i_\ell \leq 2^k$
or
$i_\ell \leq 2^k$
or
![]() $i_1 \geq 2^k$
. Thus, by our choice of
$i_1 \geq 2^k$
. Thus, by our choice of
![]() $S_{k-1}$
, there is no max-induced monotonic component of length greater than
$S_{k-1}$
, there is no max-induced monotonic component of length greater than
![]() $k+1$
in
$k+1$
in
![]() $S_k$
. Similarly, any possible
$S_k$
. Similarly, any possible
![]() $231$
pattern
$231$
pattern
![]() $(b_{i_1}, b_{i_2}, b_{i_3})$
has either
$(b_{i_1}, b_{i_2}, b_{i_3})$
has either
![]() $i_3 < 2^k$
or
$i_3 < 2^k$
or
![]() $i_1> 2^k$
by construction, so the inductive hypothesis shows
$i_1> 2^k$
by construction, so the inductive hypothesis shows
![]() $S_k$
is
$S_k$
is
![]() $231$
-avoiding.
$231$
-avoiding.
Proof of Theorem 2.2
For the forward direction, suppose (without loss of generality) that
![]() $\mathcal {F} $
contains no
$\mathcal {F} $
contains no
![]() $231$
-avoiding permutation pattern. Then each sequence in
$231$
-avoiding permutation pattern. Then each sequence in
![]() $\mathcal {F} $
contains either the pattern
$\mathcal {F} $
contains either the pattern
![]() $231$
or two elements which are equal. The sequence
$231$
or two elements which are equal. The sequence
![]() $S_k$
defined in Lemma 2.5 is an
$S_k$
defined in Lemma 2.5 is an
![]() $\mathcal F$
-avoiding sequence of length at least
$\mathcal F$
-avoiding sequence of length at least
![]() $2^k$
containing no max-induced monotonic subsequence of length greater than
$2^k$
containing no max-induced monotonic subsequence of length greater than
![]() $k+1$
.
$k+1$
.
For the backwards direction, let L and R be two permutations such that L is
![]() $132$
-avoiding and R is
$132$
-avoiding and R is
![]() $231$
-avoiding, and suppose S is a sequence of length n. We prove by induction on
$231$
-avoiding, and suppose S is a sequence of length n. We prove by induction on
![]() $t:=|L|+|R|$
that S contains at least one of L, R or a max-induced monotonic sequence of length at least
$t:=|L|+|R|$
that S contains at least one of L, R or a max-induced monotonic sequence of length at least
![]() $n^\varepsilon /2$
, where
$n^\varepsilon /2$
, where
![]() $\varepsilon = 4^{-t}$
. If
$\varepsilon = 4^{-t}$
. If
![]() $t\leq 5$
, then one of L or R has at most two elements, so the statement is clear. We therefore assume
$t\leq 5$
, then one of L or R has at most two elements, so the statement is clear. We therefore assume
![]() $t> 5$
, in which case we may assume also that n is large enough for the inequalities below.
$t> 5$
, in which case we may assume also that n is large enough for the inequalities below.
We first describe an algorithm that shows either S contains a max-induced monotonic sequence of length at least
![]() $n^{\varepsilon }/2$
or there is an index i such that
$n^{\varepsilon }/2$
or there is an index i such that
![]() $a_i$
is the maximum in a substantial interval (i.e.,
$a_i$
is the maximum in a substantial interval (i.e.,
![]() $a_j \leq a_i$
for
$a_j \leq a_i$
for
![]() $i-n^{1-\varepsilon } \leq j \leq i+n^{1-\varepsilon }$
).
$i-n^{1-\varepsilon } \leq j \leq i+n^{1-\varepsilon }$
).
We will attempt to build an increasing sequence from the leftmost element and a decreasing sequence starting from the rightmost element. Initialize index sets
![]() $I = [n]$
and
$I = [n]$
and
![]() $F_{\text {left}} = F_{\text {right}} =\emptyset $
. In the
$F_{\text {left}} = F_{\text {right}} =\emptyset $
. In the
![]() $k^{\text {th}}$
iteration of the algorithm, suppose the index
$k^{\text {th}}$
iteration of the algorithm, suppose the index
![]() $j_k \in I$
is such that
$j_k \in I$
is such that
![]() $a_{j_k} = \max _{i\in I} a_i$
. Let
$a_{j_k} = \max _{i\in I} a_i$
. Let
![]() $\ell = \max F_{\text {left}}$
and
$\ell = \max F_{\text {left}}$
and
![]() $r = \min F_{\text {right}}$
. For
$r = \min F_{\text {right}}$
. For
![]() $k = 1$
, we set
$k = 1$
, we set
![]() $\ell = 0$
and
$\ell = 0$
and
![]() $r = n+1$
. Then
$r = n+1$
. Then
-
○ if
 $j_k - \ell < n^{1-\varepsilon }$
, add
$j_k - \ell < n^{1-\varepsilon }$
, add
 $j_k$
to
$j_k$
to
 $F_{\text {left}}$
, delete all
$F_{\text {left}}$
, delete all
 $i\in I$
such that
$i\in I$
such that
 $i \leq j_k$
, and proceed to the next iteration;
$i \leq j_k$
, and proceed to the next iteration; -
○ if
 $r - j_k < n^{1-\varepsilon }$
, add
$r - j_k < n^{1-\varepsilon }$
, add
 $j_k$
to
$j_k$
to
 $F_{\text {right}}$
, delete all
$F_{\text {right}}$
, delete all
 $i\in I$
such that
$i\in I$
such that
 $i\geq j_k$
, and proceed to the next iteration;
$i\geq j_k$
, and proceed to the next iteration; -
○ otherwise, the algorithm terminates.
Observe that
![]() $(a_i)_{i\in F_{\text {left}}}$
and
$(a_i)_{i\in F_{\text {left}}}$
and
![]() $(a_i)_{i\in F_{\text {right}}}$
are max-induced monotonic sequences in S, so if either
$(a_i)_{i\in F_{\text {right}}}$
are max-induced monotonic sequences in S, so if either
![]() $|F_{\text {left}}| \geq n^{\varepsilon }/2$
or
$|F_{\text {left}}| \geq n^{\varepsilon }/2$
or
![]() $|F_{\text {right}}| \geq n^{\varepsilon }/2$
, then we have constructed a max-induced monotonic subsequence of length
$|F_{\text {right}}| \geq n^{\varepsilon }/2$
, then we have constructed a max-induced monotonic subsequence of length
![]() $n^{\varepsilon }/2$
. This must be the case if the algorithm terminates due to deleting all of I.
$n^{\varepsilon }/2$
. This must be the case if the algorithm terminates due to deleting all of I.
Otherwise, suppose the algorithm terminates on the
![]() $k^{\text {th}}$
iteration for some fixed k. Then
$k^{\text {th}}$
iteration for some fixed k. Then
![]() $j_k$
satisfies
$j_k$
satisfies
![]() $a_i \leq a_{j_k}$
for
$a_i \leq a_{j_k}$
for
![]() $j_k-n^{1-\varepsilon } \leq i \leq j_k+n^{1-\varepsilon }$
. Furthermore, for
$j_k-n^{1-\varepsilon } \leq i \leq j_k+n^{1-\varepsilon }$
. Furthermore, for
![]() $F_{\max } := \{i \in I: a_i = a_{j_k}\}$
, the constant sequence
$F_{\max } := \{i \in I: a_i = a_{j_k}\}$
, the constant sequence
![]() $(a_i)_{i\in F_{\max }}$
is a max-induced monotonic sequence in S, so we may assume
$(a_i)_{i\in F_{\max }}$
is a max-induced monotonic sequence in S, so we may assume
![]() $|F_{\max }| < n^\varepsilon /2$
.
$|F_{\max }| < n^\varepsilon /2$
.
Our goal now is to show that S must contain a max-induced copy of either L, R or a long monotonic sequence. Very roughly, we seek a large ‘blow-up’ of either 132 or 231, where a blow-up of 231 is a subsequence on
![]() $I\cup J \cup K$
such that
$I\cup J \cup K$
such that
![]() $(a_i, a_j, a_k)$
is a max-induced 231 pattern for any
$(a_i, a_j, a_k)$
is a max-induced 231 pattern for any
![]() $i\in I, j\in J, k\in K$
. Supposing we have such a blow-up of 231 with I and K large, we may apply the inductive hypothesis in I with the permutation patterns
$i\in I, j\in J, k\in K$
. Supposing we have such a blow-up of 231 with I and K large, we may apply the inductive hypothesis in I with the permutation patterns
![]() $L_{\text {left}}$
and R and on K with the permutation patterns
$L_{\text {left}}$
and R and on K with the permutation patterns
![]() $L_{\text {right}}$
and R, where
$L_{\text {right}}$
and R, where
![]() $L_{\text {left}}$
and
$L_{\text {left}}$
and
![]() $L_{\text {right}}$
are the permutation patterns to the left and right of the maximum element in any representative of the pattern L. If we find a max-induced R or long monotonic sequence, we are done, so we may assume I contains the pattern
$L_{\text {right}}$
are the permutation patterns to the left and right of the maximum element in any representative of the pattern L. If we find a max-induced R or long monotonic sequence, we are done, so we may assume I contains the pattern
![]() $L_{\text {left}}$
and K the pattern
$L_{\text {left}}$
and K the pattern
![]() $L_{\text {right}}$
, which can be joined together using the 231 blow-up structure to find the pattern L in
$L_{\text {right}}$
, which can be joined together using the 231 blow-up structure to find the pattern L in
![]() $I \cup J \cup K$
. We are not able to find a true blow-up of either 132 or 231, so first some care is needed to find a suitable replacement.
$I \cup J \cup K$
. We are not able to find a true blow-up of either 132 or 231, so first some care is needed to find a suitable replacement.
Let
![]() $I_{\text {left}} = \{i\in I: i< j_k\}$
and
$I_{\text {left}} = \{i\in I: i< j_k\}$
and
![]() $I_{\text {right}} = \{i\in I: i> j_k\}$
. Let
$I_{\text {right}} = \{i\in I: i> j_k\}$
. Let
![]() $M\,( \supset F_{\max })$
be the indices of the largest
$M\,( \supset F_{\max })$
be the indices of the largest
![]() $n^{(1-\varepsilon )/2}$
elements in
$n^{(1-\varepsilon )/2}$
elements in
![]() $(a_i)_{i\in I}$
, breaking ties arbitrarily. Either
$(a_i)_{i\in I}$
, breaking ties arbitrarily. Either
![]() $M_{\text {left}} := M \cap I_{\text {left}}$
or
$M_{\text {left}} := M \cap I_{\text {left}}$
or
![]() $M_{\text {right}} := M \setminus M_{\text {left}}$
has at least
$M_{\text {right}} := M \setminus M_{\text {left}}$
has at least
![]() $\frac 12 n^{(1-\varepsilon )/2}$
elements. Suppose the former (the argument for the latter is similar).
$\frac 12 n^{(1-\varepsilon )/2}$
elements. Suppose the former (the argument for the latter is similar).
-
○ Since
 $|I_{\text {right}}| \geq n^{1-\varepsilon }$
, there must be an interval
$|I_{\text {right}}| \geq n^{1-\varepsilon }$
, there must be an interval
 $I' \subset I_{\text {right}}$
of length at least
$I' \subset I_{\text {right}}$
of length at least
 $\frac 12 n^{(1-\varepsilon )/2}$
such that
$\frac 12 n^{(1-\varepsilon )/2}$
such that
 $I' \cap M_{\text {right}} = \emptyset $
.
$I' \cap M_{\text {right}} = \emptyset $
. -
○ Since
 $|M_{\text {left}}| \geq \frac 12n^{(1-\varepsilon )/2}$
and
$|M_{\text {left}}| \geq \frac 12n^{(1-\varepsilon )/2}$
and
 $|F_{\max }| < n^\varepsilon /2$
, there is an interval
$|F_{\max }| < n^\varepsilon /2$
, there is an interval
 $J \subset I_{\text {left}}$
such that
$J \subset I_{\text {left}}$
such that
 $|J \cap M_{\text {left}}| \geq n^{(1-3\varepsilon )/2}$
and
$|J \cap M_{\text {left}}| \geq n^{(1-3\varepsilon )/2}$
and
 $J\cap F_{\max } = \emptyset $
.
$J\cap F_{\max } = \emptyset $
.
We are not quite done: observe that there may be an element indexed by
![]() $I'$
equal to an element indexed by J. To break ties, we restrict
$I'$
equal to an element indexed by J. To break ties, we restrict
![]() $I'$
further. As before, we define
$I'$
further. As before, we define
![]() $I_{\max }' := \{i \in I': a_i = \max _{j\in I'} a_{j}\}$
. The constant sequence
$I_{\max }' := \{i \in I': a_i = \max _{j\in I'} a_{j}\}$
. The constant sequence
![]() $(a_i)_{i\in I_{\max }'}$
is a max-induced monotonic sequence in S, so we may assume
$(a_i)_{i\in I_{\max }'}$
is a max-induced monotonic sequence in S, so we may assume
![]() $|I_{\max }'| < n^\varepsilon /2$
. Then,
$|I_{\max }'| < n^\varepsilon /2$
. Then,
-
○ There is an interval
 $I" \subseteq I'$
of length at least
$I" \subseteq I'$
of length at least
 $\frac 12 n^{(1-3\varepsilon )/2}$
such that
$\frac 12 n^{(1-3\varepsilon )/2}$
such that
 $|I" \cap I_{\max }'| = \emptyset $
.
$|I" \cap I_{\max }'| = \emptyset $
.
Now, let
![]() $A = J \cap M_{\text {left}}$
and
$A = J \cap M_{\text {left}}$
and
![]() $B = I"$
. By construction, any max-induced subsequence in A or B is a max-induced subsequence of S. Also if
$B = I"$
. By construction, any max-induced subsequence in A or B is a max-induced subsequence of S. Also if
![]() $i\in A, \, j\in B$
then
$i\in A, \, j\in B$
then
![]() $a_j < a_i < a_{j_k}$
. Recall that the permutation L is
$a_j < a_i < a_{j_k}$
. Recall that the permutation L is
![]() $132$
-avoiding. Define
$132$
-avoiding. Define
![]() $L_{\text {left}}$
to be the subpermutation preceding
$L_{\text {left}}$
to be the subpermutation preceding
![]() $\max L$
and
$\max L$
and
![]() $L_{\text {right}}$
to be the subpermutation following
$L_{\text {right}}$
to be the subpermutation following
![]() $\max L$
. Observe that
$\max L$
. Observe that
![]() $L_{\text {left}}$
and
$L_{\text {left}}$
and
![]() $L_{\text {right}}$
are both 132-avoiding.
$L_{\text {right}}$
are both 132-avoiding.
We finally apply the inductive hypothesis to
![]() $S_A:= (a_i)_{i \in A}$
with the permutations
$S_A:= (a_i)_{i \in A}$
with the permutations
![]() $L_{\text {left}}$
and R, and to
$L_{\text {left}}$
and R, and to
![]() $S_B := (a_i)_{i\in B}$
with the permutations
$S_B := (a_i)_{i\in B}$
with the permutations
![]() $L_{\text {right}}$
and R. If we find a max-induced copy of R in
$L_{\text {right}}$
and R. If we find a max-induced copy of R in
![]() $S_A$
or
$S_A$
or
![]() $S_B$
, we are done. If
$S_B$
, we are done. If
![]() $S_A$
contains a max-induced monotonic subsequence of length at least
$S_A$
contains a max-induced monotonic subsequence of length at least
or
![]() $S_B$
contains a max-induced monotonic subsequence of length at least
$S_B$
contains a max-induced monotonic subsequence of length at least
we are finished. Otherwise, there is a max-induced copy of
![]() $L_{\text {left}}$
in
$L_{\text {left}}$
in
![]() $S_A$
and
$S_A$
and
![]() $L_r$
in
$L_r$
in
![]() $S_B$
, which along with
$S_B$
, which along with
![]() $a_{j_k}$
forms a max-induced copy of L in S.
$a_{j_k}$
forms a max-induced copy of L in S.
Given
![]() $n, k \in \mathbb N$
, recall
$n, k \in \mathbb N$
, recall
![]() $f(k)$
is the largest integer for which there exists some
$f(k)$
is the largest integer for which there exists some
![]() $\varepsilon> 0$
such that every sequence of length n contains either at least
$\varepsilon> 0$
such that every sequence of length n contains either at least
![]() $f(k)$
distinct max-induced patterns on k elements or a monotonic subsequence of length
$f(k)$
distinct max-induced patterns on k elements or a monotonic subsequence of length
![]() $n^\varepsilon$
.
$n^\varepsilon$
.
2.2 Separated subsequences
Up to this point, our sequence results do not use a useful fact about the
![]() $\delta $
-sequences which features often in stepping-up. A sequence
$\delta $
-sequences which features often in stepping-up. A sequence
![]() $(a_1,a_2,\ldots ,a_{k})$
has the unique maximum property if for any interval I,
$(a_1,a_2,\ldots ,a_{k})$
has the unique maximum property if for any interval I,
![]() $|\{i\in I: a_i = \max (a_i)_{i\in I}\}| = 1$
. We capitalize on this useful property in Lemma 2.6, which studies a second notion of subsequence that is used in our proof of Theorem 1.3(c). Call
$|\{i\in I: a_i = \max (a_i)_{i\in I}\}| = 1$
. We capitalize on this useful property in Lemma 2.6, which studies a second notion of subsequence that is used in our proof of Theorem 1.3(c). Call
![]() $(a_{i_1},a_{i_2},\ldots ,a_{i_t})$
with
$(a_{i_1},a_{i_2},\ldots ,a_{i_t})$
with
![]() $0<i_1<\dots <i_t\leq m$
a separated subsequence of
$0<i_1<\dots <i_t\leq m$
a separated subsequence of
![]() $(a_1,a_2,\ldots , a_m)$
if
$(a_1,a_2,\ldots , a_m)$
if
![]() $i_{j+1}>i_{j}+1$
for all
$i_{j+1}>i_{j}+1$
for all
![]() $j \in [t]$
. Similar to max-inducedness, the following simple fact captures the usefulness of this definition for stepping up: suppose
$j \in [t]$
. Similar to max-inducedness, the following simple fact captures the usefulness of this definition for stepping up: suppose
![]() $v_1 < v_2 < \dots < v_{\ell +1}$
are vectors in
$v_1 < v_2 < \dots < v_{\ell +1}$
are vectors in
![]() $\{0,1\}^m$
and let
$\{0,1\}^m$
and let
![]() $\delta _i = \delta (v_i, v_{i+1})$
. If
$\delta _i = \delta (v_i, v_{i+1})$
. If
![]() $(\delta _{i_1},\ldots , \delta _{i_k})$
is a separated subsequence of
$(\delta _{i_1},\ldots , \delta _{i_k})$
is a separated subsequence of
![]() $(\delta _1,\ldots ,\delta _\ell )$
, then there are
$(\delta _1,\ldots ,\delta _\ell )$
, then there are
![]() $v_{j_1},\ldots , v_{j_{2k}}$
such that
$v_{j_1},\ldots , v_{j_{2k}}$
such that
![]() $\delta (v_{j_{2s-1}}, v_{j_{2s}}) = \delta _{i_s}$
for each
$\delta (v_{j_{2s-1}}, v_{j_{2s}}) = \delta _{i_s}$
for each
![]() $s \in [k]$
. Given a sequence
$s \in [k]$
. Given a sequence
![]() $S= (s_1,\ldots , s_n)$
, define
$S= (s_1,\ldots , s_n)$
, define
![]() $\|S\| := |\{s_1,\ldots , s_n\}|$
– that is, the number of distinct values in the sequence. We can now state our key result on separated subsequences.
$\|S\| := |\{s_1,\ldots , s_n\}|$
– that is, the number of distinct values in the sequence. We can now state our key result on separated subsequences.
Lemma 2.6. Let
![]() $A = (a_i)_{i=1}^n$
be a sequence with the unique maximum property and
$A = (a_i)_{i=1}^n$
be a sequence with the unique maximum property and
![]() $k\in {\mathbb {N}}$
. If
$k\in {\mathbb {N}}$
. If
![]() $\|A\| < n^{1/(k+1)}$
and n is large enough, A contains every permutation pattern on
$\|A\| < n^{1/(k+1)}$
and n is large enough, A contains every permutation pattern on
![]() $[k]$
as a separated subsequence.
$[k]$
as a separated subsequence.
The proof relies on a simple density argument to find a very rich substructure that contains within it all possible small structures.
Proof of Lemma 2.6
We first find constant subsequences
![]() $A_1,\ldots , A_{k}$
such that
$A_1,\ldots , A_{k}$
such that
-
(i)
 $|A_i| \geq n^{1-i/(k+1)}$
for each
$|A_i| \geq n^{1-i/(k+1)}$
for each
 $i \in [k]$
,
$i \in [k]$
, -
(ii) if
 $a \in A_i$
(meaning a is equal to some element of
$a \in A_i$
(meaning a is equal to some element of
 $A_i$
) and
$A_i$
) and
 $a' \in A_j$
with
$a' \in A_j$
with
 $i < j$
, then
$i < j$
, then
 $a < a'$
, and
$a < a'$
, and -
(iii) (interlacing property) if
 $a_j, a_\ell \in A_i$
such that
$a_j, a_\ell \in A_i$
such that
 $j < \ell $
, then there is some
$j < \ell $
, then there is some
 $a_m \in A_{i-1}$
such that
$a_m \in A_{i-1}$
such that
 $j < m < \ell $
.
$j < m < \ell $
.
Given such subsequences, embedding an arbitrary permutation
![]() $(\sigma (1),\ldots , \sigma (k))$
is straightforward: index the elements of
$(\sigma (1),\ldots , \sigma (k))$
is straightforward: index the elements of
![]() $A_k$
by
$A_k$
by
![]() $(a_{\ell _1},\ldots , a_{\ell _s})$
. For each
$(a_{\ell _1},\ldots , a_{\ell _s})$
. For each
![]() $j \in [k]$
, use the interlacing property (and the fact
$j \in [k]$
, use the interlacing property (and the fact
![]() $s \geq n^{1/(k+1)}$
) to find a subsequence
$s \geq n^{1/(k+1)}$
) to find a subsequence
![]() $(a_{j_1}, \ldots , a_{j_k})$
of
$(a_{j_1}, \ldots , a_{j_k})$
of
![]() $A_j$
with
$A_j$
with
![]() $\ell _{m2^{k+1}} < j_m < \ell _{(m+1)2^{k+1}}$
. The (separated) subsequence
$\ell _{m2^{k+1}} < j_m < \ell _{(m+1)2^{k+1}}$
. The (separated) subsequence
![]() $(a_{\sigma (1)_1},\ldots , a_{\sigma (k)_k})$
has the same pattern as
$(a_{\sigma (1)_1},\ldots , a_{\sigma (k)_k})$
has the same pattern as
![]() $(\sigma (1),\ldots , \sigma (k))$
by property (ii).
$(\sigma (1),\ldots , \sigma (k))$
by property (ii).
We construct the desired subsequences by induction. Since
![]() $\|A\| < n^{\frac {1}{k+1}}$
, there is a constant subsequence
$\|A\| < n^{\frac {1}{k+1}}$
, there is a constant subsequence
![]() $A_1$
such that
$A_1$
such that
![]() $|A_1| \geq n^{1-1/(k+1)}$
. Note that by the unique maximum property,
$|A_1| \geq n^{1-1/(k+1)}$
. Note that by the unique maximum property,
![]() $A_1$
must be a separated subsequence. For
$A_1$
must be a separated subsequence. For
![]() $i \geq 1$
, given a constant separated subsequence
$i \geq 1$
, given a constant separated subsequence
![]() $A_i = (a_{i_j})_j$
satisfying the above properties, we construct
$A_i = (a_{i_j})_j$
satisfying the above properties, we construct
![]() $A_{i+1}$
as follows:
$A_{i+1}$
as follows:
Let
![]() $A_i' = (a_{i_j}')_j$
be the subsequence of A consisting of the maximum values between the elements of
$A_i' = (a_{i_j}')_j$
be the subsequence of A consisting of the maximum values between the elements of
![]() $A_i$
, meaning if
$A_i$
, meaning if
![]() $a_{i_j}, a_{i_{j+1}} \in A_i$
, then
$a_{i_j}, a_{i_{j+1}} \in A_i$
, then
![]() $a_{i_j}' = \max \{a_\ell : i_j \leq \ell \leq i_{j+1}\}$
. By the unique maximum property of A,
$a_{i_j}' = \max \{a_\ell : i_j \leq \ell \leq i_{j+1}\}$
. By the unique maximum property of A,
![]() $a_{i_j}'$
is well-defined and is strictly greater than
$a_{i_j}'$
is well-defined and is strictly greater than
![]() $a_{i_j}$
and
$a_{i_j}$
and
![]() $a_{i_{j+1}}$
. Then
$a_{i_{j+1}}$
. Then
![]() $|A_i'| = |A_i| - 1 \geq n^{1-i/(k+1)}-1$
, and
$|A_i'| = |A_i| - 1 \geq n^{1-i/(k+1)}-1$
, and
![]() $\|A_i'\| \leq n^{1/(k+1)} - 1$
from the assumption that
$\|A_i'\| \leq n^{1/(k+1)} - 1$
from the assumption that
![]() $\|A\| \leq n^{1/(k+1)}$
. Thus, there is a constant subsequence of
$\|A\| \leq n^{1/(k+1)}$
. Thus, there is a constant subsequence of
![]() $A_i'$
with length at least
$A_i'$
with length at least
 $$\begin{align*}\frac{|A_i'|}{\|A_i'\|} \geq n^{1-(i+1)/(k+1)},\end{align*}$$
$$\begin{align*}\frac{|A_i'|}{\|A_i'\|} \geq n^{1-(i+1)/(k+1)},\end{align*}$$
and we define
![]() $A_{i+1}$
as this subsequence. It is clear from the construction that properties (i), (ii) and (iii) are satisfied.
$A_{i+1}$
as this subsequence. It is clear from the construction that properties (i), (ii) and (iii) are satisfied.
We are now ready to employ these results in our stepping-up constructions.
3 Stepping up with many colours
In this section, we explain how the results on max-induced and separated patterns in sequences allow us to step up colourings in which all large sets of vertices span many colours. We prove Theorem 1.3 as well as Corollary 1.4. Throughout, all colourings discussed will be (hyper)edge-colourings. We say a colouring of a complete hypergraph with q colours is
![]() $(t;q,p)$
-rainbow if every set of t vertices spans at least p colours. In this language,
$(t;q,p)$
-rainbow if every set of t vertices spans at least p colours. In this language,
![]() $r_k(t;q,p)-1$
is the largest integer n for which there exists a
$r_k(t;q,p)-1$
is the largest integer n for which there exists a
![]() $(t;q,p)$
-rainbow colouring of
$(t;q,p)$
-rainbow colouring of
![]() $K_{n}^{(k)}$
. Let
$K_{n}^{(k)}$
. Let
![]() $V(K_{n}^{(r+1)})=\{0,1\}^n$
and given
$V(K_{n}^{(r+1)})=\{0,1\}^n$
and given
![]() $v,w \in V$
, recall that
$v,w \in V$
, recall that
and that
![]() $v<w$
if and only if
$v<w$
if and only if
![]() $v_\delta < w_\delta $
. To each set of vertices
$v_\delta < w_\delta $
. To each set of vertices
![]() $v_1< v_2 < \dots < v_{k+1}$
in
$v_1< v_2 < \dots < v_{k+1}$
in
![]() $K_n^{(r+1)}$
corresponds a sequence
$K_n^{(r+1)}$
corresponds a sequence
![]() $(\delta _1,\delta _2,\ldots ,\delta _{k})$
given by
$(\delta _1,\delta _2,\ldots ,\delta _{k})$
given by
![]() $\delta _i = \delta (v_i,v_{i+1})$
, which we refer to as the corresponding
$\delta _i = \delta (v_i,v_{i+1})$
, which we refer to as the corresponding
![]() $\delta $
-sequence. The crucial properties for our application of the results of Section 2 to hypergraph Ramsey theory are the following:
$\delta $
-sequence. The crucial properties for our application of the results of Section 2 to hypergraph Ramsey theory are the following:
For examples, see [Reference Graham, Rothschild and Spencer12] for proofs. A useful perspective is gained by viewing
![]() $[2^n]$
as the leaves of a binary tree of depth n, ordered from left to right as you would draw them. Given two leaves
$[2^n]$
as the leaves of a binary tree of depth n, ordered from left to right as you would draw them. Given two leaves
![]() $v,w\in [2^n]$
, the number
$v,w\in [2^n]$
, the number
![]() $2\delta (v,w)$
is simply the length of the unique path between them.
$2\delta (v,w)$
is simply the length of the unique path between them.
Recall that Corollary 2.4 shows that a sequence
![]() $(\delta _1,\delta _2,\ldots ,\delta _{\ell })$
either contains many distinct max-induced patterns or a long monotonic max-induced subsequence. In order to make use of this fact, we recall Claim 2.1, which simply says the following: suppose
$(\delta _1,\delta _2,\ldots ,\delta _{\ell })$
either contains many distinct max-induced patterns or a long monotonic max-induced subsequence. In order to make use of this fact, we recall Claim 2.1, which simply says the following: suppose
![]() $v_1 < v_2 < \dots < v_{\ell +1}$
are vectors in
$v_1 < v_2 < \dots < v_{\ell +1}$
are vectors in
![]() $\{0,1\}^m$
and let
$\{0,1\}^m$
and let
![]() $\delta _i = \delta (v_i, v_{i+1})$
. If
$\delta _i = \delta (v_i, v_{i+1})$
. If
![]() $(\delta _{i_1},\ldots , \delta _{i_k})$
is a max-induced subsequence of
$(\delta _{i_1},\ldots , \delta _{i_k})$
is a max-induced subsequence of
![]() $(\delta _1,\ldots ,\delta _\ell )$
, then there are
$(\delta _1,\ldots ,\delta _\ell )$
, then there are
![]() $v_{j_1},\ldots , v_{j_{k+1}}$
such that
$v_{j_1},\ldots , v_{j_{k+1}}$
such that
![]() $\delta (v_{j_s}, v_{j_{s+1}}) = \delta _{i_s}$
.
$\delta (v_{j_s}, v_{j_{s+1}}) = \delta _{i_s}$
.
Proof of Claim 2.1
Let
![]() $v_{j_1} = v_{i_1}$
and
$v_{j_1} = v_{i_1}$
and
![]() $v_{j_{k+1}} = v_{i_k + 1}$
. Then for
$v_{j_{k+1}} = v_{i_k + 1}$
. Then for
![]() $s>1$
, define
$s>1$
, define
![]() $v_{j_s} = v_{i_{s-1} + 1}$
if
$v_{j_s} = v_{i_{s-1} + 1}$
if
![]() $\delta _{i_{s-1}} < \delta _{i_s}$
and
$\delta _{i_{s-1}} < \delta _{i_s}$
and
![]() $v_{j_s} = v_{i_s}$
otherwise. It is straightforward to check, using property (3.2), that
$v_{j_s} = v_{i_s}$
otherwise. It is straightforward to check, using property (3.2), that
![]() $\delta (v_{j_s}, v_{j_{s+1}}) = \delta _{i_s}$
for each s.
$\delta (v_{j_s}, v_{j_{s+1}}) = \delta _{i_s}$
for each s.
We are ready to use Theorem 2.2 to prove the first two parts of Theorem 1.3.
Proof of Theorem 1.3(a) and (b)
Let
![]() $k,p,q \geq 3$
be such that
$k,p,q \geq 3$
be such that
![]() $p \leq C_k$
, the
$p \leq C_k$
, the
![]() $k^{\text {th}}$
Catalan number, and let
$k^{\text {th}}$
Catalan number, and let
![]() $c:=16^k+1$
. We first prove Part (b) – the inequality
$c:=16^k+1$
. We first prove Part (b) – the inequality
![]() $r_{k+1}(t^c;2q + p,p)> 2^{r_k(t;q,p) - 1}$
– by showing such that we can construct a
$r_{k+1}(t^c;2q + p,p)> 2^{r_k(t;q,p) - 1}$
– by showing such that we can construct a
![]() $(t^c;2q + p,p)$
-rainbow colouring
$(t^c;2q + p,p)$
-rainbow colouring
![]() $\chi '$
of
$\chi '$
of
![]() $K_{2^n}^{(k+1)}$
from any
$K_{2^n}^{(k+1)}$
from any
![]() $(t;q,p)$
-rainbow colouring
$(t;q,p)$
-rainbow colouring
![]() $\chi $
of
$\chi $
of
![]() $K_n^{(k)}$
. Let
$K_n^{(k)}$
. Let
![]() $\chi $
be such a rainbow colouring.
$\chi $
be such a rainbow colouring.
We identify
![]() $V(K_{2^n}^{(k+1)})$
and
$V(K_{2^n}^{(k+1)})$
and
![]() $V(K_{n}^{(k)})$
with
$V(K_{n}^{(k)})$
with
![]() $\{0,1\}^n$
and
$\{0,1\}^n$
and
![]() $[n]$
, respectively. Partition the set of patterns on
$[n]$
, respectively. Partition the set of patterns on
![]() $[k]$
, excluding the two monotonic permutations, into
$[k]$
, excluding the two monotonic permutations, into
![]() $p-2$
classes
$p-2$
classes
![]() $\mathcal {C} _1,\ldots , \mathcal {C} _{p-2}$
such that each class contains at least one 132-avoiding permutation pattern and one 231-avoiding permutation pattern. Let
$\mathcal {C} _1,\ldots , \mathcal {C} _{p-2}$
such that each class contains at least one 132-avoiding permutation pattern and one 231-avoiding permutation pattern. Let
![]() $\mathcal {C} _{p-1}$
be the family of patterns containing only the strictly increasing permutation and
$\mathcal {C} _{p-1}$
be the family of patterns containing only the strictly increasing permutation and
![]() $\mathcal {C} _{p}$
the family containing the strictly decreasing permutation. Observe that such a partition is guaranteed to exist by Corollary 2.4 and the assumption that
$\mathcal {C} _{p}$
the family containing the strictly decreasing permutation. Observe that such a partition is guaranteed to exist by Corollary 2.4 and the assumption that
![]() $C_{k}\geq p$
(note that a permutation may be both 132-avoiding and 231-avoiding). For a sequence S, we say
$C_{k}\geq p$
(note that a permutation may be both 132-avoiding and 231-avoiding). For a sequence S, we say
![]() $S\in \mathcal {C} _i$
if the pattern of S is in
$S\in \mathcal {C} _i$
if the pattern of S is in
![]() $\mathcal {C} _i$
. Assign to each class
$\mathcal {C} _i$
. Assign to each class
![]() $\mathcal {C} _i$
a distinct colour
$\mathcal {C} _i$
a distinct colour
![]() $c_i$
. Then, for an edge
$c_i$
. Then, for an edge
![]() $e=\{v_1,\ldots , v_{k+1}\}$
of
$e=\{v_1,\ldots , v_{k+1}\}$
of
![]() $K_{2^n}^{(k+1)}$
, with corresponding
$K_{2^n}^{(k+1)}$
, with corresponding
![]() $\delta $
-sequence
$\delta $
-sequence
![]() $(\delta _1,\ldots , \delta _k)$
, let
$(\delta _1,\ldots , \delta _k)$
, let
 $$\begin{align*}\chi'(e) = \begin{cases}\chi(\{\delta_1,\ldots, \delta_{k}\})\times 1 &\text{if } \delta_1<\delta_2<\dots < \delta_{k};\\\chi(\{\delta_1,\ldots, \delta_{k}\})\times 2 &\text{if } \delta_1>\delta_2>\dots > \delta_{k};\\c_i &\text{if } (\delta_1,\ldots, \delta_{k})\in \mathcal{C} _i,\ i \leq p-2.\end{cases} \end{align*}$$
$$\begin{align*}\chi'(e) = \begin{cases}\chi(\{\delta_1,\ldots, \delta_{k}\})\times 1 &\text{if } \delta_1<\delta_2<\dots < \delta_{k};\\\chi(\{\delta_1,\ldots, \delta_{k}\})\times 2 &\text{if } \delta_1>\delta_2>\dots > \delta_{k};\\c_i &\text{if } (\delta_1,\ldots, \delta_{k})\in \mathcal{C} _i,\ i \leq p-2.\end{cases} \end{align*}$$
We claim
![]() $\chi '$
is the desired colouring. Consider a set of
$\chi '$
is the desired colouring. Consider a set of
![]() $t^c$
vertices
$t^c$
vertices
![]() $\{v_1,\ldots ,v_{t^c}\}\subset V(K_{2^n}^{(k+1)})$
and its corresponding
$\{v_1,\ldots ,v_{t^c}\}\subset V(K_{2^n}^{(k+1)})$
and its corresponding
![]() $\delta $
-sequence
$\delta $
-sequence
![]() $(\delta _1,\ldots , \delta _{t^c-1})$
. Since each class
$(\delta _1,\ldots , \delta _{t^c-1})$
. Since each class
![]() $\mathcal {C}_i$
contains a 132-avoiding permutation pattern and a 231-avoiding permutation pattern, Theorem 2.2 tells us that
$\mathcal {C}_i$
contains a 132-avoiding permutation pattern and a 231-avoiding permutation pattern, Theorem 2.2 tells us that
![]() $(\delta _1,\ldots , \delta _{t^c-1})$
either contains a max-induced pattern from each of
$(\delta _1,\ldots , \delta _{t^c-1})$
either contains a max-induced pattern from each of
![]() $\mathcal {C} _1,\dots ,\mathcal {C} _{p}$
or a max-induced monotonic sequence of length t (the value of c was chosen for this purpose). Claim 2.1 shows that for every max-induced sequence
$\mathcal {C} _1,\dots ,\mathcal {C} _{p}$
or a max-induced monotonic sequence of length t (the value of c was chosen for this purpose). Claim 2.1 shows that for every max-induced sequence
![]() $S\subset (\delta _1,\ldots , \delta _{t^c-1})$
of length k, we can find
$S\subset (\delta _1,\ldots , \delta _{t^c-1})$
of length k, we can find
![]() $\{v_{i_1},\dots ,v_{i_{k+1}} \}\subset \{v_1,\ldots ,v_{t^c}\}$
whose corresponding
$\{v_{i_1},\dots ,v_{i_{k+1}} \}\subset \{v_1,\ldots ,v_{t^c}\}$
whose corresponding
![]() $\delta $
-sequence is S. In other words, we have that
$\delta $
-sequence is S. In other words, we have that
![]() $\chi '(\{v_{i_1},\dots ,v_{i_{k+1}}\}) = c_i$
if the pattern of S is in
$\chi '(\{v_{i_1},\dots ,v_{i_{k+1}}\}) = c_i$
if the pattern of S is in
![]() $\mathcal {C} _i$
. Therefore,
$\mathcal {C} _i$
. Therefore,
![]() $(\delta _1,\ldots , \delta _{t^c-1})$
containing a max-induced pattern from each of
$(\delta _1,\ldots , \delta _{t^c-1})$
containing a max-induced pattern from each of
![]() $\mathcal {C} _1,\dots ,\mathcal {C} _{p}$
implies that
$\mathcal {C} _1,\dots ,\mathcal {C} _{p}$
implies that
![]() $\{v_1,\ldots ,v_{t^c}\}$
spans at least p colours.
$\{v_1,\ldots ,v_{t^c}\}$
spans at least p colours.
If instead,
![]() $(\delta _1,\ldots , \delta _{t^c-1})$
contains a max-induced monotonic subsequence, say
$(\delta _1,\ldots , \delta _{t^c-1})$
contains a max-induced monotonic subsequence, say
![]() $(\delta _1,\ldots , \delta _t)$
, then by Claim 2.1, we can find
$(\delta _1,\ldots , \delta _t)$
, then by Claim 2.1, we can find
![]() $\{v_{i_1},\dots ,v_{i_{t+1}}\}\subset \{v_1,\dots ,v_{t^c}\}$
whose corresponding pattern is
$\{v_{i_1},\dots ,v_{i_{t+1}}\}\subset \{v_1,\dots ,v_{t^c}\}$
whose corresponding pattern is
![]() $(\delta _1,\dots ,\delta _t)$
. We may assume without loss of generality that
$(\delta _1,\dots ,\delta _t)$
. We may assume without loss of generality that
![]() $(\delta _1,\ldots ,\delta _t)$
is increasing, and by property (3.1),
$(\delta _1,\ldots ,\delta _t)$
is increasing, and by property (3.1),
![]() $\delta _1<\dots <\delta _t$
. Every subsequence of a strictly increasing max-induced sequence is a strictly increasing max-induced subsequence. Thus, again by Claim 2.1, for every subsequence
$\delta _1<\dots <\delta _t$
. Every subsequence of a strictly increasing max-induced sequence is a strictly increasing max-induced subsequence. Thus, again by Claim 2.1, for every subsequence
![]() $S\subset (\delta _1,\ldots , \delta _t)$
of length k, we can find a subsequence
$S\subset (\delta _1,\ldots , \delta _t)$
of length k, we can find a subsequence
![]() $S'\subset (v_{i_1},\dots ,v_{i_{t+1}})$
of length
$S'\subset (v_{i_1},\dots ,v_{i_{t+1}})$
of length
![]() $k+1$
whose corresponding
$k+1$
whose corresponding
![]() $\delta $
-sequence is S. Observe that
$\delta $
-sequence is S. Observe that
![]() $\chi '(S') = (\chi (S),1)$
, so the set of
$\chi '(S') = (\chi (S),1)$
, so the set of
![]() $(k+1)$
-edges on
$(k+1)$
-edges on
![]() $\{v_{i_1},\dots ,v_{i_{t+1}}\}$
spans at least as many colours as the set of k-edges on
$\{v_{i_1},\dots ,v_{i_{t+1}}\}$
spans at least as many colours as the set of k-edges on
![]() $\{\delta _1,\ldots ,\delta _t\}$
. By assumption, this is at least p.
$\{\delta _1,\ldots ,\delta _t\}$
. By assumption, this is at least p.
All that remains is to count the number of colours used by
![]() $\chi '$
. This is at most
$\chi '$
. This is at most
![]() $2$
colours for each of the q colours used by
$2$
colours for each of the q colours used by
![]() $\chi $
plus an extra
$\chi $
plus an extra
![]() $p-2$
for the
$p-2$
for the
![]() $c_i$
’s. Combined with the above arguments, this shows that
$c_i$
’s. Combined with the above arguments, this shows that
![]() $\chi '$
is a
$\chi '$
is a
![]() $(t^c;2q + p-2,p)$
-rainbow colouring and, in particular, a
$(t^c;2q + p-2,p)$
-rainbow colouring and, in particular, a
![]() $(t^c;2q + p,p)$
-rainbow colouring.
$(t^c;2q + p,p)$
-rainbow colouring.
We now describe the construction of the
![]() $(t^c;q,p-2)$
-rainbow colouring, say
$(t^c;q,p-2)$
-rainbow colouring, say
![]() $\chi "$
, which proves Part (a) (i.e., that
$\chi "$
, which proves Part (a) (i.e., that
![]() $r_{k+1}(t^c;q,p-2)> 2^{r_k(t;q,p-2) - 1}$
). Let a
$r_{k+1}(t^c;q,p-2)> 2^{r_k(t;q,p-2) - 1}$
). Let a
![]() $(t;q,p-2)$
-rainbow colouring
$(t;q,p-2)$
-rainbow colouring
![]() $\chi $
of
$\chi $
of
![]() $K_n^{(k)}$
be given. Partition the set of patterns on
$K_n^{(k)}$
be given. Partition the set of patterns on
![]() $[k]$
as before and assign to each class
$[k]$
as before and assign to each class
![]() $\mathcal {C} _i$
a distinct colour
$\mathcal {C} _i$
a distinct colour
![]() $c_i$
for
$c_i$
for
![]() $i\in [p-2]$
; only this time identify these colours with the first
$i\in [p-2]$
; only this time identify these colours with the first
![]() $[p-2]$
colours used by
$[p-2]$
colours used by
![]() $\chi $
(trivially we have
$\chi $
(trivially we have
![]() $q\geq p-2$
). For an edge
$q\geq p-2$
). For an edge
![]() $e=\{v_1,\ldots , v_{k+1}\}$
with corresponding
$e=\{v_1,\ldots , v_{k+1}\}$
with corresponding
![]() $\delta $
-sequence
$\delta $
-sequence
![]() $(\delta _1,\ldots , \delta _{k})$
, let
$(\delta _1,\ldots , \delta _{k})$
, let
 $$\begin{align*}\chi"(e) = \begin{cases}\chi(\{\delta_1,\ldots, \delta_{k}\}) &\text{if } \delta_1<\delta_2<\dots < \delta_{k}\text{ or } \delta_1>\delta_2>\dots > \delta_{k} ;\\c_i &\text{if } (\delta_1,\ldots, \delta_{k})\in \mathcal{C} _i.\end{cases}\end{align*}$$
$$\begin{align*}\chi"(e) = \begin{cases}\chi(\{\delta_1,\ldots, \delta_{k}\}) &\text{if } \delta_1<\delta_2<\dots < \delta_{k}\text{ or } \delta_1>\delta_2>\dots > \delta_{k} ;\\c_i &\text{if } (\delta_1,\ldots, \delta_{k})\in \mathcal{C} _i.\end{cases}\end{align*}$$
We omit the proof that
![]() $\chi "$
is in fact the desired colouring, as it is almost identical to the proof for
$\chi "$
is in fact the desired colouring, as it is almost identical to the proof for
![]() $\chi '$
. We simply note that now we can only force
$\chi '$
. We simply note that now we can only force
![]() $p-2$
colours in any set of
$p-2$
colours in any set of
![]() $t^c$
vertices, as an edge with a monotonic pattern may receive any one of the colours
$t^c$
vertices, as an edge with a monotonic pattern may receive any one of the colours
![]() $c_i$
for
$c_i$
for
![]() $i\in [p-2]$
.
$i\in [p-2]$
.
In applying our stepping-up results, we will need the following result on rainbow colorings which is proven by a standard use of the first moment method (see, for example, [Reference Alon and Spencer1]).
Proposition 3.1. For every k and q, there exists
![]() $\varepsilon> 0$
and
$\varepsilon> 0$
and
![]() $t_0$
so that for
$t_0$
so that for
![]() $t> t_0$
, there is a
$t> t_0$
, there is a
![]() $(t;q,q)$
-rainbow colouring of
$(t;q,q)$
-rainbow colouring of
![]() $K_n^{(k)}$
with
$K_n^{(k)}$
with
![]() $n = 2^{\varepsilon t^{k-1}}$
.
$n = 2^{\varepsilon t^{k-1}}$
.
Proof. Set
![]() $\varepsilon = 1/(q k!)$
and
$\varepsilon = 1/(q k!)$
and
![]() $t_0 = eq$
. Consider a uniformly random q-colouring of
$t_0 = eq$
. Consider a uniformly random q-colouring of
![]() $K_n^{(k)}$
with
$K_n^{(k)}$
with
![]() $n = 2^{\varepsilon t^{k-1}}$
. The probability a given t-set contains fewer than q colours is at most
$n = 2^{\varepsilon t^{k-1}}$
. The probability a given t-set contains fewer than q colours is at most
![]() $q(1-1/q)^{t \choose k}$
. Therefore, the expected number of t sets with fewer than q colours is at most
$q(1-1/q)^{t \choose k}$
. Therefore, the expected number of t sets with fewer than q colours is at most
 $$\begin{align*}{n \choose t}q(1-1/q)^{t \choose k} < \bigg(\frac{en}{t}\bigg)^t q e^{-{t\choose k}/q} < \bigg(\frac{q^{1/t}en}{te^{-{t\choose k}/(tq)}}\bigg)^t < 1.\end{align*}$$
$$\begin{align*}{n \choose t}q(1-1/q)^{t \choose k} < \bigg(\frac{en}{t}\bigg)^t q e^{-{t\choose k}/q} < \bigg(\frac{q^{1/t}en}{te^{-{t\choose k}/(tq)}}\bigg)^t < 1.\end{align*}$$
As the expectation is strictly less than one, there must exist some
![]() $(t;q,q)$
-rainbow colouring.
$(t;q,q)$
-rainbow colouring.
Proof of Corollary 1.4
Proposition 3.1 shows that there is an
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $r_3(t;q,q)> 2^{\varepsilon t}$
. Since the Catalan number
$r_3(t;q,q)> 2^{\varepsilon t}$
. Since the Catalan number
![]() $C_i\geq 5$
for
$C_i\geq 5$
for
![]() $i\geq 3$
, we may apply the inequality
$i\geq 3$
, we may apply the inequality
![]() $r_{i+1}(t^{c};2q + 5,5)> 2^{r_i(t;q,5)-1}$
from Theorem 1.3, once for each
$r_{i+1}(t^{c};2q + 5,5)> 2^{r_i(t;q,5)-1}$
from Theorem 1.3, once for each
![]() $i \in \{3,\dots ,k-1\}$
and with a different
$i \in \{3,\dots ,k-1\}$
and with a different
![]() $c\geq 1$
each round. This ultimately yields a lower bound of
$c\geq 1$
each round. This ultimately yields a lower bound of
![]() $r_k(t^{c'};q',5) \geq T_{k-1}(t)$
, where
$r_k(t^{c'};q',5) \geq T_{k-1}(t)$
, where
![]() $q' = 3^k q$
and
$q' = 3^k q$
and
![]() $c'\geq 1$
.
$c'\geq 1$
.
The proof of Corollary 1.5 follows the exact same procedure as the proof of Corollary 1.4, simply using the bound
![]() $r_{k+1}(t^c;3,3)> 2^{r_k(t;3,3)-1}$
in place of the bound
$r_{k+1}(t^c;3,3)> 2^{r_k(t;3,3)-1}$
in place of the bound
![]() $r_{k+1}(t^c;2q+5,3)> 2^{r_k(t;q,5) - 1}$
. We thus omit it. We now prove the final part of Theorem 1.3, which combines Lemma 2.6 with a slightly different stepping-up technique.
$r_{k+1}(t^c;2q+5,3)> 2^{r_k(t;q,5) - 1}$
. We thus omit it. We now prove the final part of Theorem 1.3, which combines Lemma 2.6 with a slightly different stepping-up technique.
Proof of Theorem 1.3(c)
Let
![]() $k,p,q \geq 3$
be such that
$k,p,q \geq 3$
be such that
![]() $p \leq k!$
and let
$p \leq k!$
and let
![]() $c:=k+2$
. We prove the inequality
$c:=k+2$
. We prove the inequality
![]() $r_{2k}(t^c;pq,p)> 2^{r_k(t;q,p) - 1}$
by showing such that we can construct a
$r_{2k}(t^c;pq,p)> 2^{r_k(t;q,p) - 1}$
by showing such that we can construct a
![]() $(t^c;pq,p)$
-rainbow colouring
$(t^c;pq,p)$
-rainbow colouring
![]() $\chi '$
of
$\chi '$
of
![]() $K_{2^n}^{(2k)}$
from any
$K_{2^n}^{(2k)}$
from any
![]() $(t;q,p)$
-rainbow colouring
$(t;q,p)$
-rainbow colouring
![]() $\chi $
of
$\chi $
of
![]() $K_n^{(k)}$
. Let such a
$K_n^{(k)}$
. Let such a
![]() $\chi $
be given.
$\chi $
be given.
We identify
![]() $V(K_{2^n}^{(2k)})$
and
$V(K_{2^n}^{(2k)})$
and
![]() $V(K_{n}^{(k)})$
with
$V(K_{n}^{(k)})$
with
![]() $\{0,1\}^n$
and
$\{0,1\}^n$
and
![]() $[n]$
, respectively. Order the
$[n]$
, respectively. Order the
![]() $k!$
permutations of
$k!$
permutations of
![]() $[k]$
and let
$[k]$
and let
![]() $P_i$
be the set of sequences whose pattern is the
$P_i$
be the set of sequences whose pattern is the
![]() $i^{\text {th}}$
permutation for
$i^{\text {th}}$
permutation for
![]() $i \in [p]$
. Then, for an edge
$i \in [p]$
. Then, for an edge
![]() $e=\{v_1,\ldots , v_{2k}\}$
with corresponding
$e=\{v_1,\ldots , v_{2k}\}$
with corresponding
![]() $\delta $
-sequence
$\delta $
-sequence
![]() $(\delta _1,\ldots , \delta _{2k-1})$
, we set
$(\delta _1,\ldots , \delta _{2k-1})$
, we set
if
![]() $(\delta _1, \delta _3, \ldots , \delta _{2k-1})\in P_i$
for some
$(\delta _1, \delta _3, \ldots , \delta _{2k-1})\in P_i$
for some
![]() $i\in [p]$
and we let
$i\in [p]$
and we let
![]() $\chi '(e)$
be arbitrary otherwise.
$\chi '(e)$
be arbitrary otherwise.
We now check that this is the desired colouring. It is clear that it uses at most
![]() $pq$
colours. Suppose
$pq$
colours. Suppose
![]() $v_1<\dots < v_{t^c}$
are vertices of
$v_1<\dots < v_{t^c}$
are vertices of
![]() $K_{2^n}^{(2k)}$
and let
$K_{2^n}^{(2k)}$
and let
![]() $(\delta _1,\dots ,\delta _{t^c-1})$
be the corresponding
$(\delta _1,\dots ,\delta _{t^c-1})$
be the corresponding
![]() $\delta $
-sequence. If
$\delta $
-sequence. If
![]() $\|(\delta _i)_{i=1}^{t^c-1}\| \geq 2t$
, then we can find an index set
$\|(\delta _i)_{i=1}^{t^c-1}\| \geq 2t$
, then we can find an index set
![]() $I \subset [t^c - 1]$
such that
$I \subset [t^c - 1]$
such that
![]() $(\delta _i)_{i\in I}$
is a separated subsequence with
$(\delta _i)_{i\in I}$
is a separated subsequence with
![]() $\|(\delta _i)_{i\in I}\| \geq t$
. Let
$\|(\delta _i)_{i\in I}\| \geq t$
. Let
![]() $f = \{\delta _{i_1},\dots ,\delta _{i_k}\}\subset (\delta _i)_{i \in I}$
, where
$f = \{\delta _{i_1},\dots ,\delta _{i_k}\}\subset (\delta _i)_{i \in I}$
, where
![]() $i_1<i_2<\dots <i_k$
. Then the edge
$i_1<i_2<\dots <i_k$
. Then the edge
![]() $e = \{v_{i_1},v_{i_1+1},v_{i_2},v_{i_2+1},\dots , v_{i_k},v_{i_k+1}\}$
has colour
$e = \{v_{i_1},v_{i_1+1},v_{i_2},v_{i_2+1},\dots , v_{i_k},v_{i_k+1}\}$
has colour
![]() $\chi '(e)= (\chi (f),\cdot )$
. As f was arbitrary, we have that
$\chi '(e)= (\chi (f),\cdot )$
. As f was arbitrary, we have that
![]() $\{v_1, \dots , v_{t^c}\}$
spans at least as many colours as
$\{v_1, \dots , v_{t^c}\}$
spans at least as many colours as
![]() $\{\delta _i\}_{i \in I}$
. But
$\{\delta _i\}_{i \in I}$
. But
![]() $\|(\delta _i)_{i\in I}\| \geq t$
and so
$\|(\delta _i)_{i\in I}\| \geq t$
and so
![]() $(\delta _i)_{i \in I}$
spans at least p colours by assumption.
$(\delta _i)_{i \in I}$
spans at least p colours by assumption.
Now suppose that
![]() $\|(\delta _i)_{i=1}^{t^c-1}\|< 2t$
. By (3.1),
$\|(\delta _i)_{i=1}^{t^c-1}\|< 2t$
. By (3.1),
![]() $(\delta _i)_{i=1}^{t^c-1}$
satisfies the unique maximum property. Therefore, by our choice of c and assumption that t is large, we can apply Lemma 2.6 with
$(\delta _i)_{i=1}^{t^c-1}$
satisfies the unique maximum property. Therefore, by our choice of c and assumption that t is large, we can apply Lemma 2.6 with
![]() $A=(\delta _i)_{i=1}^{t^c-1}$
to conclude that A contains every permutation of
$A=(\delta _i)_{i=1}^{t^c-1}$
to conclude that A contains every permutation of
![]() $[k]$
as a separated subsequence. Suppose we have a separated subsequence
$[k]$
as a separated subsequence. Suppose we have a separated subsequence
![]() $S \subset A$
whose pattern is the
$S \subset A$
whose pattern is the
![]() $i^{\text {th}}$
permutation for some
$i^{\text {th}}$
permutation for some
![]() $i \in [p]$
. As before, we can find a
$i \in [p]$
. As before, we can find a
![]() $(2k)$
-edge
$(2k)$
-edge
![]() $e\subseteq \{v_1,\dots ,v_{t^c}\}$
for whom the corresponding
$e\subseteq \{v_1,\dots ,v_{t^c}\}$
for whom the corresponding
![]() $\delta $
-pattern is S. Thus,
$\delta $
-pattern is S. Thus,
![]() $\chi '(e) = (\cdot ,i)$
. Repeating this for the first p permutations implies that
$\chi '(e) = (\cdot ,i)$
. Repeating this for the first p permutations implies that
![]() $\{v_1,\dots ,v_{t^c}\}$
spans at least p colours.
$\{v_1,\dots ,v_{t^c}\}$
spans at least p colours.
Both of our stepping-up constructions (like the original) rely on breaking the stepping-up into two parts: a lifted colouring from a lower uniformity graph and a new colouring. The constructions have the property that every large set of vertices satisfies one of the following: either it spans a colouring that is lifted from a large clique on the lower graph or it sees many distinct new colours. The number of new colours one can guarantee using this approach depends strongly on the uniformity of the hypergraphs in question. We ask a question in the concluding remarks concerning this.
4 Hedgehogs
In this section, we relate our results on many-coloured Ramsey numbers of complete hypergraphs to a Ramsey problem on a certain class of hypergraphs which we call generalized hedgehogs. We note our idea is very much inspired by the Conlon-Fox-Rödl construction described in the introduction. The main result is Theorem 1.2(a), and we also prove Lemma 1.6 for a more general family of hedgehogs.
We define the generalized hedgehog
![]() $\text {H}_{t}^{(k)}(s)$
for
$\text {H}_{t}^{(k)}(s)$
for
![]() $s,k,t\in {\mathbb {N}}$
with
$s,k,t\in {\mathbb {N}}$
with
![]() $k> s$
and
$k> s$
and
![]() $t\geq s$
to be the following k-uniform hypergraph: fix a set of t vertices called the body. The edge set of
$t\geq s$
to be the following k-uniform hypergraph: fix a set of t vertices called the body. The edge set of
![]() $\text {H}_{t}^{(k)}(s)$
consists of the following edges: for every s-subset S of the body, we add a k-edge e containing S along with
$\text {H}_{t}^{(k)}(s)$
consists of the following edges: for every s-subset S of the body, we add a k-edge e containing S along with
![]() $k-s$
additional vertices that are contained in no other edge of
$k-s$
additional vertices that are contained in no other edge of
![]() $\text {H}_{t}^{(k)}(s)$
.
$\text {H}_{t}^{(k)}(s)$
.
The k-uniform balanced hedgehog
![]() $\hat H_{t}^{(k)}$
is
$\hat H_{t}^{(k)}$
is
![]() $\text {H}_{t}^{(k)}(\lceil \frac k2 \rceil )$
, and the hedgehog introduced by Conlon, Fox and Rödl is
$\text {H}_{t}^{(k)}(\lceil \frac k2 \rceil )$
, and the hedgehog introduced by Conlon, Fox and Rödl is
![]() $\text {H}_{t}^{(k)}(k-1)$
. We note that
$\text {H}_{t}^{(k)}(k-1)$
. We note that
![]() $\text {H}_{t}^{(k)}(s)$
has
$\text {H}_{t}^{(k)}(s)$
has
![]() ${t\choose s}$
edges and
${t\choose s}$
edges and
![]() $t+ (k-s){t\choose s}$
vertices.
$t+ (k-s){t\choose s}$
vertices.
Lemma 1.6 is a corollary of the following result, which we state in its full generality.
Lemma 4.1. Given
![]() $k,q,p',t\in {\mathbb {N}}$
, let
$k,q,p',t\in {\mathbb {N}}$
, let
![]() $p={k \choose s}$
and
$p={k \choose s}$
and
![]() $q' = {q\choose p}$
. Then
$q' = {q\choose p}$
. Then
Proof of Lemma 1.6
Apply Lemma 4.1 with
![]() $2k+1, k+1$
and
$2k+1, k+1$
and
![]() $1$
playing the roles of
$1$
playing the roles of
![]() $k,s$
and
$k,s$
and
![]() $p'$
, respectively.
$p'$
, respectively.
Proof of Lemma 4.1
We prove
![]() $ r_{k}(\text {H}_{t}^{(k)}(s);q',p'+1)> r_{s}(t;q,p'p+1) -1$
by showing that given a
$ r_{k}(\text {H}_{t}^{(k)}(s);q',p'+1)> r_{s}(t;q,p'p+1) -1$
by showing that given a
![]() $(t;q,p'p+1)$
-rainbow colouring of
$(t;q,p'p+1)$
-rainbow colouring of
![]() $K_{n}^{(s)}$
, we can construct a
$K_{n}^{(s)}$
, we can construct a
![]() $q'$
-colouring
$q'$
-colouring
![]() $\chi '$
of
$\chi '$
of
![]() $K_{n}^{(k)}$
in which every copy of
$K_{n}^{(k)}$
in which every copy of
![]() $\text {H}_{t}^{(k)}(s)$
spans at least
$\text {H}_{t}^{(k)}(s)$
spans at least
![]() $p'+1$
colours. Let such a
$p'+1$
colours. Let such a
![]() $\chi $
be given. Identify the vertex sets of
$\chi $
be given. Identify the vertex sets of
![]() $K_{n}^{(k)}$
and
$K_{n}^{(k)}$
and
![]() $K_{n}^{(s)}$
. We colour
$K_{n}^{(s)}$
. We colour
![]() $e'\in E(K_{n}^{(k)})$
by
$e'\in E(K_{n}^{(k)})$
by
![]() $\chi '(e') = \{ \chi (e): e\in E(K_n^{(s)}[e'])\}$
– that is, the set of all colours of the s-edges contained in
$\chi '(e') = \{ \chi (e): e\in E(K_n^{(s)}[e'])\}$
– that is, the set of all colours of the s-edges contained in
![]() $e'$
. The number of s-edges contained in
$e'$
. The number of s-edges contained in
![]() $e'$
is exactly
$e'$
is exactly
![]() $p={k\choose s}$
, so
$p={k\choose s}$
, so
![]() $\chi '(e')$
will be a set of at most that many colours. If
$\chi '(e')$
will be a set of at most that many colours. If
![]() $|\chi '(e')|< p$
, then we add arbitrary colours to the set until
$|\chi '(e')|< p$
, then we add arbitrary colours to the set until
![]() $|\chi '(e')|=p$
. Thus, the new colouring uses at most
$|\chi '(e')|=p$
. Thus, the new colouring uses at most
![]() $q'={q\choose p}$
colours.
$q'={q\choose p}$
colours.
Now consider a copy
![]() $H\subset K_{n}^{(k)}$
of
$H\subset K_{n}^{(k)}$
of
![]() $\text {H}_{t}^{(k)}(s)$
. As the body contains t vertices, by assumption, it spans at least
$\text {H}_{t}^{(k)}(s)$
. As the body contains t vertices, by assumption, it spans at least
![]() $p'p+1$
colours under
$p'p+1$
colours under
![]() $\chi $
. Each of these colours appears as an element of
$\chi $
. Each of these colours appears as an element of
![]() $\chi '(e')$
for some
$\chi '(e')$
for some
![]() $e' \in E(H)$
(i.e.,
$e' \in E(H)$
(i.e.,
![]() $|\cup _{e'\in E(H)}\chi '(e')|\geq p'p+1$
). However, p colours appear in
$|\cup _{e'\in E(H)}\chi '(e')|\geq p'p+1$
). However, p colours appear in
![]() $\chi '(e')$
for a given
$\chi '(e')$
for a given
![]() $e'$
, so by pigeonhole there must be more than
$e'$
, so by pigeonhole there must be more than
![]() $p'$
edges
$p'$
edges
![]() $e'\in E(H)$
with distinct colours in
$e'\in E(H)$
with distinct colours in
![]() $\chi '(H)$
.
$\chi '(H)$
.
We now derive Theorem 1.2(b).
Proof of Theorem 1.2(b)
Throughout the proof, we assume
![]() $t\in {\mathbb {N}}$
is sufficiently large. Let
$t\in {\mathbb {N}}$
is sufficiently large. Let
![]() $m = \lceil \frac {e(k+1)}{\log _2 (k+1)}\rceil $
, which is chosen so that
$m = \lceil \frac {e(k+1)}{\log _2 (k+1)}\rceil $
, which is chosen so that
![]() $ m! > (\frac{m}{\mathrm{e}})^m > 2^{2k} > {2k+1\choose k+1} $
for k sufficiently large. Recall that by Proposition 3.1,
$ m! > (\frac{m}{\mathrm{e}})^m > 2^{2k} > {2k+1\choose k+1} $
for k sufficiently large. Recall that by Proposition 3.1,
![]() $r_{m}(t;m!,m!)\geq T_2(\varepsilon t)$
for some
$r_{m}(t;m!,m!)\geq T_2(\varepsilon t)$
for some
![]() $\varepsilon>0$
. We now use the inequality
$\varepsilon>0$
. We now use the inequality
![]() $r_{2k}(t^c;pq,p) \geq 2^{r_k(t;q,p)}$
from Theorem 1.3 exactly
$r_{2k}(t^c;pq,p) \geq 2^{r_k(t;q,p)}$
from Theorem 1.3 exactly
![]() $\lfloor \log _2 \frac {k+1}{m} \rfloor> \log _2\log _2 k - 3$
times, to obtain that there exists
$\lfloor \log _2 \frac {k+1}{m} \rfloor> \log _2\log _2 k - 3$
times, to obtain that there exists
![]() $q'$
and
$q'$
and
![]() $c' \geq 1$
such that
$c' \geq 1$
such that
![]() $r_{k+1}(t^{c'};q',m!) \geq T_{\log _2\log _2 k -1}(t)$
(if
$r_{k+1}(t^{c'};q',m!) \geq T_{\log _2\log _2 k -1}(t)$
(if
![]() $k+1> 2^j m$
with
$k+1> 2^j m$
with
![]() $j = \lfloor \log _2 \frac {k+1}{m} \rfloor $
we use the simple observation
$j = \lfloor \log _2 \frac {k+1}{m} \rfloor $
we use the simple observation
![]() $r_{i+1}(t; q, p)> r_{i}(t;q',p)$
for some
$r_{i+1}(t; q, p)> r_{i}(t;q',p)$
for some
![]() $q'> q$
). This is possible because the uniformity increases at each step while the number of colours imposed remains at
$q'> q$
). This is possible because the uniformity increases at each step while the number of colours imposed remains at
![]() $m!$
. Since
$m!$
. Since
![]() $m!> {2k+1\choose k+1}$
, we can apply Lemma 1.6 to get that for some
$m!> {2k+1\choose k+1}$
, we can apply Lemma 1.6 to get that for some
![]() $q"$
,
$q"$
,
![]() $r_{2k+1}(\hat H_{t};q",2)\geq T_{\log _2\log _2 k - 2}(t)$
, where we removed the exponent
$r_{2k+1}(\hat H_{t};q",2)\geq T_{\log _2\log _2 k - 2}(t)$
, where we removed the exponent
![]() $c'$
at the cost of a tower height. We choose
$c'$
at the cost of a tower height. We choose
![]() $c>0$
such that if
$c>0$
such that if
![]() $m! \leq {2k+1\choose k+1}$
, then
$m! \leq {2k+1\choose k+1}$
, then
![]() $c\log _2\log _2k \leq 1$
.
$c\log _2\log _2k \leq 1$
.
Thus, for all k,
![]() $r_{2k+1}(\hat H_{t};q",2)\geq T_{c\log _2\log _2 k }(t)$
. Furthermore, it is clear that
$r_{2k+1}(\hat H_{t};q",2)\geq T_{c\log _2\log _2 k }(t)$
. Furthermore, it is clear that
![]() $q"$
is only a function of k and of m, which is itself a function of k, as required.
$q"$
is only a function of k and of m, which is itself a function of k, as required.
Conlon, Fox and Rödl showed the following using a similar argument to Theorem 1.2(a):
Theorem 4.2 [Reference Conlon, Fox and Rödl5]
For all
![]() $k \geq 4$
, there exists
$k \geq 4$
, there exists
![]() $c>0$
such that
$c>0$
such that
For the case
![]() $k=4$
, a construction of Kostochka and Rödl [Reference Kostochka and Rödl13] shows this is approximately sharp (i.e., that
$k=4$
, a construction of Kostochka and Rödl [Reference Kostochka and Rödl13] shows this is approximately sharp (i.e., that
![]() $r_4(\text {H}_{t}^{(4)}(3);2,2) = T_2(\Omega (t))$
). We cannot prove a matching lower bound for
$r_4(\text {H}_{t}^{(4)}(3);2,2) = T_2(\Omega (t))$
). We cannot prove a matching lower bound for
![]() $k=5$
, as when we attempt to apply Lemma 1.6, we need to impose
$k=5$
, as when we attempt to apply Lemma 1.6, we need to impose
![]() $6$
colours on
$6$
colours on
![]() $4$
-uniform graphs. When stepping up to uniformity
$4$
-uniform graphs. When stepping up to uniformity
![]() $4$
, Theorem 1.3 allows us to impose at most
$4$
, Theorem 1.3 allows us to impose at most
![]() $C_3=5$
colours, so we cannot beat the random argument here. We do, however, obtain the following:
$C_3=5$
colours, so we cannot beat the random argument here. We do, however, obtain the following:
Lemma 4.3. For
![]() $ 5\leq k \leq 13 $
, there exist
$ 5\leq k \leq 13 $
, there exist
![]() $c>0$
and
$c>0$
and
![]() $q\in {\mathbb {N}}$
such that for all t,
$q\in {\mathbb {N}}$
such that for all t,
Proof. The proof mimics that of Theorem 1.2(b), but now we start from the fact that
![]() $r_4(t;14,14)\geq T_2(ct)$
(using Proposition 3.1) and leverage that
$r_4(t;14,14)\geq T_2(ct)$
(using Proposition 3.1) and leverage that
![]() $C_4=14$
. Starting from
$C_4=14$
. Starting from
![]() $\ell =4$
, we apply the relation
$\ell =4$
, we apply the relation
![]() $r_{\ell +1}(t^C;2q+p,p) \geq 2^{r_{\ell }(t;q,p)}$
from Theorem 1.3
$r_{\ell +1}(t^C;2q+p,p) \geq 2^{r_{\ell }(t;q,p)}$
from Theorem 1.3
![]() $k-5$
times. This gives us
$k-5$
times. This gives us
![]() $r_{k-1}(t;q',14)\geq T_{k-3}(t^{c'})$
for some
$r_{k-1}(t;q',14)\geq T_{k-3}(t^{c'})$
for some
![]() $q'\in {\mathbb {N}}$
and
$q'\in {\mathbb {N}}$
and
![]() $c'\geq 1$
. Applying Lemma 1.6 then gives the result using
$c'\geq 1$
. Applying Lemma 1.6 then gives the result using
![]() $q"$
colours and with
$q"$
colours and with
![]() $c'$
as c.
$c'$
as c.
We now prepare to prove our upper bounds on the Ramsey numbers of balanced hedgehogs, Theorem 1.2(a). Let H be an r-uniform hypergraph and
![]() $A\subset V(H)$
with
$A\subset V(H)$
with
![]() $|A|< r$
. The piercing number of A (denoted
$|A|< r$
. The piercing number of A (denoted
![]() $\tau _H(A)$
) is the size of the smallest set of vertices from
$\tau _H(A)$
) is the size of the smallest set of vertices from
![]() $V(H)\backslash A$
that intersects every edge of H containing A. Equivalently, it is the minimum number of vertices that must be deleted from
$V(H)\backslash A$
that intersects every edge of H containing A. Equivalently, it is the minimum number of vertices that must be deleted from
![]() $V(H)\backslash A$
to delete all edges containing A.
$V(H)\backslash A$
to delete all edges containing A.
Proposition 4.4. Suppose H is an r-uniform hypergraph and
![]() $v\in V(H)$
has
$v\in V(H)$
has
![]() $\tau (v) \geq (r-1)m$
. Then there exist m edges whose pairwise intersections are all precisely v.
$\tau (v) \geq (r-1)m$
. Then there exist m edges whose pairwise intersections are all precisely v.
Proof of Proposition 4.4
Let
![]() $X\subset V(H)$
be a witness to
$X\subset V(H)$
be a witness to
![]() $\tau (v)$
. It is clear the set of edges incident to v has order at least
$\tau (v)$
. It is clear the set of edges incident to v has order at least
![]() $(r-1)m$
. As each such edge e contains at most
$(r-1)m$
. As each such edge e contains at most
![]() $r-1$
elements of X, and
$r-1$
elements of X, and
![]() $|X|$
is minimal with respect to intersecting all edges incident to v, we can greedily find the desired m edges.
$|X|$
is minimal with respect to intersecting all edges incident to v, we can greedily find the desired m edges.
Proof of Theorem 1.2(a)
Let
![]() $G = K_{n}^{(2k+1)}$
, where
$G = K_{n}^{(2k+1)}$
, where
![]() $n \geq t^{k+3}$
, and let
$n \geq t^{k+3}$
, and let
![]() $\chi $
be an arbitrary red/blue colouring of the edges of G. We will show that there exists a monochromatic copy of
$\chi $
be an arbitrary red/blue colouring of the edges of G. We will show that there exists a monochromatic copy of
![]() $H_t^{(2k+1)}(k+1)$
in G, and thus that
$H_t^{(2k+1)}(k+1)$
in G, and thus that
![]() $\text {r}_{2k+1}(\text {H}_{t}^{(2k+1)}(k+1);2,2) \leq n$
. We will do so by using
$\text {r}_{2k+1}(\text {H}_{t}^{(2k+1)}(k+1);2,2) \leq n$
. We will do so by using
![]() $\chi $
to define a partial edge
$\chi $
to define a partial edge
![]() $2$
-colouring
$2$
-colouring
![]() $\chi '$
of
$\chi '$
of
![]() $G' :=K_{n}^{(k+1)}$
and, in turn, using
$G' :=K_{n}^{(k+1)}$
and, in turn, using
![]() $\chi '$
to define a
$\chi '$
to define a
![]() $2$
-colouring
$2$
-colouring
![]() $\chi "$
of
$\chi "$
of
![]() $V(G)$
. We will then find a large monochromatic set of vertices in
$V(G)$
. We will then find a large monochromatic set of vertices in
![]() $\chi "$
, use this to find a large (red or blue) independent set in
$\chi "$
, use this to find a large (red or blue) independent set in
![]() $G'$
and finally use this to find our monochromatic
$G'$
and finally use this to find our monochromatic
![]() $\text {H}_{t}^{(2k+1)}(k+1)$
in G.
$\text {H}_{t}^{(2k+1)}(k+1)$
in G.
Throughout the proof, let
![]() $H_t: =\text {H}_{t}^{(2k+1)}(k+1)$
. We say a set of vertices is in red danger if its red piercing number (its piercing number in the subgraph of red edges) is less than
$H_t: =\text {H}_{t}^{(2k+1)}(k+1)$
. We say a set of vertices is in red danger if its red piercing number (its piercing number in the subgraph of red edges) is less than
![]() $t^{k+1}$
and similarly define blue danger. Then for
$t^{k+1}$
and similarly define blue danger. Then for
![]() $e \in G':= K_{n}^{(k+1)}$
, let
$e \in G':= K_{n}^{(k+1)}$
, let
![]() $\chi '(e)$
be red if e is in red danger and blue if e is in blue danger. As
$\chi '(e)$
be red if e is in red danger and blue if e is in blue danger. As
![]() $\tau _G(e)> 2t^{k+1}$
, we have that this partial colouring
$\tau _G(e)> 2t^{k+1}$
, we have that this partial colouring
![]() $\chi '$
is well-defined.
$\chi '$
is well-defined.
Now say a vertex v is in red peril if its red piercing number in
![]() $G'$
(under
$G'$
(under
![]() $\chi '$
) is at most
$\chi '$
) is at most
![]() $2kt^{k+1}$
and similarly define blue peril. Let
$2kt^{k+1}$
and similarly define blue peril. Let
![]() $\chi "(v)$
be red if v is in red peril and blue if v is in blue peril, with ties broken arbitrarily. We claim that
$\chi "(v)$
be red if v is in red peril and blue if v is in blue peril, with ties broken arbitrarily. We claim that
![]() $\chi "$
assigns a colour to every vertex. Indeed, suppose that some vertex v has red piercing number and blue piercing number at least
$\chi "$
assigns a colour to every vertex. Indeed, suppose that some vertex v has red piercing number and blue piercing number at least
![]() $2k t^{k+1}$
under
$2k t^{k+1}$
under
![]() $\chi '$
.
$\chi '$
.
By Proposition 4.4, there exist
![]() $(k+1)$
-edges
$(k+1)$
-edges
![]() $e_1, \dots , e_s, f_1, \dots , f_s \in G'$
, where
$e_1, \dots , e_s, f_1, \dots , f_s \in G'$
, where
![]() $s = 2t^{k+1}$
such that
$s = 2t^{k+1}$
such that
-
○
 $e_i \cap e_j = f_i \cap f_j = \{v\}$
for all
$e_i \cap e_j = f_i \cap f_j = \{v\}$
for all
 $i \neq j$
,
$i \neq j$
, -
○
 $\chi '(e_i)$
is red for all
$\chi '(e_i)$
is red for all
 $i \in [s]$
and
$i \in [s]$
and -
○
 $\chi '(f_j)$
is blue for all
$\chi '(f_j)$
is blue for all
 $j \in [s]$
$j \in [s]$
Let
![]() $A_1, A_2, \dots , A_s$
be disjoint subsets each of size
$A_1, A_2, \dots , A_s$
be disjoint subsets each of size
![]() $k-1$
in
$k-1$
in
![]() $V(G) \setminus (\bigcup_{i=1}^s (e_i \cup f_i))$
. For each
$V(G) \setminus (\bigcup_{i=1}^s (e_i \cup f_i))$
. For each
![]() $i, j \in [s]$
, define a
$i, j \in [s]$
, define a
![]() $(2k+1)$
-edge
$(2k+1)$
-edge
![]() $g_{ij}$
to be
$g_{ij}$
to be
![]() $e_i \cup f_j$
along with an arbitrary choice of
$e_i \cup f_j$
along with an arbitrary choice of
![]() $(2k+1)-|e_i \cup f_j|$
vertices from
$(2k+1)-|e_i \cup f_j|$
vertices from
![]() $A_{(i+j-1)\mathrm {mod}\ s}$
. Observe that
$A_{(i+j-1)\mathrm {mod}\ s}$
. Observe that
![]() $e_i \cup f_j \neq e_{i'} \cup f_{j'}$
for
$e_i \cup f_j \neq e_{i'} \cup f_{j'}$
for
![]() $(i,j) \neq (i',j')$
, so in particular, these edges are all distinct.
$(i,j) \neq (i',j')$
, so in particular, these edges are all distinct.
At least half of these edges must have been, without loss of generality, red under the colouring
![]() $\chi $
of G. Therefore, there is some
$\chi $
of G. Therefore, there is some
![]() $i\in [s]$
such that
$i\in [s]$
such that
![]() $e_i$
is contained in at least
$e_i$
is contained in at least
![]() $\frac {s^2}{2s} = \frac {s}{2}> t^{k+1}$
red
$\frac {s^2}{2s} = \frac {s}{2}> t^{k+1}$
red
![]() $(2k+1)$
-edges under
$(2k+1)$
-edges under
![]() $\chi $
. But since
$\chi $
. But since
![]() $g_{ij} \cap g_{ij'} = e_i$
for
$g_{ij} \cap g_{ij'} = e_i$
for
![]() $j \neq j'$
, this contradicts the fact that
$j \neq j'$
, this contradicts the fact that
![]() $e_i$
was a red-danger edge of
$e_i$
was a red-danger edge of
![]() $G'$
. Thus, the colouring
$G'$
. Thus, the colouring
![]() $\chi "$
of
$\chi "$
of
![]() $V(G)$
colours every vertex.
$V(G)$
colours every vertex.
We now choose a set X of red vertices (without loss of generality) which has order
![]() $\frac n2$
. By the definition of
$\frac n2$
. By the definition of
![]() $\chi "$
, we have that the red piercing number under
$\chi "$
, we have that the red piercing number under
![]() $\chi '$
of each
$\chi '$
of each
![]() $v\in X$
is at most
$v\in X$
is at most
![]() $2kt^{k+1}$
. Therefore, we can greedily find a set Y of order
$2kt^{k+1}$
. Therefore, we can greedily find a set Y of order
![]() $\frac {n}{2\cdot 2kt^{k+1}}\geq t$
which contains no red edges of
$\frac {n}{2\cdot 2kt^{k+1}}\geq t$
which contains no red edges of
![]() $G'$
(here we use that t is large relative to k).
$G'$
(here we use that t is large relative to k).
All edges of
![]() $G'$
in Y are not in red danger and thus have red piercing number at least
$G'$
in Y are not in red danger and thus have red piercing number at least
![]() $t^{k+1}$
under
$t^{k+1}$
under
![]() $\chi $
. By the definition of piercing number and as
$\chi $
. By the definition of piercing number and as
![]() $t^{k+1}> t + k{t \choose k+1} = |V(\text {H}_{t}^{(2k+1)}(k+1))|$
, we can build the hedgehog greedily using Y as the body.
$t^{k+1}> t + k{t \choose k+1} = |V(\text {H}_{t}^{(2k+1)}(k+1))|$
, we can build the hedgehog greedily using Y as the body.
4.1 The Burr-Erdős Conjecture in hypergraphs
The degeneracy of a hypergraph is the minimum d such that every induced subgraph contains a vertex incident to at most d edges; such a hypergraph is called d-degenerate. Burr and Erdős conjectured that for every d, there exists a constant
![]() $c_d \geq 1$
such that every d-degenerate graph G on n vertices satisfies
$c_d \geq 1$
such that every d-degenerate graph G on n vertices satisfies
![]() $r_2(G) < c_d n$
[Reference Burr and Erdős3]. This was finally proven by Lee in [Reference Lee15], building on the previous work of several authors [(Reference Fox and Sudakov11),(Reference Kostochka and Sudakov14)]. In the case of hypergraphs, however, the conjecture fails: Kostochka and Rödl [Reference Kostochka and Rödl13] showed
$r_2(G) < c_d n$
[Reference Burr and Erdős3]. This was finally proven by Lee in [Reference Lee15], building on the previous work of several authors [(Reference Fox and Sudakov11),(Reference Kostochka and Sudakov14)]. In the case of hypergraphs, however, the conjecture fails: Kostochka and Rödl [Reference Kostochka and Rödl13] showed
![]() $r_4(H_t^{(4)}) \geq 2^{ct}$
and were able to construct for every large enough d, d-degenerate
$r_4(H_t^{(4)}) \geq 2^{ct}$
and were able to construct for every large enough d, d-degenerate
![]() $3$
-uniform hypergraphs on n vertices whose ramsey number is at least
$3$
-uniform hypergraphs on n vertices whose ramsey number is at least
![]() $n^{d^{1/4}}$
. If one allows
$n^{d^{1/4}}$
. If one allows
![]() $3$
or more colours, Conlon, Fox and Rödl [Reference Conlon, Fox and Rödl5] proved
$3$
or more colours, Conlon, Fox and Rödl [Reference Conlon, Fox and Rödl5] proved
![]() $r_3(H_t^{(3)}; 3) \geq \Omega (t^3/\log ^6 t)$
. Note that the degeneracy of hedgehogs is
$r_3(H_t^{(3)}; 3) \geq \Omega (t^3/\log ^6 t)$
. Note that the degeneracy of hedgehogs is
![]() $1$
.
$1$
.
This shows that the Burr-Erdős Conjecture fails for k-uniform hypergraphs where
![]() $k\geq 4$
and for
$k\geq 4$
and for
![]() $3$
-uniform hypergraphs provided the number of colours is at least
$3$
-uniform hypergraphs provided the number of colours is at least
![]() $3$
or the degeneracy is large enough. For the sake of completeness, we give a simple construction of
$3$
or the degeneracy is large enough. For the sake of completeness, we give a simple construction of
![]() $8$
-degenerate
$8$
-degenerate
![]() $3$
-uniform hypergraphs whose Ramsey number is not linear in the number of vertices.
$3$
-uniform hypergraphs whose Ramsey number is not linear in the number of vertices.
Proposition 4.5. There exists a
![]() $3$
-uniform hypergraph on
$3$
-uniform hypergraph on
![]() $Cn^2$
vertices which is
$Cn^2$
vertices which is
![]() $8$
-degenerate and for which the
$8$
-degenerate and for which the
![]() $2$
-colour Ramsey number is at least
$2$
-colour Ramsey number is at least
![]() $Cn^{3}.$
$Cn^{3}.$
Proof. Let V be a set of n vertices, and with
![]() $m = {n \choose 2}$
, let B be a set of
$m = {n \choose 2}$
, let B be a set of
![]() $m + 1$
vertices disjoint from V with a total ordering
$m + 1$
vertices disjoint from V with a total ordering
![]() $x_1,x_2,\ldots x_m, x_{m+1}$
. Consider an ordering on the edges E of the complete graph on V, say
$x_1,x_2,\ldots x_m, x_{m+1}$
. Consider an ordering on the edges E of the complete graph on V, say
![]() $e_1,e_2,...,e_m$
. Let H be a 3-uniform hypergraph consisting of the following: for each edge
$e_1,e_2,...,e_m$
. Let H be a 3-uniform hypergraph consisting of the following: for each edge
![]() $e_i=(x,y)\in E$
, add the two triples
$e_i=(x,y)\in E$
, add the two triples
![]() $\{x,y,x_i\}$
and
$\{x,y,x_i\}$
and
![]() $\{x,y,x_{i+1}\}$
, and for every
$\{x,y,x_{i+1}\}$
, and for every
![]() $i \in [m-3]$
, add all triples within
$i \in [m-3]$
, add all triples within
![]() $\{x_i,x_{i+1},x_{i+2},x_{i+3},x_{i+4}\}$
. By considering the smallest element of B in each subset of vertices, we see that H is
$\{x_i,x_{i+1},x_{i+2},x_{i+3},x_{i+4}\}$
. By considering the smallest element of B in each subset of vertices, we see that H is
![]() $8$
-degenerate.
$8$
-degenerate.
We claim
![]() $r_3(H) \geq n^3/8$
. Indeed, given
$r_3(H) \geq n^3/8$
. Indeed, given
![]() $K_{n^3/8}^{(3)}$
, let
$K_{n^3/8}^{(3)}$
, let
![]() $W_1,\ldots W_{n/4}$
be an arbitrary partition of the vertices where
$W_1,\ldots W_{n/4}$
be an arbitrary partition of the vertices where
![]() $|W_i|=n^2/2$
for all
$|W_i|=n^2/2$
for all
![]() $i\in [n/4]$
. We colour blue all edges inside any
$i\in [n/4]$
. We colour blue all edges inside any
![]() $W_i$
and all edges with vertices in distinct sets
$W_i$
and all edges with vertices in distinct sets
![]() $W_{i_1},W_{i_2},W_{i_3}$
. We colour red all edges with exactly two vertices in a set
$W_{i_1},W_{i_2},W_{i_3}$
. We colour red all edges with exactly two vertices in a set
![]() $W_i$
, for some
$W_i$
, for some
![]() $i\in [n/4]$
.
$i\in [n/4]$
.
Suppose there is a red copy of H. In particular, the edges induced by
![]() $S =\{x_1,x_2,x_3,x_4,x_5\}$
are all red. If S intersects distinct parts
$S =\{x_1,x_2,x_3,x_4,x_5\}$
are all red. If S intersects distinct parts
![]() $W_i,W_j$
and
$W_i,W_j$
and
![]() $W_k$
for some
$W_k$
for some
![]() $i,j,k \in [n/4]$
, then the vertices in the intersections form a blue edge. However, if
$i,j,k \in [n/4]$
, then the vertices in the intersections form a blue edge. However, if
![]() $S \subseteq W_i \cup W_j$
, then
$S \subseteq W_i \cup W_j$
, then
![]() $|S \cap W_i| \geq 3$
or
$|S \cap W_i| \geq 3$
or
![]() $|S \cap W_j| \geq 3$
, which again forms a blue edge. So we have a contradiction.
$|S \cap W_j| \geq 3$
, which again forms a blue edge. So we have a contradiction.
Suppose instead there is a blue copy of H. By pigeonhole, there are two vertices
![]() $v,w \in V$
which both lie in the same
$v,w \in V$
which both lie in the same
![]() $W_i$
. Let
$W_i$
. Let
![]() $e_j = \{v,w\}$
. The edges
$e_j = \{v,w\}$
. The edges
![]() $\{v,w,x_j\}$
and
$\{v,w,x_j\}$
and
![]() $\{v,w,x_{j+1}\}$
are both blue, so
$\{v,w,x_{j+1}\}$
are both blue, so
![]() $x_j,x_{j+1} \in W_i$
. But
$x_j,x_{j+1} \in W_i$
. But
![]() $\{x_j,x_{j+1},x_{j+2}\}$
and
$\{x_j,x_{j+1},x_{j+2}\}$
and
![]() $\{x_{j-1}, x_j,x_{j+1}\}$
are also blue, so this implies
$\{x_{j-1}, x_j,x_{j+1}\}$
are also blue, so this implies
![]() $x_{j-1}, x_{j+2} \in W_i$
. Proceeding inductively, we conclude that all of B must lie in
$x_{j-1}, x_{j+2} \in W_i$
. Proceeding inductively, we conclude that all of B must lie in
![]() $W_i$
.
$W_i$
.
However,
![]() $|W_i| = n^2/2$
and
$|W_i| = n^2/2$
and
![]() $|B| = {n \choose 2}$
, so there are
$|B| = {n \choose 2}$
, so there are
![]() $n/2$
vertices of V outside of
$n/2$
vertices of V outside of
![]() $W_i$
. Two of these vertices z and u must lie in the same
$W_i$
. Two of these vertices z and u must lie in the same
![]() $W_j$
with
$W_j$
with
![]() $j \neq i$
. Letting
$j \neq i$
. Letting
![]() $e_k = \{z,u\}$
, we get that the edge
$e_k = \{z,u\}$
, we get that the edge
![]() $\{z,u,x_k\}$
is coloured red, a contradiction which finishes the proof.
$\{z,u,x_k\}$
is coloured red, a contradiction which finishes the proof.
5 Concluding remarks
We have proved that for every positive integer h, there exist q, k and an infinite family of k-uniform hypergraphs whose
![]() $2$
-colour Ramsey numbers differ by a tower of height h from the q-colour Ramsey numbers. This reinforces the fact that the number of colours plays an important role in the behaviour of Ramsey numbers of hypergraphs and casts a shadow on Erdős’s conjecture on the
$2$
-colour Ramsey numbers differ by a tower of height h from the q-colour Ramsey numbers. This reinforces the fact that the number of colours plays an important role in the behaviour of Ramsey numbers of hypergraphs and casts a shadow on Erdős’s conjecture on the
![]() $2$
-colour Ramsey number of a
$2$
-colour Ramsey number of a
![]() $3$
-uniform clique.
$3$
-uniform clique.
Observe that both of our new stepping-up constructions rely on a dichotomy: either we can find many suitable substructures within the
![]() $\delta $
-sequences (which give rise to many colours) or we must have a long monotonic sequence (which allows us to use induction). Since for every k-edge there are at most
$\delta $
-sequences (which give rise to many colours) or we must have a long monotonic sequence (which allows us to use induction). Since for every k-edge there are at most
![]() $k!$
distinct permutations, our methods fail to give good lower bounds for
$k!$
distinct permutations, our methods fail to give good lower bounds for
![]() $r_k(t; q,p)$
whenever
$r_k(t; q,p)$
whenever
![]() $k\ll p$
. Even in the simplest case
$k\ll p$
. Even in the simplest case
![]() $r_3(t; q,3)$
, we were not able to prove a double exponential lower bound, leaving open the following question of Conlon, Fox and Rödl on
$r_3(t; q,3)$
, we were not able to prove a double exponential lower bound, leaving open the following question of Conlon, Fox and Rödl on
![]() $r_3(t; q,3)$
.
$r_3(t; q,3)$
.
Problem 5.1. [Reference Conlon, Fox and Rödl5, Problem 1] Is there an integer q, a positive constant c and a q-colouring of the
![]() $3$
-uniform hypergraph on
$3$
-uniform hypergraph on
![]() $2^{2^{ct}}$
vertices such that every subset of order t receives at least
$2^{2^{ct}}$
vertices such that every subset of order t receives at least
![]() $3$
colours?
$3$
colours?
We propose here a much weaker problem than Problem 5.1, which we were not able to resolve. We note that a negative answer would uncover a radical new phenomenon in the Ramsey numbers of hypergraphs.
Problem 5.2. Does there exist
![]() $k\in {\mathbb {N}}$
such that the following holds? For all
$k\in {\mathbb {N}}$
such that the following holds? For all
![]() $p\in {\mathbb {N}}$
, there exist
$p\in {\mathbb {N}}$
, there exist
![]() $q\in {\mathbb {N}}$
and
$q\in {\mathbb {N}}$
and
![]() $c>0$
such that
$c>0$
such that
![]() $r_k(t;q,p)\geq 2^{2^{t^c}}$
for all t sufficiently large.
$r_k(t;q,p)\geq 2^{2^{t^c}}$
for all t sufficiently large.
A similar but much more ambitious problem was posed in [Reference Conlon, Fox, He, Mubayi, Suk and Verstraëte4].
Problem 5.3. [Reference Conlon, Fox, He, Mubayi, Suk and Verstraëte4, Problem 6.3] Determine the tower height of
![]() $R_k(n; r, r - 1)=r_k(n; r,r)$
for all
$R_k(n; r, r - 1)=r_k(n; r,r)$
for all
![]() $k \geq 3$
and
$k \geq 3$
and
![]() $r \geq 2$
.
$r \geq 2$
.
The authors of [Reference Conlon, Fox, He, Mubayi, Suk and Verstraëte4] note the apparent difficulty of Problem 5.3 and ask the following weaker question. Is there a fixed integer c such that
![]() $R_k(n;r,r-1) \geq T_{k-c}(n)$
for every
$R_k(n;r,r-1) \geq T_{k-c}(n)$
for every
![]() $k\geq 3$
and
$k\geq 3$
and
![]() $r\geq 2$
? We cannot answer this question, but using Theorem 1.3(a), we can prove
$r\geq 2$
? We cannot answer this question, but using Theorem 1.3(a), we can prove
![]() $R_k(n;r, r-1)$
is at least a tower of height roughly
$R_k(n;r, r-1)$
is at least a tower of height roughly
![]() $k - 0.5\log _2 r$
. Any improvement beyond this bound would likely be very interesting.
$k - 0.5\log _2 r$
. Any improvement beyond this bound would likely be very interesting.
We make the following conjecture regarding the Ramsey numbers of k-uniform hedgehogs. This would, in particular, demonstrate that the
![]() $2$
-colour and q-colour Ramsey numbers of these hedgehogs, unlike those of balanced hedgehogs, do not differ by arbitrarily large tower heights.
$2$
-colour and q-colour Ramsey numbers of these hedgehogs, unlike those of balanced hedgehogs, do not differ by arbitrarily large tower heights.
Conjecture 5.4. There is
![]() $\ell \in \mathbb {N}$
such that for every positive integer k, for every sufficiently large t,
$\ell \in \mathbb {N}$
such that for every positive integer k, for every sufficiently large t,
Finally, recall Proposition 4.5 shows there is an infinite family of
![]() $3$
-uniform hypergraphs which are
$3$
-uniform hypergraphs which are
![]() $8$
-degenerate and for which the the
$8$
-degenerate and for which the the
![]() $2$
-colour Ramsey numbers grow faster than linear in the order of the hypergraphs. It would be interesting to improve the quantitative aspects of this result.
$2$
-colour Ramsey numbers grow faster than linear in the order of the hypergraphs. It would be interesting to improve the quantitative aspects of this result.
Problem 5.5. Give an infinite family of
![]() $1$
-degenerate
$1$
-degenerate
![]() $3$
-uniform hypergraphs whose
$3$
-uniform hypergraphs whose
![]() $2$
-colour Ramsey number is not polynomial in the order of the hypergraph.
$2$
-colour Ramsey number is not polynomial in the order of the hypergraph.
Kostochka and Rödl [Reference Kostochka and Rödl13] indicate that this may not be possible. We share this suspicion, noting that the following could be true: for any d, there is
![]() $f(d)$
such that the Ramsey number of any d-degenerate
$f(d)$
such that the Ramsey number of any d-degenerate
![]() $3$
-uniform hypergraph (on n vertices) is at most
$3$
-uniform hypergraph (on n vertices) is at most
![]() $n^{f(d)}$
.
$n^{f(d)}$
.
Acknowledgements
We thank Bhargav Narayanan for helpful conversations on this topic and the anonymous referees for their detailed and invaluable feedback, especially regarding the organization of the first two sections.
Competing interest
The authors have no competing interest to declare.
Funding statement
The first author was supported in part by Simons Foundation grant 332622. The first and fourth authors were supported in part by NSF Grant CCF-1814409 and NSF Grant DMS-1800521. The second author was supported by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy EXC-2181/1 - 390900948 (the Heidelberg STRUCTURES Cluster of Excellence) and by EPSRC grant EP/V007327/1. The third author was supported in part by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 428212407.