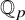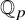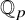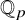Where are the zeroes of a random p-adic polynomial?

Abstract

We study the distribution of the roots of a random p-adic polynomial in an algebraic closure of ${\mathbb Q}_p$ . We prove that the mean number of roots generating a fixed finite extension K of ${\mathbb Q}_p$ depends mostly on the discriminant of K, an extension containing fewer roots when it becomes more ramified. We prove further that for any positive integer r, a random p-adic polynomial of sufficiently large degree has about r roots on average in extensions of degree at most r.

Beyond the mean, we also study higher moments and correlations between the number of roots in two given subsets of ${\mathbb Q}_p$ (or, more generally, of a finite extension of ${\mathbb Q}_p$ ). In this perspective, we notably establish results highlighting that the roots tend to repel each other and quantify this phenomenon.

1 Introduction

The distribution of roots of a random real polynomial is a classical subject of research that has been thoroughly studied since the pioneering work of Bloch and Polya [4], Littlewood and Offord [13, 14, 15] and Kac’s famous paper [10], in which an exact formula giving the average number of roots of a random polynomial with Gaussian coefficients appears for the first time.

Investigating the behaviour of roots of p-adic random polynomials is a natural question that has recently received some attention. The story started in 2006 when Evans published a paper [8] in which he managed to adapt Kac’s strategy and eventually compute the average number of zeros in ${\mathbb Z}_p$ of a random polynomial of degree n with coefficients uniformly ¹ distributed in ${\mathbb Z}_p$ . The same year, Buhler, Goldstein, Moews and Rosenberg [5] found formulas for the probability that a random p-adic polynomial has all its roots in ${\mathbb Q}_p$ . After about 10 years without further significant contributions, the subject was revived a couple of years ago by Lerario and collaborators, who began a systematic study of these phenomena. With Kulkarni [11], they notably extend Crofton’s formula to the p-adic setting and derive new estimations of the number of roots of a p-adic polynomial, establishing in particular that a uniformly distributed random polynomial of fixed degree over ${\mathbb Z}_p$ has exactly one root in ${\mathbb Q}_p$ on average, independent of p and the degree. On a slightly different note, Ait El Mannsour and Lerario [1] obtain formulas counting the average number of lines in random projective p-adic varieties. More recently, the case of nonuniform distributions has also been addressed by Shmueli [20], who came up with sharp estimations of the average number of roots.

Most of the aforementioned works are concerned with the mean of the random variable $Z_n$ counting the number of roots of a p-adic polynomial of degree n. Beyond the mean (for which one can rely on Kac’s techniques), obtaining more information about the $Z_n$ s is a fundamental question that has been recently addressed and elegantly solved by Bhargava, Cremona, Fisher and Gajović [3]. In their paper, they set up a general strategy to compute all probabilities $\mathrm {Prob}[Z_n{=}r]$ with n and r running over the integers. In addition, they observed that the formulas they obtained are all rational functions in p that are symmetric under the transformation $p \leftrightarrow p^{-1}$ . This beautiful and fascinating property remains mysterious.

Apart from the distinction between archimedean and nonarchimedean, ${\mathbb Q}_p$ differs from $\mathbb R$ in that its arithmetic is much richer; while the absolute Galois group of $\mathbb R$ is somehow boring, that of ${\mathbb Q}_p$ is large and intricate and encodes much subtle arithmetical information. In other words, the set of finite extensions of ${\mathbb Q}_p$ has a prominent structure that is part of the strength and complexity of the p-adic world. Therefore, looking at the roots of a random p-adic polynomial not only in ${\mathbb Q}_p$ but in an algebraic closure $\bar {\mathbb Q}_p$ of ${\mathbb Q}_p$ sounds like a very natural and appealing question, and we address it in the present paper.

To this end, we fix a finite extension F of ${\mathbb Q}_p$ together with an algebraic closure $\bar F$ of F. We endow $\bar F$ with the p-adic norm $\Vert \cdot \Vert $ normalised by $\Vert p \Vert = p^{-[F:{\mathbb Q}_p]}$ and use the letter q to denote the cardinality of the residue field of F. Given a positive integer n, a finite extension K of F and a compact open subset U of K, we introduce the random variable $Z_{U,n}$ counting the number of roots in U of a random polynomial of degree n with coefficients in the ring of integers ${\mathcal O}_F$ of F. Our first theorem gives an integral expression of the expected values of the $Z_{U,n}$ s.

Theorem A. There exists a family of functions $\rho _{K,n} : K \to \mathbb R^+$ (K running over the set of finite extensions of F included in $\bar F$ and n running the set of positive integers) satisfying the following property: for any positive integer n, any finite extension K of F in $\bar F$ and any open subset U of E, we have

$$ \begin{align*}\mathbb E[Z_{U,n}] \,\, = \,\, \sum_{K' \subset K} \,\, \int_{U\cap K'} \rho_{K',n}(x)\:dx,\end{align*} $$

where the sum runs over all extensions $K'$ of F included in K.

The functions $\rho _{K,n}$ s are called the density functions as their values at a given point x reflect the number of roots one may expect to find in a small neighbourhood of x. Our second theorem provides precise information about the density functions.

Theorem B. Let n be a positive integer, let $K \subset \bar F$ be a finite extension of F, and let $x \in K$ . Write r for the degree of the extension $K/F$ .

1. 1. (Vanishing) If $F[x] \neq K$ or $n < r$ , then $\rho _{K,n}(x) = 0$ .

2. 2. (Continuity) The function $\rho _{K,n}$ is continuous on K.

3. 3. (Invariance under isomorphisms) Given a second finite extension L of F and an isomorphism of F-algebras $\sigma : K \to L$ , we have $\rho _{K,n}(x) = \rho _{L,n}\big (\sigma (x)\big )$ .

4. 4. (Transformation under homography) For $\left (\begin {matrix} a & b \\ c & d \end {matrix}\right ) \in \mathrm {GL}_2({\mathcal O}_F)$ , we have

   $$ \begin{align*}\rho_{K,n}\left(\frac{ax+b}{cx+d}\right) = \Vert cx+d\Vert^{2r} \cdot \rho_{K,n}(x).\end{align*} $$

5. 5. (Monotony) We have $\rho _{K,n}(x) \leq \rho _{K,n+1}(x)$ , and the inequality is strict if and only if $F[x] = K$ and $r \leq n < 2r - 1$ .

6. 6. (Formulas for extremal degrees) If $F[x] = K$ and $x \in {\mathcal O}_K$ , then

   $$ \begin{align*}\begin{array}{rr@{\hspace{0.5ex}}l} & \rho_{K,r}(x) & = \displaystyle \Vert D_K\Vert \cdot \frac 1{\#\big({\mathcal O}_K/{\mathcal O}_F[x]\big)} \cdot \frac{q^{r+1} - q^r}{q^{r+1} - 1} \\[16pt] \text{for } n \geq 2r - 1, & \rho_{K,n}(x) & = \displaystyle \Vert D_K\Vert \cdot \int_{{\mathcal O}_F[x]} \Vert t\Vert^r\: dt \end{array},\end{align*} $$
   where $D_K$ is the discriminant of the extension $K/F$ .

A first remarkable consequence of Theorem B is that the functions $\rho _{K,n}$ are independent of n provided that $n \geq 2r - 1$ . A similar behaviour was noticed in [3] for higher moments of the random variables $Z_{F,n}$ . In addition, it is in theory feasible to derive from Theorem B closed formulas for $\rho _{K,n}$ and its integral over K, at least when $n = r$ or $n \geq 2r - 1$ . For example, Theorem C below covers the case of quadratic extensions. Before stating it, it is convenient to introduce the notation

(1.1) $$ \begin{align} \rho_n(K) = \int_K \, \rho_{K,n}(x) \: dx. \end{align} $$

By Theorem A, $\rho _n(K)$ counts the number of roots of a random polynomial of degree n that fall inside K but outside all strict subfields of K containing F.

Theorem C. Let K be a quadratic extension of F.

1. 1. If $K/F$ is unramified, we have

   $$ \begin{align*} \begin{array}{rr@{\hspace{0.5ex}}l} & \rho_2(K) & = \displaystyle \frac{q^2 - q + 1}{q^2 + q + 1}, \\ \text{for } n \geq 3, & \rho_n(K) & = \displaystyle \frac{q^4 + 1}{q^4 + q^3 + q^2 + q + 1}. \end{array}\\[-16pt]\end{align*} $$

2. 2. If $K/F$ is totally ramified, we have

   $$ \begin{align*}\begin{array}{rr@{\hspace{0.5ex}}l} & \rho_2(K) & = \displaystyle \Vert D_K \Vert \cdot \frac{q^2}{q^2 + q + 1}, \\ \text{for } n \geq 3, & \rho_n(K) & = \displaystyle \Vert D_K \Vert \cdot \frac{q^2(q^2 + 1)}{q^4 + q^3 + q^2 + q + 1}. \end{array}\\[-16pt]\end{align*} $$

When K is the quadratic unramified extension of F, we notice that $\rho _n(K)$ is a rational function in q that is self-reciprocal: that is, invariant under the transformation $q \leftrightarrow q^{-1}$ . As recalled previously, this remarkable property also holds for all higher moments of the random variable $Z_{F,n}$ . On the other hand, when $K/F$ is totally ramified, the function $\rho _n(K)$ is not self-reciprocal. One can nevertheless recover the expected symmetry by summing over all totally ramified quadratic extensions of F. Indeed, using Serre’s mass formula [18], we end up with

$$ \begin{align*}\begin{array}{rr@{\hspace{0.5ex}}l} & \displaystyle \sum_K \rho_2(K) & = \displaystyle \frac{2q}{q^2 + q + 1}, \\ \text{for } n \geq 3, & \displaystyle \sum_K \rho_n(K) & = \displaystyle \frac{2q(q^2 + 1)}{q^4 + q^3 + q^2 + q + 1} \end{array}\\[-16pt]\end{align*} $$

(where both sums run over all totally ramified quadratic extensions of F in $\bar F$ ), which are indeed self-reciprocal rational functions in q.

Another panel of interesting corollaries of Theorem B concerns the orders of magnitude of the functions $\rho _{K,n}$ s. Roughly speaking, Theorem B tells us that the size of $\rho _{K,n}$ is controlled by the p-adic norm of $D_K$ . It is in fact even more transparent when we integrate over the entire space.

Theorem D. Let $K \subset \bar F$ be a finite extension of F. Write r for the degree of $K/F$ and f for its residual degree. We have the estimations

$$ \begin{align*}\begin{array}{rr@{\hspace{0.5ex}}l} & \displaystyle \frac{\rho_r(K)}{\Vert D_K \Vert} & = \displaystyle \left( 1 - \frac 1 q \right) \cdot \sum_{m|f}\: \mu\!\left(\frac f m\right) q^{m-f} \,+\, O\left(\frac 1{q^f}\right) \\[15pt] \text{for } n \geq 2r-1, & \displaystyle \frac{\rho_n(K)}{\Vert D_K \Vert} & = \displaystyle \sum_{m|f}\: \mu\!\left(\frac f m\right) q^{m-f} \,+\, O\left(\frac 1{q^f}\right) \end{array},\\[-16pt]\end{align*} $$

where $\mu $ denotes the Moebius function and the constants hidden in the $O(-)$ are absolute.

The dominant term in the two sums above is the summand corresponding to $m = f$ and is equal to $1$ . Hence, $\rho _n(K)$ is roughly equal to $\Vert D_K \Vert $ for $n = r$ or $n \geq 2r-1$ . More precisely, one finds $\rho _n(K) = \Vert D_K \Vert \cdot (1 + O(q^{-1}))$ in both cases. It turns out that this conclusion continues to holds for all $n \geq r$ thanks to the monotony property of Theorem B.

One can also sum the estimations of Theorem D over all extensions of a fixed degree. Doing so, we obtain the following theorem.

Theorem E. For any positive integers r and n with $n \geq 2r-1$ , we have the estimation

$$ \begin{align*}\sum_{K \in \mathbf{Ex}_r} \rho_n(K) = \sum_{m|r}\: \varphi\!\left(\frac r m\right) q^{m-r} \,+\, O\left(\frac{r \cdot \log \log r}{q^r}\right),\\[-16pt]\end{align*} $$

where $\mathbf {Ex}_r$ denotes the set of all extensions of F of degree r inside $\bar F$ and $\varphi $ is the Euler’s totient function.

Again, the dominant term in the sum of Theorem E corresponds to $m = r$ , and its value is $1$ . Therefore, we conclude that a random polynomial of degree n has, on average, one root in the ground field F, one more root in the union of extensions of degree $2$ , one more root in the union of extensions of degree $3$ , and so on, until the degree n, where all roots have been found. Many variations on this theme are possible; for example, one can prove that all roots of a random polynomial lie in the maximal unramified extension of F expect $\frac 2 q + O\big (\frac 1{q^2}\big )$ of them. On the other hand, we deduce from Theorem C that the quadratic totally ramified extensions of F contain $\frac 2 q + O\big (\frac 1{q^2}\big )$ roots outside F. We then conclude that there are no more than $O\big (\frac 1{q^2}\big )$ new roots in ramified extensions of degree at least $3$ .

On a different note, it is also quite instructive to study the fluctuations of the density functions $\rho _{K,n}$ . Theorem B indicates that they are governed by the size of the ${\mathcal O}_F$ -algebra generated by x. Consequently, we deduce that elements that generate a large extension K but are close for the p-adic distance to a strict subfield of K have less chance of appearing as a root of a random polynomial. In other words, if a root x of a random polynomial is congruent to an element of a given extension K modulo a large power of p, it is very likely that x lies in K. In some sense, subfields attract all roots in a neighbourhood.

Beyond the mean, it is important to understand higher moments of the $Z_{U,n}$ s to draw a more precise picture of the behaviour of these random variables. We address this question by enlarging our setting a bit: instead of restricting ourselves to finite extensions of F, we consider more generally products of such extensions: that is, finite étale algebras over F. The nice observation is that Theorem A admits a straightforward generalisation to this extended framework. Applying it with $E = K^r$ (for some given finite extension K of F) provides information about the rth moment of $Z_{K,d}$ and, more generally, sheds some light on the distribution of r-tuples of roots in $K^r$ . For $K = F$ and $r = 2$ , this yoga has interesting consequences as it permits one to compute the covariances between the $Z_{U,n}$ s for $U \subset F$ .

Theorem F. Let U and V be two balls in ${\mathcal O}_F$ that do not meet. Pick $u \in U$ and $v \in V$ . We have

$$ \begin{align*}\frac{\mathrm{Cov}\big(Z_{U,n}, Z_{V,n}\big)} {\mathbb E[Z_{U,n}] \cdot \mathbb E[Z_{V,n}]} \,=\, - 1 \,+\, \frac{(q+1)^2}{q^2 + q + 1} {\cdot} \Vert u{-}v \Vert \,-\, \frac q{q^2 + q + 1} {\cdot} \Vert u{-}v \Vert^4\end{align*} $$

for all $n \geq 3$ .

Although the above formula might look unattractive at first glance, it is quite instructive. To begin with, it indicates that $\mathrm {Cov}\big (Z_{U,n}, Z_{V,n}\big )$ vanishes if and only if $\Vert u{-}v \Vert = 1$ . In other words, the random variables $Z_{U,n}$ and $Z_{V,n}$ are uncorrelated if and only if U and V are sufficiently far away. Otherwise, $Z_{U,n}$ and $Z_{V,n}$ are correlated and the covariance is always negative (still assuming that $U \cap V = \emptyset $ ). Moreover, the correlation becomes more significant when U and V are closer. This tends to show that roots repel each other. This conclusion can be understood as a consequence of the general principle that subalgebras attract roots; noticing that F embeds diagonally into $F^2$ , the above principle tells us that if we are given two nearby roots in F of a random polynomial, there is a huge chance that those roots coincide, which means it is unlikely to get nearby distinct roots.

Another amazing benefit of working with étale extensions is the existence of mass formulas for the density functions in the spirit of Bhargava’s extension to étale algebras of the classical Serre mass formula [2]. Given a finite étale F-algebra E, define $\rho _n(E)$ by the integral of equation (1.1), and let $\mathrm {Aut}\:_{\!F\mathrm {-alg}}(E)$ denote the group of F-automorphisms of E.

Theorem G. For any positive integers r and n with $n \geq r$ , we have

(1.2) $$ \begin{align} \sum_{E \in \acute{\mathbf{E}}\mathbf{t}_r} \, \frac{\rho_n(E)}{\# \mathrm{Aut}\:_{\!F\mathrm{-alg}}(E)} \,=\, 1, \end{align} $$

where the summation set $\acute{\mathbf{E}}\mathbf{t}_r$ consists of all isomorphism classes of étale extensions E of F of degree r (and the notation $\#$ refers to the cardinality).

When $r = 1$ , equation (1.2) reduces to $\rho _n(F) = 1$ and so asserts that a random polynomial of degree at least $1$ has exactly one root in F on average; we then recover Lerario and Kulkarni’s result in this case. When r grows, Theorem G roughly says that the above remarkable property continues to hold if we count (weighted) roots in extensions of a fixed degree, provided we are careful to include all étale algebras and not only fields! Notice however that Theorem D shows that the contribution of actual extensions to the sum in equation (1.2) is about $1/r$ . The most significant part of the mass then comes from nontrivial products of smaller degree extensions.

Organisation of the paper

The plan of the paper closely follows the progression of the introduction. In Section 2, we prove Theorems A and B. In Section 3, we study examples and obtain closed formulas for the density functions in several simple cases. In addition to treating the case of quadratic extension (in line with Theorem C) completely, we obtain partial results for extensions of prime degrees and unramified extensions. Section 4 is devoted to finding estimations of orders of magnitude of the density functions and their integrals; we notably prove Theorems D and E there. Finally, in Section 5, we present the setup of étale algebras and extend Theorems A and B to this setting. We then discuss applications to higher moments and mass formulas for density functions, establishing Theorems F and G.

Notations

Throughout the paper, we fix a prime number p, a finite extension F of ${\mathbb Q}_p$ and an algebraic closure $\bar F$ of F. We use the letter q to denote the cardinality of the residue field of F. We write $\Vert \cdot \Vert $ for the p-adic norm on $\bar F$ , normalised by $\Vert p \Vert = p^{-[F:{\mathbb Q}_p]}$ .

We let $\Omega _n$ be the space of polynomials of degree at most n with coefficients in ${\mathcal O}_F$ ; we call $\mu _n$ the probability measure on $\Omega _n$ corresponding to $\lambda _F^{\otimes {n+1}}$ under the canonical identification $\Omega _n \simeq {\mathcal O}_F^{n+1}$ . In a slight abuse of notations, we continue to write $\Vert \cdot \Vert $ for the norm on $\Omega _n$ corresponding to the sup norm on ${\mathcal O}_F^{n+1}$ (it is the so-called Gauss norm).

Throughout the paper, all finite extensions of F are implicitly supposed to be contained in $\bar F$ . If K is such an extension, we denote by ${\mathcal O}_K$ its ring of integers and by ${\mathcal O}_K^\times $ the group of invertible elements of ${\mathcal O}_K$ . We let $\lambda _K$ be the Haar measure on K normalised by $\lambda _K ({\mathcal O}_K) = 1$ . Our normalisation choices lead to the transformation formula $\lambda _K(aH) = \Vert a \Vert ^r \cdot \lambda _K(H)$ , where r is the degree of the extension $K/F$ .

Finally, we use the notation $\# A$ to denote the cardinality of a set A.

2 Density functions

The aim of this section is to define the density functions $\rho _{K,n}$ and to prove Theorems A and B. The main ingredient we will need is a p-adic version of the famous Kac-Rice formula, which gives an integral expression for a number of roots of a polynomial. We will establish it in Section 2.1. In Section 2.2, we carry out a key computation that will allow us to construct the density functions and prove Theorem B in Section 2.3. We finally move to the computation of the expected number of roots and prove Theorem A in Section 2.4.

2.1 The p-adic Kac-Rice formula

A p-adic version of the Kac-Rice formula appears in the pioneering work of Evans [8]. Nevertheless, for the purpose of this paper, it will be more convenient to use a formulation different from that of Evans (the latter is closer to what we usually call the ‘area formula’). For this reason, we will take some time to establish our version of the p-adic Kac-Rice formula and give a complete proof of it. We refer the reader to [17, Chapter 5] for the definition of strictly differentiable functions of the p-adic variable.

Theorem 2.1. Let K be a finite extension of F of degree r. Let U be a compact open subset of K, and let $f : U \to K$ be a strictly differentiable function. We assume that $(f(x), f'(x)) \neq (0,0)$ for all $x \in U$ . Then

(2.1)

Proof. Let e be the ramification index of $K/F$ . For $s \in \frac 1 e \mathbb Z$ , we denote by $B_s$ the closed ball of K of radius $q^{-s}$ and centre $0$ . If $\pi $ denotes a uniformiser of K, the set $B_s$ can be alternatively defined by $B_s = \pi ^{es} {\mathcal O}_K$ . We deduce from the latter equality that $\lambda _K(B_s) = \Vert \pi ^e \Vert ^{sr} = q^{-sr}$ .

We consider an element $a \in U$ such that $f(a) = 0$ . From our assumption, we know that $f'(a) \neq 0$ . Therefore, applying [6, Lemma 3.4], we get the existence of a positive integer $S_a$ having the following property: for any $s \in \frac 1 e \mathbb Z$ , $s \geq S_a$ , the function f induces a bijection from $a + B_s$ to $f'(a) B_s$ . Up to enlarging $S_a$ , we can further assume that $\Vert f'(x) \Vert = \Vert f'(a) \Vert $ for all $x \in a + B_{S_a}$ . We deduce for these two facts that

(2.2)

for all $s \geq S^{\prime }_a = S_a - \log _q \Vert f'(a) \Vert $ .

From the previous discussion, we also derive that a is the unique zero of f in $B_{S_a}$ . In other words, the set of zeros of f is discrete. By compacity, it follows that f has only finitely many zeros in U. Let us call them $a_1, \ldots , a_m$ . Set $S = \max (S_{a_1}, \ldots , S_{a_m})$ and $S' = \max (S^{\prime }_{a_1}, \ldots , S^{\prime }_{a_m})$ and for $i \in \{1, \ldots , m\}$ , write $U_i = a_i + B_{S_{a_i}}$ . Up to again enlarging $S_{a_i}$ s, we can assume that the $U_i$ s are pairwise disjoint. Summing the equalities in equation (2.2), we find

(2.3)

provided that $s \geq S'$ . Let V be the complement in U of $U_1 \sqcup \cdots \sqcup U_m$ . It is compact, and the function f does not vanish on it. Hence, if s is large enough, we have $\Vert f(x) \Vert> q^{-s}$ for all $x \in V$ . For those s, we thus get

(2.4)

Combining equations (2.3) and (2.4), we find that the equality

holds true when s is sufficiently large. Passing to the limit, we get the theorem.

We underline that the compacity assumption in Theorem 2.1 cannot be relaxed. For example, taking simply $U = {\mathbb Z}_p \backslash \{0\}$ and $f : x \mapsto x$ , one sees that f has no zero in U, while the right-hand side of equation (2.1) converges to $1$ . Roughly speaking, the integral continues to see the missing zero at the origin, which is expected because removing one point from the domain of integration does not alter the value of the integral.

Similarly, the assumption that the zeros of f are nondegenerate (that is, that the derivative does not vanish at these points) is definitely necessary. For example, if we take the function $f : {\mathbb Z}_p \to {\mathbb Q}_p$ , $x \mapsto x^2$ , a simple calculation shows that the right-hand side of equation (2.1) converges to $\frac p {p+1} < 1$ . More generally, one can prove that if f is a polynomial whose roots in U are $a_1, \ldots , a_m$ and have multiplicity $\mu _1, \ldots , \mu _m$ , respectively, then the right-hand side of equation (2.1) converges to

$$ \begin{align*} \sum_{i=1}^m \frac{q^{\mu_i} - q^{\mu_i-1}}{q^{\mu_i} - 1}. \end{align*} $$

In other words, a root of multiplicity $\mu $ does not contribute for $1$ but for $\frac {q^{\mu } - q^{\mu -1}}{q^{\mu } - 1} < 1$ .

2.2 A key computation

Let K be a finite extension of F of degree r, and let U be an open subset of K. We aim at computing the expected value of the random variable $Z_{U,n} : \Omega _n \to \mathbb Z \cup \{+\infty \}$ defined by

the second equality coming from Theorem 2.1. For this, roughly speaking, we would like to write the following calculation:

and introduce the density function defined by

(2.5)

However, we have to be a bit more careful because the above limit does not behave well everywhere: it takes infinite values on certain subspaces, but it turns out that those parts lead to a finite positive contribution when we integrate. The next proposition shows that these issues are somehow localised on strict subfields.

Proposition 2.2. If $n \geq r$ and if x lies in ${\mathcal O}_K$ and generates K over F, the limit in equation (2.5) exists and is equal to

$$ \begin{align*}\frac{\Vert D_K \Vert}{\#\big({\mathcal O}_K/{\mathcal O}_F[x]\big)} \cdot \int_{\Omega_{n-r}} \hspace{-1em} \Vert Q(x) \Vert^r \: dQ,\end{align*} $$

where $D_K$ denotes the discriminant of the extension $K/F$ .

Proof. For simplicity, write

Let Z be the minimal monic polynomial of x over F. By our assumptions, Z has degree r and coefficients in ${\mathcal O}_F$ . This implies that the map $\Omega _{n-r} \times \Omega _{r-1} \to \Omega _n$ taking $(Q, R)$ to $QZ + R$ preserves the measure. Performing the corresponding change of variables, we end up with the equality

We consider the evaluation morphism $\alpha _x: F \otimes _{{\mathcal O}_F} \Omega _{r-1} \to K$ taking a polynomial R to $R(x)$ . It is F-linear and bijective since the domain of $\alpha _x$ is restricted to polynomials of degree strictly less than r. Its inverse $\alpha _x^{-1}$ is F-linear, so it is continuous. Thus, there exists a positive constant $\gamma $ such that $\Vert R(x) \Vert \geq \gamma \cdot \Vert R \Vert $ for all $R \in \Omega _{r-1}$ .

Let us assume for a moment that we are given a polynomial $R \in \Omega _{r-1}$ such that $\Vert R(x) \Vert \leq q^{-s}$ . Based on the preceding, we find that $\Vert R \Vert \leq \gamma ^{-1} q^{-s}$ , from which we further deduce that $\Vert R'(x) \Vert \leq \gamma ^{-1} q^{-s}$ . Since $Z'(x)$ does not vanish, we conclude that $Z'(x)$ must divide $R'(x)$ provided that s is large enough. One can then perform the change of variables $Q \mapsto Q - \frac {R'(x)}{Z'(x)}$ in the inner integral and get

$$ \begin{align*} \int_{\Omega_{n-r}} \hspace{-1em} \Vert Q(x)Z'(x)+R'(x) \Vert^r \, dQ & = \int_{\Omega_{n-r}} \hspace{-1em} \Vert Q(x)Z'(x) \Vert^r \, dQ \\ & = \Vert Z'(x) \Vert^r \cdot \int_{\Omega_{n-r}} \hspace{-1em}\Vert Q(x) \Vert^r \, dQ. \end{align*} $$

We are then left with

(2.6)

In order to estimate the last factor, we come back to the evaluation morphism $\alpha _x$ . Since it is a F-linear isomorphism, it must act on the measures by multiplication by some scalar (namely, its determinant). In other words, there exists a positive constant $\delta $ such that $\lambda _K(\alpha _x(H)) = \delta \cdot \mu _n(H)$ for all measurable subsets H of $\Omega _{r-1}$ . Taking $H = \Omega _{r-1}$ , we find

$$ \begin{align*}\delta = \lambda_K\big(\alpha_x(\Omega_{r-1})\big) = \lambda_K\big({\mathcal O}_F[x]\big) = \frac 1{\#\big({\mathcal O}_K/{\mathcal O}_F[x]\big)}.\end{align*} $$

As in the proof of Theorem 2.1, we let $B_s$ be the closed ball of K of radius $q^{-s}$ centred at $0$ . By definition, $\alpha _x^{-1}(B_s)$ consists of polynomials R such that $\Vert R(x) \Vert \leq q^{-s}$ . Moreover, if s is sufficiently large, $\alpha _x^{-1}(B_s)$ sits inside $\Omega _{r-1}$ , and so

Plugging this input in equation (2.6), we end up with

(2.7) $$ \begin{align} I_s = \Vert Z'(x) \Vert^r \cdot \#\big({\mathcal O}_K/{\mathcal O}_F[x]\big) \cdot \int_{\Omega_{n-r}} \hspace{-1em} \Vert Q(x) \Vert^r \, dQ \end{align} $$

when s is sufficiently large. The sequence $(I_s)_{s \geq 0}$ is then eventually constant and converges to the limit given by the above formula. In order to conclude the proof of the proposition, it remains to relate the norm of $Z'(x)$ with that of the discriminant of K. We endow K with the symmetric F-bilinear form $b : K \times K \to F$ , $(u,v) \mapsto \mathrm {Tr}_{K/F}(uv)$ . Also let $\mathcal B_x = (1, x, \ldots , x^{r-1})$ be the canonical basis of ${\mathcal O}_F[x]$ over ${\mathcal O}_F $ , and set $\mathcal B^{\prime }_x = \big (\frac {x^{r-1}}{Z'(x)}, \frac {x^{r-2}}{Z'(x)}, \ldots , \frac 1 {Z'(x)}\big )$ . Both $\mathcal B_x$ and $\mathcal B^{\prime }_x$ are F-basis of K, and it follows from [19, §III.6, Lemma 2] that the matrix of b in the basis $\mathcal B_x$ and $\mathcal B^{\prime }_x$ is lower-triangular with all diagonal entries equal to $1$ . Its determinant is then $1$ as well. Performing a change of basis, we find that

$$ \begin{align*} \det \mathrm{Mat}_{\mathcal B_x}(b) = \pm\:N_{K/F}\big(Z'(x)\big),\\[-15pt] \end{align*} $$

where, by definition, $\mathrm {Mat}_{\mathcal B_x}(b)$ is the matrix of b in $\mathcal B_x$ and $N_{K/F}$ is the norm map of K over F. We now consider a basis $\mathcal B$ of ${\mathcal O}_K$ over ${\mathcal O}_F$ . By definition, the discriminant of K is the determinant of $\mathrm {Mat}_{\mathcal B}(b)$ . Therefore, if P denotes the transition matrix from $\mathcal B$ to $\mathcal B_x$ , we derive from the change-of-basis formula that $\det \mathrm {Mat}_{\mathcal B_x}(b) = (\det P)^2 \cdot D_K$ and so

$$ \begin{align*} N_{K/F}\big(Z'(x)\big) = \pm\: (\det P)^2 \cdot D_K.\\[-15pt] \end{align*} $$

On the other hand, noticing that P is also the matrix of $\alpha _x$ in the canonical basis, we deduce that

$$ \begin{align*} \Vert\!\det P \Vert = \lambda_K\big({\mathcal O}_F[x]\big) = \frac 1 {\#\big({\mathcal O}_K/{\mathcal O}_F[x]\big)}.\\[-15pt] \end{align*} $$

Combining the two previous equalities, we end up with

$$ \begin{align*}\Vert Z'(x) \Vert^r = \Vert N_{K/F}\big(Z'(x)\big) \Vert = \frac 1 {\#\big({\mathcal O}_K/{\mathcal O}_F[x]\big)^2} \cdot \Vert D_K \Vert.\\[-15pt]\end{align*} $$

Plugging this relation into equation (2.7), we obtain the proposition.

2.3 Construction and properties of the density functions

In this subsection, we construct the density functions $\rho _{K,n}$ and establish Theorem B.

Definition 2.3. Let n be a positive integer and K be a finite extension of F of degree r.

For $x \in {\mathcal O}_K$ , we set

$$ \begin{align*}\begin{array}{r@{\hspace{0.5ex}}l@{\qquad}l} \rho_{K,n}(x) & = \displaystyle \frac{\Vert D_K \Vert}{\#\big({\mathcal O}_K/{\mathcal O}_F[x]\big)} \cdot \int_{\Omega_{n-r}} \hspace{-1em} \Vert Q(x) \Vert^r \: dQ & \text{if } n \geq r \text{ and } F[x] = K, \\ & = 0 & \text{otherwise.} \end{array}\\[-15pt]\end{align*} $$

For $x \in K$ , $x \not \in {\mathcal O}_K$ , we set $\rho _{K,n}(x) = \Vert x \Vert ^{-2r} \cdot \rho _{K,n}(x^{-1})$ .

The first part of Definition 2.3 is exactly what we expect after Proposition 2.2. The second part is motivated by the observation that the transformation $P(X) \mapsto X^n P(X^{-1})$ preserves the measures on $\Omega _n$ and changes a root x into $x^{-1}$ . In any case, we notice that since K is a discrete valuation field, we have $x \in {\mathcal O}_K$ or $x^{-1} \in {\mathcal O}_K$ for all $x \in K$ . Definition 2.3 then makes sense and leads to a well-defined function $\rho _{K,n} : K \to \mathbb R^+$ , which is called the density function on K of degree n.

The rest of this subsection is devoted to the proof of Theorem B. The vanishing property and the invariance under isomorphisms (Statements 1 and 3, respectively) are clear from the definitions. In what follows, we address the other items of Theorem B one by one (in a slightly different order).

2.3.1 Continuity

The function

$$ \begin{align*}x \mapsto \int_{\Omega_{n-r}} \hspace{-1em} \Vert Q(x) \Vert^r \: dQ\\[-15pt]\end{align*} $$

is continuous on ${\mathcal O}_K$ as the integrand is obviously bounded, positive and continuous on $\Omega _{n-r} \times {\mathcal O}_K$ .

Let $x \in {\mathcal O}_K$ such that $F[x] = K$ . In this case, the index of ${\mathcal O}_F[x]$ in ${\mathcal O}_K$ is the inverse of the p-adic norm of the determinant of the matrix $M(x)$ whose ith column is filled with the coordinates of $x^i$ in a fixed basis of ${\mathcal O}_K$ . If y is a second element of ${\mathcal O}_K$ that is congruent to x modulo $p^s$ for some integer s, then the matrices $M(x)$ and $M(y)$ are also congruent modulo $p^s$ and so are their determinants. In other words, if $\Vert x - y \Vert \leq \varepsilon $ for some positive real number $\varepsilon $ , then $\Vert \!\det M(x) - \det M(y) \Vert \leq \varepsilon $ as well. When $\varepsilon < \Vert \det M(x) \Vert$ , it follows that $\Vert \!\det M(x) \Vert = \Vert \!\det M(y) \Vert $ : that is, $\#\big ({\mathcal O}_K/{\mathcal O}_F[x]\big ) = \#\big ({\mathcal O}_K/{\mathcal O}_F[y]\big )$ . This proves that the function $y \mapsto \#\big ({\mathcal O}_K/{\mathcal O}_F[y]\big )$ is constant in some neighbourhood of x; in particular, it is continuous at x and so is $\rho _{K,n}$ .

We now consider the case where $F[x] \neq K$ . Set $L = F[x]$ , and let d denote the degree of the extension $L/F$ . We consider a second element $y \in {\mathcal O}_K$ such that $F[y] = K$ and $x \equiv y \pmod {p^s}$ for some given integer s. We then have the inclusion ${\mathcal O}_F[y] \subset \mathcal O_L + p^s {\mathcal O}_K$ , from which we derive the estimation

$$ \begin{align*}\#\big({\mathcal O}_K/{\mathcal O}_F[y]\big) \geq \#\big({\mathcal O}_K/(\mathcal O_L + p^s {\mathcal O}_K)\big) = \Vert p \Vert^{s(d-r)} \geq \Vert x - y \Vert^{d-r}.\end{align*} $$

Since $d < r$ , we deduce that the quantity $\#\big ({\mathcal O}_K/{\mathcal O}_F[y]\big )$ goes to $\infty $ when y approaches x, from which we conclude that $\rho _{K,n}$ is continuous at x.

Finally, the continuity on K immediately follows from that on ${\mathcal O}_K$ .

2.3.2 Transformation under homography

It is enough to prove the transformation formula for the matrices

$$ \begin{align*}\left(\begin{matrix} a & 0 \\ 0 & a \end{matrix}\right) \, (a \in {\mathcal O}_F^\times) \quad; \quad \left(\begin{matrix} 1 & a \\ 0 & 1 \end{matrix}\right) \, (a \in {\mathcal O}_F) \quad; \quad \left(\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}\right) \end{align*} $$

since they generate $\mathrm {GL}_2({\mathcal O}_F)$ . It is obvious for scalars matrices.

For the second family of matrices, we have to check $\rho _{K,n}(x+a) = \rho _{K,n}(x)$ for $x \in K$ and $a \in {\mathcal O}_F$ . Let us assume first that $x \in {\mathcal O}_K$ . Then ${\mathcal O}_F[x] = {\mathcal O}_F[x+a]$ . Moreover, the map $\Omega _{n-r} \to \Omega _{n-r}$ , $Q(X) \mapsto Q(X+a)$ preserves the measure, implying that

$$ \begin{align*}\int_{\Omega_{n-r}} \hspace{-1em} \Vert Q(x) \Vert^r \: dQ = \int_{\Omega_{n-r}} \hspace{-1em} \Vert Q(x+a) \Vert^r \: dQ.\end{align*} $$

We conclude that the equality $\rho _{K,n}(x+a) = \rho _{K,n}(x)$ is correct in this case. We assume now that $x \not \in {\mathcal O}_K$ : that is, $\Vert x \Vert> 1$ . Since a lies in ${\mathcal O}_F$ , we have $\Vert a \Vert \leq 1$ and so $\Vert x + a \Vert = \Vert x \Vert $ . Setting $y = x^{-1}$ , we are then reduced to proving that $\rho _{K,n}(y) = \rho _{K,n}(z)$ with $z = \frac y{1+ay}$ . Observing that $\Vert y \Vert < 1$ , we can write a series expansion for the inverse of $1 + ay$ and eventually get

$$ \begin{align*}z = \sum_{i \geq 0} (-1)^i a^i y^{i+1} \in {\mathcal O}_F[y].\end{align*} $$

Similarly, we prove that $y \in {\mathcal O}_F[z]$ and hence ${\mathcal O}_F[y] = {\mathcal O}_F[z]$ . We consider the transformation $\tau : \Omega _{n-r} \to \Omega _{n-r}$ defined by $\tau \big (Q(X)\big ) = X^{n-r} Q(X^{-1})$ . It is explicitly given by the formula

$$ \begin{align*}\tau\big(a_{n-r} X^{n-r} + \cdots + a_1 X + a_0\big) = a_0 X^{n-r} + a_1 X^{n-r-1} + a_{n-r}\end{align*} $$

and hence preserves the measure. Therefore,

$$ \begin{align*} \int_{\Omega_{n-r}} \hspace{-1em} \Vert Q(y) \Vert^r \: dQ & = \Vert y \Vert^{n-r} \cdot \int_{\Omega_{n-r}} \hspace{-1em} \Vert Q(x) \Vert^r \: dQ \\ & = \Vert y \Vert^{n-r} \cdot \int_{\Omega_{n-r}} \hspace{-1em} \Vert Q(x+a) \Vert^r \: dQ \\ & = \Vert y \Vert^{n-r} \cdot \Vert x+a \Vert^{n-r} \cdot \int_{\Omega_{n-r}} \hspace{-1em} \Vert Q(z) \Vert^r \: dQ. \end{align*} $$

In addition, we remark that $y(x+a) = 1 + ay$ has norm $1$ . We then end up with

$$ \begin{align*}\int_{\Omega_{n-r}} \hspace{-1em} \Vert Q(y) \Vert^r \: dQ = \int_{\Omega_{n-r}} \hspace{-1em} \Vert Q(z) \Vert^r \: dQ,\end{align*} $$

which eventually leaves us with the desired equality $\rho _{K,n}(y) = \rho _{K,n}(z)$ .

It remains to treat the case of the antidiagonal matrix, which amounts to proving that $\rho _{K,n}(x^{-1}) = \Vert x \Vert ^{2r} \rho _{K,n}(x)$ . It is obvious from the definition when $x \not \in {\mathcal O}_K$ or $x^{-1} \not \in {\mathcal O}_K$ . We may then assume that x is invertible in ${\mathcal O}_K$ : that is, $\Vert x \Vert = 1$ . In this situation, using again that $\tau $ preserves the measure, we find

$$ \begin{align*}\int_{\Omega_{n-r}} \hspace{-1em} \Vert Q(x) \Vert^r \: dQ = \int_{\Omega_{n-r}} \hspace{-1em} \Vert Q(x^{-1}) \Vert^r \: dQ.\end{align*} $$

Let Z be the minimal polynomial of x. The constant coefficient of Z is $\pm N_{K/F}(x)$ (where we recall that $N_{K/F}$ is the norm map from K to F). Hence it has norm $1$ , which means it is invertible in ${\mathcal O}_F$ . It follows from this observation that $x^{-1}$ can be expressed as a polynomial in x with coefficients in ${\mathcal O}_F$ : that is, $x^{-1} \in {\mathcal O}_F[x]$ . Similarly, one has $x \in {\mathcal O}_F[x^{-1}]$ . Combining both results, we get ${\mathcal O}_F[x] = {\mathcal O}_F[x^{-1}]$ , from which we deduce the desired equality.

2.3.3 Formulas for extremal degrees

When $n = r$ , the density function $\rho _{r,K}$ is defined by

$$ \begin{align*}\rho_{r,K}(x) = \frac{\Vert D_K \Vert}{\#\big({\mathcal O}_K/{\mathcal O}_F[x]\big)} \cdot \int_{{\mathcal O}_F} \Vert t \Vert^r \: dt.\end{align*} $$

Let $\pi $ be a fixed uniformiser of F, and set $U_s = \pi ^s {\mathcal O}_F^\times $ . We observe that $U_s$ consists of exactly elements of norm $q^{-s}$ and that ${\mathcal O}_F \backslash \{0\}$ is the disjoint union of the $U_s$ . It follows from these observations that

$$ \begin{align*}\int_{{\mathcal O}_F} \Vert t \Vert^r \: dt = \sum_{s=0}^\infty \int_{U_s} \Vert t \Vert^r \: dt = \sum_{s=0}^\infty \lambda_F(U_s) \cdot q^{-sr}.\end{align*} $$

In addition, the measure of $U_s$ can be computed as follows:

$$ \begin{align*}\lambda_F(U_s) = \lambda_F(\pi^s {\mathcal O}_F^\times) = \Vert \pi^s \Vert \cdot \lambda_F({\mathcal O}_F^\times) = q^{-s} \cdot \left(1 - \frac 1 q\right).\end{align*} $$

We then conclude that

(2.8) $$ \begin{align} \int_{{\mathcal O}_F} \Vert t \Vert^r \: dt = \left(1 - \frac 1 q\right) \cdot \sum_{s=0}^\infty q^{-sr - s} = \frac{q^{r+1}-q^r}{q^{r+1} - 1} \end{align} $$

and the claimed formula follows.

We now move to the case $n \geq 2r - 1$ . We set $m = n-r$ . Looking at the definition of $\rho _{K,n}$ , we realise that it is enough to prove that

$$ \begin{align*}\int_{\Omega_m} \Vert Q(x) \Vert^r \: dQ = \#\big({\mathcal O}_K/{\mathcal O}_F[x]\big) \cdot \int_{{\mathcal O}_F[x]} \Vert t \Vert^r \: dt.\end{align*} $$

As in the proof of Proposition 2.2, let Z denote the minimal polynomial of x, and consider the measure-preserving morphism $\Omega _{m-r} \times \Omega _{r-1} \to \Omega _m$ mapping $(S, T)$ to $SZ + T$ . (We agree that $\Omega _{-1} = \{0\}$ when $m = r-1$ .) Performing the corresponding change of variables, we obtain

$$ \begin{align*}\int_{\Omega_m} \Vert Q(x) \Vert^r \: dQ = \int_{\Omega_{r-1}} \hspace{-0.5em} \Vert T(x) \Vert^r \: dT.\end{align*} $$

In other words, we may assume that $m = r-1$ : that is, $n = 2r-1$ . Following again the proof of Proposition 2.2, we consider the evaluation map $\alpha _x : \Omega _{r-1} \to {\mathcal O}_K$ , $T(X) \mapsto T(x)$ . We have seen that it acts on the measures by multiplication by $\#\big ({\mathcal O}_K/{\mathcal O}_F[x]\big )^{-1}$ . Therefore, performing the change of variables $t = \alpha _x(T)$ , we obtain

$$ \begin{align*}\int_{\Omega_{r-1}} \hspace{-0.5em} \Vert T(x) \Vert^r \: dT = \#\big({\mathcal O}_K/{\mathcal O}_F[x]\big) \cdot \int_{{\mathcal O}_F[x]} \Vert t \Vert^r \: dt,\end{align*} $$

which concludes the proof.

2.3.4 Monotony

Based on the preceding, it is clear that $\rho _{K,n}(x) = \rho _{K,n+1}(x)$ when $F[x] \neq K$ or $n < r$ or $n \geq 2r - 1$ . It is then enough to prove that $\rho _{K,n}(x) < \rho _{K,n+1}(x)$ in the remaining cases. Coming back to the definition of the density functions, this amounts to showing that

$$ \begin{align*}\int_{\Omega_m} \Vert Q(x) \Vert^r \: dQ \,<\, \int_{\Omega_{m+1}} \hspace{-0.5em} \Vert Q(x) \Vert^r \: dQ\end{align*} $$

provided that $0 \leq m < r-1$ and $F[x] = K$ . Let $a \in {\mathcal O}_F$ . By compacity, the function $\Omega _m \to \mathbb R$ , $Q \mapsto \Vert a x^{m+1} + Q(x) \Vert $ attains its minimum. In other words, there exists a polynomial $Q_a \in \Omega _m$ such that $\Vert a x^{m+1} + Q_a(x) \Vert \leq \Vert a x^{m+1} + Q(x) \Vert $ for all $Q \in \Omega _m$ . Write $\delta _a = \Vert a x^{m+1} + Q_a(x) \Vert $ . Notice that $\delta _a> 0$ ; otherwise, x would be annihilated by a polynomial over F of degree $m+1 < r$ , contradicting $F[x] = K$ . Also note that $\delta _a$ depends only on the norm of a; in particular the function $a \mapsto \delta _a$ is measurable.

Lemma 2.4. With the above notations, we have

$$ \begin{align*}\Vert a x^{m+1} + Q(x) \Vert = \max\big( \delta_a,\, \Vert (Q - Q_a)(x) \Vert \big)\end{align*} $$

for all $a \in {\mathcal O}_F$ and $Q \in \Omega _m$ .

Proof. Putting $S = Q - Q_a$ , the ultrametric triangle inequality gives

(2.9) $$ \begin{align} \Vert a x^{m+1} + Q(x) \Vert \leq \max\big( \delta_a,\, \Vert S(x) \Vert \big) \end{align} $$

with equality provided that $\Vert S(x) \Vert \neq \delta _a$ . We then get the lemma under this additional assumption. On the other hand, when $\Vert S(x) \Vert = \delta _a$ , we derive from the definition of $Q_a$ that $\Vert a x^{m+1} + Q(x) \Vert \geq \delta _a$ . We deduce that equation (2.9) is an equality in this case as well, which establishes the lemma.

Separating the leading coefficient in the integral over $\Omega _{m+1}$ , we obtain

$$ \begin{align*} \int_{\Omega_{m+1}} \hspace{-0.5em} \Vert Q(x) \Vert^r \: dQ & = \int_{{\mathcal O}_F} \int_{\Omega_m} \Vert a x^{m+1} + Q(x) \Vert^r \: dQ \: da \\ & = \int_{{\mathcal O}_F} \int_{\Omega_m} \max\big( \delta_a^r,\, \Vert (Q-Q_a)(x) \Vert^r\big) \: dQ \: da \\ & = \int_{{\mathcal O}_F} \int_{\Omega_m} \max\big( \delta_a^r,\, \Vert Q(x) \Vert^r\big) \: dQ \: da, \end{align*} $$

which eventually shows that

$$ \begin{align*}\int_{\Omega_{m+1}} \hspace{-0.5em} \Vert Q(x) \Vert^r \: dQ \, \geq \, \int_{\Omega_m} \Vert Q(x) \Vert^r \: dQ\end{align*} $$

with strict inequality, provided that the set of pairs $(a,Q) \in {\mathcal O}_F \times \Omega _m$ for which $\Vert Q(x) \Vert < \delta _a$ has positive measure. But the latter property always holds true because $\delta _a = \delta _1> 0$ for all $a \in {\mathcal O}_F^\times $ , and ${\mathcal O}_F^\times $ has positive measure in ${\mathcal O}_F$ . This concludes the proof of Theorem B.

2.4 From density functions to average number of roots

We now focus on Theorem A. After Proposition 2.2, we are encouraged to treat separately roots lying in strict subextensions of K. We materialise this idea by introducing the notion of new roots.

Definition 2.5. Let K be a finite extension of F. An element $x \in \bar F$ is new in K if it is in K but not in any strict subextension of K.

Given an open subset U of a finite extension K of F together with a positive integer n, we define the random variable $Z^{\mathrm {new}}_{U,f} : \Omega _n \to \mathbb Z$ taking a polynomial of P to the number of roots of P that lie in U and are new in K. After what we have achieved so far, one strongly expects the mean value of $Z^{\mathrm {new}}_{U,n}$ to be related to the integral of the expression of the limit that appears in Proposition 2.2.

Theorem 2.6. Let n be a positive integer. Let K be a finite extension of F, and let U be an open subset of K. Then

(2.10) $$ \begin{align} \mathbb E\big[Z^{\mathrm{new}}_{U,n}\big] = \int_U \rho_{K,n}(x) \: dx. \end{align} $$

Proof. As usual, let r be the degree of the extension $K/F$ . Let $K^{\mathrm {new}}$ be the subset of K consisting of elements x for which $F[x] = K$ . Since K contains only finitely many subextensions and each subextension is a closed subspace of K, we deduce that $K^{\mathrm {new}}$ is open in K. We set ${\mathcal O}_K^{\mathrm {new}} = {\mathcal O}_K \cap K^{\mathrm {new}}$ .

To start with, we assume that U is compact and included in ${\mathcal O}_K^{\mathrm {new}}$ . We then have $Z^{\mathrm {new}}_{U,n} = Z_{U,n}$ . Since a random polynomial has almost surely only simple roots, we deduce from the p-adic Kac-Rice formula (compare Theorem 2.1) that

It is clear that $I_s(x,P)$ is nonnegative everywhere. As in the proof of Theorem 2.1, let $B_s$ be the closed ball of K of radius $q^{-s}$ and centre $0$ . From [8, Proposition 2.3], we deduce that

$$ \begin{align*}\int_{P^{-1}(B_s)} \hspace{-0.2em} \Vert P'(x) \Vert^r \, dx \,=\, \int_{B_s} \# P^{-1}(y) \, dy \,\leq\, n \lambda_K(B_s) \,=\, n q^{-rs}\end{align*} $$

for any polynomial $P \in \Omega _n$ . Hence

$$ \begin{align*}\int_U I_s(x, P) \, dx = q^{sr} \int_{U \cap P^{-1}(B_s)} \Vert P'(x) \Vert^r \, dx \,\leq\, n.\end{align*} $$

We can then apply Lebesgue’s dominated convergence theorem and get

$$ \begin{align*}\mathbb E[Z_{U,n}] = \lim_{s \to \infty} \, \int_{\Omega_n} \int_U I_s(x, P) \, dx\, dP = \lim_{s \to \infty} \, \int_U \int_{\Omega_n} I_s(x, P) \, dP\, dx,\end{align*} $$

where the second equality comes from Fubini’s theorem. We now want to use a similar argument to swap the limit on s and the integral over U. In order to proceed, we fix an element $x \in U$ and denote by $\alpha _x : F \otimes _{{\mathcal O}_F} \Omega _n \to K$ the evaluation morphism at x already considered in the proof of Proposition 2.2. Noticing that $\Vert P'(x) \Vert ^r \leq 1$ for all $P \in \Omega _n$ , we find

$$ \begin{align*} \int_{\Omega_n} I_s(x, P) \, dP & \leq q^{sr} \cdot \mu_n\big(\Omega_n \cap \alpha_x^{-1}(B_s)\big) \\ & \leq q^{sr} \cdot \mu_n\big(\alpha_x^{-1}(B_s)\big) = \#\big({\mathcal O}_K/{\mathcal O}_F[x]\big). \end{align*} $$

We saw in Section 2.3.1 that the function $x \mapsto \#\big ({\mathcal O}_K/{\mathcal O}_F[x]\big )$ is continuous; hence it is integrable on the compact set U. The dominated convergence theorem then again applies and gives

$$ \begin{align*}\mathbb E[Z_{U,n}] = \int_U \, \lim_{s \to \infty} \int_{\Omega_n} I_s(x, P) \, dP\, dx = \int_U \rho_{K,n}(x) \, dx.\end{align*} $$

Theorem 2.6 is then proved when U is compact and included in ${\mathcal O}_K^{\mathrm {new}}$ .

One can extend the result to any open subset of ${\mathcal O}_K$ using a standard limit argument. Precisely, if U is open in ${\mathcal O}_K$ , one can construct an increasing sequence $(U_m)_{m \geq 0}$ of compact open subsets of ${\mathcal O}_K^{\mathrm {new}}$ such that $\bigcup _{m \geq 0} U_m = U \cap {\mathcal O}_K^{\mathrm {new}}$ . Applying what we have done before with $U_m$ , we find

(2.11) $$ \begin{align} \mathbb E[Z_{U_m,n}] = \int_{U_m} \rho_{K,n}(x) \: dx. \end{align} $$

Moreover, the sequence $Z_{U_m,n}$ is nondecreasing and simply converges to $Z^{\mathrm {new}}_{U,n}$ . By the monotone convergence theorem, we find that $\mathbb E[Z_{U_m,n}]$ converges to $\mathbb E[Z^{\mathrm {new}}_{U,n}]$ . Passing to the limit in equation (2.11), we obtain the theorem for U.

For a general U, we write $U = U_0 \sqcup U_\infty $ with $U_0 = U \cap {\mathcal O}_K$ and $U_\infty = U \backslash U_0$ . Since both sides of equation (2.10) are additive with respect to U, it is enough to prove the theorem for $U_\infty $ . For this, as in Section 2.3.2, we consider the measure-preserving map $\tau : \Omega _n \to \Omega _n$ defined by

$$ \begin{align*}\tau\big(a_n X^n + \cdots + a_1 X + a_0\big) = a_0 X^n + \cdots + a_{n-1} X + a_n.\end{align*} $$

An element $x \in K$ is a root of a polynomial P if and only if $x^{-1}$ is a root of $\tau (P)$ . It is also obvious that $x \in K^{\mathrm {new}}$ if and only if $x^{-1} \in K^{\mathrm {new}}$ . Thus we get $\mathbb E\big [Z^{\mathrm {new}}_{U_\infty ,n}\big ] = \mathbb E\big [Z^{\mathrm {new}}_{V_\infty ,n}\big ]$ , where $V_\infty $ is the image of $U_\infty $ under the map $x \mapsto x^{-1}$ . In addition, $V_\infty \subset {\mathcal O}_K$ ; we can then apply the theorem with $V_\infty $ and conclude that

$$ \begin{align*}\mathbb E\big[Z^{\mathrm{new}}_{U_\infty,n}\big] = \int_{V_\infty} \rho_{K,n}(x) \: dx = \int_{U_\infty} \rho_{K,n}(x^{-1}) \cdot \Vert x \Vert^{-2r} \: dx = \int_{U_\infty} \rho_{K,n}(x) \: dx,\end{align*} $$

which finally proves the theorem in all cases.

We conclude this section by explaining how Theorem A can be derived from Theorem 2.6. It is actually easy once we notice that, given a finite extension E of F, any root $x \in K$ of a polynomial $P \in \Omega _n$ is new in a unique subextension $K'$ of E, namely $K' = F[x]$ . Hence, if U is an open subset of E, one has

$$ \begin{align*}Z_{U,n} = \sum_{K' \subset K} Z^{\mathrm{new}}_{U \cap K',n},\end{align*} $$

and Theorem A follows by additivity of the mean.

3 Examples and closed formulas

As we saw in Section 2, the distribution of roots in $\bar F$ of a random polynomial of degree n over ${\mathcal O}_F$ is governed by the density functions $\rho _{K,n}$ . However, it is not clear how useful this result could be for deriving explicit formulas, given that the density functions are defined by intricate integral expressions that do not look easily tractable at first glance.

The aim of this section is to become more familiar with those integrals and fully compute them in certain simple cases. The case of quadratic extensions will be covered in full generality in Section 3.1, culminating with a proof of Theorem C. Partial results in the case of prime degree extensions and unramified extensions will be given in Section 3.2 and Section 3.3, respectively.

Before getting to the heart of the matter and dealing with extensions, it is important to elucidate the case of the ground field F itself. This base case is addressed by the following proposition.

Proposition 3.1. For all positive integers n and all $x \in F$ , we have

$$ \begin{align*}\begin{array}{l@{\hspace{0.5ex}}l@{\qquad}l} \rho_{F,n}(x) & = \displaystyle \frac q{q+1} & \text{if } x \in {\mathcal O}_F \\[10pt] & = \displaystyle \frac q{q+1} \cdot \Vert x \Vert^{-2} & \text{otherwise.} \end{array}\end{align*} $$

Proof. It follows from Theorem B that $\rho _{F,n}$ does not depend on n provided that $n \geq 1$ . The values of $\rho _{F,n}$ on ${\mathcal O}_F$ are given by the explicit formula for $\rho _{F,1}(x)$ , which appears again in Theorem B. The values on $F\backslash {\mathcal O}_F$ are deduced from that on ${\mathcal O}_F$ , coming back to Definition 2.3.

Integrating over F, we recover (one more time) the fact that a random polynomial over ${\mathcal O}_F$ has exactly one root on average in F. In a similar fashion, if U is an open subset of ${\mathcal O}_F$ , we find $\mathbb E[Z_{U,n}] = \frac q{q+1} \cdot \lambda (U)$ . In particular, when $F = {\mathbb Q}_p$ and $U = {\mathbb Z}_p$ , we recover Evans’ theorem [8], which states that a random polynomial over the p-adics has $\frac p{p+1}$ roots in $\mathbb Z_p$ on average.

3.1 Quadratic extensions

Throughout this subsection, we fix a quadratic extension K of F together with an integer $n \geq 1$ . We aim at finding a closed expression for $\rho _{K,n}(x)$ for $x \in {\mathcal O}_K$ . Our starting point is Theorem B, which provides us with the following expression:

• ○ if $n = 2$ , then $\displaystyle \rho _{K,2}(x) = \Vert D_K \Vert \cdot \frac {1}{\#\big ({\mathcal O}_K/{\mathcal O}_F[x]\big )} \cdot \frac {q^2}{q^2 + q + 1}$ ,

• ○ if $n \geq 3$ , then $\displaystyle \rho _{K,n}(x) = \Vert D_K \Vert \cdot \int _{{\mathcal O}_F[x]} \Vert t \Vert ^2 \: dt$ .

We now distinguish between two cases depending on whether $K/F$ is ramified.

Proposition 3.2. Let K be the unramified quadratic extension of F. Then for all $x \in {\mathcal O}_K$ , we have

$$ \begin{align*}\begin{array}{lr@{\hspace{0.5ex}}l} & \rho_{K,2}(x) & \displaystyle = \frac{q^2}{q^2 + q + 1} \cdot \mathrm{dist}(x, F), \\[10pt] \text{for } n \geq 3, & \rho_{K,n}(x) & \displaystyle = \frac{q^2}{q^2 + q + 1} \cdot \mathrm{dist}(x, F) + \frac{q^3}{(q^2 + 1) \: (q^2 + q + 1)} \cdot \mathrm{dist}(x,F)^4 ,\end{array}\end{align*} $$

where $\mathrm {dist}(x, F)$ denotes the distance from x to F.

Proof. Since $K/F$ is unramified, its discriminant has norm $1$ and thus does not contribute. We fix an element $\zeta \in {\mathcal O}_K$ with norm $1$ such that ${\mathcal O}_K = {\mathcal O}_F[\zeta ]$ . The family $\mathcal B = (1, \zeta )$ is a basis of ${\mathcal O}_K$ over ${\mathcal O}_F$ . Let $x \in {\mathcal O}_K$ , $x \not \in {\mathcal O}_F$ , and write $x = a + b \zeta $ with $a, b \in {\mathcal O}_F$ , $b \neq 0$ . We have ${\mathcal O}_F[x] = {\mathcal O}_F[b \zeta ]$ , which shows that a basis of ${\mathcal O}_F[x]$ over ${\mathcal O}_F$ is simply $\mathcal B_x = (1, b\zeta )$ . Comparing $\mathcal B$ and $\mathcal B_x$ , we find $\#\big ({\mathcal O}_K/{\mathcal O}_F[x]\big ) = \#\big ({\mathcal O}_F/b{\mathcal O}_F\big ) = \Vert b \Vert ^{-1}$ . Observing in addition that a is the closest element of x in F, we can reinterpret the norm of b as the distance of x to F. Putting all ingredients together, we obtain the announced formula for $\rho _{K,2}(x)$ . This formula has been established when $x \not \in {\mathcal O}_F$ ; however, it obviously also holds true when $x \in {\mathcal O}_F$ since $\rho _{K,2}(x)$ vanishes in this case by definition.

We now move to the computation of $\rho _{K,n}$ for $n \geq 3$ . We continue to consider an element $x \in {\mathcal O}_K$ , $x \not \in {\mathcal O}_F$ and write $x = a + b \zeta $ with $a, b \in {\mathcal O}_F$ , $b \neq 0$ . Performing a change of variables or, more simply, coming back to Definition 2.3, we have

$$ \begin{align*}\rho_{K,n}(x) = \frac 1 {\#\big({\mathcal O}_K/{\mathcal O}_F[x]\big)} \cdot \int_{{\mathcal O}_F^2} \Vert u + vx \Vert^2 \: du \: dv = \Vert b \Vert \cdot \int_{{\mathcal O}_F^2} \Vert u + vx \Vert^2 \: du \: dv.\end{align*} $$

Replacing t by $t - ua$ , this reduces to

$$ \begin{align*}\rho_{K,n}(x) = \Vert b \Vert \cdot \int_{{\mathcal O}_F^2} \Vert u + vb\zeta \Vert^2 \: du \: dv = \Vert b \Vert \cdot \int_{{\mathcal O}_F^2} \max\big(\Vert tu\Vert^2, \Vert vb \Vert^2 \big) \: du \: dv.\end{align*} $$

As in Section 2.3.3, we decompose ${\mathcal O}_F$ as the disjoint union ${\mathcal O}_F = \{0\} \sqcup \bigcup _{s \geq 0} U_s$ , where $U_s$ consists of elements of norm $q^{-s}$ . Decomposing the integral accordingly and writing $\Vert b \Vert = q^{-\delta }$ , we find

$$ \begin{align*}\rho_{K,n}(x) = \left( 1 - \frac 1 q\right)^2 q^{-\delta} \cdot \sum_{s=0}^\infty \sum_{t=0}^\infty q^{-s-t-2\min(s, t+\delta)}.\end{align*} $$

Computing the latter double sum is painful but straightforward. We split the domain of summation into three regions, namely

$$ \begin{align*} D_1 & = \big\{ \, (s,t) \in \mathbb Z_{\geq 0}^2 \quad \text{such that} \quad s < \delta \,\big\}, \\ D_2 & = \big\{ \, (s,t) \in \mathbb Z_{\geq 0}^2 \quad \text{such that} \quad \delta \leq s \leq t + \delta \,\big\}, \\ D_3 & = \big\{ \, (s,t) \in \mathbb Z_{\geq 0}^2 \quad \text{such that} \quad s> t + \delta \,\big\}. \end{align*} $$

We then compute the double sum separately on each domain:

• ○ over $D_1$ : $\displaystyle \sum _{s=0}^{\delta -1} \sum _{t=0}^\infty q^{-3s-t} = \frac {q^4}{(q-1)(q^3-1)}\cdot (1 - q^{-3\delta })$ ,

• ○ over $D_2$ : $\displaystyle \sum _{s=\delta }^\infty \sum _{t=s-\delta }^\infty q^{-3s-t} = q^{-3\delta } \sum _{s=0}^\infty \sum _{t=s}^\infty q^{-3s-t} = \frac {q^5}{(q-1)(q^4-1)} \cdot q^{-3\delta }$ ,

• ○ over $D_3$ : $\displaystyle \sum _{t=0}^\infty \sum _{s=t+\delta +1}^\infty q^{-s-3t-2\delta } = q^{-3\delta -1} \sum _{t=0}^\infty \sum _{s=t}^\infty q^{-s-3t} = \frac {q^4}{(q-1)(q^4-1)} \cdot q^{-3\delta }$ .

Summing the contributions and noticing $q^{-\delta } = \Vert b \Vert = \mathrm {dist}(x,F)$ , we finally find the expression given in the statement of the proposition. As previously, we notice that this formula continues to hold when $x \in {\mathcal O}_F$ , given that $\rho _{K,n}(x)$ vanishes by definition in this case.

Proposition 3.3. Let K be a totally ramified quadratic extension of F. Then for all $x \in {\mathcal O}_K$ , we have

$$ \begin{align*}\begin{array}{lr@{\hspace{0.5ex}}l} & \displaystyle \frac{\rho_{K,2}(x)}{\Vert D_K \Vert} & \displaystyle = \frac{q^{3/2}}{q^2 + q + 1} \cdot \mathrm{dist}(x, F), \\[10pt] \text{for } n \geq 3, & \displaystyle \frac{\rho_{K,n}(x)}{\Vert D_K \Vert} & \displaystyle = \frac{q^{3/2}}{q^2 + q + 1} \cdot \mathrm{dist}(x, F) + \frac{1}{q \:(q + 1) \: (q^2 + q + 1)} \cdot \mathrm{dist}(x,F)^4, \end{array}\end{align*} $$

where $\mathrm {dist}(x, F)$ denotes the distance from x to F.

Proof. The proof is similar to that of Proposition 3.2, so we only sketch the argument. We fix a uniformiser $\pi $ of K. The family $(1,\pi )$ forms a basis of ${\mathcal O}_K$ over ${\mathcal O}_F$ . Let $x \in {\mathcal O}_K$ , $x \not \in {\mathcal O}_F$ , and write $x = a + b\pi $ with $a, b \in {\mathcal O}_F$ , $b \neq 0$ . From the fact that $(1, b\pi )$ is a ${\mathcal O}_F$ -basis of ${\mathcal O}_F[x]$ , we deduce that the cardinality of ${\mathcal O}_K/{\mathcal O}_F[x]$ is $\Vert b \Vert ^{-1}$ . Noticing that $\mathrm {dist}(x, F) = \Vert b \pi \Vert = \sqrt {q} \cdot \Vert b \Vert $ , we get the announced formula for $\rho _{K,2}(x)$ .

When $n \geq 3$ , we start with the formula

$$ \begin{align*}\rho_{K,n}(x) = \frac {\Vert D_K \Vert}{\#\big({\mathcal O}_K/{\mathcal O}_F[x]\big)} \cdot \int_{{\mathcal O}_F^2} \Vert u + vx \Vert^2 \: du \: dv.\end{align*} $$

Decomposing the integral into slices where $\Vert u \Vert $ and $\Vert v \Vert $ are constant, we obtain

$$ \begin{align*}\frac{\rho_{K,n}(x)}{\Vert D_K \Vert} = \left( 1 - \frac 1 q\right)^2 q^{-\delta} \cdot \sum_{s=0}^\infty \sum_{t=0}^\infty q^{-s-t-\min(2s, 2t+2\delta+1)},\end{align*} $$

where $\delta $ is defined by $\Vert b \Vert = q^{-\delta }$ . Finally, splitting the previous double sum into three parts exactly as we did in the unramified case, we end up after some calculations with the formula displayed in the statement of the proposition.

Theorem C can be deduced from Propositions 3.2 and 3.3 by integrating over K. For this, the first ingredient is the observation that the transformation law of Theorem B permits one to relate the integral of $\rho _{K,n}$ outside ${\mathcal O}_K$ to its integral over another domain in ${\mathcal O}_K$ . Precisely, applying it with the homography $h : x \mapsto x^{-1}$ , we get $\rho _{K,n}\big (h(x)\big ) = \Vert x \Vert ^4 \cdot \rho _{K,n}(x)$ . Noticing in addition that h maps bijectively $K\backslash {\mathcal O}_K$ to the maximal ideal $\mathfrak m_K$ of ${\mathcal O}_K$ , we obtain

$$ \begin{align*}\int_{K\backslash{\mathcal O}_K} \hspace{-0.4em} \rho_{K,n}(x)\: dx = \int_{\mathfrak m_K} \rho_{K,n}\big(h(x)\big) {\cdot} \Vert h'(x) \Vert^2 \: dx = \int_{\mathfrak m_K} \rho_{K,n}(x) \: dx.\end{align*} $$

Summing the contributions over ${\mathcal O}_K$ and $K\backslash {\mathcal O}_K$ , we end up with

$$ \begin{align*}\int_K \, \rho_{K,n}(x)\: dx = \int_{{\mathcal O}_K} \rho_{K,n}(x)\: dx \, + \, \int_{\mathfrak m_K} \rho_{K,n}(x)\: dx.\end{align*} $$

Theorem C now easily follows from the next lemma.

Lemma 3.4. Let d be a positive integer, and set $\displaystyle \alpha _d = \frac {q-1}{q^{d+1} - 1} = \frac 1{q^d + q^{d-1} \cdots + 1}$ .

1. 1. If $K/F$ is unramified, we have

   $$ \begin{align*}\int_{{\mathcal O}_K} \mathrm{dist}(x,F)^d \: dx = q^d \alpha_d \quad \text{and} \quad \int_{\mathfrak m_K} \mathrm{dist}(x,F)^d \: dx = q^{-2} \alpha_d.\end{align*} $$

2. 2. If $K/F$ is totally ramified, we have

   $$ \begin{align*}\int_{{\mathcal O}_K} \mathrm{dist}(x,F)^d \: dx = q^{d/2} \alpha_d \quad \text{and} \quad \int_{\mathfrak m_K} \mathrm{dist}(x,F)^d \: dx = q^{d/2\,-\,1} \alpha_d.\end{align*} $$

Proof. We first assume that $K/F$ is unramified. Writing ${\mathcal O}_K = {\mathcal O}_F[\zeta ]$ as in the proof of Proposition 3.2, we find

$$ \begin{align*}\int_{{\mathcal O}_K} \mathrm{dist}(x,F)^d \: dx \,=\, \int_{{\mathcal O}_F} \Vert b \Vert^d \: db = q^d \alpha_d,\end{align*} $$

the last equality being nothing but equation (2.8) established in Section 2.3.3. Similarly noticing that $x = a + b \zeta $ lies in $\mathfrak m_K$ if and only if both a and b falls in the maximal ideal $\mathfrak m_F$ of ${\mathcal O}_F$ , we obtain

$$ \begin{align*}\int_{\mathfrak m_K} \mathrm{dist}(x,F)^d \: dx \,=\, \lambda(\mathfrak m_F) \cdot \int_{\mathfrak m_F} \Vert b \Vert^d \: db \,=\, q^{-1} \int_{\mathfrak m_F} \Vert b \Vert^d \: db.\end{align*} $$

Fixing a uniformiser $\pi _F$ of F and performing the change of variables $b = \pi _F t$ , we finally get

$$ \begin{align*}\int_{\mathfrak m_K} \mathrm{dist}(x,F)^d \: dx \,=\, q^{-d-2} \int_{{\mathcal O}_F} \Vert t \Vert^d \: dt = q^{-2} \alpha_d.\end{align*} $$

The argument in the totally ramified case is similar. We pick a uniformiser $\pi $ of K and, writing ${\mathcal O}_K = {\mathcal O}_F[\pi ]$ , find

$$ \begin{align*}\int_{{\mathcal O}_K} \mathrm{dist}(x,F)^d \: dx \,=\, \int_{{\mathcal O}_F} \Vert b \pi \Vert^d \: db \,=\, \Vert \pi \Vert^d \cdot q^d \alpha_d \,=\, q^{d/2} \alpha_d.\end{align*} $$

For the integral over $\mathfrak m_K$ , we observe that $a + b\pi \in {\mathcal O}_K$ if and only if $a \in \mathfrak m_F$ . Therefore

$$ \begin{align*}\int_{\mathfrak m_K} \mathrm{dist}(x,F)^d \: dx \,=\, \lambda(\mathfrak m_F) \cdot \int_{{\mathcal O}_F} \Vert b \pi \Vert^d \: db \,=\, q^{d/2\,-\,1} \alpha_d,\end{align*} $$

which concludes the proof.

3.2 Prime degree extensions

The strategy we have presented above in the case of quadratic extensions extends to all extensions of prime degree, the crucial point being that $K/F$ does not admit any nontrivial subextension. Nonetheless, the computations become much longer and more painful in this generality, although they remain feasible in theory. However, the case of polynomials of minimal degree remains reasonable.

Proposition 3.5. Let r be a prime number, and let K be an extension of F of degree r.

1. 1. If $K/F$ is unramified, then for all $x \in {\mathcal O}_K$ , we have

   $$ \begin{align*}\rho_{r,K}(x) = \frac{q^{r+1}-q^r}{q^{r+1}-1} \cdot \mathrm{dist}(x,F)^{r(r-1)/2}.\end{align*} $$

2. 2. If $K/F$ is totally ramified, then for all $x \in {\mathcal O}_K$ , we have

   $$ \begin{align*}\rho_{r,K}(x) = \Vert D_K \Vert \cdot \frac{q^{(r+3)/2}-q^{(r+1)/2}}{q^{r+1}-1} \cdot \mathrm{dist}(x,F)^{r(r-1)/2}.\end{align*} $$

Proof. We assume first that $K/F$ is unramified. Let $x \in {\mathcal O}_K$ , $x \not \in {\mathcal O}_F$ . By compacity, there exists $a \in {\mathcal O}_F$ such that $\Vert x - a \Vert = \mathrm {dist}(x, F)$ . We pick such an element a and write $x - a = \pi ^\delta \zeta $ , where $\pi $ is a fixed uniformiser of F and $\zeta \in {\mathcal O}_K$ has norm $1$ . Let $k_F$ and $k_K$ denote the residue fields of F and K, respectively, and let $\bar \zeta $ be the image of $\zeta $ in $k_K$ . We claim that $\bar \zeta \not \in k_F$ ; otherwise, there would exist $b \in {\mathcal O}_F$ with $b \equiv \zeta \pmod \pi $ and so $\Vert x - (a + \pi ^\delta b) \Vert \leq q^{-\delta -1} < q^{-\delta } = \Vert x - a \Vert $ , contradicting the minimality property of a. Given that the extension $k_K/k_F$ has prime degree, we deduce that $k_K = k_F[\bar \zeta ]$ and, consequently, that ${\mathcal O}_K = {\mathcal O}_F[\zeta ]$ . The family $(1, \zeta , \ldots , \zeta ^{r-1})$ is then a basis of ${\mathcal O}_K$ over ${\mathcal O}_F$ , while $(1, \pi ^\delta \zeta , \ldots , (\pi ^\delta \zeta )^{r-1})$ is a basis of ${\mathcal O}_F[x]$ over ${\mathcal O}_F$ . This shows that

$$ \begin{align*}\#\big({\mathcal O}_K/{\mathcal O}_F[x]\big) = q^{\delta + 2\delta + \cdots + (r-1)\delta} = q^{\delta r(r-1)/2} = \mathrm{dist}(x,F)^{-r(r-1)/2},\end{align*} $$

from which we deduce the claimed formula for $\rho _{r,K}(x)$ .

We now move to the totally ramified case. Let $\pi _F$ (respectively, $\pi _K$ ) denote a fixed uniformiser of F (respectively, K). Then ${\mathcal O}_K = {\mathcal O}_F[\pi _K]$ and the family $\mathcal B = (1, \pi _K, \ldots , \pi _K^{r-1})$ is a ${\mathcal O}_F$ -basis of ${\mathcal O}_K$ . Let $x \in {\mathcal O}_K$ . As before, if $x \in {\mathcal O}_F$ , both sides of the equality we want to prove vanish, and there is nothing more to do. We then assume $x \not \in {\mathcal O}_F$ and consider $a \in {\mathcal O}_F$ such that $\Vert x - a \Vert = \mathrm {dist}(x,F)$ . Write $x - a = \pi _K^\delta u$ with $\delta \in \mathbb Z_{\geq 0}$ and $u \in {\mathcal O}_K^\times $ . The minimality condition in the definition of a implies that $\delta \not \equiv 0 \pmod r$ . In addition, the family $\mathcal B_x = (1, \pi _K^\delta u, \ldots , (\pi _K^\delta u)^{r-1})$ is a ${\mathcal O}_F$ -basis of ${\mathcal O}_F[x]$ . For $i \in \{0, \ldots , r{-}1\}$ , we decompose $(\pi _K^\delta u)^i$ in the basis $\mathcal B$ : that is, we write

(3.1) $$ \begin{align} (\pi_K^\delta u)^i = \sum_{j=0}^{r-1} a_{ij} \pi_K^j \end{align} $$

with $a_{ij} \in {\mathcal O}_F$ . Set $c = q^{1/r}$ . Taking norms in equation (3.1), we get $c^{-\delta i} = \max _{1 \leq j < r} \big (\Vert a_{ij} \Vert {\cdot } c^{-j}\big )$ . In other words, $\Vert a_{ij} \Vert \leq c^{j-\delta i}$ for all j, and the equality holds for at least one index j. On the other hand, the inequality is certainly strict as soon as r does not divide $j-\delta i$ because $\Vert a_{ij} \Vert $ is a power of $q = c^r$ . Therefore, if $j_i$ denotes the remainder in the division of $\delta i$ by r, we conclude that $\Vert a_{ij} \Vert \leq c^{j-\delta i}$ for all j with equality if and only if $j = j_i$ . Let A be the change-of-basis matrix from $\mathcal B$ to $\mathcal B_x$ . By definition, its entries are exactly the $a_{ij}$ s. Let P be the permutation matrix associated to $i \mapsto j_i$ , and define

$$ \begin{align*}B = \left(\begin{matrix} \pi_F^{-\delta_0} \\ & \ddots \\ & & \pi_F^{-\delta_{r-1}} \end{matrix} \right) \cdot P^{-1} \cdot A \qquad \text{with} \quad \delta_i = \frac{\delta i - j_i}r.\end{align*} $$

The estimations on $\Vert a_{ij} \Vert $ we have obtained previously show that B has entries in ${\mathcal O}_F$ and that $B \text { mod } \pi _F$ is lower-triangular with nonzero diagonal entries. Hence B is invertible over ${\mathcal O}_F$ , which gives $\Vert \!\det B \Vert = 1$ . Since P is clearly invertible as well, we conclude that

$$ \begin{align*}\#\big({\mathcal O}_K/{\mathcal O}_F[x]\big) = \Vert\!\det A \Vert^{-1} = q^{\delta_0 + \cdots + \delta_r} = q^{(\delta-1)(r-1)/2}.\end{align*} $$

Remembering that $\mathrm {dist}(x,F) = \Vert x-a \Vert = \Vert \pi _K^\delta u \Vert = q^{-\delta /r}$ , we finally find the formula given in the proposition.

Extending Proposition 3.5 to larger degrees does not require more conceptual arguments but leads to much more laborious calculations. It follows from Definition 2.3 that for $n \geq r$ and $x \in {\mathcal O}_K \backslash {\mathcal O}_F$ , one has

$$ \begin{align*}\rho_{n,K}(x) = \frac{\Vert D_K \Vert}{\#\big({\mathcal O}_K/{\mathcal O}_F[x]\big)} \cdot \int_{{\mathcal O}_F^{m+1}} \max\big( \Vert u_0 \Vert^r, \, q^{-\delta r} \Vert u_1 \Vert^r,\, \ldots, \, q^{-\delta rm} \Vert u_m \Vert^r \big) \: du_0 \cdots du_m,\end{align*} $$

where $q^{-\delta } = \mathrm {dist}(x,F)$ and $m = \min (r{-}1, n{-}r)$ . In addition, after the proof of Proposition 3.5, we know an explicit formula for $\#\big ({\mathcal O}_K/{\mathcal O}_F[x]\big )$ . The integral can be computed by splitting the domain of integration, namely ${\mathcal O}_F^{m+1}$ , into $m{+}1$ subdomains depending on the index at which the maximum is reached. Computing all contributions separately and summing them, we can conclude. As far as we tried, it seems that the final formula does not take a simple form in full generality.

3.3 Unramified extensions

For general unramified extensions K, it is possible to compute at a lower cost some values of $\rho _{K,n}$ (for any n).

Proposition 3.6. Let r be a positive integer, and let K be the unramified extension of F of degree r. Let $x \in {\mathcal O}_K$ . We assume that ${\mathcal O}_F[x] = {\mathcal O}_K$ . Then

$$ \begin{align*}\rho_{n,K}(x) = \frac{q^{n'+1} - q^r}{q^{n'+1} - 1} \qquad \text{with} \quad n' = \min(n, 2r{-}1)\\[-15pt]\end{align*} $$

for all $n \geq r$ .

Proof. Set $m = n'-r$ . Let $k_F$ (respectively, $k_K$ ) denote the residue field of F (respectively, K). Let $\xi \in k_K$ be the image of x. Our assumption implies that $k_F[\xi ] = k_K$ . Therefore, if an expression of the form $u_0 + u_1 x + \cdots + u_m x^m$ with $u_i \in {\mathcal O}_F$ vanishes in $k_K$ , then all $u_i$ have to vanish in $k_F$ . We deduce from this property that

$$ \begin{align*}\Vert u_0 + u_1 x + \cdots + u_m x^m \Vert = \max\big(\Vert u_0 \Vert, \, \Vert u_1 \Vert,\, \ldots, \, \Vert u_m \Vert \big)\\[-15pt]\end{align*} $$

for all $u_0, \ldots , u_m \in {\mathcal O}_F$ . It then follows from Definition 2.3 and our assumptions that

$$ \begin{align*}\rho_{n,K}(x) = \int_{{\mathcal O}_F^{m+1}} \max\big( \Vert u_0 \Vert^r, \, \Vert u_1 \Vert^r,\, \ldots, \, \Vert u_m \Vert^r \big) \: du_0 \cdots du_m.\\[-15pt]\end{align*} $$

Contrary to what we said at the end of Section 3.2, the latter integral can be easily computed. Let us fix a uniformiser $\pi $ of F and, for each nonnegative integer s, set $U_s = (\pi ^s {\mathcal O}_F)^{m+1}$ . The $U_s$ s then form a decreasing sequence of open subsets of ${\mathcal O}_F^{m+1}$ . Moreover, it is easy to check that $U_s$ is exactly the domain over which the integrand $\max \big (\Vert u_0 \Vert ^r, \, \ldots , \, \Vert u_m \Vert ^r \big )$ is less than or equal to $q^{-sr}$ . We deduce from this that

$$ \begin{align*}\rho_{n,K}(x) = \sum_{s=0}^\infty \big(\lambda_F^{\otimes{m+1}}(U_s) - \lambda_F^{\otimes{m+1}}(U_{s+1})\big) \cdot q^{-sr}.\\[-15pt]\end{align*} $$

Observing that $\lambda _F^{\otimes {m+1}}(U_s) = \lambda _F(\pi ^s {\mathcal O}_F)^{m+1} = q^{-s(m+1)}$ , we end up with

$$ \begin{align*}\rho_{n,K}(x) = \big( 1 - q^{-m-1}\big) \cdot \sum_{s=0}^\infty q^{-s(m+1+r)} = \frac{q^{m+1+r} - q^r}{q^{m+1+r} - 1},\end{align*} $$

which is what we wanted to prove.

3.4 Numerical simulations

We have conducted several numerical experiments illustrating the theoretical results obtained in Section 2 and Section 3. First, for $p \in \{2, 5\}$ , we picked a sample of $500{,}000$ random polynomials over $\mathbb Z_p$ of degree up to $5$ and counted the number of (new) roots these polynomials have in ${\mathbb Q}_p$ and all its extensions of degree $2$ and $3$ . The results are reported on Figure 1 for $p = 2$ and in Figure 2 for $p = 5$ (the colours in the figures represent the number of new roots in each field). In both cases, we observe that the empirical average number of roots in $\mathbb Q_p$ is $1$ , as predicted by Proposition 3.1.

Figure 1 Average number of new roots of a polynomial in various extensions. Sample of $500,\!000$ polynomials over $\mathbb Z_2$ picked uniformly at random.

Figure 2 Average number of new roots of a polynomial in various extensions. Sample of $500,\!000$ polynomials over $\mathbb Z_5$ picked uniformly at random.

We can also check that the number of new roots heavily depends on the discriminant of the extension. When $p = 5$ , for example, the discriminant of $\mathbb Q_{5^2}$ has norm $1$ , whereas the discriminant of the two other quadratic extensions, namely $\mathbb Q_5[\sqrt 5]$ and $\mathbb Q_5[\sqrt {10}]$ , has norm $1/5$ ; looking at Figure 2, we see that the height of the dark blue area is roughly $5$ times larger that the height of the light blue area. Similarly, when $p = 2$ , the discriminant of $\mathbb Q_4$ has norm $1$ , the discriminant of $\mathbb Q_2[\sqrt 3]$ and $\mathbb Q_2[\sqrt 7]$ has norm $1/4$ and that of the four remaining quadratic extensions has norm $1/8$ . Again, we can check in Figure 1 that one has approximately the same ratios for the heights of the corresponding areas.

Another property we can visualise in Figure 1 and Figure 2 is the monotony statement of Theorem B. We see that the heights of the areas tend to slightly increase with the degree until they stabilise at degree $3$ for quadratic extensions and degree $5$ for cubic extensions.

In a slightly different direction, Figure 3 shows the empiric distribution of new roots of a sample of $500{,}000$ random polynomials of degree $5$ over $\mathbb Z_2$ in the ring of integers of two quadratic extensions, namely $\mathbb Z_4$ , presented as $\mathbb Z_2[\zeta ]$ with $\zeta ^2 + \zeta + 1 = 0$ (on the left) and $\mathbb Z_2[\pi ]$ , where $\pi $ is a root of the Eisenstein polynomial $X^2 + 2X - 2$ (on the right). In the figures, each bullet corresponds to a class modulo $2^5$ . The darkness of the bullet encodes the number of roots we got in the corresponding class: the bullet is black if we observed more than $400$ roots (total, in our sample of $500{,}000$ polynomials), white if we do not have any roots and gray for intermediate numbers of hits. On each $\mathbb Z_2$ -line, the classes are ordered as follows:

$$ \begin{align*} \begin{array}{c} 0, 16, 8, 24, 4, 20, 12, 28, 2, 18, 10, 26, 6, 22, 14, 30, \\ 1, 17, 9, 25, 5, 21, 13, 29, 3, 19, 11, 27, 7, 23, 15, 31. \end{array}\end{align*} $$

That is, the even classes come first, followed by the odd ones. In each subgroup, the classes are grouped according to their congruence modulo $4$ , then modulo $8$ , and so on. This organisation is appropriate for our purpose but reflects the $2$ -adic distance.

Figure 3 Distribution of new roots of a polynomial in $\mathbb Z_4$ (on the left) and in $\mathbb Z_2[\pi ]$ with $\pi ^2 + 2\pi - 2 = 0$ (on the right). Sample of $500,\!000$ polynomials over $\mathbb Z_2$ picked uniformly at random.

In each figure, it is striking that the bullets become much brighter when we approach the $\mathbb Z_2$ -line on the bottom. This empirical observation is in perfect compliance with the explicit formulas of Propositions 3.2 and 3.3 that clearly indicate that the size of $\rho _{K,n}(x)$ is governed by the distance of x to $\mathbb Q_2$ . The bullets in the figure on the right are much brighter than the bullets on the left. Again, this is because the discriminant of $\mathbb Q_2[\pi ]$ has a smaller norm than the discriminant of $\mathbb Q_4$ ; we expect more roots, and thus darker bullets, in the case of $\mathbb Q_4$ .

4 Some orders of magnitude

In the previous section, we tried to write exact formulas for the density function $\rho _{K,n}$ s. However, in many cases, it is sufficient – and sometimes even more useful – to know their orders of magnitude. In this section, we focus on the quantities

$$ \begin{align*} \rho_n(K) = \int_K \rho_{K,n}(x) \: dx \end{align*} $$

that count the average number of new roots in K: that is, $\rho _n(K) = \mathbb E[Z^{\mathrm {new}}_{K,n}]$ (see Definition 2.5 and Theorem 2.6). We obtain sharp asymptotic estimations when q and r grow, proving in particular Theorems D and E.

4.1 Counting generators over finite fields

This subsection gathers several preliminary lemmas concerning the number of generators of an extension of finite fields. Write ${\mathbb F}_q$ (respectively, $\bar {\mathbb F}_q$ ) for the residue field of F (respectively, $\bar F$ ). It is well-known that $\bar {\mathbb F}_q$ is an algebraic closure of ${\mathbb F}_q$ . For any given a positive integer f, let $\mathbb F_{q^f}$ denote the unique extension of ${\mathbb F}_q$ of degree f in $\bar {\mathbb F}_q$ . Let $G_f$ be the number of elements $x \in \mathbb F_{q^f}$ such that ${\mathbb F}_q[x] = \mathbb F_{q^f}$ . From the obvious fact that each $x \in \mathbb F_{q^f}$ generates some $\mathbb F_{q^m}$ for a divisor m of f, we deduce the relation

(4.1) $$ \begin{align} \sum_{m|f} G_m = q^f. \end{align} $$

This relation can be ‘inverted’ using the Moebius inversion formula. We recall that the Moebius function $\mu : \mathbb Z_{> 0} \to \{0, 1\}$ is defined by $\mu (p_1 \ldots p_s) = (-1)^s$ if $p_1, \ldots , p_s$ are distinct prime numbers and $\mu (n) = 0$ as soon as n is divisible by a square. Equation (4.1) then becomes

(4.2) $$ \begin{align} G_f = \sum_{m|f} \mu\left(\frac f m \right) q^m. \end{align} $$

From the latter formula, one easily derive that $G_f = q^f + O\big (q^{f/2}\big )$ . Here is another estimation of the same type that we will need in the sequel.

Lemma 4.1. For all positive integer f, we have

$$ \begin{align*} \sum_{\substack{m|f\\m < f}} G_m q^m \, \leq \, 2 q^f. \end{align*} $$

Proof. A strict divisor of f cannot exceed $f/2$ . On the other hand, it is obvious from the definition that $G_m \leq q^m$ for all m. Hence, the sum of the lemma is bounded from above by

$$ \begin{align*}\sum_{m < f/2} q^{2m} \leq \frac{q^{f+2} - 1}{q^2 - 1} \leq \frac{q^f}{1 - q^{-2}} \leq 2 q^f\end{align*} $$

given that $q \geq 2$ .

Let $\varphi $ be Euler’s totient function. We recall that $\varphi (n)$ is by definition the number of integers that are less than n and coprime with n. If the decomposition of n in prime factors reads $n = p_1^{\alpha _1} \cdots p_s^{\alpha _s}$ , one has the formula

$$ \begin{align*} \varphi(n) = n \cdot \left( 1 - \frac 1{p_1}\right) \cdots \left( 1 - \frac 1{p_s}\right). \end{align*} $$

The next beautiful lemma, which harmoniously relates the Moebius and Euler functions, is classical; we nevertheless include a proof for completeness.

Lemma 4.2. For any positive integer n, one has the relation

$$ \begin{align*} \sum_{m|n} \frac{\mu(m)} m \,=\, \frac{\varphi(n)} n. \end{align*} $$

Proof. Write $n = p_1^{\alpha _1} \cdots p_s^{\alpha _s}$ , where the $p_i$ s are pairwise distinct prime numbers. The divisors m of n are exactly the integers of the form $m = p_1^{\beta _1} \cdots p_s^{\beta _s}$ with $\beta _i \leq \alpha _i$ for all i. We then deduce from the definition of the Moebius function that

$$ \begin{align*} \sum_{m|n} \frac{\mu(m)} m = \sum_{\beta_1 = 0}^1 \cdots \sum_{\beta_s = 0}^1 \frac{(-1)^{\beta_1 + \cdots + \beta_s}}{p_1^{\beta_1}\ldots p_s^{\beta_s}} = \prod_{i=1}^s \left( 1 - \frac 1 {p_i}\right) = \frac{\varphi(n)}n, \end{align*} $$

which proves the lemma.

Lemma 4.3. For any positive integer r, one has the relation

$$ \begin{align*} r \cdot \sum_{f|r} \frac{G_f}f \,=\, \sum_{m|r} \varphi\left(\frac r m \right) q^m. \end{align*} $$

Proof. The lemma follows from the following sequence of equalities:

$$ \begin{align*} \begin{array}{@{}r@{\hspace{0.5ex}}l@{\qquad}l@{}} \displaystyle r \cdot \sum_{f|r} \frac{G_f}f & = \displaystyle r \cdot \sum_{m|f|r} \mu\left(\frac f m\right)\frac{q^m}f. & \text{by equation 4.2} \\ & = \displaystyle r \cdot \sum_{m|r} \, \sum_{n| \frac r m} \frac{\mu(n)} n \, \cdot \frac{q^m} m. & (\text{change of variables } n = \frac f m) \\ & = \displaystyle \sum_{m|r} \, \varphi\left(\frac r m\right) q^m & \text{by Lemma 4.2}. \end{array}\\[-45pt] \end{align*} $$

4.2 Isolating the main contribution to $\rho _n(K)$

We come back to the p-adic situation and our problem of finding a sharp asymptotic of $\rho _n(K)$ . In what follows, we fix a finite extension K of F. We denote its degree by r and its residual degree by f. The residue field of K is then $\mathbb F_{q^f}$ . Let $\mathcal G_K$ be the set of generators of ${\mathcal O}_K$ : that is,

$$ \begin{align*} \mathcal G_K = \big\{\, x \in {\mathcal O}_K \quad \text{such that} \quad {\mathcal O}_F[x] = {\mathcal O}_K \, \big\}. \end{align*} $$

Similarly, for a positive integer f, we define $\mathcal G_f$ as the set of generators of $\mathbb F_{q^f}$ over $\mathbb F_q$ . By definition, the number $G_f$ we introduced in Section 4.1 is the cardinality of $\mathcal G_f$ . For each $\alpha \in \mathbb F_{q^f}$ , we let $U_\alpha $ denote the open subset of ${\mathcal O}_K$ consisting of elements whose image in the residue field is $\alpha $ . The $U_\alpha $ s are then pairwise disjoint and $\lambda _K(U_\alpha ) = q^{-f}$ for all $\alpha $ .

Lemma 4.4. For $\alpha \in \mathbb F_{q^f}$ , we have

$$ \begin{align*}\begin{array}{r@{\hspace{0.5ex}}l@{\qquad}l} q^{-f} \cdot \big(1 - q^{-f}\big) \,\leq\, \lambda_K(\mathcal G_K \cap U_\alpha) & \,\leq\, q^{-f} & \text{if } \alpha \in \mathcal G_f, \\ \mathcal G_K \cap U_\alpha & \,=\, \emptyset & \text{if } \alpha \not\in \mathcal G_f. \end{array}\end{align*} $$

Proof. If $x \in {\mathcal O}_K$ generates ${\mathcal O}_K$ over ${\mathcal O}_F$ , its image in the residue field must generate $\mathbb F_{q^f}$ over $\mathbb F_q$ . This proves the lemma when $\alpha \not \in \mathcal G_f$ .

We now assume that $\alpha \in \mathcal G_f$ . First, it is clear that $\lambda _K(\mathcal G_K \cap U_\alpha ) \leq \lambda _K(U_\alpha ) = q^{-f}$ . Let $\bar Z$ be the minimal polynomial of $\alpha $ over $\mathbb F_q$ . Also let $a \in {\mathcal O}_K$ be a lifting of $\alpha $ and $Z \in \Omega _f$ be a polynomial lifting $\bar Z$ . We fix in addition a uniformiser $\pi $ of K. Then $Z(a)$ is a multiple of $\pi $ , and we write $Z(a) = \pi b$ . In addition, $\bar Z'(a)$ does not vanish given that $\mathbb F_{q^f}/ \mathbb F_q$ is a separable extension. For $x \in {\mathcal O}_K$ , the congruence

$$ \begin{align*}Z(a + \pi x) \,\equiv\, Z(a) + Z'(a) \pi x \,\equiv\, \pi \cdot \big(b + Z'(a)\:x\big)\quad \pmod{\pi^2} \end{align*} $$

shows that $Z(a + \pi x)$ is a uniformiser of K as soon as the image of x in the residue field is different from $\frac {-b}{Z'(a)}$ . When this occurs, ${\mathcal O}_F[x]$ then contains a uniformiser of K together with a generator of the residue field, implying that ${\mathcal O}_F[x] = {\mathcal O}_K$ . The lemma follows.

Proposition 4.5. For all $n \geq r$ , we have

$$ \begin{align*} \frac 1 {\Vert D_K\Vert} \cdot \int_{K\backslash\mathcal G_K} \rho_{K,n}(x) \: dx \, \leq \, 4 q^{-f}. \end{align*} $$

Proof. Set $V = K \backslash \mathcal G_K$ and $V_\alpha = V \cap U_\alpha $ for $\alpha \in \mathbb F_{q^f}$ . Also set $V_\infty = K\backslash {\mathcal O}_K$ . The set V then appears as the disjoint union of the $V_\alpha $ s for $\alpha $ varying in $\mathbb P^1(\mathbb F_{q^f})$ . We will bound the integral of $\rho _{K,n}$ on each $V_\alpha $ separately. When $\alpha \in \mathcal G_f$ , it follows from Lemma 4.4 that $\lambda _K(V_\alpha ) \leq q^{-2f}$ . In addition, coming back to Definition 2.3, we remark that $\rho _{K,n}$ is upper bounded by $\Vert D_K \Vert $ on ${\mathcal O}_K$ and so on $V_\alpha $ . We then deduce, in this case, that

$$ \begin{align*} \frac 1 {\Vert D_K \Vert} \cdot \int_{V_\alpha} \rho_{K,n}(x) \: dx \, \leq \, q^{-2f}. \end{align*} $$

We now consider the case where $\alpha \in \mathbb F_{q^f}$ , $\alpha \not \in \mathcal G_f$ . Write $\ell = {\mathbb F}_q[\alpha ]$ , and let $m(\alpha )$ be the degree of the extension $\ell /{\mathbb F}_q$ . By assumption, $m(\alpha ) < f$ . On the other hand, the reduction morphism ${\mathcal O}_K \to \mathbb F_{q^f}$ takes ${\mathcal O}_F[x]$ to $\ell $ . We deduce that the cardinality of the quotient ${\mathcal O}_K/{\mathcal O}_F[x]$ is bounded from below by the cardinality of $\mathbb F_{q^f}/\ell $ , which is $q^{f-m(\alpha )}$ . Injecting this bound into the definition of $\rho _{n,K}$ , we find

$$ \begin{align*} \frac 1 {\Vert D_K \Vert} \cdot \int_{V_\alpha} \rho_{K,n}(x) \: dx \, \leq \, \lambda_K(V_\alpha) \cdot q^{m(\alpha) - f} \, = \, q^{m(\alpha) - 2f}. \end{align*} $$

Finally, when $\alpha = \infty $ , we perform the change of variables $x \mapsto x^{-1}$ , which leaves us with

$$ \begin{align*}\int_{V_\infty} \rho_{K,n}(x) \: dx \,=\, \int_{V_0} \rho_{K,n}(x) \: dx \,\leq\, \Vert D_K \Vert \cdot q^{1 - 2f}.\end{align*} $$

Summing all the upper bounds, we find

$$ \begin{align*} \frac 1 {\Vert D_K \Vert} \cdot \int_{K\backslash\mathcal G_K} \rho_{K,n}(x) \: dx \,\leq\, q^{1-2f} \,+\, G_f q^{-2f} + \sum_{\substack{m|f\\m<f}} G_m q^{m - 2f} \end{align*} $$

given that the number of $\alpha \in \mathbb F_{q^f} \backslash \mathcal G_K$ for which $m(\alpha ) = m$ is equal to $G_m$ by definition. Remembering that $G_f \leq q^f$ and using Lemma 4.1, we end up with

$$ \begin{align*} \frac 1 {\Vert D_K \Vert} \cdot \int_{K\backslash\mathcal G_K} \rho_{K,n}(x) \: dx \,\leq\, q^{1-2f} + q^{-f} + 2 q^{-f} \,\leq\, 4 q^{-f}.\end{align*} $$

The proposition is proved.

The next corollary can be seen as an effective version of Theorem D (use equation (4.2)).

Corollary 4.6. We have the estimations

$$ \begin{align*}\begin{array}{rr@{\hspace{0.5ex}}l} & \displaystyle - q^{-f} \, \leq\, \frac{\rho_r(K)}{\Vert D_K \Vert} \,-\, \frac{q^{r+1} - q^r}{q^{r+1} - 1} \cdot \frac{G_f}{q^f} & \, \leq \, 4 q^{-f} \\[16pt] \text{for } n \geq 2r-1, & \displaystyle - q^{-f} \, \leq\, \frac{\rho_n(K)}{\Vert D_K \Vert} \,-\, \frac{q^f}{q^f + 1} \cdot \frac{G_f}{q^f} & \, \leq \, 4 q^{-f}. \end{array}\end{align*} $$

Proof. Let $n = r$ or $n \geq 2r - 1$ . Recall that by definition

$$ \begin{align*}\rho_n(K) = \int_K \rho_{K,n}(x) \: dx \,=\, \int_{\mathcal G_K} \rho_{K,n}(x) \: dx \,+\, \int_{K\backslash\mathcal G_K} \rho_{K,n}(x) \:dx.\end{align*} $$

By Proposition 4.5, we know that the integral over $K \backslash \mathcal G_K$ is upper bounded by $4 q^{-f}$ . It is also obviously nonnegative since the integrand is nonnegative. Therefore, it is enough to prove that

$$ \begin{align*}0 \, \leq \, c_n \: \frac{G_f}{q^f} \,-\, \int_{\mathcal G_K} \frac{\rho_{K,n}(x)}{\Vert D_K \Vert} \: dx \, \leq\, q^{-f}\end{align*} $$

with $c_r = \frac {q^{r+1} - q^r}{q^{r+1} - 1}$ and $c_n = \frac {q^r}{q^r + 1}$ for $n \geq 2r -1$ . On the other hand, a computation similar to the one we carried out in Section 2.3.3 gives

$$ \begin{align*}\int_{{\mathcal O}_K} \Vert t \Vert^r \: dt = \frac{q^f}{q^f + 1}.\end{align*} $$

Hence, it follows from the explicit formulas of Theorem B that $\rho _{K,n}$ is constant equal to $c_n {\cdot } \Vert D_K \Vert $ on $\mathcal G_K$ . We are then reduced to checking that $0 \leq q^{-f} G_f - \lambda _K(\mathcal G_K) \leq q^{-f} c_n^{-1}$ . This follows from Lemma 4.4 after remarking that $0 \leq c_n \leq 1$ .

By the monotony result of Theorem B, the previous corollary also provides estimations of $\rho _n(K)$ when n varies between r and $2r{-}1$ . However, they are less sharp since the error term is a priori only in $O\big (q^{-1}\big )$ instead of $O\big (q^{-f}\big )$ . We can nevertheless recover more accuracy when the extension $K/F$ is unramified.

Theorem 4.7. If $K/F$ is unramified, we have the estimation

$$ \begin{align*}- q^{-r} \, \leq\, \frac{\rho_n(K)}{\Vert D_K \Vert} \,-\, \frac{q^{n+1} - q^r}{q^{n+1} - 1} \cdot \frac{G_r}{q^r} \, \leq \, 4 q^{-r}\end{align*} $$

for all n between r and $2r-1$ .

Proof. It is exactly the same as the proof of Corollary 4.6, except that the value of $\rho _{K,n}$ on $\mathcal G_K$ is now given by Proposition 3.6. (Also note that $f = r$ in the unramified case.)

Replacing $G_r$ by its expression given by equation (4.2), we end up with the following asymptotic development in the spirit of Theorem D:

(4.3) $$ \begin{align} \rho_n(K) = \left( 1 - \frac 1 {q^{n-r+1}} \right) \cdot \sum_{m|r}\: \mu\!\left(\frac r m\right) q^{m-r} \,+\, O\left(\frac 1{q^r}\right).\\[-16pt]\nonumber \end{align} $$

This estimation holds true for any unramified extension $K/F$ and an integer n in the range $[r,\: 2r{-}1]$ ; moreover, the constant hidden in the $O(-)$ is absolute.

4.3 Summing over extensions of fixed degree

The aim of this subsection is to prove Theorem E. The strategy we will follow is simple: we sum the surroundings of Corollary 4.6 over all extensions K of a fixed degree r. The main new ingredient we will need is Serre’s mass formula, which we recall below. If K is a finite extension of F, we write $\mathrm {Aut}\:_{\!F\mathrm {-alg}}(K)$ for the group of automorphisms of F-algebras of K.

Theorem 4.8 (Serre’s mass formula)

For any positive integer r, we have

$$ \begin{align*}q^{r-1} \sum_K \frac{\Vert D_K \Vert}{\#\:\mathrm{Aut}\:_{\!F\mathrm{-alg}}(K)} = 1,\\[-16pt]\end{align*} $$

where the sum runs over all isomorphism classes of totally ramified extensions K of F of degree r.

Proof. See [18].

We need to be careful that in the formulation of Theorem 4.8, the sum runs over isomorphism classes of extensions and not extensions in $\bar F$ as we usually work with in this paper. To switch between those two viewpoints, we observe that an abstract extension K of F of degree r admits r embeddings into $\bar F$ . However, two such embeddings have the same image (and so define the same subfield of $\bar F$ ) when they differ by an automorphism of K. The number of subfields of $\bar F$ that are isomorphic to K is then exactly equal to $\frac r {\#\:\mathrm {Aut}\:_{\!F\mathrm {-alg}}(K)}$ . Therefore, Serre’s mass formula can be rewritten as follows:

(4.4) $$ \begin{align} \sum_{K \in \mathbf{Ex}_{r,1}} \Vert D_K \Vert = \frac r{q^{r-1}},\\[-16pt]\nonumber \end{align} $$

where the indexation set $\mathbf {Ex}_{r,1}$ consists of all subfields K of $\bar F$ that are totally ramified extensions of F of degree r. More generally, given an auxiliary positive integer f dividing r, we define $\mathbf {Ex}_{r,f}$ as the set of embedded extensions of F of degree r and residual degree f. Serre’s mass formula extends without difficulty to extensions in $\mathbf {Ex}_{r,f}$ .

Proposition 4.9. For all positive integers r and all divisors f or r, we have

$$ \begin{align*}\sum_{K \in \mathbf{Ex}_{r,f}} \Vert D_K \Vert = \frac r{q^r} \cdot \frac{q^f}f.\\[-16pt]\end{align*} $$

Proof. Let $F_f$ be the unique unramified extension of F of degree f in $\bar F$ . Its residue field is $\mathbb F_{q^f}$ and the normalised norm on $F_f$ is the fth power of $\Vert \cdot \Vert $ . Moreover, any extension K in $\mathbf {Ex}_{r,f}$ canonically contains $F_f$ and then appears uniquely as a totally ramified extension of $F_f$ . In addition, the discriminant of $K/F$ , still denoted by $D_K$ , is the fth power of the discriminant $D_{K/F_f}$ of $K/F_f$ . Hence $\Vert D_{K/F_f} \Vert ^f = \Vert D_K \Vert $ . The formula (4.4) applied with the base field $F_f$ then gives

$$ \begin{align*}\sum_{K \in \mathbf{Ex}_{r,f}} \Vert D_K \Vert = \sum_{K \in \mathbf{Ex}_{r,f}} \Vert D_{K/F_f} \Vert^f = \frac r f \cdot \frac 1 { (q^f)^{r\!/\!f\, -\,1}} = \frac r {q^r} \cdot \frac {q^f} f,\\[-16pt]\end{align*} $$

which establishes the proposition.

We now fix two positive integers r and n with $n \geq 2r-1$ . For a given divisor f or r, observing that

$$ \begin{align*}1 - \frac 1{q^f} \leq 1 - \frac 1{q^r} \leq \frac{q^r}{q^r + 1} \leq 1,\end{align*} $$

we derive from Corollary 4.6 that

$$ \begin{align*}\left| \frac{\rho_n(K)}{\Vert D_K \Vert} - \frac{G_f}{q^f} \right| \leq \frac 5{q^f}\end{align*} $$

for any extension $K \in \mathbf {Ex}_{r,f}$ . Summing over all such extensions, we find

$$ \begin{align*}\left| \sum_{K \in \mathbf{Ex}_{r,f}} \hspace{-0.5em} \rho_n(K) \,-\, \frac{G_f}{q^f} \sum_{K \in \mathbf{Ex}_{r,f}} \hspace{-0.2em} \Vert D_K \Vert \, \right| \, \leq \, \frac 5{q^f} \sum_{K \in \mathbf{Ex}_{r,f}} \Vert D_K \Vert,\end{align*} $$

which gives after Proposition 4.9

$$ \begin{align*}\left| \sum_{K \in \mathbf{Ex}_{r,f}} \hspace{-0.5em} \rho_n(K) \,-\, \frac r{q^r} {\cdot} \frac{G_f}f \, \right| \, \leq \, \frac {5}{q^r}\cdot \frac r f.\end{align*} $$

Writing that $\mathbf {Ex}_r$ is the disjoint union of the $\mathbf {Ex}_{r,f}$ s for f varying in the set of divisors of r and summing all the above estimations, we end up with

(4.5) $$ \begin{align} \left| \sum_{K \in \mathbf{Ex}_r} \rho_n(K) \,-\, \frac r{q^r} \sum_{f|r} \frac{G_f}f \, \right| \, \leq \, \frac {5}{q^r} \sum_{f|r} \frac r f \, = \, \frac 5 {q^r} \sum_{f|r} f. \end{align} $$

Finally, the error term is controlled thanks to the following classical result:

$$ \begin{align*}\displaystyle \sum_{f|r} f \,=\, O\big(r \cdot \log\log r\big)\end{align*} $$

(see for instance [9]). Injecting it into equation (4.5) and using the summation formula of Lemma 4.3, we finally get Theorem E.

Remark 4.10. It is amusing to observe that Theorems D and E have a very similar shape, except that the former involves the Moebius function whereas the latter implicates the Euler function. Comparing both results and writing $\delta = \varphi - \mu $ , we obtain for $n \geq 2r - 1$

$$ \begin{align*}\sum_{K \in \mathbf{Ex}^{\text{ram}}_r} \rho_n(K) = \sum_{m|r}\: \delta\!\left(\frac r m\right) q^{m-r} \,+\, O\left(\frac{r \cdot \log \log r}{q^r}\right),\end{align*} $$

where the indexation set $\mathbf {Ex}^{\text {ram}}_r$ consists of all ramified extensions of F of degree r in $\bar F$ . Since $\delta (1) = 0$ , the dominant term of the sum on the right-hand side is obtained for $m = r/\ell $ , where $\ell $ is the smallest divisor of m. Its value is $\delta (\ell )\:q^{-r(1-\frac 1 \ell )}$ . Since $\ell $ is necessarily prime, we have moreover $\mu (\ell ) = -1$ and $\varphi (\ell ) = \ell - 1$ , giving $\delta (\ell ) = \ell $ . As a consequence, we obtain the approximation

$$ \begin{align*}\sum_{K \in \mathbf{Ex}^{\text{ram}}_r} \rho_n(K) \,\approx\, \ell \cdot q^{-r(1-\frac 1 \ell)}.\end{align*} $$

For example, when $r = 2$ , we find that the order of magnitude of $\sum _{K \in \mathbf {Ex}^{\text {ram}}_2} \rho _n(K)$ is $2/q$ . If q is odd, the set $\mathbf {Ex}^{\text {ram}}_2$ consists of exactly two elements (namely, the extensions $F\big [\sqrt \pi \big ]$ and $F\big [\sqrt {a\pi }\big ]$ , where $\pi $ is a uniformiser of F and a is an element of ${\mathcal O}_F$ that is not a square in the residue field) and each corresponding summand contributes for $1/q$ .

5 The setup of étale algebras

In the previous section, we exclusively focused our interest on the mean of the $Z_{U,n}$ s. However, it is evident that the mean captures only a small part of the complexity of the phenomena; beyond it, we would like to study higher moments or correlations between the $Z_{U,n}$ s to get a more precise picture of the situation.

In this section, we propose to attack these questions by applying the same methods as before in some suitable enlarged framework, which is that of finite étale algebras (which are finite products of finite extensions of F). On the one hand, allowing this flexibility is harmless because all the techniques we developed in the previous sections extend without difficulty. On the other hand, it is interesting because it sheds new light on many natural questions. For instance, it turns out that the average number of roots in power algebras of the form $K^m$ is closely related to higher moments of the random variables $Z_{U,n}$ for $U \subset K$ . Similarly, studying the average number of roots in products of type $K_1 \times K_2$ provides valuable information on the correlations between $Z_{K_1,n}$ and $Z_{K_2,n}$ .

This section is organised as follows. In Section 5.1, we introduce the random variables $Z_{E,n}$ and $Z^{\mathrm {new}}_{E,n}$ for a finite étale algebra E and relate them to products of the $Z_{K,n}$ s. In Section 5.2, we extend Theorems A and B to our new setup. In Section 5.3, we spend some time on the special case of the étale algebra $F^2$ , making everything explicit in this example. We then derive from our calculations precise information about the variance and the correlations between the $Z_{U,n}$ s where U is an open subset of F, proving in particular Theorem F. Finally, we prove Theorem G in Section 5.4.

5.1 Roots and new roots

Before getting to the heart of the matter, we gather standard facts about finite étale F-algebras. To begin with, let us recall that a finite étale algebra over F is defined as a finite algebra over F without nilpotent elements [7, Definition 2.1.2]. It is well known (see [7, Corollary 2.1.6]) that any finite étale algebra over F can be decomposed as a product $K_1 \times K_2 \times \cdots \times K_m$ , where each $K_i$ is a finite extension of F. In what follows, we will often pick such a decomposition and work with it. The two next (classical) results will be useful to check that all our forthcoming constructions are intrinsic: that is, they do not depend on the choice of a decomposition as above.

Lemma 5.1. Let $K, K_1, \ldots , K_m$ be finite extensions of $F $ , and set $E = K_1 \times \cdots \times K_m$ . Let $f : E \to K$ be a surjective morphism of F-algebras. Then there exists an index i such that $f = \varphi \circ \text {pr}_i$ , where $\varphi : K_i \to K$ is an isomorphism and $\text {pr}_i$ denotes the projection on the ith factor.

Proof. Let $e_i = (0, \ldots , 0, 1, 0, \ldots , 0) \in E$ with the $1$ in ith position. If x lies in the kernel of f, so does $e_i x$ for all i. This proves that $\ker f$ decomposed as $I_1 \times \cdots \times I_m$ , where $I_i$ is some ideal of $K_i$ . Since $K_i$ is a field, one must have $I_i = 0$ or $I_i = K_i$ . Moreover, since f is surjective, $\ker f$ is a maximal ideal. This shows that there exists a special index i such that $I_i = 0$ and $I_j = K_j$ for all $j \neq i$ . Hence f factors through $\text {pr}_i$ and the lemma follows.

Corollary 5.2. Let $K_1, \ldots , K_m$ be pairwise nonisomorphic finite extensions of F. Let $(a_1, \ldots , a_m)$ and $(b_1, \ldots , b_m)$ be two tuples of nonnegative integers. Let

$$ \begin{align*}f :\, K_1^{a_1} \times \cdots \times K_m^{a_m} \longrightarrow K_1^{b_1} \times \cdots \times K_m^{b_m}\end{align*} $$

be a surjective morphism of F-algebras. Then for each $i \in \{1, \ldots , m\}$ , there exists an injection $\sigma _i \{1, \ldots , b_i\} \to \{1, \ldots , a_i\}$ and a tuple $(\varphi _{i,1}, \ldots , \varphi _{i,b_i})$ of automorphisms of $K_i$ such that

$$ \begin{align*}f\big((x_{i,j})_{1 \leq i \leq m, 1 \leq j \leq a_i}\big) = \big(\varphi_{i,j}(x_{i,\sigma_i(j)})\big)_{1 \leq i \leq m, 1 \leq j \leq b_i}.\end{align*} $$

Proof. Write $x = (x_{i,j})_{1 \leq i \leq m, 1 \leq j \leq a_i}$ . Given $i \in \{1, \ldots , m\}$ and $j \in \{1, \ldots , b_i\}$ , Lemma 5.1 tells us that the $(i,j)$ coordinate of $f(x)$ must be of the form $\varphi _{i,j}(x_{i,\sigma _i(j)})$ for some automorphism $\varphi _{i,j}$ of $K_i$ and some $\sigma _i(j) \in \{1, \ldots , b_i\}$ . This establishes the shape we have given for f. Finally, the fact that the $\sigma _i$ s are injective follows from the surjectivity of f.

When $a_i = b_i$ for all i, Corollary 5.2 indicates that the group of automorphisms of F-algebras of $E = K_1^{a_1} \times \cdots \times K_m^{a_m}$ , denoted by $\mathrm {Aut}\:_{\!F\mathrm {-alg}}(E)$ , is canonically isomorphic to

$$ \begin{align*}\prod_{i=1}^m \big(\mathfrak S_{a_i} \ltimes \mathrm{Aut}\:_{\!F\mathrm{-alg}}(K_i)^{a_i}\big),\end{align*} $$

where $\mathfrak S_{a_i}$ is the symmetric group on $a_i$ letters and acts on $\mathrm {Aut}\:_{F\mathrm {-alg}}(K_i)^{a_i}$ by permuting the automorphisms. In particular we deduce that

$$ \begin{align*}\# \mathrm{Aut}\:_{\!F\mathrm{-alg}}(E) = \prod_{i=1}^m \,\, a_i! \ \big(\#\mathrm{Aut}\:_{\!F\mathrm{-alg}}(K_i)\big)^{a_i}.\end{align*} $$

Another property of étale algebras it will be important to keep in mind in the sequel is recorded in the next proposition.

Proposition 5.3. Any F-subalgebra of a finite étale F-algebra is finite étale.

Proof. It is obvious from the definition.

We now go back to our topic. Given a polynomial $P \in F[X]$ , a root of P in a finite étale F-algebra E is, by definition, an element $x \in E$ such that $P(x) = 0$ . It is a standard fact that the datum of a root of P in E is equivalent to the datum of a morphism of F-algebras $F[X]/P \to E$ : to a root x, we associate the morphism taking X to x; and, conversely, to a morphism $\varphi : F[X]/P \to E$ , we associate the root $\varphi (X)$ .

The notion of new elements we introduced in the case of extensions in Definition 2.5 immediately extends to finite étale algebras.

Definition 5.4. Let E be a finite étale algebra over F. An element $x \in E$ is new in E if it does not belong to any strict F-subalgebra of E: that is, if $F[x] = E$ .

Lemma 5.5. Let P be a polynomial over F. Let $x \in E$ be a root of P and $\varphi : F[X]/P \to E$ be its associated morphism. Then x is new in E if and only if $\varphi $ is surjective.

Proof. It follows from the fact that the image of $\varphi $ is the F-algebra generated by x.

Given a positive integer n, a finite étale F-algebra E and an open subset $U \subset E$ , we define the random variables $Z_{U,n} : \Omega _n \to \mathbb Z$ and $Z^{\mathrm {new}}_{U,n} : \Omega _n \to \mathbb Z$ by

$$ \begin{align*} Z_{U,n}(P) & = \text{number of roots of } P \text{ in } U, \\ Z^{\mathrm{new}}_{U,n}(P) & = \text{number of roots of } P \text{ in } U \text{ that are new in } E. \end{align*} $$

It follows from Lemma 5.5 that $Z_{U,n}(P)$ (respectively, $Z^{\mathrm {new}}_{U,n}(P)$ ) is also the number of morphisms (respectively, surjective morphisms) of F-algebras $\varphi : F[X]/P \to E$ such that $\varphi (X) \in U$ . In particular, $Z_{E,n}(P) = \#\: \mathrm {Hom}_{F\mathrm {-alg}}\big (F[X]/P, E\big )$ and $Z^{\mathrm {new}}_{E,n}(P) = \#\: \mathrm {Hom}^{\mathrm {surj}}_{F\mathrm {-alg}}\big (F[X]/P, E\big )$ (where the notations are transparent). This reformulation shows directly that $Z^{\mathrm {new}}_{E,n}$ identically vanishes when $n < [E:F]$ . In addition, the random variables $Z_{U,n}$ and $Z^{\mathrm {new}}_{U,n}$ are related by the formula

(5.1) $$ \begin{align} Z_{U,n} = \sum_{E' \subset E} Z^{\mathrm{new}}_{E'\cap U, n}, \end{align} $$

which simply comes from the observation that an element $x \in E$ is new in a unique subalgebra $E'$ of E, namely $E' = F[x]$ . This algebra is moreover necessarily étale over F by Proposition 5.3. We note furthermore that the construction $Z_{U,n}$ is multiplicative with respect to the parameter U: that is,

$$ \begin{align*}Z_{U_1 \times U_2, n} = Z_{U_1, n} \cdot Z_{U_2, n}\end{align*} $$

for any positive integer n, any finite étale F-algebras $E_1$ and $E_2$ and any open subsets $U_1$ and $U_2$ of $E_1$ and $E_2$ , respectively. This property is interesting for us because it implies the formula

(5.2) $$ \begin{align} \mathrm{Cov}\big(Z_{U_1,n},\, Z_{U_2,n}\big) = \mathbb E\big[Z_{U_1 \times U_2, n}\big] - \mathbb E\big[Z_{U_1, n}\big] {\cdot} \mathbb E\big[Z_{U_2, n}\big], \end{align} $$

which shows that the covariance of $Z_{U_1,n}$ and $Z_{U_2,n}$ can be computed in terms of means of random variables of the form $Z_{U,n}$ . The next proposition highlights a similar property for the higher (factorial) moments of certain random variables $Z^{\mathrm {new}}_{U,n}$ .

Proposition 5.6. Let K be a finite extension of $F $ , and set $a = \# \: \mathrm {Aut}\:_{\!F\mathrm {-alg}}(K)$ . Let $m, n$ be two positive integers, and let U be an open subset of K stable by all morphisms in $\mathrm {Aut}\:_{\!F\mathrm {-alg}}(K)$ . Then

$$ \begin{align*}Z^{\mathrm{new}}_{U^m, n} = Z^{\mathrm{new}}_{U,n} \cdot \big(Z^{\mathrm{new}}_{U,n} - a\big) \cdot \big(Z^{\mathrm{new}}_{U,n} - 2a\big) \cdots \big(Z^{\mathrm{new}}_{U,n} - (m{-}1)a\big).\end{align*} $$

Proof. Write $r = [K:F]$ , and pick a polynomial $P \in \Omega _n$ . Let $x = (x_1, \ldots , x_m) \in U^m$ . We claim that x is a new root of P in E if and only if $x_i$ is a new root of P in K for all i and the $x_i$ s are pairwise nonconjugate. To prove the claim, we let Z be the minimal polynomial of x over F; similarly, for all $i \in \{1, \ldots , m\}$ , we denote by $Z_i$ the minimal polynomial of $x_i$ over F. We then have $Z = \text {lcm} (Z_1,\ldots , Z_m)$ . Notice that all the $Z_i$ s are irreducible since we assume that K is a field. On the other hand, the fact that x is new in E (respectively, $x_i$ is new in K) is equivalent to the equality $\deg Z = rm$ (respectively, $\deg Z_i = r$ ). We deduce from this that x is new in E if and only if $x_i$ is new in K for all i and the $Z_i$ s are pairwise coprime. By irreducibility, the coprimality condition is equivalent to the fact that the $Z_i$ s are pairwise distinct, which is further equivalent to the fact that the $x_i$ s are pairwise nonconjugate. This establishes our claim.

We are now ready to count the number of new roots of P in $U^m$ . Based on the preceding, it is equivalent to count the number of tuples $(x_1, \ldots , x_m) \in U^m$ of new roots in K that are pairwise nonconjugate. By definition of $Z^{\mathrm {new}}_{U,n}$ , we have $Z^{\mathrm {new}}_{U,n}(P)$ possibilities for $x_1$ . The fact that $x_2$ cannot be conjugate to $x_1$ eliminates exactly a possibilities because we have assumed that U is stable under the action of $\mathrm {Aut}\:_{\!F\mathrm {-alg}}(K)$ . There then remain $Z^{\mathrm {new}}_{U,n}(P) - a$ possibilities for $x_2$ . Similarly, we have $Z^{\mathrm {new}}_{U,n}(P) - 2a$ possibilities for $x_3$ because it has to be nonconjugate to both $x_1$ and $x_2$ . Repeating this argument m times, we end up with the formula of the proposition.

5.2 Density functions

In this subsection, we aim at extending the definition of density functions to the setting of étale algebras and at proving variants of Theorems A and B in this framework. For this, the first step is to find an adequate generalisation of the p-adic Kac-Rice formula.

Kac-Rice formula

If E is a finite étale algebra over F presented as $E = K_1 \times K_2 \times \cdots \times K_m$ (where the $K_i$ s are finite extensions of F), we endow it with the norm $\Vert \cdot \Vert $ defined by

$$ \begin{align*}\Vert (x_1, x_2, \ldots, x_m) \Vert = \max\big( \Vert x_1 \Vert, \Vert x_2 \Vert, \ldots, \Vert x_m \Vert \big) \qquad (x_i \in K_i).\end{align*} $$

We deduce from Corollary 5.2 and the discussion just after that the above definition is intrinsic in the sense that it does not depend on the chosen identification $E \simeq K_1 \times \cdots \times K_m$ . We let ${\mathcal O}_E$ be the subring of E consisting of elements of norm at most $1$ . When E is presented as $E = K_1 \times \cdots \times K_m$ , we have ${\mathcal O}_E = \mathcal O_{K_1} \times \cdots \times \mathcal O_{K_m}$ .

Given E as above, we also define the norm map $N_{E/F} : E \to F$ taking an element $x \in E$ to the determinant of the F-linear mapping $E \to E$ , $y \mapsto xy$ . When $E = K_1 \times \cdots \times K_m$ , we have

$$ \begin{align*}N_{E/F}\big((x_1, \ldots, x_m)\big) = N_{K_1/F}(x_1) \cdots N_{K_m/F}(x_m)\end{align*} $$

from which we derive

$$ \begin{align*} \Vert N_{E/F}\big((x_1, \ldots, x_m)\big) \Vert & = \Vert N_{K_1/F}(x_1) \Vert \cdots \Vert N_{K_m/F}(x_m) \Vert \\ & = \Vert x_1 \Vert^{[K_1:F]} \cdots \Vert x_m \Vert^{[K_m:F]}. \end{align*} $$

The latter formula shows in particular that $N_{E/F}$ maps ${\mathcal O}_E$ to ${\mathcal O}_F$ .

With the above preparation, the extension of the p-adic Kac-Rice formula to our new setting can be formulated as follows.

Theorem 5.7. Let E be a finite étale algebra over $F $ , and set $r = [E:F]$ . Let U be a compact open subset of E, and let $f : U \to E$ be a strictly differentiable function. We assume that $f'(x)$ is invertible in E for all $x \in E$ such that $f(x) = 0$ . Then

Proof. It is entirely similar to that of Theorem 2.1.

Density functions

We define the discriminant $D_E$ of a finite étale F-algebra $E = K_1 \times \cdots \times K_m$ as the product $D_{K_1} \cdots D_{K_m}$ . One checks that $D_E$ is also the discriminant of the bilinear form $E \times E \to F$ , $(x,y) \mapsto \mathrm {Tr}_{E/F}(xy)$ , where $\mathrm {Tr}_{E/F}$ is the trace map of E over F. This alternative definition shows in particular that $D_E$ does not depend (up to multiplication by an invertible element) on the choice of the presentation $E = K_1 \times \cdots \times K_m$ .

In the case of étale algebras, the density functions cannot be defined exactly the same way as for extensions (see Definition 2.3) because it may happen that neither x nor $x^{-1}$ falls in the ring of integers. We will then proceed in a slightly different manner. We denote by $\lambda _E$ the Haar measure on E normalised by $\lambda _E({\mathcal O}_E) = 1$ . If $E = K_1 \times \cdots \times K_m$ , we simply have $\lambda _E = \lambda _{K_1} \otimes \cdots \otimes \lambda _{K_m}$ . A second important ingredient we will need is a height function $H : E \to \mathbb R$ ; writing again $E = K_1 \times \cdots \times K_m$ , it is defined as follows:

$$ \begin{align*}H\big((x_1, \ldots, x_m)\big) = \prod_{i=1}^m\, \max\!\Big(1,\, \Vert x_i \Vert^{[K_i:F]}\Big) \qquad (x_i \in K_i).\end{align*} $$

Again using Corollary 5.2, we conclude that this notion does not depend on the choice of the identification $E = K_1 \times \cdots \times K_m$ .

Given a positive integer n and a finite étale F-algebra E of degree r, we set

$$ \begin{align*}\rho_{E,n}(x) = \frac{\Vert D_E \Vert \cdot \lambda_E\big({\mathcal O}_F[x]\big)} {H(x)^{n+1}} \cdot \int_{\Omega_{n-r}} \hspace{-1em} \Vert N_{E/F}(Q(x)) \Vert \: dQ.\end{align*} $$

The main benefit of the above expression is its validity for any $x \in E$ . In particular, when x is not new in E, we observe that ${\mathcal O}_F[x]$ is included in a strict F-linear subalgebra of E and thus has measure zero; $\rho _{E,n}(x)$ then vanishes as well in this case. In a similar fashion, when x is new in ${\mathcal O}_E$ , the height of x is $1$ and the measure of ${\mathcal O}_F[x]$ is the inverse of the cardinality of ${\mathcal O}_E/{\mathcal O}_F[x]$ ; we then get in this case

$$ \begin{align*}\rho_{E,n}(x) = \frac{\Vert D_E \Vert}{\#\big({\mathcal O}_E/{\mathcal O}_F[x]\big)} \cdot \int_{\Omega_{n-r}} \hspace{-1em} \Vert N_{E/F}(Q(x)) \Vert \: dQ,\end{align*} $$

which is exactly the formula of Definition 2.3. Theorems A and B now extend almost verbatim but with one notable exception: the monotony property of Theorem B no longer holds in the framework of étale algebras and there only remains the fact that the sequence $(\rho _{E,n})_{n \geq 1}$ is eventually constant.

Theorem 5.8. For any positive integer n, any finite étale F-algebra E and any open subset U of E, we have

$$ \begin{align*} \mathbb E\big[Z^{\mathrm{new}}_{U,n}\big] & \,\, = \,\, \int_U \rho_{E,n}(x)\:dx \\ \mathbb E[Z_{U,n}] & \,\, = \,\, \sum_{E' \subset E} \,\, \int_{U\cap E'} \rho_{E',n}(x)\:dx, \end{align*} $$

where the latter sum runs over all F-subalgebras $E'$ of E. Moreover, writing $r = [E:F]$ , the function $\rho _{E,n}$ satisfies the following list of properties, in which x denotes an element of E:

1. 1. (Vanishing) If $F[x] \neq E$ or $n < r$ , then $\rho _{E,n}(x) = 0$ .

2. 2. (Continuity) The function $\rho _{E,n}$ is continuous on K.

3. 3. (Transformation under homography) For $\left (\begin {matrix} a & b \\ c & d \end {matrix}\right ) \in \mathrm {GL}_2({\mathcal O}_F)$ , we have

   $$ \begin{align*}\rho_{E,n}\left(\frac{ax+b}{cx+d}\right) = \Vert N_{E/F}(cx+d) \Vert^2 \cdot \rho_{E,n}(x).\end{align*} $$

4. 4. (Ultimate constancy) If $n \geq 2r-1$ , then $\rho _{E,n} = \rho _{E,2r-1}$ .

5. 5. (Formulas for extremal degrees) If $F[x] = E$ and $x \in {\mathcal O}_E$ , then

   $$ \begin{align*}\begin{array}{rr@{\hspace{0.5ex}}l} & \rho_{E,r}(x) & = \displaystyle \Vert D_E\Vert \cdot \frac 1{\#\big({\mathcal O}_E/{\mathcal O}_F[x]\big)} \cdot \frac{q^{r+1} - q^r}{q^{r+1} - 1} \\[15pt] \text{for } n \geq 2r - 1, & \rho_{E,n}(x) & = \displaystyle \Vert D_E\Vert \cdot \int_{{\mathcal O}_F[x]} \Vert N_{E/F}(t)\Vert\: dt. \end{array}\end{align*} $$

Proof. The proof follows the same pattern than in the case of extensions. The first step is to extend Proposition 2.2 and show that

(5.3)

when x is new in E. As in the proof of Proposition 2.2, we write $I_s$ for the above integral. Let Z be the minimal monic polynomial of x; it does not need to be irreducible, but it has degree r since x is assumed to be new in E. Let $c \in F$ be the content of Z that is, by definition, the gcd of the coefficients of Z. Using that the content of a product is the product of the contents, we find that a product $QZ \in {\mathcal O}_F[x]$ if and only if $Q \in c^{-1} {\mathcal O}_F[X]$ . Moreover, we saw in the proof of Proposition 2.2 that there exists a positive constant $\gamma $ such that $\Vert R(x) \Vert \geq \gamma {\cdot } \Vert R \Vert $ for all polynomials R of degree at most $r{-}1$ . We deduce from these facts that for any fixed R with $\Vert R \Vert \leq \gamma $ , the property $QZ + R \in \Omega _n$ is equivalent to $Q \in c^{-1} \Omega _{n-r}$ . Remarking in addition that the mapping $(Q,R) \mapsto QZ + R$ preserves the measure (it is linear and has determinant one in the canonical bases), we obtain the equality

which holds true provided that s is sufficiently large. Repeating the argument presented in the proof of Proposition 2.2, we end up with

$$ \begin{align*} I_s & = \Vert D_E \Vert \cdot \lambda_E\big({\mathcal O}_F[x]\big) \cdot \int_{c^{-1} \Omega_{n-r}} \hspace{-1em} \Vert N_{E/F} (Q(x)) \Vert \cdot dQ \\ & = \Vert D_E \Vert \cdot \lambda_E\big({\mathcal O}_F[x]\big) \cdot \Vert c \Vert^{-n-1} \int_{\Omega_{n-r}} \hspace{-1em} \Vert N_{E/F} (Q(x)) \Vert \cdot dQ \end{align*} $$

for s large enough. Consider a decomposition $E = K_1 \times \cdots \times K_m$ , and write $x = (x_1, \ldots , x_m)$ accordingly. For each index i, set $r_i = [K_i:F]$ , and let $Z_i$ be the minimal monic polynomial of $x_i$ . Then Z is the lcm of the $Z_i$ s and comparing degrees, we get $Z = Z_1 \cdots Z_m$ . On the other hand, using relations between coefficients and roots, we find that the coefficient on $Z_i$ in $X^j$ has norm at most $\Vert x_i \Vert ^{r_i-j}$ , and equality is reached for $j \in \{0, r_i\}$ . Therefore, the content $c_i$ of $Z_i$ is $1$ when $x_i \in \mathcal O_{K_i}$ and is equal to $N_{K_i/F}(x_i)$ otherwise. Hence $\Vert c_i \Vert = \max \!\big (1,\, \Vert x_i \Vert ^{r_i}\big )$ in all cases. By the multiplicativity property of the contents, we conclude that $\Vert c \Vert = H(x)$ , which finally establishes equation (5.3). After this result, the proof of the first part of the theorem is totally similar to that of Theorem 2.6.

It remains to establish the properties of the density functions. Continuity and formulas for extremal degrees are derived exactly as in the case of extensions (see Section 2.3.1 and Section 2.3.3, respectively). Although the transformation formula under homography can be tackled as in Section 2.3.2, it is probably easier, in the case of étale algebras, to use a different argument that we present now. First, we remark that thanks to continuity, the set of equalities

$$ \begin{align*} \mathbb E\big[Z^{\mathrm{new}}_{U,n}\big] \,\, = \,\, \int_U \rho_{E,n}(x)\:dx \end{align*} $$

(when U varies) entirely determines the density function $\rho _{E,n}$ . Given an homography $h : t \mapsto \frac {at+b} {ct+d}$ , it is then enough to prove that $\mathbb E\big [Z^{\mathrm {new}}_{U,n}\big ] = \mathbb E\big [Z^{\mathrm {new}}_{h(U),n}\big ]$ for any open subset U of E, which follows from the fact that the transformation

$$ \begin{align*} \Omega_n \to \Omega_n, \quad P(X) \mapsto (cX+d)^n \cdot P\left(\frac{aX+b}{cX+d}\right) \end{align*} $$

preserves the measure.

It finally only remains to prove that $\rho _{E,n} = \rho _{E,2r-1}$ as soon as $n \geq 2r-1$ . Let x be a new element in E. As in the first part of the proof, we consider the minimal monic polynomial $Z \in {\mathcal O}_F[X]$ of x and let $c \in {\mathcal O}_F$ be its content. We pick a decomposition $E = K_1 \times \cdots \times K_m$ , and we let $E_0$ (respectively, $E_\infty $ ) be the product of the $K_i$ s for which x falls in the ring of integers (respectively, outside the ring of integers). We thus have the decomposition $E = E_0 \times E_\infty $ , and we write $x = (x_0, x_\infty )$ accordingly. It follows from the definition of the height function that $H(x) = \Vert N_{E_\infty /F} (x_\infty ) \Vert $ . For $t \in \{0, \infty \}$ , set $r_t = [E_t:F]$ , and let $Z_t$ be the minimal monic polynomial of $x_t$ . From the fact that x is new in E, we find $\deg Z = r$ , from which we deduce that $\deg Z_t = r_t$ and $Z = Z_0 Z_\infty $ . In addition, both polynomials $Z_0$ and $c^{-1} Z_\infty $ have integral coefficients. Even better, if we write

(5.4) $$ \begin{align} c^{-1} Z_\infty = \lambda_0 + \lambda_1 X + \cdots + \lambda_{r_\infty} X^{r_\infty}, \end{align} $$

the fact that the roots in $\bar F$ of $Z_\infty $ all have positive valuation implies that the constant coefficient $\lambda _0$ is invertible in ${\mathcal O}_F$ while the next ones lie in the maximal ideal of ${\mathcal O}_F$ : that is, $\Vert \lambda _0 \Vert = 1$ and $\Vert \lambda _i \Vert < 1$ for $i \in \{1, \ldots , r_\infty \}$ . For a polynomial $Q \in \Omega _n$ , we define $Q \hspace {0.6ex}\%\hspace {0.6ex} Z_0$ as the remainder of the division of Q by $Z_0$ and $Q \hspace {0.6ex}\%^\tau \hspace {0.6ex} Z_\infty $ as the remainder of the division by increasing power order of Q by $Z_\infty $ . The notation $\hspace {0.6ex}\%^\tau \hspace {0.6ex}$ comes from the fact that

$$ \begin{align*}Q \hspace{0.6ex}\%^\tau\hspace{0.6ex} Z_\infty = \tau\big(\tau(Q) \hspace{0.6ex}\%\hspace{0.6ex} \tau(Z_\infty)\big),\end{align*} $$

where $\tau $ is the involution of $\Omega _n$ taking $P(X)$ to $X^n P(X^{-1})$ . We derive from the fact that $Z_0 \in {\mathcal O}_F[X]$ (respectively, from equation (5.4)) that $Q \hspace {0.6ex}\%\hspace {0.6ex} Z_0$ (respectively, $Q \hspace {0.6ex}\%^\tau \hspace {0.6ex} Z_\infty $ ) has integral coefficients when Q has. We consider the ${\mathcal O}_F$ -linear mapping

$$ \begin{align*}\begin{array}{rcl} \varphi : \quad \Omega_n & \longrightarrow & (\Omega_{r_0-1}) \times (X^{n-r_\infty+1} \Omega_{r_\infty - 1}) \\ Q & \mapsto & \big(Q \hspace{0.6ex}\%\hspace{0.6ex} Z_0, \, Q \hspace{0.6ex}\%^\tau\hspace{0.6ex} Z_\infty\big) \end{array}.\end{align*} $$

We claim that $\varphi $ is surjective. Given $P \in \Omega _{r_0-1}$ , checking that $(P,0)$ is in the image of $\varphi $ amounts to proving that there exists a polynomial that is divisible by $Z_\infty $ and congruent to P modulo $Z_0$ . This follows from the fact that $Z_\infty $ is invertible in the quotient ${\mathcal O}_F[X]/Z_0$ , which is itself a consequence of equation (5.4), which implies that the series $\sum _{i=1}^\infty \big ( \lambda _0 - c^{-1} Z_\infty \big )^i$ converges in ${\mathcal O}_F[X]/Z_0$ . Twisting by $\tau $ , we prove similarly that all elements of the form $(0, X^{n-r_\infty +1}B)$ with $B \in \Omega _{r_\infty - 1}$ are attained by $\varphi $ . Hence the surjectivity.

We deduce that $\Omega _n$ can be decomposed (noncanonically) as follows:

$$ \begin{align*}\Omega_n \simeq \big(\!\ker\varphi\big) \times \big(\Omega_{r_0-1}\big) \times \big(X^{n-r_\infty+1} \Omega_{r_\infty - 1}\big).\end{align*} $$

This isomorphism moreover preserves the measure since it is ${\mathcal O}_F$ -linear. Thus, if we set

$$ \begin{align*}J_t = \int_{\Omega_{r_t-1}} \hspace{-0.5em} \Vert N_{E_t/F}(Q(x_t)) \Vert \: dQ \qquad (t \in \{0, \infty\})\end{align*} $$

we get

$$ \begin{align*} \frac 1{H(x)^{n+1}} \int_{\Omega_n} \Vert N_{E/F}(Q(x)) \Vert \: dQ & \,=\, \frac{\Vert N_{E_\infty/F}(x_\infty) \Vert^{n-r_\infty+1}}{H(x)^{n+1}} \cdot J_0 \cdot J_\infty \\ & \,=\, \frac 1{H(x)^{r_\infty}} \cdot J_0 \cdot J_\infty, \end{align*} $$

which shows that the latter quantity does not depend on n (provided that $n \geq 2r - 1$ ) and so neither does $\rho _{n,E}(x)$ .

5.3 The case of $F^2$

The algebra $E = F^2$ is the simplest example of finite étale algebra that is not a field, but it leads to nontrivial and interesting results about the distribution of roots in F of a random polynomial. It allows us to compute precisely the second moment and covariances between the random variables $Z_{U,n}$ when U is an open subset of F. In what follows, we present a panorama of results in this direction.

Proposition 5.9. For $x, y \in {\mathcal O}_F$ , we have

$$ \begin{align*}\begin{array}{l@{\quad}r@{\hspace{0.5ex}}l} & \rho_{F^2,2}(x,y) & = \displaystyle \frac{q^2}{q^2 + q + 1} {\cdot} \Vert x-y \Vert \\ \text{for } n \geq 3, & \rho_{F^2,n}(x,y) & = \displaystyle \frac{q^2}{q^2 + q + 1} {\cdot} \Vert x-y \Vert - \frac{q^3}{(q+1)^2\:(q^2+q+1)} {\cdot} \Vert x-y \Vert^4. \end{array}\end{align*} $$

Proof. First, observe that $\Vert D_{F^2} \Vert = \Vert D_F \Vert ^2 = 1$ . Set $h = x - y$ , and let A be the ${\mathcal O}_F$ -subalgebra of ${\mathcal O}_F^2$ generated by $(x,y)$ . A basis of A is formed by the vectors $e_1 = (1, 1)$ and $e_2 = (0, h)$ . Hence $\#(\mathcal O_{F^2}/A) = \Vert h \Vert ^{-1}$ , and the proposition follows when $n = 2$ using the explicit formulas of Theorem 5.8. For $n \geq 3$ , we have to compute the integral of $\Vert N_{F^2/F}(t) \Vert $ over A. Applying the linear change of variables ${\mathcal O}_F^2 \stackrel \sim \to A$ , $(u,v) \mapsto ue_1 + v e_2 = (u, u+hv)$ , we obtain

(5.5) $$ \begin{align} \int_A \Vert N_{F^2/F}(t) \Vert \:dt = \Vert h \Vert \int_{{\mathcal O}_F^2} \Vert a \Vert {\cdot} \Vert u + hv \Vert \: du \: dv. \end{align} $$

In order to compute the latter integral, we first integrate with respect to the variable v. For a fixed $u \in {\mathcal O}_F$ , we claim that

$$ \begin{align*}\begin{array}{l@{\hspace{0.5em}}l@{\qquad}l} \displaystyle \int_{{\mathcal O}_F} \Vert u + hv \Vert \: dv & = \Vert u \Vert & \text{if } \Vert u \Vert> \Vert h \Vert \\ & = \displaystyle \frac q{q+1} \cdot \Vert h \Vert & \text{otherwise.} \end{array}\end{align*} $$

Indeed, when $\Vert u \Vert> \Vert h \Vert $ , the integrand is constant equal to $\Vert u \Vert $ . On the other hand, when $\Vert u \Vert \leq \Vert h \Vert $ , we can perform the change to variables $v \mapsto v - h^{-1}u$ and conclude by using equation (2.8). Injecting the above result into equation (5.5) and decomposing the integral according to the values of $\Vert u \Vert $ , we obtain

$$ \begin{align*}\int_A \Vert N_{F^2/F}(t) \Vert \:dt = \Vert h \Vert \cdot \left( 1 - \frac 1 q\right) {\cdot} \left( \sum_{s=0}^{\delta-1} q^{-3s} \,+\, \frac q{q+1} {\cdot} \Vert h \Vert {\cdot} \sum_{s=\delta}^\infty q^{-2s}\right),\end{align*} $$

where $\delta $ is defined by $\Vert h \Vert = q^{-\delta }$ . A straightforward computation now gives

$$ \begin{align*}\int_A \Vert N_{F^2/F}(t) \Vert \:dt = \frac{q^2}{q^2 + q + 1} {\cdot} \Vert h \Vert - \frac{q^3}{(q+1)^2\:(q^2+q+1)} {\cdot} \Vert h \Vert^4,\end{align*} $$

which concludes the proof thanks to the formulas for extremal degrees of Theorem 5.8.

Using the transformation formulas reported in Theorem 5.8, we can derive from Proposition 5.9 the values of $\rho _{F^2,n}$ on the whole domain $F^2$ . Indeed, if $x \in {\mathcal O}_F$ and $y \in F \backslash {\mathcal O}_F$ , considering the homography $t \mapsto \frac 1{1-x+t}$ , we get

$$ \begin{align*}\rho_{F^2,n}(x,y) = \Vert 1{-}x{+}y \Vert^{-2} \cdot \rho_{F^2,n}(1,y') = \Vert y \Vert^{-2} \cdot \rho_{F^2,n}(1,y')\end{align*} $$

with $y' = \frac 1 {1-x+y}$ . From the fact that $1-x+y \not \in {\mathcal O}_F$ , we deduce that $y'$ is in the maximal ideal of F and so $\Vert 1 - y'\Vert = 1$ . Applying Proposition 5.9, we finally find

$$ \begin{align*}\begin{array}{l@{\quad}r@{\hspace{0.5ex}}l} & \rho_{F^2,2}(x,y) & = \displaystyle \frac{q^2}{q^2 + q + 1} \cdot \Vert y \Vert^{-2} \\ \text{for } n \geq 3, & \rho_{F^2,n}(x,y) & = \displaystyle \frac{q^2}{(q+1)^2} \cdot \Vert y \Vert^{-2} \end{array}\end{align*} $$

in this case. Similarly when both x and y do not belong to ${\mathcal O}_F$ , we use the homography $t \mapsto t^{-1}$ and get

$$ \begin{align*}\begin{array}{l@{\quad}r@{\hspace{0.5ex}}l} & \rho_{F^2,2}(x,y) & = \displaystyle \frac{q^2}{q^2 + q + 1} {\cdot} \frac{\Vert x-y \Vert}{\Vert x \Vert^2 {\cdot} \Vert y \Vert^2} \\ \text{for } n \geq 3, & \rho_{F^2,n}(x,y) & = \displaystyle \frac{q^2}{q^2 + q + 1} {\cdot} \frac{\Vert x-y \Vert}{\Vert x \Vert^2 {\cdot} \Vert y \Vert^2} - \frac{q^3}{(q+1)^2\:(q^2+q+1)} {\cdot} \frac{\Vert x-y \Vert}{\Vert x \Vert^5 {\cdot} \Vert y \Vert^5}. \end{array}\end{align*} $$

Applications to covariances

Proposition 5.6 tells us that the integral of $\rho _{F^2,n}$ over $F^2$ gives twice the second factorial of the random variable $Z^{\mathrm {new}}_{F,n} = Z_{F,n}$ (which was computed as the value called $\rho (2,n)$ in [3]). Similarly, it turns out that we can obtain information about the variances and covariances of the random variables $Z_{U,n}$ for $U \subset F$ by integrating over smaller domains.

Proposition 5.10. For any positive integer n and any open subsets U and V of F, we have

$$ \begin{align*}\mathbb E\big[Z_{U,n}{\cdot}Z_{V,n}\big] \,=\, \int_U \int_V \rho_{F^2,n}(x,y)\:dx\:dy \,\,+\,\, \int_{U \cap V} \rho_{F,n}(x)\:dx.\end{align*} $$

Proof. The étale algebra $F^2$ admits a unique subalgebra, which is F embedded diagonally. Hence, applying Theorem 5.8 with the open subset $W = U \times V \subset F^2$ , we get

$$ \begin{align*}\mathbb E\big[Z_{U,n}{\cdot}Z_{V,n}\big] = \mathbb E\big[Z_{W,n}\big] = \int_W \rho_{F^2,n}(x)\:dx \,\,+\,\, \int_{W \cap F} \rho_{F,n}(x)\:dx.\end{align*} $$

Given that F is embedded diagonally in $F^2$ , the intersection $W \cap F$ is the set of elements $x \in F$ such that $(x,x) \in W = U \times V$ : that is, $W \cap F = U \cap V$ . The proposition follows.

When U and V are open balls of ${\mathcal O}_F$ , one can fully compute the integrals of Proposition 5.10 and come up with closed formulas for the mean of $Z_{U,n}{\cdot } Z_{V,n}$ and then for the covariance of $Z_{U,n}$ and $Z_{V,n}$ . The easiest case occurs when U are V are disjoint; under this additional assumption, the distance $\Vert x - y \Vert $ does not vary when x runs over U and y runs over V. According to Proposition 5.9, the function $\rho _{F^2,n}$ is then constant over $U \times V$ and easy to integrate. Doing so, we end up with the formula given in Theorem F (in the introduction).

On the other hand, when $V \subset U$ , the computation is a bit more painful but can nevertheless be carried out without trouble. For $n \geq 3$ , the final result we obtain reads

$$ \begin{align*} \mathbb E\big[Z_{U,n}{\cdot}Z_{V,n}\big] & \,=\, \frac q{q+1} {\cdot} \lambda(V) \,+\, \frac {q^3}{(q+1)\:(q^2+q+1)} {\cdot} \lambda(U)^2{\cdot}\lambda(V) \\ & \hspace{3em}-\, \frac {q^7}{(q+1)^2\:(q^2+q+1)\:(q^4+q^3+q^2+q+1)} {\cdot} \lambda(U)^5{\cdot}\lambda(V), \end{align*} $$

where we recall that $\lambda $ denotes the Haar measure on F.

Numerical simulations

As we did in Section 3.4, we conducted some numerical experiments illustrating the results of this subsection: we picked a sample of $500{,}000$ random polynomials over $\mathbb Z_2$ and located the pairs of distinct roots of those polynomials (which are exactly their new roots in $\mathbb Q_2^2$ ) in the $2$ -adic plane. The results we obtained are reported in Figure 4; we refer to Section 3.4 for an explanation of how to read this figure. In agreement with Proposition 5.9, we observe that pairs of roots are less and less numerous when we get closer to the diagonal.

Figure 4 Distribution of pairs of distinct roots of a polynomial. Sample of $500,\!000$ polynomials over $\mathbb Z_2$ picked uniformly at random.

It is also interesting to compare Figure 4 with Figure 3 (on page 24). Indeed, given that $\mathbb Q_2^2$ and $\mathbb Q_4$ both have discriminants of norm $1$ , we might expect at first glance that the number of new roots in both algebras will be comparable. However, looking at the figures, we clearly see that Figure 4 is much brighter than its counterpart. In other words, the conclusion of our numerical experiments is that there are significantly more new roots in $\mathbb Q_4$ than in $\mathbb Q_2^2$ . Coming back to Propositions 3.2 and 5.9, we realise that the aforementioned phenomenon can be explained by looking at the higher-order term (that is, the term in $\mathrm {dist}(x,\mathbb Q_2)^4$ in the case of $\mathbb Q_4$ and the term in $\Vert x -y\Vert ^4$ in the case of $\mathbb Q_2^2$ ); this term contributes positively – that is, it comes with a plus sign – in the case of $\mathbb Q_4$ , whereas it contributes negatively in the case of $\mathbb Q_2^2$ . When we are sufficiently far from $\mathbb Q_2$ , this error term is no longer negligible, and the sign change makes a significant difference.

5.4 A mass formula

In this last subsection, we prove Theorem G. For a positive integer r, we denote by $\acute{\mathbf{E}}\mathbf{t}_r$ the set of isomorphism classes of étale algebras of degree r over F. To simplify notation, we set

$$ \begin{align*} \Sigma(r,n) = \sum_{E \in \acute{\mathbf{E}}\mathbf{t}_r} \frac{\rho_n(E)}{\# \mathrm{Aut}\:_{\!F\mathrm{-alg}}(E)} \end{align*} $$

for all integers r and n. Our goal is to prove that $\Sigma (r,n) = 1$ provided that $n \geq r$ . We first consider the extreme case where $n = r$ , for which we have the following nice reinterpretation of the summands above.

Proposition 5.11. For a finite étale F-algebra E of degree r, we have

Proof. From Theorem 5.8, we know that

(5.6) $$ \begin{align} \rho_r(E) = \mathbb E\big[Z^{\mathrm{new}}_{E,r}\big] = \int_{\Omega_r} \# \mathrm{Hom}^{\mathrm{surj}}_{\!F\mathrm{-alg}}\big(F[X]/P,\,E\big) \: dP. \end{align} $$

If P is a polynomial of degree r, the quotient algebra $F[X]/P$ has degree r as well, so any surjective homomorphism of F-algebras $F[X]/P \to E$ has to be an isomorphism. Consequently, the integrand in equation (5.6) is equal to $\# \mathrm {Aut}\:_{\!F\mathrm {-alg}}(E)$ if $F[X]/P \simeq E$ , and it vanishes otherwise. The proposition follows.

Proposition 5.11 tells us that $\rho _r(E)/\# \mathrm {Aut}\:_{\!F\mathrm {-alg}}(E)$ is exactly the probability that a random polynomial $P \in \Omega _r$ satisfies $F[X]/P \simeq E$ . On the other hand, note that the quotient $F[X]/P$ is an étale F-algebra of degree r as soon as P is separable. This event almost certainly occurs. Therefore the probabilities that $F[X]/P \simeq E$ sum to $1$ when E runs over $\acute{\mathbf{E}}\mathbf{t}_r$ : that is, $\Sigma (r,r) = 1$ . Theorem G is then proved when $n = r$ . For higher n, the key ingredient of the proof is the following symmetry result.

Lemma 5.12. For $n> r$ , we have $\Sigma (r,n) = \Sigma (n{-}r, n)$ .

Proof. Unrolling the definitions of $\Sigma (r,n)$ and $\rho _n(E)$ , we obtain

$$ \begin{align*} \Sigma(r,n) = \int_{\Omega_n} \sum_{E \in \acute{\mathbf{E}}\mathbf{t}_r} \frac{\# \mathrm{Hom}^{\mathrm{surj}}_{\!F\mathrm{-alg}}\big(F[X]/P,\,E\big)} {\# \mathrm{Aut}\:_{\!F\mathrm{-alg}}(E)} \: dP. \end{align*} $$

Pick a separable polynomial $P \in \Omega _n $ , and set $E_P = F[X]/P$ ; it is an étale F-algebra of degree n. Define ${\acute{\mathbf{E}}\mathbf{t}}_r[P]$ as the subset of $\acute{\mathbf{E}}\mathbf{t}_r$ consisting of étale algebras E for which there exists a surjective morphism of F-algebras $E_P \to E$ . Let $E \in \acute{\mathbf{E}}\mathbf{t}_r[P]$ , and choose writings $E_P = K_1^{a_1} \times \cdots \times K_m^{a_m}$ and $E = K_1^{b_1} \times \cdots \times K_m^{b_m}$ , where the $K_i$ s are pairwise nonisomorphic finite extensions of F and $a_i, b_i \in \mathbb Z_{\geq 0}$ . From Corollary 5.2, we deduce that $a_i \geq b_i$ for all $i \in \{1, \ldots , m\}$ and that

$$ \begin{align*} \frac{\# \mathrm{Hom}^{\mathrm{surj}}_{\!F\mathrm{-alg}}(E_P,\,E)} {\# \mathrm{Aut}\:_{\!F\mathrm{-alg}}(E)} = \binom{a_1}{b_1} \cdot \binom{a_2}{b_2} \cdots \binom{a_m}{b_m}. \end{align*} $$

Hence, if we define $E^\vee = K_1^{a_1-b_1} \times \cdots \times K_m^{a_m-b_m}$ , we find

$$ \begin{align*}\frac{\# \mathrm{Hom}^{\mathrm{surj}}_{\!F\mathrm{-alg}}(E_P,\,E)} {\# \mathrm{Aut}\:_{\!F\mathrm{-alg}}(E)} = \frac{\# \mathrm{Hom}^{\mathrm{surj}}_{\!F\mathrm{-alg}}(E_P,\,E^\vee)} {\# \mathrm{Aut}\:_{\!F\mathrm{-alg}}(E^\vee)}.\end{align*} $$

Moreover, it follows again from Corollary 5.2 that the association $E \mapsto E^\vee $ induces a well-defined function $\acute{\mathbf{E}}\mathbf{t}_r[P] \to \acute{\mathbf{E}}\mathbf{t}_{n-r}[P]$ . This function is moreover bijective because its inverse can be built in a similar fashion. We conclude that, for a fixed separable polynomial $P \in \Omega _n$ , we have

$$ \begin{align*} \sum_{E \in \acute{\mathbf{E}}\mathbf{t}_r[P]} \frac{\# \mathrm{Hom}^{\mathrm{surj}}_{\!F\mathrm{-alg}}(E_P,\,E)} {\# \mathrm{Aut}\:_{\!F\mathrm{-alg}}(E)}\,= \sum_{E^\vee \in \acute{\mathbf{E}}\mathbf{t}_{n-r}[P]} \hspace{-0.5em} \frac{\# \mathrm{Hom}^{\mathrm{surj}}_{\!F\mathrm{-alg}}(E_P,\,E^\vee)} {\# \mathrm{Aut}\:_{\!F\mathrm{-alg}}(E^\vee)}, \end{align*} $$

which further gives

$$ \begin{align*} \sum_{E \in \acute{\mathbf{E}}\mathbf{t}_r} \frac{\# \mathrm{Hom}^{\mathrm{surj}}_{\!F\mathrm{-alg}}(E_P,\,E)} {\# \mathrm{Aut}\:_{\!F\mathrm{-alg}}(E)}\,= \sum_{E^\vee \in \acute{\mathbf{E}}\mathbf{t}_{n-r}} \frac{\# \mathrm{Hom}^{\mathrm{surj}}_{\!F\mathrm{-alg}}(E_P,\,E^\vee)} {\# \mathrm{Aut}\:_{\!F\mathrm{-alg}}(E^\vee)} \end{align*} $$

since all the additional summands that appear in both sums are zero. Finally, we obtain the lemma by taking the integral over $\Omega _n$ and remembering that a polynomial in $\Omega _n$ is almost surely separable.

After Lemma 5.12, it is easy to conclude the proof of Theorem G by induction on n. When $n = 1$ , the condition $n \geq r$ indicates that $r = 1$ as well, and we fall in the case where $n = r$ , which has already been treated. We now pick an integer $n> 1$ and assume that $\Sigma (r,m) = 1$ provided that $1 \leq r \leq m < n$ . Also let $r \in \{1, \ldots , n\}$ . If $n = r$ , we have already seen that $\Sigma (r,n) = 1$ , and there is nothing more to prove. If $r \leq n/2$ , it follows from the fourth property of Theorem 5.8 that $\Sigma (r,n) = \Sigma (r, 2r{-}1)$ , from which we deduce that $\Sigma (r,n) = 1$ thanks to our induction hypothesis. Finally, if $n/2 \leq r < n$ , we use Lemma 5.12 to write $\Sigma (r,n) = \Sigma (n{-}r, n)$ ; and, observing that $0 < n{-}r \leq n/2$ , we conclude by applying the previous case.