Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T06:16:18.978Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPACT TOEPLITZ OPERATORS WITH CONTINUOUS SYMBOLS

Published online by Cambridge University Press:  01 May 2009

TRIEU LE
TRIEU LE*
Affiliation:
Department of Pure Mathematics, University of Waterloo, 200 University Avenue West, Waterloo, ON, N2L 3G1, Canada e-mail: t29le@math.uwaterloo.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For any rotation-invariant positive regular Borel measure ν on the closed unit ball 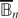whose support contains the unit sphere 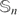, let L2a be the closure in L2 = L2(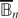, dν) of all analytic polynomials. For a bounded Borel function f on 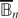, the Toeplitz operator Tf is defined by Tf(ϕ) = P(fϕ) for ϕ ∈ L2a, where P is the orthogonal projection from L2 onto L2a. We show that if f is continuous on 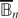, then Tf is compact if and only if f(z) = 0 for all z on the unit sphere. This is well known when L2a is replaced by the classical Bergman or Hardy space.

Keywords

Primary 47B35
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 51 , Issue 2 , May 2009 , pp. 257 - 261
Copyright
Copyright © Glasgow Mathematical Journal Trust 2008

References

REFERENCES

1.Lewis, A.Coburn, Singular integral operators and Toeplitz operators on odd spheres, Indiana Univ. Math. J. 23 (1973–1974), 433–439. MR 0322595 (48 #957)Google Scholar
2.Takahiko, Nakazi and Yoneda, Rikio, Compact Toeplitz operators with continuous symbols on weighted Bergman spaces, Glasgow Math. J. 42 (1) (2000), 31–35. MR 1739694 (2000i:47052)Google Scholar
3.Walter, Rudin, Function theory in the unit ball of Cn, vol. 241 (Springer-Verlag, New York, 1980). MR 601594 (82i:32002)Google Scholar
4.Kehe, Zhu, Spaces of holomorphic functions in the unit ball, vol. 226 (Springer-Verlag, New York, 2005). MR 2115155 (2006d:46035)Google Scholar