Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Castorena, Abel
2010.
Remarks on the Gieseker-Petri divisor in genus eight.
Rendiconti del Circolo Matematico di Palermo,
Vol. 59,
Issue. 1,
p.
143.
Lelli–Chiesa, Margherita
2012.
The Gieseker-Petri divisor in $${\mathcal{M}_g}$$ for g ≤ 13.
Geometriae Dedicata,
Vol. 158,
Issue. 1,
p.
149.


 of smooth and complex irreducible projective curves of genus
of smooth and complex irreducible projective curves of genus  be the locus of curves that do not satisfy the Gieseker-Petri theorem. Let
be the locus of curves that do not satisfy the Gieseker-Petri theorem. Let 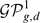 be the subvariety of
be the subvariety of