Killing rational characteristic classes by surgery

Extract

Let f_r: X_r → BO(r) be a sequence of fibrations with maps g_r: X_r → X_r+1 such that the usual diagram commutes. For such a situation R. Lashof defines the concept of an X-structure on manifolds (see [3]), and proves a Thom-isomorphism for the cobordism groups of such manifolds. Let n, m be positive integers which are fixed throughout this paper. If r is very big in comparison with n + m then X, is a simply connected CW-complex and the map 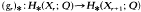is an isomorphism up to dimension n. Let γ be the pull-back over X_r of the universal r-linear bundle (which is, of course, a bundle over BO(r)). If r is very big in comparison with n + m, then we put X = X_r, and we assume that γ is orientable and oriented. The elements of H*(X; Q) of dimension not greater than n, will be called rational universal X-characteristic classes. It is well-known that many of the usual classes of manifolds may be described in terms of X-structures, (e.g. SO, SU, Spin-manifolds etc.).