No CrossRef data available.
Article contents
On an arithemtical inequality
Published online by Cambridge University Press: 18 May 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Here we extend an arithmetical inequality about multiplicative functions obtained by K. Alladi, P. Erdős and J. D. Vaaler, to include also the case of submultiplicative functions. Also an alternative proof of an extension of a result used for this purpose is given.
Let Uk, for integral k, denote the set {1,2,…, k}, and Vk denote the collection of all subsets of Uk. In the following, all unspecified sets like A,…, are assumed to be subsets of Uk. Let σ = {Si} and τ = {Tj} be two given collections of subsets of Uk. Set
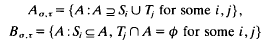
and
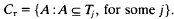
Let ′ denote complementation in Uk (but for in the proof of (3) where it denotes complementation in C). For any collection p of subsets of Uk, let p′ denote the collection of the complements of members of p.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1994
References
REFERENCES
1.Alladi, K., Erdős, P., and Vaaler, J. D., Multiplicative functions and small divisors, in Analytic Number Theory and Diophantine Problems, Proc. 1984 Conf. on Number Theory, Stillwater, Progress in Math., 70 (1987), 1–13.Google Scholar
2.Alladi, K., Erdős, P. and Vaaler, J. D., Multiplicative functions and smaller divisors II, J. Number Theory, 31 (1989), 183–190.CrossRefGoogle Scholar
4.Hall, P., On representatives of subsets, J. London Math. Soc. 10 (1935), 26–30.CrossRefGoogle Scholar
5.Landreau, B., Majorations de Fonctions Arithmétiques en moyenne sur des ensembles de faible densité (Ph.D. thesis), L'Université de Bordeaux I (1987).Google Scholar
6.Soundararajan, K., An inequality for multiplicative functions, J. Number Theory 41 (1992), 225–230.CrossRefGoogle Scholar
You have
Access