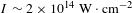1 Introduction
Reproducing astrophysical magnetized dynamical processes in the laboratory has become possible due to the emergence of platforms able to couple high-power laser-produced plasmas and external magnetic fields[Reference Albertazzi, Ciardi, Nakatsutsumi, Vinci, Béard, Bonito, Billette, Borghesi, Burkley, Chen, Cowan, Herrmannsdörfer, Higginson, Kroll, Pikuz, Naughton, Romagnani, Riconda, Revet, Riquier, Schlenvoigt, Yu Skobelev, Ya Faenov, Soloviev, Huarte-Espinosa, Frank, Portugall, Pépin and Fuchs1–Reference Revet, Chen, Bonito, Khiar, Filippov, Argiroffi, Higginson, Orlando, Béard, Blecher, Borghesi, Burdonov, Khaghani, Naughton, Pépin, Portugall, Riquier, Rodriguez, Ryazantsev, Skobelev, Soloviev, Willi, Pikuz, Ciardi and Fuchs3]. One of the major advantages of this coupling platform is the possibility to produce compressible, radiative magnetohydrodynamic (MHD) plasmas which have enough similarities[Reference Ryutov, Drake and Remington4] with astrophysical objects to investigate some fundamental physical processes[Reference Remington, Drake and Ryutov5], not accessible to astronomical observations, while also benchmarking large-scale simulations. In the particular case of highly magnetized plasmas, fundamental processes involved in magnetic cataclysmic variables (MCV) of polar type[Reference Warner6] can be studied[Reference Falize, Michaut and Bouquet7, Reference Cross, Reville and Gregori8]. This system is composed of a white dwarf (WD) and a companion star where a supersonic plasma flow (
![]() $v\sim 1000~\text{km}/\text{s}$
), coming from the companion star, falls down onto the WD along an accretion column when the magnetic field is over 1000 T, preventing the formation of an accretion disk around the WD[Reference Wu9]. After impact on the WD photosphere, a radiative steady reverse-shock forms that heats the accretion column up to 10 keV. As a consequence, a strong emission from soft to hard X-rays[Reference Warner6] due to bremsstrahlung cooling and other radiative processes is observed. Moreover, unexplained luminosity oscillations[10–Reference Mouchet, Bonnet-Bidaud, Van Box Som, Falize, Buckley, Breytenbach, Ashley, Marsh and Dhillon12] which could be related, for example, to unstable thermal oscillations of the shock front[Reference Chevalier and Imamura13] or MHD instabilities in the accretion column have been reported. As the reverse-shock position in polar systems is too close to the WD photosphere (of the order of 100–1000 km), observations cannot provide structural parameters such as shock height
$v\sim 1000~\text{km}/\text{s}$
), coming from the companion star, falls down onto the WD along an accretion column when the magnetic field is over 1000 T, preventing the formation of an accretion disk around the WD[Reference Wu9]. After impact on the WD photosphere, a radiative steady reverse-shock forms that heats the accretion column up to 10 keV. As a consequence, a strong emission from soft to hard X-rays[Reference Warner6] due to bremsstrahlung cooling and other radiative processes is observed. Moreover, unexplained luminosity oscillations[10–Reference Mouchet, Bonnet-Bidaud, Van Box Som, Falize, Buckley, Breytenbach, Ashley, Marsh and Dhillon12] which could be related, for example, to unstable thermal oscillations of the shock front[Reference Chevalier and Imamura13] or MHD instabilities in the accretion column have been reported. As the reverse-shock position in polar systems is too close to the WD photosphere (of the order of 100–1000 km), observations cannot provide structural parameters such as shock height
![]() $h_{s}$
and shock temperature. Therefore, several experimental studies have been initiated to study such objects in the laboratory[Reference Falize, Ravasio, Loupias, Dizière, Gregory, Michaut, Busschaert, Cavet and Koenig14–Reference Cross, Gregori, Foster, Graham, Bonnet-Bidaud, Busschaert, Charpentier, Danson, Doyle, Drake, Fyrth, Gumbrell, Koenig, Krauland, Kuranz, Loupias, Michaut, Mouchet, Patankar, Skidmore, Spindloe, Tubman, Woolsey, Yurchak and Falize18], where it has been shown that both ionization and radiation losses are important in the reverse-shock dynamics. However, in these experiments, the plasma flow was collimated by an additional tube[Reference Busschaert, Falize, Loupias, Michaut, Ravasio, Pelka, Yurchak and Koenig19] that disturbed the dynamics of the flow. As a result, it was not possible to observe if MHD instabilities such as the firehose instability or others[Reference Matsakos, Chièze, Stehlé, González, Ibgui, de Sá, Lanz, Orlando, Bonito, Argiroffi, Reale and Peres20] can occur in an accretion column. The recent development of platforms able to produce strong external magnetic field[Reference Albertazzi, Béard, Ciardi, Vinci, Albrecht, Billette, Burris-Mog, Chen, Da Silva, Dittrich, Herrmannsdörfer, Hirardin, Kroll, Nakatsutsumi, Nitsche, Riconda, Romagnagni, Schlenvoigt, Simond, Veuillot, Cowan, Portugall, Pépin and Fuchs21] in a laser environment allowed us to collimate the plasma flow without using a tube. It is an important point as recent radiations of hydrodynamic simulations[Reference Busschaert, Falize, Michaut, Bonnet-Bidaud and Mouchet22, Reference Toth and Draine23] showed the importance of the coupling between magnetic fields, radiation processes and extreme hydrodynamics, which can give rise to a wide variety of dynamical behaviors depending on which regime we are located.
$h_{s}$
and shock temperature. Therefore, several experimental studies have been initiated to study such objects in the laboratory[Reference Falize, Ravasio, Loupias, Dizière, Gregory, Michaut, Busschaert, Cavet and Koenig14–Reference Cross, Gregori, Foster, Graham, Bonnet-Bidaud, Busschaert, Charpentier, Danson, Doyle, Drake, Fyrth, Gumbrell, Koenig, Krauland, Kuranz, Loupias, Michaut, Mouchet, Patankar, Skidmore, Spindloe, Tubman, Woolsey, Yurchak and Falize18], where it has been shown that both ionization and radiation losses are important in the reverse-shock dynamics. However, in these experiments, the plasma flow was collimated by an additional tube[Reference Busschaert, Falize, Loupias, Michaut, Ravasio, Pelka, Yurchak and Koenig19] that disturbed the dynamics of the flow. As a result, it was not possible to observe if MHD instabilities such as the firehose instability or others[Reference Matsakos, Chièze, Stehlé, González, Ibgui, de Sá, Lanz, Orlando, Bonito, Argiroffi, Reale and Peres20] can occur in an accretion column. The recent development of platforms able to produce strong external magnetic field[Reference Albertazzi, Béard, Ciardi, Vinci, Albrecht, Billette, Burris-Mog, Chen, Da Silva, Dittrich, Herrmannsdörfer, Hirardin, Kroll, Nakatsutsumi, Nitsche, Riconda, Romagnagni, Schlenvoigt, Simond, Veuillot, Cowan, Portugall, Pépin and Fuchs21] in a laser environment allowed us to collimate the plasma flow without using a tube. It is an important point as recent radiations of hydrodynamic simulations[Reference Busschaert, Falize, Michaut, Bonnet-Bidaud and Mouchet22, Reference Toth and Draine23] showed the importance of the coupling between magnetic fields, radiation processes and extreme hydrodynamics, which can give rise to a wide variety of dynamical behaviors depending on which regime we are located.
Similarity criteria between the astrophysical problem under study and the laboratory experiment allow making a bridge between the experiment and the polar system. The huge magnetic field associated with these astrophysical systems (
![]() ${>}$
1000 T) implies, in the laboratory, an extremely high magnetic field (of the order of 100000 T)[Reference Van Box Som, Falize, Koenig, Sakawa, Albertazzi, Barroso, Bonnet-Bidaud, Busschaert, Ciardi, Hara, Katsuki, Kumar, Lefevre, Michaut, Michel, Miura, Morita, Mouchet, Rigon, Sano, Shiiba, Shimogawara and Tomiya24], based on Alfven similarity[Reference Ryutov, Drake and Remington4], which is unrealistic to achieve. However, in this polar regime (i.e., for magnetic field below 3000 T), the B-field has only one predominant effect: the collimation of the accreted plasma flow. In that case, some of the most important parameters to evaluate in the experiment are the magnetic Reynolds number
${>}$
1000 T) implies, in the laboratory, an extremely high magnetic field (of the order of 100000 T)[Reference Van Box Som, Falize, Koenig, Sakawa, Albertazzi, Barroso, Bonnet-Bidaud, Busschaert, Ciardi, Hara, Katsuki, Kumar, Lefevre, Michaut, Michel, Miura, Morita, Mouchet, Rigon, Sano, Shiiba, Shimogawara and Tomiya24], based on Alfven similarity[Reference Ryutov, Drake and Remington4], which is unrealistic to achieve. However, in this polar regime (i.e., for magnetic field below 3000 T), the B-field has only one predominant effect: the collimation of the accreted plasma flow. In that case, some of the most important parameters to evaluate in the experiment are the magnetic Reynolds number
![]() $R_{m}$
(which gives an indication on the diffusivity of the B-field inside the plasma,
$R_{m}$
(which gives an indication on the diffusivity of the B-field inside the plasma,
![]() $R_{m}=\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70E}uL$
, where
$R_{m}=\unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D70E}uL$
, where
![]() $u$
is the flow velocity,
$u$
is the flow velocity,
![]() $L$
is the characteristic length and
$L$
is the characteristic length and
![]() $\unicode[STIX]{x1D70E}$
is the electrical conductivity) and the
$\unicode[STIX]{x1D70E}$
is the electrical conductivity) and the
![]() $\unicode[STIX]{x1D6FD}_{\text{ram}}$
parameter (which evaluates the ratio between the ram pressure
$\unicode[STIX]{x1D6FD}_{\text{ram}}$
parameter (which evaluates the ratio between the ram pressure
![]() $\unicode[STIX]{x1D70C}v^{2}$
and the magnetic pressure
$\unicode[STIX]{x1D70C}v^{2}$
and the magnetic pressure
![]() $B^{2}/2\unicode[STIX]{x1D707}_{0}$
), to compare to the polar case where
$B^{2}/2\unicode[STIX]{x1D707}_{0}$
), to compare to the polar case where
![]() $R_{m}\gg 10$
and
$R_{m}\gg 10$
and
![]() $\unicode[STIX]{x1D6FD}_{\text{ram}}\sim 10^{-2}{-}10^{-4}$
. In such systems, radiation plays an important role as the cooling parameter is of the order of
$\unicode[STIX]{x1D6FD}_{\text{ram}}\sim 10^{-2}{-}10^{-4}$
. In such systems, radiation plays an important role as the cooling parameter is of the order of
![]() $\unicode[STIX]{x1D712}\sim 10^{-2}$
where
$\unicode[STIX]{x1D712}\sim 10^{-2}$
where
![]() $\unicode[STIX]{x1D712}\sim t_{\text{rad}}/t_{\text{hydro}}$
is defined as the ratio between the radiative cooling time
$\unicode[STIX]{x1D712}\sim t_{\text{rad}}/t_{\text{hydro}}$
is defined as the ratio between the radiative cooling time
![]() $t_{\text{rad}}$
and the characteristic hydrodynamic time
$t_{\text{rad}}$
and the characteristic hydrodynamic time
![]() $t_{\text{hydro}}$
. Finally, to be almost similar, the laser produced plasma should have (i) a magnetic pressure dominant over ram pressure, (ii) B-field frozen in the plasma and (iii) important radiation cooling. Other parameters such as density, temperature, and velocity can be found in Ref. [Reference Cross, Gregori, Foster, Graham, Bonnet-Bidaud, Busschaert, Charpentier, Danson, Doyle, Drake, Fyrth, Gumbrell, Koenig, Krauland, Kuranz, Loupias, Michaut, Mouchet, Patankar, Skidmore, Spindloe, Tubman, Woolsey, Yurchak and Falize18].
$t_{\text{hydro}}$
. Finally, to be almost similar, the laser produced plasma should have (i) a magnetic pressure dominant over ram pressure, (ii) B-field frozen in the plasma and (iii) important radiation cooling. Other parameters such as density, temperature, and velocity can be found in Ref. [Reference Cross, Gregori, Foster, Graham, Bonnet-Bidaud, Busschaert, Charpentier, Danson, Doyle, Drake, Fyrth, Gumbrell, Koenig, Krauland, Kuranz, Loupias, Michaut, Mouchet, Patankar, Skidmore, Spindloe, Tubman, Woolsey, Yurchak and Falize18].
Here we present our experimental platform developed to study the dynamics of the reverse shock occurring in polar systems, using the coupling between high energy lasers and external magnetic field. The paper is organized as follows. In Section 2, we present the experimental platform that has been developed at LULI2000 laser facility Ecole Polytechnique (Palaiseau, France) in collaboration with HZDR (Dresden, Germany) to mimic a polar system using an external magnetic field. Section 3 is devoted to the experimental results while Section 4 focuses on the numerical simulations performed with the 2D/3D MHD FLASH code developed by the University of Chicago (US) and the comparison with the experimental data. Finally, Section 5 presents further discussion about magnetic effects occurring in such plasmas and concludes the study.
2 Experimental setup
The experiment has been performed on the LULI2000 laser facility at LULI laboratory (Ecole Polytechnique, France). A long pulse (
![]() $\unicode[STIX]{x1D70F}\sim 1.5~\text{ns}$
), high energy (
$\unicode[STIX]{x1D70F}\sim 1.5~\text{ns}$
), high energy (
![]() $E_{L}\sim 400~\text{J}$
at the wavelength
$E_{L}\sim 400~\text{J}$
at the wavelength
![]() $\unicode[STIX]{x1D706}_{L}=527~\text{nm}$
) beam has been used to produce a strong shock wave in a multilayer solid target (referred to as the main target in the following): a layer of 25-
$\unicode[STIX]{x1D706}_{L}=527~\text{nm}$
) beam has been used to produce a strong shock wave in a multilayer solid target (referred to as the main target in the following): a layer of 25-
![]() $\unicode[STIX]{x03BC}\text{m}$
-thick CH, acting as the ablator, and a layer of 6-
$\unicode[STIX]{x03BC}\text{m}$
-thick CH, acting as the ablator, and a layer of 6-
![]() $\unicode[STIX]{x03BC}\text{m}$
-thick Sn, acting as an X-ray shield against radiation produced in the corona. The main target is glued onto a 4-mm-diameter holder having a 1-mm-diameter inner hole
$\unicode[STIX]{x03BC}\text{m}$
-thick Sn, acting as an X-ray shield against radiation produced in the corona. The main target is glued onto a 4-mm-diameter holder having a 1-mm-diameter inner hole
![]() $\pm 0.2~\text{mm}$
(see Figure 1(a)). The holder is made of aluminum. A hybrid phase plate (HPP) produced a flat-topped, 400-
$\pm 0.2~\text{mm}$
(see Figure 1(a)). The holder is made of aluminum. A hybrid phase plate (HPP) produced a flat-topped, 400-
![]() $\unicode[STIX]{x03BC}\text{m}$
-diameter focal spot, leading to an on-target intensity of the order of
$\unicode[STIX]{x03BC}\text{m}$
-diameter focal spot, leading to an on-target intensity of the order of
![]() $2\times 10^{14}~\text{W}\cdot \text{cm}^{-2}$
. When the shock breaks out from the rear Sn surface, a plasma flow is generated that propagates into vacuum and impacts an obstacle located at a distance ranging from 2 to 3 mm depending on the shot. The obstacle used in this experiment was a 3 mm diameter, 1 mm thick Al plate. We diagnosed the dense (
$2\times 10^{14}~\text{W}\cdot \text{cm}^{-2}$
. When the shock breaks out from the rear Sn surface, a plasma flow is generated that propagates into vacuum and impacts an obstacle located at a distance ranging from 2 to 3 mm depending on the shot. The obstacle used in this experiment was a 3 mm diameter, 1 mm thick Al plate. We diagnosed the dense (
![]() ${>}10^{20}~\text{cm}^{-3}$
) outgoing plasma by X-ray backlighting. To this end, an X-ray source was produced by irradiating a
${>}10^{20}~\text{cm}^{-3}$
) outgoing plasma by X-ray backlighting. To this end, an X-ray source was produced by irradiating a
![]() $25~\unicode[STIX]{x03BC}\text{m}$
diameter vanadium wire with the Pico2000 laser pulse (80 J,
$25~\unicode[STIX]{x03BC}\text{m}$
diameter vanadium wire with the Pico2000 laser pulse (80 J,
![]() ${\sim}$
10 ps, defocused to
${\sim}$
10 ps, defocused to
![]() ${\sim}$
a
${\sim}$
a
![]() $50~\unicode[STIX]{x03BC}\text{m}$
diameter focal spot). The backlighter source (wire) was located 3 cm below the main target (see Figure 1(b)), the radiograph image being recorded on an imaging plate (IP) positioned
$50~\unicode[STIX]{x03BC}\text{m}$
diameter focal spot). The backlighter source (wire) was located 3 cm below the main target (see Figure 1(b)), the radiograph image being recorded on an imaging plate (IP) positioned
![]() ${\sim}$
60 cm above the target-chamber center, leading to a 20x magnification (see Figure 1(c)). The spatial resolution was checked using a gold grid of 400 lines per inch. The measured value of
${\sim}$
60 cm above the target-chamber center, leading to a 20x magnification (see Figure 1(c)). The spatial resolution was checked using a gold grid of 400 lines per inch. The measured value of
![]() $25~\unicode[STIX]{x03BC}\text{m}$
is similar to the diameter of the V wire, as expected[Reference Brambrink, Baton, Koenig, Yurchak, Bidaut, Albertazzi, Cross, Gregori, Rigby, Falize, Pelka, Kroll, Pikuz, Sakawa, Ozaki, Kuranz, Manuel, Li, Tzeferacos and Lamb25]. The V wire produces a K
$25~\unicode[STIX]{x03BC}\text{m}$
is similar to the diameter of the V wire, as expected[Reference Brambrink, Baton, Koenig, Yurchak, Bidaut, Albertazzi, Cross, Gregori, Rigby, Falize, Pelka, Kroll, Pikuz, Sakawa, Ozaki, Kuranz, Manuel, Li, Tzeferacos and Lamb25]. The V wire produces a K
![]() $_{\unicode[STIX]{x1D6FC}}$
emission line at an energy of 4.95 keV. However, energetic electrons produced by the short pulse laser emit hard X-ray through bremsstrahlung process (see Section 3.2 for more details). Various optical diagnostics were implemented perpendicular to the main laser beam. A probe laser beam (few mJ, 7 ns at
$_{\unicode[STIX]{x1D6FC}}$
emission line at an energy of 4.95 keV. However, energetic electrons produced by the short pulse laser emit hard X-ray through bremsstrahlung process (see Section 3.2 for more details). Various optical diagnostics were implemented perpendicular to the main laser beam. A probe laser beam (few mJ, 7 ns at
![]() $\unicode[STIX]{x1D706}=532~\text{nm}$
) provided some of the fundamental variables of the plasma flow: (i) a simple shadowgraphy recorded the global shape of the plasma, and (ii) a modified Nomarski interferometer enabled inference of the electron density of the flow in the range
$\unicode[STIX]{x1D706}=532~\text{nm}$
) provided some of the fundamental variables of the plasma flow: (i) a simple shadowgraphy recorded the global shape of the plasma, and (ii) a modified Nomarski interferometer enabled inference of the electron density of the flow in the range
![]() ${\sim}5\times 10^{17}{-}1\times 10^{20}~\text{cm}^{-3}$
. Both diagnostics were coupled to gated optical imagers (GOIs) with a 200 ps time frame. We also implemented optical pyrometry (either streaked or gated with GOI) to record the self-emission of the flow at a central wavelength of 450 nm having a 40 nm bandwidth. The streaked self-emission gave us the flow expansion velocity on each shot while the gated self-emission provided (2D) images of the plasma emission of the plasma at a given time. These numerous diagnostics are of prime importance both to determine the dimensionless parameters of the generated plasma (the magnetic Reynolds number, the
${\sim}5\times 10^{17}{-}1\times 10^{20}~\text{cm}^{-3}$
. Both diagnostics were coupled to gated optical imagers (GOIs) with a 200 ps time frame. We also implemented optical pyrometry (either streaked or gated with GOI) to record the self-emission of the flow at a central wavelength of 450 nm having a 40 nm bandwidth. The streaked self-emission gave us the flow expansion velocity on each shot while the gated self-emission provided (2D) images of the plasma emission of the plasma at a given time. These numerous diagnostics are of prime importance both to determine the dimensionless parameters of the generated plasma (the magnetic Reynolds number, the
![]() $\unicode[STIX]{x1D6FD}$
parameter, …) and as a constraint for the 2D MHD simulations.
$\unicode[STIX]{x1D6FD}$
parameter, …) and as a constraint for the 2D MHD simulations.
In our experiment, the plasma flow is immersed in an external magnetic field of 10 T generated by a specially designed coil. The coil is coupled to a pulsed power generator[Reference Albertazzi, Béard, Ciardi, Vinci, Albrecht, Billette, Burris-Mog, Chen, Da Silva, Dittrich, Herrmannsdörfer, Hirardin, Kroll, Nakatsutsumi, Nitsche, Riconda, Romagnagni, Schlenvoigt, Simond, Veuillot, Cowan, Portugall, Pépin and Fuchs21]. The capacitor-based pulse generator is charged up to a voltage of 9.3 kV and provides a peak current of 31.75 kA to the coil. The magnetic field inside the coil reaches its maximum after
![]() ${\sim}90~\unicode[STIX]{x03BC}\text{s}$
and stays constant (less than 2% variation) for a few
${\sim}90~\unicode[STIX]{x03BC}\text{s}$
and stays constant (less than 2% variation) for a few
![]() $\unicode[STIX]{x03BC}\text{s}$
, i.e., a duration much greater than the typical hydrodynamical time scale of the experiment. The magnetic-field maximum was synchronized to optical lasers. The coil, designed and fabricated by HZDR, is composed of two solenoids in a Helmholtz-like configuration. The coil windings remain in air to avoid technical problems such as electric flashovers. The magnet features three bores of
$\unicode[STIX]{x03BC}\text{s}$
, i.e., a duration much greater than the typical hydrodynamical time scale of the experiment. The magnetic-field maximum was synchronized to optical lasers. The coil, designed and fabricated by HZDR, is composed of two solenoids in a Helmholtz-like configuration. The coil windings remain in air to avoid technical problems such as electric flashovers. The magnet features three bores of
![]() ${\sim}$
1 cm diameter: one for the high-power laser beam and two for diagnostic purposes (optical and X-ray). All bores intersect in the middle of the split-pair coil where the plasma flow is generated.
${\sim}$
1 cm diameter: one for the high-power laser beam and two for diagnostic purposes (optical and X-ray). All bores intersect in the middle of the split-pair coil where the plasma flow is generated.
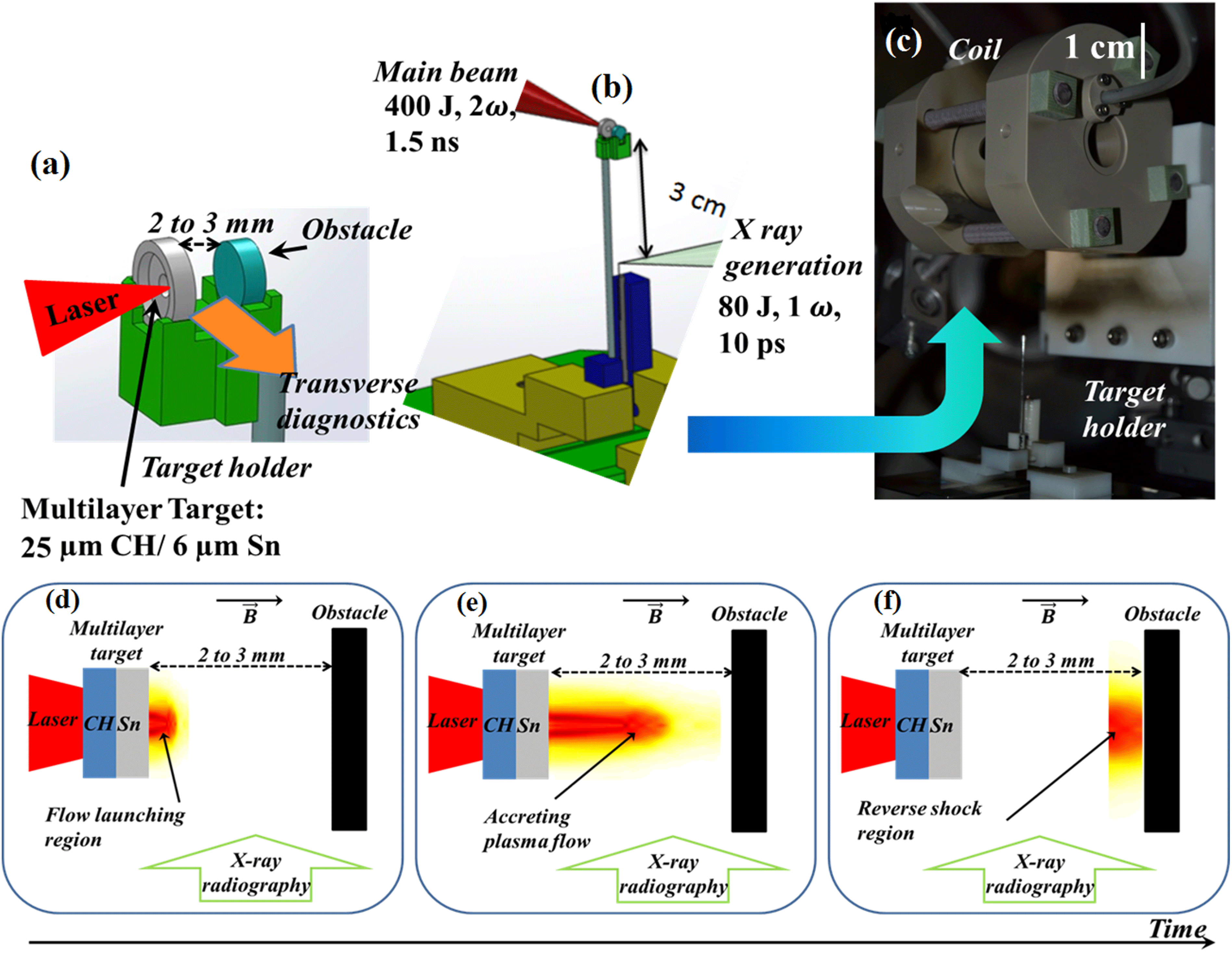
Figure 1. Experimental setup at LULI2000. (a) Main target and obstacle assembly. (b) Target holder showing the main target and a
![]() $25~\unicode[STIX]{x03BC}\text{m}$
V wire which is positioned 3 cm below to create the X-ray source. (c) The target holder is then inserted inside the coil from the bottom. Schematic illustration of the different terminology used in the paper. (d) After the shock breakout, a plasma flow is launched from the main target rear side. When the plasma propagates between both targets, we refer to (e) the accreting plasma flow and finally (f) the reverse-shock region.
$25~\unicode[STIX]{x03BC}\text{m}$
V wire which is positioned 3 cm below to create the X-ray source. (c) The target holder is then inserted inside the coil from the bottom. Schematic illustration of the different terminology used in the paper. (d) After the shock breakout, a plasma flow is launched from the main target rear side. When the plasma propagates between both targets, we refer to (e) the accreting plasma flow and finally (f) the reverse-shock region.
3 Experimental results
This section presents the fundamental experimental parameters inferred from the measurements made by our set of diagnostics described above.
3.1 Plasma and reverse-shock velocity
The optical emission of the plasma at a wavelength of 450 nm, with 40 nm bandwidth, has been recorded and used to determine the experimental rear side plasma flow velocities. As can be seen in Figure 2, it is possible to deduce three relevant velocities: (i) an initial, high flow velocity
![]() $v_{\text{init}}$
for the first
$v_{\text{init}}$
for the first
![]() $400~\unicode[STIX]{x03BC}\text{m}$
from the rear side of the main target, called the flow-launching region in Figure 1(d), (ii) the mean velocity before impact
$400~\unicode[STIX]{x03BC}\text{m}$
from the rear side of the main target, called the flow-launching region in Figure 1(d), (ii) the mean velocity before impact
![]() $\langle v\rangle$
of the outflow on the obstacle, i.e., the accreting plasma flow velocity (see Figure 1(e)), and (iii) the reverse-shock velocity
$\langle v\rangle$
of the outflow on the obstacle, i.e., the accreting plasma flow velocity (see Figure 1(e)), and (iii) the reverse-shock velocity
![]() $v_{\text{rev}}$
. Indeed, the collision of the plasma flow onto the obstacle compresses and heats the material giving rise to a bright visible emission associated to the reverse shock. The measured velocities are similar in both cases (with and without the B-field): initial velocity of the outflow
$v_{\text{rev}}$
. Indeed, the collision of the plasma flow onto the obstacle compresses and heats the material giving rise to a bright visible emission associated to the reverse shock. The measured velocities are similar in both cases (with and without the B-field): initial velocity of the outflow
![]() $v_{\text{init}}\sim 83\pm 5~\text{km}/\text{s}$
, the mean velocity before impact being of the order of
$v_{\text{init}}\sim 83\pm 5~\text{km}/\text{s}$
, the mean velocity before impact being of the order of
![]() $\langle v\rangle \sim 46{-}60\pm 5~\text{km}/\text{s}$
depending on the shot and the reverse-shock velocity
$\langle v\rangle \sim 46{-}60\pm 5~\text{km}/\text{s}$
depending on the shot and the reverse-shock velocity
![]() $v_{\text{rev}}\sim 15{-}20\pm 5~\text{km}/\text{s}$
. These data are used to constrain our 2D radiative MHD simulations.
$v_{\text{rev}}\sim 15{-}20\pm 5~\text{km}/\text{s}$
. These data are used to constrain our 2D radiative MHD simulations.
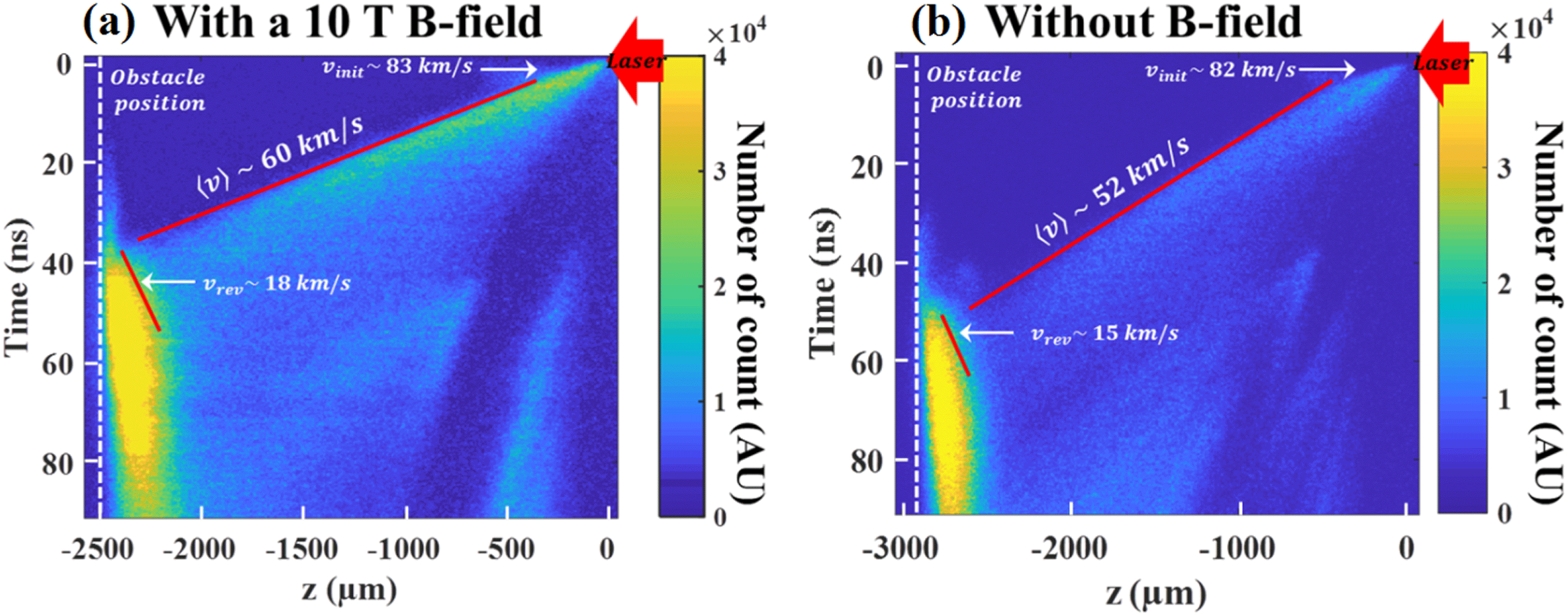
Figure 2. Streaked optical emission of the plasma at a wavelength of 450 nm obtained during the experiment giving the different velocities of the plasma flow, (a) with a 10 T B-field using 406 J laser energy and (b) without B-field using 402 J laser energy.
Figure 3 summarizes the three different velocities determined from the experimental data as a function of the distance between the main target and the obstacle and as a function of the laser energy.

Figure 3. Experimental results of the flow-launching velocity, accreting plasma flow velocity and reverse-shock velocity as a function of (a) the distance between the main target and the obstacle (the laser energy for each shot is displayed) and (b) the laser energy. The different velocities (
![]() $v_{\text{init}}$
,
$v_{\text{init}}$
,
![]() $\langle v\rangle$
,
$\langle v\rangle$
,
![]() $v_{\text{rev}}$
) are defined in Figure 2.
$v_{\text{rev}}$
) are defined in Figure 2.
As can be seen in Figure 3, there is no significant difference between the case with or without a 10 T external B-field.
There is an important caveat associated with this analysis. What is actually seen by the self-emission diagnostic is the movement of the plasma that is emitting brightly at
![]() ${\sim}$
450 nm at a high enough density. Plasma that has cooled or rarefied too much would not be seen. This is unlikely to be an issue for the reverse shock, but might affect the measurements of the flow toward the obstacle. Indeed, one would expect the freely flowing plasma to include faster components at lower density, for reasons discussed in Ref. [Reference Zeldovich and Raizer26]. The existence of such components is one possible explanation for the earliest emission (seen between
${\sim}$
450 nm at a high enough density. Plasma that has cooled or rarefied too much would not be seen. This is unlikely to be an issue for the reverse shock, but might affect the measurements of the flow toward the obstacle. Indeed, one would expect the freely flowing plasma to include faster components at lower density, for reasons discussed in Ref. [Reference Zeldovich and Raizer26]. The existence of such components is one possible explanation for the earliest emission (seen between
![]() ${\sim}$
20 to
${\sim}$
20 to
![]() ${\sim}$
40 ns and
${\sim}$
40 ns and
![]() $z\sim 2400{-}2500~\unicode[STIX]{x03BC}\text{m}$
in Figure 2(a) and
$z\sim 2400{-}2500~\unicode[STIX]{x03BC}\text{m}$
in Figure 2(a) and
![]() ${\sim}$
30 to 50 ns and
${\sim}$
30 to 50 ns and
![]() $z\sim 2900~\unicode[STIX]{x03BC}\text{m}$
in Figure 2(b)) near the obstacle, which is dimmer than the main emission produced by the reverse shock. This emission could be as well related to the pre heating of the obstacle although the Sn layer should stop most of the X-rays which heat the obstacle.
$z\sim 2900~\unicode[STIX]{x03BC}\text{m}$
in Figure 2(b)) near the obstacle, which is dimmer than the main emission produced by the reverse shock. This emission could be as well related to the pre heating of the obstacle although the Sn layer should stop most of the X-rays which heat the obstacle.
3.2 X-ray radiography of the plasma
The X-ray source is produced by irradiating a 25-
![]() $\unicode[STIX]{x03BC}\text{m}$
-diameter, vanadium (V) wire using the Pico2000 laser (80 J,
$\unicode[STIX]{x03BC}\text{m}$
-diameter, vanadium (V) wire using the Pico2000 laser (80 J,
![]() ${\sim}$
10 ps, defocused to
${\sim}$
10 ps, defocused to
![]() ${\sim}$
50-
${\sim}$
50-
![]() $\unicode[STIX]{x03BC}\text{m}$
-diameter focal spot). The objective is to obtain a quasi-monochromatic X-ray spectrum with the main contribution coming from the K
$\unicode[STIX]{x03BC}\text{m}$
-diameter focal spot). The objective is to obtain a quasi-monochromatic X-ray spectrum with the main contribution coming from the K
![]() $\unicode[STIX]{x1D6FC}$
at 4.952 keV. The IP detector, situated at
$\unicode[STIX]{x1D6FC}$
at 4.952 keV. The IP detector, situated at
![]() ${\sim}$
60 cm above the target, is covered with a 11.4-
${\sim}$
60 cm above the target, is covered with a 11.4-
![]() $\unicode[STIX]{x03BC}\text{m}$
- thick Ti layer that cuts off X-ray photons in the range 0 to
$\unicode[STIX]{x03BC}\text{m}$
- thick Ti layer that cuts off X-ray photons in the range 0 to
![]() ${\sim}$
2 keV and 5 keV to
${\sim}$
2 keV and 5 keV to
![]() ${\sim}$
8–9 keV. In order to evaluate the X-ray spectrum incident on the IP, additional step filters (Al and Sn) with different thicknesses have been added. The experimental results show, in analyzing transmission through the step filters, that the spectrum is not monochromatic and that a nonnegligible part of the photons have energy above 10 keV due to the emission of continuous radiation via bremsstrahlung process.
${\sim}$
8–9 keV. In order to evaluate the X-ray spectrum incident on the IP, additional step filters (Al and Sn) with different thicknesses have been added. The experimental results show, in analyzing transmission through the step filters, that the spectrum is not monochromatic and that a nonnegligible part of the photons have energy above 10 keV due to the emission of continuous radiation via bremsstrahlung process.
Figure 4 displays typical experimental results obtained during the experimental campaign with and without magnetic field. The time
![]() $t=0$
is defined at the beginning of the laser–matter interaction. The temporal dynamics is obtained by delaying the Pico2000 beam with respect to the main drive laser beam. As one can see, two characteristic shapes are observed. The plasma flow has a bubble-like structure close to the rear side of the main target (see Figures 4(c) and 4(d)) which is not the case in Figures 4(a) and 4(b). As the bubble-like structure is produced in both cases with and without B-field, its generation is not related to the presence of the B-field. This topology could be connected to the shape of the target holder, which gives rise to the emergence of the bubble-like structure. It will be investigated in more details in Section 4.4.
$t=0$
is defined at the beginning of the laser–matter interaction. The temporal dynamics is obtained by delaying the Pico2000 beam with respect to the main drive laser beam. As one can see, two characteristic shapes are observed. The plasma flow has a bubble-like structure close to the rear side of the main target (see Figures 4(c) and 4(d)) which is not the case in Figures 4(a) and 4(b). As the bubble-like structure is produced in both cases with and without B-field, its generation is not related to the presence of the B-field. This topology could be connected to the shape of the target holder, which gives rise to the emergence of the bubble-like structure. It will be investigated in more details in Section 4.4.

Figure 4. Experimental results of X-ray radiography in the case without external B-field at (a) 60 ns and (d) 75 ns and with B-field at (b) 60 ns and (c) 75 ns. The laser irradiates the target from the bottom of the image. The plasma expansion from the rear surface of the target is visible. The thin, darkened feature seen near the edges of the plasma, especially in the bottom two images, suggests the presence of a denser shell of material seen by limb-darkening. The dark band at the bottom of the image (located between
![]() $z=0$
and
$z=0$
and
![]() $z\sim 0.5{-}0.8~\text{mm}$
) is an additional Al filter to prevent unexpected X-ray emission from the front of the target. The lighter box above corresponds to the area where no additional filters are present.
$z\sim 0.5{-}0.8~\text{mm}$
) is an additional Al filter to prevent unexpected X-ray emission from the front of the target. The lighter box above corresponds to the area where no additional filters are present.
3.3 Effect of the external magnetic field onto the collimation of the plasma flow
This section is devoted to the analysis of the radial extension of the plasma flow with or without the 10 T external magnetic field. One can see in Figure 4, the plasma has a definite outer radial boundary over some distance. We measured the location of the edges of the plasma by finding the midpoint of the change in intensity of the radiograph near this boundary (located approximately at
![]() $z\sim \pm 0.5{-}0.8~\text{mm}$
in Figure 4), and inferred the plasma diameter from these measurements. The uncertainties using this method give
$z\sim \pm 0.5{-}0.8~\text{mm}$
in Figure 4), and inferred the plasma diameter from these measurements. The uncertainties using this method give
![]() $\pm 50~\unicode[STIX]{x03BC}\text{m}$
. Figure 5(a) shows the evolution of the diameter of the plasma against the distance from the rear surface of the target, either with or without magnetic field. As one can see, there is little difference between the two cases at distances below
$\pm 50~\unicode[STIX]{x03BC}\text{m}$
. Figure 5(a) shows the evolution of the diameter of the plasma against the distance from the rear surface of the target, either with or without magnetic field. As one can see, there is little difference between the two cases at distances below
![]() ${\sim}$
1.5 mm from the main target. This is a strong indication that the dynamic of the plasma flow (at
${\sim}$
1.5 mm from the main target. This is a strong indication that the dynamic of the plasma flow (at
![]() $t\sim 75~\text{ns}$
) is not affected below 1.5 mm by the magnetic field, the magnetic pressure being too small compared to the plasma pressure. However, in the case without magnetic field, the diameter of the plasma continues to increase, as the plasma propagates further from the rear surface of the target. In the case with the magnetic field, we observe a clear difference: at
$t\sim 75~\text{ns}$
) is not affected below 1.5 mm by the magnetic field, the magnetic pressure being too small compared to the plasma pressure. However, in the case without magnetic field, the diameter of the plasma continues to increase, as the plasma propagates further from the rear surface of the target. In the case with the magnetic field, we observe a clear difference: at
![]() ${\sim}$
1.6 mm, the radial expansion of the plasma stops, the plasma being focused. Our interpretation, discussed below, is that the gradient in magnetic pressure has become large enough to overcome the gradient in thermal pressure and focus the plasma.
${\sim}$
1.6 mm, the radial expansion of the plasma stops, the plasma being focused. Our interpretation, discussed below, is that the gradient in magnetic pressure has become large enough to overcome the gradient in thermal pressure and focus the plasma.
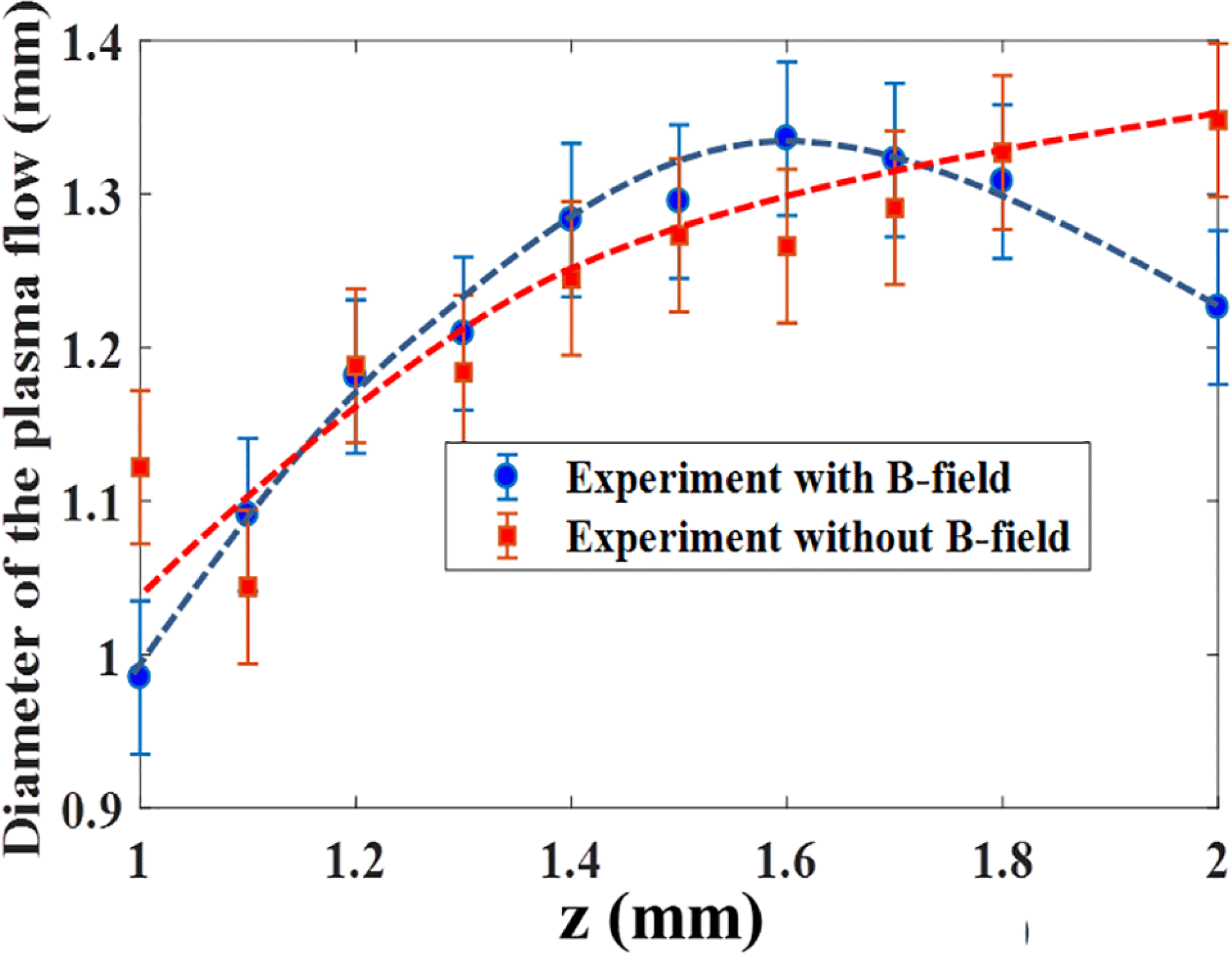
Figure 5. Diameter of the plasma flow as a function of the distance from the rear surface of the target in the case with and without magnetic field at 75 ns after the beginning of the interaction. Uncertainties are of the order of
![]() $\pm 50~\unicode[STIX]{x03BC}\text{m}$
and come mainly from the determination of the edge of the plasma flow. The data stop at 2 mm from the main target due to the low plasma density and the resulting low contrast (see Figure 4).
$\pm 50~\unicode[STIX]{x03BC}\text{m}$
and come mainly from the determination of the edge of the plasma flow. The data stop at 2 mm from the main target due to the low plasma density and the resulting low contrast (see Figure 4).
4 Radiative MHD simulation of the experiment
This section presents the comparison between the experimental results and the simulation using the FLASH code[27], developed at the University of Chicago. FLASH is a two-dimensional (2D) or 3D MHD code, with adaptive mesh refinement. A nonideal MHD solver with an unsplit, staggered mesh is used together with physical modules that allow modeling high energy density laser experiments. These include a laser energy deposition module, SESAME equation of state and the radiation transfer solved in the multi-group diffusion approximation using 40 radiation groups. The simulation domain is initialized with a homogeneous and constant magnetic field of 10 T oriented in the direction of propagation of the flow. The effective resolution of the simulation is
![]() $5.08~\unicode[STIX]{x03BC}\text{m}$
enabling resolution of the Sn layer of the target. In order to save computational resources, the simulation is 2D axis-symmetric. The laser intensity distribution on target has been initialized with a super Gaussian function of a
$5.08~\unicode[STIX]{x03BC}\text{m}$
enabling resolution of the Sn layer of the target. In order to save computational resources, the simulation is 2D axis-symmetric. The laser intensity distribution on target has been initialized with a super Gaussian function of a
![]() $200~\unicode[STIX]{x03BC}\text{m}$
radius to simulate the experiment. The time profile of the laser has a rising time of 200 ps followed by a plateau of 1.3 ns at
$200~\unicode[STIX]{x03BC}\text{m}$
radius to simulate the experiment. The time profile of the laser has a rising time of 200 ps followed by a plateau of 1.3 ns at
![]() $I=1.6\times 10^{14}~\text{W}\cdot \text{cm}^{-2}$
, and a decrease of 100 ps. The laser intensity in the simulation has been reduced to reproduce the mean flow velocity (
$I=1.6\times 10^{14}~\text{W}\cdot \text{cm}^{-2}$
, and a decrease of 100 ps. The laser intensity in the simulation has been reduced to reproduce the mean flow velocity (
![]() $\langle v\rangle$
see Figure 3) measured in the experiment by optical diagnostics. Finally, the target holder is modeled as a 5 mm thick plate using aluminum EOS and opacities. The initial conditions of the simulation are displayed in Figure 6. The target is composed of two layers: a
$\langle v\rangle$
see Figure 3) measured in the experiment by optical diagnostics. Finally, the target holder is modeled as a 5 mm thick plate using aluminum EOS and opacities. The initial conditions of the simulation are displayed in Figure 6. The target is composed of two layers: a
![]() $25~\unicode[STIX]{x03BC}\text{m}$
thick CH and a
$25~\unicode[STIX]{x03BC}\text{m}$
thick CH and a
![]() $6~\unicode[STIX]{x03BC}\text{m}$
thick Sn. The washer has a 1 mm hole diameter.
$6~\unicode[STIX]{x03BC}\text{m}$
thick Sn. The washer has a 1 mm hole diameter.
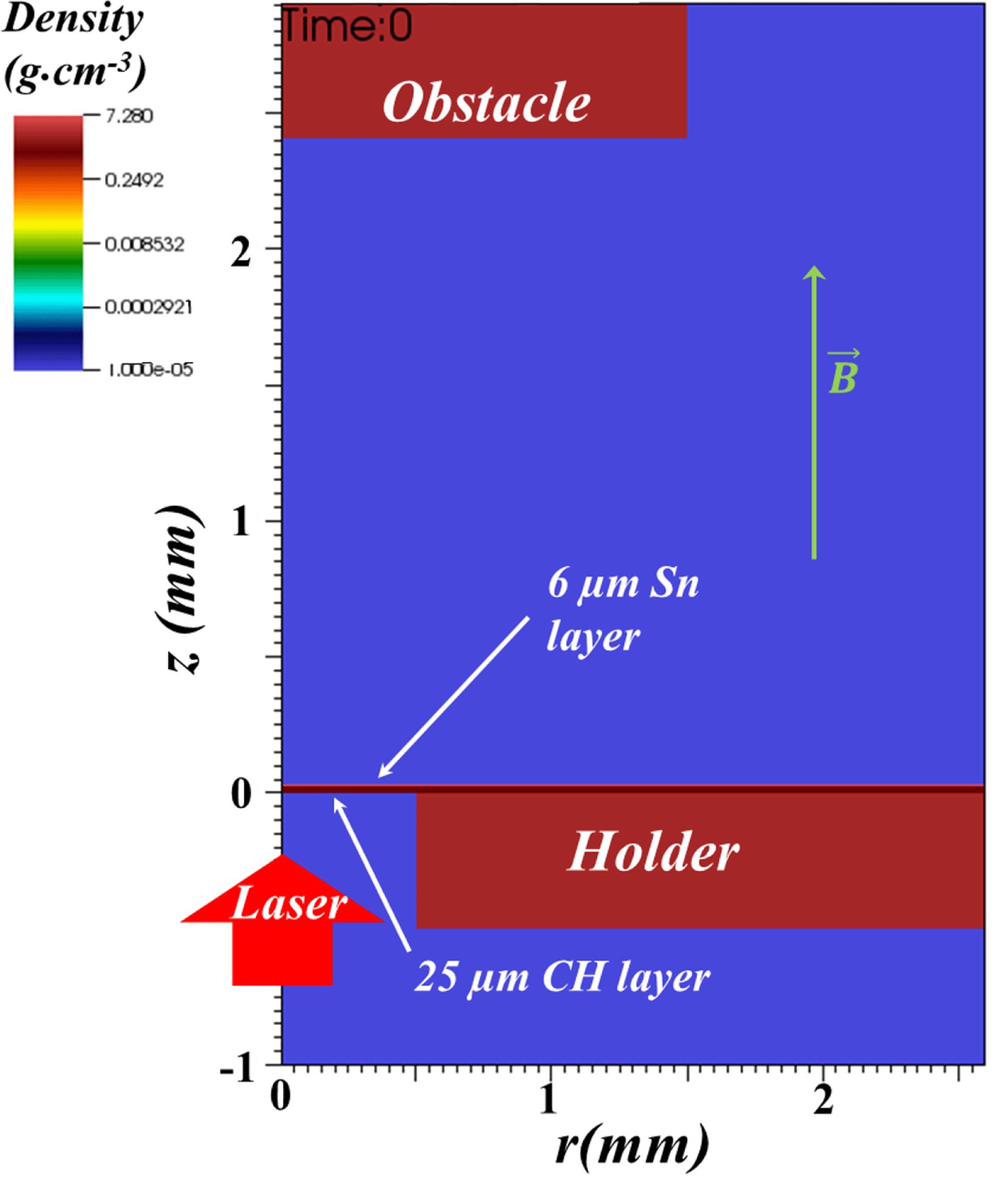
Figure 6. General setup of the 2D axis-symmetric radiative MHD FLASH simulation using a 1 mm hole diameter and a 10 T B-field.
In this section, we compare experimental results with radiative MHD simulation in order to quantify the importance of (i) magnetic field and (ii) radiation for the reverse-shock dynamics. As indicated previously, the experimental distance between the target and the obstacle varies between 2.4 and 3.1 mm. We have here, chosen for the FLASH simulation, a short distance, i.e., 2.4 mm.
4.1 Effects of the B-field
The magnetic field controls part of the system dynamics. In order to tackle its effect, we compared two simulations using a short target–obstacle distance (
![]() $l=2.4~\text{mm}$
) with and without B-field. The short distance results in a higher mass flux (
$l=2.4~\text{mm}$
) with and without B-field. The short distance results in a higher mass flux (
![]() $\text{d}m/\text{d}t$
) toward the obstacle and thus leading to a denser and more visible reverse shock. However, the B-field has a smaller effect on the dynamics when the target–obstacle distance is small, as the ram pressure (
$\text{d}m/\text{d}t$
) toward the obstacle and thus leading to a denser and more visible reverse shock. However, the B-field has a smaller effect on the dynamics when the target–obstacle distance is small, as the ram pressure (
![]() $\unicode[STIX]{x1D70C}v^{2}$
) is higher in the case of a short target–obstacle distance for a constant magnetic pressure
$\unicode[STIX]{x1D70C}v^{2}$
) is higher in the case of a short target–obstacle distance for a constant magnetic pressure
![]() $B^{2}/(2\unicode[STIX]{x1D707}_{0})$
, i.e., the
$B^{2}/(2\unicode[STIX]{x1D707}_{0})$
, i.e., the
![]() $\unicode[STIX]{x1D6FD}_{\text{ram}}$
is higher than in the case of a longer target–obstacle distance (see Figure 5).
$\unicode[STIX]{x1D6FD}_{\text{ram}}$
is higher than in the case of a longer target–obstacle distance (see Figure 5).
In Figure 7(a), the mass density is displayed 75 ns after the beginning of the interaction for both cases with and without B-field. The magnetic field has a strong effect on the collimation of the flow building a surrounding envelope due to the accumulation of plasma. In this region,
![]() $\unicode[STIX]{x1D6FD}_{\text{ram}}\sim 1$
and
$\unicode[STIX]{x1D6FD}_{\text{ram}}\sim 1$
and
![]() $R_{m}\geqslant 1$
(see Figure 7(b)), respectively the beta parameter and the magnetic Reynolds number, which indicate that the magnetic-field lines are frozen in the plasma. They are bent, and add an additional component to the Lorentz forces, allowing the collimation of the plasma flow. As a consequence, the radial extension of the reverse shock is constrained while it is not the case without B-field.
$R_{m}\geqslant 1$
(see Figure 7(b)), respectively the beta parameter and the magnetic Reynolds number, which indicate that the magnetic-field lines are frozen in the plasma. They are bent, and add an additional component to the Lorentz forces, allowing the collimation of the plasma flow. As a consequence, the radial extension of the reverse shock is constrained while it is not the case without B-field.
In conclusion, at late time after the beginning of the interaction (i.e., few tens of nanosecond), the magnetic field has an important effect, even at 10 T B-field, to constrain the radial expansion both of the accreting plasma flow and the reverse shock as can be seen in Figure 7.
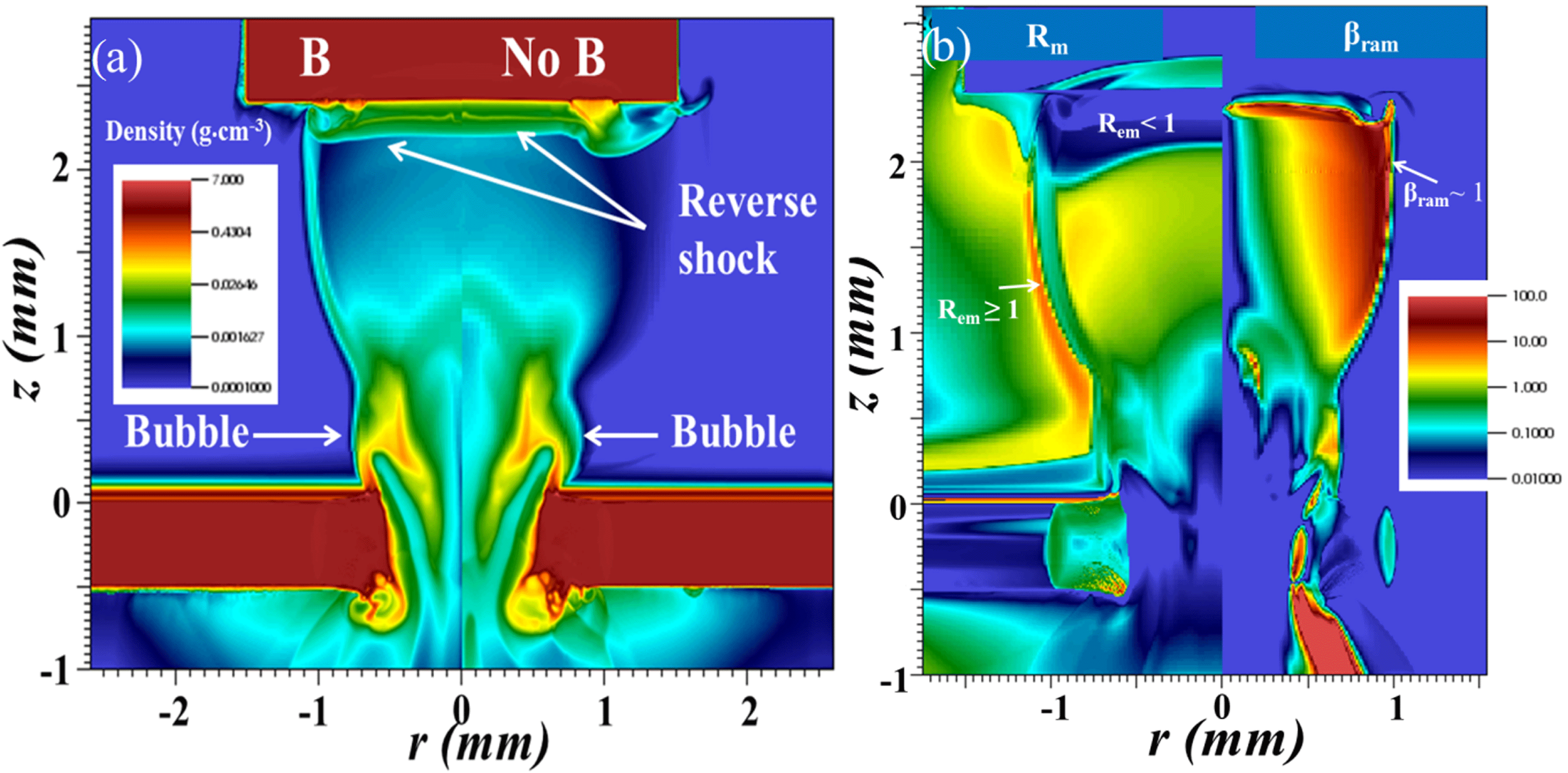
Figure 7. (a) 2D MHD radiative simulation of the experiment performed with and without a 10 T B-field at 75 ns after the beginning of the interaction showing the mass density. Radiation module is on. The left panel corresponds to the case with the B-field and the right panel without. (b) Numerical results of the simulation showing the dimensionless number
![]() $\unicode[STIX]{x1D6FD}_{\text{ram}}$
and
$\unicode[STIX]{x1D6FD}_{\text{ram}}$
and
![]() $R_{m}$
for the simulation of (a) left (using the 10 T B-field, radiation module on and at 75 ns after the beginning of the interaction).
$R_{m}$
for the simulation of (a) left (using the 10 T B-field, radiation module on and at 75 ns after the beginning of the interaction).
![]() $R_{m}$
is evaluated using the conduction model of Lee and More[Reference Lee and More30].
$R_{m}$
is evaluated using the conduction model of Lee and More[Reference Lee and More30].
4.2 Effects of radiation
Radiation can as well have a strong influence in the dynamics of the accreting plasma flow and of the reverse shock. In order to assess its effect, we performed two 2D MHD simulations with a 10 T B-field: the first one uses the radiation module, the radiation transfer being solved in the multi-group diffusion approximation using 40 radiation groups and the second without the radiation module (see Figure 8). No strong differences are observed in the cold accreting plasma flow (
![]() $T_{e}\sim 1{-}3~\text{eV}$
) underlining its nonradiative nature. The obstacle is slightly heated up to 0.1–0.3 eV. A small expansion is also observed. However, it is difficult to be quantitative on this particular point as the FLASH code is an Eulerian code. Further numerical and experimental investigations are needed. However, strong differences appear in the reverse-shock region. With radiation on, the temperature, so the ionization state, shows a heating of the matter ahead of the shock front up to
$T_{e}\sim 1{-}3~\text{eV}$
) underlining its nonradiative nature. The obstacle is slightly heated up to 0.1–0.3 eV. A small expansion is also observed. However, it is difficult to be quantitative on this particular point as the FLASH code is an Eulerian code. Further numerical and experimental investigations are needed. However, strong differences appear in the reverse-shock region. With radiation on, the temperature, so the ionization state, shows a heating of the matter ahead of the shock front up to
![]() ${\sim}400~\unicode[STIX]{x03BC}\text{m}$
from the target rear surface (see Figures 8(a) and 8(c)). This resembles a radiative precursor as produced in radiative shocks[Reference Bouquet, Stéhlé, Koenig, Chièze, Benuzzi-Mounaix, Batani, Leygnac, Fleury, Merdji, Michaut, Thais, Grandjouan, Hall, Henry, Malka and Lafon28, Reference Michaut, Falize, Cavet, Bouquet, Koenig, Vinci, Reighard and Drake29] although the structure of the shock here seems to be different by nature, as it can be seen in Figure 8(b).
${\sim}400~\unicode[STIX]{x03BC}\text{m}$
from the target rear surface (see Figures 8(a) and 8(c)). This resembles a radiative precursor as produced in radiative shocks[Reference Bouquet, Stéhlé, Koenig, Chièze, Benuzzi-Mounaix, Batani, Leygnac, Fleury, Merdji, Michaut, Thais, Grandjouan, Hall, Henry, Malka and Lafon28, Reference Michaut, Falize, Cavet, Bouquet, Koenig, Vinci, Reighard and Drake29] although the structure of the shock here seems to be different by nature, as it can be seen in Figure 8(b).
The differences observed here, in the longitudinal expansion of the reverse shock, especially in temperature and ionization state could be studied experimentally by our SOP diagnostic.
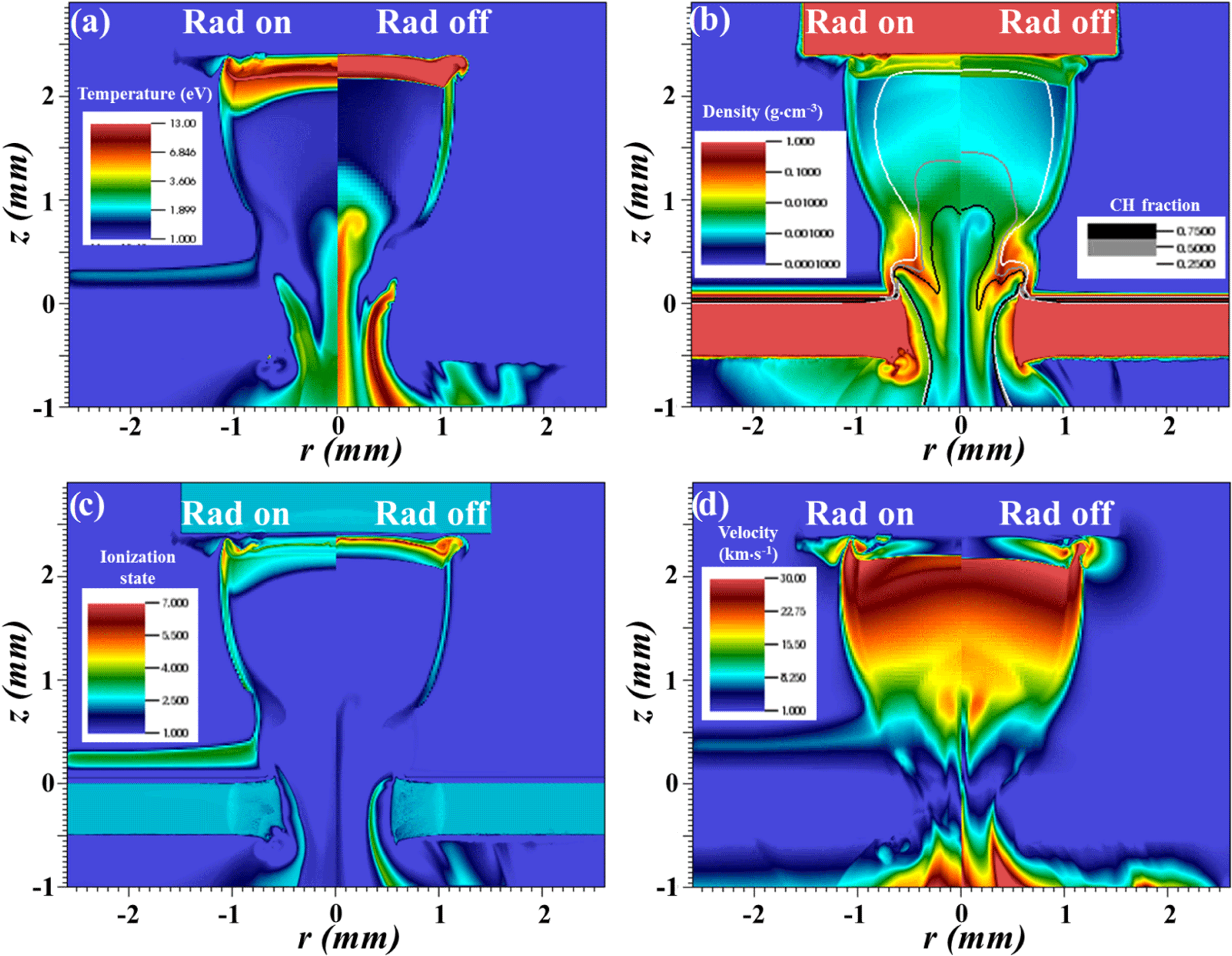
Figure 8. 2D MHD radiative simulation of the experiment performed with and without radiation at 75 ns after the beginning of the interaction. A 10 T B-field is present. (a) Temperature in eV, (b) density in
![]() $\text{g}\cdot \text{cm}^{-3}$
with isocontours of CH fraction compared with Al and Sn, (c) ionization state and (d) modulus of velocity in
$\text{g}\cdot \text{cm}^{-3}$
with isocontours of CH fraction compared with Al and Sn, (c) ionization state and (d) modulus of velocity in
![]() $\text{km}\cdot \text{s}^{-1}$
.
$\text{km}\cdot \text{s}^{-1}$
.
4.3 Direct comparison between experimental data and simulations
This section is devoted to comparing experimental data with the results of the 2D MHD simulation to interpret in details, the fundamental processes involved in the accretion processes and reverse-shock generation.
An X-ray radiography postprocessing of the 2D FLASH simulation has been developed to allow a direct comparison with the experimental data (see Figures 9(c) and 9(d)). The Henke (cold) opacities have been used to obtain the specific opacity for each element
![]() $\unicode[STIX]{x1D705}$
(
$\unicode[STIX]{x1D705}$
(
![]() $\text{cm}^{2}/\text{g}$
) and the absorption at each wavelength is
$\text{cm}^{2}/\text{g}$
) and the absorption at each wavelength is
![]() $I=I_{0}\exp (-\int \unicode[STIX]{x1D705}\unicode[STIX]{x1D70C}dl)$
where
$I=I_{0}\exp (-\int \unicode[STIX]{x1D705}\unicode[STIX]{x1D70C}dl)$
where
![]() $\unicode[STIX]{x1D705}$
is assumed to be constant with temperature and density. This approximation is valid in our plasma conditions.
$\unicode[STIX]{x1D705}$
is assumed to be constant with temperature and density. This approximation is valid in our plasma conditions.
According to Figures 9(a) and 9(b), a clear difference is observed that can be partly due to a nonmonochromatic X-ray source. Indeed, in ultra-high intensity laser driven sources, a large contribution from hard X-rays (
![]() ${>}$
10 keV) exists that has not been used in the postprocessing process. In order to overcome this issue, we postprocessed the simulation using two different X-ray energies: 4.952 keV and 11.92 keV.
${>}$
10 keV) exists that has not been used in the postprocessing process. In order to overcome this issue, we postprocessed the simulation using two different X-ray energies: 4.952 keV and 11.92 keV.
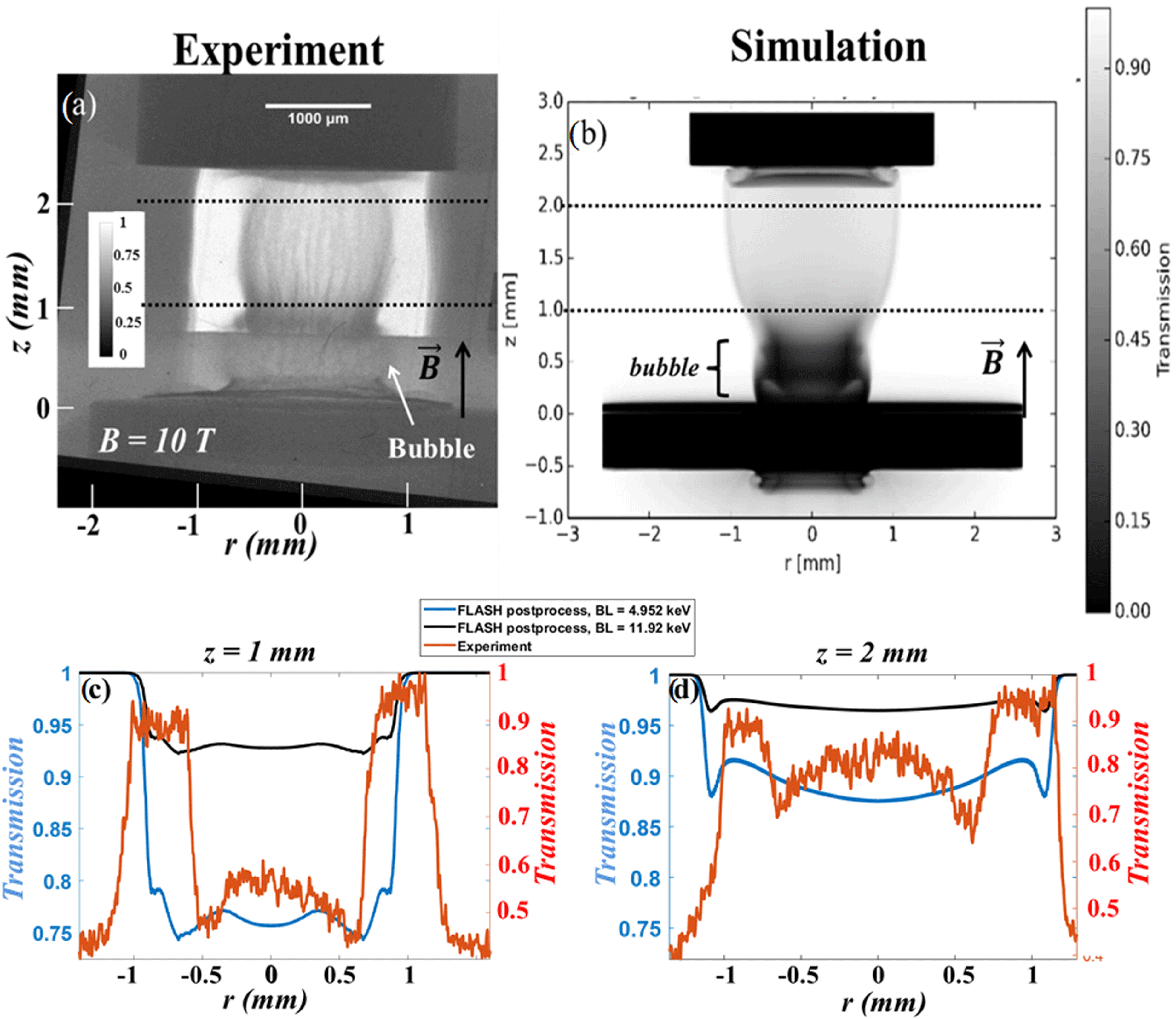
Figure 9. Radiographs obtained at 75 ns from (a) experimental results renormalized between 0 and 1, and (b) FLASH MHD radiative simulation, postprocessed using a 4.952 keV monochromatic X-ray source (corresponding to the vanadium K
![]() $\unicode[STIX]{x1D6FC}$
emission of the backlighter in the experiment). Horizontal lineouts of radiograph transmission at different positions (c)
$\unicode[STIX]{x1D6FC}$
emission of the backlighter in the experiment). Horizontal lineouts of radiograph transmission at different positions (c)
![]() $z=1~\text{mm}$
and (d)
$z=1~\text{mm}$
and (d)
![]() $z=2~\text{mm}$
(dashed lines in (a) and (b)) and direct comparison between two different X-ray source energies: 4.952 keV (reproducing the K
$z=2~\text{mm}$
(dashed lines in (a) and (b)) and direct comparison between two different X-ray source energies: 4.952 keV (reproducing the K
![]() $\unicode[STIX]{x1D6FC}$
emission of the backlighter in the experiment) and 11.92 keV (to observe the influence of a higher photon energy on the morphology of the X-ray radiography).
$\unicode[STIX]{x1D6FC}$
emission of the backlighter in the experiment) and 11.92 keV (to observe the influence of a higher photon energy on the morphology of the X-ray radiography).
4.3.1 Plasma flow dynamics
As can be seen in Figures 9(c) and 9(d), the best fit is obtained for a V backlighter at 4.952 keV, where the different features are observed for both experiment and FLASH simulation: (i) a central region of low transmission (between
![]() $r\sim -0.5$
and 0.6 mm in the experiment and
$r\sim -0.5$
and 0.6 mm in the experiment and
![]() $r\sim -0.65$
and
$r\sim -0.65$
and
![]() $r\sim 0.65~\text{mm}$
in the FLASH simulation for
$r\sim 0.65~\text{mm}$
in the FLASH simulation for
![]() $z=1~\text{mm}$
), (ii) an envelope surrounding the plasma flow due to the accumulation of plasma where
$z=1~\text{mm}$
), (ii) an envelope surrounding the plasma flow due to the accumulation of plasma where
![]() $\unicode[STIX]{x1D6FD}_{\text{ram}}\sim 1$
and
$\unicode[STIX]{x1D6FD}_{\text{ram}}\sim 1$
and
![]() $R_{ms}\gg 1$
early in time, as discussed below. This area is located at
$R_{ms}\gg 1$
early in time, as discussed below. This area is located at
![]() $r\sim -0.5$
and
$r\sim -0.5$
and
![]() $r=0.6~\text{mm}$
in the experiment and
$r=0.6~\text{mm}$
in the experiment and
![]() $r\sim -0.65~\text{mm}$
and
$r\sim -0.65~\text{mm}$
and
![]() $r\sim 0.65~\text{mm}$
in the FLASH simulation (see Figure 9(c)). We attribute this structure to the dynamics discussed below: at early times, the magnetic field is swept outward, until the magnetic pressure stops the radial expansion of the plasma. The FLASH simulations find a compression of the magnetic field to
$r\sim 0.65~\text{mm}$
in the FLASH simulation (see Figure 9(c)). We attribute this structure to the dynamics discussed below: at early times, the magnetic field is swept outward, until the magnetic pressure stops the radial expansion of the plasma. The FLASH simulations find a compression of the magnetic field to
![]() ${\sim}$
14 T in the envelope region at 75 ns and
${\sim}$
14 T in the envelope region at 75 ns and
![]() ${\sim}$
13 T at 85 ns. The outflowing plasma forms a reverse shock against the layer of increased magnetic field, so that the accumulating, stagnated plasma creates the zone of increased absorption enhanced in the radiographs by limb-darkening.
${\sim}$
13 T at 85 ns. The outflowing plasma forms a reverse shock against the layer of increased magnetic field, so that the accumulating, stagnated plasma creates the zone of increased absorption enhanced in the radiographs by limb-darkening.
Hard X-rays (
![]() ${>}$
10 keV) increase the signal-to-noise ratio on the X-ray and so decrease the contrast of the X-ray radiography. As a conclusion, one should note that the agreement between the experiment and the simulation is qualitative but not quantitative.
${>}$
10 keV) increase the signal-to-noise ratio on the X-ray and so decrease the contrast of the X-ray radiography. As a conclusion, one should note that the agreement between the experiment and the simulation is qualitative but not quantitative.
4.3.2 Reverse-shock dynamics
In this section, we discuss the reverse-shock optical emission and X-ray radiography and the FLASH simulation using a 10 T external B-field. Figures 10(a) and 10(b) show the optical emission and the electron and radiation temperatures given by FLASH at two different times, measured along the flow propagation. In order to quantify the influence of radiation in the experiment, we compared to simulations with the radiation module on, and without (see Figure 8). The observed optical emission is a nonlinear, line-integrated function of electron temperature, species density, and ionization state, and is detected mainly from different absorption depth in the plasma depending if the plasma is optically thick or not. The emission is thus unlikely to be simply proportional to electron temperature, especially near the axis. Even so, the emission will be stronger where the plasma is hotter. As one can see, the dynamic of the emission is well correlated to the electron and radiation temperatures given by the simulation when radiation module is on. Indeed, the peak of the optical emission located around
![]() $z_{\text{peak}}\sim 200~\unicode[STIX]{x03BC}\text{m}$
from the obstacle position (
$z_{\text{peak}}\sim 200~\unicode[STIX]{x03BC}\text{m}$
from the obstacle position (
![]() $z\sim 2.2~\text{mm}$
from the rear side of the main target) agrees well with the peak of the electron and radiation temperatures in the simulation for the two different times. The longitudinal expansion of the emission zone is also well reproduced by the FLASH simulation (it is
$z\sim 2.2~\text{mm}$
from the rear side of the main target) agrees well with the peak of the electron and radiation temperatures in the simulation for the two different times. The longitudinal expansion of the emission zone is also well reproduced by the FLASH simulation (it is
![]() ${\sim}400~\unicode[STIX]{x03BC}\text{m}$
in Figure 10(b)). This is in contrast with the simulation without radiation (see black curve of Figure 10(b)) where a strong disagreement is observed between the width of the emission zone obtained in the experiment and the temperature profile given by the simulation. These results indicate that to reproduce the optical self-emission, radiation has to be taken into account.
${\sim}400~\unicode[STIX]{x03BC}\text{m}$
in Figure 10(b)). This is in contrast with the simulation without radiation (see black curve of Figure 10(b)) where a strong disagreement is observed between the width of the emission zone obtained in the experiment and the temperature profile given by the simulation. These results indicate that to reproduce the optical self-emission, radiation has to be taken into account.
Figure 10(c) presents a lineout of Figures 9(a) and 9(b) and the case without radiation taken at
![]() $r=0.02~\text{mm}$
. The longitudinal expansion of the reverse-shock front is in each case close to
$r=0.02~\text{mm}$
. The longitudinal expansion of the reverse-shock front is in each case close to
![]() ${\sim}240~\unicode[STIX]{x03BC}\text{m}$
from the obstacle, i.e., at the position where the maximum of the optical emission peak is observed. The length of the reverse shock is better reproduced when radiation is on; however, the difference is not significative enough to conclude.
${\sim}240~\unicode[STIX]{x03BC}\text{m}$
from the obstacle, i.e., at the position where the maximum of the optical emission peak is observed. The length of the reverse shock is better reproduced when radiation is on; however, the difference is not significative enough to conclude.
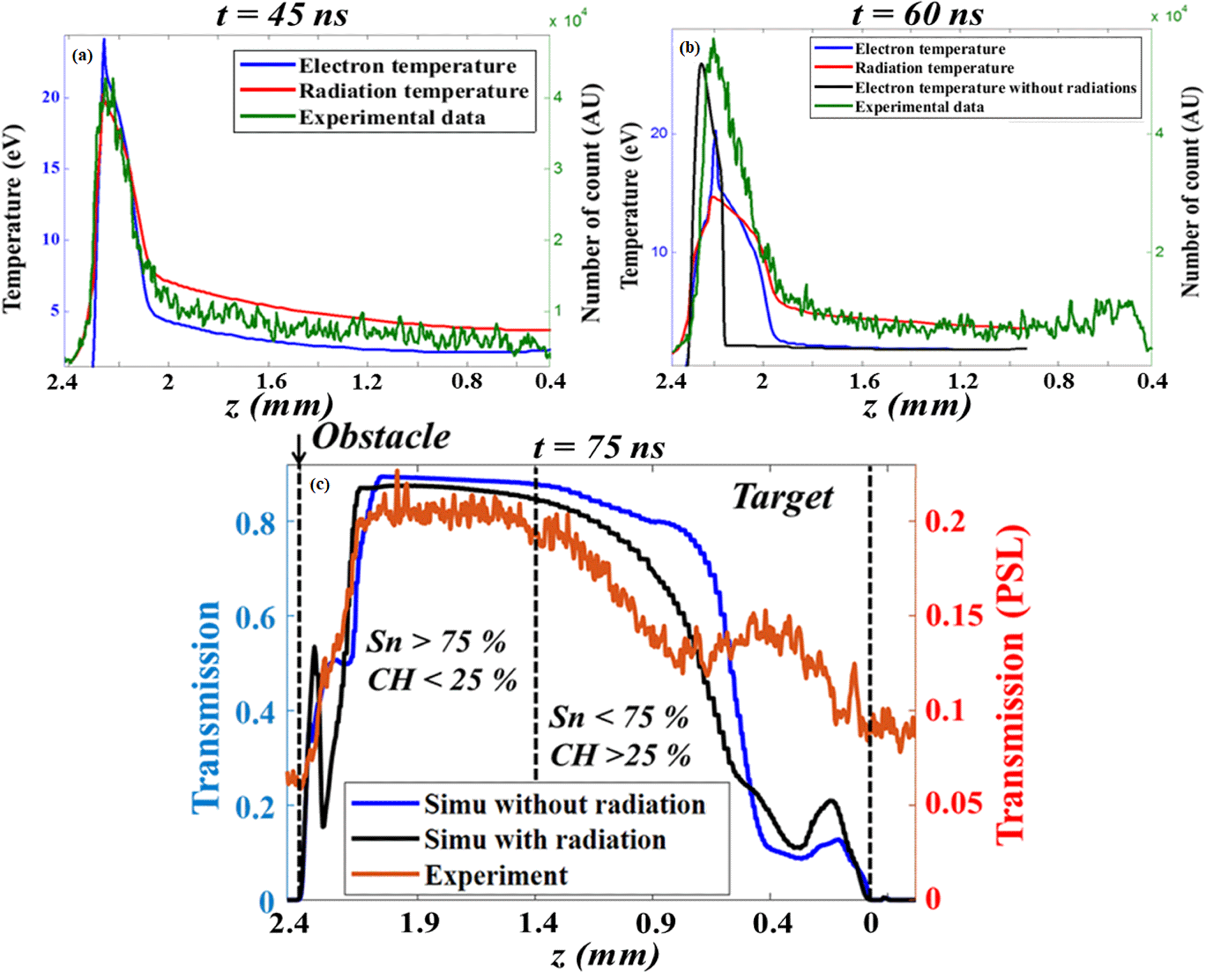
Figure 10. Comparison between lineout of the optical emission (see Figure 2(a) for an example), measured in the experiment (left axis) and electron and radiation temperature given by the FLASH simulation (right axis at
![]() $r=0.2~\text{mm}$
) at (a) 45 ns and (b) 60 ns after the laser drive for two different FLASH simulations: without radiation modules (black curve) and with radiation module on (blue and red) using 40 radiation groups. (c) Vertical lineout of radiograph transmission, at
$r=0.2~\text{mm}$
) at (a) 45 ns and (b) 60 ns after the laser drive for two different FLASH simulations: without radiation modules (black curve) and with radiation module on (blue and red) using 40 radiation groups. (c) Vertical lineout of radiograph transmission, at
![]() $r=0.2~\text{mm}$
of Figure 9(a) (experiment, red curve), Figure 9(b) (simulation with radiations, black curve) and without radiations (blue curve).
$r=0.2~\text{mm}$
of Figure 9(a) (experiment, red curve), Figure 9(b) (simulation with radiations, black curve) and without radiations (blue curve).
In conclusion, according to our diagnostics, it is difficult to distinguish whether the reverse shock itself is radiative or radiation changes the nature of the plasma flow. Moreover, a study of the dominant effects due to radiation is necessary. It will give an important input for the understanding of the dynamics of the astrophysical system.
4.4 Effect of the hole diameter on the dynamics of the plasma flow
Understanding the features observed in Figure 4 is of great importance for the platform optimization. In particular, on some shots at the base of the plasma flow (see Figures 4(c) and 4(d)), a bubble-like structure can be observed. It is clearly not related to the addition of the external magnetic field as it appears in both cases with and without B-field. One of the possible explanations leading to such a feature could be related to the hole diameter of the target holder. In order to assess its effect, we performed two types of two dimensional FLASH simulations: the first one with a 1 mm hole diameter and the second one with a 2 mm hole diameter (see Figure 11).
The coronal plasma formed on the laser side expands into vacuum, has a high temperature and is able to strongly heat and launch a shock wave in the target holder. As a consequence, a large amount of the material from the holder is ablated and disturbs the dynamics of the plasma for the 1 mm hole diameter (see Figure 11).
The use of a 2 mm hole greatly reduces this effect. It is clearly visible in the experimental data (see Figures 4(c) and 4(d)) as well as in the simulation (see Figure 11) where at the base of the plasma flow, an elongated bubble is observed using a 1 mm hole diameter while on other shots (see Figure 4(a) and 4(b)), the bubble is not present, which indicate a different hole diameter. However, as can be seen in Figure 11, the dynamics of the reverse shock seems not to be strongly influenced by the size of the hole diameter of the target.
5 Discussion
We can identify three regions in the system under study (see Figure 1). There is a flow-launching region, a region of accreting plasma flow, and a region behind the reverse shock. Each of these has distinct dynamics and so has specific dimensionless parameters that govern their behavior. Only the second and third regions have a clear connection to astrophysical systems, and so we will focus on these here. The first relevant basic equations in both regions is the MHD momentum equation,
in which the pressure is p, the permeability of free space is
![]() $\unicode[STIX]{x1D707}$
, the density is
$\unicode[STIX]{x1D707}$
, the density is
![]() $\unicode[STIX]{x1D70C}$
, the magnetic-field vector is
$\unicode[STIX]{x1D70C}$
, the magnetic-field vector is
![]() $\mathbf{B}$
, and the fluid velocity of the plasma is
$\mathbf{B}$
, and the fluid velocity of the plasma is
![]() $\mathbf{u}$
, which we distinguish from the directed speed of the plasma flow,
$\mathbf{u}$
, which we distinguish from the directed speed of the plasma flow,
![]() $v$
. Here one can see that the motion involves a competition between gradients of thermal pressure,
$v$
. Here one can see that the motion involves a competition between gradients of thermal pressure,
![]() $p_{\text{th}}$
, and magnetic effects. The two magnetic effects involve the gradient of magnetic pressure,
$p_{\text{th}}$
, and magnetic effects. The two magnetic effects involve the gradient of magnetic pressure,
![]() $B^{2}/(2\unicode[STIX]{x1D707}_{\text{0}})$
, and the magnetic-curvature force. The parameter
$B^{2}/(2\unicode[STIX]{x1D707}_{\text{0}})$
, and the magnetic-curvature force. The parameter
![]() $\unicode[STIX]{x1D6FD}_{\text{th}}=2\unicode[STIX]{x1D707}_{\text{0}}p_{\text{th}}/B^{2}$
characterizes the competition between thermal and magnetic forces in any region. In studies of accreting flows, the thermal pressure of the shocked plasma at an obstacle is of the order of the ram pressure of the accreting flow,
$\unicode[STIX]{x1D6FD}_{\text{th}}=2\unicode[STIX]{x1D707}_{\text{0}}p_{\text{th}}/B^{2}$
characterizes the competition between thermal and magnetic forces in any region. In studies of accreting flows, the thermal pressure of the shocked plasma at an obstacle is of the order of the ram pressure of the accreting flow,
![]() $\unicode[STIX]{x1D70C}v^{2}$
. More is firmly known about the incoming flow, than about the shocked plasma at an obstacle, and as a consequence, this has led the community that studies such flows to focus on a ‘ram
$\unicode[STIX]{x1D70C}v^{2}$
. More is firmly known about the incoming flow, than about the shocked plasma at an obstacle, and as a consequence, this has led the community that studies such flows to focus on a ‘ram
![]() $\unicode[STIX]{x1D6FD}$
’, defined as
$\unicode[STIX]{x1D6FD}$
’, defined as
![]() $\unicode[STIX]{x1D6FD}_{\text{ram}}=2\unicode[STIX]{x1D707}_{\text{0}}\unicode[STIX]{x1D70C}v^{2}/B^{2}$
. Thus,
$\unicode[STIX]{x1D6FD}_{\text{ram}}=2\unicode[STIX]{x1D707}_{\text{0}}\unicode[STIX]{x1D70C}v^{2}/B^{2}$
. Thus,
![]() $\unicode[STIX]{x1D6FD}_{\text{ram}}\sim \unicode[STIX]{x1D6FD}_{\text{th}}$
within the shocked plasma at the obstacle. Note that, as
$\unicode[STIX]{x1D6FD}_{\text{ram}}\sim \unicode[STIX]{x1D6FD}_{\text{th}}$
within the shocked plasma at the obstacle. Note that, as
![]() $\unicode[STIX]{x1D6FD}_{\text{ram }}\sim \unicode[STIX]{x1D6FD}_{\text{th}},\unicode[STIX]{x1D6FD}_{\text{ram}}$
characterizes the competition between thermal effects and magnetic effects in the shocked matter but not in the accreting flow. Taking the accreting flow to be
$\unicode[STIX]{x1D6FD}_{\text{ram }}\sim \unicode[STIX]{x1D6FD}_{\text{th}},\unicode[STIX]{x1D6FD}_{\text{ram}}$
characterizes the competition between thermal effects and magnetic effects in the shocked matter but not in the accreting flow. Taking the accreting flow to be
![]() ${\sim}$
Mach 8, as typical in our experiment, so that the sound speed,
${\sim}$
Mach 8, as typical in our experiment, so that the sound speed,
![]() $c_{\text{s}}$
, is
$c_{\text{s}}$
, is
![]() ${\sim}v/8$
, we have
${\sim}v/8$
, we have
![]() $\unicode[STIX]{x1D6FD}_{\text{th}}\sim \unicode[STIX]{x1D6FD}_{\text{ram}}/64$
.
$\unicode[STIX]{x1D6FD}_{\text{th}}\sim \unicode[STIX]{x1D6FD}_{\text{ram}}/64$
.
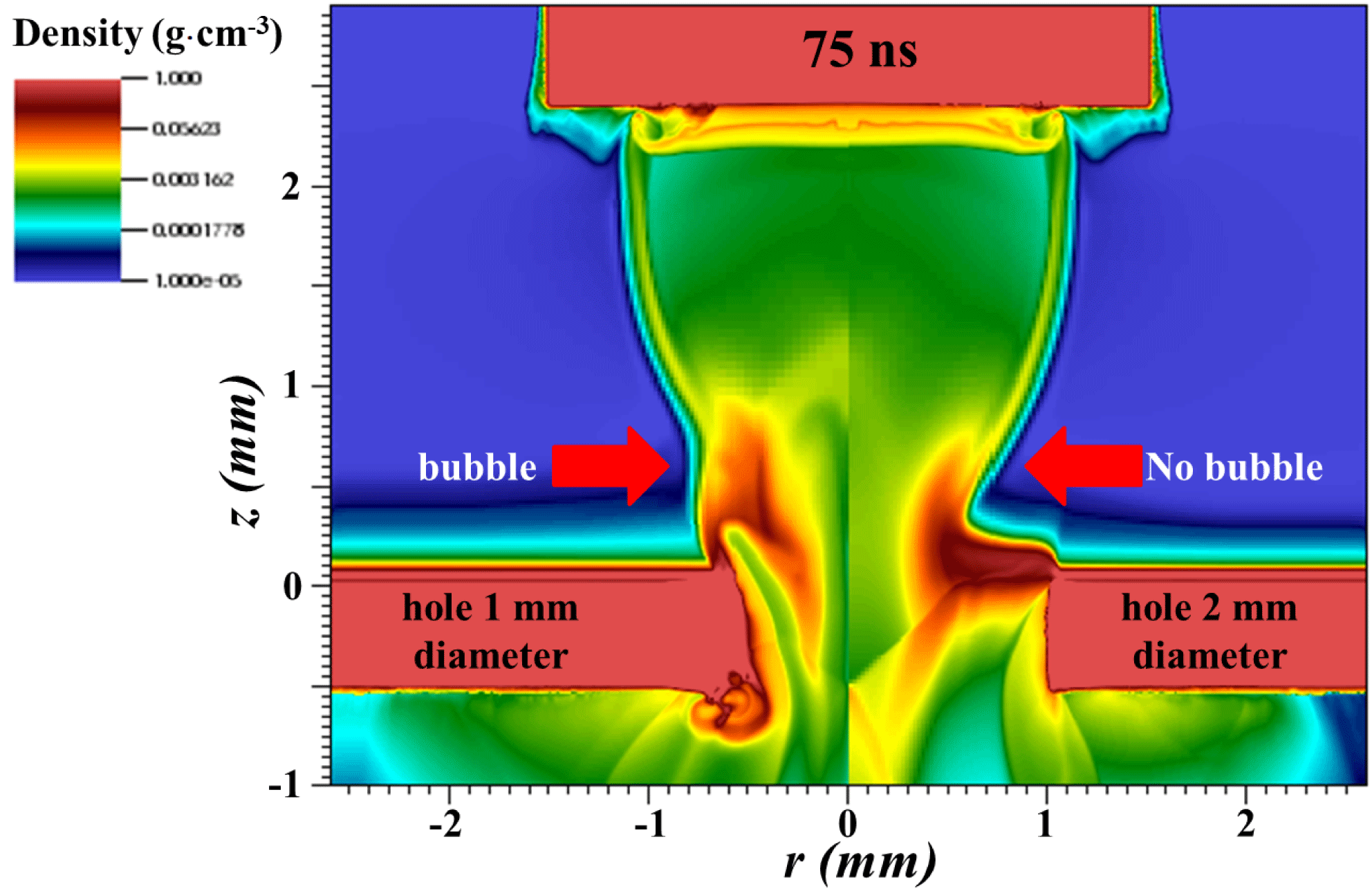
Figure 11. MHD radiative FLASH simulation of the experiment using a 1 mm hole diameter (left panel) and a 2 mm hole diameter (right panel) and a 10 T B-field. An obvious difference is observed at the base of the jet where the plasma shape is strongly affected by the size of the hole.
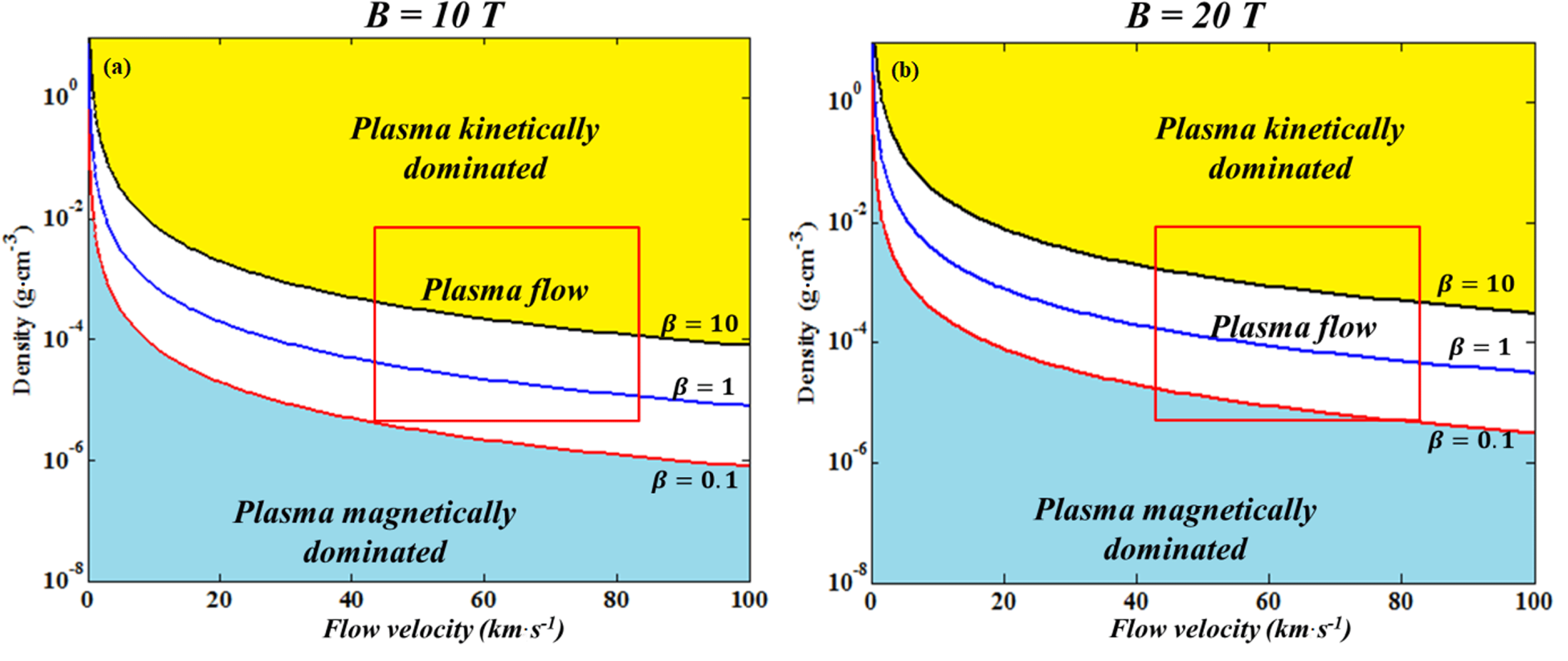
Figure 12. Illustration of the
![]() $\unicode[STIX]{x1D6FD}_{\text{ram}}$
parameter as a function of the shock velocity and the density for an external magnetic field of (a) 10 T and (b) 20 T. The red rectangle corresponds to the experimental conditions deduced from the combination of diagnostics.
$\unicode[STIX]{x1D6FD}_{\text{ram}}$
parameter as a function of the shock velocity and the density for an external magnetic field of (a) 10 T and (b) 20 T. The red rectangle corresponds to the experimental conditions deduced from the combination of diagnostics.
Our diagnostics allowed us to directly infer the propagation velocity, the reverse-shock velocity, the longitudinal and radial extent of the plasma, and the electron density in the range from
![]() $5\times 10^{17}$
to
$5\times 10^{17}$
to
![]() $1\times 10^{20}~\text{cm}^{-3}$
. For reasonable values of ionization (between 1 and 5), this corresponds to a mass density ranging from
$1\times 10^{20}~\text{cm}^{-3}$
. For reasonable values of ionization (between 1 and 5), this corresponds to a mass density ranging from
![]() $10^{-5}~\text{g}\cdot \text{cm}^{-3}$
to more than
$10^{-5}~\text{g}\cdot \text{cm}^{-3}$
to more than
![]() $10^{-3}~\text{g}\cdot \text{cm}^{-3}$
. This lets us evaluate the range of
$10^{-3}~\text{g}\cdot \text{cm}^{-3}$
. This lets us evaluate the range of
![]() $\unicode[STIX]{x1D6FD}_{\text{ram}}$
that is present in the experiment. Figure 12(a) shows
$\unicode[STIX]{x1D6FD}_{\text{ram}}$
that is present in the experiment. Figure 12(a) shows
![]() $\unicode[STIX]{x1D6FD}_{\text{ram}}$
for the 10 T magnetic field of the experiment, and Figure 12(b) shows
$\unicode[STIX]{x1D6FD}_{\text{ram}}$
for the 10 T magnetic field of the experiment, and Figure 12(b) shows
![]() $\unicode[STIX]{x1D6FD}_{\text{ram}}$
for the 20 T B-field of future perspectives. One finds
$\unicode[STIX]{x1D6FD}_{\text{ram}}$
for the 20 T B-field of future perspectives. One finds
![]() $\unicode[STIX]{x1D6FD}_{\text{ram}}<1$
for densities below
$\unicode[STIX]{x1D6FD}_{\text{ram}}<1$
for densities below
![]() ${\sim}10^{-5}~\text{g}\,\cdot \,\text{cm}^{-3}$
for the 10 T case and below
${\sim}10^{-5}~\text{g}\,\cdot \,\text{cm}^{-3}$
for the 10 T case and below
![]() ${\sim}10^{-4}~\text{g}\cdot \text{cm}^{-3}$
for the 20 T case. This implies that the magnetic field should not be dynamically important for the accreted plasma flow at early time (
${\sim}10^{-4}~\text{g}\cdot \text{cm}^{-3}$
for the 20 T case. This implies that the magnetic field should not be dynamically important for the accreted plasma flow at early time (
![]() $t<10~\text{ns}$
), the collimation time being of the order of
$t<10~\text{ns}$
), the collimation time being of the order of
![]() ${\sim}$
8–10 ns. However, when the density of the leading edge of the accreting flow is small enough, the B-field will constrain its radial extension. Even then, increasing the field to 20 T would reduce the time it takes for the B-field to have an influence on the collimation of the accreting plasma flow. However, for the accreting flow
${\sim}$
8–10 ns. However, when the density of the leading edge of the accreting flow is small enough, the B-field will constrain its radial extension. Even then, increasing the field to 20 T would reduce the time it takes for the B-field to have an influence on the collimation of the accreting plasma flow. However, for the accreting flow
![]() $\unicode[STIX]{x1D6FD}_{\text{th}}\sim \unicode[STIX]{x1D6FD}_{\text{ram}}/64$
so one can infer from Figure 12(a) that the magnetic field may be dynamically important, as indeed it appears to be from the observed deflection of this material. This does require that the magnetic field diffuses slowly enough into the plasma so that the plasma can compress the field enough to establish a significant gradient of magnetic pressure. We examine this issue next.
$\unicode[STIX]{x1D6FD}_{\text{th}}\sim \unicode[STIX]{x1D6FD}_{\text{ram}}/64$
so one can infer from Figure 12(a) that the magnetic field may be dynamically important, as indeed it appears to be from the observed deflection of this material. This does require that the magnetic field diffuses slowly enough into the plasma so that the plasma can compress the field enough to establish a significant gradient of magnetic pressure. We examine this issue next.
The second relevant equation for the system of interest is the magnetic induction equation,
in which the resistivity is
![]() $\unicode[STIX]{x1D702}$
. (Note that in SI mks units
$\unicode[STIX]{x1D702}$
. (Note that in SI mks units
![]() $\unicode[STIX]{x1D702}$
is in
$\unicode[STIX]{x1D702}$
is in
![]() $\unicode[STIX]{x03A9}\,\cdot \,\text{m}$
and
$\unicode[STIX]{x03A9}\,\cdot \,\text{m}$
and
![]() $\unicode[STIX]{x1D707}$
is in Henries/m, which is
$\unicode[STIX]{x1D707}$
is in Henries/m, which is
![]() $\unicode[STIX]{x03A9}\,\cdot \,\text{s}/\text{m}$
, so that
$\unicode[STIX]{x03A9}\,\cdot \,\text{s}/\text{m}$
, so that
![]() $\unicode[STIX]{x1D702}/\unicode[STIX]{x1D707}$
has the units of a kinematic diffusion coefficient, as is required.) The two terms on the right-hand side of this equation characterize the competition between convection of magnetic flux by the plasma and the resistive diffusion of magnetic field into the plasma. If the first term is dominant, then any components of
$\unicode[STIX]{x1D702}/\unicode[STIX]{x1D707}$
has the units of a kinematic diffusion coefficient, as is required.) The two terms on the right-hand side of this equation characterize the competition between convection of magnetic flux by the plasma and the resistive diffusion of magnetic field into the plasma. If the first term is dominant, then any components of
![]() $\mathbf{u}$
that are perpendicular to
$\mathbf{u}$
that are perpendicular to
![]() $\mathbf{B}$
displace the magnetic-field lines. If this term was dominant, then the radial expansion of the flow would compress the field surrounding it, increasing
$\mathbf{B}$
displace the magnetic-field lines. If this term was dominant, then the radial expansion of the flow would compress the field surrounding it, increasing
![]() $B$
there. If the second term was dominant, then the field would diffuse through the plasma before any displacement could develop. If we set
$B$
there. If the second term was dominant, then the field would diffuse through the plasma before any displacement could develop. If we set
![]() $\unicode[STIX]{x1D6FB}\sim 1/L_{1}$
in the first term and
$\unicode[STIX]{x1D6FB}\sim 1/L_{1}$
in the first term and
![]() $\unicode[STIX]{x1D6FB}\sim 1/L_{2}$
in the second term, then the ratio of these two terms,
$\unicode[STIX]{x1D6FB}\sim 1/L_{2}$
in the second term, then the ratio of these two terms,
![]() $R_{12}$
, is
$R_{12}$
, is
in which the traditional magnetic Reynolds number is
![]() $R_{m}$
, with all scale lengths taken to be of order of some reference number
$R_{m}$
, with all scale lengths taken to be of order of some reference number
![]() $L\sim L_{2}\sim L_{1}$
. For some period of time after the flow emerges from the solid target,
$L\sim L_{2}\sim L_{1}$
. For some period of time after the flow emerges from the solid target,
![]() $u\sim c_{s}$
and the radial expansion of its edges is characterized by
$u\sim c_{s}$
and the radial expansion of its edges is characterized by
![]() $L_{1}\sim c_{s}t$
, for sound speed
$L_{1}\sim c_{s}t$
, for sound speed
![]() $c_{s}$
, while in contrast
$c_{s}$
, while in contrast
![]() $L_{2}$
is very large (much larger than the plasma diameter), as the field is nearly uniform. This means that
$L_{2}$
is very large (much larger than the plasma diameter), as the field is nearly uniform. This means that
![]() $L_{2}/L_{1}>1$
, where
$L_{2}/L_{1}>1$
, where
![]() $L_{2}$
is several times of the plasma diameter. During this period, we find that
$L_{2}$
is several times of the plasma diameter. During this period, we find that
![]() $\unicode[STIX]{x1D702}$
is small enough that
$\unicode[STIX]{x1D702}$
is small enough that
![]() $R_{12}\gg 1$
in the flow, enabling the radial expansion of the plasma to push the field aside and compress it. The resulting gradient of magnetic-field pressure resists the plasma expansion. Since the expanding flow is supersonic, a layer of shocked material may form. This would explain the apparent observation of a dense shell near the outer edges of the plasma, as seen in Figure 4 and in the simulation (see Figure 8(b)).
$R_{12}\gg 1$
in the flow, enabling the radial expansion of the plasma to push the field aside and compress it. The resulting gradient of magnetic-field pressure resists the plasma expansion. Since the expanding flow is supersonic, a layer of shocked material may form. This would explain the apparent observation of a dense shell near the outer edges of the plasma, as seen in Figure 4 and in the simulation (see Figure 8(b)).
Once the gradients approach a common value,
![]() $L\sim L_{2}\sim L_{1}$
, the field will diffuse a distance
$L\sim L_{2}\sim L_{1}$
, the field will diffuse a distance
![]() $\unicode[STIX]{x1D6FF}\sim L/\sqrt{R_{m}}$
during the time it takes an acoustic disturbance to cross the plasma column, with
$\unicode[STIX]{x1D6FF}\sim L/\sqrt{R_{m}}$
during the time it takes an acoustic disturbance to cross the plasma column, with
![]() $R_{m}=c_{s}\unicode[STIX]{x1D707}L/\unicode[STIX]{x1D702}$
here. Even then, there are two distinct values of
$R_{m}=c_{s}\unicode[STIX]{x1D707}L/\unicode[STIX]{x1D702}$
here. Even then, there are two distinct values of
![]() $R_{m}$
, one in the accreting flow (
$R_{m}$
, one in the accreting flow (
![]() $R_{mf}$
) and a different one (
$R_{mf}$
) and a different one (
![]() $R_{ms}$
) in the post-shock (accreted matter). Since
$R_{ms}$
) in the post-shock (accreted matter). Since
![]() $c_{s}\sim v$
in the post-shock matter, one could say
$c_{s}\sim v$
in the post-shock matter, one could say
![]() $R_{ms}=v\unicode[STIX]{x1D707}L/\unicode[STIX]{x1D702}$
there, with
$R_{ms}=v\unicode[STIX]{x1D707}L/\unicode[STIX]{x1D702}$
there, with
![]() $\unicode[STIX]{x1D702}$
evaluated for the post-shock ionization and temperature. For reference, using temperatures from the simulation discussed above, the Lee and More model[Reference Lee and More30] gives
$\unicode[STIX]{x1D702}$
evaluated for the post-shock ionization and temperature. For reference, using temperatures from the simulation discussed above, the Lee and More model[Reference Lee and More30] gives
![]() $\unicode[STIX]{x1D702}\sim 2\times 10^{-6}~\unicode[STIX]{x03A9}\cdot \text{cm}$
at the center of the plasma flow and decreases to
$\unicode[STIX]{x1D702}\sim 2\times 10^{-6}~\unicode[STIX]{x03A9}\cdot \text{cm}$
at the center of the plasma flow and decreases to
![]() ${\sim}4\times 10^{-7}~\unicode[STIX]{x03A9}\cdot \text{cm}$
at its edge. However, it is not so clear what value of
${\sim}4\times 10^{-7}~\unicode[STIX]{x03A9}\cdot \text{cm}$
at its edge. However, it is not so clear what value of
![]() $L$
to use. Using the plasma diameter as
$L$
to use. Using the plasma diameter as
![]() $L$
, one obtains the results shown in Figure 13. The rectangular area indicates values of
$L$
, one obtains the results shown in Figure 13. The rectangular area indicates values of
![]() $R_{m}$
achieved in the experiment. One concludes that dynamic interaction of the shocked plasma and the field has the potential to produce large-scale structures but that small-scale modulations will be damped by magnetic diffusion. To enable more complex interactions, one needs to increase the plasma temperature.
$R_{m}$
achieved in the experiment. One concludes that dynamic interaction of the shocked plasma and the field has the potential to produce large-scale structures but that small-scale modulations will be damped by magnetic diffusion. To enable more complex interactions, one needs to increase the plasma temperature.
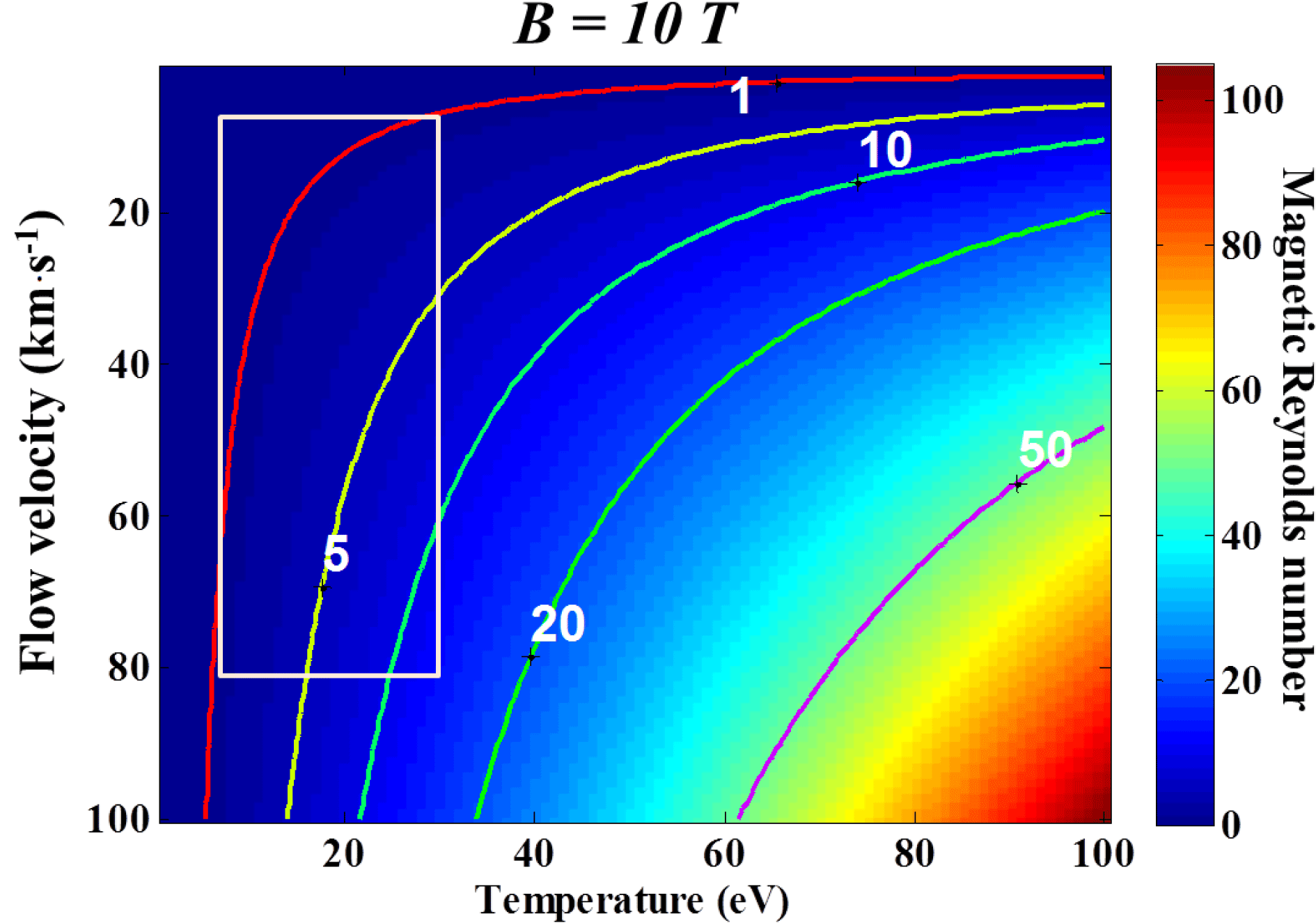
Figure 13. Map of magnetic Reynolds number in the shocked matter,
![]() $R_{ms}$
, which depends on the incoming flow velocity, resistivity and temperature. The resistivity was evaluated using a Coulomb logarithm of 10 and ionization from 1 to 6. Results are shown for an external magnetic field of 10 T. The white rectangle corresponds to the experimental conditions, as deduced from the combination of diagnostics. The lines are isolines of
$R_{ms}$
, which depends on the incoming flow velocity, resistivity and temperature. The resistivity was evaluated using a Coulomb logarithm of 10 and ionization from 1 to 6. Results are shown for an external magnetic field of 10 T. The white rectangle corresponds to the experimental conditions, as deduced from the combination of diagnostics. The lines are isolines of
![]() $R_{ms}$
for values of 1, 5, 10, 20 and 50.
$R_{ms}$
for values of 1, 5, 10, 20 and 50.
6 Conclusion
In conclusion, we have developed a new experimental platform that couples a strong external magnetic field with high-power lasers (
![]() ${\sim}$
kJ), enabling the study of magnetized-reverse-shock dynamics of interest for astrophysical systems such as cataclysmic variables of polar type. A clear and visible reverse shock is formed when a plasma flow, constrained by the addition of a 10 T B-field, impacts an obstacle. It will add an additional magnetic pressure which helps to the collimation of the plasma flow. As a consequence a higher mass flux (
${\sim}$
kJ), enabling the study of magnetized-reverse-shock dynamics of interest for astrophysical systems such as cataclysmic variables of polar type. A clear and visible reverse shock is formed when a plasma flow, constrained by the addition of a 10 T B-field, impacts an obstacle. It will add an additional magnetic pressure which helps to the collimation of the plasma flow. As a consequence a higher mass flux (
![]() $\text{d}m/\text{d}t$
) propagates toward the obstacle and leads to the generation of a reverse shock. However, no magnetic instabilities such as the firehose instability have been reported due to the presence of the B-field. An instability seems to develop where density fluctuations are tracked in the X-ray radiographic data. This might be due to the Sn layer at the rear surface of the target. Further experimental and numerical investigations are needed. One should note as well that the density fluctuations associated with the firehose instability should be small. An improvement of the spatial resolution and an optimization of the contrast for the X-ray radiography diagnostic are therefore mandatory.
$\text{d}m/\text{d}t$
) propagates toward the obstacle and leads to the generation of a reverse shock. However, no magnetic instabilities such as the firehose instability have been reported due to the presence of the B-field. An instability seems to develop where density fluctuations are tracked in the X-ray radiographic data. This might be due to the Sn layer at the rear surface of the target. Further experimental and numerical investigations are needed. One should note as well that the density fluctuations associated with the firehose instability should be small. An improvement of the spatial resolution and an optimization of the contrast for the X-ray radiography diagnostic are therefore mandatory.
The experiment and 2D MHD radiative simulations qualitatively agree although nonnegligible differences exist. In particular, the simulations agree with the longitudinal reverse-shock extension of the optical emission seen in the experiment when the radiation module is on. However, the radial extension of the plasma flow does not match the experimental results. Improvement should be done in this direction. The investigation of the radiation effects should as well be improved to evaluate, in the astrophysical system, whether radiative losses are important or if the plasma can be considered optically thin and here only emission is important.
Future developments will be made to increase the external B-field amplitude to 20 T, allowing a higher magnetic pressure and allowing experiments to approach the case where diffusion of the magnetic field is negligible. This will also result in a higher mass flux allowing a more visible reverse shock. Increasing the magnetic field should as well permit the development of the firehose instability at the boundary between the magnetic field and the accreting plasma flow; however, this must be combined with an improvement of the spatial resolution of the X-ray radiography.
Acknowledgements
The authors would like to thank the LULI staff for their great support. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 654148 Laserlab-Europe. The work was supported by RAS Presidium Program for Basic Research #11 and by Competitiveness Program of NRNU MEPhI. R. P. Drake and C. C. Kuranz were supported by the NNSA-DS and SC-OFES Joint Program in High Energy Density Laboratory Plasmas, grant No. DE-NA0002956.