1 Introduction
Magnetic fields are applied in various areas of modern physics and engineering. In the past 50 years, researchers have strived to realize strong magnetic fields in laboratories for fundamental studies and diverse applications[ Reference Sagdeev 1 – Reference Santos, Bailly-Grandvaux, Ehret, Arefiev, Batani, Beg, Calisti, Ferri, Florido, Forestier-Colleoni, Fujioka, Gigosos, Giuffrida, Gremillet, Honrubia, Kojima, Korneev, Law, Marquès, Morace, Mossé, Peyrusse, Rose, Roth, Sakata, Schaumann, Suzuki-Vidal, Tikhonchuk, Toncian, Woolsey and Zhang 9 ]. Approaches include high explosives[ Reference Sakharov, Lyudaev, Smirnov, Plyushchev, Pavlovskii, Chernyshev, Feoktistova, Zharinov and Zysin 10 , Reference Fowler, Garn and Caird 11 ], electromagnetic implosions[ Reference Cnare 12 , Reference Miura and Nojiri 13 ], high-power lasers[ Reference Sheng and Meyer-ter-Vehn 14 – Reference Meinecke, Doyle, Miniati, Bell, Bingham, Crowston, Drake, Fatenejad, Koenig, Kuramitsu, Kuranz, Lamb, Lee, MacDonald, Murphy, Park, Pelka, Ravasio, Sakawa, Schekochihin, Scopatz, Tzeferacos, Wan, Woolsey, Yurchak, Reville and Gregori 19 ] and Z pinches[ Reference Velikovich, Gol’berg, Liberman and Felber 20 , Reference Felber, Malley and Wessel 21 ]. The principal physical mechanism of these methods is based on magnetic flux compression (MFC)[ Reference Sakharov, Lyudaev, Smirnov, Plyushchev, Pavlovskii, Chernyshev, Feoktistova, Zharinov and Zysin 10 ] using hollow cylindrical structures and pre-seeded magnetic fields. To date, the highest magnetic field experimentally observed remains of the kilotesla (kT) order[ Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi 22 – Reference Law, Abe, Morace, Arikawa, Sakata, Lee, Matsuo, Morita, Ochiai, Liu, Yogo, Okamoto, Golovin, Ehret, Ozaki, Nakai, Sentoku, Santos, d'Humières, Korneev and Fujioka 24 ].
Recently, a novel concept called a microtube implosion (MTI)[ Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov 25 ] has been proposed. MTI utilizes a structured target and intense laser pulses. Particle simulations have demonstrated that MTI can generate ultrahigh magnetic fields of the megatesla (MT) order. This increase is three orders of magnitude higher than any experimental data. Although MTI uses a similar physical configuration as MFC, it differs from MFC because the ultrahigh magnetic fields in MTI are generated by the spin currents induced by collective Larmor gyromotions.
Irradiating a micrometer-sized, cylindrically hollow target with relativistically intense laser pulses generates hot electrons (Figure 1). These laser-produced relativistic electrons launch a cylindrically symmetric implosion of the inner wall ions toward the central axis. The kilotesla-order, uniform, pre-seeded magnetic fields[ Reference Fujioka, Zhang, Ishihara, Shigemori, Hironaka, Johzaki, Sunahara, Yamamoto, Nakashima, Watanabe, Shiraga, Nishimura and Azechi 22 , Reference Daido, Miki, Mima, Fujita, Sawai, Fujita, Kitagawa, Nakai and Yamanaka 26 – Reference Zhang, Zhu, Li, Jiang, Yuan, Wei, Liang, Wang, Zhao, Zhong, Han, Hua, Zhu, Zhu, Wang, Fang and Zhang 31 ] parallel to the target central axis launch Larmor gyromotions of electrons and ions, deflecting their trajectories in the opposite direction. Near the target center, currents running on the envelope curves due to the deflected ions and electrons (referred to as Larmor holes[ Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov 25 ]) form a strong spin current. Consequently, ultrahigh magnetic fields are generated in a collective manner, amplifying the original seed magnetic field by two to three orders of magnitude. Note, if the cylindrical cavity is replaced by a spherical one, based on another physical concept referred to as microbubble implosion[ Reference Murakami, Arefiev and Zosa 32 – Reference Koga, Murakami, Arefiev, Nakamiya, Bulanov and Bulanov 35 ], ultrahigh electric fields may be obtained close to the Shwinger limit[ Reference Schwinger 36 ] instead of an ultrahigh magnetic field.

Figure 1 Illustration of a microtube implosion. Due to the laser-produced hot electrons with megaelectron volt energies, cold ions in the inner wall surface implode toward the central axis. By pre-seeding uniform magnetic fields of the kilotesla order, the Lorentz force induces a Larmor gyromotion of the imploding ions and electrons. Due to the resultant collective motion of relativistic charged particles around the central axis, strong spin currents of approximately peta-ampere/cm
![]() ${}^2$
are produced with a few tens of nm size, generating megatesla-order magnetic fields.
${}^2$
are produced with a few tens of nm size, generating megatesla-order magnetic fields.
Previously, we proposed the principle of MTI and used two-dimensional (2D) particle-in-cell (PIC) simulations to demonstrate its characteristic behavior in terms of plasma parameters, such as the plasma density, the current and the temperature of the electrons[ Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov 25 ]. In this work, we clarify the achievable maximum magnetic fields as a function of external parameters, including the applied laser intensity, laser energy and target structure. This study provides indispensable information to conduct real experiments in a laboratory setting.
Previous studies have discussed a surprising phenomenon called polarity switching[
Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov
25
,
Reference Weichman, Murakami, Robinson and Arefiev
37
]. Polarity switching causes a plasma-current-driven magnetic field of the order of 0.1–1 MT to initially grow on the central axis in the direction opposite to the seed magnetic field (antiparallel or reverse field regime)[
Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov
25
,
Reference Weichman, Murakami, Robinson and Arefiev
37
]. In a later stage, the central magnetic field abruptly changes its direction to become parallel to the original seed field (forward polarity regime) and quickly grows to reach a similar or higher magnetic field than the early stage. Polarity switching is observed at relatively low seed magnetic fields of less than a few kT. However, its detailed physical mechanism is debatable. Our strategy in this work is straightforward. To clarify the quantitative relation between the achievable magnetic field, applied laser and target parameters, we avoid the polarity switching regime by assuming a relatively strong seed magnetic field,
![]() ${B}_0=6$
kT.
${B}_0=6$
kT.
In addition to employing a relatively strong seed magnetic field, we also employ one more condition to assure forward polarity (i.e., a square cross-section microtube, which has a square-shaped outer cross-section and a circular-shaped inner cross-section). Circular cross-section microtubes (Figure 1) induce both forward and reverse polarities, depending on several external parameters, such as the wall thickness and the strength of the seed magnetic field[ Reference Weichman, Robinson, Murakami and Arefiev 38 ]. On the other hand, square cross-section microtubes are reported to generate more robust ultrahigh magnetic fields than circular cross-section microtubes. This is due to the following reason. The polarity of the magnetic field generated at the center depends on whether the electron fluxes originating from the laser-interaction spots are clockwise or anticlockwise with respect to the target center. With a circular-shaped target, the collective behavior of the electron fluxes is more sensitive to the laser conditions, which determines the absorption pattern on the target surface, than with the square-shaped target[ Reference Weichman, Murakami, Robinson and Arefiev 37 ]. Hence, this study employs square cross-section microtubes.
The rest of this paper is organized as follows. Section 2 provides the three-dimensional (3D) simulation result to demonstrate that MTI is indeed feasible in 3D configurations under a realistic target-laser interplay. Furthermore, dozens of 2D simulations are conducted to show both the qualitative and quantitative dependencies of the laser parameters on magnetic field generation. Section 3 employs a simple model to explain the simulation results in Section 2 and the scaling of the maximum magnetic field is established in terms of the laser intensity and energy. Finally, Section 4 provides a discussion to conclude this paper.
2 Simulation results
2.1 3D EPOCH simulations
We conducted 3D PIC simulations using the open-source fully relativistic code EPOCH[
Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz, Bell and Ridgers
39
]. In the simulations, the overall computational domain and a single unit cell are both cubic with sizes of
![]() $16\ \unicode{x3bc}\text{m}\times 16\ \unicode{x3bc}\text{m}\times 16$
μm and
$16\ \unicode{x3bc}\text{m}\times 16\ \unicode{x3bc}\text{m}\times 16$
μm and
![]() $20\ \text{nm}\times 20\ \text{nm}\times 20$
nm, respectively. Initially, a cubic aluminum target with the size of
$20\ \text{nm}\times 20\ \text{nm}\times 20$
nm, respectively. Initially, a cubic aluminum target with the size of
![]() $14\ \unicode{x3bc}\text{m}\times 14\ \unicode{x3bc}\text{m}\times 14\ \unicode{x3bc}\text{m}$
is set at the center, which has a cylindrical cavity with a radius of
$14\ \unicode{x3bc}\text{m}\times 14\ \unicode{x3bc}\text{m}\times 14\ \unicode{x3bc}\text{m}$
is set at the center, which has a cylindrical cavity with a radius of
![]() ${R}_0=5$
μm, and its axis overlaps the
${R}_0=5$
μm, and its axis overlaps the
![]() $z$
-axis. The length of the target along the z-axis is chosen to be
$z$
-axis. The length of the target along the z-axis is chosen to be
![]() ${L}_0=7$
μm. The target is composed of a cold and charge-neutral plasma with ion and electron densities of
${L}_0=7$
μm. The target is composed of a cold and charge-neutral plasma with ion and electron densities of
![]() ${n}_{\mathrm{i}0}=5.0\times {10}^{22}$
cm
${n}_{\mathrm{i}0}=5.0\times {10}^{22}$
cm
![]() ${}^{-3}$
and
${}^{-3}$
and
![]() ${n}_{\mathrm{e}0}={Zn}_{\mathrm{i}0}=6.5\times {10}^{23}$
cm
${n}_{\mathrm{e}0}={Zn}_{\mathrm{i}0}=6.5\times {10}^{23}$
cm
![]() ${}^{-3}$
, respectively, with the ionization state
${}^{-3}$
, respectively, with the ionization state
![]() $Z=13$
. Note that, in the following simulations, we assume the fully ionized states of the target materials, that is,
$Z=13$
. Note that, in the following simulations, we assume the fully ionized states of the target materials, that is,
![]() $Z=6$
for carbon and
$Z=6$
for carbon and
![]() $Z=13$
for aluminum, which are well validated under the applied laser intensities
$Z=13$
for aluminum, which are well validated under the applied laser intensities
![]() ${I}_{\mathrm{L}}\gtrsim {10}^{20}$
W cm
${I}_{\mathrm{L}}\gtrsim {10}^{20}$
W cm
![]() ${}^{-2}$
. In addition, because the characteristic electron energies of MTI are of the order of the mega-electron volt (MeV), the plasma is postulated to be collisionless. For a solid cell, 10 and 20 pseudo particles, which respectively correspond to ions and electrons, are assigned. A seed magnetic field
${}^{-2}$
. In addition, because the characteristic electron energies of MTI are of the order of the mega-electron volt (MeV), the plasma is postulated to be collisionless. For a solid cell, 10 and 20 pseudo particles, which respectively correspond to ions and electrons, are assigned. A seed magnetic field
![]() ${B}_0=6$
kT parallel to the
${B}_0=6$
kT parallel to the
![]() $z$
-axis is uniformly set over the entire domain. Owing to limitations in our computational ability, the above cell size and particle numbers assigned to a solid cell are substantially coarser than those treated in 2D simulations, as discussed below.
$z$
-axis is uniformly set over the entire domain. Owing to limitations in our computational ability, the above cell size and particle numbers assigned to a solid cell are substantially coarser than those treated in 2D simulations, as discussed below.
The four faces of the target parallel to the
![]() $z$
-axis are normally irradiated by four laser pulses simultaneously. The pulses are polarized such that the laser electric fields are perpendicular to the seed magnetic field. The applied laser pulses are spatially uniform (planar waves) with a Gaussian shape in time, a laser wavelength
$z$
-axis are normally irradiated by four laser pulses simultaneously. The pulses are polarized such that the laser electric fields are perpendicular to the seed magnetic field. The applied laser pulses are spatially uniform (planar waves) with a Gaussian shape in time, a laser wavelength
![]() ${\lambda}_{\mathrm{L}}=0.8\kern0.1em$
μm, a peak intensity
${\lambda}_{\mathrm{L}}=0.8\kern0.1em$
μm, a peak intensity
![]() ${I}_{\mathrm{L}}=3.0\times {10}^{21}$
W cm
${I}_{\mathrm{L}}=3.0\times {10}^{21}$
W cm
![]() ${}^{-2}$
and a pulse duration
${}^{-2}$
and a pulse duration
![]() ${\tau}_{\mathrm{L}}=50$
fs (FWHM: full width at half maximum). Figures 2(a) and 2(b) show the perspective views of the normalized ion density
${\tau}_{\mathrm{L}}=50$
fs (FWHM: full width at half maximum). Figures 2(a) and 2(b) show the perspective views of the normalized ion density
![]() ${n}_{\mathrm{i}}/{n}_{\mathrm{i}0}$
and the
${n}_{\mathrm{i}}/{n}_{\mathrm{i}0}$
and the
![]() $z$
-component of the magnetic field
$z$
-component of the magnetic field
![]() ${B}_{{z}}$
, respectively, when the peak value
${B}_{{z}}$
, respectively, when the peak value
![]() ${B}_{{z}}=1.03$
MT is achieved at
${B}_{{z}}=1.03$
MT is achieved at
![]() $t\simeq 200$
fs on the central axis. The figures show a quarter of the full target volume where the two centrally orthogonal surfaces are on the left and their magnified views are on the right. Comparing the 2D and 3D results indicates that the overall plasma behavior and the achieved key physical quantities, such as the maximum magnetic field and current, agree with each other. In fact,
$t\simeq 200$
fs on the central axis. The figures show a quarter of the full target volume where the two centrally orthogonal surfaces are on the left and their magnified views are on the right. Comparing the 2D and 3D results indicates that the overall plasma behavior and the achieved key physical quantities, such as the maximum magnetic field and current, agree with each other. In fact,
![]() ${B}_{\mathrm{max}}=1.2$
MT is obtained in the 2D EPOCH simulation, as shown below, instead of
${B}_{\mathrm{max}}=1.2$
MT is obtained in the 2D EPOCH simulation, as shown below, instead of
![]() ${B}_{\mathrm{max}}=1.0$
MT in the 3D simulations.
${B}_{\mathrm{max}}=1.0$
MT in the 3D simulations.
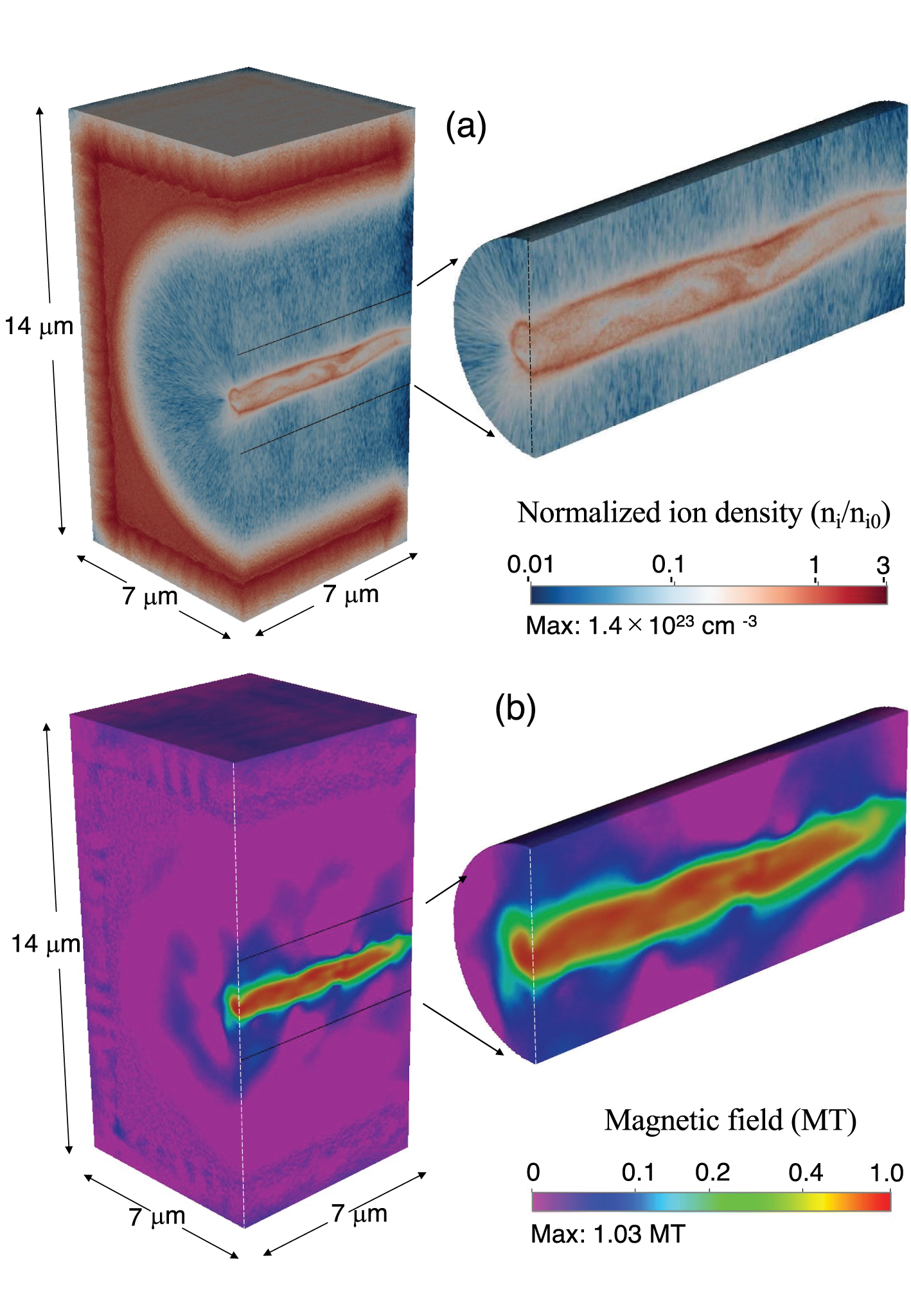
Figure 2 Perspective views of the normalized ion density
![]() ${n}_{\mathrm{i}}/{n}_{\mathrm{i}0}$
and the
${n}_{\mathrm{i}}/{n}_{\mathrm{i}0}$
and the
![]() $z$
-component of the magnetic field
$z$
-component of the magnetic field
![]() ${B}_{{z}}$
, respectively, observed at
${B}_{{z}}$
, respectively, observed at
![]() $t\sim 200$
fs, which is obtained by a 3D EPOCH simulation. A cubic aluminum target with a size of
$t\sim 200$
fs, which is obtained by a 3D EPOCH simulation. A cubic aluminum target with a size of
![]() $14\ \unicode{x3bc}\text{m}\times 14\ \unicode{x3bc}\text{m}\times 14\ \unicode{x3bc}\text{m}$
is set at the center, which has a cylindrical cavity with a radius of
$14\ \unicode{x3bc}\text{m}\times 14\ \unicode{x3bc}\text{m}\times 14\ \unicode{x3bc}\text{m}$
is set at the center, which has a cylindrical cavity with a radius of
![]() ${R}_0=5\kern0.1em$
μm and an axis overlapping the
${R}_0=5\kern0.1em$
μm and an axis overlapping the
![]() $z$
-axis. The seed magnetic field
$z$
-axis. The seed magnetic field
![]() ${B}_0=6$
kT parallel to the
${B}_0=6$
kT parallel to the
![]() $z$
-axis is uniformly set over the entire domain. The four faces of the target parallel to the
$z$
-axis is uniformly set over the entire domain. The four faces of the target parallel to the
![]() $z$
-axis are normally irradiated by uniform laser pulses simultaneously, which are characterized by
$z$
-axis are normally irradiated by uniform laser pulses simultaneously, which are characterized by
![]() ${\lambda}_{\mathrm{L}}=0.8\kern0.1em$
μm,
${\lambda}_{\mathrm{L}}=0.8\kern0.1em$
μm,
![]() ${I}_{\mathrm{L}}=3\times {10}^{21}$
W cm
${I}_{\mathrm{L}}=3\times {10}^{21}$
W cm
![]() ${}^{-2}$
and
${}^{-2}$
and
![]() ${\tau}_{\mathrm{L}}=50$
fs.
${\tau}_{\mathrm{L}}=50$
fs.
Owing to the expansion of the inner wall plasma toward the central axis, the plasma density value drops two orders of magnitude lower in the middle of the cylindrical cavity. However, both the ions and electrons are rapidly compressed near the center due to the cylindrical converging effect, which reaches a few times the value of the solid density. As a result, a hollow cylindrical structure with a diameter of approximately
![]() $700$
nm forms along the
$700$
nm forms along the
![]() $z$
-axis (Figure 2(a)). This round-shaped cross-section forms the Larmor ring[
Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov
25
], which is composed of an envelope of the converging and diverging ion trajectories under the effect of the seed magnetic field. The ions and electrons around the Larmor ring collectively work to generate ultrahigh magnetic fields of the MT order at the center, as confirmed in Figure 2(b). Thus, Figure 2 demonstrates that the MTI concept indeed works under the 3D configuration with practical target and laser conditions. From the 3D simulations, a target structure with
$z$
-axis (Figure 2(a)). This round-shaped cross-section forms the Larmor ring[
Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov
25
], which is composed of an envelope of the converging and diverging ion trajectories under the effect of the seed magnetic field. The ions and electrons around the Larmor ring collectively work to generate ultrahigh magnetic fields of the MT order at the center, as confirmed in Figure 2(b). Thus, Figure 2 demonstrates that the MTI concept indeed works under the 3D configuration with practical target and laser conditions. From the 3D simulations, a target structure with
![]() ${L}_0/{R}_0\gtrsim$
1–2 is sufficient to achieve the same degree of the maximum magnetic field as the 2D results (not described in detail in this paper).
${L}_0/{R}_0\gtrsim$
1–2 is sufficient to achieve the same degree of the maximum magnetic field as the 2D results (not described in detail in this paper).
2.2 2D EPOCH simulations
We also conducted 2D PIC simulations under similar conditions to the above 3D case. Here we employ solid aluminum as the target material. For a solid element, we set 50 and 100 pseudo particles/cell for ions and electrons, respectively. The full size of a computational box is
![]() $22\ \unicode{x3bc}\text{m}\times 22\ \unicode{x3bc}\text{m}$
, while the size of a single cell is 10 nm. This corresponds to a resolution of 100 cells/μm with a total simulation domain size of
$22\ \unicode{x3bc}\text{m}\times 22\ \unicode{x3bc}\text{m}$
, while the size of a single cell is 10 nm. This corresponds to a resolution of 100 cells/μm with a total simulation domain size of
![]() $2200\times 2200$
meshes. Although uniformity issues with respect to laser illumination and plasma implosion are crucial topics of MTI, especially in terms of the number of laser beams[
Reference Murakami and Nishi
40
], they are beyond the scope of this study.
$2200\times 2200$
meshes. Although uniformity issues with respect to laser illumination and plasma implosion are crucial topics of MTI, especially in terms of the number of laser beams[
Reference Murakami and Nishi
40
], they are beyond the scope of this study.
The square-shaped microtube target with a coaxial circular void is placed at the center of the computational box. The initial inner radius of the microtube
![]() ${R}_0=5\kern0.1em$
μm and the minimum thickness of the wall
${R}_0=5\kern0.1em$
μm and the minimum thickness of the wall
![]() $\Delta R=2\kern0.1em$
μm are fixed. The side lengths of the square are
$\Delta R=2\kern0.1em$
μm are fixed. The side lengths of the square are
![]() ${D}_0=2\left({R}_0+\Delta R\right)=14\kern0.1em$
μm. The seed magnetic field is again
${D}_0=2\left({R}_0+\Delta R\right)=14\kern0.1em$
μm. The seed magnetic field is again
![]() ${B}_0=6$
kT along the
${B}_0=6$
kT along the
![]() $z$
-axis. Note that
$z$
-axis. Note that
![]() ${B}_0=4$
kT produces almost the same simulation results as
${B}_0=4$
kT produces almost the same simulation results as
![]() ${B}_0=6$
kT, while
${B}_0=6$
kT, while
![]() ${B}_0=2$
kT has a significantly lower performance for the magnetic field generation than
${B}_0=2$
kT has a significantly lower performance for the magnetic field generation than
![]() ${B}_0=6$
kT (not discussed in detail in this paper). Similar to the 3D case, the four faces of the microtube are normally and simultaneously irradiated by uniform laser pulses with
${B}_0=6$
kT (not discussed in detail in this paper). Similar to the 3D case, the four faces of the microtube are normally and simultaneously irradiated by uniform laser pulses with
![]() ${\lambda}_{\mathrm{L}}=0.8\kern0.1em$
μm and
${\lambda}_{\mathrm{L}}=0.8\kern0.1em$
μm and
![]() $\tau =50$
fs (FWHM). In the 2D simulations, the laser peak intensity ranges from
$\tau =50$
fs (FWHM). In the 2D simulations, the laser peak intensity ranges from
![]() ${I}_{\mathrm{L}}=3.7\times {10}^{19}$
to
${I}_{\mathrm{L}}=3.7\times {10}^{19}$
to
![]() $2.7\times {10}^{22}$
W cm
$2.7\times {10}^{22}$
W cm
![]() ${}^{-2}$
.
${}^{-2}$
.
Figure 3 shows the temporal evolution of the magnetic field generation with four different laser intensities. The sign of the generated magnetic fields is positive if the generated fields are in the same direction as the seed magnetic field. At
![]() $t\sim 110$
fs, the peak of the laser pulse reaches the target center. The maximum magnetic fields generated by MTI depend on the applied laser intensity. As the laser intensity increases, the magnetic field is generated earlier and reaches a higher peak
$t\sim 110$
fs, the peak of the laser pulse reaches the target center. The maximum magnetic fields generated by MTI depend on the applied laser intensity. As the laser intensity increases, the magnetic field is generated earlier and reaches a higher peak
![]() ${B}_{\mathrm{max}}$
. This is because the imploding plasma driven by hot electrons, which has a higher temperature due to heating with a higher laser intensity[
Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov
25
], fills the microtube cavity more quickly. As expected, all those curves show that the magnetic fields are generated in the same direction as that of the seed magnetic field.
${B}_{\mathrm{max}}$
. This is because the imploding plasma driven by hot electrons, which has a higher temperature due to heating with a higher laser intensity[
Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov
25
], fills the microtube cavity more quickly. As expected, all those curves show that the magnetic fields are generated in the same direction as that of the seed magnetic field.
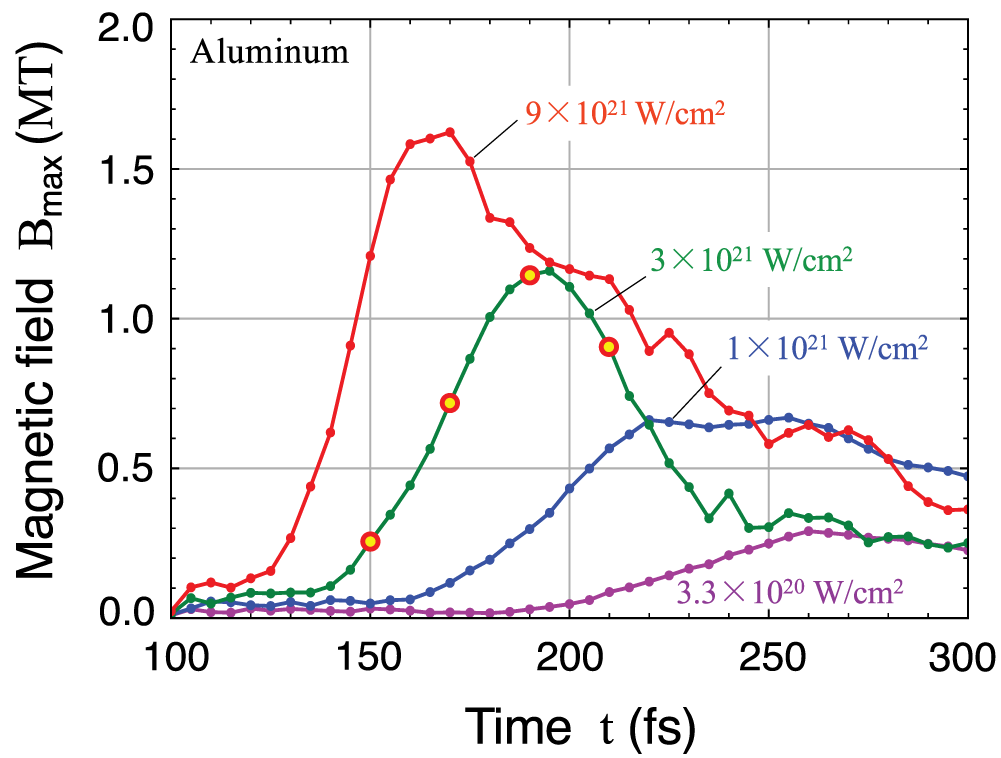
Figure 3 Temporal evolution of the central magnetic field, obtained from 2D EPOCH simulations, under four different laser intensities
![]() ${I}_{\mathrm{L}}$
, which are labelled and applied to an aluminum target (
${I}_{\mathrm{L}}$
, which are labelled and applied to an aluminum target (
![]() ${n}_{\mathrm{i}0}=5\times {10}^{22}$
cm
${n}_{\mathrm{i}0}=5\times {10}^{22}$
cm
![]() ${}^{-3}$
,
${}^{-3}$
,
![]() $A=27$
and
$A=27$
and
![]() $Z=13$
). Other fixed parameters are
$Z=13$
). Other fixed parameters are
![]() ${R}_0=5\kern0.1em$
μm,
${R}_0=5\kern0.1em$
μm,
![]() ${D}_0=14\kern0.1em$
μm,
${D}_0=14\kern0.1em$
μm,
![]() ${\lambda}_{\mathrm{L}}=0.8\kern0.1em$
μm,
${\lambda}_{\mathrm{L}}=0.8\kern0.1em$
μm,
![]() ${\tau}_{\mathrm{L}}=50$
fs and
${\tau}_{\mathrm{L}}=50$
fs and
![]() ${B}_0=6$
kT. The target is assumed to be uniformly irradiated on the four sides. The laser peak time is
${B}_0=6$
kT. The target is assumed to be uniformly irradiated on the four sides. The laser peak time is
![]() $t=75$
fs. The four highlighted circles on the green curve correspond to the sampling times for the 2D patterns given in Figure 4.
$t=75$
fs. The four highlighted circles on the green curve correspond to the sampling times for the 2D patterns given in Figure 4.
Figure 4 shows snapshots of the 2D patterns for the magnetic field (upper row), the total current (middle row) and the electron density (lower row) normalized by the initial value (
![]() ${n}_{\mathrm{e}0}={Zn}_{\mathrm{i}0}=6.5\times {10}^{23}$
cm
${n}_{\mathrm{e}0}={Zn}_{\mathrm{i}0}=6.5\times {10}^{23}$
cm
![]() ${}^{-3}$
), which correspond to the four highlighted times on the green curve in Figure 3 (
${}^{-3}$
), which correspond to the four highlighted times on the green curve in Figure 3 (
![]() ${I}_{\mathrm{L}}=3.0\times {10}^{21}$
W cm
${I}_{\mathrm{L}}=3.0\times {10}^{21}$
W cm
![]() ${}^{-2}$
). Just after the collapse of the microtube cavity at
${}^{-2}$
). Just after the collapse of the microtube cavity at
![]() $t=130$
fs (Figure 3), spin currents run around the center form. The currents reach 0.3 PA cm
$t=130$
fs (Figure 3), spin currents run around the center form. The currents reach 0.3 PA cm
![]() ${}^{-2}$
with a characteristic diameter of
${}^{-2}$
with a characteristic diameter of
![]() $\sim 1\kern0.1em$
μm at
$\sim 1\kern0.1em$
μm at
![]() $t=190$
fs when the maximum magnetic field
$t=190$
fs when the maximum magnetic field
![]() ${B}_{\mathrm{max}}\simeq 1.2$
MT. These spin currents are produced mainly by electrons. This is also supported by the fact that the ring structures of the electron density correspond to the solid density,
${B}_{\mathrm{max}}\simeq 1.2$
MT. These spin currents are produced mainly by electrons. This is also supported by the fact that the ring structures of the electron density correspond to the solid density,
![]() ${n}_{\mathrm{e}}\sim 0.3{n}_{\mathrm{e}0}\simeq 2\times {10}^{23}$
cm
${n}_{\mathrm{e}}\sim 0.3{n}_{\mathrm{e}0}\simeq 2\times {10}^{23}$
cm
![]() ${}^{-3}$
. Meanwhile, practically no electrons are contained in the central area, which is referred to as the Larmor hole in Ref. [Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov25].
${}^{-3}$
. Meanwhile, practically no electrons are contained in the central area, which is referred to as the Larmor hole in Ref. [Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov25].

Figure 4 Snapshots of the 2D patterns for the magnetic field (upper row), the total current vectors (middle row) and the electron density (lower row) normalized by the initial value (
![]() ${n}_{\mathrm{e}0}={Zn}_{\mathrm{i}0}=6.5\times {10}^{23}$
cm
${n}_{\mathrm{e}0}={Zn}_{\mathrm{i}0}=6.5\times {10}^{23}$
cm
![]() ${}^{-3}$
), corresponding to the four highlighted times on the green curve in Figure 3 (
${}^{-3}$
), corresponding to the four highlighted times on the green curve in Figure 3 (
![]() ${I}_{\mathrm{L}}=3.0\times {10}^{21}$
W/cm
${I}_{\mathrm{L}}=3.0\times {10}^{21}$
W/cm
![]() ${}^2$
). Generated magnetic fields are assumed to be positive if they are in the same direction as the seed magnetic field (
${}^2$
). Generated magnetic fields are assumed to be positive if they are in the same direction as the seed magnetic field (
![]() ${B}_0=6$
kT). Just after the collapse of the microtube cavity at around
${B}_0=6$
kT). Just after the collapse of the microtube cavity at around
![]() $t=130$
fs, the spin-structured plasma flow due to the seed magnetic field is formed, increasing the magnetic strength, as observed in the current patterns.
$t=130$
fs, the spin-structured plasma flow due to the seed magnetic field is formed, increasing the magnetic strength, as observed in the current patterns.
3 Model for laser scaling
The achievable magnetic field of an MTI is given as[ Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov 25 ]
 \begin{align}{B}_{\mathrm{max}}\kern0.1em \left[\mathrm{MT}\right]=\frac{{\left(Z/6\right)}^{3/2}}{{\left(A/12\right)}^{1/2}}\left(\frac{n_{\mathrm{i}0}}{10^{23}\kern0.1em {\mathrm{cm}}^{-3}}\right)\left(\frac{R_0}{3\,\,\unicode{x3bc}\mathrm{m}}\right)\sqrt{\frac{{\mathrm{\mathcal{E}}}_{\mathrm{av}}}{6\ \mathrm{MeV}}},\end{align}
\begin{align}{B}_{\mathrm{max}}\kern0.1em \left[\mathrm{MT}\right]=\frac{{\left(Z/6\right)}^{3/2}}{{\left(A/12\right)}^{1/2}}\left(\frac{n_{\mathrm{i}0}}{10^{23}\kern0.1em {\mathrm{cm}}^{-3}}\right)\left(\frac{R_0}{3\,\,\unicode{x3bc}\mathrm{m}}\right)\sqrt{\frac{{\mathrm{\mathcal{E}}}_{\mathrm{av}}}{6\ \mathrm{MeV}}},\end{align}
where
![]() $A$
and
$A$
and
![]() ${\mathrm{\mathcal{E}}}_{\mathrm{av}}$
are the atomic mass number for the target material and the average energy of the hot electrons, respectively. The derivation of Equation (1) assumes that the electron energy distribution follows the Maxwell–Jüttner (M-J) distribution[
Reference Jüttner
41
], which is characterized by a single temperature
${\mathrm{\mathcal{E}}}_{\mathrm{av}}$
are the atomic mass number for the target material and the average energy of the hot electrons, respectively. The derivation of Equation (1) assumes that the electron energy distribution follows the Maxwell–Jüttner (M-J) distribution[
Reference Jüttner
41
], which is characterized by a single temperature
![]() ${T}_{\mathrm{e}}$
, because the
${T}_{\mathrm{e}}$
, because the
![]() ${\mathrm{\mathcal{E}}}_{\mathrm{av}}$
of interest spans the relativistic regime. For the M-J distribution (
${\mathrm{\mathcal{E}}}_{\mathrm{av}}$
of interest spans the relativistic regime. For the M-J distribution (
![]() ${\mathrm{\mathcal{E}}}_{\mathrm{av}}\gg {mc}^2$
), the two variables are approximately related as
${\mathrm{\mathcal{E}}}_{\mathrm{av}}\gg {mc}^2$
), the two variables are approximately related as
![]() ${\mathrm{\mathcal{E}}}_{\mathrm{av}}\simeq 3{T}_{\mathrm{e}}$
. Here, we use Equation (1) to derive the scaling in terms of the practical laser and target parameters, and then to confirm that the scaling well reproduces the simulation results.
${\mathrm{\mathcal{E}}}_{\mathrm{av}}\simeq 3{T}_{\mathrm{e}}$
. Here, we use Equation (1) to derive the scaling in terms of the practical laser and target parameters, and then to confirm that the scaling well reproduces the simulation results.
Firstly, we simply estimate the averaged electron energy
![]() ${\mathrm{\mathcal{E}}}_{\mathrm{av}}$
assuming that the absorbed laser energy is uniformly transferred to all the electrons contained in the target as
${\mathrm{\mathcal{E}}}_{\mathrm{av}}$
assuming that the absorbed laser energy is uniformly transferred to all the electrons contained in the target as
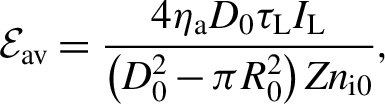 \begin{align}{\mathrm{\mathcal{E}}}_{\mathrm{a}\mathrm{v}}=\frac{4{\eta}_{\mathrm{a}}{D}_0{\tau}_{\mathrm{L}}{I}_{\mathrm{L}}}{\left({D}_0^2-\pi {R}_0^2\right){Zn}_{\mathrm{i}0}},\end{align}
\begin{align}{\mathrm{\mathcal{E}}}_{\mathrm{a}\mathrm{v}}=\frac{4{\eta}_{\mathrm{a}}{D}_0{\tau}_{\mathrm{L}}{I}_{\mathrm{L}}}{\left({D}_0^2-\pi {R}_0^2\right){Zn}_{\mathrm{i}0}},\end{align}
where
![]() ${\eta}_{\mathrm{a}}$
and
${\eta}_{\mathrm{a}}$
and
![]() ${D}_0$
denote the laser absorption efficiency and the initial length of each side of the square cross-section target, respectively. To derive Equation (2), we assume that the target is irradiated on its four sides by spatially uniform lasers at an intensity of
${D}_0$
denote the laser absorption efficiency and the initial length of each side of the square cross-section target, respectively. To derive Equation (2), we assume that the target is irradiated on its four sides by spatially uniform lasers at an intensity of
![]() ${I}_{\mathrm{L}}$
with a Gaussian pulse duration of
${I}_{\mathrm{L}}$
with a Gaussian pulse duration of
![]() ${\tau}_{\mathrm{L}}$
(FWHM).
${\tau}_{\mathrm{L}}$
(FWHM).
A previous study summarized various experimental data on the laser absorption efficiency for the domain
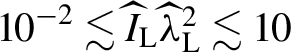 ${10}^{-2}\lesssim {\widehat{I}}_{\mathrm{L}}{\widehat{\lambda}}_{\mathrm{L}}^2\lesssim 10$
, and gave the laser absorption efficiency in the form of
${10}^{-2}\lesssim {\widehat{I}}_{\mathrm{L}}{\widehat{\lambda}}_{\mathrm{L}}^2\lesssim 10$
, and gave the laser absorption efficiency in the form of
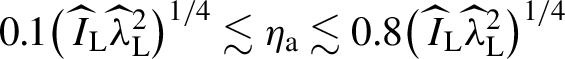 $0.1{\left({{\kern2pt}\widehat{I}}_{\mathrm{L}}{\widehat{\lambda}}_{\mathrm{L}}^2\right)}^{1/4}\lesssim {\eta}_{\mathrm{a}}\lesssim 0.8{\left({{\kern2pt}\widehat{I}}_{\mathrm{L}}{\widehat{\lambda}}_{\mathrm{L}}^2\right)}^{1/4}$
, where
$0.1{\left({{\kern2pt}\widehat{I}}_{\mathrm{L}}{\widehat{\lambda}}_{\mathrm{L}}^2\right)}^{1/4}\lesssim {\eta}_{\mathrm{a}}\lesssim 0.8{\left({{\kern2pt}\widehat{I}}_{\mathrm{L}}{\widehat{\lambda}}_{\mathrm{L}}^2\right)}^{1/4}$
, where
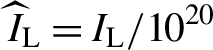 ${\widehat{I}}_{\mathrm{L}}={I}_{\mathrm{L}}/{10}^{20}$
W cm
${\widehat{I}}_{\mathrm{L}}={I}_{\mathrm{L}}/{10}^{20}$
W cm
![]() ${}^{-2}$
and
${}^{-2}$
and
 ${\widehat{\lambda}}_{\mathrm{L}}={\lambda}_{\mathrm{L}}/1$
μm[
Reference Levy, Wilks, Tabak, Libby and Baring
42
]. The complementary domains,
${\widehat{\lambda}}_{\mathrm{L}}={\lambda}_{\mathrm{L}}/1$
μm[
Reference Levy, Wilks, Tabak, Libby and Baring
42
]. The complementary domains,
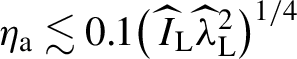 ${\eta}_{\mathrm{a}}\lesssim 0.1{\left({{\kern2pt}\widehat{I}}_{\mathrm{L}}{\widehat{\lambda}}_{\mathrm{L}}^2\right)}^{1/4}$
and
${\eta}_{\mathrm{a}}\lesssim 0.1{\left({{\kern2pt}\widehat{I}}_{\mathrm{L}}{\widehat{\lambda}}_{\mathrm{L}}^2\right)}^{1/4}$
and
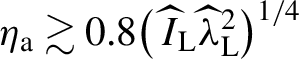 ${\eta}_{\mathrm{a}}\gtrsim 0.8{\left({{\kern2pt}\widehat{I}}_{\mathrm{L}}{\widehat{\lambda}}_{\mathrm{L}}^2\right)}^{1/4}$
correspond to the ‘forbidden’ domain[
Reference Levy, Wilks, Tabak, Libby and Baring
42
], in which no experimental results can be found. In principle,
${\eta}_{\mathrm{a}}\gtrsim 0.8{\left({{\kern2pt}\widehat{I}}_{\mathrm{L}}{\widehat{\lambda}}_{\mathrm{L}}^2\right)}^{1/4}$
correspond to the ‘forbidden’ domain[
Reference Levy, Wilks, Tabak, Libby and Baring
42
], in which no experimental results can be found. In principle,
![]() ${\eta}_{\mathrm{a}}$
is bounded as
${\eta}_{\mathrm{a}}$
is bounded as
![]() ${\eta}_{\mathrm{a}}\leqq 1$
. Thus,
${\eta}_{\mathrm{a}}\leqq 1$
. Thus,
![]() ${\eta}_{\mathrm{a}}$
can be approximately formulated in a simple form that can also be used for a higher intensity domain
${\eta}_{\mathrm{a}}$
can be approximately formulated in a simple form that can also be used for a higher intensity domain
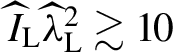 ${\widehat{I}}_{\mathrm{L}}{\widehat{\lambda}}_{\mathrm{L}}^2\gtrsim 10$
:
${\widehat{I}}_{\mathrm{L}}{\widehat{\lambda}}_{\mathrm{L}}^2\gtrsim 10$
:
 \begin{align}{\eta}_{\mathrm{a}}\approx {\left(1+\frac{1}{\eta_0{\left({{\kern2pt}\widehat{I}}_{\mathrm{L}}{\widehat{\lambda}}_{\mathrm{L}}^2\right)}^{1/4}}\right)}^{-1},\kern1em 0.1\lesssim {\eta}_0\lesssim 0.8.\end{align}
\begin{align}{\eta}_{\mathrm{a}}\approx {\left(1+\frac{1}{\eta_0{\left({{\kern2pt}\widehat{I}}_{\mathrm{L}}{\widehat{\lambda}}_{\mathrm{L}}^2\right)}^{1/4}}\right)}^{-1},\kern1em 0.1\lesssim {\eta}_0\lesssim 0.8.\end{align}
From Equations (1)–(3), the scaling for the maximum magnetic fields is obtained in terms of the laser and target parameters as
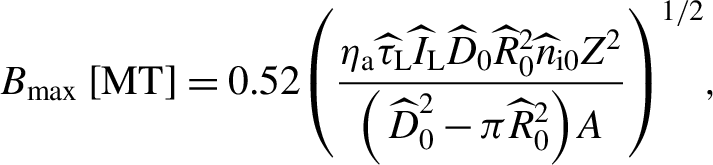 \begin{align}{B}_{\mathrm{max}}\kern0.1em \left[\mathrm{MT}\right]=0.52{\left(\frac{\eta_{\mathrm{a}}{\widehat{\tau}}_{\mathrm{L}}{\widehat{I}}_{\mathrm{L}}{\widehat{D}}_0{\widehat{R}}_0^2{\widehat{n}}_{\mathrm{i}0}{Z}^2}{\left({{\kern2pt}\widehat{D}}_0^2-\pi {\widehat{R}}_0^2\right)A}\right)}^{1/2},\end{align}
\begin{align}{B}_{\mathrm{max}}\kern0.1em \left[\mathrm{MT}\right]=0.52{\left(\frac{\eta_{\mathrm{a}}{\widehat{\tau}}_{\mathrm{L}}{\widehat{I}}_{\mathrm{L}}{\widehat{D}}_0{\widehat{R}}_0^2{\widehat{n}}_{\mathrm{i}0}{Z}^2}{\left({{\kern2pt}\widehat{D}}_0^2-\pi {\widehat{R}}_0^2\right)A}\right)}^{1/2},\end{align}
where
![]() ${\widehat{n}}_{\mathrm{i}0}={n}_{\mathrm{i}0}/{10}^{23}$
cm
${\widehat{n}}_{\mathrm{i}0}={n}_{\mathrm{i}0}/{10}^{23}$
cm
![]() ${}^{-3}$
,
${}^{-3}$
,
![]() ${\widehat{\tau}}_{\mathrm{L}}={\tau}_{\mathrm{L}}/1$
ps,
${\widehat{\tau}}_{\mathrm{L}}={\tau}_{\mathrm{L}}/1$
ps,
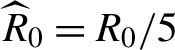 ${\widehat{R}}_0={R}_0/5\kern0.1em$
μm and
${\widehat{R}}_0={R}_0/5\kern0.1em$
μm and
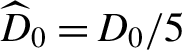 ${\widehat{D}}_0={D}_0/5\kern0.1em$
μm.
${\widehat{D}}_0={D}_0/5\kern0.1em$
μm.
Figure 5 shows the scaling for the maximum magnetic field
![]() ${B}_{\mathrm{max}}$
, laser energy
${B}_{\mathrm{max}}$
, laser energy
![]() ${E}_{\mathrm{L}}$
and laser power
${E}_{\mathrm{L}}$
and laser power
![]() ${P}_{\mathrm{L}}$
in terms of the laser intensity
${P}_{\mathrm{L}}$
in terms of the laser intensity
![]() ${I}_{\mathrm{L}}$
for a square target with
${I}_{\mathrm{L}}$
for a square target with
![]() ${R}_0=5\kern0.1em$
μm and
${R}_0=5\kern0.1em$
μm and
![]() ${D}_0=14$
μm and a seed magnetic field
${D}_0=14$
μm and a seed magnetic field
![]() ${B}_0=6$
kT. Laser pulses with
${B}_0=6$
kT. Laser pulses with
![]() ${\lambda}_{\mathrm{L}}=0.8\kern0.1em$
μm,
${\lambda}_{\mathrm{L}}=0.8\kern0.1em$
μm,
![]() ${\tau}_{\mathrm{L}}=50$
ps are assumed to uniformly irradiate the four target surfaces. For the 2D EPOCH simulations, here we employ two different solid materials: aluminum (
${\tau}_{\mathrm{L}}=50$
ps are assumed to uniformly irradiate the four target surfaces. For the 2D EPOCH simulations, here we employ two different solid materials: aluminum (
![]() ${n}_{\mathrm{i}0}=5\times {10}^{22}$
cm
${n}_{\mathrm{i}0}=5\times {10}^{22}$
cm
![]() ${}^{-3}$
,
${}^{-3}$
,
![]() $Z=13$
and
$Z=13$
and
![]() $A=27$
) and carbon (
$A=27$
) and carbon (
![]() ${n}_{\mathrm{i}0}=1\times {10}^{23}$
cm
${n}_{\mathrm{i}0}=1\times {10}^{23}$
cm
![]() ${}^{-3}$
,
${}^{-3}$
,
![]() $Z=6$
and
$Z=6$
and
![]() $A=12$
), to compare the performance of magnetic field generation. The blue and red circles denote aluminum and carbon, respectively.
$A=12$
), to compare the performance of magnetic field generation. The blue and red circles denote aluminum and carbon, respectively.
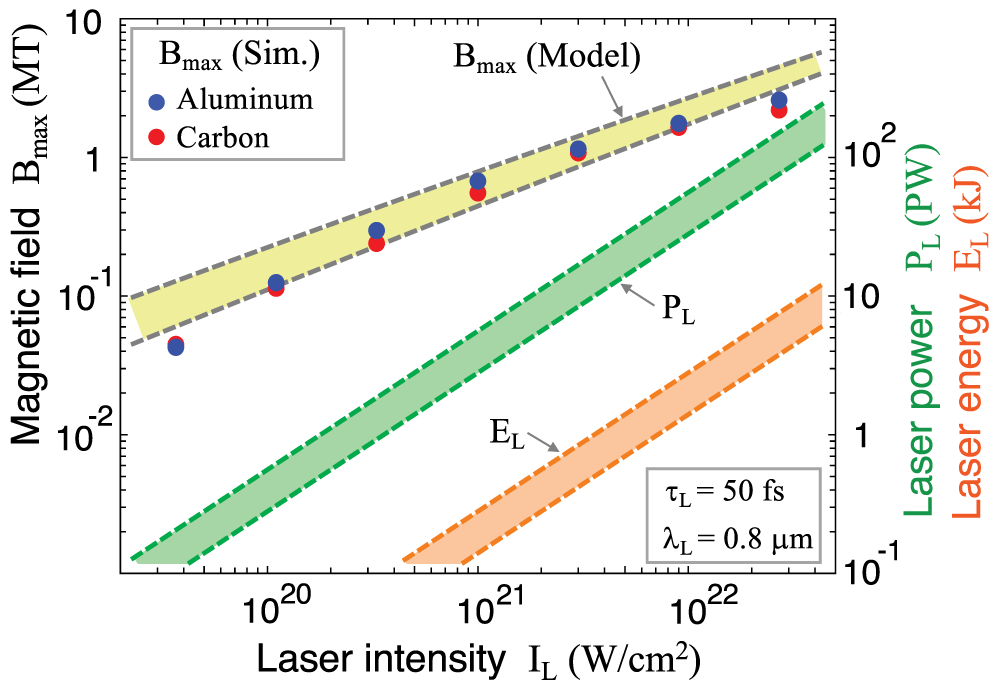
Figure 5 Scaling for
![]() ${B}_{\mathrm{max}}$
,
${B}_{\mathrm{max}}$
,
![]() ${P}_{\mathrm{L}}$
and
${P}_{\mathrm{L}}$
and
![]() ${E}_{\mathrm{L}}$
in terms of
${E}_{\mathrm{L}}$
in terms of
![]() ${I}_{\mathrm{L}}$
. A square target is used with parameters
${I}_{\mathrm{L}}$
. A square target is used with parameters
![]() ${R}_0=5\kern0.1em$
μm and
${R}_0=5\kern0.1em$
μm and
![]() ${D}_0=14\kern0.1em$
μm. The laser is assumed to uniformly irradiate the four target surfaces. The fixed parameters for the 2D simulations are
${D}_0=14\kern0.1em$
μm. The laser is assumed to uniformly irradiate the four target surfaces. The fixed parameters for the 2D simulations are
![]() ${\lambda}_{\mathrm{L}}=0.8\kern0.1em$
μm,
${\lambda}_{\mathrm{L}}=0.8\kern0.1em$
μm,
![]() ${\tau}_{\mathrm{L}}=50$
ps and
${\tau}_{\mathrm{L}}=50$
ps and
![]() ${B}_0=6$
kT. Yellow shading denotes the model prediction, which is given in Equation (4), and the two bounding dashed curves correspond to the minimum and maximum laser absorption efficiencies (
${B}_0=6$
kT. Yellow shading denotes the model prediction, which is given in Equation (4), and the two bounding dashed curves correspond to the minimum and maximum laser absorption efficiencies (
![]() $0.1\lesssim {\eta}_0\lesssim 0.8$
) in Equation (3). To draw the model curve for
$0.1\lesssim {\eta}_0\lesssim 0.8$
) in Equation (3). To draw the model curve for
![]() ${P}_{\mathrm{L}}$
and
${P}_{\mathrm{L}}$
and
![]() ${E}_{\mathrm{L}}$
, an optimized aspect ratio
${E}_{\mathrm{L}}$
, an optimized aspect ratio
![]() $1\lesssim {L}_0/{R}_0\lesssim 2$
is postulated.
$1\lesssim {L}_0/{R}_0\lesssim 2$
is postulated.
Surprisingly, the simulation results for these two materials are in close vicinity to each other at all applied laser intensities. This coherent behavior can be explained by Equation (4), because the material-dependent part of Equation (4) has similar values for the two materials (i.e.,
![]() ${\widehat{n}}_{\mathrm{i}0}{Z}^2/A\simeq 3$
). At first glance, the results appear to be independent of the material.
${\widehat{n}}_{\mathrm{i}0}{Z}^2/A\simeq 3$
). At first glance, the results appear to be independent of the material.
The yellow shading in Figure 5 denotes the model prediction, where Equation (4) is applied with the above laser and target parameters. The shading is bounded by the two dashed curves, which correspond to the minimum and maximum laser absorption efficiency (
![]() $0.1\lesssim {\eta}_0\lesssim 0.8$
) in Equation (3). The simulation results are well reproduced by the model prediction, especially in the range of
$0.1\lesssim {\eta}_0\lesssim 0.8$
) in Equation (3). The simulation results are well reproduced by the model prediction, especially in the range of
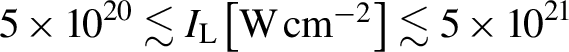 $5\times {10}^{20}\lesssim {I}_{\mathrm{L}}\left[\mathrm{W}\kern0.1em {\mathrm{cm}}^{-2}\right]\lesssim 5\times {10}^{21}$
. It should be noted that a lower seed magnetic field
$5\times {10}^{20}\lesssim {I}_{\mathrm{L}}\left[\mathrm{W}\kern0.1em {\mathrm{cm}}^{-2}\right]\lesssim 5\times {10}^{21}$
. It should be noted that a lower seed magnetic field
![]() ${B}_0=4$
kT gives similar simulation results to those in Figure 5 with
${B}_0=4$
kT gives similar simulation results to those in Figure 5 with
![]() ${B}_0=6$
kT. Moreover, the model, which is given by Equation (4), can well reproduce the EPOCH simulation results not only for the specific values of
${B}_0=6$
kT. Moreover, the model, which is given by Equation (4), can well reproduce the EPOCH simulation results not only for the specific values of
![]() ${R}_0=5\kern0.1em$
μm and
${R}_0=5\kern0.1em$
μm and
![]() ${D}_0=14\;$
μm, but also for targets with different values of
${D}_0=14\;$
μm, but also for targets with different values of
![]() ${R}_0$
and
${R}_0$
and
![]() ${D}_0$
ranging
${D}_0$
ranging
![]() $3\ \unicode{x3bc} \mathrm{m}\lesssim {R}_0\lesssim 7\ \unicode{x3bc}$
m and
$3\ \unicode{x3bc} \mathrm{m}\lesssim {R}_0\lesssim 7\ \unicode{x3bc}$
m and
![]() $10\ \unicode{x3bc} \mathrm{m}\lesssim {D}_0\lesssim 18\ \unicode{x3bc}$
m, respectively. The scaling,
$10\ \unicode{x3bc} \mathrm{m}\lesssim {D}_0\lesssim 18\ \unicode{x3bc}$
m, respectively. The scaling,
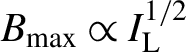 ${B}_{\mathrm{max}}\propto {I}_{\mathrm{L}}^{1/2}$
, can be roughly concluded from Figure 5, which is also confirmed in Equation (4).
${B}_{\mathrm{max}}\propto {I}_{\mathrm{L}}^{1/2}$
, can be roughly concluded from Figure 5, which is also confirmed in Equation (4).
The MTI process has two characteristic timescales: the laser pulse duration
![]() ${\tau}_{\mathrm{L}}$
and the hydrodynamic time scale
${\tau}_{\mathrm{L}}$
and the hydrodynamic time scale
![]() ${\tau}_{\mathrm{H}}\sim {R}_0/{c}_{\mathrm{s}}$
, where
${\tau}_{\mathrm{H}}\sim {R}_0/{c}_{\mathrm{s}}$
, where
![]() ${c}_{\mathrm{s}}={\left({ZT}_{\mathrm{e}}/{m}_{\mathrm{i}}\right)}^{1/2}$
denotes the sound speed, at which the microtube wall expands[
Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov
25
,
Reference Grevich, Pariskaya and Pitaevskii
43
]. From Equation (2),
${c}_{\mathrm{s}}={\left({ZT}_{\mathrm{e}}/{m}_{\mathrm{i}}\right)}^{1/2}$
denotes the sound speed, at which the microtube wall expands[
Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov
25
,
Reference Grevich, Pariskaya and Pitaevskii
43
]. From Equation (2),
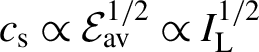 ${c}_{\mathrm{s}}\propto {\mathrm{\mathcal{E}}}_{\mathrm{av}}^{1/2}\propto {I}_{\mathrm{L}}^{1/2}$
, and therefore
${c}_{\mathrm{s}}\propto {\mathrm{\mathcal{E}}}_{\mathrm{av}}^{1/2}\propto {I}_{\mathrm{L}}^{1/2}$
, and therefore
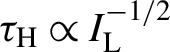 ${\tau}_{\mathrm{H}}\propto {I}_{\mathrm{L}}^{-1/2}$
. To enhance the magnetic field generation in MTI,
${\tau}_{\mathrm{H}}\propto {I}_{\mathrm{L}}^{-1/2}$
. To enhance the magnetic field generation in MTI,
![]() ${\tau}_{\mathrm{L}}$
and
${\tau}_{\mathrm{L}}$
and
![]() ${\tau}_{\mathrm{H}}$
must have coherent lengths. If
${\tau}_{\mathrm{H}}$
must have coherent lengths. If
![]() ${\tau}_{\mathrm{L}}\ll {\tau}_{\mathrm{H}}$
, the absorbed laser energy cannot be effectively transferred to the central core, where strong spin currents and, consequently, strong magnetic fields are generated. Thus, the hydrodynamic efficiency is reduced. On the other hand, if
${\tau}_{\mathrm{L}}\ll {\tau}_{\mathrm{H}}$
, the absorbed laser energy cannot be effectively transferred to the central core, where strong spin currents and, consequently, strong magnetic fields are generated. Thus, the hydrodynamic efficiency is reduced. On the other hand, if
![]() ${\tau}_{\mathrm{L}}\gg {\tau}_{\mathrm{H}}$
, the timing for a substantial part of the laser absorption is out of phase with MTI, reducing the practical absorption efficiency. In fact, the discrepancy between the simulation results and the model prediction in Figure 5 increases for both the laser intensity regimes,
${\tau}_{\mathrm{L}}\gg {\tau}_{\mathrm{H}}$
, the timing for a substantial part of the laser absorption is out of phase with MTI, reducing the practical absorption efficiency. In fact, the discrepancy between the simulation results and the model prediction in Figure 5 increases for both the laser intensity regimes,
![]() ${I}_{\mathrm{L}}\lesssim {10}^{20}$
W cm
${I}_{\mathrm{L}}\lesssim {10}^{20}$
W cm
![]() ${}^{-2}$
and
${}^{-2}$
and
![]() ${I}_{\mathrm{L}}\gtrsim {10}^{22}$
W cm
${I}_{\mathrm{L}}\gtrsim {10}^{22}$
W cm
![]() ${}^{-2}$
, which respectively correspond to
${}^{-2}$
, which respectively correspond to
![]() ${\tau}_{\mathrm{L}}\ll {\tau}_{\mathrm{H}}$
and
${\tau}_{\mathrm{L}}\ll {\tau}_{\mathrm{H}}$
and
![]() ${\tau}_{\mathrm{L}}\gg {\tau}_{\mathrm{H}}$
. In addition, for such an ultrahigh intensity regime,
${\tau}_{\mathrm{L}}\gg {\tau}_{\mathrm{H}}$
. In addition, for such an ultrahigh intensity regime,
![]() ${I}_{\mathrm{L}}\gg {10}^{22}$
W cm
${I}_{\mathrm{L}}\gg {10}^{22}$
W cm
![]() ${}^{-2}$
, both laser-accelerated ions and electrons become highly relativistic, degrading the generation of ultrahigh spin currents and ultrahigh magnetic fields.
${}^{-2}$
, both laser-accelerated ions and electrons become highly relativistic, degrading the generation of ultrahigh spin currents and ultrahigh magnetic fields.
The interplay between the converging and diverging relativistic charged particles, which is driven by the laser-heated quasi-isothermal plasma, is responsible for the physics ofMTI[
Reference Murakami and Basko
44
]. The most dominant physical quantity is the average electron energy
![]() ${\mathrm{\mathcal{E}}}_{\mathrm{av}}$
, which characterizes the fundamental structure around the Larmor hole, the spin current and the resultant ultrahigh magnetic field[
Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov
25
]. The Larmor hole radius
${\mathrm{\mathcal{E}}}_{\mathrm{av}}$
, which characterizes the fundamental structure around the Larmor hole, the spin current and the resultant ultrahigh magnetic field[
Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov
25
]. The Larmor hole radius
![]() ${R}_{\mathrm{H}}$
, which corresponds to the peak magnetic field at the center, is given by
${R}_{\mathrm{H}}$
, which corresponds to the peak magnetic field at the center, is given by
 \begin{align}{R}_{\mathrm{H}}\kern0.1em \left[\mathrm{nm}\right]=37\kern0.1em {\widehat{B}}_0{\widehat{R}}_0^2{\left(\frac{\left({{\kern2pt}\widehat{D}}_0^2-\pi {\widehat{R}}_0^2\right){\widehat{n}}_{\mathrm{i}0}{Z}^2}{\eta_{\mathrm{a}}{\widehat{D}}_0{\widehat{\tau}}_{\mathrm{L}}{\widehat{I}}_{\mathrm{L}}A}\right)}^{1/2},\end{align}
\begin{align}{R}_{\mathrm{H}}\kern0.1em \left[\mathrm{nm}\right]=37\kern0.1em {\widehat{B}}_0{\widehat{R}}_0^2{\left(\frac{\left({{\kern2pt}\widehat{D}}_0^2-\pi {\widehat{R}}_0^2\right){\widehat{n}}_{\mathrm{i}0}{Z}^2}{\eta_{\mathrm{a}}{\widehat{D}}_0{\widehat{\tau}}_{\mathrm{L}}{\widehat{I}}_{\mathrm{L}}A}\right)}^{1/2},\end{align}
where
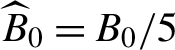 ${\widehat{B}}_0={B}_0/5$
(in kT). The maximum spin current density running around the Larmor hole,
${\widehat{B}}_0={B}_0/5$
(in kT). The maximum spin current density running around the Larmor hole,
![]() ${J}_{\mathrm{H}}\propto \left({R}_0/{R}_{\mathrm{H}}\right){Zn}_{\mathrm{i}0}{c}_{\mathrm{s}}$
, is coherently given as
${J}_{\mathrm{H}}\propto \left({R}_0/{R}_{\mathrm{H}}\right){Zn}_{\mathrm{i}0}{c}_{\mathrm{s}}$
, is coherently given as
 \begin{align}{J}_{\mathrm{H}}\kern0.1em \left[\mathrm{PA}\ {\mathrm{cm}}^{-2}\right]=0.63\kern0.1em \frac{\eta_{\mathrm{a}}{\widehat{D}}_0{\widehat{\tau}}_{\mathrm{L}}{\widehat{I}}_{\mathrm{L}}}{{\widehat{B}}_0{\widehat{R}}_0\left({{\kern2pt}\widehat{D}}_0^2-\pi {\widehat{R}}_0^2\right)}.\end{align}
\begin{align}{J}_{\mathrm{H}}\kern0.1em \left[\mathrm{PA}\ {\mathrm{cm}}^{-2}\right]=0.63\kern0.1em \frac{\eta_{\mathrm{a}}{\widehat{D}}_0{\widehat{\tau}}_{\mathrm{L}}{\widehat{I}}_{\mathrm{L}}}{{\widehat{B}}_0{\widehat{R}}_0\left({{\kern2pt}\widehat{D}}_0^2-\pi {\widehat{R}}_0^2\right)}.\end{align}
Here it should be stressed that
![]() ${J}_{\mathrm{H}}$
does not depend on the material constants of
${J}_{\mathrm{H}}$
does not depend on the material constants of
![]() $A$
,
$A$
,
![]() $Z$
and
$Z$
and
![]() ${n}_{\mathrm{i}0}$
. Moreover, it is confirmed from Equations (4)–(6) that the product of the characteristic current
${n}_{\mathrm{i}0}$
. Moreover, it is confirmed from Equations (4)–(6) that the product of the characteristic current
![]() ${J}_{\mathrm{H}}$
and the radius
${J}_{\mathrm{H}}$
and the radius
![]() ${R}_{\mathrm{H}}$
around the Larmor hole has a coherent parametric relation with the maximum central magnetic field
${R}_{\mathrm{H}}$
around the Larmor hole has a coherent parametric relation with the maximum central magnetic field
![]() ${B}_{\mathrm{max}}$
, which is expressed as
${B}_{\mathrm{max}}$
, which is expressed as
![]() ${B}_{\mathrm{max}}\sim 4\pi {J}_{\mathrm{H}}{R}_{\mathrm{H}}$
, according to Ampere’s law. Applying the specific parameters used in Figure 4, Equations (5) and (6) yield the diameter of a Larmor hole as
${B}_{\mathrm{max}}\sim 4\pi {J}_{\mathrm{H}}{R}_{\mathrm{H}}$
, according to Ampere’s law. Applying the specific parameters used in Figure 4, Equations (5) and (6) yield the diameter of a Larmor hole as
![]() $2{R}_{\mathrm{H}}\simeq 240$
nm and the maximum spin current density
$2{R}_{\mathrm{H}}\simeq 240$
nm and the maximum spin current density
![]() ${J}_{\mathrm{H}}\simeq 0.23$
PA cm
${J}_{\mathrm{H}}\simeq 0.23$
PA cm
![]() ${}^{-2}$
, respectively, where
${}^{-2}$
, respectively, where
![]() ${\eta}_{\mathrm{a}}=0.5$
is fixed as an example. These values agree well with the size of the electron-free area and maximum current density observed at
${\eta}_{\mathrm{a}}=0.5$
is fixed as an example. These values agree well with the size of the electron-free area and maximum current density observed at
![]() $t=190$
fs in Figure 4.
$t=190$
fs in Figure 4.
The total laser power
![]() ${P}_{\mathrm{L}}$
and laser energy
${P}_{\mathrm{L}}$
and laser energy
![]() ${E}_{\mathrm{L}}$
are simply evaluated as
${E}_{\mathrm{L}}$
are simply evaluated as
where
![]() ${L}_0$
denotes the target length along the microtube axis. The laser power and energy missing the target are not counted in Equations (7) and (8). Figure 5 plots
${L}_0$
denotes the target length along the microtube axis. The laser power and energy missing the target are not counted in Equations (7) and (8). Figure 5 plots
![]() ${P}_{\mathrm{L}}$
and
${P}_{\mathrm{L}}$
and
![]() ${E}_{\mathrm{L}}$
obtained by Equations (7) and (8), respectively, by applying the same specific numbers used for the simulations, except
${E}_{\mathrm{L}}$
obtained by Equations (7) and (8), respectively, by applying the same specific numbers used for the simulations, except
![]() ${L}_0/{R}_0\simeq 1$
–2, which are inferred to be acceptable minimum lengths of microtubes to achieve similar values for the maximum magnetic fields obtained by the 2D simulations. Figure 5 also shows the model predictions for
${L}_0/{R}_0\simeq 1$
–2, which are inferred to be acceptable minimum lengths of microtubes to achieve similar values for the maximum magnetic fields obtained by the 2D simulations. Figure 5 also shows the model predictions for
![]() ${P}_{\mathrm{L}}$
and
${P}_{\mathrm{L}}$
and
![]() ${E}_{\mathrm{L}}$
, which are obtained by Equations (7) and (8), respectively, using
${E}_{\mathrm{L}}$
, which are obtained by Equations (7) and (8), respectively, using
![]() $1\lesssim {L}_0/{R}_0\lesssim 2$
.
$1\lesssim {L}_0/{R}_0\lesssim 2$
.
The 2D and 3D performances of magnetic field generation using microtube targets are similar. The results given in Figure 5 show that, for example,
![]() ${B}_{\mathrm{max}}\sim 0.5$
–0.7 MT with
${B}_{\mathrm{max}}\sim 0.5$
–0.7 MT with
![]() ${E}_{\mathrm{L}}\sim 150$
–300 J and
${E}_{\mathrm{L}}\sim 150$
–300 J and
![]() ${P}_{\mathrm{L}}\sim 3$
–6 PW can be achieved upon uniformly irradiating the target at
${P}_{\mathrm{L}}\sim 3$
–6 PW can be achieved upon uniformly irradiating the target at
![]() ${I}_{\mathrm{L}}={10}^{21}$
W cm
${I}_{\mathrm{L}}={10}^{21}$
W cm
![]() ${}^{-2}$
. Such high-power laser performances are accessible by today’s laser technology[
Reference Korn
45
–
Reference Danson, Haefner, Bromage, Butcher and Chanteloup
48
].
${}^{-2}$
. Such high-power laser performances are accessible by today’s laser technology[
Reference Korn
45
–
Reference Danson, Haefner, Bromage, Butcher and Chanteloup
48
].
4 Discussion
We here briefly discuss a criterion of the seed magnetic field in terms of the target and laser parameters to accomplish the current MTI scenario. In MTI, a cylindrically converging flow composed of energetic electrons and ions, which are twisted by the seed magnetic field in opposite directions with respect to the target center, that is, clockwise and anticlockwise, collectively works to produce ultrahigh spin currents and, consequently, ultrahigh magnetic fields. This scenario can be ensured when the Larmor hole radius
![]() ${R}_{\mathrm{H}}$
is sufficiently larger than the local electron Debye length
${R}_{\mathrm{H}}$
is sufficiently larger than the local electron Debye length
![]() ${\lambda}_{\mathrm{D}}$
, that is,
${\lambda}_{\mathrm{D}}$
, that is,
![]() ${R}_{\mathrm{H}}>{\lambda}_{\mathrm{D}}$
, otherwise the flow of relativistic electrons around the center becomes unstable and generates magnetic fields in the opposite direction to the seed field (polarity switching)[
Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov
25
]. This condition is explicitly given as
${R}_{\mathrm{H}}>{\lambda}_{\mathrm{D}}$
, otherwise the flow of relativistic electrons around the center becomes unstable and generates magnetic fields in the opposite direction to the seed field (polarity switching)[
Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov
25
]. This condition is explicitly given as
 \begin{align}\frac{R_{\mathrm{H}}}{\lambda_{\mathrm{D}}}\sim 0.39\frac{{\widehat{R}}_0^2\left({{\kern2pt}\widehat{D}}_0^2-\pi {\widehat{R}}_0^2\right){\widehat{n}}_{\mathrm{i}0}^{3/2}{Z}^2}{\eta_{\mathrm{a}}{\widehat{D}}_0{\widehat{\tau}}_{\mathrm{L}}{\widehat{I}}_{\mathrm{L}}\sqrt{A}}{\widehat{B}}_0>1,\end{align}
\begin{align}\frac{R_{\mathrm{H}}}{\lambda_{\mathrm{D}}}\sim 0.39\frac{{\widehat{R}}_0^2\left({{\kern2pt}\widehat{D}}_0^2-\pi {\widehat{R}}_0^2\right){\widehat{n}}_{\mathrm{i}0}^{3/2}{Z}^2}{\eta_{\mathrm{a}}{\widehat{D}}_0{\widehat{\tau}}_{\mathrm{L}}{\widehat{I}}_{\mathrm{L}}\sqrt{A}}{\widehat{B}}_0>1,\end{align}
where the local electron density at the center just after the cavity collapse is approximated as
![]() ${n}_{\mathrm{e}}\sim {Zn}_{\mathrm{i}0}$
, which is demonstrated by EPOCH simulations[
Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov
25
].
${n}_{\mathrm{e}}\sim {Zn}_{\mathrm{i}0}$
, which is demonstrated by EPOCH simulations[
Reference Murakami, Honrubia, Weichman, Arefiev and Bulanov
25
].
In summary, 2D and 3D PIC simulations indicate that the concept of MTI can work in a realistic configuration by taking practical laser-plasma interaction conditions into account. To enhance the magnetic field generation in MTI, the two different time scales – the laser pulse duration
![]() ${\tau}_{\mathrm{L}}$
and the hydrodynamic time scale
${\tau}_{\mathrm{L}}$
and the hydrodynamic time scale
![]() ${\tau}_{\mathrm{H}}$
– must have coherent lengths, otherwise the absorbed laser energy cannot be effectively transferred to the central core. From the 3D simulations, a target structure with
${\tau}_{\mathrm{H}}$
– must have coherent lengths, otherwise the absorbed laser energy cannot be effectively transferred to the central core. From the 3D simulations, a target structure with
![]() ${L}_0/{R}_0\gtrsim$
1–2 is found to reproduce the same degree of maximum magnetic field as the 2D results. One of the most important parameters in MTI is the average electron energy, which is explicitly shown as a function of the laser and target parameters by the simple model. The model scaling for the maximum magnetic field
${L}_0/{R}_0\gtrsim$
1–2 is found to reproduce the same degree of maximum magnetic field as the 2D results. One of the most important parameters in MTI is the average electron energy, which is explicitly shown as a function of the laser and target parameters by the simple model. The model scaling for the maximum magnetic field
![]() ${B}_{\mathrm{max}}$
and core parameters, such as the spin current
${B}_{\mathrm{max}}$
and core parameters, such as the spin current
![]() ${J}_{\mathrm{H}}$
and the Larmor hole radius
${J}_{\mathrm{H}}$
and the Larmor hole radius
![]() ${R}_{\mathrm{H}}$
, reproduce well the simulation results. The scaling should facilitate practical experiments toward the realization of megatesla-order magnetic fields, which have yet to be achieved in laboratories.
${R}_{\mathrm{H}}$
, reproduce well the simulation results. The scaling should facilitate practical experiments toward the realization of megatesla-order magnetic fields, which have yet to be achieved in laboratories.
Acknowledgments
M. Murakami was supported by the Japan Society for the Promotion of Science (JSPS). D. Shokov acknowledges fruitful discussions with Y. Gu. This work used computing resources at the Cybermedia Center of Osaka University.



















































