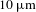1 Introduction
The development of short pulse lasers at relativistic intensities has aroused exciting progress in high energy density physics. Especially, relativistically intense laser–solid interactions are of crucial importance to many great applications, such as fast ignition of fusion energy[Reference Van Woerkom, Akli, Bartal, Beg, Chawla, Chen, Chowdhury, Freeman, Hey, Key, King, Link, Ma, MacKinnon, MacPhee, Offermann, Ovchinnikov, Patel, Schumacher, Stephens and Tsui1–Reference White, Hartley, Borm, Crowley, Harris, Hochhaus, Kaempfer, Li, Neumayer, Pattison, Pfeifer, Richardson, Robinson, Uschmann and Gregori8], hadron therapy[Reference Bulanov, Esirkepov, Khoroshkov, Kuznetsov and Pegoraro9–Reference Kraft, Richter, Zeil, Baumann, Beyreuther, Bock, Bussmann, Cowan, Dammene, Enghardt, Helbig, Karsch, Kluge, Laschinsky, Lessmann, Metzkes, Naumburger, Sauerbrey, Schurer, Sobiella, Woithe, Schramm and Pawelke12], proton radiography[Reference Li, Seguin, Frenje, Manuel, Casey, Sinenian, Petrasso, Amendt, Landen, Rygg, Town, Betti, Delettrez, Knauer, Marshall, Meyerhofer, Sangster, Shvarts, Smalyuk, Soures, Back, Kilkenny and Nikroo13–Reference Ravasio, Romagnani, Le Pape, Benuzzi-Mounaix, Cecchetti, Batani, Boehly, Borghesi, Dezulian, Gremillet, Henry, Hicks, Loupias, MacKinnon, Ozaki, Park, Patel, Schiavi, Vinci, Clarke, Notley, Bandyopadhyay and Koenig15] and high quality ion beam source[Reference Bin, Ma, Wang, Streeter, Kreuzer, Kiefer, Yeung, Cousens, Foster, Dromey, Yan, Ramis, Meyer-ter-Vehn, Zepf and Schreiber16–Reference Wu, Zheng, Qiao, Zhou, Yan, Yu and He19]. When an intense laser beam irradiates a solid target, relativistic electrons can be produced in front of the target. These energetic electrons can propagate through the bulk solid and trigger abundant plasma–atomic processes, which typically include return current, resistive electric and magnetic fields[Reference Leblanc and Sentoku20], bulk heating, ionization dynamics[Reference Huang, Kluge and Cowan21] and Bremsstrahlung X-ray generation[Reference Jiang, Krygier, Schumacher, Akli and Freeman22–Reference Hanus, Drska, dHumieres and Tikhonchuk24].
In the past decades, there are increasing number of researches focusing on laser–solid interactions. These studies can be roughly categorized into two subjects, determined by whether it is the intense laser fields or the solid-density effects that play the dominant roles. When an intense laser beam irradiates a solid, it will be reflected back by the encountered high-density plasmas. Within the low-density region in front of the target, the two conflicting laser pulses (incident and reflected) can efficiently accelerate electrons therein[Reference Beg, Bell, Dangor, Danson, Fews, Glinsky, Hammel, Lee, Norreys and Tatarakis25–Reference Sorokovikova, Arefiev, McGuffey, Qiao, Robinson, Wei, McLean and Beg32]. This acceleration mechanism is usually referred to as direct laser acceleration (DLA), which is a pure plasma physics process and can be well modelled by the widely used particle-in-cell (PIC) codes. Typically, temperature of these energetic electrons can be well formulated by Beg’s scaling law[Reference Beg, Bell, Dangor, Danson, Fews, Glinsky, Hammel, Lee, Norreys and Tatarakis25] or Wilks’ scaling law[Reference Wilks, Kruer, Tabak and Langdon26]. However, when there exists large-scale preformed plasma in front of the solid, the electron heating is beyond predictions of Beg’s and Wilks’ scaling laws. In such cases, one has to take into account the synergetic effects of both charge separation electric fields and the two conflicting laser fields[Reference Paradkar, Wei, Yabuuchi, Stephens, Haines, Krasheninnikov and Beg29–Reference Sorokovikova, Arefiev, McGuffey, Qiao, Robinson, Wei, McLean and Beg32]. Recently, a two-stage electron acceleration model was proposed[Reference Wu, Krasheninnikov, Luan and Yu33–Reference Wu, Luan, Wang, Yu, Gong, Cao, Zheng and He35] in order to describe the electron dynamics influenced by both charge separation electric fields and the two conflicting laser fields. The dependence of the energetic electrons generation on both the pre-plasma scale length and the laser intensity was figured out. An energy scaling law of the energetic electrons with
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D716}\sim (IL_{p})^{1/2}$
was obtained, where
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D716}\sim (IL_{p})^{1/2}$
was obtained, where
![]() $I$
is the laser intensity and
$I$
is the laser intensity and
![]() $L_{p}$
is the pre-plasma scale length.
$L_{p}$
is the pre-plasma scale length.
In front of the target, it is the intense laser fields that dominate the interactions. However except the electromagnetic dynamics, some atomic processes might also play important roles, like field ionization (multi-photon ionization, tunnelling ionization and barrier-suppression ionization)[Reference Wu, Qiao, McGuffey, He and Beg36] and quantum electrodynamics (QED)[Reference Wu, Qiao and He37]. In our recent works[Reference Wu, Qiao, McGuffey, He and Beg36, Reference Wu, Qiao and He37], both field ionization and QED models had been established and implemented into the PIC code. However the greatest challenge of PIC simulations is the fact that one has to include the regions where solid-density effects also dominate. The transport of energetic electrons within the solid triggers a lot of coupled atomic and plasma processes. To trace these processes, several hybrid simulation codes were established[Reference Robinson, Sherlock and Norreys38–Reference Kim, McGuffey, Qiao, Wei, Grabowski and Beg43]. In hybrid simulations, the energetic electrons are treated kinetically using the Vlasov Fokker–Planck approach and the bulk solid is regarded as a resistive fluid. The most recent work[Reference Kim, Qiao, McGuffey, Wei, Grabowski and Beg42, Reference Kim, McGuffey, Qiao, Wei, Grabowski and Beg43] also invoked the Saha–Boltzmann model[Reference Hutchinson44] (or Thomas–Fermi model[Reference Salzmann45]) to synchronously update the ionization of the bulk solid. Note for the existing hybrid simulations, the laser–plasma interactions have not been considered directly. Instead, the energetic electrons are injected with a temperature obeying certain scaling laws. Most of all, the correctness of the hydrodynamic and hybrid methods is based on the local thermal equilibrium assumption. The time scale of laser–solid interactions at relativistic intensities is much shorter than those processes in inertial confinement fusion (ICF) studies, such as ablation, shock wave tuning, and hydrodynamic instabilities. The typical time scale of ICF is on the order of nanosecond, while the time scale of laser–solid interactions at relativistic intensities is on the order of picosecond or even femtosecond. Therefore the local thermal equilibrium assumption needs to be seriously retreated.
In order to figure out the above dynamics with significant nonequilibrium features, a first principle approach should be constructed from the very beginning. Here, in this paper, we have developed a PIC code. The PIC code takes advantage of the newly developed ionization and collision dynamics models, which enables us to calculate intense laser–solid interactions in a more realistic way. Furthermore, the numerical self-heating of PIC simulations, which usually appears in solid-density plasmas, is well controlled by the proposed ‘layered density’ method. As an application of the new code, the generation and transport of energetic electrons in front of and within the solid target when irradiated by intense laser beams are studied. For the considered case, in which laser intensity is
![]() $10^{20}~\text{W}\cdot \text{cm}^{-2}$
and pre-plasma scale length in front of the solid target is
$10^{20}~\text{W}\cdot \text{cm}^{-2}$
and pre-plasma scale length in front of the solid target is
![]() $10~\unicode[STIX]{x03BC}\text{m}$
, several quantitative conclusions are drawn: (i) the collisional damping (although it is very weak) can significantly affect the energetic electrons generation in front of the target, (ii) the Bremsstrahlung radiation will be enhanced by 2–3 times when the solid is dramatically heated and ionized, (iii) the ‘cut-off’ electron energy is lowered by an amount of 25% when both collision damping and Bremsstrahlung radiations are included and finally, (iv) the resistive electromagnetic fields due to Ohmic heating play nonignorable roles and must be taken into account in such interactions.
$10~\unicode[STIX]{x03BC}\text{m}$
, several quantitative conclusions are drawn: (i) the collisional damping (although it is very weak) can significantly affect the energetic electrons generation in front of the target, (ii) the Bremsstrahlung radiation will be enhanced by 2–3 times when the solid is dramatically heated and ionized, (iii) the ‘cut-off’ electron energy is lowered by an amount of 25% when both collision damping and Bremsstrahlung radiations are included and finally, (iv) the resistive electromagnetic fields due to Ohmic heating play nonignorable roles and must be taken into account in such interactions.
2 Atomic models and numerical scheme of the PIC code
Although the PIC method is a first principle scheme derived from the Vlasov and the coupled Maxwell’s equations, it is a tool originally designed to describe plasmas at high temperature and low densities. Typical plasmas of high temperature and low density are fully dominated by the electromagnetic effects. For solid-density plasmas (matter), advanced atomic models need to be taken into account. These models should allow one to calculate ionization dynamics. Such models should also allow one to directly depict the close interactions in the plasmas and thus, accounts for the multi-particle nature of real plasmas. In addition, PIC method is a kind of numerical schemes, which usually suffer significant self-heating. In general, it is challenging for a PIC code to simulate extremely dense and low-temperature (less than 1 keV) plasmas. This is because the grid size of PIC is restricted by the plasma Debye length,
![]() $\unicode[STIX]{x1D706}_{d}\sim \sqrt{T_{e}/n_{e}}$
, in order to avoid the numerical self-heating[Reference Langdon46]. Due to the great demand of huge number of grids and/or particles in the PIC simulations of solid-density plasmas, it is not realistic to perform even with the current fastest super-computers. Therefore, in order to investigate intense laser–solid interactions by using a PIC approach, one has to solve challenges, both physically and numerically.
$\unicode[STIX]{x1D706}_{d}\sim \sqrt{T_{e}/n_{e}}$
, in order to avoid the numerical self-heating[Reference Langdon46]. Due to the great demand of huge number of grids and/or particles in the PIC simulations of solid-density plasmas, it is not realistic to perform even with the current fastest super-computers. Therefore, in order to investigate intense laser–solid interactions by using a PIC approach, one has to solve challenges, both physically and numerically.
2.1 Ionization dynamics
The main challenge to the ionization dynamics of solid-density plasmas is to incorporate both the matter’s response to the surrounding plasmas and plasmas’ response to the matter. In a recent work[Reference Wu, He, Yu and Fritzsche3], we have proposed and analysed a Monte Carlo approach that can be configured and embedded into the PIC code. In this approach, we use a collection of macro-particles to describe a plasma or matter of finite ion density. Here, a macro-particle can be regarded as the ensemble of real particles, i.e., a group of particles with ‘same’ mass, charge state, position and momentum. The electrons are classified moreover into bound and free ones, where the former are regarded as part of ions or atoms, and the latter are isolated as the surrounding plasmas. Here, both impact (collision) ionization (CI)[Reference Lotz47] and electron–ion recombination (RE)[Reference Hahn and Li48] are taken into account. Furthermore, the ionization potential depression (IPD)[Reference Stewart and Pyatt49, Reference Ecker and Kroll50] by the surrounding ions and free electrons is also taken into consideration.
When compared with Saha–Boltzmann or Thomas–Fermi models, which are applied in the literature for plasmas near thermal equilibrium, the temporal relaxation of ionization dynamics can also be simulated by the recently proposed model. Here as a benchmark, the ionization dynamics of an Al bulk (with density
![]() $2.7~\text{g}\cdot \text{cm}^{-3}$
) is calculated with our PIC code. We consider only a few computational cells, connected by periodic boundary conditions, with each cell containing 200 ion macro-particles and 200 electron macro-particles initially (nonuniform weight). In these calculations, electromagnetic effects are turned off. Figure 1(a) shows the total plasma energy within a computational cell as a function of time, where the initial Al charge state is assumed to be
$2.7~\text{g}\cdot \text{cm}^{-3}$
) is calculated with our PIC code. We consider only a few computational cells, connected by periodic boundary conditions, with each cell containing 200 ion macro-particles and 200 electron macro-particles initially (nonuniform weight). In these calculations, electromagnetic effects are turned off. Figure 1(a) shows the total plasma energy within a computational cell as a function of time, where the initial Al charge state is assumed to be
![]() $4+$
, and the initial free electron temperature is set to
$4+$
, and the initial free electron temperature is set to
![]() $150~\text{eV}$
. Following the energy history, at initial time, the CI rate of Al is larger than RE. The former one would reduce the plasma energy and increase the averaged ionization degree as a function of time. After 6 ps relaxation, the normalized charge state distribution is presented in blue bars, and the averaged ionization degree is
$150~\text{eV}$
. Following the energy history, at initial time, the CI rate of Al is larger than RE. The former one would reduce the plasma energy and increase the averaged ionization degree as a function of time. After 6 ps relaxation, the normalized charge state distribution is presented in blue bars, and the averaged ionization degree is
![]() $\bar{Z}=5.82$
with
$\bar{Z}=5.82$
with
![]() $T_{e}=74~\text{eV}$
. In Figure 1(a), the ionization distributions calculated by the Saha–Boltzmann equation are also presented in the red curves covered on the inlets, showing good consistence with the PIC calculations. Following the same routine, by varying the reasonable guesses of initial temperature and charge state configuration, the dependence of averaged ionization degree on final thermal equilibrium temperatures covering a large variation is obtained by the PIC code, as shown in black square lines in Figure 2(b), also showing good consistence with results from the Saha–Boltzmann equation.
$T_{e}=74~\text{eV}$
. In Figure 1(a), the ionization distributions calculated by the Saha–Boltzmann equation are also presented in the red curves covered on the inlets, showing good consistence with the PIC calculations. Following the same routine, by varying the reasonable guesses of initial temperature and charge state configuration, the dependence of averaged ionization degree on final thermal equilibrium temperatures covering a large variation is obtained by the PIC code, as shown in black square lines in Figure 2(b), also showing good consistence with results from the Saha–Boltzmann equation.
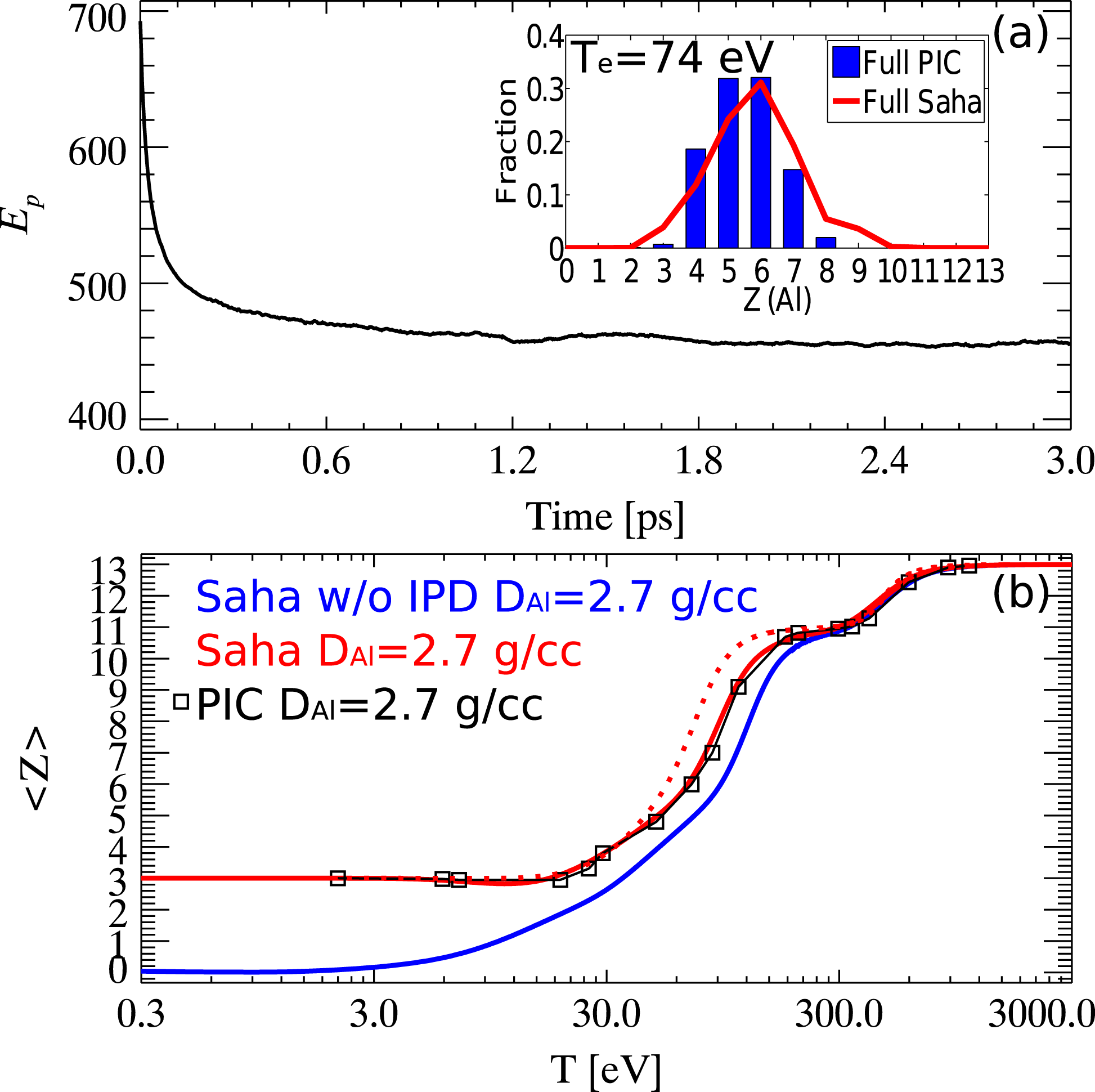
Figure 1. (a) The total plasma energy within a computational cell as a function of time, with initial plasma temperature
![]() $150~\text{eV}$
and pre-defined charge state
$150~\text{eV}$
and pre-defined charge state
![]() $4+$
. The red line covered on the inlets is the ionization distributions of Al calculated by the Saha–Boltzmann equation with defined temperature,
$4+$
. The red line covered on the inlets is the ionization distributions of Al calculated by the Saha–Boltzmann equation with defined temperature,
![]() $T_{e}=74~\text{eV}$
. (b) The averaged ionization degree as a function of temperature, where red and green lines are the results calculated by the Saha–Boltzmann equation, including IPD and excluding IPD, with fixed Al density
$T_{e}=74~\text{eV}$
. (b) The averaged ionization degree as a function of temperature, where red and green lines are the results calculated by the Saha–Boltzmann equation, including IPD and excluding IPD, with fixed Al density
![]() $2.7~\text{g}\cdot \text{cm}^{-3}$
. The solid red line is with the SP[Reference Stewart and Pyatt49] model of IPD, while the dashed red line is with EK[Reference Ecker and Kroll50] model of IPD. The black square line is picked up from the equilibrium states calculated by our PIC code.
$2.7~\text{g}\cdot \text{cm}^{-3}$
. The solid red line is with the SP[Reference Stewart and Pyatt49] model of IPD, while the dashed red line is with EK[Reference Ecker and Kroll50] model of IPD. The black square line is picked up from the equilibrium states calculated by our PIC code.
2.2 Collision with Bremsstrahlung corrections
It is well known in plasma physics that electron–electron, electron–ion and ion–ion scatterings can be described by means of the Monte Carlo binary collision model, thanks to the pioneering works of Takizuka and Abe[Reference Takizuka and Abe51], Nanbu and Yonemura[Reference Nanbu and Yonemura52], and Sentoku and Kemp[Reference Sentoku and Kemp53]. Within these PIC calculations, three steps are made iteratively: (i) pair of particles are selected randomly in the cell, i.e., either electron–electron, electron–ion or ion–ion pairs; (ii) for these pair of particles, the binary collisions are associated with changes in the velocity of the particles within the time interval
![]() $\unicode[STIX]{x1D6FF}t$
and are calculated; (iii) and then the velocity of each particle is replaced by the newly calculated one. The collision frequency of fully ionized plasmas between charged particles, used in these PIC calculations, is
$\unicode[STIX]{x1D6FF}t$
and are calculated; (iii) and then the velocity of each particle is replaced by the newly calculated one. The collision frequency of fully ionized plasmas between charged particles, used in these PIC calculations, is
![]() $\unicode[STIX]{x1D708}=2\unicode[STIX]{x1D70B}e^{4}Z_{a}^{2}Z_{b}^{2}n_{\min }\ln (\unicode[STIX]{x1D6EC}_{\text{f}})/(3m_{e}^{2}\unicode[STIX]{x1D6FD}^{3})$
, where
$\unicode[STIX]{x1D708}=2\unicode[STIX]{x1D70B}e^{4}Z_{a}^{2}Z_{b}^{2}n_{\min }\ln (\unicode[STIX]{x1D6EC}_{\text{f}})/(3m_{e}^{2}\unicode[STIX]{x1D6FD}^{3})$
, where
![]() $Z_{a}$
and
$Z_{a}$
and
![]() $Z_{b}$
are charge state of colliding particles,
$Z_{b}$
are charge state of colliding particles,
![]() $n_{\min }$
is the minimal density of the two species
$n_{\min }$
is the minimal density of the two species
![]() $a$
and
$a$
and
![]() $b$
, and
$b$
, and
![]() $\unicode[STIX]{x1D6FD}$
is the relative velocity between the two colliding particles. The Coulomb logarithm,
$\unicode[STIX]{x1D6FD}$
is the relative velocity between the two colliding particles. The Coulomb logarithm,
![]() $\ln (\unicode[STIX]{x1D6EC}_{\text{f}})$
, is usually defined as
$\ln (\unicode[STIX]{x1D6EC}_{\text{f}})$
, is usually defined as
![]() $L\equiv \ln (\unicode[STIX]{x1D706}_{\text{D}}/b)$
, where the Debye length,
$L\equiv \ln (\unicode[STIX]{x1D706}_{\text{D}}/b)$
, where the Debye length,
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
, is a dynamic value changing as
$\unicode[STIX]{x1D706}_{\text{D}}$
, is a dynamic value changing as
![]() $\unicode[STIX]{x1D706}_{\text{D}}=\sqrt{(T_{e}/4\unicode[STIX]{x1D70B}n_{e})(1+\unicode[STIX]{x1D6FD}^{2}/v_{\text{th}}^{2})}$
, where
$\unicode[STIX]{x1D706}_{\text{D}}=\sqrt{(T_{e}/4\unicode[STIX]{x1D70B}n_{e})(1+\unicode[STIX]{x1D6FD}^{2}/v_{\text{th}}^{2})}$
, where
![]() $T_{e}$
and
$T_{e}$
and
![]() $v_{\text{th}}$
are the temperature and thermal velocity of background electrons. Parameter
$v_{\text{th}}$
are the temperature and thermal velocity of background electrons. Parameter
![]() $b$
is the distance of the closest approach between the two charges. In classical scattering, we have
$b$
is the distance of the closest approach between the two charges. In classical scattering, we have
![]() $b=Z_{a}Z_{b}e^{2}/m_{e}\unicode[STIX]{x1D6FD}^{2}$
. This condition is not satisfied in the relativistic case, so that the scattering must be treated quantum mechanically using the Born approximation. In this case, i.e.,
$b=Z_{a}Z_{b}e^{2}/m_{e}\unicode[STIX]{x1D6FD}^{2}$
. This condition is not satisfied in the relativistic case, so that the scattering must be treated quantum mechanically using the Born approximation. In this case, i.e.,
![]() $e^{2}/\hbar \unicode[STIX]{x1D6FD}\ll 1$
, the Coulomb logarithm is then expressed as
$e^{2}/\hbar \unicode[STIX]{x1D6FD}\ll 1$
, the Coulomb logarithm is then expressed as
![]() $L=\ln (\unicode[STIX]{x1D706}_{\text{D}}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}/\hbar )$
, which is the ratio of the Debye length and the de Broglie wavelength. This definition of Coulomb logarithm works well for low-density and high-temperature plasmas. However, for plasmas of solid density and at low temperatures, as
$L=\ln (\unicode[STIX]{x1D706}_{\text{D}}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}/\hbar )$
, which is the ratio of the Debye length and the de Broglie wavelength. This definition of Coulomb logarithm works well for low-density and high-temperature plasmas. However, for plasmas of solid density and at low temperatures, as
![]() $b$
is larger than
$b$
is larger than
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
, the Coulomb logarithm expression will become negative. Existing works[Reference Takizuka and Abe51–Reference Sentoku and Kemp53] do not address this issue of negative Coulomb logarithm, as the collision models are initially proposed for high-temperature plasmas.
$\unicode[STIX]{x1D706}_{\text{D}}$
, the Coulomb logarithm expression will become negative. Existing works[Reference Takizuka and Abe51–Reference Sentoku and Kemp53] do not address this issue of negative Coulomb logarithm, as the collision models are initially proposed for high-temperature plasmas.

Figure 2. Schematic of charged particle collision. For neutral atoms, when all electrons are bounded at the nuclei with the radius on the order of Bohr unit
![]() $a_{0}$
, only projectile that could penetrate through the electron can be deflected by the Coulomb force of the nuclei. When temperature is high, some of the bound electrons are ionized and form plasmas around the nuclei, projectile with a collision distance
$a_{0}$
, only projectile that could penetrate through the electron can be deflected by the Coulomb force of the nuclei. When temperature is high, some of the bound electrons are ionized and form plasmas around the nuclei, projectile with a collision distance
![]() $b$
smaller than
$b$
smaller than
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
(usually
$\unicode[STIX]{x1D706}_{\text{D}}$
(usually
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
is much larger than
$\unicode[STIX]{x1D706}_{\text{D}}$
is much larger than
![]() $a_{0}$
) can also be deflected by the Coulomb force.
$a_{0}$
) can also be deflected by the Coulomb force.
We here obtain a general Coulomb logarithm by considering the scattering of charged particles by sheathed Coulomb force,
![]() $\exp (-r/\unicode[STIX]{x1D706}_{\text{D}})/r$
. Rigorous calculation results in the expression of Coulomb logarithm as
$\exp (-r/\unicode[STIX]{x1D706}_{\text{D}})/r$
. Rigorous calculation results in the expression of Coulomb logarithm as
![]() $L=\ln [(1+\unicode[STIX]{x1D702})/\unicode[STIX]{x1D702}]$
(appendix A), where
$L=\ln [(1+\unicode[STIX]{x1D702})/\unicode[STIX]{x1D702}]$
(appendix A), where
![]() $\unicode[STIX]{x1D702}=b/\unicode[STIX]{x1D706}_{\text{D}}$
. This expression of Coulomb logarithm will converge to
$\unicode[STIX]{x1D702}=b/\unicode[STIX]{x1D706}_{\text{D}}$
. This expression of Coulomb logarithm will converge to
![]() $L=\ln (\unicode[STIX]{x1D706}_{\text{D}}/b)$
when
$L=\ln (\unicode[STIX]{x1D706}_{\text{D}}/b)$
when
![]() $b\ll \unicode[STIX]{x1D706}_{\text{D}}$
for high-temperature plasmas. In addition, when plasma temperature is smaller than the so-called Fermi energy
$b\ll \unicode[STIX]{x1D706}_{\text{D}}$
for high-temperature plasmas. In addition, when plasma temperature is smaller than the so-called Fermi energy
![]() $\unicode[STIX]{x1D716}_{\text{F}}$
, collision in the degenerate regime is also taken into account. In the degenerate regime, the dynamics of electrons are mainly determined by Pauli–Dirac statistics, which tends to lower the classical collision frequency by a factor of
$\unicode[STIX]{x1D716}_{\text{F}}$
, collision in the degenerate regime is also taken into account. In the degenerate regime, the dynamics of electrons are mainly determined by Pauli–Dirac statistics, which tends to lower the classical collision frequency by a factor of
![]() $(T_{e}/\unicode[STIX]{x1D716}_{\text{F}})^{2}$
[Reference Kittel54]. The degenerate collision frequency is
$(T_{e}/\unicode[STIX]{x1D716}_{\text{F}})^{2}$
[Reference Kittel54]. The degenerate collision frequency is
![]() $\unicode[STIX]{x1D708}=(4m_{e}e^{4}/3\unicode[STIX]{x1D70B}\hbar ^{3})L$
. When
$\unicode[STIX]{x1D708}=(4m_{e}e^{4}/3\unicode[STIX]{x1D70B}\hbar ^{3})L$
. When
![]() $\unicode[STIX]{x1D6FD}$
is smaller than the value
$\unicode[STIX]{x1D6FD}$
is smaller than the value
![]() $n_{\max }^{1/3}\hbar /m_{e}c$
, where
$n_{\max }^{1/3}\hbar /m_{e}c$
, where
![]() $n_{\max }$
is the maximal density between species
$n_{\max }$
is the maximal density between species
![]() $a$
and
$a$
and
![]() $b$
,
$b$
,
![]() $\unicode[STIX]{x1D708}=(4m_{e}e^{4}/3\unicode[STIX]{x1D70B}\hbar ^{3})L$
is used instead. For the given Al solid of density
$\unicode[STIX]{x1D708}=(4m_{e}e^{4}/3\unicode[STIX]{x1D70B}\hbar ^{3})L$
is used instead. For the given Al solid of density
![]() $2.7~\text{g}\cdot \text{cm}^{-3}$
, Figure 3(a) shows the collision frequencies as functions of temperatures, given by our PIC code. The electron–electron collision frequency is displayed by black square line and the electron–ion collision frequency is displayed in black diamond line. In these calculations, the changing of averaged ionization degree with temperature is also taken into account. The collision frequency is calculated by averaging over 1000 pairs of colliding particles. For moderate temperatures, for example with
$2.7~\text{g}\cdot \text{cm}^{-3}$
, Figure 3(a) shows the collision frequencies as functions of temperatures, given by our PIC code. The electron–electron collision frequency is displayed by black square line and the electron–ion collision frequency is displayed in black diamond line. In these calculations, the changing of averaged ionization degree with temperature is also taken into account. The collision frequency is calculated by averaging over 1000 pairs of colliding particles. For moderate temperatures, for example with
![]() $T_{e}$
greater than
$T_{e}$
greater than
![]() $10~\text{eV}$
, the collision frequency nicely converges to the Spitzer model[Reference Takizuka and Abe51–Reference Sentoku and Kemp53], i.e.,
$10~\text{eV}$
, the collision frequency nicely converges to the Spitzer model[Reference Takizuka and Abe51–Reference Sentoku and Kemp53], i.e.,
![]() $\unicode[STIX]{x1D708}\sim T_{e}^{-1.5}$
, which decreases rapidly with the raising of temperatures. However, at low-temperature limit, when
$\unicode[STIX]{x1D708}\sim T_{e}^{-1.5}$
, which decreases rapidly with the raising of temperatures. However, at low-temperature limit, when
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
is extremely small, the Fermi–Dirac statistics tends to suppress the collision frequency, by a factor of
$\unicode[STIX]{x1D706}_{\text{D}}$
is extremely small, the Fermi–Dirac statistics tends to suppress the collision frequency, by a factor of
![]() $(T_{e}/\unicode[STIX]{x1D716}_{\text{F}})^{2}$
. In Figure 3(b), we have compared the resistivity given by our PIC code with that of experimental measurements[Reference Milchberg, Freeman, Davey and More55]. These measurements were obtained by rapid heating of the Al solid using a short pulse laser (this is considered to be a disadvantage of these measurements, as they do not give time for equilibrium to be established). The basic behaviour of resistivity as a function of temperature is well depicted by our PIC code, i.e., the resistivity is first increasing with the raising of temperature and then converges to the predictions of the Spitzer model.
$(T_{e}/\unicode[STIX]{x1D716}_{\text{F}})^{2}$
. In Figure 3(b), we have compared the resistivity given by our PIC code with that of experimental measurements[Reference Milchberg, Freeman, Davey and More55]. These measurements were obtained by rapid heating of the Al solid using a short pulse laser (this is considered to be a disadvantage of these measurements, as they do not give time for equilibrium to be established). The basic behaviour of resistivity as a function of temperature is well depicted by our PIC code, i.e., the resistivity is first increasing with the raising of temperature and then converges to the predictions of the Spitzer model.
The above collision model works well for fully ionized plasmas. However in laser–solid interactions, the inner part of the bulk target is usually partially ionized. Therefore, the contribution of bound electrons must also be taken into consideration. In a recent work[Reference Wu, He, Yu and Fritzsche4], we have studied the ion stopping in warm dense matter (or/and partially ionized plasma), where contribution of both the bound and free electrons is included by modifying the ion–electron collision frequency as
where
![]() $\ln (\unicode[STIX]{x1D6EC}_{\text{b}})\equiv \ln |2\unicode[STIX]{x1D6FE}^{2}m_{e}\unicode[STIX]{x1D6FD}^{2}/\bar{I}_{A}(Z)|-\unicode[STIX]{x1D6FD}^{2}-C_{\text{K}}/A-\unicode[STIX]{x1D6FF}/2$
,
$\ln (\unicode[STIX]{x1D6EC}_{\text{b}})\equiv \ln |2\unicode[STIX]{x1D6FE}^{2}m_{e}\unicode[STIX]{x1D6FD}^{2}/\bar{I}_{A}(Z)|-\unicode[STIX]{x1D6FD}^{2}-C_{\text{K}}/A-\unicode[STIX]{x1D6FF}/2$
,
![]() $I_{A}(z)$
is the effective ionization potential,
$I_{A}(z)$
is the effective ionization potential,
![]() $\unicode[STIX]{x1D6FF}/2$
is the density effect contribution and
$\unicode[STIX]{x1D6FF}/2$
is the density effect contribution and
![]() $(A-Z)/Z$
(
$(A-Z)/Z$
(
![]() $A$
is the atomic number,
$A$
is the atomic number,
![]() $A=13$
for Al and
$A=13$
for Al and
![]() $Z$
is the ionization state) defines the ratio of bound electrons contributions. For a fully ionized plasma,
$Z$
is the ionization state) defines the ratio of bound electrons contributions. For a fully ionized plasma,
![]() $Z\rightarrow A$
, the collision frequency between ions and electrons in Equation (1) converges to
$Z\rightarrow A$
, the collision frequency between ions and electrons in Equation (1) converges to
![]() $\unicode[STIX]{x1D708}_{\text{i}\text{-}\text{e}}\sim (8\sqrt{2\unicode[STIX]{x1D70B}}Z_{b}^{2}e^{4}Zn_{i}/3m_{e}^{2}\unicode[STIX]{x1D6FD}^{3})\ln (\unicode[STIX]{x1D6EC}_{\text{f}})$
. For neutral atoms,
$\unicode[STIX]{x1D708}_{\text{i}\text{-}\text{e}}\sim (8\sqrt{2\unicode[STIX]{x1D70B}}Z_{b}^{2}e^{4}Zn_{i}/3m_{e}^{2}\unicode[STIX]{x1D6FD}^{3})\ln (\unicode[STIX]{x1D6EC}_{\text{f}})$
. For neutral atoms,
![]() $Z\rightarrow 0$
, in contrast, the frequency in Equation (1) is
$Z\rightarrow 0$
, in contrast, the frequency in Equation (1) is
![]() $\unicode[STIX]{x1D708}_{\text{i}\text{-}\text{e}}\sim (8\sqrt{2\unicode[STIX]{x1D70B}}Z_{b}^{2}e^{4}An_{i}/3m_{e}^{2}\unicode[STIX]{x1D6FD}^{3})\ln (\unicode[STIX]{x1D6EC}_{\text{b}})$
. If the projectile is electron, the value of
$\unicode[STIX]{x1D708}_{\text{i}\text{-}\text{e}}\sim (8\sqrt{2\unicode[STIX]{x1D70B}}Z_{b}^{2}e^{4}An_{i}/3m_{e}^{2}\unicode[STIX]{x1D6FD}^{3})\ln (\unicode[STIX]{x1D6EC}_{\text{b}})$
. If the projectile is electron, the value of
![]() $\ln (\unicode[STIX]{x1D6EC}_{\text{b}})$
must be estimated in the centre-of-mass frame, and the expression becomes
$\ln (\unicode[STIX]{x1D6EC}_{\text{b}})$
must be estimated in the centre-of-mass frame, and the expression becomes
![]() $\ln (\unicode[STIX]{x1D6EC}_{\text{b}})\equiv \ln |(\unicode[STIX]{x1D6FE}-1)\sqrt{(\unicode[STIX]{x1D6FE}+1)/2}m_{e}c^{2}/\bar{I}_{A}(Z)|-\unicode[STIX]{x1D6FD}^{2}/2-\unicode[STIX]{x1D6FF}/2$
.
$\ln (\unicode[STIX]{x1D6EC}_{\text{b}})\equiv \ln |(\unicode[STIX]{x1D6FE}-1)\sqrt{(\unicode[STIX]{x1D6FE}+1)/2}m_{e}c^{2}/\bar{I}_{A}(Z)|-\unicode[STIX]{x1D6FD}^{2}/2-\unicode[STIX]{x1D6FF}/2$
.

Figure 3. For given Al solid of density
![]() $2.7~\text{g}\cdot \text{cm}^{-3}$
, (a) the electron–electron (black square line) and electron–ion (black diamond line) collision frequency given by our PIC code as functions of temperatures; (b) the resistivity given by our PIC code versus experimental values[Reference Milchberg, Freeman, Davey and More55]. In these calculations, the variation of averaged ionization degree with temperature is also taken into account. The values given by the PIC code are averaged over 1000 particle pairs.
$2.7~\text{g}\cdot \text{cm}^{-3}$
, (a) the electron–electron (black square line) and electron–ion (black diamond line) collision frequency given by our PIC code as functions of temperatures; (b) the resistivity given by our PIC code versus experimental values[Reference Milchberg, Freeman, Davey and More55]. In these calculations, the variation of averaged ionization degree with temperature is also taken into account. The values given by the PIC code are averaged over 1000 particle pairs.

Figure 4. Stopping power of different materials, (a) for Al and (b) for Cu, as a function of projected electron kinetic energy. Results from our PIC simulations, at low-temperature limit, are compared with that from the NIST database. The solid black line is the collisional stopping power (
![]() $S_{\text{c}}$
), the solid blue line is the radiation stopping power (
$S_{\text{c}}$
), the solid blue line is the radiation stopping power (
![]() $S_{\text{r}}$
) and the solid red line is the total stopping power, with
$S_{\text{r}}$
) and the solid red line is the total stopping power, with
![]() $S_{\text{t}}=S_{\text{c}}+S_{\text{r}}$
from the NIST database. The black square line is the collisional stopping power calculated by PIC code, and the red square line is the total stopping power calculated by PIC code, where dashed lines represent the one excluding density effect
$S_{\text{t}}=S_{\text{c}}+S_{\text{r}}$
from the NIST database. The black square line is the collisional stopping power calculated by PIC code, and the red square line is the total stopping power calculated by PIC code, where dashed lines represent the one excluding density effect
![]() $\unicode[STIX]{x1D6FF}/2$
. (c) The stopping power of Al as a function of projected electron kinetic energy at different temperatures.
$\unicode[STIX]{x1D6FF}/2$
. (c) The stopping power of Al as a function of projected electron kinetic energy at different temperatures.
As a benchmark of our collision model, Figure 4 shows the variation of stopping power as functions of energy. Solid black line represents the collisional stopping power (
![]() $S_{\text{c}}$
) obtained from the National Institute of Standard and Technology (NIST)[56] database. Results given by our PIC code (black square lines) are also displayed to compare with that from the NIST database. Results given by our PIC code nicely reproduce the collisional stopping powers as obtained from the NIST database, for both Al as shown in Figure 4(a) and copper (Cu) as shown in Figure 4(b). For the stopping power calculation of energetic electrons, the density effect, i.e.,
$S_{\text{c}}$
) obtained from the National Institute of Standard and Technology (NIST)[56] database. Results given by our PIC code (black square lines) are also displayed to compare with that from the NIST database. Results given by our PIC code nicely reproduce the collisional stopping powers as obtained from the NIST database, for both Al as shown in Figure 4(a) and copper (Cu) as shown in Figure 4(b). For the stopping power calculation of energetic electrons, the density effect, i.e.,
![]() $\unicode[STIX]{x1D6FF}/2$
term, plays an important role. When excluding this effect, as dashed black square lines show, the stopping power is significantly larger than the values from the NIST database. While this is not the simple relationship available for the corrections
$\unicode[STIX]{x1D6FF}/2$
term, plays an important role. When excluding this effect, as dashed black square lines show, the stopping power is significantly larger than the values from the NIST database. While this is not the simple relationship available for the corrections
![]() $\unicode[STIX]{x1D6FF}/2$
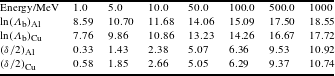
between the magnitude and atomic number of the stopping medium, fortunately, it has already been tabulated for all elemental targets[56, 57]. In Table 1, we have organized
$\unicode[STIX]{x1D6FF}/2$
between the magnitude and atomic number of the stopping medium, fortunately, it has already been tabulated for all elemental targets[56, 57]. In Table 1, we have organized
![]() $\ln (\unicode[STIX]{x1D6EC}_{\text{b}})$
and
$\ln (\unicode[STIX]{x1D6EC}_{\text{b}})$
and
![]() $\unicode[STIX]{x1D6FF}/2$
as functions of electron kinetic energies, where
$\unicode[STIX]{x1D6FF}/2$
as functions of electron kinetic energies, where
![]() $\ln (\unicode[STIX]{x1D6EC}_{\text{b}})$
is calculated with the PIC code by averaging over 1000 projected electrons and values of density effects are obtained from the NIST database. It is shown that the value of density effect is increasing with the raising of projected electron energy. This is comparable to that of
$\ln (\unicode[STIX]{x1D6EC}_{\text{b}})$
is calculated with the PIC code by averaging over 1000 projected electrons and values of density effects are obtained from the NIST database. It is shown that the value of density effect is increasing with the raising of projected electron energy. This is comparable to that of
![]() $\ln (\unicode[STIX]{x1D6EC}_{\text{b}})$
when the projected electron energy is high, especially when the kinetic energy is greater than
$\ln (\unicode[STIX]{x1D6EC}_{\text{b}})$
when the projected electron energy is high, especially when the kinetic energy is greater than
![]() $10~\text{MeV}$
.
$10~\text{MeV}$
.
When the kinetic energy of projected electrons is, for example, higher than
![]() $10~\text{MeV}$
, the radiation stopping also becomes nonignorable. This is because, when charged particles collide, they will accelerate in each other’s electric field and as a result, radiating electromagnetic waves. Generally, the total energy radiated in this collision is given for the instantaneous radiated power by an accelerated charge,
$10~\text{MeV}$
, the radiation stopping also becomes nonignorable. This is because, when charged particles collide, they will accelerate in each other’s electric field and as a result, radiating electromagnetic waves. Generally, the total energy radiated in this collision is given for the instantaneous radiated power by an accelerated charge,
![]() $P\sim \dot{\unicode[STIX]{x1D6FD}}^{2}Z^{2}$
, integrated over the duration time of collision,
$P\sim \dot{\unicode[STIX]{x1D6FD}}^{2}Z^{2}$
, integrated over the duration time of collision,
![]() $\unicode[STIX]{x1D70F}$
. For an energetic electron propagating through a target, following the classical text by Jackson[Reference Jackson58], we can obtain the energy radiated per unit length per unit frequency as
$\unicode[STIX]{x1D70F}$
. For an energetic electron propagating through a target, following the classical text by Jackson[Reference Jackson58], we can obtain the energy radiated per unit length per unit frequency as
where
![]() $n$
is the ion density of the target,
$n$
is the ion density of the target,
![]() $A$
is the atomic number of the target material (
$A$
is the atomic number of the target material (
![]() $A=13$
for Al),
$A=13$
for Al),
![]() $\unicode[STIX]{x1D6FC}=e^{2}/\hbar c$
is the fine structure constant,
$\unicode[STIX]{x1D6FC}=e^{2}/\hbar c$
is the fine structure constant,
![]() $r_{e}=e^{2}/m_{e}c^{2}$
is the classical electron radius and
$r_{e}=e^{2}/m_{e}c^{2}$
is the classical electron radius and
![]() $\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D6FE}-\hbar \unicode[STIX]{x1D714}$
is the relativistic factor of the electron after the photon has been emitted. For energetic electrons, the radiation of energetic electrons is emitted mainly in the forward direction. The average angle between the directions of the electron and the emitted light is
$\unicode[STIX]{x1D6FE}^{\prime }=\unicode[STIX]{x1D6FE}-\hbar \unicode[STIX]{x1D714}$
is the relativistic factor of the electron after the photon has been emitted. For energetic electrons, the radiation of energetic electrons is emitted mainly in the forward direction. The average angle between the directions of the electron and the emitted light is
![]() ${\sim}1/\unicode[STIX]{x1D6FE}$
. Within the PIC simulations, the angular distribution of emitted photons can therefore be approximated as
${\sim}1/\unicode[STIX]{x1D6FE}$
. Within the PIC simulations, the angular distribution of emitted photons can therefore be approximated as
where a delta-function approximation is used to describe the direction of photon emissions.
Table 1. Coulomb logarithm and
![]() $\unicode[STIX]{x1D6FF}/2$
as a function of energy of projected electrons for solid Al and Cu at low-temperature limit, where
$\unicode[STIX]{x1D6FF}/2$
as a function of energy of projected electrons for solid Al and Cu at low-temperature limit, where
![]() $\ln (\unicode[STIX]{x1D6EC}_{\text{b}})$
is calculated with the PIC code by averaging over
$\ln (\unicode[STIX]{x1D6EC}_{\text{b}})$
is calculated with the PIC code by averaging over
![]() $1000$
projected electrons and values of
$1000$
projected electrons and values of
![]() $\unicode[STIX]{x1D6FF}/2$
are obtained from the NIST database.
$\unicode[STIX]{x1D6FF}/2$
are obtained from the NIST database.
Following the definition of collision stopping power, the radiation stopping power has the following form by integrating Equation (2) with
![]() $\hbar \unicode[STIX]{x1D714}$
from 0 to
$\hbar \unicode[STIX]{x1D714}$
from 0 to
![]() $\unicode[STIX]{x1D6FE}m_{e}c^{2}$
,
$\unicode[STIX]{x1D6FE}m_{e}c^{2}$
,
In Equation (4), we need to account for the screening of nuclear potential by surrounding electrons at the nuclei when the collisions are distant. Similar to the approach applied for the Coulomb logarithm calculation (appendix A), when impact parameter is larger than a particular value, the potential is artificially set to be zero. At low-temperature limit, when all electrons are bound at the nuclei, the ‘Thomas–Fermi’ potential is an approximation to the screened nuclear potential. It can be approximated as
![]() $\unicode[STIX]{x1D719}=(Ze/r)\exp (-r/a)$
, with the characteristic length
$\unicode[STIX]{x1D719}=(Ze/r)\exp (-r/a)$
, with the characteristic length
![]() $a=1.4a_{0}A^{-1/3}$
, where
$a=1.4a_{0}A^{-1/3}$
, where
![]() $a_{0}$
is the Bohr unit. This kind of screening will reduce the power radiated, because it essentially lowers the maximal effective impact parameter to
$a_{0}$
is the Bohr unit. This kind of screening will reduce the power radiated, because it essentially lowers the maximal effective impact parameter to
![]() ${\sim}a$
. Under relativistic collisions, the screening is so important that
${\sim}a$
. Under relativistic collisions, the screening is so important that
![]() $\ln (\unicode[STIX]{x1D6EC})$
in Equation (4) can be written as constant
$\ln (\unicode[STIX]{x1D6EC})$
in Equation (4) can be written as constant
![]() $\ln (\unicode[STIX]{x1D6EC})=\ln |am_{e}c/\hbar |$
. Under such conditions, radiation stopping power, as represented by Equation (4), is a linear function of energy. This kind of behaviour is also well confirmed by the solid blue line, picked from the NIST database, as shown in Figure 4. When temperature is high, some of the bound electrons are ionized and form plasmas surrounding the nuclei. As schematically shown in Figure 2, this will increase the maximal effective impact parameter from
$\ln (\unicode[STIX]{x1D6EC})=\ln |am_{e}c/\hbar |$
. Under such conditions, radiation stopping power, as represented by Equation (4), is a linear function of energy. This kind of behaviour is also well confirmed by the solid blue line, picked from the NIST database, as shown in Figure 4. When temperature is high, some of the bound electrons are ionized and form plasmas surrounding the nuclei. As schematically shown in Figure 2, this will increase the maximal effective impact parameter from
![]() ${\sim}a$
to
${\sim}a$
to
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
; here
$\unicode[STIX]{x1D706}_{\text{D}}$
; here
![]() $\unicode[STIX]{x1D706}_{\text{D}}=\sqrt{T_{e}/4\unicode[STIX]{x1D70B}n_{e}}$
is the Debye length of plasmas. When including ionization effect, the radiation stopping power, which is originally shown in Equation (4), can be rewritten as
$\unicode[STIX]{x1D706}_{\text{D}}=\sqrt{T_{e}/4\unicode[STIX]{x1D70B}n_{e}}$
is the Debye length of plasmas. When including ionization effect, the radiation stopping power, which is originally shown in Equation (4), can be rewritten as
where
![]() $L_{a}=\ln |am_{e}c/\hbar |$
and
$L_{a}=\ln |am_{e}c/\hbar |$
and
![]() $L_{\text{D}}=\ln |\unicode[STIX]{x1D706}_{\text{D}}/a|$
. This updated radiation stopping power can converge to neutral atom limit when
$L_{\text{D}}=\ln |\unicode[STIX]{x1D706}_{\text{D}}/a|$
. This updated radiation stopping power can converge to neutral atom limit when
![]() $Z\rightarrow 0$
and also to purely plasma cases when
$Z\rightarrow 0$
and also to purely plasma cases when
![]() $Z\rightarrow A$
, noting that
$Z\rightarrow A$
, noting that
![]() $L_{a}+L_{\text{D}}=\ln |\unicode[STIX]{x1D706}_{\text{D}}m_{e}c/\hbar |$
.
$L_{a}+L_{\text{D}}=\ln |\unicode[STIX]{x1D706}_{\text{D}}m_{e}c/\hbar |$
.
In PIC simulations, as the average angle between photon and electron can be handled by a delta-function approximation, the Bremsstrahlung radiation does not further change the deflection of the electron. This approximation will significantly simplify the implementation of Bremsstrahlung correction into the binary collision models. In such models, after the second step of calculation cycles, the electron energy is updated by including the Bremsstrahlung correction, i.e.,
![]() $\unicode[STIX]{x1D6FE}_{\text{Br}}=\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6FE}$
with
$\unicode[STIX]{x1D6FE}_{\text{Br}}=\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6FE}$
with
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6FE}m_{e}c^{2}=c\unicode[STIX]{x1D6FF}tS_{\text{r}}$
. The electron momentum is also updated with
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6FE}m_{e}c^{2}=c\unicode[STIX]{x1D6FF}tS_{\text{r}}$
. The electron momentum is also updated with
![]() $\boldsymbol{p}_{\text{Br}}=\sqrt{(\unicode[STIX]{x1D6FE}_{\text{Br}}-1)/(\unicode[STIX]{x1D6FE}-1)}\boldsymbol{p}$
, where
$\boldsymbol{p}_{\text{Br}}=\sqrt{(\unicode[STIX]{x1D6FE}_{\text{Br}}-1)/(\unicode[STIX]{x1D6FE}-1)}\boldsymbol{p}$
, where
![]() $\unicode[STIX]{x1D6FF}t$
is the time step of PIC simulations.
$\unicode[STIX]{x1D6FF}t$
is the time step of PIC simulations.
When the Bremsstrahlung radiation correction is included, red square lines in Figures 4(a) and 4(b) show the total stopping power (including both radiation and collision) as functions of projected electron energy, where Figure 4(a) is for Al and Figure 4(b) is for Cu. Our stopping power values given by the PIC code nicely reproduce that from the NIST database. Note that data from the NIST databases are obtained at the neutral atom limit. When temperature is high, some of the bound electrons are ionized and form surrounding plasmas, the corresponding radiation stopping power should also be increased accordingly. As shown in Figure 4(c), the total stopping powers calculated by the PIC code at different temperatures,
![]() $T_{e}=100~\text{eV}$
with
$T_{e}=100~\text{eV}$
with
![]() $Z=8.0$
(red diamond line) and
$Z=8.0$
(red diamond line) and
![]() $T_{e}=1000~\text{eV}$
with
$T_{e}=1000~\text{eV}$
with
![]() $Z=13$
(red triangle line), are presented. As expected, the radiation stopping power is increased by 2–3 times when the temperature (and ionization) of the target is increased to hundreds of eV.
$Z=13$
(red triangle line), are presented. As expected, the radiation stopping power is increased by 2–3 times when the temperature (and ionization) of the target is increased to hundreds of eV.
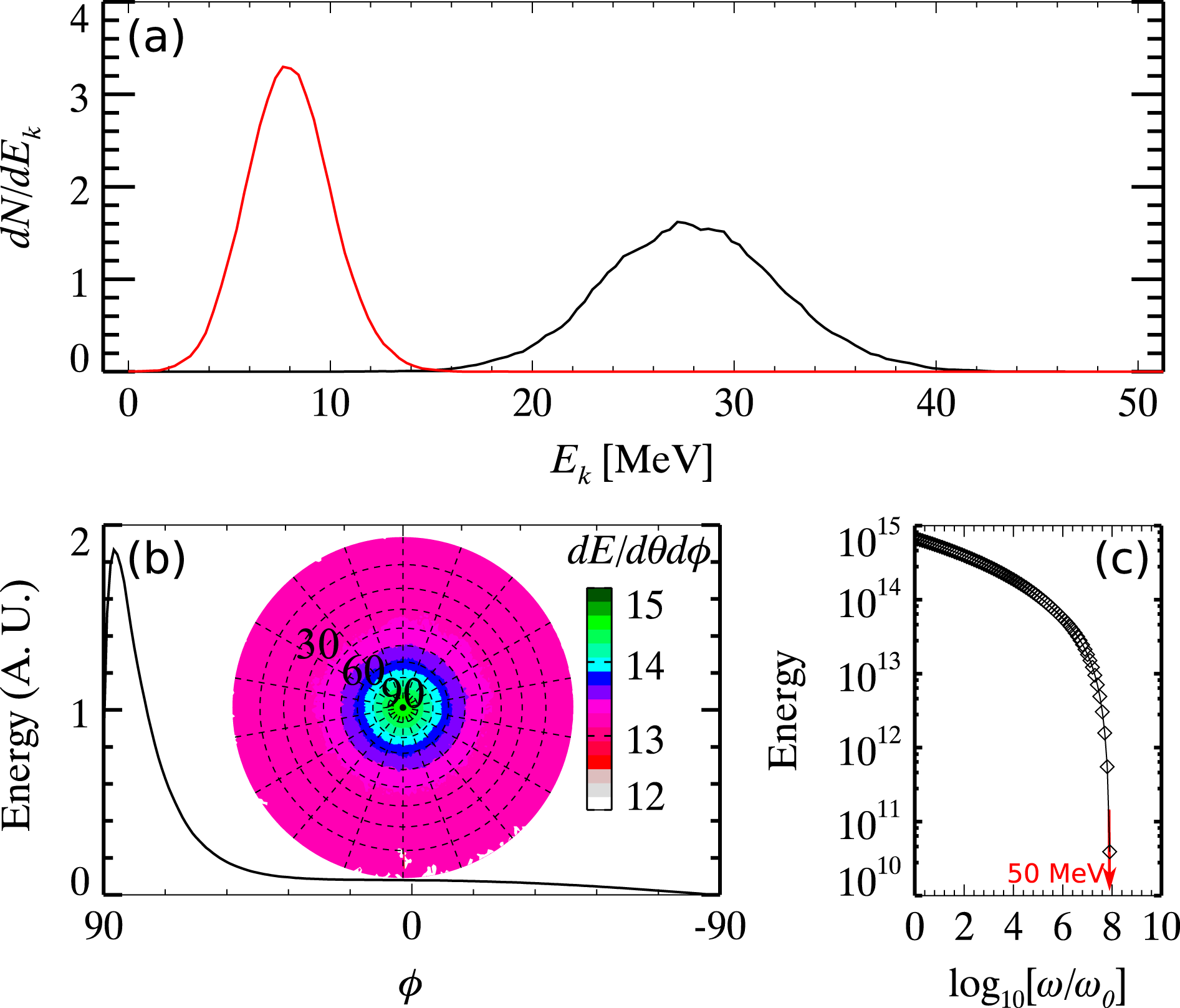
Figure 5. Comparison of PIC simulations when including and excluding Bremsstrahlung radiation correction. Initially, a mono-energetic electron beam of
![]() $E=50~\text{MeV}$
is launched into a bulk Al. The final energy spectrum after
$E=50~\text{MeV}$
is launched into a bulk Al. The final energy spectrum after
![]() $150~\text{ps}$
is shown in (a), where the red line is the case including Bremsstrahlung and the black line is the one excluding Bremsstrahlung. (b) is the angular distribution of emitted photons due to Bremsstrahlung radiation. See text for the explanation of coordinate setup. (c) is the frequency spectra of emitted photons due to Bremsstrahlung radiation, where we have plotted
$150~\text{ps}$
is shown in (a), where the red line is the case including Bremsstrahlung and the black line is the one excluding Bremsstrahlung. (b) is the angular distribution of emitted photons due to Bremsstrahlung radiation. See text for the explanation of coordinate setup. (c) is the frequency spectra of emitted photons due to Bremsstrahlung radiation, where we have plotted
![]() $\int _{\hbar \unicode[STIX]{x1D714}_{\text{k}}}^{\infty }[\text{d}E/\text{d}(\hbar \unicode[STIX]{x1D714})]\text{d}(\hbar \unicode[STIX]{x1D714})$
as a function of cut-off frequency
$\int _{\hbar \unicode[STIX]{x1D714}_{\text{k}}}^{\infty }[\text{d}E/\text{d}(\hbar \unicode[STIX]{x1D714})]\text{d}(\hbar \unicode[STIX]{x1D714})$
as a function of cut-off frequency
![]() $\unicode[STIX]{x1D714}_{\text{k}}$
. Note
$\unicode[STIX]{x1D714}_{\text{k}}$
. Note
![]() $\hbar \unicode[STIX]{x1D714}_{0}=1.24$
eV, corresponding to the energy of a photon with wavelength
$\hbar \unicode[STIX]{x1D714}_{0}=1.24$
eV, corresponding to the energy of a photon with wavelength
![]() $1~\unicode[STIX]{x03BC}\text{m}$
.
$1~\unicode[STIX]{x03BC}\text{m}$
.
In order to give details of the comparison between collision model with and without the Bremsstrahlung radiation correction, the ‘EM-field mode’ in PIC simulations is turned off. Initially, a mono-energetic electron beam of
![]() $E_{k}=50~\text{MeV}$
is launched along
$E_{k}=50~\text{MeV}$
is launched along
![]() $x$
direction into a bulk Al. After
$x$
direction into a bulk Al. After
![]() $150$
ps, the final energy spectra with and without Bremsstrahlung radiation correction are shown in Figure 5(a). The red line is the case including Bremsstrahlung and black line is the one excluding Bremsstrahlung. We can see, as expected, the peak energy of electron beam is
$150$
ps, the final energy spectra with and without Bremsstrahlung radiation correction are shown in Figure 5(a). The red line is the case including Bremsstrahlung and black line is the one excluding Bremsstrahlung. We can see, as expected, the peak energy of electron beam is
![]() $8~\text{MeV}$
(with Bremsstrahlung radiation correction) versus
$8~\text{MeV}$
(with Bremsstrahlung radiation correction) versus
![]() $28~\text{MeV}$
(without Bremsstrahlung radiation correction). The energy spread is also significantly contracted by the Bremsstrahlung radiation.
$28~\text{MeV}$
(without Bremsstrahlung radiation correction). The energy spread is also significantly contracted by the Bremsstrahlung radiation.
The angular distribution of emitted photons due to Bremsstrahlung radiation is presented in Figure 5(b). Here the definition of the angle is similar to the longitude and latitude system on a map of the Earth. Here the longitude angle
![]() $\unicode[STIX]{x1D703}$
spans from
$\unicode[STIX]{x1D703}$
spans from
![]() $-180^{\circ }$
to
$-180^{\circ }$
to
![]() $180^{\circ }$
, which is defined as the azimuthal angle of transverse momentum of the photon. The latitude angle
$180^{\circ }$
, which is defined as the azimuthal angle of transverse momentum of the photon. The latitude angle
![]() $\unicode[STIX]{x1D719}$
spans from
$\unicode[STIX]{x1D719}$
spans from
![]() $-90^{\circ }$
to
$-90^{\circ }$
to
![]() $90^{\circ }$
, which is defined as the angle between the
$90^{\circ }$
, which is defined as the angle between the
![]() $x$
-axis and the photon propagation direction. We can see that the radiation of photons is almost of forward direction, although a slight deflection from the
$x$
-axis and the photon propagation direction. We can see that the radiation of photons is almost of forward direction, although a slight deflection from the
![]() $x$
-axis of
$x$
-axis of
![]() $3^{\circ }{-}5^{\circ }$
is observed. In Figure 5(c), we also present the frequency spectrum of emitted photons, where we have plotted
$3^{\circ }{-}5^{\circ }$
is observed. In Figure 5(c), we also present the frequency spectrum of emitted photons, where we have plotted
![]() $\int _{\hbar \unicode[STIX]{x1D714}_{\text{k}}}^{\infty }[\text{d}E/\text{d}(\hbar \unicode[STIX]{x1D714})]\text{d}(\hbar \unicode[STIX]{x1D714})$
as a function of cut-off frequency
$\int _{\hbar \unicode[STIX]{x1D714}_{\text{k}}}^{\infty }[\text{d}E/\text{d}(\hbar \unicode[STIX]{x1D714})]\text{d}(\hbar \unicode[STIX]{x1D714})$
as a function of cut-off frequency
![]() $\unicode[STIX]{x1D714}_{\text{k}}$
. Note that the cut-off energy of the radiated photons is exactly equal to the maximum electron energy, i.e.,
$\unicode[STIX]{x1D714}_{\text{k}}$
. Note that the cut-off energy of the radiated photons is exactly equal to the maximum electron energy, i.e.,
![]() $50~\text{MeV}$
. The cut-off frequency is as high as
$50~\text{MeV}$
. The cut-off frequency is as high as
![]() ${\sim}0.4\times 10^{8}\hbar \unicode[STIX]{x1D714}_{0}$
, where
${\sim}0.4\times 10^{8}\hbar \unicode[STIX]{x1D714}_{0}$
, where
![]() $\hbar \unicode[STIX]{x1D714}_{0}=1.24~\text{eV}$
is the energy of a photon with wavelength
$\hbar \unicode[STIX]{x1D714}_{0}=1.24~\text{eV}$
is the energy of a photon with wavelength
![]() $1~\unicode[STIX]{x03BC}\text{m}$
.
$1~\unicode[STIX]{x03BC}\text{m}$
.

Figure 6. The value of self-heating as a function of simulation time. Plasma is of density
![]() $100n_{c}$
(
$100n_{c}$
(
![]() $n_{c}$
is the corresponding critical density for electromagnetic wave of wavelength
$n_{c}$
is the corresponding critical density for electromagnetic wave of wavelength
![]() $1~\unicode[STIX]{x03BC}\text{m}$
), plasma temperature is
$1~\unicode[STIX]{x03BC}\text{m}$
), plasma temperature is
![]() $T_{e}=10~\text{eV}$
, the simulation grid size is
$T_{e}=10~\text{eV}$
, the simulation grid size is
![]() $0.02~\unicode[STIX]{x03BC}\text{m}$
and 100 electrons are filled into a computational cell. Different coloured lines represent different combinations of numerical schemes, fourth/second order and with/without current smoothing.
$0.02~\unicode[STIX]{x03BC}\text{m}$
and 100 electrons are filled into a computational cell. Different coloured lines represent different combinations of numerical schemes, fourth/second order and with/without current smoothing.
2.3 ‘Layered density’ method
It is well known that PIC codes are prone to a phenomenon known as self-heating. In general, the grid size of PIC is restricted by the plasma Debye length
![]() $\unicode[STIX]{x1D706}_{\text{D}}\sim \sqrt{T_{e}/n_{e}}$
, to avoid the numerical self-heating[Reference Langdon46]. However the analysis presented there concentrates primarily on the case in which particle forces are assigned to the nearest-neighbour grid points. Here we refer this method as the first-order scheme. Recently, high-order explicit electromagnetic fields solver and smoother particle shape functions have been implemented into PIC codes. Significant advantages over first-order scheme have been reported[Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz, Bell and Ridgers59], and the restriction of grid size in PIC simulations is also increased from plasma Debye length
$\unicode[STIX]{x1D706}_{\text{D}}\sim \sqrt{T_{e}/n_{e}}$
, to avoid the numerical self-heating[Reference Langdon46]. However the analysis presented there concentrates primarily on the case in which particle forces are assigned to the nearest-neighbour grid points. Here we refer this method as the first-order scheme. Recently, high-order explicit electromagnetic fields solver and smoother particle shape functions have been implemented into PIC codes. Significant advantages over first-order scheme have been reported[Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz, Bell and Ridgers59], and the restriction of grid size in PIC simulations is also increased from plasma Debye length
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
to skin depth
$\unicode[STIX]{x1D706}_{\text{D}}$
to skin depth
![]() $l\sim \sqrt{m_{e}c^{2}/n_{e}}$
.
$l\sim \sqrt{m_{e}c^{2}/n_{e}}$
.
In Figure 6, we have presented the value of self-heating as a function of the simulation time. In these simulations, the plasma density is
![]() $100n_{c}$
. Here
$100n_{c}$
. Here
![]() $n_{c}$
is the corresponding critical density for electromagnetic wave of wavelength
$n_{c}$
is the corresponding critical density for electromagnetic wave of wavelength
![]() $1~\unicode[STIX]{x03BC}\text{m}$
. The plasma temperature is of
$1~\unicode[STIX]{x03BC}\text{m}$
. The plasma temperature is of
![]() $T_{e}=10~\text{eV}$
. The plasma Debye length is
$T_{e}=10~\text{eV}$
. The plasma Debye length is
![]() $\unicode[STIX]{x1D706}_{\text{D}}=4\times 10^{-6}~\unicode[STIX]{x03BC}\text{m}$
and skin depth is
$\unicode[STIX]{x1D706}_{\text{D}}=4\times 10^{-6}~\unicode[STIX]{x03BC}\text{m}$
and skin depth is
![]() $l=0.024~\unicode[STIX]{x03BC}\text{m}$
. The simulation grid size is
$l=0.024~\unicode[STIX]{x03BC}\text{m}$
. The simulation grid size is
![]() $0.02~\unicode[STIX]{x03BC}\text{m}$
, which is smaller than skin depth. We fill 100 electrons into each computational cell. Different coloured lines represent the combinations of different numerical schemes. In Figure 6, larger and smoother particle shape functions coupled with multi-points electromagnetic field solvers are regarded as high-order schemes. It is clearly demonstrated that fourth-order numerical scheme coupled with current smoothing technique shows significant advantage over others. Therefore, in our following simulations, this combination is regarded as the default setup.
$0.02~\unicode[STIX]{x03BC}\text{m}$
, which is smaller than skin depth. We fill 100 electrons into each computational cell. Different coloured lines represent the combinations of different numerical schemes. In Figure 6, larger and smoother particle shape functions coupled with multi-points electromagnetic field solvers are regarded as high-order schemes. It is clearly demonstrated that fourth-order numerical scheme coupled with current smoothing technique shows significant advantage over others. Therefore, in our following simulations, this combination is regarded as the default setup.
The combination of fourth-order numerical scheme coupled with current smoothing technique is a useful approach to avoid significant numerical self-heating. However if plasma density is further increased, it is still a great challenge for the present PIC codes. For example the electron density can be as high as
![]() $10^{24}~\text{cm}^{-3}$
in solid metals, or even as high as
$10^{24}~\text{cm}^{-3}$
in solid metals, or even as high as
![]() $10^{25}~\text{cm}^{-3}$
in the compressed D-T core which exists in fast-ignition inertial confinement fusion research. It is nowadays a well accepted fact that the numerical self-heating arises from the high-density background plasmas. For extremely high-density plasmas, it is the collision effects that dominate, while the electromagnetic effects tend to be significantly suppressed. If one turns off the electromagnetic field solver for the high-density background electrons, the self-heating can be definitely avoided. However, by doing so, one also lost some important physics, like the generation of return current and resistive electric and magnetic fields.
$10^{25}~\text{cm}^{-3}$
in the compressed D-T core which exists in fast-ignition inertial confinement fusion research. It is nowadays a well accepted fact that the numerical self-heating arises from the high-density background plasmas. For extremely high-density plasmas, it is the collision effects that dominate, while the electromagnetic effects tend to be significantly suppressed. If one turns off the electromagnetic field solver for the high-density background electrons, the self-heating can be definitely avoided. However, by doing so, one also lost some important physics, like the generation of return current and resistive electric and magnetic fields.
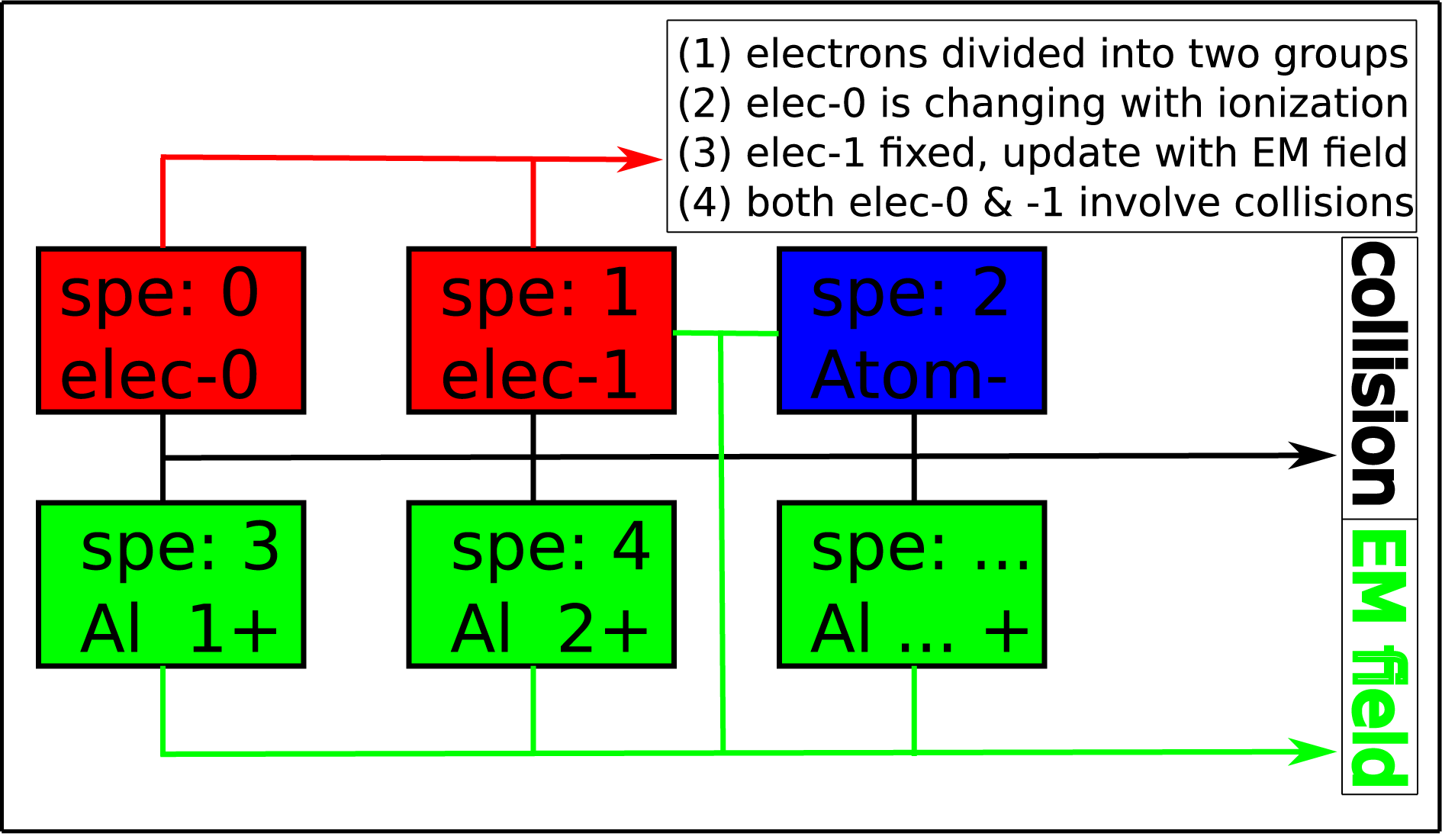
Figure 7. The schematic of ‘layered density’ method. Here ‘layered density’ means electrons are divided into two groups, i.e., electron-0 and electron-1. During the PIC simulation, electron-0 updates following the ionization dynamics. For the calculation of electromagnetic fields, only electron-1 is involved. For collisions, both electron-0 and electron-1 are involved.

Figure 8. Thermal equilibrium benchmark of the ‘layered density’ (LD) method. Electron and ion kinetic energy as a function of time. Initial plasma density is set to be
![]() $100n_{c}$
, initial electron temperature is
$100n_{c}$
, initial electron temperature is
![]() $50~\text{eV}$
and initial proton temperature is
$50~\text{eV}$
and initial proton temperature is
![]() $100~\text{eV}$
. For the LD method, electrons are divided into two groups, and the density of each group is
$100~\text{eV}$
. For the LD method, electrons are divided into two groups, and the density of each group is
![]() $50n_{c}$
. In PIC simulations, these two groups of electrons are treated as different species.
$50n_{c}$
. In PIC simulations, these two groups of electrons are treated as different species.
Here we suggest a ‘layered density’ method, which can well deal with plasmas with extremely high densities. This method is not a rigorous numerical scheme, but an empirical method. A schematic structure is shown in Figure 7. In this method, we divide the high-density background electrons into two groups, regarded as ele-0 and ele-1. In PIC simulations, although both ele-0 and ele-1 have the same mass and charge, they are treated as different particle species. Usually density
![]() $n_{e0}$
of ele-0 is close to the original background density
$n_{e0}$
of ele-0 is close to the original background density
![]() $n_{e}$
, while density of ele-1 is
$n_{e}$
, while density of ele-1 is
![]() $n_{e1}=n_{e}-n_{e0}$
. In PIC simulations, the movement of charged particles generates a distribution of current density, and this current density will in turn update the electromagnetic fields. In the ‘layered density’ method, the contribution to the current density from ele-0 is turned off, while only ele-1’s contribution is reserved. The variation of
$n_{e1}=n_{e}-n_{e0}$
. In PIC simulations, the movement of charged particles generates a distribution of current density, and this current density will in turn update the electromagnetic fields. In the ‘layered density’ method, the contribution to the current density from ele-0 is turned off, while only ele-1’s contribution is reserved. The variation of
![]() $n_{e0}$
is restricted to ionization dynamics, while the variation of
$n_{e0}$
is restricted to ionization dynamics, while the variation of
![]() $n_{e1}$
is due to the actions of electromagnetic fields. However, both ele-0 and ele-1 involve in the collision effects. Although, this ‘layered density’ method can avoid numerical self-heating, whether this kind of setup is applicable or not still demands rigorous benchmarks: (i) thermal equilibrium benchmark; (ii) return current and resistive electric field or magnetic field benchmark.
$n_{e1}$
is due to the actions of electromagnetic fields. However, both ele-0 and ele-1 involve in the collision effects. Although, this ‘layered density’ method can avoid numerical self-heating, whether this kind of setup is applicable or not still demands rigorous benchmarks: (i) thermal equilibrium benchmark; (ii) return current and resistive electric field or magnetic field benchmark.
In Figure 8, thermal equilibrium benchmark of the ‘layered density’ method is demonstrated. In this benchmark, initial plasma density is set to be
![]() $100n_{c}$
, initial electron temperature is
$100n_{c}$
, initial electron temperature is
![]() $50~\text{eV}$
and initial proton temperature is
$50~\text{eV}$
and initial proton temperature is
![]() $100~\text{eV}$
. The black triangle and red triangle lines represent the relaxation processes of electrons and protons with initially different temperatures. For the ‘layered density’ method, electrons are divided into two groups, and the density of each group is
$100~\text{eV}$
. The black triangle and red triangle lines represent the relaxation processes of electrons and protons with initially different temperatures. For the ‘layered density’ method, electrons are divided into two groups, and the density of each group is
![]() $50n_{c}$
. In PIC simulations, these two groups of electrons are treated as different species. The black square and red square lines represent the one calculated by ‘layered density’ method PIC. When comparing with results obtained by the full PIC, we do not find any significant differences. This is because, the collision frequency between charged particles is a linear function of density, i.e.,
$50n_{c}$
. In PIC simulations, these two groups of electrons are treated as different species. The black square and red square lines represent the one calculated by ‘layered density’ method PIC. When comparing with results obtained by the full PIC, we do not find any significant differences. This is because, the collision frequency between charged particles is a linear function of density, i.e.,
![]() $\unicode[STIX]{x1D708}\sim n_{e}$
. Therefore, a linear decomposition of electrons into different sub-groups does not affect the whole collision dynamics.
$\unicode[STIX]{x1D708}\sim n_{e}$
. Therefore, a linear decomposition of electrons into different sub-groups does not affect the whole collision dynamics.
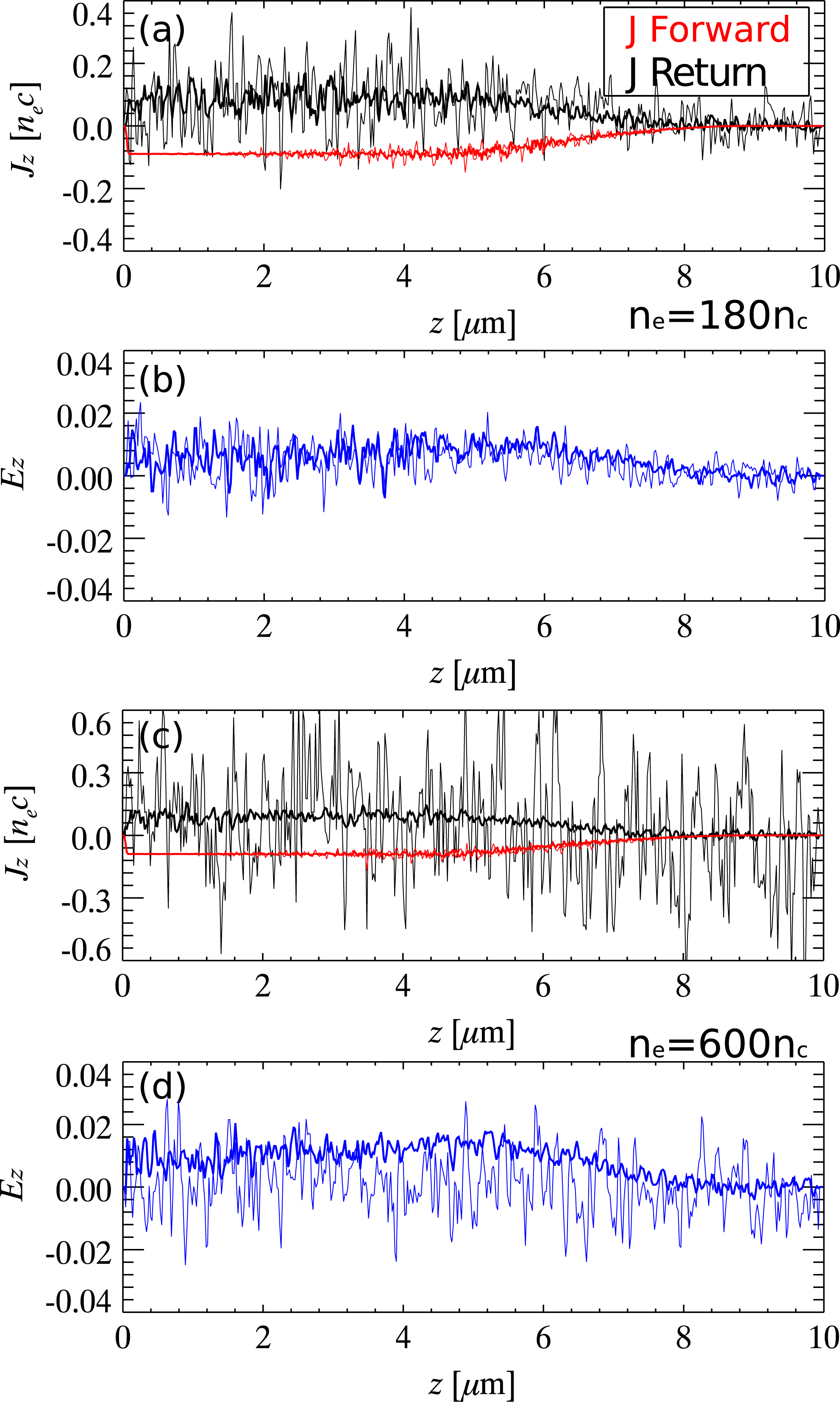
Figure 9. (a) and (c) The current density distribution,
![]() $\boldsymbol{J}$
, of forward-propagating fast electrons (red line) and returning background electrons (black line), when a fast electron beam of 1 MeV with density
$\boldsymbol{J}$
, of forward-propagating fast electrons (red line) and returning background electrons (black line), when a fast electron beam of 1 MeV with density
![]() $0.1n_{c}$
is launched into uniform plasmas. (b) and (d) The resistive electric fields, normalized by
$0.1n_{c}$
is launched into uniform plasmas. (b) and (d) The resistive electric fields, normalized by
![]() $eE/m_{e}\unicode[STIX]{x1D714}_{0}c$
, generated by the launched electron beam. Here background plasma density in (a) and (b) is of
$eE/m_{e}\unicode[STIX]{x1D714}_{0}c$
, generated by the launched electron beam. Here background plasma density in (a) and (b) is of
![]() $180n_{c}$
(
$180n_{c}$
(
![]() $n_{c}$
is the corresponding critical density for electromagnetic wave of wavelength
$n_{c}$
is the corresponding critical density for electromagnetic wave of wavelength
![]() $\unicode[STIX]{x1D706}_{0}=1~\unicode[STIX]{x03BC}\text{m}$
and
$\unicode[STIX]{x1D706}_{0}=1~\unicode[STIX]{x03BC}\text{m}$
and
![]() $\unicode[STIX]{x1D714}_{0}=2\unicode[STIX]{x1D70B}c/\unicode[STIX]{x1D706}_{0}$
) and temperature is of
$\unicode[STIX]{x1D714}_{0}=2\unicode[STIX]{x1D70B}c/\unicode[STIX]{x1D706}_{0}$
) and temperature is of
![]() $T_{e}=10~\text{eV}$
. In (c) and (d), plasma density of
$T_{e}=10~\text{eV}$
. In (c) and (d), plasma density of
![]() $600n_{c}$
is used. Thick lines are the results calculated by ‘layered density’ methods, and thin lines are the ones obtained from full-PIC method.
$600n_{c}$
is used. Thick lines are the results calculated by ‘layered density’ methods, and thin lines are the ones obtained from full-PIC method.
For extremely high-density plasmas, the electromagnetic effects are significantly suppressed. However, if one turns off the electromagnetic field solver for the high-density background electrons, some important physics, like the generation of return current and resistive electric or/and magnetic field, is lost. In the ‘layered density’ method, the high-density background electrons are divided into two groups, ele-0 and ele-1, and only the latter one is set up to update the electromagnetic fields. As a benchmark of return current and resistive electromagnetic fields, we consider a fast electron beam of 1 MeV with density
![]() $0.1n_{c}$
launching into uniform plasmas. In Figures 9(a) and 9(b), the density and temperature of the uniform plasmas are set to
$0.1n_{c}$
launching into uniform plasmas. In Figures 9(a) and 9(b), the density and temperature of the uniform plasmas are set to
![]() $180n_{c}$
(
$180n_{c}$
(
![]() $n_{c}$
is the corresponding critical density for electromagnetic wave of wavelength
$n_{c}$
is the corresponding critical density for electromagnetic wave of wavelength
![]() $\unicode[STIX]{x1D706}_{0}=1~\unicode[STIX]{x03BC}\text{m}$
and
$\unicode[STIX]{x1D706}_{0}=1~\unicode[STIX]{x03BC}\text{m}$
and
![]() $\unicode[STIX]{x1D714}_{0}=2\unicode[STIX]{x1D70B}c/\unicode[STIX]{x1D706}_{0}$
) and
$\unicode[STIX]{x1D714}_{0}=2\unicode[STIX]{x1D70B}c/\unicode[STIX]{x1D706}_{0}$
) and
![]() $10~\text{eV}$
. The corresponding skin depth is
$10~\text{eV}$
. The corresponding skin depth is
![]() $0.021~\unicode[STIX]{x03BC}\text{m}$
, and grid size in PIC simulation is set to
$0.021~\unicode[STIX]{x03BC}\text{m}$
, and grid size in PIC simulation is set to
![]() $0.02~\unicode[STIX]{x03BC}\text{m}$
. As shown in Figure 9(a), thin red line is the current density
$0.02~\unicode[STIX]{x03BC}\text{m}$
. As shown in Figure 9(a), thin red line is the current density
![]() $J_{\text{fw}}$
of launched fast electrons calculated by full PIC, and black line is the return current
$J_{\text{fw}}$
of launched fast electrons calculated by full PIC, and black line is the return current
![]() $J_{\text{rt}}$
. We can see that the total current is almost zero, because the
$J_{\text{rt}}$
. We can see that the total current is almost zero, because the
![]() $J_{\text{fw}}$
is almost compensated by
$J_{\text{fw}}$
is almost compensated by
![]() $J_{\text{rt}}$
. The thick red and black lines are the one calculated by ‘layered density’ method PIC, where density of ele-0 is
$J_{\text{rt}}$
. The thick red and black lines are the one calculated by ‘layered density’ method PIC, where density of ele-0 is
![]() $130n_{c}$
and density of ele-1 is
$130n_{c}$
and density of ele-1 is
![]() $50n_{c}$
. When comparing the results obtained by two different methods, we do not find any significant differences, except that the numerical noises calculated by ‘layered density’ method PIC are significantly depressed. The corresponding resistive electric field is shown in Figure 9(b), where thin blue line represents the one calculated by full PIC and thick blue line is the one by ‘layered density’ method PIC. As for the resistive electric fields, except that the numerical noises calculated by ‘layered density’ method PIC appear relatively small, we also do not find any significant differences between them. When increasing the uniform background plasma density from
$50n_{c}$
. When comparing the results obtained by two different methods, we do not find any significant differences, except that the numerical noises calculated by ‘layered density’ method PIC are significantly depressed. The corresponding resistive electric field is shown in Figure 9(b), where thin blue line represents the one calculated by full PIC and thick blue line is the one by ‘layered density’ method PIC. As for the resistive electric fields, except that the numerical noises calculated by ‘layered density’ method PIC appear relatively small, we also do not find any significant differences between them. When increasing the uniform background plasma density from
![]() $180n_{c}$
to
$180n_{c}$
to
![]() $600n_{c}$
and keeping other parameters the same, as shown in Figures 9(c) and 9(d), the results obtained from full PIC are fully ‘swallowed’ by numerical noises. In contrast, the results calculated by the ‘layered density’ method PIC are proved to be stable.
$600n_{c}$
and keeping other parameters the same, as shown in Figures 9(c) and 9(d), the results obtained from full PIC are fully ‘swallowed’ by numerical noises. In contrast, the results calculated by the ‘layered density’ method PIC are proved to be stable.
It seems that the decomposition of high-density background plasmas is an arbitrary approach; however one still needs to obey some restricted rules. When a fast electron beam launches into high-density plasmas, the induced return current will increase with time, asymptotically approaching steady state given by Ohm’s law
![]() $\boldsymbol{J}=\unicode[STIX]{x1D70E}\boldsymbol{E}$
[Reference Davies60]. The variation of return current density with time can be obtained by seeking a time-dependent solution to the Drude model[Reference Davies60] for electron transport,
$\boldsymbol{J}=\unicode[STIX]{x1D70E}\boldsymbol{E}$
[Reference Davies60]. The variation of return current density with time can be obtained by seeking a time-dependent solution to the Drude model[Reference Davies60] for electron transport,
![]() $\boldsymbol{J}(t)=\unicode[STIX]{x1D70E}\boldsymbol{E}[1-\exp (-t/\unicode[STIX]{x1D70F})]$
, where
$\boldsymbol{J}(t)=\unicode[STIX]{x1D70E}\boldsymbol{E}[1-\exp (-t/\unicode[STIX]{x1D70F})]$
, where
![]() $\unicode[STIX]{x1D70E}=e^{2}n_{e}\unicode[STIX]{x1D70F}/m_{e}$
is conductivity and
$\unicode[STIX]{x1D70E}=e^{2}n_{e}\unicode[STIX]{x1D70F}/m_{e}$
is conductivity and
![]() $\unicode[STIX]{x1D70F}$
is the typical collision time of background electrons, which is usually much smaller than
$\unicode[STIX]{x1D70F}$
is the typical collision time of background electrons, which is usually much smaller than
![]() $2\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D714}_{pe}$
. In the ‘layered density’ method, we have
$2\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D714}_{pe}$
. In the ‘layered density’ method, we have
![]() $\boldsymbol{J}_{e1}(t)\sim en_{e1}\bar{\boldsymbol{v}}_{e1}\sim e^{2}n_{e1}\boldsymbol{E}\unicode[STIX]{x1D6FF}t/m_{e}\sim \unicode[STIX]{x1D70E}\boldsymbol{E}[1-\exp (-\unicode[STIX]{x1D6FF}t/\unicode[STIX]{x1D70F})]$
. Within one time step, if the product of
$\boldsymbol{J}_{e1}(t)\sim en_{e1}\bar{\boldsymbol{v}}_{e1}\sim e^{2}n_{e1}\boldsymbol{E}\unicode[STIX]{x1D6FF}t/m_{e}\sim \unicode[STIX]{x1D70E}\boldsymbol{E}[1-\exp (-\unicode[STIX]{x1D6FF}t/\unicode[STIX]{x1D70F})]$
. Within one time step, if the product of
![]() $n_{e1}\unicode[STIX]{x1D6FF}t$
is much larger than
$n_{e1}\unicode[STIX]{x1D6FF}t$
is much larger than
![]() $n_{e}\unicode[STIX]{x1D70F}$
, then one cannot distinguish the differences whether all the background electrons
$n_{e}\unicode[STIX]{x1D70F}$
, then one cannot distinguish the differences whether all the background electrons
![]() $n_{e}$
or just
$n_{e}$
or just
![]() $n_{e1}$
involve in return current or/and resistive electromagnetic fields calculations. After the abrupt building of return current, whose following evolution is much slow, any small variation of return current
$n_{e1}$
involve in return current or/and resistive electromagnetic fields calculations. After the abrupt building of return current, whose following evolution is much slow, any small variation of return current
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{J}(\unicode[STIX]{x1D6FF}t)$
can be compensated by the redistribution of
$\unicode[STIX]{x1D6FF}\boldsymbol{J}(\unicode[STIX]{x1D6FF}t)$
can be compensated by the redistribution of
![]() $n_{e1}$
and
$n_{e1}$
and
![]() $\bar{\boldsymbol{v}}_{e1}$
within
$\bar{\boldsymbol{v}}_{e1}$
within
![]() $\unicode[STIX]{x1D6FF}t$
. Here we present an empirical formula, where for the given PIC simulation time step
$\unicode[STIX]{x1D6FF}t$
. Here we present an empirical formula, where for the given PIC simulation time step
![]() $\unicode[STIX]{x1D6FF}t$
and initial background plasma temperatures
$\unicode[STIX]{x1D6FF}t$
and initial background plasma temperatures
![]() $T_{e}$
, the threshold density of ele-1 is
$T_{e}$
, the threshold density of ele-1 is
In the simulation setup, we have
![]() $n_{e1}\gg n_{e1}^{\text{th}}$
. Note that the ‘layered density’ method is still an empirical method instead of a rigorous numerical scheme. To ensure that the simulation results are physically correct, we would suggest to re-run the simulation by increasing the ele-1 density twice to confirm the convergence of final results.
$n_{e1}\gg n_{e1}^{\text{th}}$
. Note that the ‘layered density’ method is still an empirical method instead of a rigorous numerical scheme. To ensure that the simulation results are physically correct, we would suggest to re-run the simulation by increasing the ele-1 density twice to confirm the convergence of final results.
3 Applications
In this part, as an application of the new code, the generation and transport of energetic electrons in front of and within the solid target when irradiated by intense laser beams are studied by using the LAPINE (appendix B) code. Thanks to the ‘layered density’ method and the coupled high-order numerical scheme and current smoothing technique, the simulation grid size can be significantly larger than the plasma Debye length. Larger simulation grid would dramatically reduce the simulation burden, which makes it possible for a small cluster with only 10 nodes (with each node containing 12 cores) to simulate realistic laser–solid interactions in large scales, both spatially and temporally.
Figure 10. (a) The initial parameter setup, with pre-plasma scale length
![]() $10~\unicode[STIX]{x03BC}\text{m}$
, initial density
$10~\unicode[STIX]{x03BC}\text{m}$
, initial density
![]() $180n_{c}$
(
$180n_{c}$
(
![]() $Z=3$
) and temperature
$Z=3$
) and temperature
![]() $10~\text{eV}$
. In the ‘layered density’ method, density of ele-0 is
$10~\text{eV}$
. In the ‘layered density’ method, density of ele-0 is
![]() $n_{e0}=160n_{c}$
and ele-1 is
$n_{e0}=160n_{c}$
and ele-1 is
![]() $n_{e1}=20n_{c}$
. Here
$n_{e1}=20n_{c}$
. Here
![]() $n_{c}=1.1\times 10^{21}~\text{cm}^{-3}$
is the corresponding critical density of electromagnetic wave with wavelength
$n_{c}=1.1\times 10^{21}~\text{cm}^{-3}$
is the corresponding critical density of electromagnetic wave with wavelength
![]() $1~\unicode[STIX]{x03BC}\text{m}$
. (b) Electron density and temperature at the end of simulations.
$1~\unicode[STIX]{x03BC}\text{m}$
. (b) Electron density and temperature at the end of simulations.
3.1 1D simulations
The simulation setup of 1D PIC is shown in Figure 10(a). The simulation box is
![]() $400~\unicode[STIX]{x03BC}\text{m}$
, an Al target with maximal density of
$400~\unicode[STIX]{x03BC}\text{m}$
, an Al target with maximal density of
![]() $2.7~\text{g}\cdot \text{cm}^{-3}$
(or ion density of
$2.7~\text{g}\cdot \text{cm}^{-3}$
(or ion density of
![]() $60n_{c}$
for laser of wavelength
$60n_{c}$
for laser of wavelength
![]() $1~\unicode[STIX]{x03BC}\text{m}$
) and temperature of
$1~\unicode[STIX]{x03BC}\text{m}$
) and temperature of
![]() $10~\text{eV}$
is applied. The simulation grid size is
$10~\text{eV}$
is applied. The simulation grid size is
![]() $\unicode[STIX]{x1D6FF}z=0.02~\unicode[STIX]{x03BC}\text{m}$
, which is smaller than the skin depth
$\unicode[STIX]{x1D6FF}z=0.02~\unicode[STIX]{x03BC}\text{m}$
, which is smaller than the skin depth
![]() $l\sim 0.021~\unicode[STIX]{x03BC}\text{m}$
. In the ‘layered density’ method, density of ele-1 is
$l\sim 0.021~\unicode[STIX]{x03BC}\text{m}$
. In the ‘layered density’ method, density of ele-1 is
![]() $n_{e1}(z)=n_{e1}/\{1+\exp [-2(z-180)/L_{p}]\}$
, where
$n_{e1}(z)=n_{e1}/\{1+\exp [-2(z-180)/L_{p}]\}$
, where
![]() $n_{e1}=20n_{c}$
is the solid plasma density and
$n_{e1}=20n_{c}$
is the solid plasma density and
![]() $L_{p}=10$
is the pre-plasma scale length. The density of ele-0 is
$L_{p}=10$
is the pre-plasma scale length. The density of ele-0 is
![]() $n_{e0}(z)=160n_{c}$
when
$n_{e0}(z)=160n_{c}$
when
![]() $z>250$
and otherwise
$z>250$
and otherwise
![]() $n_{e0}(z)=0$
. The simulation time step is
$n_{e0}(z)=0$
. The simulation time step is
![]() $\unicode[STIX]{x1D6FF}t=3.9\times 10^{-2}~\text{fs}$
. Therefore, according to Equation (6), the corresponding density threshold is
$\unicode[STIX]{x1D6FF}t=3.9\times 10^{-2}~\text{fs}$
. Therefore, according to Equation (6), the corresponding density threshold is
![]() $n_{e1}^{\text{th}}=7n_{c}$
, which is much smaller than
$n_{e1}^{\text{th}}=7n_{c}$
, which is much smaller than
![]() $n_{e1}=20n_{c}$
. The laser intensity is
$n_{e1}=20n_{c}$
. The laser intensity is
![]() $10^{20}~\text{W}\cdot \text{cm}^{-2}$
or normalized amplitude
$10^{20}~\text{W}\cdot \text{cm}^{-2}$
or normalized amplitude
![]() $a=8.54$
(with laser wavelength
$a=8.54$
(with laser wavelength
![]() $1~\unicode[STIX]{x03BC}\text{m}$
). It enters the simulation box from the left boundary, where the laser amplitude rises over 33 fs and then remains constant.
$1~\unicode[STIX]{x03BC}\text{m}$
). It enters the simulation box from the left boundary, where the laser amplitude rises over 33 fs and then remains constant.
The final electron density and temperature (at
![]() $t=1.3~\text{ps}$
) are presented in Figure 10(b). We can see that along the laser propagation direction, both electron density and temperature decrease rapidly. As the thermal equilibrium is not yet established within such a short time, here we use ‘temperature’ to represent the average kinetic energy of electrons. In Figure 10(b), at
$t=1.3~\text{ps}$
) are presented in Figure 10(b). We can see that along the laser propagation direction, both electron density and temperature decrease rapidly. As the thermal equilibrium is not yet established within such a short time, here we use ‘temperature’ to represent the average kinetic energy of electrons. In Figure 10(b), at
![]() $z=380$
, temperature is
$z=380$
, temperature is
![]() $T_{e}=1000~\text{eV}$
, while the corresponding electron density is
$T_{e}=1000~\text{eV}$
, while the corresponding electron density is
![]() $660n_{c}$
(or
$660n_{c}$
(or
![]() $Z=11$
). This is already much smaller than the thermal equilibrium ionization degree,
$Z=11$
). This is already much smaller than the thermal equilibrium ionization degree,
![]() $Z=12.9$
with
$Z=12.9$
with
![]() $T_{e}=1000~\text{eV}$
as shown in Figure 1(b). At earlier times, as expected, the deviation from the thermal equilibrium values could be more significant than at final times. The detailed comparison is not shown in this paper, but one can refer to Figure 1(a) to find the evolution of ionization dynamics with time.
$T_{e}=1000~\text{eV}$
as shown in Figure 1(b). At earlier times, as expected, the deviation from the thermal equilibrium values could be more significant than at final times. The detailed comparison is not shown in this paper, but one can refer to Figure 1(a) to find the evolution of ionization dynamics with time.
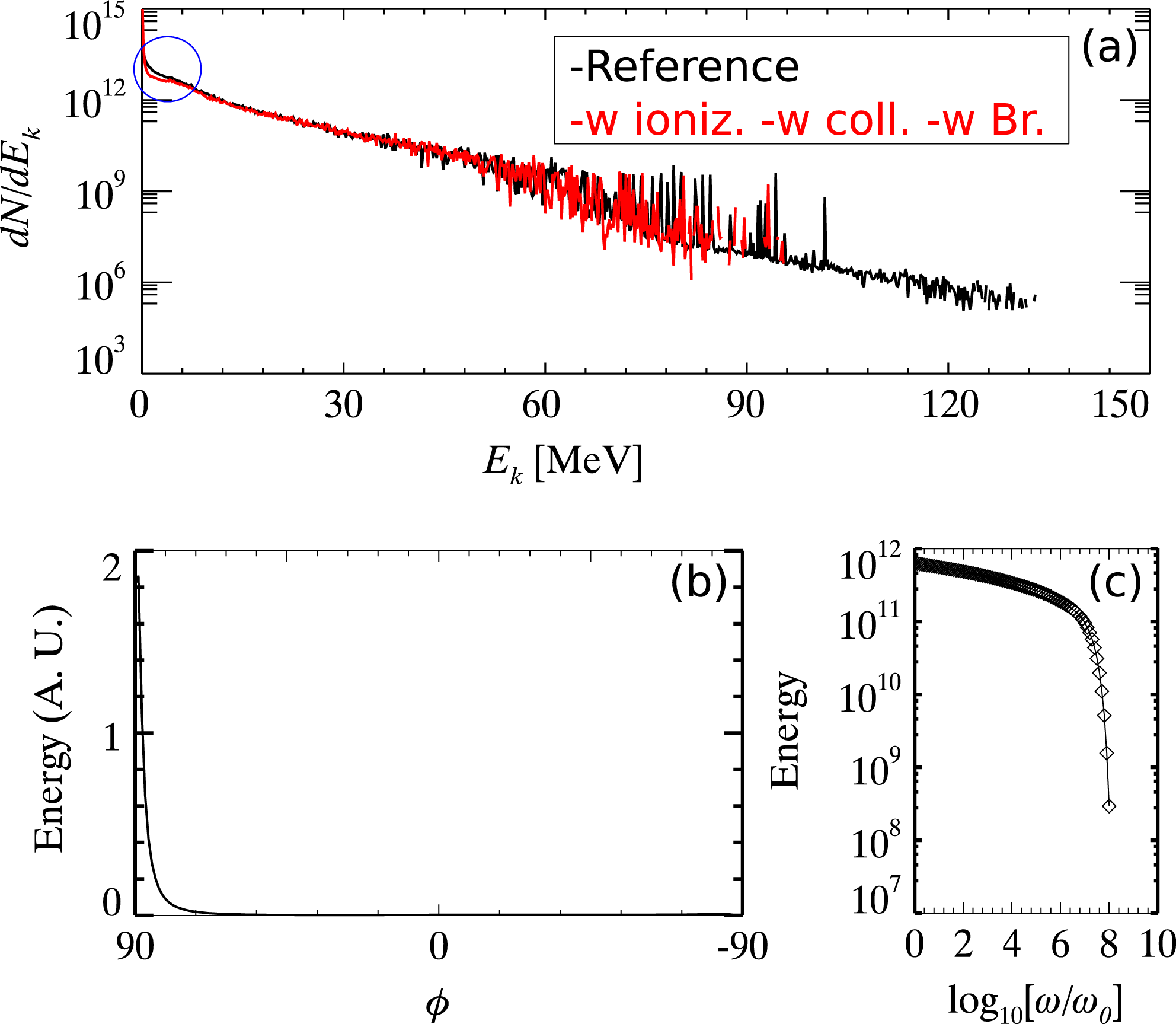
Figure 11. (a) The final energy spectra of electrons, with the black line representing the reference case without considering atomic processes, and the red line representing the one including both ionization and collision with Bremsstrahlung radiation corrections. (b) The angular distribution of emitted photons. (c) The frequency spectra of emitted photons, where we have plotted
![]() $\int _{\hbar \unicode[STIX]{x1D714}_{\text{k}}}^{\infty }[\text{d}E/\text{d}(\hbar \unicode[STIX]{x1D714})]\text{d}(\hbar \unicode[STIX]{x1D714})$
as a function of cut-off frequency
$\int _{\hbar \unicode[STIX]{x1D714}_{\text{k}}}^{\infty }[\text{d}E/\text{d}(\hbar \unicode[STIX]{x1D714})]\text{d}(\hbar \unicode[STIX]{x1D714})$
as a function of cut-off frequency
![]() $\unicode[STIX]{x1D714}_{\text{k}}$
. Note
$\unicode[STIX]{x1D714}_{\text{k}}$
. Note
![]() $\hbar \unicode[STIX]{x1D714}_{0}=1.24$
eV, corresponding to the energy of a photon with wavelength
$\hbar \unicode[STIX]{x1D714}_{0}=1.24$
eV, corresponding to the energy of a photon with wavelength
![]() $1~\unicode[STIX]{x03BC}\text{m}$
.
$1~\unicode[STIX]{x03BC}\text{m}$
.

Figure 12. The
![]() $z$
–
$z$
–
![]() $p_{z}$
phase-space plot of electrons, with the same simulation parameters as shown in Figure 10. (a) The one without considering ionization, collision and Bremsstrahlung radiation correction. (b) The one turning on both ionization and collision with Bremsstrahlung radiation corrections. Different columns represent values at different times, here
$p_{z}$
phase-space plot of electrons, with the same simulation parameters as shown in Figure 10. (a) The one without considering ionization, collision and Bremsstrahlung radiation correction. (b) The one turning on both ionization and collision with Bremsstrahlung radiation corrections. Different columns represent values at different times, here
![]() $t=0.67$
ps for (1),
$t=0.67$
ps for (1),
![]() $t=1.0$
ps for (2) and
$t=1.0$
ps for (2) and
![]() $t=1.3$
ps for (3). The red curves covered on the phase-space plots are the electrostatic potential curves (
$t=1.3$
ps for (3). The red curves covered on the phase-space plots are the electrostatic potential curves (
![]() $\int ^{z}E_{z}\,\text{d}z$
), normalized by
$\int ^{z}E_{z}\,\text{d}z$
), normalized by
![]() $-e\unicode[STIX]{x1D719}/m_{e}c^{2}$
. The blue lines are the
$-e\unicode[STIX]{x1D719}/m_{e}c^{2}$
. The blue lines are the
![]() $E_{x}(\times 0.25)$
, normalized by
$E_{x}(\times 0.25)$
, normalized by
![]() $eE/m_{e}\unicode[STIX]{x1D714}_{0}c$
, components of the superposition of incoming and reflected laser pulses.
$eE/m_{e}\unicode[STIX]{x1D714}_{0}c$
, components of the superposition of incoming and reflected laser pulses.
In Figure 11(a), we have presented the electron energy spectra, comparing different cases without/with ionization, collision and Bremsstrahlung radiation interactions. The black line represents the reference case without considering these atomic processes, and red line represents the one including these atomic processes. We can see that the electron ‘cut-off’ energy is significantly lowered by 25%. In addition, as the blue circle shows, the number of electrons with low energies, i.e., less than 3 MeV, is also significantly reduced. The latter one can be interpreted by collisional damping. While for the former one, it might be due to the Bremsstrahlung radiation, as this radiation is very efficient for those energetic electrons, with energy larger than 10 MeV. The angular distribution of emitted photons is shown in Figure 11(b). We can see that the direction of emitted photons is along the laser propagation direction, with a small diffraction angle of
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D719}\sim 10^{\circ }$
. The frequency spectrum of emitted photons, where we have plotted
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D719}\sim 10^{\circ }$
. The frequency spectrum of emitted photons, where we have plotted
![]() $\int _{\hbar \unicode[STIX]{x1D714}_{\text{k}}}^{\infty }[\text{d}E/\text{d}(\hbar \unicode[STIX]{x1D714})]\,\text{d}(\hbar \unicode[STIX]{x1D714})$
as a function of cut-off frequency
$\int _{\hbar \unicode[STIX]{x1D714}_{\text{k}}}^{\infty }[\text{d}E/\text{d}(\hbar \unicode[STIX]{x1D714})]\,\text{d}(\hbar \unicode[STIX]{x1D714})$
as a function of cut-off frequency
![]() $\unicode[STIX]{x1D714}_{\text{k}}$
, is shown in Figure 11(c). The cut-off frequency is of
$\unicode[STIX]{x1D714}_{\text{k}}$
, is shown in Figure 11(c). The cut-off frequency is of
![]() $\unicode[STIX]{x1D714}_{\text{k}}\sim 10^{8}\unicode[STIX]{x1D714}_{0}\sim 100$
MeV, which is equal to the ‘cut-off’ energy of electrons.
$\unicode[STIX]{x1D714}_{\text{k}}\sim 10^{8}\unicode[STIX]{x1D714}_{0}\sim 100$
MeV, which is equal to the ‘cut-off’ energy of electrons.
However the Bremsstrahlung radiation alone cannot fully explain the 25% reduction of ‘cut-off’ energy. This is because, as shown in Figure 4(c), for Al, the stopping power of electrons with energy 100 MeV is only
![]() $5\times 10^{-3}~\text{MeV}\cdot \,\unicode[STIX]{x03BC}\text{m}^{-1}$
. For a propagation distance of
$5\times 10^{-3}~\text{MeV}\cdot \,\unicode[STIX]{x03BC}\text{m}^{-1}$
. For a propagation distance of
![]() $200~\unicode[STIX]{x03BC}\text{m}$
, the energy reduction is only 1 MeV. Bremsstrahlung radiation only contributes
$200~\unicode[STIX]{x03BC}\text{m}$
, the energy reduction is only 1 MeV. Bremsstrahlung radiation only contributes
![]() ${\sim}1$
MeV energy reduction, and therefore, there must exist other mechanisms that significantly reduce the generation of energetic electrons. (Note by the authors: As the values of stopping power heavily depend on target materials,
${\sim}1$
MeV energy reduction, and therefore, there must exist other mechanisms that significantly reduce the generation of energetic electrons. (Note by the authors: As the values of stopping power heavily depend on target materials,
![]() $S\sim A^{2}$
(
$S\sim A^{2}$
(
![]() $A=29$
for Cu and
$A=29$
for Cu and
![]() $A=79$
for gold), if the target material is of Cu and/or gold, the energy reduction can be as high as 5 MeV and/or 37 MeV. Note that the material dependence of electron heating/acceleration is not the purpose of this paper, which shall be detailed in the following works. The present paper is focused on presenting a global simulation code and addressing the influences of the coupled atomic processes on laser–solid interactions.)
$A=79$
for gold), if the target material is of Cu and/or gold, the energy reduction can be as high as 5 MeV and/or 37 MeV. Note that the material dependence of electron heating/acceleration is not the purpose of this paper, which shall be detailed in the following works. The present paper is focused on presenting a global simulation code and addressing the influences of the coupled atomic processes on laser–solid interactions.)
In order to figure out the other mechanisms that significantly play roles, we now refer to the phase-space plots of electrons, as shown in Figure 12. The phase-space density
![]() $\text{d}N/\text{d}z\,\text{d}p$
gives a value proportional to the number of electrons found between
$\text{d}N/\text{d}z\,\text{d}p$
gives a value proportional to the number of electrons found between
![]() $z$
and
$z$
and
![]() $z+\text{d}z$
having longitudinal momentum ranged between
$z+\text{d}z$
having longitudinal momentum ranged between
![]() $p_{z}$
and
$p_{z}$
and
![]() $p_{z}+\text{d}p_{z}$
. Energetic electrons are generated in front of the target. Figures 12(a) and 12(b) show the generation of energetic electrons at
$p_{z}+\text{d}p_{z}$
. Energetic electrons are generated in front of the target. Figures 12(a) and 12(b) show the generation of energetic electrons at
![]() $t=0.67$
ps and
$t=0.67$
ps and
![]() $t=1.0$
ps, respectively. Figure 12(c) shows the global pictures containing both the generation and transport of energetic electrons at
$t=1.0$
ps, respectively. Figure 12(c) shows the global pictures containing both the generation and transport of energetic electrons at
![]() $t=1.3$
ps. We can see that generation of energetic electrons is dramatically depressed when collision is included in front of the target. As we know, in front of the target, plasma density therein is low, and collision effect is relatively small when compared to electromagnetic effects. However, we found that this weak collision effect can still have significant effects on the generation of energetic electrons.
$t=1.3$
ps. We can see that generation of energetic electrons is dramatically depressed when collision is included in front of the target. As we know, in front of the target, plasma density therein is low, and collision effect is relatively small when compared to electromagnetic effects. However, we found that this weak collision effect can still have significant effects on the generation of energetic electrons.
When a laser propagates in underdense preformed plasmas, part of electrons are swept away in the forward direction by the laser ponderomotive force, leaving behind immobile ions. The electric field
![]() $E_{z}$
due to charge separation within the underdense plasma region tries to pull the electrons in the backward direction. When the laser arrives at the critical density surface and is reflected back, the ponderomotive force of the reflected laser pulse can further accelerate the electrons in the backward direction. The synergetic effects by this longitudinal charge separation field
$E_{z}$
due to charge separation within the underdense plasma region tries to pull the electrons in the backward direction. When the laser arrives at the critical density surface and is reflected back, the ponderomotive force of the reflected laser pulse can further accelerate the electrons in the backward direction. The synergetic effects by this longitudinal charge separation field
![]() $E_{z}$
and the ponderomotive force of the reflected laser pulse can efficiently accelerate electrons in the backward direction. Here we briefly explain this mechanism. We know that a single electron in vacuum, oscillating coherently with a propagating plane laser pulse would gain zero cycle averaged energy since the electron energy gain in one half cycle is exactly equal to the energy loss in the next half cycle. In Figure 13, we have presented single particle simulations. This shows the dynamics of an electron of initial momentum
$E_{z}$
and the ponderomotive force of the reflected laser pulse can efficiently accelerate electrons in the backward direction. Here we briefly explain this mechanism. We know that a single electron in vacuum, oscillating coherently with a propagating plane laser pulse would gain zero cycle averaged energy since the electron energy gain in one half cycle is exactly equal to the energy loss in the next half cycle. In Figure 13, we have presented single particle simulations. This shows the dynamics of an electron of initial momentum
![]() $p_{z}=0.1$
under a laser pulse of amplitude
$p_{z}=0.1$
under a laser pulse of amplitude
![]() $a=1.5$
. The maximal energy gain from the laser field is
$a=1.5$
. The maximal energy gain from the laser field is
![]() $m_{e}c^{2}a^{2}/2=1.125$
, and this value is the same as that obtained by single particle simulations, Figure 13(a). However, when there exists an external electric field, even though this field is very weak, the Woodward–Lawson theorem can be broken and the electron can obtain nonzero energy from the synergetic effects by the external electric field and the laser pulse. If the extension of external electric field is of infinity, the electron will always stay in phase with the laser and be accelerated to energy of infinity. In Figure 13(b), when we add a small external electric field,
$m_{e}c^{2}a^{2}/2=1.125$
, and this value is the same as that obtained by single particle simulations, Figure 13(a). However, when there exists an external electric field, even though this field is very weak, the Woodward–Lawson theorem can be broken and the electron can obtain nonzero energy from the synergetic effects by the external electric field and the laser pulse. If the extension of external electric field is of infinity, the electron will always stay in phase with the laser and be accelerated to energy of infinity. In Figure 13(b), when we add a small external electric field,
![]() $E_{z}=-0.1$
, the electron dynamics is dramatically changed. The energy gain is significantly higher than
$E_{z}=-0.1$
, the electron dynamics is dramatically changed. The energy gain is significantly higher than
![]() $m_{e}c^{2}a^{2}/2=1.125$
. In a recent work[Reference Wu, Krasheninnikov, Luan and Yu33], we have proved that the maximal energy gain is scaled as
$m_{e}c^{2}a^{2}/2=1.125$
. In a recent work[Reference Wu, Krasheninnikov, Luan and Yu33], we have proved that the maximal energy gain is scaled as
![]() ${\sim}aL^{1/2}$
, where
${\sim}aL^{1/2}$
, where
![]() $L$
is the propagation length.
$L$
is the propagation length.
In front of the target, although the charge separation is very small, it has significant influences on electron dynamics. Similarly, the weak collisional damping might also play important roles in these interactions. Let us first estimate the collision frequency. The considered plasma is of
![]() $1.0n_{c}$
, temperature is of
$1.0n_{c}$
, temperature is of
![]() $\unicode[STIX]{x1D6FE}m_{e}c^{2}$
and the collision frequency is
$\unicode[STIX]{x1D6FE}m_{e}c^{2}$
and the collision frequency is
![]() $\unicode[STIX]{x1D708}_{\text{c}}=10^{-5}\unicode[STIX]{x1D6FE}^{-3/2}$
. In the single particle simulation, we have added the weak collisional damping term
$\unicode[STIX]{x1D708}_{\text{c}}=10^{-5}\unicode[STIX]{x1D6FE}^{-3/2}$
. In the single particle simulation, we have added the weak collisional damping term
![]() $-\unicode[STIX]{x1D708}_{\text{c}}\boldsymbol{p}_{e}$
into the electrons equation of motion. As shown in Figure 13(c), when the collision frequency is
$-\unicode[STIX]{x1D708}_{\text{c}}\boldsymbol{p}_{e}$
into the electrons equation of motion. As shown in Figure 13(c), when the collision frequency is
![]() $10^{-5}\unicode[STIX]{x1D6FE}^{-3/2}$
, the maximal energy gain within
$10^{-5}\unicode[STIX]{x1D6FE}^{-3/2}$
, the maximal energy gain within
![]() $100T_{0}$
is 2.0. In Figure 13(d), when the collision frequency is
$100T_{0}$
is 2.0. In Figure 13(d), when the collision frequency is
![]() $10^{-4}\unicode[STIX]{x1D6FE}^{-3/2}$
, the maximal energy gain within
$10^{-4}\unicode[STIX]{x1D6FE}^{-3/2}$
, the maximal energy gain within
![]() $100T_{0}$
is 4.0. Although the energy gains of electrons are significantly depressed when compared to collision-less cases, they are still much larger than that value 1.125.
$100T_{0}$
is 4.0. Although the energy gains of electrons are significantly depressed when compared to collision-less cases, they are still much larger than that value 1.125.
3.2 2D simulations
In this section, we shall present how the ‘layered density’ method PIC works in 2D simulations. Here to avoid the extensive calculation burden, we use a smaller simulation box and shorter laser pulse duration. The simulation box is
![]() $40~\unicode[STIX]{x03BC}\text{m}\times 40~\unicode[STIX]{x03BC}\text{m}$
(
$40~\unicode[STIX]{x03BC}\text{m}\times 40~\unicode[STIX]{x03BC}\text{m}$
(
![]() $L_{z}\times L_{y}$
), with grid size
$L_{z}\times L_{y}$
), with grid size
![]() $\unicode[STIX]{x1D6FF}z=0.02~\unicode[STIX]{x03BC}\text{m}$
and
$\unicode[STIX]{x1D6FF}z=0.02~\unicode[STIX]{x03BC}\text{m}$
and
![]() $\unicode[STIX]{x1D6FF}y=0.1~\unicode[STIX]{x03BC}\text{m}$
. The pre-plasma scale length used in 2D simulation is
$\unicode[STIX]{x1D6FF}y=0.1~\unicode[STIX]{x03BC}\text{m}$
. The pre-plasma scale length used in 2D simulation is
![]() $5~\unicode[STIX]{x03BC}\text{m}$
. Other parameters, like plasma density division, temperatures and laser intensity, are the same as in the 1D simulation.
$5~\unicode[STIX]{x03BC}\text{m}$
. Other parameters, like plasma density division, temperatures and laser intensity, are the same as in the 1D simulation.

Figure 13. Dynamics of an electron calculated with single particle simulations. The gained energy from laser beam as a function of propagation length. The total simulation time is
![]() $100T_{0}$
. (a) An electron with initial momentum
$100T_{0}$
. (a) An electron with initial momentum
![]() $p_{z}=0.1$
, a single laser pulse of amplitude
$p_{z}=0.1$
, a single laser pulse of amplitude
![]() $a_{x}=1.5$
. (b) An electron with initial momentum
$a_{x}=1.5$
. (b) An electron with initial momentum
![]() $p_{z}=0.1$
, a single laser pulse of amplitude
$p_{z}=0.1$
, a single laser pulse of amplitude
![]() $a_{x}=1.5$
, and a constant external electric field of
$a_{x}=1.5$
, and a constant external electric field of
![]() $E_{z}=-0.1$
. (c) An electron with initial momentum
$E_{z}=-0.1$
. (c) An electron with initial momentum
![]() $p_{z}=0.1$
, a single laser pulse of amplitude
$p_{z}=0.1$
, a single laser pulse of amplitude
![]() $a_{x}=1.5$
, a constant external electric field of
$a_{x}=1.5$
, a constant external electric field of
![]() $E_{z}=-0.1$
and initial collision frequency of
$E_{z}=-0.1$
and initial collision frequency of
![]() $10^{-5}$
. (d) An electron with initial momentum
$10^{-5}$
. (d) An electron with initial momentum
![]() $p_{z}=0.1$
, a single laser pulse of amplitude
$p_{z}=0.1$
, a single laser pulse of amplitude
![]() $a_{x}=1.5$
, a constant external electric field of
$a_{x}=1.5$
, a constant external electric field of
![]() $E_{z}=-0.1$
and initial collision frequency of
$E_{z}=-0.1$
and initial collision frequency of
![]() $10^{-4}$
.
$10^{-4}$
.

Figure 14. Results of 2D PIC simulations. The plasma density perturbations in front of the target at the end of simulation.
The plasma distortion in front of the target is shown in Figure 14. In this region, energetic electrons are generated directly by laser fields. When these electrons propagate into the bulk solid, abundant plasma and atomic interactions take place therein. As shown in Figures 15(a) and 15(b), collision ionization would dramatically increase the electron density. Typically, the ionization and plasma temperature decrease rapidly along the electron propagation direction. When comparing with 1D simulations, we find some filamentation structures in the electron density and temperature distributions. This kind of filamentation is due to two-stream or/and Weibel instabilities.
The propagation of electrons could generate magnetic fields. Except electromagnetic instabilities, like Weibel instability, there are two sources that can generate strong magnetic fields: (i)
![]() $\unicode[STIX]{x1D6FB}\times \boldsymbol{B}=4\unicode[STIX]{x1D70B}\boldsymbol{J}/c$
; (ii)
$\unicode[STIX]{x1D6FB}\times \boldsymbol{B}=4\unicode[STIX]{x1D70B}\boldsymbol{J}/c$
; (ii)
![]() $-\unicode[STIX]{x2202}\boldsymbol{B}/\unicode[STIX]{x2202}t=\unicode[STIX]{x1D6FB}\times \boldsymbol{E}$
. As shown in Figure 15(c1), in front of the target, this magnetic field is fully due to the forward
$-\unicode[STIX]{x2202}\boldsymbol{B}/\unicode[STIX]{x2202}t=\unicode[STIX]{x1D6FB}\times \boldsymbol{E}$
. As shown in Figure 15(c1), in front of the target, this magnetic field is fully due to the forward
![]() $\boldsymbol{J}_{e}$
, i.e., the first-generation mechanism, which could cause the divergence of electron beams. When these electrons propagate into the solid, the forward
$\boldsymbol{J}_{e}$
, i.e., the first-generation mechanism, which could cause the divergence of electron beams. When these electrons propagate into the solid, the forward
![]() $\boldsymbol{J}_{e}$
is quickly neutralized by return current. The total current density is close to zero, and therefore the first mechanism is not effective any more. However, because of the strong collision effect, a resistive electric field
$\boldsymbol{J}_{e}$
is quickly neutralized by return current. The total current density is close to zero, and therefore the first mechanism is not effective any more. However, because of the strong collision effect, a resistive electric field
![]() $E_{z}=\boldsymbol{J}_{e}/\unicode[STIX]{x1D70E}$
can be generated, which in turn could induce the resistive magnetic field, through the second-generation mechanism. This magnetic field, as shown in Figure 15(c2), could collimate electron beams.
$E_{z}=\boldsymbol{J}_{e}/\unicode[STIX]{x1D70E}$
can be generated, which in turn could induce the resistive magnetic field, through the second-generation mechanism. This magnetic field, as shown in Figure 15(c2), could collimate electron beams.

Figure 15. Results of 2D PIC simulations. (a) The plasma density in the inner part of the target at the end of simulation time. (b) The plasma temperature in the inner part of the target at the end of simulation time. (c1) The magnetic fields, normalized by
![]() $eB/m_{e}\unicode[STIX]{x1D714}_{0}$
, generated by the forward-propagating fast electrons. (c2) The resistive magnetic fields, normalized by
$eB/m_{e}\unicode[STIX]{x1D714}_{0}$
, generated by the forward-propagating fast electrons. (c2) The resistive magnetic fields, normalized by
![]() $eB/m_{e}\unicode[STIX]{x1D714}_{0}$
, generated by the Ohmic return current.
$eB/m_{e}\unicode[STIX]{x1D714}_{0}$
, generated by the Ohmic return current.
In Figure 16, we also present the angular distribution and energy spectra of emitted photons. The diffraction angle obtained in the 2D simulation is significantly higher than 1D, which can be as large as
![]() $30^{\circ }$
. The ‘cut-off’ frequency of emitted photons is significantly smaller than in 1D simulations. This is because, short laser pulse and pre-plasma scale length are used in 2D simulations. The maximal electron energy in 2D simulations is much smaller than that in 1D simulations.
$30^{\circ }$
. The ‘cut-off’ frequency of emitted photons is significantly smaller than in 1D simulations. This is because, short laser pulse and pre-plasma scale length are used in 2D simulations. The maximal electron energy in 2D simulations is much smaller than that in 1D simulations.
4 Discussions and conclusions
In summary, we have presented a full-PIC code, which enables us to calculate intense laser–solid interactions in a ‘first principle’ way, covering almost ‘all’ the coupled physical mechanisms. For ionizations, we have taken into account CI, RE and IPD. For collisions, we have taken into account both bound and free electrons contributions. A modified Coulomb logarithm is used in the binary collision model, which has the ability to deal with collisions at low temperatures, when the closest approach distance is larger than Debye length. For collisions with energetic electrons, Bremsstrahlung radiation correction is also included in our model. The ‘layered density’ method PIC is proposed to simulate plasma dynamics at extremely high densities. The numerical self-heating of PIC simulations with solid-density plasmas can be well controlled by this method.
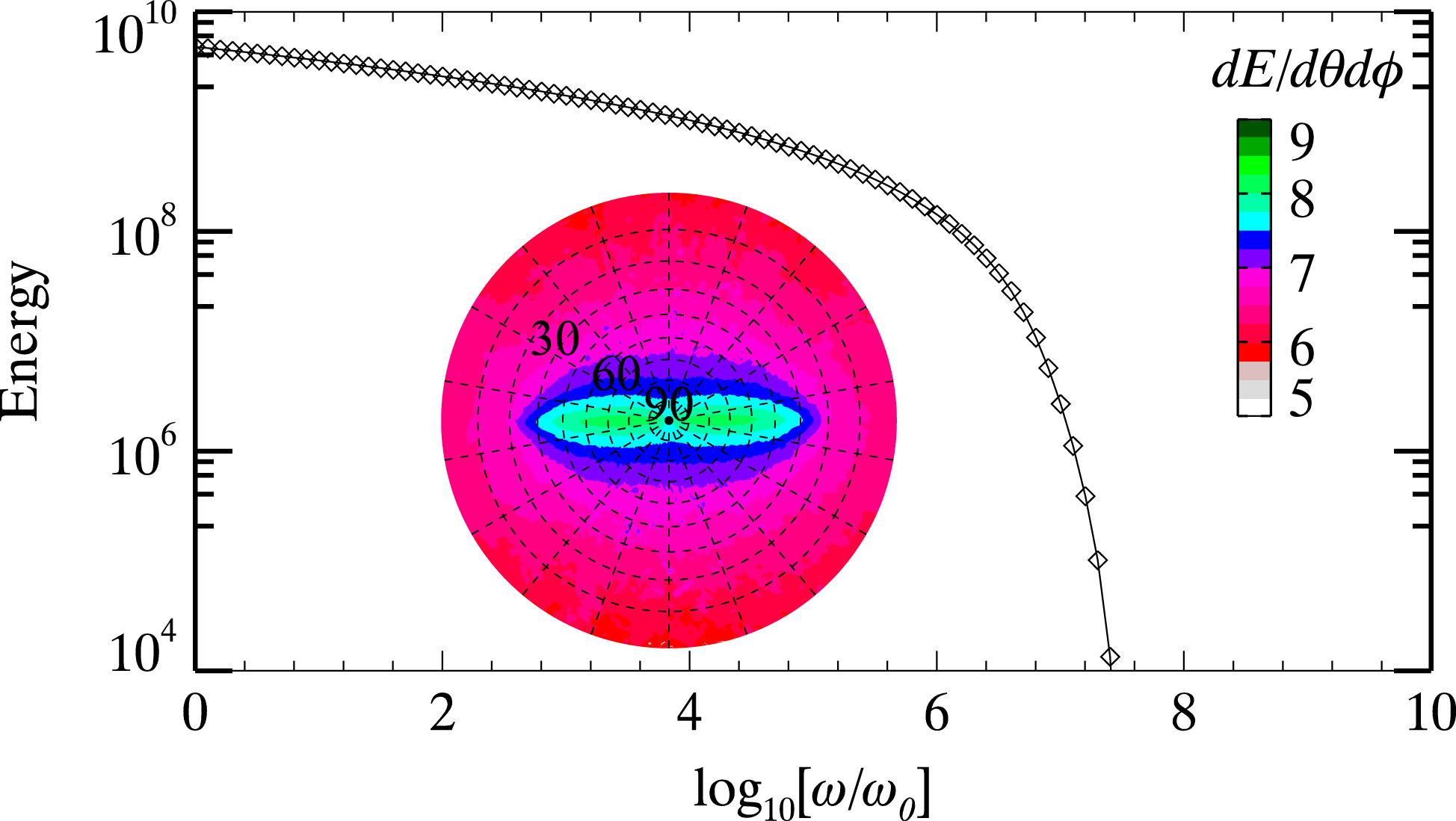
Figure 16. Results of 2D PIC simulations. Figure shows the angular distribution of emitted photons and the frequency spectra of emitted photons, where we have plotted
![]() $\int _{\hbar \unicode[STIX]{x1D714}_{\text{k}}}^{\infty }[\text{d}E/\text{d}(\hbar \unicode[STIX]{x1D714})]\,\text{d}(\hbar \unicode[STIX]{x1D714})$
as a function of cut-off frequency
$\int _{\hbar \unicode[STIX]{x1D714}_{\text{k}}}^{\infty }[\text{d}E/\text{d}(\hbar \unicode[STIX]{x1D714})]\,\text{d}(\hbar \unicode[STIX]{x1D714})$
as a function of cut-off frequency
![]() $\unicode[STIX]{x1D714}_{\text{k}}$
. Note
$\unicode[STIX]{x1D714}_{\text{k}}$
. Note
![]() $\hbar \unicode[STIX]{x1D714}_{0}=1.24$
eV, corresponding to the energy of a photon with wavelength
$\hbar \unicode[STIX]{x1D714}_{0}=1.24$
eV, corresponding to the energy of a photon with wavelength
![]() $1~\unicode[STIX]{x03BC}\text{m}$
.
$1~\unicode[STIX]{x03BC}\text{m}$
.
Especially, as an application of the new code, the generation and transport of energetic electrons in front of and within the solid target when irradiated by intense laser beams are studied. For the considered case, where laser intensity is
![]() $10^{20}~\text{W}\cdot \text{cm}^{-2}$
and pre-plasma scale length in front of the solid is
$10^{20}~\text{W}\cdot \text{cm}^{-2}$
and pre-plasma scale length in front of the solid is
![]() $10~\unicode[STIX]{x03BC}\text{m}$
, several quantitative conclusions are drawn: (i) the collisional damping (although it is very weak) can significantly affect the energetic electrons generation in front of the target, (ii) the Bremsstrahlung radiation will be enhanced by 2–3 times when the solid is dramatically heated and ionized, (iii) the ‘cut-off’ electron energy is lowered by an amount of 25% when both collision damping and Bremsstrahlung radiations are included and finally, (iv) the resistive electromagnetic fields due to Ohmic heating play nonignorable roles and must be taken into account in such interactions.
$10~\unicode[STIX]{x03BC}\text{m}$
, several quantitative conclusions are drawn: (i) the collisional damping (although it is very weak) can significantly affect the energetic electrons generation in front of the target, (ii) the Bremsstrahlung radiation will be enhanced by 2–3 times when the solid is dramatically heated and ionized, (iii) the ‘cut-off’ electron energy is lowered by an amount of 25% when both collision damping and Bremsstrahlung radiations are included and finally, (iv) the resistive electromagnetic fields due to Ohmic heating play nonignorable roles and must be taken into account in such interactions.
Acknowledgements
This work was supported by the Science Challenge Project (No. TZ2016005), the National Natural Science Foundation of China (Nos. 11605269, 11674341, and 11675245), and the National Basic Research Program of China (No. 2013CBA01504). D. Wu wishes to acknowledge the financial support from German Academic Exchange Service (DAAD) and China Scholarship Council (CSC).
Appendix A. The calculation of Coulomb logarithm
To calculate Coulomb logarithm, one of the practical approaches, as used in models in Refs. [Reference Takizuka and Abe51–Reference Sentoku and Kemp53], is to sum binary collisions over a distance of the order of the Debye length. Under the potential of
![]() $1/r$
, the differential cross section reads,
$1/r$
, the differential cross section reads,
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\sim 1/\sin ^{4}(\unicode[STIX]{x1D703}/2)$
, and the Coulomb logarithm reads,
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\sim 1/\sin ^{4}(\unicode[STIX]{x1D703}/2)$
, and the Coulomb logarithm reads,
![]() $L\sim \int _{0}^{\unicode[STIX]{x1D70B}}\sin \unicode[STIX]{x1D703}\sin ^{2}(\unicode[STIX]{x1D703}/2)\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\,\text{d}\unicode[STIX]{x1D703}\sim \ln [\sin (\unicode[STIX]{x1D703}/2)]|_{0}^{\unicode[STIX]{x1D70B}}$
. This integration is not a convergent value, when
$L\sim \int _{0}^{\unicode[STIX]{x1D70B}}\sin \unicode[STIX]{x1D703}\sin ^{2}(\unicode[STIX]{x1D703}/2)\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\,\text{d}\unicode[STIX]{x1D703}\sim \ln [\sin (\unicode[STIX]{x1D703}/2)]|_{0}^{\unicode[STIX]{x1D70B}}$
. This integration is not a convergent value, when
![]() $\unicode[STIX]{x1D703}\rightarrow 0$
. While in plasmas, the potential of a charged particle should be screened. When
$\unicode[STIX]{x1D703}\rightarrow 0$
. While in plasmas, the potential of a charged particle should be screened. When
![]() $b$
(i.e., the distance of the closest approach between the two charges) is larger than
$b$
(i.e., the distance of the closest approach between the two charges) is larger than
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
, the potential is artificially set to be zero. Therefore, the lower limit
$\unicode[STIX]{x1D706}_{\text{D}}$
, the potential is artificially set to be zero. Therefore, the lower limit
![]() $\unicode[STIX]{x1D703}_{\min }$
of scattering angle is obtained when
$\unicode[STIX]{x1D703}_{\min }$
of scattering angle is obtained when
![]() $b=\unicode[STIX]{x1D706}_{\text{D}}$
, i.e.,
$b=\unicode[STIX]{x1D706}_{\text{D}}$
, i.e.,
![]() $\unicode[STIX]{x1D703}_{\text{min}}/2=b/\unicode[STIX]{x1D706}_{\text{D}}$
. Thus we have
$\unicode[STIX]{x1D703}_{\text{min}}/2=b/\unicode[STIX]{x1D706}_{\text{D}}$
. Thus we have
![]() $L\sim \ln (\unicode[STIX]{x1D706}_{D}/b)$
.
$L\sim \ln (\unicode[STIX]{x1D706}_{D}/b)$
.
However instead of the above method, a rigorous way is to sum full binary collisions with all particles using the screened potential
![]() $\exp (-r/\unicode[STIX]{x1D706}_{\text{D}})/r$
. Acted by this screened potential, the differential cross section reads,
$\exp (-r/\unicode[STIX]{x1D706}_{\text{D}})/r$
. Acted by this screened potential, the differential cross section reads,
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\sim 1/[\sin ^{2}(\unicode[STIX]{x1D703}/2)+\unicode[STIX]{x1D702}]$
, where
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\sim 1/[\sin ^{2}(\unicode[STIX]{x1D703}/2)+\unicode[STIX]{x1D702}]$
, where
![]() $\unicode[STIX]{x1D702}$
is the smallest value between
$\unicode[STIX]{x1D702}$
is the smallest value between
![]() $\hbar /\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D706}_{\text{D}}$
(quantum) and
$\hbar /\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D706}_{\text{D}}$
(quantum) and
![]() $Z_{a}Z_{b}e^{2}/m_{e}\unicode[STIX]{x1D6FD}^{2}\unicode[STIX]{x1D706}_{\text{D}}$
(classical). The Coulomb logarithm
$Z_{a}Z_{b}e^{2}/m_{e}\unicode[STIX]{x1D6FD}^{2}\unicode[STIX]{x1D706}_{\text{D}}$
(classical). The Coulomb logarithm
![]() $L\sim \int _{0}^{\unicode[STIX]{x1D70B}}\sin \unicode[STIX]{x1D703}\sin ^{2}(\unicode[STIX]{x1D703}/2)\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\,\text{d}\unicode[STIX]{x1D703}$
by applying the new differential cross section is
$L\sim \int _{0}^{\unicode[STIX]{x1D70B}}\sin \unicode[STIX]{x1D703}\sin ^{2}(\unicode[STIX]{x1D703}/2)\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\,\text{d}\unicode[STIX]{x1D703}$
by applying the new differential cross section is
![]() $L\sim \ln (1+2\unicode[STIX]{x1D702}-\cos \unicode[STIX]{x1D703})|_{0}^{\unicode[STIX]{x1D70B}}$
. This is a convergent value, with
$L\sim \ln (1+2\unicode[STIX]{x1D702}-\cos \unicode[STIX]{x1D703})|_{0}^{\unicode[STIX]{x1D70B}}$
. This is a convergent value, with
![]() $L\sim \ln [(1+\unicode[STIX]{x1D702})/\unicode[STIX]{x1D702}]$
. This expression of Coulomb logarithm will converge to
$L\sim \ln [(1+\unicode[STIX]{x1D702})/\unicode[STIX]{x1D702}]$
. This expression of Coulomb logarithm will converge to
![]() $L=\ln (\unicode[STIX]{x1D706}_{\text{D}}/b)$
when
$L=\ln (\unicode[STIX]{x1D706}_{\text{D}}/b)$
when
![]() $b\ll \unicode[STIX]{x1D706}_{\text{D}}$
for high-temperature plasmas.
$b\ll \unicode[STIX]{x1D706}_{\text{D}}$
for high-temperature plasmas.
Appendix B. A brief introduction to LAPINE code
LAPINE[Reference Xu, Chang, Zhuo, Cao and Yue61] is the abbreviation of LAser-Plasma-INtEraction, and along with KLAPS[Reference Chen, Sheng, Zheng, Ma and Zhang62] and LARED-P[Reference Zhu and Zhang63] codes, it is one of the first-generation PIC codes fully developed by Chinese. LAPINE is a parallel PIC code, written in C++ language, capable of performing 1D, 2D and 3D simulations. The 1D, 2D and 3D versions are self-consistently written into a single group of files. Setup of 1D, 2D or 3D is defined in pre-compilation to compile the code to the specific LAPINE-1D, 2D or 3D.
Physical models. Many advanced physical modules have been implemented into LAPINE code, which include bulk ionization[Reference Wu, He, Yu and Fritzsche3] (coupling impact ionization, electron–ion recombination and ionization potential depression by surrounding plasmas), binary collisions[Reference Wu, He, Yu and Fritzsche4] (partially ionized plasmas and also pure plasmas for all temperature ranges), field ionization[Reference Wu, Qiao, McGuffey, He and Beg36] and QED[Reference Wu, Qiao and He37] modules. Note that all the physical modules have been well benchmarked and applied for related physical research.
Numerical scheme. High-order electromagnetic field solver, high-order particle shape and current smooth technique have been implemented into LAPINE to improve its ability in calculating high-density plasmas. The proposed ‘layered density’ method is first implemented into the LAPINE code, showing strong power in performing laser–solid simulations in large scale.