PN Jeffreys-Vicente Equation

Extract

In our work (Xu et al. 2000) for the first time a complete and closed set of post-Newtonian dynamical equations for elastically deformable, rotating astronomical bodies has been deduced. These bodies are assumed to differ only slightly from corresponding stationary and axisymmetric fluid reference bodies and show no internal dissipation, i.e., they are composed of a perfectly elastic medium. For such bodies a set of perturbation equations is derived by means of the Carter and Quintana formalism in a suitably defined rotating coordinate system. The post-Newtonian dynamical equation for the displacement field is the central result of this paper together with the various equations that define the quantities appearing therein. It is the post-Newtonian version of the well-known Jeffreys-Vicente (J-V) equation (Jeffreys & Vicente 1957) that forms the basis of any local theory of global geodynamics. PN J-V equation reads:

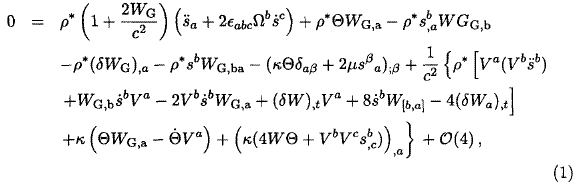
where s_a is the covariant displacement field, 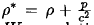(ρ is the density of tolal mass-energy, p is the isotropic pressure), W_G a relativistic geopotential in rotating coordinate, Θ the volume dilation, δW_G Euler variation of W_G, K the compression modulus, 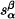is the shear tensor, W and W^α are the scalar and vector potential in rotating coordinate.