A Geometrical origin of the Pulsar Core and Conal Emissions

Extract

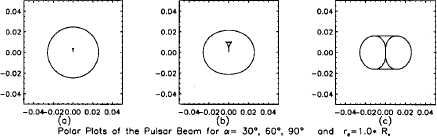
We have analysed the dipole magnetic field geometry for the general case of an oblique rotator and have found that open field lines which define the polar cap divide into two branches (Kapoor and Shukre 1996) which appear naturally relevant for distinguishing the core and conal emissions. The polar cap shape is actually determined by a quadratic equation having two roots leading to two values of the polar angle, θ⁺ and θ⁻ with respect to the magnetic axis for a given azimuth φ. For the north pole both θ⁺ and θ⁻ branches are shown as polar plots in Fig. 1 for various inclination angles α and a typical pulsar period 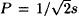. The discussion of pulsar polar caps hitherto (e.g. Biggs 1990) had not distinguished between the θ⁺ and the θ⁻ solutions. The region defined by the θ⁺ solution is completely contained inside the polar cap. It has a peculiar triangular shape whose lowest vertex is always on the magnetic axis. This naturally suggests an identification of the θ⁺ and the θ⁻ regions with the core and conal emission zones.