Article contents
Normal and stable approximation to subgraph counts in superpositions of Bernoulli random graphs
Published online by Cambridge University Press: 18 August 2023
Abstract
Real networks often exhibit clustering, the tendency to form relatively small groups of nodes with high edge densities. This clustering property can cause large numbers of small and dense subgraphs to emerge in otherwise sparse networks. Subgraph counts are an important and commonly used source of information about the network structure and function. We study probability distributions of subgraph counts in a community affiliation graph. This is a random graph generated as an overlay of m partly overlapping independent Bernoulli random graphs (layers) 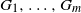 $G_1,\dots,G_m$ with variable sizes and densities. The model is parameterised by a joint distribution of layer sizes and densities. When m grows linearly in the number of nodes n, the model generates sparse random graphs with a rich statistical structure, admitting a nonvanishing clustering coefficient and a power-law limiting degree distribution. In this paper we establish the normal and
$G_1,\dots,G_m$ with variable sizes and densities. The model is parameterised by a joint distribution of layer sizes and densities. When m grows linearly in the number of nodes n, the model generates sparse random graphs with a rich statistical structure, admitting a nonvanishing clustering coefficient and a power-law limiting degree distribution. In this paper we establish the normal and  $\alpha$-stable approximations to the numbers of small cliques, cycles, and more general 2-connected subgraphs of a community affiliation graph.
$\alpha$-stable approximations to the numbers of small cliques, cycles, and more general 2-connected subgraphs of a community affiliation graph.
Keywords
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 3
- Cited by


