Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T09:58:25.393Z Has data issue: false hasContentIssue false
  • English
  • Français

Adaptive simulation using perfect control variates

Part of: Markov processes Operations research and management science Probabilistic methods, simulation and stochastic differential equations

Published online by Cambridge University Press:  14 July 2016

Shane G. Henderson  and
Burt Simon
Shane G. Henderson*
Affiliation:
Cornell University
Burt Simon*
Affiliation:
University of Colorado at Denver
*
∗ Postal address: School of Operations Research and Industrial Engineering, Cornell University, Ithaca, NY 14853, USA. Email address: shane@orie.cornell.edu
∗∗ Postal address: Department of Mathematics, University of Colorado at Denver, Campus Box 170, PO Box 173364, Denver, CO 80217-3364, USA. Email address: bsimon@math.cudenver.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce adaptive-simulation schemes for estimating performance measures for stochastic systems based on the method of control variates. We consider several possible methods for adaptively tuning the control-variate estimators, and describe their asymptotic properties. Under certain assumptions, including the existence of a ‘perfect control variate’, all of the estimators considered converge faster than the canonical rate of n −1/2, where n is the simulation run length. Perfect control variates for a variety of stochastic processes can be constructed from ‘approximating martingales’. We prove a central limit theorem for an adaptive estimator that converges at rate 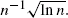A similar estimator converges at rate n −1. An exponential rate of convergence is also possible under suitable conditions.

Keywords

Adaptive Monte Carlovariance reductionefficiency improvementapproximating martingalecontrol variate

MSC classification

Primary: 65C05: Monte Carlo methods
Secondary: 60J22: Computational methods in Markov chains 90B99: None of the above, but in this section
Type
Research Papers
Information
Journal of Applied Probability , Volume 41 , Issue 3 , September 2004 , pp. 859 - 876
Copyright
Copyright © Applied Probability Trust 2004 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Al-Qaq, W. A., Devetsikiotis, M., and Townsend, J.-K. (1995). Stochastic gradient optimization of importance sampling for the efficient simulation of digital communication systems. IEEE Trans. Commun. 43, 2975–2985.10.1109/26.477500Google Scholar
Baggerly, K., Cox, D., and Picard, R. (2000). Exponential convergence of adaptive importance sampling for Markov chains. J. Appl. Prob. 37, 342–358.10.1239/jap/1014842541Google Scholar
Billingsley, P. (1968). Convergence of Probability Measures. John Wiley, New York.Google Scholar
Booth, T. E. (1985). Exponential convergence for Monte-Carlo particle-transport. Trans. Amer. Nuclear Soc. 50, 267–268.Google Scholar
Booth, T. E. (1989). Zero-variance solutions for linear Monte-Carlo. Nuclear Sci. Eng. 102, 332–340.10.13182/NSE89-A23646Google Scholar
Booth, T. E. (2001). An approximate Monte Carlo adaptive importance sampling method. Nuclear Sci. Eng. 138, 96–103.10.13182/NSE01-A2204Google Scholar
Borkar, V. S., Juneja, S., and Kherani, A. A. (2004). Performance analysis conditioned on rare events: an adaptive simulation scheme. To appear in Commun. Inf.Google Scholar
Desai, P. Y. (2001). Adaptive Monte Carlo methods for solving eigenvalue problems. , Department of Management Science and Engineering, Stanford University.Google Scholar
Desai, P., and Glynn, P. W. (2001). A Markov chain perspective on adaptive Monte Carlo algorithms. In Proc. 2001 Winter Simulation Conf. (Piscataway, NJ, 2001), eds Peters, B. A., Smith, J. S., Medeiros, D. J. and Rohrer, M. W., IEEE, pp. 379–384.Google Scholar
Fitzgerald, M., and Picard, R. (2001). Accelerated Monte Carlo for particle dispersion. Commun. Statist. Theory Meth. 30, 2459–2471.10.1081/STA-100107698Google Scholar
Henderson, S., Meyn, S. P. and Tadić, V. (2003). Performance evaluation and policy selection in multiclass networks. Discrete Event Dynamic Systems 13, 149–189.10.1023/A:1022197004856Google Scholar
Henderson, S. G., and Glynn, P. W. (2002). Approximating martingales for variance reduction in Markov process simulation. Math. Operat. Res. 27, 253–271.10.1287/moor.27.2.253.329Google Scholar
Hsieh, M. (2002). Adaptive Monte Carlo methods for rare event simulations. In Proc. 2002 Winter Simulation Conf. (Piscataway, NJ, 2002), eds Yücesan, E., Chen, C.-H., Snowdon, J. L. and Charnes, J. M., IEEE, pp. 108–115.10.1109/WSC.2002.1172874Google Scholar
Karlin, S., and Taylor, H. M. (1981). A Second Course in Stochastic Processes. Academic Press, Boston, MA.Google Scholar
Kollman, C., Baggerly, K., Cox, D., and Picard, R. (1999). Adaptive importance sampling on discrete Markov chains. Ann. Appl. Prob. 9, 391–412.Google Scholar
Law, A. M., and Kelton, W. D. (2000). Simulation Modeling and Analysis, 3rd edn. McGraw-Hill, New York.Google Scholar
Lieber, D., Nemirovskii, A., and Rubinstein, R. Y. (1999). A fast Monte Carlo method for evaluating reliability indexes. IEEE Trans. Reliab. 48, 256–261.10.1109/24.799896Google Scholar
Liptser, R. S., and Shiryayev, A. N. (1989). Theory of Martingales. Kluwer, Boston, MA.10.1007/978-94-009-2438-3Google Scholar
Picard, R. R., Fitzgerald, M., and Brown, M. J. (2001). Accelerating convergence in stochastic particle dispersion simulation codes. J. Computational Physics 173, 231–255.10.1006/jcph.2001.6874Google Scholar
Resnick, S. I. (2001). A Probability Path. Birkhäuser, Boston, MA.Google Scholar
Rubinstein, R. Y. (1999). The cross-entropy method for combinatorial and continuous optimization. Methodology Comput. Appl. Prob. 1, 127–190.10.1023/A:1010091220143Google Scholar
Su, Y., and Fu, M. C. (2000). Importance sampling in derivative securities pricing. In Proc. 2000 Winter Simulation Conf. (Piscataway, NJ, 2000), eds Joines, J. A., Barton, R. R., Kang, K. and Fishwick, P. A., IEEE, pp. 587–596.Google Scholar
Vázquez-Abad, F., and Dufresne, D. (1998). Accelerated simulation for pricing Asian options. In Proc. 1998 Winter Simulation Conf. (Piscataway, NJ, 1998), eds Medeiros, D., Watson, E., Carson, J. S. and Manivannan, M. S., IEEE, pp. 1493–1500.Google Scholar