No CrossRef data available.
Article contents
Differences between Lyapunov exponents for the simple random walk in Bernoulli potentials
Published online by Cambridge University Press: 23 June 2023
Abstract
We consider the simple random walk on the d-dimensional lattice 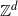 $\mathbb{Z}^d$ (
$\mathbb{Z}^d$ (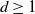 $d \geq 1$), traveling in potentials which are Bernoulli-distributed. The so-called Lyapunov exponent describes the cost of traveling for the simple random walk in the potential, and it is known that the Lyapunov exponent is strictly monotone in the parameter of the Bernoulli distribution. Hence the aim of this paper is to investigate the effect of the potential on the Lyapunov exponent more precisely, and we derive some Lipschitz-type estimates for the difference between the Lyapunov exponents.
$d \geq 1$), traveling in potentials which are Bernoulli-distributed. The so-called Lyapunov exponent describes the cost of traveling for the simple random walk in the potential, and it is known that the Lyapunov exponent is strictly monotone in the parameter of the Bernoulli distribution. Hence the aim of this paper is to investigate the effect of the potential on the Lyapunov exponent more precisely, and we derive some Lipschitz-type estimates for the difference between the Lyapunov exponents.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust
References
Cerf, R. and Dembin, B. (2022). The time constant for Bernoulli percolation is Lipschitz continuous strictly above
 $p_c$
. Ann. Prob. 50, 1781–1812.CrossRefGoogle Scholar
$p_c$
. Ann. Prob. 50, 1781–1812.CrossRefGoogle Scholar
Dembin, B. (2020). Anchored isoperimetric profile of the infinite cluster in supercritical bond percolation is Lipschitz continuous. Electron. Commun. Prob. 25, 1–13.CrossRefGoogle Scholar
Dembin, B. (2021). Regularity of the time constant for a supercritical Bernoulli percolation. ESAIM Prob. Statist. 25, 109–132.CrossRefGoogle Scholar
Flury, M. (2007). Large deviations and phase transition for random walks in random nonnegative potentials. Stoch. Process. Appl. 117, 596–612.CrossRefGoogle Scholar
Flury, M. (2008). Coincidence of Lyapunov exponents for random walks in weak random potentials. Ann. Prob. 36, 1528–1583.CrossRefGoogle Scholar
Fontes, L. and Newman, C. M. (1993). First passage percolation for random colorings of
 $\mathbb{Z}^d$
. Ann. Appl. Prob. 3, 746–762.CrossRefGoogle Scholar
$\mathbb{Z}^d$
. Ann. Appl. Prob. 3, 746–762.CrossRefGoogle Scholar
Grimmett, G. (1999). Percolation (Grundlehren der mathematischen Wissenschaften 321). Springer.CrossRefGoogle Scholar
Kosygina, E., Mountford, T. S. and Zerner, M. P. (2011). Lyapunov exponents of Green’s functions for random potentials tending to zero. Prob. Theory Related Fields 150, 43–59.CrossRefGoogle Scholar
Kubota, N. (2020). Strict comparison for the Lyapunov exponents of the simple random walk in random potentials. Available at arXiv:2010.08798.Google Scholar
Le, T. T. H (2017). On the continuity of Lyapunov exponents of random walk in random potential. Bernoulli 23, 522–538.Google Scholar
Mourrat, J.-C. (2012). Lyapunov exponents, shape theorems and large deviations for the random walk in random potential. ALEA Lat. Am. J. Prob. Math. Statist. 9, 165–209.Google Scholar
Scholler, J. (2014). On the time constant in a dependent first passage percolation model. ESAIM Prob. Statist. 18, 171–184.CrossRefGoogle Scholar
Wang, W.-M. (2001). Mean field bounds on Lyapunov exponents in
 $\textrm{Z}^d$
at the critical energy. Prob. Theory Related Fields 119, 453–474.CrossRefGoogle Scholar
$\textrm{Z}^d$
at the critical energy. Prob. Theory Related Fields 119, 453–474.CrossRefGoogle Scholar
Wang, W.-M. (2002). Mean field upper and lower bounds on Lyapunov exponents. Amer. J. Math. 124, 851–878.CrossRefGoogle Scholar
Wu, X.-Y. and Feng, P. (2009). On a lower bound for the time constant of first-passage percolation. Acta Math. Sinica Chinese Series 52, 81–86.Google Scholar
Zerner, M. P. (1998). Directional decay of the Green’s function for a random nonnegative potential on
 $\textrm{Z}^d$
. Ann. Appl. Prob. 8, 246–280.CrossRefGoogle Scholar
$\textrm{Z}^d$
. Ann. Appl. Prob. 8, 246–280.CrossRefGoogle Scholar
Zygouras, N. (2009). Lyapounov norms for random walks in low disorder and dimension greater than three. Prob. Theory Related Fields 143, 615–642.CrossRefGoogle Scholar


