Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T00:26:47.455Z Has data issue: false hasContentIssue false
  • English
  • Français

On an inequality for the normal distribution arising in bioequivalence studies

Part of: Distribution theory - Probability

Published online by Cambridge University Press:  14 July 2016

Yi-Ching Yao  and
Hari Iyer
Yi-Ching Yao*
Affiliation:
Academia Sinica
Hari Iyer*
Affiliation:
Colorado State University
*
∗Postal address: Institute of Statistical Science, Academia Sinica, Taipei, Taiwan, R.O.C. Email address: yao@stat.sinica.edu.tw
∗∗Postal address: Department of Statistics, Colorado State University, Fort Collins, CO 80523, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

For (μ,σ2) ≠ (0,1), and 0 < z < ∞, we prove that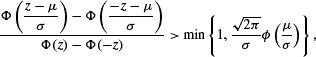 where φ and Φ are, respectively, the p.d.f. and the c.d.f. of a standard normal random variable. This inequality is sharp in the sense that the right-hand side cannot be replaced by a larger quantity which depends only on μ and σ. In other words, for any given (μ,σ) ≠ (0,1), the infimum, over 0 < z < ∞, of the left-hand side of the inequality is equal to the right-hand side. We also point out how this inequality arises in the context of defining individual bioequivalence.

Keywords

Individual bioequivalencetherapeutic windowbioavailability

MSC classification

Primary: 60E15: Inequalities; stochastic orderings
Type
Short Communications
Information
Journal of Applied Probability , Volume 36 , Issue 1 , March 1999 , pp. 279 - 286
Copyright
Copyright © Applied Probability Trust 1999 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, S., and Hauck, W. W. (1990). Consideration of individual bioequivalence. Journal of Pharmacokinetics and Biopharmaceutics 18, 259–274.Google Scholar
Schall, R. (1995). Assessment of individual and population bioequivalence using the probability that bioavailabilities are similar. Biometrics 51, 615–626.CrossRefGoogle ScholarPubMed
Schall, R., and Luus, H. G. (1993). On population and individual bioequivalence. Statistics in Medicine 12, 1109–1124.CrossRefGoogle ScholarPubMed