Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-27T22:58:05.924Z Has data issue: false hasContentIssue false
  • English
  • Français

On Markov chain approximations for computing boundary crossing probabilities of diffusion processes

Part of: Markov processes Probabilistic methods, simulation and stochastic differential equations

Published online by Cambridge University Press:  11 May 2023

Vincent Liang  and
Konstantin Borovkov Open the ORCID record for Konstantin Borovkov [Opens in a new window]
Vincent Liang*
Affiliation:
The University of Melbourne
Konstantin Borovkov*
Affiliation:
The University of Melbourne
*
*Postal address: School of Mathematics and Statistics, The University of Melbourne, Parkville 3010, Australia
*Postal address: School of Mathematics and Statistics, The University of Melbourne, Parkville 3010, Australia
Get access Rights & Permissions [Opens in a new window]

Abstract

We propose a discrete-time discrete-space Markov chain approximation with a Brownian bridge correction for computing curvilinear boundary crossing probabilities of a general diffusion process on a finite time interval. For broad classes of curvilinear boundaries and diffusion processes, we prove the convergence of the constructed approximations in the form of products of the respective substochastic matrices to the boundary crossing probabilities for the process as the time grid used to construct the Markov chains is getting finer. Numerical results indicate that the convergence rate for the proposed approximation with the Brownian bridge correction is 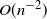$O(n^{-2})$ in the case of 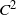$C^2$ boundaries and a uniform time grid with n steps.

Keywords

boundary crossing probabilitydiffusion processesMarkov chains

MSC classification

Primary: 60J60: Diffusion processes
Secondary: 60J70: Applications of Brownian motions and diffusion theory (population genetics, absorption problems, etc.) 65C30: Stochastic differential and integral equations
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 4 , December 2023 , pp. 1386 - 1415
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ait-Sahalia, Y. (2002). Maximum-likelihood estimation of discretely sampled diffusions: A closed-form approach. Econometrica 70, 223–262.CrossRefGoogle Scholar
Anderson, T. W. (1960). A modification of the sequential probability ratio test to reduce the sample size. Ann. Math. Statist. 31, 165–197.CrossRefGoogle Scholar
Baldi, P. and Caramellino, L. (2010). Asymptotics of hitting probabilities for general one-dimensional pinned diffusions. Ann. Appl. Prob. 12, 1071–1095.Google Scholar
Beskos, A., Papaspiliopoulos, O. and Roberts, G. O. (2006). Retrospective exact simulation of diffusion sample paths with applications. Bernoulli 12, 1077–1098.CrossRefGoogle Scholar
Beskos, A. and Roberts, G. O. (2005). Exact simulation of diffusions. Ann. Appl. Prob. 15, 2422–2444.Google Scholar
Billingsley, P. (1968). Convergence of Probability Measures. Wiley, New York.Google Scholar
Borodin, A. N. and Salminen, P. (1996). Handbook of Brownian Motion – Facts and Formulae. Birkhäuser, Basel.CrossRefGoogle Scholar
Borovkov, K. and Novikov, A. (2005). Explicit bounds for approximation rates of boundary crossing probabilities for the Wiener process. J. Appl. Prob. 42, 82–92.CrossRefGoogle Scholar
Broadie, M., Glasserman, P. and Kou, S. (1997). A continuity correction for discrete barrier options. Math. Finance 7, 325–349.CrossRefGoogle Scholar
Buonocore, A., Giorno, V., Nobile, A. G. and Ricciardi, L. M. (1990). On the two-boundary first-crossing-time problem for diffusion processes. J. Appl. Prob. 27, 102–114.Google Scholar
Buonocore, A., Nobile, A. G. and Ricciardi, L. M. (1987). A new integral equation for the evaluation of first-passage-time probability densities. Adv. Appl. Prob. 19, 784–800.CrossRefGoogle Scholar
Cherkasov, I. D. (1957). On the transformation of the diffusion process to a Wiener process. Theor. Prob. Appl. 2, 373–377.CrossRefGoogle Scholar
Cheuk, T. H. F. and Vorst, T. C. F. (1996). Complex barrier options. J. Derivatives 4, 8–22.CrossRefGoogle Scholar
Daniels, H. E. (1969). The minimum of a stationary Markov process superimposed on a U-shaped trend. J. Appl. Prob. 6, 399–408.Google Scholar
Downes, A. N. and Borovkov, K. A. (2008). First passage densities and boundary crossing probabilities for diffusion processes. Methodology Comput. Appl. Prob. 10, 621–644.CrossRefGoogle Scholar
Elerian, O. (1998). A Note on the Existence of a Closed-Form Conditional Transition Density for the Milstein Scheme . Economics Discussion Paper 1998–W18, Nuffield College, Oxford.Google Scholar
Erdös, P. and Kac, M. (1946). On certain limit theorems of the theory of probability. Bull. Amer. Math. Soc. 52, 292–302.Google Scholar
Ethier, S. N. and Kurtz, T. G. (1986). Markov Processes. Wiley, New York.CrossRefGoogle Scholar
Fu, J. C. and Wu, T.-L. (2010). Linear and nonlinear boundary crossing probabilities for Brownian motion and related processes. J. Appl. Prob. 47, 1058–1071.CrossRefGoogle Scholar
Giorno, V., Nobile, A. G., Ricciardi, L. M. and Sato, S. (1989). On the evaluation of first-passage-time probability densities via non-singular integral equations. Adv. Appl. Prob. 21, 20–36.CrossRefGoogle Scholar
Gobet, E. (2000). Weak approximation of killed diffusion using Euler schemes. Stoch. Process. Appl. 87, 167–197.CrossRefGoogle Scholar
Gobet, E. and Menozzi, S. (2010). Stopped diffusion processes: Boundary corrections and overshoot. Stoch. Process. Appl. 120, 130–162.CrossRefGoogle Scholar
Goodwin, E. T. (1949). The evaluation of integrals of the form $\int^\infty_{-\infty}\, f(x) \mathrm{e}^{-x^{2}}\, \mathrm{d} x$ . Proc. Camb. Phil.. Soc. 45, 241–245.CrossRefGoogle Scholar
Gutiérrez, R., Ricciardi, L. M., Román, P, and Torres, F. (1997). First-passage-time densities for time-non-homogeneous diffusion processes. J. Appl. Prob. 34, 623–631.CrossRefGoogle Scholar
Hall, W. J. (1997). The distribution of Brownian motion on linear stopping boundaries. Sequent. Anal. 16, 345–352.CrossRefGoogle Scholar
Hamana, Y. and Matsumoto, H. (2013). The probability distributions of the first hitting times of Bessel processes. Trans. Amer. Math. Soc. 365, 5237–5257.CrossRefGoogle Scholar
Herrmann, S. and Zucca, C. (2019). Exact simulation of the first-passage time of diffusions. J. Sci. Comput. 3, 1477–1504.Google Scholar
Herrmann, S. and Zucca, C. (2020). Exact simulation of first exit times for one-dimensional diffusion processes. ESAIM: M2AN 54, 811–844.CrossRefGoogle Scholar
Hille, E. and Phillips, R. S. (1996). Functional Analysis and Semi-groups, reprint, rev. (AMS Colloquium Publications 31). AMS, Providence, RA.Google Scholar
Hurn, A. S., Jeisman, J. I. and Lindsay, K. A. (2007). Seeing the wood for the trees: A critical evaluation of methods to estimate the parameters of stochastic differential equations. J. Financial Econometrics 5, 390–455.CrossRefGoogle Scholar
Ichiba, T. and Kardaras, C. (2011). Efficient estimation of one-dimensional diffusion first passage time densities via Monte Carlo simulation. J. Appl. Prob. 48, 390–455.CrossRefGoogle Scholar
Jáimez, R. G., Gonzalez, A. J. and Román, P. R. (1991). Construction of first-passage-time densities for a diffusion process which is not necessarily time-homogeneous. J. Appl. Prob. 28, 903–909.CrossRefGoogle Scholar
Ji, H. and Shao, J. (2015). First passage probabilities of one-dimensional diffusion processes. Front. Math. China 10, 901–916.CrossRefGoogle Scholar
Khintchine, A. (1933). Asymptotische Gesetze der Wahrscheinlichkeitsrechnung. Springer, Berlin. [Reprinted by Chelsea Publishing Company, 1948.]Google Scholar
Kloeden, P. E. and Platen, E. (1992). Numerical Solution of Stochastic Differential Equations. Springer, Berlin.CrossRefGoogle Scholar
Kolmogorov, A. (1931). Eine Verallgemeinerung des Laplace–Liapounoffschen Satzes. Bulletin de l’Académie des Sciences de l’URSS. Classe des sciences mathématiques et naturelles, 959–962.Google Scholar
Kolmogorov, A. (1933). Über die Grenzwertsätze der Wahrscheinlichkeitsrechnung. Bulletin de l’Académie des Sciences de l’URSS. Classe des sciences mathématiques et naturelles, 363–372.Google Scholar
Lerche, H. R. (1986). Boundary Crossing of Brownian Motion: Its Relation to the Law of the Iterated Logarithm and to Sequential Analysis. Springer, Berlin.Google Scholar
Li, C. (2013). Maximum-likelihood estimation for diffusion processes via closed-form density expansions. Ann. Statist. 41, 1350–1380.CrossRefGoogle Scholar
Linz, P. (1987). Analytical and Numerical Methods for Volterra Equations. SIAM, Philadelphia, PA.Google Scholar
Loader, C. R. and Deely, J. J. (1987). Computations of boundary crossing probabilities for the Wiener process J. Statist. Comput. Simul. 27, 95–105.CrossRefGoogle Scholar
Lyness, J. N. and Ninham, B. W. (1967). Numerical quadrature and asymptotic expansions. Math. Comput. 21, 162–178.Google Scholar
Nagaev, S. V. (1970). On the speed of convergence in a boundary problem I. Theory Prob. Appl. 15, 163–186.CrossRefGoogle Scholar
Nagaev, S. V. (1970). On the speed of convergence in a boundary problem II. Theory Prob. Appl. 15, 403–429.CrossRefGoogle Scholar
Novikov, A., Frishling, V. and Kordzakhia, N. (1999). Approximations of boundary crossing probabilities for a Brownian motion. J. Appl. Prob. 36, 1019–1030.CrossRefGoogle Scholar
Olver, F. W. J. (1974). Asymptotics and Special Functions. Academic Press, New York.Google Scholar
Park, C. and Schuurmann, F. J. (1976). Evaluations of barrier-crossing probabilities of Wiener paths. J. Appl. Prob. 13, 267–275.Google Scholar
Patie, P. and Winter, C. (2008). First exit time probability for multidimensional diffusions: A PDE-based approach. J. Comput. Appl. Math. 222, 42–53.Google Scholar
Peskir, G. (2002). On integral equations arising in the first-passage problem for Brownian motion. J. Integral Equ. Appl. 14, 397–423.Google Scholar
Pötzelberger, K. and Wang, L. (2001). Boundary crossing probability for Brownian motion. J. Appl. Prob. 38, 152–164.CrossRefGoogle Scholar
Ricciardi, L. M. (1976). On the transformation of diffusion processes into the Wiener process. J. Math. Anal. Appl. 54, 185–199.CrossRefGoogle Scholar
Ricciardi, L. M., Sacerdote, L. and Sato, S. (1984). On an integral equation for first-passage-time probability densities. J. Appl. Prob. 21, 302–314.CrossRefGoogle Scholar
Ricciardi, L. M. and Sato, S. (1983). A note on the evaluation of first-passage-time probability densities. J. Appl. Prob. 20, 197–201.CrossRefGoogle Scholar
Rogers, L. C. G. (1985). Smooth transition densities for one-dimensional diffusions. Bull. London Math. Soc. 17, 157–161.CrossRefGoogle Scholar
Sacerdote, L. and Tomassetti, F. (1996). Smooth transition densities for one-dimensional diffusions. Adv. Appl. Prob. 28, 270–284.CrossRefGoogle Scholar
Sazonov, V. V. (1981). Normal Approximation – Some Recent Advances (Lect. Notes Math. 879). Springer, Berlin.Google Scholar
Sidi, A. (2003). Practical Extrapolation Methods. Cambridge University Press.CrossRefGoogle Scholar
Siegmund, D. and Yuh, Y. S. (1982). Brownian approximations to first passage probabilities. Z. Wahrscheinlichkeitst. 59, 239–248.CrossRefGoogle Scholar
Stein, E. M. and Weiss, G. (1971). Introduction to Fourier Analysis on Euclidean Spaces. Princeton University Press.Google Scholar
Takahasi, H. and Mori, M. (1973). Double exponential formulas for numerical integration. Publ. Res. Inst. Math. Sci. 9, 721–741.CrossRefGoogle Scholar
Wang, L. and Pötzelberger, K. (1997). Boundary crossing probability for Brownian motion and general boundaries. J. Appl. Prob. 34, 54–65.Google Scholar
Wang, L. and Pötzelberger, K. (2007). Crossing probabilities for diffusion processes with piecewise continuous boundaries. Methodology Comput. Appl. Prob. 9, 21–40.CrossRefGoogle Scholar