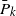On some properties of distributions possessing a bathtub-shaped failure rate average

Abstract

The life distribution of a device subject to shocks governed by a homogeneous Poisson process is shown to have a bathtub failure rate average (BFRA) when the probabilities $\bar{P}_k$ of surviving k shocks possess the corresponding discrete property. We prove closure under the formation of weak limits for BFRA distributions and explore related moment convergence issues within the BFRA family. Similar results for increasing and decreasing failure rate average distributions are obtained either independently or as consequences of our results. We also establish some results outlining the positions of various non-monotonic ageing classes such as bathtub failure rate, increasing initially then decreasing mean residual life, new worse then better than used in expectation, and increasing initially then decreasing mean time to failure in the hierarchy. Finally, an open problem is posed and a partial solution provided.

1. Introduction

Usually, ageing is the process of ‘growing up’ and ‘growing old’ for mechanical devices or biological systems. It begins at birth and ends with death. In reliability theory, the term ageing of a system with a lifetime distribution implies that the residual life of the system is affected by its age in some probabilistic sense. This interpretation allows cases in which a system may typically face positive ageing, negative ageing, or no ageing.

In ‘positive ageing’, the age of the system has an adverse effect on the residual lifetime, i.e. the residual lifetime of the system decreases in some probabilistic sense with increase in age. This type of ageing pattern is the most common, since the majority of systems experience gradual wear and tear under usual operating conditions. ‘Negative ageing’ describes the opposite beneficial effect on the life of the unit as age progresses. In fact, negative ageing is the dual of positive ageing. ‘No ageing’ is equivalent to saying that the age of the system has no effect on the distribution of its residual lifetime.

Monotonic ageing is the phenomenon where the pattern of ageing remains the same during the entire lifespan of a system. Interestingly enough, in many practical situations the ageing pattern happens to be non-monotonic, typically characterized by a ‘burn-in phase’ (negative ageing), a useful life phase (no ageing), and finally a ‘wear-out phase’ (positive ageing). A well-known example is that of human beings, where ageing is beneficial during infancy and young adulthood, i.e. a person becomes stronger with increase in age, and subsequently the reverse phenomenon of gradual degeneration is observed. This is also the case with mechanical systems that may have a high initial failure probability due to design or manufacturing errors, but after some point of time the system improves its performance due to work hardening (see [1, 58]). Moreover, in this context, [25] gave two real-life examples: (i) [42] found in a study of curability of breast cancer that the peak of mortality occurred after about three years and then declines slowly; (ii) [11] analyzed lung cancer data from the Veterans Administration, presented in [54], and showed that the empirical failure rates for both low and high potassium sulfide groups are non-monotonic. So the modelling of these types of phenomena necessitates the use of various non-monotonic ageing families of life distributions. The specific time point where the ageing profile changes trend is called a change point or turning point of that family. Attempts to model such scenarios have led to several non-parametric classes of distributions such as bathtub failure rate (BFR) [23], increasing initially then decreasing mean residual life (IDMRL) [24], new worse then better than used in expectation (NWBUE) [47], increasing initially then decreasing mean time to failure (IDMTTF) [27] etc. [46] observed a trend change in the failure rate average which results in the family of bathtub failure rate average (BFRA) distributions, subsequently developed and studied in detail in [12].

At this juncture, we recall some basic notation and definitions in the context of BFRA distributions. Suppose that the lifetime of a system (or a component thereof) is represented by a random variable X with cumulative distribution function F(x) and survival function $\bar{F}(x)\;:\!=\;1-F(x)$ .

Definition 1.1. The failure rate average function of a life distribution F is defined by $r(x) = -({\ln{\bar{F}(x)}})/{x}$ , $x>0$ .

If F is absolutely continuous with respect to the Lebesgue measure on the real line, then $r(x)=({1}/{x})\int_0^x h(u) \, \mathrm{d} u$ , where $h(u)={f(u)}/{\bar{F}(u)}$ is called the hazard rate of F and f denotes the probability density function of F.

Definition 1.2. A life distribution F is said to be a BFRA distribution if there exists a point $x_0 \geq 0$ such that the failure rate average function r(x) is non-increasing on $(0, x_0)$ and non-decreasing on $[x_0, \infty)$ . The point $x_0$ is referred to as a turning point (or change point) of F in the BFRA sense.

In this case, we write F is BFRA $(x_0)$ . For $x_0=0$ , the BFRA class reduces to increasing failure rate average (IFRA). We also include all decreasing failure rate average (DFRA) distributions in the BFRA class by adopting the notion that a BFRA distribution having ‘a change point at infinity’ is in fact DFRA. The upside-down bathtub failure rate average (UBFRA) class, which is the dual of the BFRA class, can be obtained in an obvious way by reversing the monotonicity in the above definition. Note that $r(x)=R(x)/x$ , where $R(x) = {-}\log{\bar{F}(x)}$ is the hazard function of F. Singpurwalla [56] referred to this hazard function as ‘hazard potential’ and provided an innovative interpretation of it. Moreover, another equivalent condition for BFRA distributions can be written as ‘ $\bar{F}(x)^{1/x}$ is non-decreasing on $(0, x_0)$ and non-increasing on $[x_0, \infty)$ ’.

Failure rate average (FRA) is a very important fundamental concept in reliability and survival analysis (see [8, 41]). The IFRA class of distributions, first introduced in [16], generalizes the increasing failure rate (IFR) family and is equivalent to the class of distribution functions where R(x) is star-shaped. The class of IFRA distributions is the smallest ageing class that is closed under the formation of coherent structures and contains the limiting case of no wear (see [16]). Further, this class arises from the cumulative damage shock model when a device is subjected to shocks driven by a Poisson process (see [21, 22]). Tests of exponentiality against nonexponential IFRA distributions have been proposed by several authors [5, 37, 39, 43, 57, 59]. [46] and [12] both showed that if a twice-differentiable life distribution function F is BFR $(t_0)$ , then F is BFRA $(x_0)$ where $x_0\geq t_0$ . The relationship between the discrete versions of BFR and BFRA was also given in [45]. [12] proposed a non-parametric test of exponentiality against BFRA alternatives by assuming that the proportion of early failures is known, and investigated the closure of BFRA property under some reliability operations.

Throughout the paper, we follow the convention that ‘increasing’ (‘decreasing’) means ‘non-decreasing’ (‘non-increasing’).

The rest of the paper is organized as follows. Section 2 extends the results of [22], specifically in the context of the BFRA class of life distributions. Shock model theory is developed when the shock survival probabilities $\bar{P}_k$ are discrete BFRA and the shock arrivals follow a homogeneous Poisson process. The BFRA property of the discrete failure distribution $P_k$ is shown to be reflected as the BFRA property of $\bar{H}(t)$ . Section 3 deals with closure under weak convergence within the BFRA family and, as a consequence, we obtain closure under the formation of weak limits within the IFRA (DFRA) family. Moreover, the relation between convergence of moment sequences and weak convergence within BFRA and IFRA classes is explored. Further, we show that these connections are not meaningful in the context of UBFRA and DFRA distributions. In Section 4, we prove that the BFRA class of distributions contains all BFR distributions. Further, we establish some results to investigate the interrelationships among well-known non-monotonic ageing families. Finally, we conclude by suggesting possible avenues of future work, and also pose an interesting open problem in this area.

2. Shock model theory

We focus on a system where failure is caused by a sequence of shocks occurring randomly in time according to a counting process $\lbrace N(t)\colon t\geq 0\rbrace$ . Let the system have a probability $\bar{P}_k$ of surviving the first k shocks, $k=0, 1, 2, \dots$ , where the $\bar{P}_k$ satisfy the inheritance condition $1= \bar{P}_0 \geq \bar{P}_1 \geq \bar{P}_2 \geq \cdots$ , and $\sum_{i=0}^\infty \bar{P}_{i} = \gamma < \infty$ , i.e. the expected number of shocks required to cause failure of the system is finite. Assume that only the shocks are responsible for failure, and constant wear and tear is completely absent. Then, using a conditioning argument, the probability $\bar{H}(t)$ that the system will survive beyond time t may be written as $\bar{H}(t) = \sum_{k=0}^\infty \mathbb{P}[N(t)=k]\bar{P}_k$ . Now, this can be written as

(2.1) \begin{equation} \bar{H}(t)= \sum_{k=0}^\infty \mathrm{e}^{-\lambda t}\frac{(\lambda t)^k}{k!}\bar{P}_k\end{equation}

when the shock arrivals follow a homogeneous Poisson process with intensity $\lambda>0$ . A shock model of this kind was considered in [22] for the first time in the context of ageing scenarios. ‘Shocks’ can be interpreted as claims, the technical reasons for failure in a running machine, or the cause of deterioration of a biological organ. Thus, the Poisson shock model has various applications in several fields, including risk, survival, and reliability analysis (see [51] and the references therein). In the vast literature concerning shock model theory, [3, 17, 19, 20, 40, 53, 55] and others are important. Thus, it is relevant to investigate the origin of the ageing class under consideration via discrete survival probabilities.

In reliability shock models, for the discrete distribution $P_k$ , $k=0,1,2,\dots$ , most research tries to establish that properties of $P_k$ are reflected in corresponding properties of the continuous life distribution H(t). This is shown in [22] for ILR, IFR, IFRA, DMRL, NBU, and NBUE classes, [35, 38] for HNBUE and $\mathcal{L}$ classes, [18] for strong increasing failure rate and SNBU, and [2] for NBUFR and NBAFR. For non-monotonic ageing scenarios, [49] first proved such results in the context of NWBUE and BFR classes. Analogous results have been established in [4, 32] in the context of the IDMRL and IDMTTF distribution families. For a more detailed overview, see [50] and the references therein.

In this section we establish the corresponding results for BFRA classes of life distributions, which remains unexplored. The following definition introduces the notion of the discrete version of the BFRA property.

Definition 2.1. The sequence $\lbrace \bar{P}_k, k=0,1,\dots \rbrace$ is said to have the discrete BFRA (D-BFRA) property if there exists $k_0 \geq 0$ such that $\bar{P_k}^{1/k}$ is increasing in k for $k<k_0$ and decreasing in k for $k\geq k_0$ .

At the outset, we recapitulate some results of total positivity theory and establish two lemmas before going on to prove the main result in this section.

Lemma 2.1. Consider a function $\phi\colon [a, b) \rightarrow (0, 1]$ where $a, b\in [0, \infty)$ . Then $\phi(s)^{1/s}$ is increasing (decreasing) in s if, for every $c\geq 0$ , $\phi(s)-\mathrm{e}^{-cs}$ has at most one change of sign, and if one change occurs, it occurs in the order $-,+$ ( $+,-$ ).

Proof. Let $s_1, s_2 \in [a, b)$ , $s_1<s_2$ . We want to show that $\phi(s_1)^{1/s_1}\leq \phi(s_2)^{1/s_2}$ , i.e. $({1}/{s_1})\log{(\phi(s_1))}\leq ({1}/{s_2})\log{(\phi(s_2))}$ , i.e. $g(s_1)/s_1\geq g(s_2)/s_2$ where $g(s)=-\log{(\phi(s))}$ . Let $c_1=g(s_1)/s_1$ and $c_2=g(s_2)/s_2$ . Suppose that, for every $c\geq 0$ , $\phi(s)-\mathrm{e}^{-cs}$ has at most one change of sign, from $-$ to $+$ if one occurs. So, in particular, this happens for $c_1$ and $c_2$ . Thus, $\log{(\phi(s))}+c_i s$ has at most one change of sign from $-$ to $+$ for $i=1,2$ , i.e. $c_i s -g(s)$ has at most one change of sign $-$ to $+$ if one occurs for $i=1,2$ . Now, by choice of $c_1$ and $c_2$ , we have $g(s) \leq c_i s$ for $s\leq s_i$ and $g(s) \geq c_i s$ for $s > s_i$ . If possible, let $c_1=g(s_1)/s_1 < g(s_2)/s_2=c_2$ . Then, for $s_1<s<s_2$ , $g(s) \leq c_1 s$ as $s>s_1$ , $g(s) < c_2 s$ as $c_1<c_2$ , and $g(s) \leq g(s)$ as $s<s_2$ , which is a contradiction. So $\phi(s)^{1/s}$ is increasing in s. The proof for the ‘decreasing’ case is analogous.

Lemma 2.1 shows the characterization of monotonicity of $\phi(s)^{1/s}$ in terms of the sign changes. Before proceeding further, we recall the definition of a totally positive function and an important theorem of Karlin ([29, p. 21]).

Definition 2.2. Let $X, Y \subseteq \mathbb{R}$ . A function $L\colon X\times Y \rightarrow \mathbb{R}$ is called a totally positive function of order n ( $TP_n$ ) if, for every $i=1,2,\dots , n$ ,

\begin{align*} \begin{vmatrix} L(s_1, t_1) & L(s_1, t_2) & \dots & L(s_1, t_i) \\[5pt] L(s_2, t_1) & L(s_2, t_2) & \dots & L(s_2, t_i) \\[5pt] \vdots & \vdots & \ddots &\vdots \\[5pt] L(s_i, t_1) & L(s_i, t_2) & \dots & L(s_i, t_i) \end{vmatrix} \geq 0 , \end{align*}

where $ s_1<s_2<\cdots <s_i$ ( $s_j \in X$ , $j=1,2,\dots, i$ ) and $t_1<t_2<\cdots <t_i$ ( $t_j \in Y$ , $j=1,2,\dots, i$ ).

Definition 2.3. A function L is called totally positive (TP) when L is $TP_n$ for every $n\geq1$ .

Consider a subset $\lbrace x_i\mid 1\leq i \leq m \rbrace$ of $\mathbb{R}$ and let $S^-(x_1, x_2, \dots x_m)$ be the number of sign changes in $x_1, x_2, \dots x_m$ ignoring zero terms. Let Q be an ordered subset of $\mathbb{R}$ and $g\colon Q\rightarrow \mathbb{R}$ be a function. Define $S^-(g)\;:\!=\;\sup_{y_1<y_2<\cdots <y_m \in Q} S^-( g(y_1), g(y_2), \dots , g(y_m))$ .

Let L(x, y) defined on $X\times Y$ be Borel measurable, and assume for simplicity that the integral $\int_Y L(x, y) \, \mathrm{d} \mu (y)$ exists for every x in X. Here, $\mu$ represents a fixed sigma-finite regular measure defined on Y such that $\mu(U)>0$ for each open set U for which $U\cap Y$ is non-empty.

Theorem 2.1. Let L(x, y) be $TP_r$ on $X\times Y$ . Let g be a bounded Borel-measurable function on Y. Let the transformation $f(x)=\int_Y L(x, y) g(y) \, \mathrm{d} \mu (y)$ be finite for each x on X. Then $S^-(f) \leq S^-(g)$ provided $S^-(g)\leq r-1$ . Moreover, if $S^-(f) = S^-(g) \leq r-1$ , then g and f exhibit the same sequence of signs when their respective arguments traverse the domain of definition from left to right.

Theorem 2.1 is called the variation diminishing property (VDP) of TP functions; see [29, Chapter 5] for a proof. The following main theorem demonstrates that $\bar{H}(t)$ inherits the BFRA property if the sequence $\lbrace\bar{P}_k,\,k\geq 0\rbrace$ possesses the discrete BFRA property.

Theorem 2.2. Let the sequence $\lbrace\bar{P}_k,\,k\geq 0\rbrace$ possess the D-BFRA property. Then $\bar{H}(t)$ defined in (2.1) is BFRA.

Proof. Let $\eta\in[0,1]$ . Now, from Definition 2.1, as ${\bar{P}_k}^{1/k}$ is increasing in k for $k<k_0$ and ${\bar{P}_k}^{1/k}$ is decreasing in k for $k\geq k_0$ for some $k_0\in \mathbb{N}$ , $\bar{P}_k - \eta^{k}$ has at most two sign changes in the direction $-,+,-$ . Now,

\begin{equation*} \bar{H}(t) - \mathrm{e}^{-(1- \eta)\lambda t } = \sum_{k=0}^\infty \mathrm{e}^{-\lambda t}\frac{(\lambda t)^k}{k!}\bar{P}_k - \sum_{k=0}^\infty \mathrm{e}^{-\lambda t} \frac{{(\lambda \eta t)}^k}{k!} \nonumber = \sum_{k=0}^\infty (\bar{P}_k-\eta^k) \mathrm{e}^{-\lambda t} \frac{(\lambda t)^k}{k!}. \nonumber \end{equation*}

In the first case, suppose $\bar{P}_k - \eta^{k}$ has two sign changes in the direction $-,+,-$ . Note that $\mathrm{e}^{-\lambda t}{(\lambda t)^k}/{k!}$ is a $TP_3$ function for $s>0$ and $k\in \mathbb{N}\cup \lbrace 0\rbrace$ , since $\mathrm{e}^{-\lambda t}{(\lambda t)^k}/{k!}$ is a TP function for any $\lambda>0$ . Then, by the VDP, $S^-(\bar{H}(t) -\mathrm{e}^{-(1- \eta)\lambda t })=0$ , 1, or 2. If $S^-(\bar{H}(t) -\mathrm{e}^{-(1- \eta)\lambda t })=2$ , then, by the VDP, $\bar{H}(t) -\mathrm{e}^{-(1- \eta)\lambda t }$ has the same sign change property in t. Note that $\bar{H}(t)\geq \mathrm{e}^{-\lambda t}$ since the hazard rate $h(t)\leq \lambda$ for all $t>0$ (see [22, p. 629]). Hence, for any $c\leq \lambda$ , $\bar{H}(t) -\mathrm{e}^{-c t }$ has the same sign change property in t, and the choice for $\eta$ is $1-c/\lambda$ . Moreover, for any $c> \lambda$ , $\bar{H}(t) -\mathrm{e}^{-c t }$ is always positive for $t>0$ . Thus, there exists $d\in [0, \infty)$ such that, for any $c\geq 0$ , $\bar{H}(t) -\mathrm{e}^{-c t }$ has at most one change of sign from $-$ to $+$ for $t\leq d$ , and $\bar{H}(t) -\mathrm{e}^{-c t }$ has at most one change of sign from $+$ to $-$ for $t> d$ . Applying Lemma 2.1 on [0, d) and $[d, \infty)$ , we get the result that $\bar{H}(t)$ is BFRA. If $\bar{H}(t) -\mathrm{e}^{-(1- \eta)\lambda t }$ has at most one change of sign, then the sign of $\bar{H}(t) -\mathrm{e}^{-(1- \eta)\lambda t }$ can change from $+$ to $-$ or $-$ to $+$ . Again, an application of Lemma 2.1 together with the fact that $\bar{H}(t)\geq \mathrm{e}^{-\lambda t}$ yields the result.

In the second case, suppose $\bar{P}_k - \eta^{k} $ has one sign change from $+,-$ or $-,+$ . Then, by the VDP, $\bar{H}(t) -\mathrm{e}^{-(1- \eta)\lambda t }$ has the same sign change property in t, if sign change occurs in $\bar{P}_k - \eta^{k} $ . Again, using the fact that $\bar{H}(t)\geq \mathrm{e}^{-\lambda t}$ and arguing as in [22], we can conclude that, for any $c\geq 0$ , $\bar{H}(t) -\mathrm{e}^{-c t }$ has at most one sign change in t, if one occurs. Again, Lemma 2.1 yields the result that $\bar{H}(t)$ is IFRA or DFRA.

Corollary 2.1. $\bar{H}(t)$ belongs to the IFRA (DFRA) class if $\lbrace\bar{P}_k,\,k\geq 0\rbrace$ satisfies the discrete IFRA (DFRA) property.

Remark 2.1. It is important to note that [22, (3.4) of Theorem 3.1] is identical to Corollary 2.1.

3. Weak convergence issues within BFRA class

During the last few decades, the topic of weak convergence in various ageing classes has generated substantial interest among reliability experts. Weak convergence issues within a class of distributions has been addressed in [10] for IFR, [9] for HNBUE, [33] for IMIT, [47, 48] for NWBUE and BFR, [4] for IDMRL, [32] for IDMTTF distributions. Let $F_n$ , $n=1,2, \dots $ be a sequence of BFRA distributions with $F_n$ converging to F in distribution. In this section, we first try to establish that F belongs to the BFRA class, i.e. closure under the formation of weak limits within the BFRA family.

Theorem 3.1. Suppose $\lbrace F_n,\,n\geq 1 \rbrace$ is a sequence of BFRA distributions. Let $x_{0n}$ be a change point of $F_n$ , and suppose that $F_n$ converges to F in distribution, where F is assumed to be continuous. Then F is BFRA.

Proof. Let $r(x)=\Lambda_{F_n}(x)=R_{F_n}(x)/x$ be the corresponding FRA function. By the BFRA property, $\Lambda_{F_n}$ is decreasing on $(0, x_{0n})$ and increasing on $[ x_{0n}, \infty)$ , where $R_{F_n}(x)=-\ln{\bar{F}_n(x)}$ . Now, $F_n \stackrel{\mathcal{L}}{\rightarrow} F$ implies $R_{F_n}(x) \rightarrow R_{F}(x)$ , and consequently $\Lambda_{F_n} \rightarrow \Lambda_{F}$ pointwise, where $\stackrel{\mathcal{L}}{\rightarrow}$ denotes convergence in distribution. For any BFRA distribution H, we define $C_H = \lbrace x_0\colon \Lambda_{H}(x)$ is decreasing on $(0, x_{0})$ and increasing on $[ x_{0}, \infty) \rbrace$ . Now, $x_{0n}\in C_{F_n}$ , $n=1,2, \dots$ . Two cases may arise: (i) $\lbrace x_{0n}\rbrace$ is bounded; (ii) $\lbrace x_{0n}\rbrace$ is unbounded.

For case (i), $\lbrace x_{0n}\rbrace_{n=1}^{\infty}$ is bounded, an application of the Bolzano–Weierstrass theorem yields a subsequence $\lbrace x_{0n_k}\rbrace$ of $\lbrace x_{0n}\rbrace$ such that $x_{0n_k}\rightarrow l$ (finite) as $k\rightarrow\infty$ . Thus, for any $\epsilon>0$ , there exists $k_0\in \mathbb{N}$ such that $l - \epsilon < \lbrace x_{0n_k}\rbrace < l + \epsilon$ for all $k\geq k_0$ . Now, for any $x_1, x_2 > 0$ such that $x_1<x_2<l -\epsilon$ , we have $\Lambda_{F_{n_k}}(x_1) \geq \Lambda_{F_{n_k}}(x_2)$ since $\Lambda_{F_{n_k}}(x)$ is decreasing on $(0, x_{0n_k})$ . Consequently, using the fact that $\Lambda_{F_n}\rightarrow \Lambda_{F}$ , we get $\Lambda_{F}(x_1) \geq \Lambda_{F}(x_2)$ as $k\rightarrow \infty$ . Thus, $\Lambda_F(x)$ is decreasing on $(0, l - \epsilon)$ . Similarly, we can show that $\Lambda_F(x)$ is increasing on $(l + \epsilon, \infty)$ . Since $\epsilon>0$ is arbitrary, F is BFRA with l as a change point.

For case (ii), $\lbrace x_{0n}\rbrace_{n=1}^{\infty}$ is unbounded, there exists a subsequence $\lbrace x_{0n_k}\rbrace$ such that $x_{0n_k}\rightarrow \infty$ as $k\rightarrow \infty$ . Now, for any $0<x_1<x_2<\infty$ there exists $k_0\in\mathbb{N}$ sufficiently large that $x_1 < x_2 < x_{0n_k}$ for all $k\geq k_0$ . Thus, $\Lambda_{F_{n_k}}(x_1) \geq \Lambda_{F_{n_k}}(x_2)$ , as $\Lambda_{F_{n_k}}(x)$ is decreasing on $(0, x_{0n_k})$ . Consequently, using the fact that $\Lambda_{F_{n_k}}\rightarrow \Lambda_{F}$ pointwise as $k\rightarrow \infty$ , we get $\Lambda_{F}(x_1) \geq \Lambda_{F}(x_2)$ . Hence, $\Lambda_F(x)$ is DFRA, i.e. BFRA with a change point at $\infty$ .

The weak limit of a sequence of IFRA and DFRA distributions is not known so far. However, as a consequence of Theorem 3.1, we obtain the following corollary which shows closure under the formation of weak limits within the IFRA (DFRA) family of distributions.

Corollary 3.1. Let $\lbrace F_n,\,n\geq 1\rbrace$ be a sequence of IFRA (DFRA) distributions. Let F be a continuous distribution function, and $F_n$ converge to F in distribution. Then F is IFRA (DFRA).

The next theorem deals with convergence of the sequence of change points of $F_n$ .

Theorem 3.2. Suppose $\lbrace F_n,\,n\geq 1\rbrace$ is a sequence of BFRA distributions having unique change points $x_{0n}$ . Let F be a continuous distribution function with unique change point $x_0$ in the BFRA sense, $F_n$ converging to F in distribution. Then $\lim_{n\rightarrow \infty}x_{0n}=x_0$ ( $\leq \infty$ ).

Proof. Note that the unique change point means the FRA function is not constant in any neighborhood of its change. We again prove this theorem by considering two cases: (i) $\lbrace x_{0n}\rbrace$ is bounded; (ii) $\lbrace x_{0n}\rbrace$ is unbounded.

For case (i), $\lbrace x_{0n}\rbrace_{n=1}^{\infty}$ is bounded, following case (i) of the proof of Theorem 3.1, it can be easily shown that there exists a convergent subsequence of $\lbrace x_{0n}\rbrace$ whose limit is a change point of F. Then, by the uniqueness of the change point of F, it follows that $\lim_{n\rightarrow \infty}x_{0n}=x_0$ ( $< \infty$ ).

For case (ii), $\lbrace x_{0n}\rbrace_{n=1}^{\infty}$ is unbounded, case (ii) of the proof of Theorem 3.1 implies that F is necessarily a DFRA distribution, i.e. a BFRA distribution with unique change point $x_0=\infty$ . Now suppose that $\lbrace x_{0n}\rbrace \nrightarrow \infty$ as $n\rightarrow\infty$ . Then there exists $M>0$ such that $x_{0n}\leq M$ infinitely often, so that it should be possible to find a subsequence $\lbrace x_{0n_k}\rbrace$ converging to a finite limit $\alpha$ , say. But then, by case (i) in the proof of Theorem 3.1, along with the uniqueness of the change point of F, we have the contradiction that $\infty=\alpha <\infty$ . Thus, $x_{0n} \rightarrow x_0=\infty$ as $n\rightarrow \infty$ .

In the next theorem we explore the convergence of the corresponding moment sequences of all orders.

Theorem 3.3. Let $\lbrace F_n,\,n\geq 1\rbrace$ be a sequence of absolutely continuous BFRA distributions having a unique change point $x_{0n}$ . Assume that $\lbrace x_{0n}\rbrace_{n=1}^{\infty}$ is bounded. If $F_n$ converges to F in distribution where F is continuous, then, for every $r>0$ , $\mathbb{E}_{F_n}(X^r) \rightarrow \mathbb{E}_F(X^r)$ as $n\rightarrow \infty$ .

Proof. Using [12, Theorem 3.2] we get finiteness of moments of $F_n$ . Now, following Theorem 3.1 we conclude that F is BFRA. If F is BFRA with a finite change point then again an application of [12, Theorem 3.2] yields finiteness of moments of F. Now we consider the case when F is BFRA with a change point at infinity, i.e. DFRA. Note that there exists B such that $x_{0n}\leq B$ for all n since $\lbrace x_{0n}\rbrace_{n=1}^{\infty}$ is bounded. Take $B<x<y$ . Then $\Lambda_{F_n}(x)\leq \Lambda_{F_n}(y)$ , since the FRA function of $F_n$ is increasing on $[x_{0n}, \infty)$ . Consequently, taking limits of both sides as $n\rightarrow\infty$ , we get $\Lambda_{F}(x)\leq \Lambda_{F}(y)$ . Now, the DFRA property of F leads to $\Lambda_{F}(x)\geq \Lambda_{F}(y)$ . Thus, $\Lambda_{F}(x)$ is constant for all $x>B$ . Suppose $\Lambda_{F}(x)=c$ for all $x>B$ . Thus $\bar{F}(x) \leq 1$ for $x\leq B$ and $\bar{F}(x) = \mathrm{e}^{-{c x}}$ for $x>B$ , and hence $\int_0^{\infty} x^{r-1} \bar{F}(x) \, \mathrm{d} x <\infty$ . Consequently, it suffices to show that, for all $r>0$ , $\lim_{n\rightarrow\infty}\int_0^{\infty} x^{r-1} \bar{F}_n(x) \, \mathrm{d} x = \int_0^{\infty} x^{r-1} \bar{F}(x) \, \mathrm{d} x$ . Suppose $\epsilon>0$ is such that $\epsilon + \bar{F}(M) = \mathrm{e}^{-\theta}$ for some $\theta>0$ , where $M\in \mathbb{R}^+$ such that $M>B$ . Now, $F_n$ converges to F in distribution implies that there exists $N\in\mathbb{N}$ depending on $\epsilon$ such that $\bar{F}_n(M) < \mathrm{e}^{-\theta}$ for all $n\geq N$ . Note that the FRA function of $F_n$ increasing on $[x_{0n}, \infty)$ implies that $\lbrace \bar{F}_n(x)\rbrace^{{1}/{x}}$ is decreasing on $[x_{0n},\infty)$ . Consequently, $\bar{F}_n(x)\leq V(x)$ , where $V(x) = 1$ for $x\leq M$ , and $V(x) = \mathrm{e}^{-{\theta x}/{M}}$ for $x>M$ . Thus, $x^{r-1} \bar{F}_n(x)$ is bounded by the integrable function $x^{r-1} V(x)$ on $(0,\infty)$ . Hence, the theorem follows in view of the dominated convergence theorem, since $F_n(x)\rightarrow F(x)$ pointwise.

In the next theorem we explore the convergence of moment sequences for the IFRA family. Here we even relax the condition of absolute continuity.

Theorem 3.4. Let $\lbrace F_n,\,n\geq 1\rbrace$ be a sequence of continuous distributions which are IFRA with finite means. If $F_n$ converges to F in distribution where F is continuous with finite mean, then, for every $r\geq 1$ , $\mathbb{E}_{F_n}(X^r) \rightarrow \mathbb{E}_F(X^r)$ as $n\rightarrow \infty$ .

Proof. For an IFRA distribution G with mean $\mu$ , from [8] we get that

(3.1) \begin{equation} \mathbb{E}_G(X^r)\leq \Gamma(r+1)\mu^r \quad \text{if } r\geq 1 , \end{equation}

and there exists $\zeta_p$ such that $F(\zeta_p)=p$ , $0<p<1$ , for which

(3.2) \begin{equation} \bar{G}(x)\leq \begin{cases} 1 & \text{ for } x\leq \zeta_p , \\[5pt] \mathrm{e}^{-\alpha x } & \text{ for } x>\zeta_p , \end{cases} \end{equation}

where $\alpha=-({1}/{\zeta_p})\ln{(1-p)}$ . Corollary 3.1 ensures that F is IFRA, and (3.1) implies that $\mathbb{E}_F(X^r)<\infty$ for all $r>1$ . Now, using (3.1) and (3.2), and following the argument of the proof of Theorem 3.3, we get the result.

Theorem 3.5. Suppose F is an absolutely continuous BFRA distribution with a finite change point at $x_0$ . Then F is uniquely determined by its moment sequence.

Proof. [12, Theorem 3.2] shows that, for all $r\geq 1$ ,

\begin{equation*} \mathbb{E}_F(X^r) \;:\!=\; \int_0^{\infty} x^r \, \mathrm{d} F(x) \leq \frac{\Gamma (r+1)} {\big(\min_{u\in[0,t_0]}{\lambda (u)}\big)^r} , \end{equation*}

from which it can be shown that the power series $\sum_{r=0}^{\infty} ({u^r}/{r!}) \mathbb{E}_F(X^r)$ has a non-null radius of convergence. The theorem now follows easily using [44, p. 217].

Using (3.1) together with [44, p. 217], the following theorem holds.

Theorem 3.6. Suppose F is a continuous IFRA distribution with finite mean. Then F is uniquely determined by its moment sequence.

The following theorem is related to the converse of Theorem 3.3.

Theorem 3.7. Let $\lbrace F_n,\,n\geq 1\rbrace$ be a sequence of absolutely continuous BFRA distributions with a unique change point $x_{0n}<\infty$ for all $n\geq 1$ , and suppose that F is an absolutely continuous BFRA with unique finite change point $x_0$ such that, for all integers $r>0$ ,

(3.3) \begin{equation} \lim_{n\rightarrow\infty}\int_0^{\infty} x^r \, \mathrm{d} F_n(x) = \int_0^{\infty} x^r \, \mathrm{d} F(x). \end{equation}

Then $F_n$ converges to F in distribution.

Proof. As a consequence of Theorem 3.5 and (3.3), every weakly convergent subsequence of $\lbrace F_n,\,n\geq 1\rbrace$ necessarily converges to the distribution F. This concludes the proof.

The converse of Theorem 3.4 also holds for IFRA family following an argument analogous to the proof of Theorem 3.7, using Theorem 3.6 instead of Theorem 3.5.

Theorem 3.8. Let $F_n,\, n=1, 2, \dots ,$ be a sequence of continuous IFRA distributions. Suppose that F is continuous and IFRA such that, for all integers $r\geq 1$ , $\mathbb{E}_{F_n}(X^r) \rightarrow \mathbb{E}_F(X^r)$ as $n\rightarrow \infty$ . Then $F_n$ converges to F in distribution.

Example 3.1. Consider a survival function $\bar{F_1}(x)=(x^2+1)^{-1}$ , $x\geq 0$ , of a life distribution. It is easily seen that $F_1$ is a UBFR distribution with a change point at 1. Then, from [46, Theorem 1] or [12, Theorem 2.1], it can be concluded that $F_1$ is a UBFRA distribution since $F_1$ is a twice-differentiable function. Further, it can also be shown that the change point of $F_1$ in UBFRA sense is finite. Note that $\mathbb{E}_F(X)=\pi/2<\infty$ and $\mathbb{E}_F(X^r)=\infty$ for all $r>1$ . Consequently, the versions of Theorems 3.3, 3.5, and 3.7 are not meaningful in the context of UBFRA distributions.

Remark 3.1. The versions of Theorems 3.4, 3.6, and 3.8 are not meaningful in the context of DFRA distributions.

4. Interrelationships among non-monotonic ageing classes

Interrelationships among ageing classes have received widespread attention in the literature from the very beginning [7, 28, 36, 41]. In this section, we study the interrelationships between the BFR family of [23], the IDMRL family of [24], the NWBUE family of [47], and the IDMTTF family of [27]. In the context of the abovementioned non-monotonic ageing classes, see the recent works [13, 14, 15, 26, 30, 31, 34]. Exploiting ‘total time on test’ (TTT) transform characterizations, [47] established that the NWBUE family of life distributions contains both IDMRL and BFR classes. [46] proved that BFR implies both BFRA and IDMRL for a twice-differentiable distribution function. [27] established that $\{\mathrm{BFR}\} \subset \{\mathrm{IDMTTF}\} \subset \{\mathrm{NWBUE}\}$ . [32] proved that a BFR life distribution F with change point $t_0$ implies F is IDMRL with a change point $\tau$ where $\tau\leq t_0$ , and that the $\{\mathrm{IDMRL}\}$ and $\{\mathrm{IDMTTF}\}$ families intersect each other. Moreover, [32] summarized the following interrelationships among the abovementioned classes of life distributions:

Here, $x^\prime$ , $\tau$ , $t_0$ , and $t_0^\prime$ denote the change points of F in BFRA, IDMRL, IDMTTF, and NWBUE senses respectively. If each of the classes in the preceding chain is replaced by its dual, the corresponding structure also holds. [46] and [12] both proved that a BFR family of twice-differentiable distributions is necessarily BFRA. Here we establish a general result that a BFRA family of distributions contains a BFR class of distributions, where we do not consider any assumptions like ‘twice differentiability of distribution F’. The following lemma plays a key role in establishing the main result.

Lemma 4.1. Suppose $y^*,y^{**}\in [0,\infty)$ and $g\colon[y^*,y^{**}]\rightarrow \mathbb{R}^+$ is a convex function. Let $A_g= \lbrace \alpha \mid g(y) = \alpha y \text{ has at least one solution in } [y^*,y^{**}] \rbrace$ . Now define

\begin{align*} \tilde{y}_1 & = \min \lbrace y \mid y \text{ is a solution of } g(y) = \tilde{\alpha}y \text{ in } [y^*,y^{**}] \rbrace , \\[5pt] \tilde{y}_2 & = \max \lbrace y \mid y \text{ is a solution of } g(y) = \tilde{\alpha}y \text{ in } [y^*,y^{**}] \rbrace , \end{align*}

where $\tilde{a}=\min A_g$ . Then:

1. (i) ${g(y)}/{y}$ is decreasing in y for all $y\in [y^*,y^{**}]$ if $\tilde{y}_2=y^{**}$ .

2. (ii) ${g(y)}/{y}$ is increasing in y for all $y\in [y^*,y^{**}]$ if $\tilde{y}_1=y^*$ .

3. (iii) ${f(y)}/{y}$ is decreasing in y for all $y\in [y^*,\tilde{y}]$ and increasing in y for all $y\in [\tilde{y},y^{**}]$ , where $\tilde{y}\in [\tilde{y}_1, \tilde{y}_2]$ if $y^*<\tilde{y_1}\leq \tilde{y_2}<y^{**}$ .

Proof. The proof is similar to the proof of [27, Lemma 1].

The following theorem is the main result of this section.

Theorem 4.1. If a life distribution F is BFR $(x^\prime)$ then F is BFRA $(x_0)$ , where $x^\prime\leq x_0$ .

Proof. There are three separate cases to consider.

Case (i): $x^\prime=0$ . In this case, F is IFR. [6] showed that IFR implies IFRA. Thus, F is BFRA with change point $x_0 =0$ .

Case (ii): $0<x^\prime<\infty$ . If F is BFR $(x^\prime)$ , then $R(x)=-\ln{\bar{F}(x)}$ is a positive concave function on $(0, x^\prime]$ . Hence, for all $x\in (0, x^\prime]$ and for $0< \beta< 1$ , $\ln{\bar{F}(\beta x)} = \ln{\bar{F}(\beta x+ \bar{\beta} 0)}$ , where $\bar{\beta}=1-\beta$ , i.e. $\ln{\bar{F}(\beta x)} \leq \beta \ln{\bar{F}(x)}$ , i.e. $\lbrace \bar{F}(\beta x)\rbrace^{{1}/{\beta x}} \leq \lbrace \bar{F}(x)\rbrace^{{1}/{x}}$ . Thus, $\lbrace \bar{F}(x)\rbrace^{{1}/{x}}$ is increasing in $x\in (0, x^\prime]$ , i.e. the FRA of F is decreasing on $(0, x^\prime]$ . Again, note that $R(x)=-\ln{\bar{F}(x)}$ is a positive convex function on $[x^\prime, \infty)$ , since F is a BFR distribution with a change point at $x^\prime$ . By using Lemma 4.1, the result follows immediately.

Case (iii): $x^\prime$ is a change point at $\infty$ . In this case, F is DFR. [6] showed that DFR implies DFRA. Thus, F is BFRA with a change point at infinity.

Note that [12, Example 2.1] indicates that the BFR class of life distributions is strictly smaller than the BFRA class. We now investigate the relationships between BFRA, IDMRL, IDMTTF, and NWBUE, since IDMRL, NWBUE and IDMTTF are larger classes of distributions than the BFR class.

In the next example we try to find the connection between the BFRA and IDMRL distribution classes.

Example 4.1. Consider the distribution function given by

\begin{equation*} F_2(x)= \begin{cases} 1 - \mathrm{e}^{-x}, & 0 \leq x < 1 , \\[3pt] 1 - (\mathrm{e} x)^{-1}, & 1 \leq x < 2 , \\[3pt] 1 - \frac{1}{2}\mathrm{e}^{-2}\exp\big[{-}\frac{1}{2}x(x-3)\big], & 2 \leq x < 3 , \\[3pt] 1 - \frac{1}{2}\mathrm{e}^{\frac{19}{4}}\exp\big[{-}\frac{1}{4}x(12-x)\big], & 3 \leq x < 3.5 , \\[3pt] 1 - \frac{1}{2}\mathrm{e}^{-\frac{1}{2}}\exp\big[{-}\frac{5}{28}x^2\big], & x \geq 3.5. \end{cases} \end{equation*}

It was shown in [12] that $F_2$ is a BFRA distribution. The change point $x_0$ in the BFRA sense turns out to be $2.320\,84$ . Note that the values $e_{F_2}(2.7) = 0.715\,849$ , $e_{F_2}(2.84) = 0.701\,676$ , and $e_{F_2}(3.1) = 0.704\,291$ clearly indicate that $F_2$ does not have the IDMRL property. A plot of the mean residual life (MRL) function $e_{F_2}(x)$ of $F_2$ is given in Figure 1.

Figure 1. Mean residual life function of $F_2$ .

Example 4.2. [4] considered an IDMRL distribution with change point 2 given by

\begin{equation*} F_3(x)= \begin{cases} 1 - (1+x)^{-2}, & 0 < x \leq 1 , \\[3pt] 1 - 4x^{-2}{\mathrm{e}^{(1-x)/2x}}, & 1 \leq x < 2 , \\[3pt] 1 - ({18-x})/({2^8 \mathrm{e}^{1/4}}), & 2 \leq x < 10 , \\[3pt] 1 - {\big(6-\frac{x}{5}\big)^4}/({2^{13} \mathrm{e}^{1/4}}), & 10 \leq x < 25 , \\[3pt] 1 - {2^{-13}}{\mathrm{e}^{3/4}}\exp[x-25-\mathrm{e}^{x-25}], & x \geq 25 . \end{cases} \end{equation*}

Let $r_{F_3}(t)$ be the FRA function of $F_3$ . The fact that $F_3$ is not BFRA is clear from the values $r_{F_3}(0.5) = 1.621\,86$ , $r_{F_3}(1) = 1.386\,29$ , $r_{F_3}(1.5) = 1.575\,93$ , and $r_{F_3}(3) = 1.029\,04$ . Figure 2 displays the FRA function of $F_3$ .

Figure 2. Failure rate average function of $F_3$ .

Examples 4.1 and 4.2 show that neither of the BFRA and IDMRL classes is contained in the other. Next, we investigate the connection between BFRA and NWBUE distributions.

Example 4.3. Consider the distribution function given by

\begin{equation*} F_4(x)= \begin{cases} 1 - ({1+2 x})^{-2}, & 0 \leq x < 2 , \\[3pt] \frac{24}{25}, & 2 \leq x < 3 , \\[3pt] 1 - \frac{9}{25}(2 x-3)^{-2}, & 3 \leq x < 4 , \\[3pt] 1 - \frac{9}{2500}x\exp[{({16-x^2})/{20}}], & x \geq 4. \end{cases} \end{equation*}

The MRL function of $F_4$ , given by

\begin{equation*} e_{F_4}(x)= \begin{cases} \frac{1}{2}({1+2 x}), & 0 \leq x < 2 , \\[5pt] \frac{1}{2}(9-2 x), & 2 \leq x < 3 , \\[5pt] \frac{1}{2}({x-3}), & 3 \leq x < 4 , \\[5pt] {10}{x}^{-1}, & x \geq 4, \end{cases} \end{equation*}

shows that $F_4$ is NWBUE with change point $t_0^\prime = 20$ in the NWBUE sense. The values $r_{F_4}(3) = 1.072\,96$ , $r_{F_4}(3.4) = 1.085\,78$ , and $r_{F_4}(4) = 1.060\,13$ illustrate that $F_4$ does not possess the BFRA property. A plot of the FRA function $r_{F_4}$ of $F_4$ is given in Figure 3.

Figure 3. Failure rate average function of $F_4$ .

Remark 4.1. Examples 4.1 and 4.2 show that neither of the BFRA and IDMRL classes is contained in the other. Moreover, Theorem 4.1 and [32, Theorem 16] show that BFRA and IDMRL classes of distributions contain all BFR distributions.

Remark 4.2. Theorem 4.1 and [47, Proposition 2.1] show that BFRA and NWBUE classes of distributions contain the BFR family of distributions. Now, from Example 4.3 we can conclude that either $\{\mathrm{BFRA}\} \subset \{\mathrm{NWBUE}\}$ or neither of the classes is contained in the other.

Remark 4.3. Theorem 4.1 and [27, Theorem 4] show that both BFRA and IDMTTF classes of distributions contain the BFR family.

From the remarks above it can be easily seen that the BFRA, IDMRL, NWBUE, and IDMTTF classes of distributions contain BFR distributions. Moreover, we are unable to establish any clear connection between IDMTTF and BFRA distributions. But at this juncture we would like to pose an open problem:

(4.1) \begin{equation}{If \, a \, life \, distribution} \, F \, {is \, BFRA}(x_0) \, {then} \, F \, {is \, IDMTTF}(t_0), \, {where} \, t_0 \geq x_0.\end{equation}

In the next theorem we have tried to provide a partial answer to (4.1) by following an argument similar to [52] that attempts to show that if F is IFRA then $\tau(u)/u$ is decreasing in u, where

(4.2) \begin{equation} \tau(u)=\int_0^{F^{-1}(u)}\bar{F}(x) \, \mathrm{d} x, \qquad u\in[0,1] ,\end{equation}

is the total-time-on-test (TTT) transform of F, and $F^{-1}(u)=\inf\lbrace x \colon F(x) \geq u \rbrace$ .

Theorem 4.2. Suppose an absolutely continuous lifetime distribution F is BFRA $(x_0)$ . Then the mean time to failure (MTTF) function is increasing on $(0,x_0]$ .

Proof. In order to prove this theorem we first assume that F is absolutely continuous with respect to Lebesgue measure, and later we extend the argument to the ‘continuous’ case. Note that the MTTF function $M_F(t)$ of F can be written as

\begin{align*} M_F(t) = \frac{\int_0^t \bar{F}(x) \, \mathrm{d} x}{\int_0^t \lambda(x)\bar{F}(x) \, \mathrm{d} x}, \end{align*}

since F is absolutely continuous with respect to Lebesgue measure. Now the numerator of $\frac{\mathrm{d}}{\mathrm{d} t} M_F(t)$ is given by

\begin{equation*} Q(t) = \bar{F}(t) \int_0^t \lambda(x)\bar{F}(x) \, \mathrm{d} x - \lambda(t)\bar{F}(t) \int_0^t \bar{F}(x) \, \mathrm{d} x \nonumber = \bar{F}(t) \int_0^t [ \lambda(x) - \lambda(t) ] \bar{F}(x) \, \mathrm{d} x . \nonumber \end{equation*}

Thus, to prove this theorem it is enough to show that $S(t)=\int_0^t[ \lambda(x) - \lambda(t)] \bar{F}(x) \, \mathrm{d} x \geq 0$ for $t \leq x_0$ . Using integration by parts, S(t) can be written as

\begin{equation*} S(t) = \bigg[\frac{-\ln{\bar{F}(t)}}{t} - \lambda(t) \bigg]t\bar{F}(t) + \int_0^t\bigg[\frac{-\ln{\bar{F}(x)}}{x} - \lambda(t) \bigg] x \, \mathrm{d} \bar{F}(x) . \end{equation*}

Note that, for all $t\leq x_0$ ,

\begin{equation*} S(t) \geq \bigg[\frac{-\ln{\bar{F}(t)}}{t} - \lambda(t) \bigg] \bigg[ t\bar{F}(t) + \int_0^t x \, \mathrm{d} \bar{F}(x) \bigg] \nonumber \geq 0 , \end{equation*}

since $({-\!\ln{\bar{F}(t)}})/{t}$ is decreasing on $(0, x_0]$ . Thus, $M_F(t)$ is increasing on $(0,x_0]$ .

At this stage, the following hierarchy represents the updated interrelationships among the non-monotonic ageing classes.

5. Discussion

The main contributions of this paper center around the homogeneous Poisson shock model in the framework of BFRA distributions, weak convergence issues within the BFRA class, and interrelationships among non-monotonic ageing classes. However, there is substantial scope for future work, for example, non-homogeneous Poisson shock models and pure birth shock models for the BFRA class remain to be explored. Further, in this scenario we can also consider shock models in a more general setup where failure occurs due to shocks in the presence of continuous wear and tear.

In Section 3 we posed the open problem (4.1). The TTT transform, defined in (4.2), plays an important role in characterizing ageing classes of life distributions (see [36]). Thus, (4.1) has the following equivalent formulation in terms of the TTT transform: ‘If F is BFRA then there exists $\tilde{u}\in [0,1]$ such that $\tau(x)/x$ is increasing on $[0,\tilde{u}]$ and decreasing on $(\tilde{u},1]$ .’ In this regard, the following comments would be in order. We believe that the result contained in (4.1) is true. In fact, the distribution in Example 4.1 (due to [12]) is BFRA with change point $2.320\,84$ and IDMTTF with change point $2.404\,25$ $(\!>\!2.320\,84)$ , as can be seen from Figure 4.

Figure 4. Mean time to failure function of $F_2$ .

If, indeed, that result does hold, then the hierarchy would turn out as follows: