Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-15T16:26:49.254Z Has data issue: false hasContentIssue false
  • English
  • Français

An Analytical Comparison of Variance and Semivariance Capital Market Theories

Published online by Cambridge University Press:  06 April 2009

Timothy J. Nantell  and
Barbara Price
Get access Rights & Permissions [Opens in a new window]

Extract

Most research in modern portfolio theory and capital market theory is based on investor selection of portfolios that are efficient in the sense that they are not dominated by other portfolios in terms of their risk-expected return characteristics. The most widely used measure of portfolio risk is the variance about the mean of the exante distribution of portfolio returns. The theoretical framework from which this measure of risk is usually derived was initially suggested by Markowitz [12], and is by now well known. Although variance has the attention of most researchers, another measure, semivariance, had some early support from Markowitz himself, and from Quirk and Saposnik [17], Mao [10], and others. Semivariance as a measure of risk can be derived from the same theoretical framework as is variance; it requires only a slightly different utility function. The semivariance of returns of portfolio p below some point h is defined as

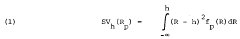
where fp (R) represents the probability density function of returns for portfolio p. Semivariance portfolio theory is enjoying something of a revival in the works of Porter [15, 16], Hogan and Warren [6] and Klemkosky [8], and semivariance capital market models have been developed by Hogan and Warren [7] and Greene [5].

Type
Research Article
Information
Journal of Financial and Quantitative Analysis , Volume 14 , Issue 2 , June 1979 , pp. 221 - 242
Copyright
Copyright © School of Business Administration, University of Washington 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bateman Manuscript Project edited by Erdelyi, A. et al. , Tables of Integral Transforms, Vol. 1. N.Y.: McGraw-Hill (1954).Google Scholar
[2]Baumol, W. J. “An Expected Gain-Confidence Limit Criterion for Portfolio Selection”. Management Science (10 1963).CrossRefGoogle Scholar
[3]Fama, Eugene F., and Miller, Merton. The Theory of Finance. N.Y.: Holt, Rinehart and Winston (1972).Google Scholar
[4]Gradshteyn, I. S., and Ryzhik, I. M.. Table of Integrals, Series, and Products, 4th ed.N.Y.: Academic Press (1965).Google Scholar
[5]Greene, James B. “A Mean-Semivariance Capital Asset Pricing Model”. Unpublished Ph.D. dissertation, University of Michigan (1975).Google Scholar
[6]Hogan, W. W., and Warren, J. M.. “Computation of the Efficient Boundary in the E-S Portfolio Selection Model”. Journal of Financial and Quantitative Analysis (05 1970), pp. 349–60.Google Scholar
[7]Hogan, W. W., and Warren, J. M.. “Toward the Development of an Equilibrium Capital-Market Model Based on Semivariance”. Journal of Financial and Quantitative Analysis (01 1974), pp. 1–11.CrossRefGoogle Scholar
[8]Klemkosky, Robert. “The Bias in Composite Performance Measures”. Journal of Financial and Quantitative Analysis (06 1973), pp. 505–14.CrossRefGoogle Scholar
[9]Kraus, Alan, and Litzenberger, Robert H.. “Skewness Preference and the Valuation of Risk Assets”. Journal of Finance (12 1976).CrossRefGoogle Scholar
[10]Mao, J. C. T. “Models of Capital Budgeting, E-V versus E-S”. Journal of Financial and Quantitative Analysis (01 1970), pp. 657– 75.CrossRefGoogle Scholar
[11]Mao, J. C. T.. “Survey of Capital Budgeting: Theory and Practice”. Journal of Finance (05 1970), pp. 349–60.CrossRefGoogle Scholar
[12]Markowitz, H. M.Portfolio Selection. N. Y.: John Wiley and Sons, Inc. (1959).Google Scholar
[13]McEnally, R. W. “A Note on the Behavior of High Risk Common Stock”. Journal of Finance (03 1974).CrossRefGoogle Scholar
[14]Nantell, Timothy J., and Greene, James B.. “Semivariance: Portfolio Theory and Capital Market Theory”. Presented at 1974 meetings of Western Finance Association.Google Scholar
[15]Porter, R. Burr. “Semivariance and Stochastic Dominance: A Comparison”. The American Economic Review (03 1974), pp. 200–4.Google Scholar
[10]Porter, R. Burr; Bey, Roger; and Lewis, David. “The Development of a Mean-Semivariance Approach to Capital Budgeting.” Journal of Financial and Quantitative Analysis (11 1975).CrossRefGoogle Scholar
[17]Quirk, J. P., and Saposnik, R.. “Admissability and Measurable Utility Functions”. Review of Economic Studies (02 1962), pp. 140–46.CrossRefGoogle Scholar
[18]Sharpe, W. F. “Capital Asset Prices: A Theory of Market Equilibrium Under Conditions of Risk”. Journal of Finance (09 1964).CrossRefGoogle Scholar
[10]Swalm, R. O. “Utility Theory—Insights into Risk Taking”. Harvard Business Review (12 1966).Google Scholar