Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-15T14:32:14.842Z Has data issue: false hasContentIssue false
  • English
  • Français

A Model of Capital Asset Risk

Published online by Cambridge University Press:  19 October 2009

R. Richardson Pettit  and
Randolph Westerfield
Get access Rights & Permissions [Opens in a new window]

Extract

The “market model” of capital asset pricing theory posits that the oneperiod return on an asset is a linear function of the one-period return on a “market factor” plus the effect of factors that are unique to that asset. The coefficients of the model, estimated using realized returns, can be used for predicting asset returns conditional on market returns, and the slope or “beta” coefficient provides an estimate of the asset's risk. Although the market model has been applied to a wide variety of capital market studies and is now being applied by practitioners for assessing asset risk, very little research has been undertaken to discover the determinants of the beta coefficient.

Type
Research Article
Information
Journal of Financial and Quantitative Analysis , Volume 7 , Issue 2 , March 1972 , pp. 1649 - 1668
Copyright
Copyright © School of Business Administration, University of Washington 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Beaver, , Kettler, , and Scholes, , “The Association between Market Determined and Accounting Determined Risk Measures,” The Accounting Review (October 1970)Google Scholar, examined the degree of association between various accounting ratios and the beta coefficient of the market model.

2 See Blume, M., “Portfolio Theory: A Step towards Its Practical Application,” Journal of Business. (April 1970) and “On the Assessment of Risk,” Journal of Finance (March 1971).Google Scholar

3 To show how equation (2) was derived consider the following perpetuity discounted cash flow valuation model:

(a)

Pi is the price of the ith asset, in this case a share of common stock issued by the ith firm. Although equation (a) is a simplification of a more complex valuation model, it incorporates two important variables always considered in asset price determination; namely, espected cash and the rate at which expected cash flows are capitalized. A small, unanticipated change in the asset's market price, dPi, can be represented as the differential equation:

(b)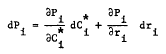

or, evaluating the partial derivatives,

(c)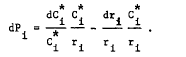

The realized rate of return from holding asset i is defined as:

(d)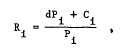

where, from the investor's viewpoint, Ci. is the anticipated dividends plus capital gains generated and will equal expected cash flows C*. The value of dPi. is the realized but unanticipated (windfall) gains attributable to changes in actual cash flows generated by the firm, changes in expected future cash flows, and changes in the rate at which these cash flows are discounted.

Substituting equation (c) into (d) and assuming that the elasticity of expected cash flows with respect to reported cash flows is unity (a much more restrictive assumption than is necessary), the realized rate of return, Rj, on asset i can be expressed in terms of changes in its realized cash flows and changes in its capitalization rate as shown in equation (2). It's important to remember that, given our assumption about the elasticity of expected cash flows, .

4 The assumption is made that there is a valuation equation for the market asset given by 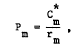and that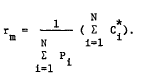

Then the derivation of Rm can proceed in exactly the same way as Ri was derived in footnote 3.

5 Rie, Daniel, “Preliminary Test of a Theory of Market Returns When Capitalization Rates Are Variable” (unpublished manuscript, Wharton School of Finance and Commerce, University of Pennsylvania, 1970).Google Scholar

6 Equation (3) appears to be equivalent to a version of a model developed by Rie, “Preliminary Test.” Rie shows that prediction error of the market model can be traced to two kinds of macroeconomic variables. Rie was the first to introduce the terminology of a cash flow variable and a capitalization rate variable. Also, Michael Brennan, in “Capital Asset Pricing and the Structure of Security Returns” (unpublished manuscript, University of British Columbia, 1970) has shown that the prediction error of the market model is associated with two factors, using a factor analytic technique.

7 Equation (4) can be derived easily by expressing the market model beta coefficient as

where COV(Ri, Rm) is the covariance between the returns on asset i and the market factor, and VARm (Rm) is the variance of the returns on the market factor. If definitions (2a) and (2b) are substituted into equation (a) and if all cross-product terms have zero expectation, then,

(b)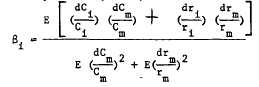

and equation (b) can be rewritten as equation (4) in the text.

8 The Fisher Index is an equally weighted index of returns on all New York Stock Exchange securities during that period. An investment relative is defined as an assets end-of-period price plus dividends in the period divided by the price at the beginning of the period.

9 Writers in the theory of finance have often assumed that growth and risk are positively related. For examples, see Lerner, E. M. and Carleton, W. T., A Theory of Financial Analysis (New York: Harcourt, Brace & World, Inc., 1966), p. 114Google Scholar, and Gordon, Myron, “Optimal Investment and Financing Policy,” Journal of Finance (May 1963), p. 267.Google Scholar

10 The estimates for OLS will be biased downwards and will be inconsistent. For a proof see Johnson, J., Econometric Methods (New York: McGraw Hill Book Co., 1963), Chapter 6. The one necessary condition is that measurement errors be independently distributed.Google Scholar

11 A similar kind of grouping technique has been used in Beaver, Kettler, and Scholes, “Association” and Brennan, “Capital Asset Pricing.”

12 The discussion implies our belief that the payout ratio is an endogenous variable at least partially dependent on growth expectations. Thus the model as developed here is not correctly identified, resulting in a biased coefficient for the payout variable. Time has prevented the two stage approach that would give an unbiased estimate of coefficient and its standard error.

13 The economic interpretation of the constant term given in the previous section becomes irrelevant when payout and growth are added as explanatory variables.

14 “The result is not inconsistent with studies that have found a strong relation between growth and the price-earnings ratio. However, a strong relation between P/E and growth confounds the effect of growth expectations with the effect of risk on the P/E ratio. What our results say is that the relation between growth and P/E is unrelated to risk because growth and risk are unrelated.