Article contents
Benjamin’s gravity current into an ambient fluid with an open surface in a channel of general cross-section
Published online by Cambridge University Press: 27 November 2018
Abstract
We present the solution of the idealized steady-state gravity current of height  $h$ and density
$h$ and density 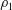 $\unicode[STIX]{x1D70C}_{1}$ that propagates into an ambient motionless fluid of height
$\unicode[STIX]{x1D70C}_{1}$ that propagates into an ambient motionless fluid of height 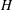 $H$ and density
$H$ and density 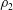 $\unicode[STIX]{x1D70C}_{2}$ in a channel of general non-rectangular cross-section, with an upper surface open to the atmosphere, at high Reynolds number. The current propagates with speed
$\unicode[STIX]{x1D70C}_{2}$ in a channel of general non-rectangular cross-section, with an upper surface open to the atmosphere, at high Reynolds number. The current propagates with speed 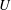 $U$ and causes a depth decrease
$U$ and causes a depth decrease  $\unicode[STIX]{x1D712}$ of the top surface. This is a significant extension of Benjamin’s (J. Fluid Mech., vol. 31, 1968, pp. 209–248) seminal solution for the gravity current in a rectangular (or laterally unbounded) channel with a fixed top (
$\unicode[STIX]{x1D712}$ of the top surface. This is a significant extension of Benjamin’s (J. Fluid Mech., vol. 31, 1968, pp. 209–248) seminal solution for the gravity current in a rectangular (or laterally unbounded) channel with a fixed top (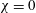 $\unicode[STIX]{x1D712}=0$). The determination of
$\unicode[STIX]{x1D712}=0$). The determination of 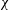 $\unicode[STIX]{x1D712}$ is a part of the problem. Supposing that the direction of propagation is
$\unicode[STIX]{x1D712}$ is a part of the problem. Supposing that the direction of propagation is  $x$ and gravity acceleration
$x$ and gravity acceleration 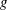 $g$ acts in the
$g$ acts in the  $-z$ direction, the sidewalls are specified by
$-z$ direction, the sidewalls are specified by 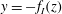 $y=-f_{I}(z)$ and
$y=-f_{I}(z)$ and  $y=f_{II}(z),~z\in [0.H]$, and the width is
$y=f_{II}(z),~z\in [0.H]$, and the width is 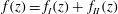 $f(z)=f_{I}(z)+\,f_{II}(z)$. The dimensionless parameters of the problem are
$f(z)=f_{I}(z)+\,f_{II}(z)$. The dimensionless parameters of the problem are 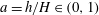 $a=h/H\in (0,1)$ and
$a=h/H\in (0,1)$ and 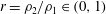 $r=\unicode[STIX]{x1D70C}_{2}/\unicode[STIX]{x1D70C}_{1}\in (0,1)$. We show that a control-volume analysis of the type used by Benjamin produces a system of algebraic equations for
$r=\unicode[STIX]{x1D70C}_{2}/\unicode[STIX]{x1D70C}_{1}\in (0,1)$. We show that a control-volume analysis of the type used by Benjamin produces a system of algebraic equations for  $\tilde{\unicode[STIX]{x1D712}}=\unicode[STIX]{x1D712}/H$ and
$\tilde{\unicode[STIX]{x1D712}}=\unicode[STIX]{x1D712}/H$ and 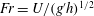 $Fr=U/(g^{\prime }h)^{1/2}$ as functions of
$Fr=U/(g^{\prime }h)^{1/2}$ as functions of  $a$ and
$a$ and  $r$, where
$r$, where  $g^{\prime }=(r^{-1}-1)g$ is the reduced gravity. The geometry enters the equation via the width function
$g^{\prime }=(r^{-1}-1)g$ is the reduced gravity. The geometry enters the equation via the width function 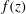 $f(z)$. We present solutions for typical
$f(z)$. We present solutions for typical 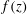 $f(z)$: rectangle, semi-circle,
$f(z)$: rectangle, semi-circle, 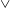 $\vee$ triangle and trapezoid
$\vee$ triangle and trapezoid 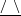 $\text{}\underline{/~\backslash }$ . The results are physically acceptable and insightful. The non-negative dissipation condition defines the domain of validity
$\text{}\underline{/~\backslash }$ . The results are physically acceptable and insightful. The non-negative dissipation condition defines the domain of validity 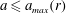 $a\leqslant a_{max}(r)$ (also depending on
$a\leqslant a_{max}(r)$ (also depending on  $f(z)$); the equality sign corresponds to energy-conserving cases. The critical speed limitation (with respect to the characteristics) is also considered briefly and suggests a slightly smaller
$f(z)$); the equality sign corresponds to energy-conserving cases. The critical speed limitation (with respect to the characteristics) is also considered briefly and suggests a slightly smaller 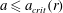 $a\leqslant a_{crit}(r)$. The open-top results in the Boussinesq limit
$a\leqslant a_{crit}(r)$. The open-top results in the Boussinesq limit 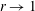 $r\rightarrow 1$ coincide with the fixed-top solution. Upon the reduction of
$r\rightarrow 1$ coincide with the fixed-top solution. Upon the reduction of  $r$, for a fixed thickness
$r$, for a fixed thickness  $a$, the value of
$a$, the value of 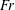 $Fr$ decreases and
$Fr$ decreases and 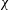 $\unicode[STIX]{x1D712}$ increases, until the point of energy-conserving (non-dissipative) flow; for smaller
$\unicode[STIX]{x1D712}$ increases, until the point of energy-conserving (non-dissipative) flow; for smaller  $r$, a negative non-physical dissipation appears. The trends are more pronounced for a converging cross-section geometry (like
$r$, a negative non-physical dissipation appears. The trends are more pronounced for a converging cross-section geometry (like 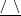 $\text{}\underline{/~\backslash }$ ) than for the opposite shape (like
$\text{}\underline{/~\backslash }$ ) than for the opposite shape (like 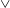 $\vee$ triangle). The previously investigated Benjamin-type steady-state
$\vee$ triangle). The previously investigated Benjamin-type steady-state 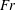 $Fr$ and dissipation results are particular cases of the new formulation:
$Fr$ and dissipation results are particular cases of the new formulation: 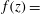 $f(z)=$ const. reproduces the two-dimensional results, and
$f(z)=$ const. reproduces the two-dimensional results, and 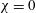 $\unicode[STIX]{x1D712}=0$ recovers the fixed-top solution.
$\unicode[STIX]{x1D712}=0$ recovers the fixed-top solution.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 2
- Cited by

