Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhou, Xingyu
Zuo, Jingying
Li, Xin
Zhang, Silong
Qin, Jiang
and
Bao, Wen
2022.
Thermal behavior of supercritical CO2 inside scramjet cooling channels with different structural parameters.
Applied Thermal Engineering,
Vol. 217,
Issue. ,
p.
119153.
Zhang, Junqiang
Zou, Zhengping
and
Wang, Yifan
2022.
Large-Eddy Simulation on the Aerodynamic and Thermal Characteristics in a Micropipe of the Hypersonic Engine Precooler.
Micromachines,
Vol. 13,
Issue. 4,
p.
637.
Wang, Yusen
Cheng, Yuxiang
Li, Minghao
Jiang, Peixue
and
Zhu, Yinhai
2022.
Online measurement of mean residence time of supercritical-pressure fluid with/without chemical reaction in pipe flow: A particle image statistics method considering optical distortion and radial uneven distribution of tracer particles.
Chemical Engineering Science,
Vol. 258,
Issue. ,
p.
117772.
Cinnella, P.
and
Gloerfelt, X.
2023.
Insights into the turbulent flow of dense gases through high-fidelity simulations.
Computers & Fluids,
Vol. 267,
Issue. ,
p.
106067.
Kumar, Nitesh
and
Basu, Dipankar N.
2023.
Thermalhydraulic assessment and design optimization of incorporating flow obstructors in a supercritical minichannel heat sink.
Applied Energy,
Vol. 349,
Issue. ,
p.
121666.
Wang, Yusen
Zhu, Yinhai
Cheng, Yuxiang
and
Jiang, Pei-Xue
2023.
Heat and mass transfer correlations of supercritical n-decane considering the influence of pyrolysis reaction by simplifying internal heat and mass sources as pseudo-wall fluxes.
International Journal of Heat and Mass Transfer,
Vol. 217,
Issue. ,
p.
124636.
Wu, Dingchen
Wei, Mingshan
He, Jundi
He, Shuisheng
and
Tian, Ran
2023.
Direct numerical simulations of cooling flow and heat transfer in supercritical CO2 Brayton cycle coupled with solar energy.
Applied Thermal Engineering,
Vol. 230,
Issue. ,
p.
120790.
Cao, Yuli
Xu, Ruina
and
Jiang, Peixue
2023.
Physics-informed machine learning based RANS turbulence modeling convection heat transfer of supercritical pressure fluid.
International Journal of Heat and Mass Transfer,
Vol. 201,
Issue. ,
p.
123622.
He, Shuisheng
2023.
NEW INSIGHT INTO HEAT TRANSFER DETERIORATION.
p.
15.
Zhang, Junqiang
Zou, Zhengping
and
Fu, Chao
2023.
A Review of the Complex Flow and Heat Transfer Characteristics in Microchannels.
Micromachines,
Vol. 14,
Issue. 7,
p.
1451.
Cao, Yuli
Xu, Ruina
He, S.
and
Jiang, Peixue
2023.
Accelerating turbulence in heated micron tubes at supercritical pressure.
Journal of Fluid Mechanics,
Vol. 972,
Issue. ,
Zhang, Xirui
Shao, Qihan
Liu, Jian
Xi, Wenxiong
Liu, Chaoyang
and
Sunden, Bengt
2024.
Recent Development of Heat Transfer and Fluid Flow of Supercritical CO2 in Tubes: Mechanisms and Applications.
Journal of Thermal Science,
Vol. 33,
Issue. 6,
p.
2274.
Zeng, Gang
Chen, Lin
Yang, Dong
Yuan, Haizhuan
Zang, Jinguang
and
Huang, Yanping
2024.
Measurement and comparison of transient thermal boundary layer of a Local-Heated Mini-Channel under sub- and super-critical conditions.
Applied Thermal Engineering,
Vol. 247,
Issue. ,
p.
123053.
Bai, Yifan
Wang, Han
Liu, Minyun
Wu, Jinghui
Lyu, Haicai
and
Huang, Yanping
2024.
Direct numerical simulation of flow and heat transfer of supercritical water with different heat fluxes.
International Journal of Heat and Mass Transfer,
Vol. 221,
Issue. ,
p.
125132.
Yuan, Baoqiang
Wang, Wei
Xin, Gongming
and
Du, Wenjing
2024.
Numerical Analysis of Heat Transfer Characteristics to Supercritical CO2 in a Vertical Mini-Channel: Transition and Pseudo-Boiling.
Journal of Thermal Science,
Vol. 33,
Issue. 1,
p.
101.
Zhou, Xingyu
Zhang, Silong
Li, Xin
Zuo, Jingying
Wei, Jianfei
and
Wang, Heyang
2024.
Numerical study on thermal–hydraulic performance of hydrocarbon fuel under trans-critical states and supercritical CO2 in a zigzag printed circuit heat exchanger.
Applied Thermal Engineering,
Vol. 236,
Issue. ,
p.
121496.
Yuan, Baoqiang
Wang, Wei
and
Du, Wenjing
2024.
Assessment of advanced RANS models to predict the heat transfer for supercritical fluids in vertical tubes.
International Journal of Heat and Mass Transfer,
Vol. 219,
Issue. ,
p.
124829.
Chou, Che-Yen
Kuo, Geng-Chun
and
Chueh, Chih-Che
2024.
Numerical analysis of thermal-hydraulic influence of geometric flow baffles on multistage Tesla valves in printed circuit heat exchangers.
Applied Thermal Engineering,
Vol. 251,
Issue. ,
p.
123601.
Wang, Haodong
Xu, Ruina
Jiang, Peixue
and
Wang, Chao
2024.
Investigation on heat transfer enhancement of supercritical hydrocarbon fuel in rotating channel interpolated with spiral wire.
Applied Thermal Engineering,
Vol. 248,
Issue. ,
p.
123151.
Xiao, Mingfei
Ren, Yangjian
Yang, Junjiao
and
Hu, Zhan-Chao
2024.
Turbulent Rayleigh–Bénard convection in a supercritical CO2-based binary mixture with cross-diffusion effects.
International Journal of Heat and Mass Transfer,
Vol. 228,
Issue. ,
p.
125648.
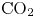 $\textrm {CO}_2$ in a vertical tube with buoyancy and thermal acceleration effects
$\textrm {CO}_2$ in a vertical tube with buoyancy and thermal acceleration effects
 $\textrm {CO}_2$ in a small vertical tube influenced by coupled effects of buoyancy and thermal acceleration are numerically investigated using direct numerical simulation. Both upward and downward flows with an inlet Reynolds number of 3540 and pressure of 7.75 MPa have been simulated and the results are compared with corresponding experimental data. The flow and heat transfer results reveal that under buoyancy and thermal acceleration, the turbulent flow and heat transfer exhibit four developing periods in which buoyancy and thermal acceleration alternately dominate. The results suggest a way to distinguish the dominant factor of heat transfer in different periods and a criterion for heat transfer degradation under the complex coupling of buoyancy and thermal acceleration. An analysis of the orthogonal decomposition and the generative mechanism of turbulent structures indicates that the flow acceleration induces a stretch-to-disrupt mechanism of coherent turbulent structures. The significant flow acceleration can destroy the three-dimensional flow structure and stretch the vortices resulting in dissipation.
$\textrm {CO}_2$ in a small vertical tube influenced by coupled effects of buoyancy and thermal acceleration are numerically investigated using direct numerical simulation. Both upward and downward flows with an inlet Reynolds number of 3540 and pressure of 7.75 MPa have been simulated and the results are compared with corresponding experimental data. The flow and heat transfer results reveal that under buoyancy and thermal acceleration, the turbulent flow and heat transfer exhibit four developing periods in which buoyancy and thermal acceleration alternately dominate. The results suggest a way to distinguish the dominant factor of heat transfer in different periods and a criterion for heat transfer degradation under the complex coupling of buoyancy and thermal acceleration. An analysis of the orthogonal decomposition and the generative mechanism of turbulent structures indicates that the flow acceleration induces a stretch-to-disrupt mechanism of coherent turbulent structures. The significant flow acceleration can destroy the three-dimensional flow structure and stretch the vortices resulting in dissipation.