Article contents
Dynamic transition from Mach to regular reflection of shock waves in a steady flow
Published online by Cambridge University Press: 09 June 2014
Abstract
The steady, two-dimensional transition criteria between regular and Mach reflection are well established. Little has been done on the dynamic effect on transition due to a rapidly rotating wedge. Results from experiments and computations done on steady and unsteady shock wave transition from Mach reflection to regular reflection, MR  $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\rightarrow $ RR, are described. The measured motion and the initial shock incidence was used to mimic the experiment with a two-dimensional numerical code. The maximum rotation speed achieved at transition was approximately
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\rightarrow $ RR, are described. The measured motion and the initial shock incidence was used to mimic the experiment with a two-dimensional numerical code. The maximum rotation speed achieved at transition was approximately 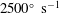 $2500^\circ \ {\mathrm{s}}^{-1}$. Rapid wedge rotation was shown to have a significant measurable effect on transition. The code was also applied to the dependence of dynamic MR
$2500^\circ \ {\mathrm{s}}^{-1}$. Rapid wedge rotation was shown to have a significant measurable effect on transition. The code was also applied to the dependence of dynamic MR  $\rightarrow $ RR transition on other variables in the parameter space. These include rotation about the leading or trailing edge, initial incidence and rotation speed at two free-stream conditions. Impulsively started rotation in these cases was used with the rotation specified by
$\rightarrow $ RR transition on other variables in the parameter space. These include rotation about the leading or trailing edge, initial incidence and rotation speed at two free-stream conditions. Impulsively started rotation in these cases was used with the rotation specified by 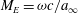 $M_E = \omega c/a_{\infty }$ where
$M_E = \omega c/a_{\infty }$ where 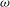 $\omega $ is constant angular velocity (negative anticlockwise),
$\omega $ is constant angular velocity (negative anticlockwise),  $c$ the distance from the edge considered to the pivot point and
$c$ the distance from the edge considered to the pivot point and 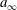 $a_{\infty }$ the free-stream sound speed. For the Mach numbers and range of rotation speeds tested, both the wedge and shock angle at transition decreased with increased rotation speed. The sensitivity of the transition angle to changing the rotation point from the trailing edge to the experimental model pivot point was investigated briefly at a free-stream Mach number of
$a_{\infty }$ the free-stream sound speed. For the Mach numbers and range of rotation speeds tested, both the wedge and shock angle at transition decreased with increased rotation speed. The sensitivity of the transition angle to changing the rotation point from the trailing edge to the experimental model pivot point was investigated briefly at a free-stream Mach number of 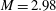 $M = 2.98$ with
$M = 2.98$ with 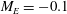 $M_E = -0.1$. The wedge angle at transition increased by 1.5° and the shock angle at transition decreased by 1.5°, a significant variation. The effect of the initial incidence was also investigated. By reducing the initial wedge angle from 24.5 to 23.5° for these initial conditions the shock angle at transition decreased by approximately 1.8°, also a marked sensitivity. The flow field development for impulsive rotation about the wedge trailing and leading edges at
$M_E = -0.1$. The wedge angle at transition increased by 1.5° and the shock angle at transition decreased by 1.5°, a significant variation. The effect of the initial incidence was also investigated. By reducing the initial wedge angle from 24.5 to 23.5° for these initial conditions the shock angle at transition decreased by approximately 1.8°, also a marked sensitivity. The flow field development for impulsive rotation about the wedge trailing and leading edges at 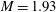 $M = 1.93$ for
$M = 1.93$ for 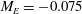 $M_E = -0.075$ was analysed in some detail. The flow field development is very sensitive to the rotation centre, more especially at large rotation rates. Four phases of the Mach stem development were identified in both cases. For rotation about the wedge leading edge the Mach stem height remains constant until the expansion waves arrive at the triple point. This is followed by an increase in Mach stem height, which then remains constant for a short period after which it decreases until transition to RR. For rotation about the wedge trailing edge the impulsive start generates a disturbance on the incident wave which propagates down the wave, through the triple point and down the Mach stem. The stem height is constant until the arrival of the incident wave disturbance. This causes a sudden decrease in Mach stem height. Subsequently, the Mach stem height remains constant for a short time, before it decreases until transition to RR. Similar effects in the variation of stem height with wedge angle occur at the higher Mach number of 2.98. It was demonstrated that MR can be maintained for a while at zero wedge incidence with a sufficiently large rotation rate of
$M_E = -0.075$ was analysed in some detail. The flow field development is very sensitive to the rotation centre, more especially at large rotation rates. Four phases of the Mach stem development were identified in both cases. For rotation about the wedge leading edge the Mach stem height remains constant until the expansion waves arrive at the triple point. This is followed by an increase in Mach stem height, which then remains constant for a short period after which it decreases until transition to RR. For rotation about the wedge trailing edge the impulsive start generates a disturbance on the incident wave which propagates down the wave, through the triple point and down the Mach stem. The stem height is constant until the arrival of the incident wave disturbance. This causes a sudden decrease in Mach stem height. Subsequently, the Mach stem height remains constant for a short time, before it decreases until transition to RR. Similar effects in the variation of stem height with wedge angle occur at the higher Mach number of 2.98. It was demonstrated that MR can be maintained for a while at zero wedge incidence with a sufficiently large rotation rate of 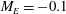 $M_E = -0.1$, with
$M_E = -0.1$, with 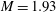 $M=1.93$, for both leading and trailing edge pivot points.
$M=1.93$, for both leading and trailing edge pivot points.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 11
- Cited by


