Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T15:04:25.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamical similarity and universality of drop size and velocity spectra in sprays

Published online by Cambridge University Press:  07 December 2018

K. Dhivyaraja ,
D. Gaddes ,
E. Freeman ,
S. Tadigadapa  and
M. V. Panchagnula Open the ORCID record for M. V. Panchagnula [Opens in a new window]
K. Dhivyaraja
Affiliation:
Department of Applied Mechanics, National Centre for Combustion Research and Development, Indian Institute of Technology Madras, Chennai 600036, India
D. Gaddes
Affiliation:
Department of Electrical Engineering, Pennsylvania State University, University Park, PA 16802, USA
E. Freeman
Affiliation:
Department of Electrical Engineering, Pennsylvania State University, University Park, PA 16802, USA
S. Tadigadapa
Affiliation:
Department of Electrical Engineering, Pennsylvania State University, University Park, PA 16802, USA
M. V. Panchagnula*
Affiliation:
Department of Applied Mechanics, National Centre for Combustion Research and Development, Indian Institute of Technology Madras, Chennai 600036, India
*
†Email address for correspondence: mvp@iitm.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Sprays are a class of multiphase flows which exhibit a wide range of drop size and velocity scales spanning several orders of magnitude. The objective of the current work is to experimentally investigate the prospect of dynamical similarity in these flows. We are also motivated to identify a choice of length and time scales which could lead towards a universal description of the drop size and velocity spectra. Towards this end, we have fabricated a cohort of geometrically similar pressure swirl atomizers using micro-electromechanical systems (MEMS) as well as additive manufacturing technology. We have characterized the dynamical characteristics of the sprays as well as the drop size and velocity spectra (in terms of probability density functions, p.d.f.s) over a wide range of Reynolds ($Re$) and Weber numbers (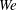$We$) using high-speed imaging and phase Doppler interferometry, respectively. We show that the dimensionless Sauter mean diameter (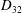$D_{32}$) scaled to the boundary layer thickness in the liquid sheet at the nozzle exit (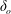$\unicode[STIX]{x1D6FF}_{o}$) exhibits self-similarity in the core region of the spray, but not in the outer zone. In addition, we show that global drop size spectra in the sprays show two distinct characteristics. The spectra from varying 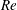$Re$ and 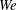$We$ collapse onto a universal p.d.f. for drops of size $x$ where 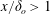$x/\unicode[STIX]{x1D6FF}_{o}>1$. For 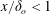$x/\unicode[STIX]{x1D6FF}_{o}<1$, a residual effect of 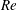$Re$ and 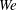$We$ persists in the size spectra. We explain this characteristic by the fact that the physical mechanisms that cause large drops is different from that which is responsible for the small drops. Similarly, with the liquid sheet velocity at the nozzle exit (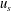$u_{s}$) as the choice of velocity scale, we show that drops moving with a velocity $u$ such that 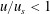$u/u_{s}<1$ collapse onto a universal p.d.f., while drops with 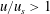$u/u_{s}>1$ exhibit a residual effect of 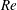$Re$ and 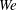$We$. From these observations, we suggest that physically accurate models for drop size and velocity spectra should rely on piecewise descriptions of the p.d.f. rather than invoking a single mathematical form for the entire distribution. Finally, we show from a dynamical modal analysis that the conical liquid sheet flapping characteristics exhibit a sharp transition in Strouhal number (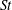$St$) at a critical 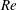$Re$.

JFM classification

Drops and Bubbles: Aerosols/atomization Drops and Bubbles: Drops Micro-/Nano-fluid dynamics: MEMS/NEMS
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 860 , 10 February 2019 , pp. 510 - 543
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alter, O., Brown, P. O. & Botstein, D. 2000 Singular value decomposition for genome-wide expression data processing and modeling. Proc. Natl Acad. Sci. USA 97 (18), 10101–10106.Google Scholar
Amini, G. 2016 Liquid flow in a simplex swirl nozzle. Intl J. Multiphase Flow. 79 (Suppl. C), 225–235.Google Scholar
Artium Technologies2015 PDI-300 MD User Manual. Artium Technologies, Inc., Sunnyvale, CA, USA.Google Scholar
Babinsky, E. & Sojka, P. E. 2002 Modeling drop size distributions. Prog. Energy Combust. Sci. 28 (4), 303–329.Google Scholar
Bayvel, L. P. & Orzechowski, Z. 1993 Liquid Atomization. Taylor & Francis.Google Scholar
Bearman, P. W. 1969 On vortex shedding from a circular cylinder in the critical Reynolds number regime. J. Fluid Mech. 37 (3), 577–585.Google Scholar
Benjamin, M. & Harvey, R. J. 1996 Performance comparison of micro-, macro, conventionally machined simplex atomizers. In 9th ILASS AMERICAS, Institute of Liquid Atomization and Sprays.Google Scholar
Binnie, A. M. & Harris, D. P. 1950 The application of boundary-layer theory to swirling liquid flow through a nozzle. Q. J. Mech. Appl. Math. 3 (1), 89–106.Google Scholar
Bloor, M. I. G. & Ingham, D. B. 1977 On the use of a Pohlhausen method in three dimensional boundary layers. Z. Angew. Math. Phys. 28 (2), 289–299.Google Scholar
Chatterjee, A. 2000 An introduction to the proper orthogonal decomposition. Curr. Sci. 78 (7), 808–817.Google Scholar
Chua, C. K., Leong, K. F. & Lim, C. S. 2010 Rapid Prototyping: Principles and Applications, 3rd edn. World Scientific.Google Scholar
Coles, S. 2001 An Introduction to Statistical Modeling of Extreme Values. Springer.Google Scholar
De Vega, M., Rodríguez, P. & Lecuoa, A. 2000 Mean structure and droplet behavior in a coaxial airblast atomized spray: self-similarity and velocity decay functions. Atomiz. Sprays 10 (6), 603–626.Google Scholar
Déjean, B., Berthoumieu, P. & Gajan, P. 2016a Experimental study on the influence of liquid and air boundary conditions on a planar air-blasted liquid sheet. Part I. Liquid and air thicknesses. Intl J. Multiphase Flow 79, 202–213.Google Scholar
Déjean, B., Berthoumieu, P. & Gajan, P. 2016b Experimental study on the influence of liquid and air boundary conditions on a planar air-blasted liquid sheet. Part II. Prefilming zone length. Intl J. Multiphase Flow 79, 214–224.Google Scholar
Dhivyaraja, K., Gaddes, D., Panchagnula, M. V. & Tadigadapa, S. 2015 Geometrical scaling effects on the properties of pressure swirl microsprays. In 13th Triennial International Conference on Liquid Atomization and Spray Systems.Google Scholar
Dumouchel, C., Bloor, M. I. G., Dombrowski, N., Ingham, D. B. & Ledoux, M. 1992 Boundary-layer characteristics of a swirl atomizer. Atomiz. Sprays 2 (3), 225–237.Google Scholar
Giffen, E. & Muraszew, A. 1953 The Atomization of Liquid Fuels. Chapman and Hall.Google Scholar
Gorokhovski, M. & Herrmann, M. 2008 Modeling primary atomization. Annu. Rev. Fluid Mech. 40, 343–366.Google Scholar
Guildenbecher, D., López-Rivera, C. & Sojka, P. 2009 Secondary atomization. Exp. Fluids 46, 371–402.Google Scholar
Halder, M. R., Dash, S. K. & Som, S. K. 2002 Initiation of air core in a simplex nozzle and the effects of operating and geometrical parameters on its shape and size. Exp. Therm. Fluid Sci. 26 (8), 871–878.Google Scholar
Hardalupas, Y., Taylor, A. M. K. P. & Whitelaw, J. H. 1989 Velocity and particle-flux characteristics of turbulent particle-laden jets. Proc. R. Soc. Lond. A 426 (1870), 31–78.Google Scholar
Ko, N. W. M. & Chan, W. T. 1978 Similarity in the initial region of annular jets: three configurations. J. Fluid Mech. 84 (4), 641–656.Google Scholar
Kostoglou, M. 2003 Exact self-similar solutions to the fragmentation equation with homogeneous discrete kernel. Physica A 320, 84–96.Google Scholar
Kumar, K. & Kumar, G. S. 2015 An experimental and theoretical investigation of surface roughness of poly-jet printed parts. Virtual and Physical Prototyping 10 (1), 23–34.Google Scholar
Laermer, F., Schilp, A., Funk, K. & Offenberg, M. 1999 Bosch deep silicon etching: improving uniformity and etch rate for advanced mems applications.. In Technical Digest. IEEE International MEMS 99 Conference. Twelfth IEEE International Conference on Micro Electro Mechanical Systems (Cat. No.99CH36291), pp. 211–216.Google Scholar
Lasheras, J. C. & Hopfinger, E. J. 2000 Liquid jet instability and atomization in a coaxial gas stream. Annu. Rev. Fluid Mech. 32, 275–308.Google Scholar
Lasheras, J. C., Villermaux, E. & Hopfinger, E. J. 1998 Break-up and atomization of a round water jet by a high-speed annular air jet. J. Fluid Mech. 357, 351–379.Google Scholar
Lefebvre, A. H. 1989 Atomization and Sprays. Hemisphere.Google Scholar
Lefebvre, A. H. & Suyari, M. 1986 Film thickness measurements in a simplex swirl atomizer. J. Propul. Power 2 (6), 528–533.Google Scholar
Lin, S. P. & Reitz, R. D. 1998 Drop and spray formation from a liquid jet. Annu. Rev. Fluid Mech. 30 (1), 85–105.Google Scholar
Longmire, E. K. & Eaton, J. K. 1992 Structure of a particle-laden round jet. J. Fluid Mech. 236, 217–257.Google Scholar
Marmottant, P. & Villermaux, E. 2004 On spray formation. J. Fluid Mech. 498, 73–111.Google Scholar
Matas, J.-P., Marty, S., Dem, M. S. & Cartellier, A. 2015 Influence of gas turbulence on the instability of an air–water mixing layer. Phys. Rev. Lett. 115, 074501.Google Scholar
Otsu, N. 1979 Threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. SMC‐9 (1), 62–66.Google Scholar
Panchagnula, M. V., Sojka, P. E. & Santangelo, P. J. 1996 On the three-dimensional instability of a swirling, annular, inviscid liquid sheet subject to unequal gas velocities. Phys. Fluids 8, 3300–3312.Google Scholar
Panchagnula, M. V. & Sojka, P. E. 1999 Spatial droplet velocity and size profiles in effervescent atomizer-produced sprays. Fuel 78 (6), 729–741.Google Scholar
Payri, F., Bermudez, V., Payri, R. & Salvador, F. J. 2004 The influence of cavitation on the internal flow and the spray characteristics in diesel injection nozzles. Fuel 83 (4), 419–431.Google Scholar
Rajamanickam, K. & Basu, S. 2017 Insights into the dynamics of spray-swirl interactions. J. Fluid Mech. 810, 82–126.Google Scholar
Rajan, N., Mehregany, M., Zorman, C. A., Stefanescu, S. & Kicher, T. P. 1999 Fabrication and testing of micromachined silicon carbide and nickel fuel atomizers for gas turbine engines. J. Microelectromech. Syst. 8 (3), 251–257.Google Scholar
Rayapati, N. P., Bhamidipati, S., Peddieson, J. & Panchagnula, M. V. 2010 Analytical solutions for particulate pipe flows with fragmentation, evaporation, and diffusion. Mech. Res. Commun. 37 (6), 604–610.Google Scholar
Rizk, N. K. & Lefebvre, A. H. 1985 Internal flow characteristics of simplex swirl atomizers. J. Propul. Power 1 (3), 193–199.Google Scholar
Sampath, R. & Chakravarthy, S. R. 2014 Proper orthogonal and dynamic mode decompositions of time-resolved piv of confined backward-facing step flow. Exp. Fluids 55 (9), 1792.Google Scholar
Shen, J. & Li, X. 1996 Instability of an annular viscous liquid jet. Acta Mechanica 114 (1–4), 167–183.Google Scholar
Simmons, H. C. & Harvey, R. J.1995 Spray nozzle and method of manufacturing same, US Patent 5,435,884.Google Scholar
Singh, A., Mehregany, M., Phillips, S. M. & Harvey, R. J. 1998 Micromachined silicon fuel atomizers for gas turbine engines. Atomiz. Sprays 8 (4), 405–418.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Part I. Coherent structures. Q. Appl. Maths 45 (3), 561–571.Google Scholar
Som, S. K. 2012 Air core in pressure swirl atomizing nozzles. Atomiz. Sprays 22 (4), 283–303.Google Scholar
Taylor, G. I. 1948 The mechanics of swirl atomizers. In Proceedings of the Seventh International Congress for Applied Mechanics, pp. 280–285.Google Scholar
Taylor, G. I. 1950 The boundary layer in the converging nozzle of a swirl atomizer. Q. J. Mech. Appl. Maths 3 (2), 129–139.Google Scholar
Tratnig, A. & Brenn, G. 2010 Drop size spectra in sprays from pressure-swirl atomizers. Int. J. Multiphase Flow. 36 (5), 349–363.Google Scholar
Vadivukkarasan, M. & Panchagnula, M. V. 2016 Helical modes in combined Rayleigh–Taylor and Kelvin–Helmholtz instability of a cylindrical interface. Int. J. Spray Comb. Dyn. 8 (4), 219–234.Google Scholar
Vadivukkarasan, M. & Panchagnula, M. V. 2017 Combined Rayleigh–Taylor and Kelvin–Helmholtz instabilities on an annular liquid sheet. J. Fluid Mech. 812, 152–177.Google Scholar
Villermaux, E. 2007 Fragmentation. Annu. Rev. Fluid Mech. 39 (1), 419–446.Google Scholar
Wahono, S., Honnery, D., Soria, J. & Ghojel, J. 2008 High-speed visualisation of primary break-up of an annular liquid sheet. Exp. Fluids 44 (3), 451–459.Google Scholar
Xianguo, L. & Tankin, R. S. 1991 On the temporal instability of a two-dimensional viscous liquid sheet. J. Fluid Mech. 226, 425–443.Google Scholar