Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2025-01-02T16:03:14.778Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics in a stably stratified tilted square cavity

Published online by Cambridge University Press:  29 November 2019

Hezekiah Grayer Open the ORCID record for Hezekiah Grayer [Opens in a new window] ,
Jason Yalim Open the ORCID record for Jason Yalim [Opens in a new window] ,
Bruno D. Welfert Open the ORCID record for Bruno D. Welfert [Opens in a new window]  and
Juan M. Lopez Open the ORCID record for Juan M. Lopez [Opens in a new window]
Hezekiah Grayer
Affiliation:
School of Mathematical and Statistical Sciences, Arizona State University, TempeAZ85287, USA
Jason Yalim
Affiliation:
School of Mathematical and Statistical Sciences, Arizona State University, TempeAZ85287, USA
Bruno D. Welfert
Affiliation:
School of Mathematical and Statistical Sciences, Arizona State University, TempeAZ85287, USA
Juan M. Lopez*
Affiliation:
School of Mathematical and Statistical Sciences, Arizona State University, TempeAZ85287, USA
*
†Email address for correspondence: juan.m.lopez@asu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamics of a fluid flow in a differentially heated square container is investigated numerically. Two opposite conducting walls are maintained at constant temperatures, one hot and the other cold, and the other two walls are insulated. When the conducting walls are horizontal with the lower one cold, the static linearly stratified state is stable. When the container is tilted, the static equilibrium ceases to exist and the fluid flows due to the baroclinic torque arising from the bending of isotherms near the tilted insulated walls. 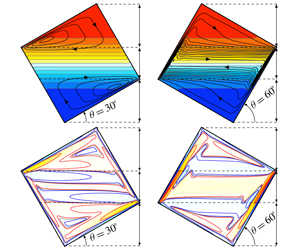This flow is found to be steady for tilt angles less than $45^{\circ }$, regardless of the relative balance between buoyancy and viscous effects (quantified by a buoyancy number $R_{N}$). For tilt angles above $45^{\circ }$, the flow becomes unsteady above a critical $R_{N}$ with localized boundary layer undulations at the conducting walls, at the heights of the horizontally opposite corners. From these corners emanate horizontal shear layers, which become thinner and more intense with increasing $R_{N}$. As the tilt angle approaches $90^{\circ }$, the nature of the instability changes, corresponding to that of the well-studied laterally heated cavity flow.

JFM classification

Convection: Buoyancy-driven instability Geophysical and Geological Flows: Baroclinic flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 883 , 25 January 2020 , A62
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Åkervik, E., Brandt, L., Henningson, D. S., Hœpffner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18, 068102.CrossRefGoogle Scholar
Baïri, A. 2008 Nusselt–Rayleigh correlations for design of industrial elements: experimental and numerical investigation of natural convection in tilted square air filled enclosures. Energy Convers. Manage. 49, 771–782.CrossRefGoogle Scholar
Bejan, A., Al-Homoud, A. A. & Imberger, J. 1981 Experimental study of high-Rayleigh-number convection in a horizontal cavity with different end temperatures. J. Fluid Mech. 109, 283–299.CrossRefGoogle Scholar
Cliffe, K. A. & Winters, K. H. 1984 A numerical study of the cusp catastrophe for Bénard convection in tilted cavities. J. Comput. Phys. 54, 531–534.CrossRefGoogle Scholar
Corvaro, F., Paroncini, M. & Sotte, M. 2012 PIV and numerical analysis of natural convection in tilted enclosures filled with air and with opposite active walls. Intl J. Heat Mass Transfer 55, 6349–6362.CrossRefGoogle Scholar
Gill, A. E. 1966 The boundary-layer regime for convection in a rectangular cavity. J. Fluid Mech. 26, 515–536.CrossRefGoogle Scholar
Hart, J. E. 1971 Stability of the flow in a differentially heated inclined box. J. Fluid Mech. 47, 547–576.CrossRefGoogle Scholar
Inaba, H. & Fukuda, T. 1984 Natural convection in an inclined square cavity in regions of density inversion of water. J. Fluid Mech. 142, 363–381.CrossRefGoogle Scholar
Ivey, G. N. 1984 Experiments on transient natural convection in a cavity. J. Fluid Mech. 144, 389–401.CrossRefGoogle Scholar
Jiang, L., Sun, C. & Calzavarini, E. 2019 Robustness of heat transfer in confined inclined convection at high Prandtl number. Phys. Rev. E 99, 013108.CrossRefGoogle ScholarPubMed
Le Quéré, P. & Behnia, M. 1998 From onset of unsteadiness to chaos in a differentially heated square cavity. J. Fluid Mech. 359, 81–107.CrossRefGoogle Scholar
Lopez, J. M., Welfert, B. D., Wu, K. & Yalim, J. 2017 Transition to complex dynamics in the cubic lid-driven cavity. Phys. Rev. Fluids 2, 074401.CrossRefGoogle Scholar
Oteski, L., Duguet, Y., Pastur, L. R. & Le Quéré, P. 2015 Quasiperiodic routes to chaos in confined two-dimensional differential convection. Phys. Rev. E 92, 043020.CrossRefGoogle ScholarPubMed
Ozoe, H., Yamamoto, K., Sayama, H. & Churchill, S. W. 1974 Natural circulation in an enclosed rectangular channel heated on one side and cooled on the opposing side. Intl J. Heat Mass Transfer 17, 1209–1217.Google Scholar
Page, M. A. 2011 Combined diffusion-driven and convective flow in a tilted square container. Phys. Fluids 23, 056602.CrossRefGoogle Scholar
Paolucci, S. & Chenoweth, D. R. 1989 Transition to chaos in a differentially heated vertical cavity. J. Fluid Mech. 201, 379–410.CrossRefGoogle Scholar
Patterson, J. & Imberger, J. 1980 Unsteady natural convection in a rectangular cavity. J. Fluid Mech. 100, 65–86.CrossRefGoogle Scholar
Peacock, T., Stocker, R. & Aristoff, J. M. 2004 An experimental investigation of the angular dependence of diffusion-driven flow. Phys. Fluids 16, 3503.CrossRefGoogle Scholar
Phillips, O. M. 1970 On flows induced by diffusion in a stably stratified fluid. Deep-Sea Res. 17, 435–443.Google Scholar
Pordes, R., Petravick, D., Kramer, B., Olson, D., Livny, M., Roy, A., Avery, P., Blackburn, K., Wenaus, T., Würthwein, F. et al. 2007 The Open Science Grid. J. Phys. Conf. Ser. 78, 012057.CrossRefGoogle Scholar
Quon, C. 1976 Diffusively induced boundary layers in a tilted square cavity: a numerical study. J. Comput. Phys. 22, 459–485.CrossRefGoogle Scholar
Quon, C. 1983 Convection induced by insulated boundaries in a square. Phys. Fluids 26, 632–637.CrossRefGoogle Scholar
Sfiligoi, I., Bradley, D. C., Holzman, B., Mhashilkar, P., Padhi, S. & Wurthwein, F. 2009 The pilot way to grid resources using glideinWMS. In 2009 WRI World Congress on Computer Science and Information Engineering, vol. 2, pp. 428–432. IEEE.CrossRefGoogle Scholar
Shishkina, O. & Horn, S. 2016 Thermal convection in inclined cylindrical containers. J. Fluid Mech. 790, R3.CrossRefGoogle Scholar
Torres, J. F., Henry, D., Komiya, A., Maruyama, S. & Ben Haldid, H. 2013 Three-dimensional continuation study of convection in a tilted rectangular enclosure. Phys. Rev. E 88, 043015.CrossRefGoogle Scholar
Ulloa, M. J. & Ochoa, J. 1997 Horizontal convective rolls in a tilted square duct of conductive and insulating walls. Comput. Fluids 26, 1–17.CrossRefGoogle Scholar
Wu, K., Welfert, B. D. & Lopez, J. M. 2018 Complex dynamics in a stratified lid-driven square cavity flow. J. Fluid Mech. 855, 43–66.CrossRefGoogle Scholar
Wunsch, C. 1970 On oceanic boundary mixing. Deep-Sea Res. 17, 293–301.Google Scholar
Xin, S. & Le Quéré, P. 2006 Natural-convection flows in air-filled differentially heated cavities with adiabatic horizontal walls. Numer. Heat Transfer 50, 437–466.CrossRefGoogle Scholar
Yalim, J., Welfert, B. D. & Lopez, J. M. 2019 Parametrically forced stably stratified cavity flow: complicated nonlinear dynamics near the onset of instability. J. Fluid Mech. 871, 1067–1096.CrossRefGoogle Scholar

Grayer et al. supplementary movie 1

Isotherms and vorticity of the steady states. Unstable steady states were computed using selective frequency damping.

Download Grayer et al. supplementary movie 1(Video)
Video 9.2 MB

Grayer et al. supplementary movie 2

Pointwise and setwise invariant limit cycles L1.

Download Grayer et al. supplementary movie 2(Video)
Video 472.4 KB

Grayer et al. supplementary movie 3

States near the double-Hopf bifurcation dH12.

Download Grayer et al. supplementary movie 3(Video)
Video 3.7 MB

Grayer et al. supplementary movie 4

States near the double-Hopf bifurcation dH23.

Download Grayer et al. supplementary movie 4(Video)
Video 11.8 MB