Published online by Cambridge University Press: 14 February 2018
Previous studies on capsule dynamics in shear flow have dealt with Newtonian fluids, while the effect of fluid viscoelasticity remains an unresolved fundamental question. In this paper, we report a numerical investigation of the dynamics of capsules enclosing a viscoelastic fluid and which are freely suspended in a Newtonian fluid under simple shear. Systematic simulations are performed at small but non-zero Reynolds numbers (i.e. 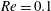 $Re=0.1$) using a three-dimensional front-tracking finite-difference model, in which the fluid viscoelasticity is introduced via the Oldroyd-B constitutive equation. We demonstrate that the internal fluid viscoelasticity presents significant effects on the deformation behaviour of initially spherical capsules, including transient evolution and equilibrium values of their deformation and orientation. Particularly, the capsule deformation decreases slightly with the Deborah number De increasing from 0 to
$Re=0.1$) using a three-dimensional front-tracking finite-difference model, in which the fluid viscoelasticity is introduced via the Oldroyd-B constitutive equation. We demonstrate that the internal fluid viscoelasticity presents significant effects on the deformation behaviour of initially spherical capsules, including transient evolution and equilibrium values of their deformation and orientation. Particularly, the capsule deformation decreases slightly with the Deborah number De increasing from 0 to 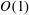 $O(1)$. In contrast, with De increasing within high levels, i.e.
$O(1)$. In contrast, with De increasing within high levels, i.e. 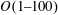 $O(1{-}100)$, the capsule deformation increases continuously and eventually approaches the Newtonian limit having a viscosity the same as the Newtonian part of the viscoelastic capsule. By analysing the viscous stress, pressure and viscoelastic stress acting on the capsule membrane, we reveal that the mechanism underlying the effects of the internal fluid viscoelasticity on the capsule deformation is the alterations in the distribution of the viscoelastic stress at low De and its magnitude at high De, respectively. Furthermore, we find some new features in the dynamics of initially non-spherical capsules induced by the internal fluid viscoelasticity. Particularly, the transition from tumbling to swinging of oblate capsules can be triggered at very high viscosity ratios by increasing De alone. Besides, the critical viscosity ratio for the tumbling-to-swinging transition is remarkably enlarged with De increasing at relatively high levels, i.e.
$O(1{-}100)$, the capsule deformation increases continuously and eventually approaches the Newtonian limit having a viscosity the same as the Newtonian part of the viscoelastic capsule. By analysing the viscous stress, pressure and viscoelastic stress acting on the capsule membrane, we reveal that the mechanism underlying the effects of the internal fluid viscoelasticity on the capsule deformation is the alterations in the distribution of the viscoelastic stress at low De and its magnitude at high De, respectively. Furthermore, we find some new features in the dynamics of initially non-spherical capsules induced by the internal fluid viscoelasticity. Particularly, the transition from tumbling to swinging of oblate capsules can be triggered at very high viscosity ratios by increasing De alone. Besides, the critical viscosity ratio for the tumbling-to-swinging transition is remarkably enlarged with De increasing at relatively high levels, i.e. 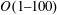 $O(1{-}100)$, while it shows little change at low De, i.e. below
$O(1{-}100)$, while it shows little change at low De, i.e. below 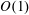 $O(1)$.
$O(1)$.