Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hearst, R. Jason
and
Ganapathisubramani, Bharathram
2017.
Tailoring incoming shear and turbulence profiles for lab‐scale wind turbines.
Wind Energy,
Vol. 20,
Issue. 12,
p.
2021.
Mydlarski, Laurent
2017.
A turbulent quarter century of active grids: from Makita (1991) to the present.
Fluid Dynamics Research,
Vol. 49,
Issue. 6,
p.
061401.
Diaz-Daniel, Carlos
Laizet, Sylvain
and
Vassilicos, J. Christos
2017.
Direct numerical simulations of a wall-attached cube immersed in laminar and turbulent boundary layers.
International Journal of Heat and Fluid Flow,
Vol. 68,
Issue. ,
p.
269.
Ikhennicheu, Maria
Gaurier, Benoît
Druault, Philippe
and
Germain, Grégory
2018.
Experimental analysis of the floor inclination effect on the turbulent wake developing behind a wall mounted cube.
European Journal of Mechanics - B/Fluids,
Vol. 72,
Issue. ,
p.
340.
Hearst, R. Jason
Dogan, Eda
and
Ganapathisubramani, Bharathram
2018.
Robust features of a turbulent boundary layer subjected to high-intensity free-stream turbulence.
Journal of Fluid Mechanics,
Vol. 851,
Issue. ,
p.
416.
Jeon, Jeongsook
Lee, Ji Yong
and
Kang, Seokkoo
2018.
Experimental Investigation of Three‐Dimensional Flow Structure and Turbulent Flow Mechanisms Around a Nonsubmerged Spur Dike With a Low Length‐to‐Depth Ratio.
Water Resources Research,
Vol. 54,
Issue. 5,
p.
3530.
Shinde, Siddhesh
Maki, Kevin
and
Johnsen, Eric
2018.
Understanding the Dependence of Near-Wake Characteristics on the Cube Height in a Turbulent Boundary Layer.
Rinoshika, Hiroka
Rinoshika, Akira
and
Fujimoto, Shun
2018.
Visualization of a finite wall-mounted cylinder wake controlled by a horizontal or inclined hole.
Journal of Visualization,
Vol. 21,
Issue. 4,
p.
543.
Manolesos, Marinos
Gao, Zhiqiu
and
Bouris, Demetri
2018.
Experimental investigation of the atmospheric boundary layer flow past a building model with openings.
Building and Environment,
Vol. 141,
Issue. ,
p.
166.
Wang, F.
Lam, K.M.
Zu, G.B.
and
Cheng, L.
2019.
Coherent structures and wind force generation of square-section building model.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 188,
Issue. ,
p.
175.
Fang, Xingjun
and
Tachie, Mark F.
2019.
Flows over surface-mounted bluff bodies with different spanwise widths submerged in a deep turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
p.
717.
Güemes, A.
Sanmiguel Vila, C.
Örlü, R.
Vinuesa, R.
Schlatter, P.
Ianiro, A.
and
Discetti, S.
2019.
Flow organization in the wake of a rib in a turbulent boundary layer with pressure gradient.
Experimental Thermal and Fluid Science,
Vol. 108,
Issue. ,
p.
115.
Hearst, R. Jason
2019.
Progress in Turbulence VIII.
Vol. 226,
Issue. ,
p.
173.
Yauwenas, Yendrew
Porteous, Ric
Moreau, Danielle J.
and
Doolan, Con J.
2019.
The effect of aspect ratio on the wake structure of finite wall-mounted square cylinders.
Journal of Fluid Mechanics,
Vol. 875,
Issue. ,
p.
929.
Kozmar, Hrvoje
and
Laschka, Boris
2019.
Wind-tunnel modeling of wind loads on structures using truncated vortex generators.
Journal of Fluids and Structures,
Vol. 87,
Issue. ,
p.
334.
Aliferis, Alexander D.
Jessen, Marius Stette
Bracchi, Tania
and
Hearst, R. Jason
2019.
Performance and wake of a Savonius vertical‐axis wind turbine under different incoming conditions.
Wind Energy,
Vol. 22,
Issue. 9,
p.
1260.
Wang, F.
Cheng, L.
and
Lam, K. M.
2019.
POD characterisation of extreme wake patterns of turbulent wind fields past rectangular buildings.
Environmental Fluid Mechanics,
Vol. 19,
Issue. 4,
p.
879.
Wang, F.
and
Lam, K. M.
2019.
Geometry effects on mean wake topology and large-scale coherent structures of wall-mounted prisms.
Physics of Fluids,
Vol. 31,
Issue. 12,
Ikhennicheu, Maria
Germain, Grégory
Druault, Philippe
and
Gaurier, Benoît
2019.
Experimental study of coherent flow structures past a wall-mounted square cylinder.
Ocean Engineering,
Vol. 182,
Issue. ,
p.
137.
Ikhennicheu, Maria
Germain, Grégory
Druault, Philippe
and
Gaurier, Benoît
2019.
Experimental investigation of the turbulent wake past real seabed elements for velocity variations characterization in the water column..
International Journal of Heat and Fluid Flow,
Vol. 78,
Issue. ,
p.
108426.
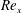 $Re_{x}$) and the ratio of the cube height (
$Re_{x}$) and the ratio of the cube height ( $h$) to the boundary layer thickness (
$h$) to the boundary layer thickness (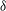 $\unicode[STIX]{x1D6FF}$) are held constant at
$\unicode[STIX]{x1D6FF}$) are held constant at 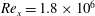 $Re_{x}=1.8\times 10^{6}$ and
$Re_{x}=1.8\times 10^{6}$ and 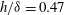 $h/\unicode[STIX]{x1D6FF}=0.47$. It is demonstrated that the stagnation point on the upstream side of the cube and the reattachment length in the wake of the cube are independent of the incoming profile for the conditions investigated here. In contrast, the wake length monotonically decreases for increasing turbulence intensity but fixed normalised shear – both quantities measured at the cube height. The wake shortening is a result of heightened turbulence levels promoting wake recovery from high local velocities and the reduction in strength of a dominant shedding frequency.
$h/\unicode[STIX]{x1D6FF}=0.47$. It is demonstrated that the stagnation point on the upstream side of the cube and the reattachment length in the wake of the cube are independent of the incoming profile for the conditions investigated here. In contrast, the wake length monotonically decreases for increasing turbulence intensity but fixed normalised shear – both quantities measured at the cube height. The wake shortening is a result of heightened turbulence levels promoting wake recovery from high local velocities and the reduction in strength of a dominant shedding frequency.