Article contents
Effects of reverberating waves and interface coupling on a divergent Richtmyer–Meshkov instability
Published online by Cambridge University Press: 22 November 2023
Abstract
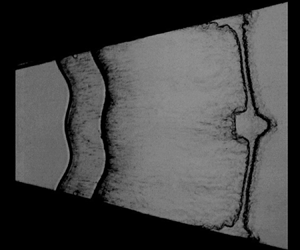
Shock-tube experiments on Richtmyer–Meshkov (RM) instability at a perturbed SF $_6$ layer surrounded by air, induced by a cylindrical divergent shock, are reported. To explore the effects of reverberating waves and interface coupling on instability growth, gas layers with various shapes are created: unperturbed inner interface and sinusoidal outer interface (case US); sinusoidal inner and outer interfaces that have identical phase (case IP); sinusoidal inner and outer interfaces that have opposite phase (case AP). For each case, three thicknesses are considered. Results show that reverberating waves inside the layer dominate the early-stage instability growth, while interface coupling dominates the late-stage growth. The influences of waves on divergent RM instability are more pronounced than the planar and convergent counterparts, which are estimated accurately based on gas dynamics theory. Both the wave influence and interface coupling depend heavily on the layer shape, leading to diverse growth rates: the quickest growth for case AP, medium growth for case US, the slowest growth for case IP. In particular, for the IP case, there exists a critical thickness below which the instability growth is suppressed by both the reverberating waves and interface coupling. This provides an efficient way to modulate the growth of divergent RM instability. It is found that divergent RM instability involves weak nonlinearity and strong interface coupling such that the linear theory of Mikaelian (Phys. Fluids, vol. 17, 2005, 094105) can well reproduce the instability growth at late stages for all cases. This constitutes the first experimental confirmation of the Mikaelian theory.
$_6$ layer surrounded by air, induced by a cylindrical divergent shock, are reported. To explore the effects of reverberating waves and interface coupling on instability growth, gas layers with various shapes are created: unperturbed inner interface and sinusoidal outer interface (case US); sinusoidal inner and outer interfaces that have identical phase (case IP); sinusoidal inner and outer interfaces that have opposite phase (case AP). For each case, three thicknesses are considered. Results show that reverberating waves inside the layer dominate the early-stage instability growth, while interface coupling dominates the late-stage growth. The influences of waves on divergent RM instability are more pronounced than the planar and convergent counterparts, which are estimated accurately based on gas dynamics theory. Both the wave influence and interface coupling depend heavily on the layer shape, leading to diverse growth rates: the quickest growth for case AP, medium growth for case US, the slowest growth for case IP. In particular, for the IP case, there exists a critical thickness below which the instability growth is suppressed by both the reverberating waves and interface coupling. This provides an efficient way to modulate the growth of divergent RM instability. It is found that divergent RM instability involves weak nonlinearity and strong interface coupling such that the linear theory of Mikaelian (Phys. Fluids, vol. 17, 2005, 094105) can well reproduce the instability growth at late stages for all cases. This constitutes the first experimental confirmation of the Mikaelian theory.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 2
- Cited by


