Article contents
The electrophoretic mobilities of a circular cylinder in close proximity to a dielectric wall
Published online by Cambridge University Press: 08 September 2016
Abstract
In their bipolar-coordinate analysis of circular-cylinder electrophoresis near a dielectric wall, Keh et al. (J. Fluid Mech., vol. 231, 1991, pp. 211–228) found that, when an electric field is applied parallel to the wall, the translational and rotational electrophoretic mobilities increase monotonically as the ratio 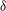 $\unicode[STIX]{x1D6FF}$ of the cylinder–wall separation to the cylinder radius decreases, eventually diverging as
$\unicode[STIX]{x1D6FF}$ of the cylinder–wall separation to the cylinder radius decreases, eventually diverging as 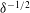 $\unicode[STIX]{x1D6FF}^{-1/2}$ when
$\unicode[STIX]{x1D6FF}^{-1/2}$ when 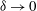 $\unicode[STIX]{x1D6FF}\rightarrow 0$. Considering the singular limit
$\unicode[STIX]{x1D6FF}\rightarrow 0$. Considering the singular limit 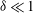 $\unicode[STIX]{x1D6FF}\ll 1$ from the outset, we conduct here an asymptotic analysis of that electrokinetic problem, providing insight to the manner by which the intense electric field in the narrow gap is transformed into
$\unicode[STIX]{x1D6FF}\ll 1$ from the outset, we conduct here an asymptotic analysis of that electrokinetic problem, providing insight to the manner by which the intense electric field in the narrow gap is transformed into 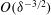 $O(\unicode[STIX]{x1D6FF}^{-3/2})$ shear stresses; these stresses, in turn, overcome the large Stokes resistance so as to provide the large electrophoretic mobilities. In a companion problem, where the cylinder is exposed to a uniform current emanating from a nearby reactive electrode, the intense gap-scale electric field results in an
$O(\unicode[STIX]{x1D6FF}^{-3/2})$ shear stresses; these stresses, in turn, overcome the large Stokes resistance so as to provide the large electrophoretic mobilities. In a companion problem, where the cylinder is exposed to a uniform current emanating from a nearby reactive electrode, the intense gap-scale electric field results in an 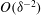 $O(\unicode[STIX]{x1D6FF}^{-2})$ pressure, giving rise in turn to a large repulsive force. In that problem we find that the cylinder velocity perpendicular to the wall approaches a finite limit as
$O(\unicode[STIX]{x1D6FF}^{-2})$ pressure, giving rise in turn to a large repulsive force. In that problem we find that the cylinder velocity perpendicular to the wall approaches a finite limit as 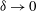 $\unicode[STIX]{x1D6FF}\rightarrow 0$. We also discuss the role of ‘dielectrophoretic’ forces which are inevitable in the above semi-bounded configurations.
$\unicode[STIX]{x1D6FF}\rightarrow 0$. We also discuss the role of ‘dielectrophoretic’ forces which are inevitable in the above semi-bounded configurations.
- Type
- Rapids
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 4
- Cited by



