Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-27T16:24:25.515Z Has data issue: false hasContentIssue false
  • English
  • Français

Enstrophy and circulation scaling for Navier–Stokes reconnection

Published online by Cambridge University Press:  25 January 2018

Robert M. Kerr Open the ORCID record for Robert M. Kerr [Opens in a new window]
Robert M. Kerr*
Affiliation:
Department of Mathematics, University of Warwick, Coventry CV4 7AL, UK
*
†Email address for correspondence: Robert.Kerr@warwick.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

As reconnection begins and the enstrophy 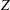$Z$ grows for two configurations, helical trefoil knots and anti-parallel vortices, two regimes of self-similar collapse are observed. First, during trefoil reconnection a new 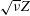$\sqrt{\unicode[STIX]{x1D708}}Z$ scaling, where $\unicode[STIX]{x1D708}$ is viscosity, is identified before any 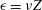$\unicode[STIX]{x1D716}=\unicode[STIX]{x1D708}Z$ dissipation scaling begins. Further rescaling shows linearly decreasing 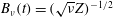$B_{\unicode[STIX]{x1D708}}(t)=(\sqrt{\unicode[STIX]{x1D708}}Z)^{-1/2}$ at configuration-dependent crossing times 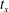$t_{x}$. Gaps in the vortex structures identify the 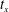$t_{x}$ as when reconnection ends and collapse onto $\unicode[STIX]{x1D708}$-independent curves can be obtained using 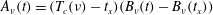$A_{\unicode[STIX]{x1D708}}(t)=(T_{c}(\unicode[STIX]{x1D708})-t_{x})(B_{\unicode[STIX]{x1D708}}(t)-B_{\unicode[STIX]{x1D708}}(t_{x}))$. The critical times 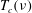$T_{c}(\unicode[STIX]{x1D708})$ are identified empirically by extrapolating the linear 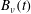$B_{\unicode[STIX]{x1D708}}(t)$ regimes to 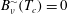$B_{\unicode[STIX]{x1D708}}^{{\sim}}(T_{c})=0$, yielding an 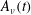$A_{\unicode[STIX]{x1D708}}(t)$ collapse that forms early as $\unicode[STIX]{x1D708}$ varies by 256. These solutions are regular or non-singular, as shown by decreasing cubic velocity norms 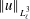$\Vert u\Vert _{L_{\ell }^{3}}^{}$. For the anti-parallel vortices, first there is an exchange of circulation, from 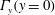$\unicode[STIX]{x1D6E4}_{y}(y=0)$ to 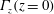$\unicode[STIX]{x1D6E4}_{z}(z=0)$, mediated by the viscous circulation exchange integral 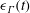$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D6E4}}(t)$, which is followed by a modified 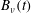$B_{\unicode[STIX]{x1D708}}(t)$ collapse until the reconnection ends at 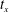$t_{x}$. Singular Leray scaling and mathematical bounds for higher-order Sobolev norms are used to help explain the origins of the new scaling and why the domain size 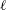$\ell$ has to increase to maintain the collapse of 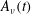$A_{\unicode[STIX]{x1D708}}(t)$ and 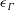$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D6E4}}$ as $\unicode[STIX]{x1D708}$ decreases.

JFM classification

Mathematical Foundations: Mathematical Foundations Mathematical Foundations: Topological fluid dynamics Vortex Flows: Vortex dynamics
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 839 , 25 March 2018 , R2
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beale, J. T., Kato, T. & Majda, A. 1984 Remarks on the breakdown of smooth solutions of the 3-D Euler equations. Commun. Math. Phys. 94, 61–66.CrossRefGoogle Scholar
Constantin, P. 1986 Note on loss of regularity for solutions of the 3D incompressible Euler and related equations. Commun. Math. Phys. 104, 311–326.Google Scholar
Constantin, P. & Foias, C. 1988 The Navier–Stokes Equations. University of Chicago Press.Google Scholar
Doering, C. R. 2009 The 3D Navier–Stokes problem. Annu. Rev. Fluid Mech. 41, 109–128.CrossRefGoogle Scholar
Doering, C. R. & Gibbon, J. D. 1995 Applied Analysis of the Navier–Stokes Equations (Appendix A). Cambridge University Press.Google Scholar
Donzis, D., Gibbon, J. D., Gupta, A., Kerr, R. M., Pandit, R. & Vincenzi, D. 2013 Vorticity moments in four numerical simulations of the 3D Navier–Stokes equations. J. Fluid Mech. 732, 316–331.Google Scholar
Escauriaza, L., Seregin, G. & Sverák, V. 2003 L 3, ∞ -solutions to the Navier–Stokes equations and backward uniqueness. Russian Math. Surveys 58, 211–250.Google Scholar
Gibbon, J. D. 2010 Regularity and singularity in solutions of the three-dimensional Navier–Stokes equations. Proc. R. Soc. Lond. A 466, 2587–2604.Google Scholar
Gibbon, J. D. 2012 A hierarchy of length scales for solutions of the three-dimensional Navier–Stokes equations. Commun. Math. Sci. 10, 131–136.Google Scholar
Kerr, R. M. 2013a Swirling, turbulent vortex rings formed from a chain reaction of reconnection events. Phys. Fluids 25, 065101.Google Scholar
Kerr, R. M. 2013b Bounds for Euler from vorticity moments and line divergence. J. Fluid Mech. 729, R2.Google Scholar
Kerr, R. M. 2018 Trefoil knot timescales for reconnection and helicity. Fluid Dyn. Res. 50, 011422.Google Scholar
Kleckner, D. & Irvine, W. T. M. 2013 Creation and dynamics of knotted vortices. Nat. Phys. 9, 253–258.Google Scholar
Leray, J. 1934 Sur le mouvement d’un liquide visqueux emplissant l’espace. Acta Math. 63, 193–248.Google Scholar
Necas, J., Ruzicka, M. & Sverák, V. 1996 On Leray’s self-similar solutions of the Navier–Stokes equations. Acta Math. 176, 283–294.Google Scholar
Melander, M. V. & Hussain, F. 1989 Cross-linking of two antiparallel vortex tubes. Phys. Fluids A 1, 633–636.Google Scholar
Moffatt, H. K. & Ricca, R. 1992 Helicity and the Calugareanu invariant. Proc. R. Soc. Lond. A 439, 411–429.Google Scholar
Robinson, J. C., Rodrigo, J. & Sadowski, W. 2016 The Three-Dimensional Navier–Stokes Equations, Classical Theory, Cambridge Studies in Advanced Mathematics. Cambridge University Press.Google Scholar
Scheeler, M. W., Kleckner, D., Proment, D., Kindlmann, G. L. & Irvine, W. T. M. 2014 Helicity conservation by flow across scales in reconnecting vortex links and knots. Proc. Natl Acad. Sci. USA 111, 15350–15355.Google Scholar
Virk, D., Hussain, F. & Kerr, R. M. 1995 Compressible vortex reconnection. J. Fluid Mech. 304, 47–86.Google Scholar