Published online by Cambridge University Press: 19 September 2014
Thrust-generating flapping foils are known to produce jets inclined to the free stream at high Strouhal numbers 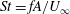 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{St} = fA/U_{\infty }$, where
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{St} = fA/U_{\infty }$, where 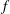 $f$ is the frequency and
$f$ is the frequency and 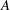 $A$ is the amplitude of flapping and
$A$ is the amplitude of flapping and 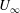 $U_{\infty }$ is the free-stream velocity. Our experiments, in the limiting case of
$U_{\infty }$ is the free-stream velocity. Our experiments, in the limiting case of 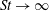 $\mathit{St} \rightarrow \infty $ (zero free-stream speed), show that a purely oscillatory pitching motion of a chordwise flexible foil produces a coherent jet composed of a reverse Bénard–Kármán vortex street along the centreline, albeit over a specific range of effective flap stiffnesses. We obtain flexibility by attaching a thin flap to the trailing edge of a rigid NACA0015 foil; length of flap is
$\mathit{St} \rightarrow \infty $ (zero free-stream speed), show that a purely oscillatory pitching motion of a chordwise flexible foil produces a coherent jet composed of a reverse Bénard–Kármán vortex street along the centreline, albeit over a specific range of effective flap stiffnesses. We obtain flexibility by attaching a thin flap to the trailing edge of a rigid NACA0015 foil; length of flap is 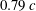 $0.79\, c$ where
$0.79\, c$ where  $c$ is rigid foil chord length. It is the time-varying deflections of the flexible flap that suppress the meandering found in the jets produced by a pitching rigid foil for zero free-stream condition. Recent experiments (Marais et al., J. Fluid Mech., vol. 710, 2012, p. 659) have also shown that the flexibility increases the
$c$ is rigid foil chord length. It is the time-varying deflections of the flexible flap that suppress the meandering found in the jets produced by a pitching rigid foil for zero free-stream condition. Recent experiments (Marais et al., J. Fluid Mech., vol. 710, 2012, p. 659) have also shown that the flexibility increases the 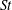 $\mathit{St}$ at which non-deflected jets are obtained. Analysing the near-wake vortex dynamics from flow visualization and particle image velocimetry (PIV) measurements, we identify the mechanisms by which flexibility suppresses jet deflection and meandering. A convenient characterization of flap deformation, caused by fluid–flap interaction, is through a non-dimensional ‘effective stiffness’,
$\mathit{St}$ at which non-deflected jets are obtained. Analysing the near-wake vortex dynamics from flow visualization and particle image velocimetry (PIV) measurements, we identify the mechanisms by which flexibility suppresses jet deflection and meandering. A convenient characterization of flap deformation, caused by fluid–flap interaction, is through a non-dimensional ‘effective stiffness’, 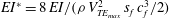 $EI^{*} = 8 \, EI/(\rho \, V_{{{TE_{{max}}}}}^2 \, s_{{{f}}} \, c_{{{f}}}^3/2)$, representing the inverse of the flap deflection due to the fluid-dynamic loading; here,
$EI^{*} = 8 \, EI/(\rho \, V_{{{TE_{{max}}}}}^2 \, s_{{{f}}} \, c_{{{f}}}^3/2)$, representing the inverse of the flap deflection due to the fluid-dynamic loading; here, 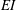 $EI$ is the bending stiffness of flap,
$EI$ is the bending stiffness of flap, 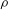 $\rho $ is fluid density,
$\rho $ is fluid density, 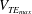 $V_{{{TE_{{max}}}}}$ is the maximum velocity of rigid foil trailing edge,
$V_{{{TE_{{max}}}}}$ is the maximum velocity of rigid foil trailing edge, 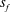 $s_{{{f}}}$ is span and
$s_{{{f}}}$ is span and 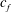 $c_{{{f}}}$ is chord length of the flexible flap. By varying the amplitude and frequency of pitching, we obtain a variation in
$c_{{{f}}}$ is chord length of the flexible flap. By varying the amplitude and frequency of pitching, we obtain a variation in 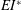 $EI^{*}$ over nearly two orders of magnitude and show that only moderate
$EI^{*}$ over nearly two orders of magnitude and show that only moderate 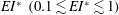 $EI^{*}\ (0.1 \lesssim EI^{*} \lesssim 1)$ generates a sustained, coherent, orderly jet. Relatively ‘stiff’ flaps (
$EI^{*}\ (0.1 \lesssim EI^{*} \lesssim 1)$ generates a sustained, coherent, orderly jet. Relatively ‘stiff’ flaps (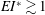 $EI^{*} \gtrsim 1$), including the extreme case of no flap, produce meandering jets, whereas highly ‘flexible’ flaps (
$EI^{*} \gtrsim 1$), including the extreme case of no flap, produce meandering jets, whereas highly ‘flexible’ flaps (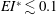 $EI^{*} \lesssim 0.1$) produce spread-out jets. Obtained from the measured mean velocity fields, we present values of thrust coefficients for the cases for which orderly jets are observed.
$EI^{*} \lesssim 0.1$) produce spread-out jets. Obtained from the measured mean velocity fields, we present values of thrust coefficients for the cases for which orderly jets are observed.
Present address: Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Bangalore 560064, India.
This video shows the dye visualization in a horizontal plane along the mid-span for the airfoil with flexible flap over 10 oscillation cycles (for amplitude of oscillation ±15°, and frequency 2 Hz). The rigid airfoil chord is 38 mm and flexible flap chord is 30 mm. Laser sheet is passed from bottom side of the visualization window. The transparent flap is blackened in the plane of visualization, except for a 3 mm portion near the trailing edge to identify the start of the flap. Two large vortices, which eventually become part of the ‘reverse Benard-Karman vortex street’, along with a few smaller vortices are shed per oscillation cycle. Movie clearly shows the role of flexible flap in the formation of non-meandering unidirectional vortex jet aligned along the center-line. The vortices are shed at the appropriate space and appropriate phase of the cycle. Note also that a vortex once shed is pushed downstream by flap induced motion. The movement of a streak of dye present below the airfoil clearly shows the pulling of the fluid towards the airfoil and the flap. Note that, the movie clearly shows that the leading edge vortices are not generated by the pitching foil. The small ‘blobs’ of dye near the leading edge and also on the airfoil surface are not the vortices, but they are formed due to the following two reasons: one, intermittent release of dye from the dye port, and two, since the motion of fluid is small near the leading edge, the dye accumulates there. These ‘blobs’ of dye are eventually convected downstream by the flow.