Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-14T03:08:22.180Z Has data issue: false hasContentIssue false
  • English
  • Français

Global and local aspects of entrainment in temporal plumes

Published online by Cambridge University Press:  22 December 2016

Dominik Krug Open the ORCID record for Dominik Krug [Opens in a new window] ,
Daniel Chung Open the ORCID record for Daniel Chung [Opens in a new window] ,
Jimmy Philip  and
Ivan Marusic
Dominik Krug*
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Daniel Chung
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Jimmy Philip
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Ivan Marusic
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: dominik.krug@unimelb.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

To date, the understanding of the role buoyancy plays in the entrainment process in unstable configurations such as turbulent plumes remains incomplete. Towards addressing this question, we set up a flow in which a plume evolves in time instead of space. We demonstrate that the temporal problem is equivalent to a spatial plume in a strong coflow and address in detail how the temporal plume can be realized via direct numerical simulation. 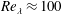Using numerical data of plume simulations up to $Re_{\unicode[STIX]{x1D706}}\approx 100$, we show that the entrainment coefficient can be determined consistently using a global entrainment analysis in an integral framework as well as via a local approach. The latter is based on a study of the local propagation of the turbulent/non-turbulent interface relative to the fluid. Locally, this process is dominated by small-scale diffusion which is amplified by interface convolutions such that the total entrained flux is independent of viscosity. Further, we identify a direct buoyancy contribution to entrainment by baroclinic torque, which accounts for 8 %–12 % of the entrained flux locally, comparable to the 15 % buoyancy contribution at the integral level. It appears that the baroclinic torque is a mechanism that might explain higher values of the entrainment coefficient in spatial plumes compared with jets.

JFM classification

Convection: Convection Convection: Plumes/thermals Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 812 , 10 February 2017 , pp. 222 - 250
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bisset, D. K., Hunt, J. C. R. & Rogers, M. M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.CrossRefGoogle Scholar
van den Bremer, T. S. & Hunt, G. R. 2014 Two-dimensional planar plumes and fountains. J. Fluid Mech. 750, 210–244.CrossRefGoogle Scholar
Carazzo, G., Kaminski, E. & Tait, S. 2006 The route to self-similarity in turbulent jets and plumes. J. Fluid Mech. 547, 137–148.Google Scholar
Chung, D. & Matheou, G. 2012 Direct numerical simulation of stationary homogeneous stratified sheared turbulence. J. Fluid Mech. 696, 434–467.CrossRefGoogle Scholar
Chung, D. & Pullin, D. I. 2009 Large-eddy simulation and wall modelling of turbulent channel flow. J. Fluid Mech. 631, 281–309.Google Scholar
Corrsin, S. & Kistler, A.1954 The free-stream boundaries of turbulent flows. NACA TN-3133, TR-1244, 1033–1064.Google Scholar
Craske, J. & van Reeuwijk, M. 2015 Energy dispersion in turbulent jets. Part 1. Direct simulation of steady and unsteady jets. J. Fluid Mech. 763, 500–537.CrossRefGoogle Scholar
Craske, J. & van Reeuwijk, M. 2016 Generalised unsteady plume theory. J. Fluid Mech. 792, 1013–1052.Google Scholar
Fox, D. G. 1970 Forced plume in a stratified fluid. J. Geophys. Res. 75 (33), 6818–6835.Google Scholar
Holzner, M., Liberzon, A., Nikitin, N., Lüthi, B., Kinzelbach, W. & Tsinober, A. 2008 A Lagrangian investigation of the small-scale features of turbulent entrainment through particle tracking and direct numerical simulation. J. Fluid Mech. 598, 465–475.Google Scholar
Holzner, M. & Lüthi, B. 2011 Laminar superlayer at the turbulence boundary. Phys. Rev. Lett. 106 (13), 134503.Google Scholar
Holzner, M., Song, B., Avila, M. & Hof, B. 2013 Lagrangian approach to laminar–turbulent interfaces in transitional pipe flow. J. Fluid Mech. 723, 140–162.CrossRefGoogle Scholar
Hou, T. Y. & Li, R. 2007 Computing nearly singular solutions using pseudo-spectral methods. J. Comput. Phys. 226 (1), 379–397.Google Scholar
Hunt, G. R. & Van den Bremer, T. S. 2011 Classical plume theory: 1937–2010 and beyond. IMA J. Appl. Maths 76 (3), 424–448.Google Scholar
Kaminski, E., Tait, S. & Carazzo, G. 2005 Turbulent entrainment in jets with arbitrary buoyancy. J. Fluid Mech. 526, 361–376.Google Scholar
Krug, D., Holzner, M., Lüthi, B., Wolf, M., Kinzelbach, W. & Tsinober, A. 2015 The turbulent/non-turbulent interface in an inclined dense gravity current. J. Fluid Mech. 765, 303–324.Google Scholar
List, E. J. 1982 Turbulent jets and plumes. Annu. Rev. Fluid Mech. 14 (1), 189–212.Google Scholar
Mater, P. D. & Venayagamoorthy, S. K. 2014 A unifying framework for parameterizing stably stratified shear-flow turbulence. Phys. Fluids 26 (3), 036601.Google Scholar
Mathew, J. & Basu, A. J. 2002 Some characteristics of entrainment at a cylindrical turbulence boundary. Phys. Fluids 14 (7), 2065–2072.Google Scholar
Morton, B. R. 1959 Forced plumes. J. Fluid Mech. 5 (01), 151–163.Google Scholar
Morton, B. R., Taylor, G. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Paillat, S. & Kaminski, E. 2014 Entrainment in plane turbulent pure plumes. J. Fluid Mech. 755, R2.CrossRefGoogle Scholar
Philip, J., Bermejo-Moreno, I., Chung, D. & Marusic, I.2015 Characteristics of the entrainment velocity in a developing wake. In International Symposium on Turbulence and Shear Flow Phenomena, TSFP-9, Melbourne, Australia. Available at: http://www.tsfp-conference.org/proceedings/proceedings-of-tsfp-9-2015-melbourne.html.Google Scholar
Philip, J., Meneveau, C., de Silva, C. M. & Marusic, I. 2014 Multiscale analysis of fluxes at the turbulent/non-turbulent interface in high Reynolds number boundary layers. Phys. Fluids 26 (1), 015105.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Priestley, C. H. B. & Ball, F. K. 1955 Continuous convection from an isolated source of heat. Q. J. R. Meteorol. Soc. 81 (348), 144–157.Google Scholar
Ramaprian, B. R. & Chandrasekhara, M. S. 1989 Measurements in vertical plane turbulent plumes. Trans. ASME J. Fluids Engng 111 (1), 69–77.Google Scholar
Redford, J. A., Castro, I. P. & Coleman, G. N. 2012 On the universality of turbulent axisymmetric wakes. J. Fluid Mech. 710, 419–452.Google Scholar
van Reeuwijk, M. & Craske, J. 2015 Energy-consistent entrainment relations for jets and plumes. J. Fluid Mech. 782, 333–355.Google Scholar
van Reeuwijk, M. & Holzner, M. 2014 The turbulence boundary of a temporal jet. J. Fluid Mech. 739, 254–275.Google Scholar
van Reeuwijk, M., Salizzoni, P., Hunt, G. R & Craske, J. 2016 Turbulent transport and entrainment in jets and plumes: a DNS study. Phys. Rev. Fluids 1, 074301.Google Scholar
de Rooy, W. C., Bechtold, P., Fröhlich, K., Hohenegger, C., Jonker, H., Mironov, D., Siebesma, P., Teixeira, J. & Yano, J.-I. 2013 Entrainment and detrainment in cumulus convection: an overview. Q. J. R. Meteorol. Soc. 139 (670), 1–19.CrossRefGoogle Scholar
da Silva, C. B., Hunt, J. C. R., Eames, I. & Westerweel, J. 2014 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46, 567–590.Google Scholar
da Silva, C. B. & Pereira, J. C. F. 2008 Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets. Phys. Fluids 20 (5), 55101.Google Scholar
Sreenivasan, K. R., Ramshankar, R. & Meneveau, C. 1989 Mixing, entrainment and fractal dimensions of surfaces in turbulent flows. Proc. R. Soc. Lond. A 421 (1860), 79–108.Google Scholar
Taveira, R. R. & da Silva, C. B. 2013 Kinetic energy budgets near the turbulent/nonturbulent interface in jets. Phys. Fluids 25 (1), 015114.Google Scholar
Tennekes, H. & Lumley, J. L. 1994 A First Course in Turbulence. MIT.Google Scholar
Townsend, A. A. R. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Tsinober, A. 2009 An Informal Conceptual Introduction to Turbulence: Second Edition of An Informal Introduction to Turbulence. Springer.Google Scholar
Turner, J. S. 1986 Turbulent entrainment – the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.Google Scholar
Watanabe, T., Sakai, Y., Nagata, K., Ito, Y. & Hayase, T. 2014 Enstrophy and passive scalar transport near the turbulent/non-turbulent interface in a turbulent planar jet flow. Phys. Fluids 26 (10), 105103.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.Google Scholar
Wolf, M., Holzner, M., Lüthi, B., Krug, D., Kinzelbach, W. & Tsinober, A. 2013 Effects of mean shear on the local turbulent entrainment process. J. Fluid Mech. 731, 95–116.CrossRefGoogle Scholar
Wolf, M., Lüthi, B., Holzner, M., Krug, D., Kinzelbach, W. & Tsinober, A. 2012 Investigations on the local entrainment velocity in a turbulent jet. Phys. Fluids 24 (10), 105110.CrossRefGoogle Scholar
Woods, A. W. 2010 Turbulent plumes in nature. Annu. Rev. Fluid Mech. 42, 391–412.Google Scholar
Zeldovich, Y. B. 1937 The asymptotic laws of freely-ascending convective flows. Zh. Eksp. Teor. Fiz. 7, 1463–1465.Google Scholar