Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Arietaleaniz, S.
Malgaretti, P.
Pagonabarraga, I.
and
Hidalgo, R. C.
2018.
Rheological behavior of colloidal suspension with long-range interactions.
Physical Review E,
Vol. 98,
Issue. 4,
Deng, Pan
Fu, Cheng-Jie
and
Wu, Zhigang
2018.
High purity and viability cell separation of a bacterivorous jakobid flagellate based on a steep velocity gradient induced soft inertial force.
RSC Advances,
Vol. 8,
Issue. 62,
p.
35512.
Jiang, Maoqiang
Qian, Shizhi
and
Liu, Zhaohui
2018.
Fully resolved simulation of single-particle dynamics in a microcavity.
Microfluidics and Nanofluidics,
Vol. 22,
Issue. 12,
Gupta, Anupam
Magaud, Pascale
Lafforgue, Christine
and
Abbas, Micheline
2018.
Conditional stability of particle alignment in finite-Reynolds-number channel flow.
Physical Review Fluids,
Vol. 3,
Issue. 11,
Stoecklein, Daniel
and
Di Carlo, Dino
2019.
Nonlinear Microfluidics.
Analytical Chemistry,
Vol. 91,
Issue. 1,
p.
296.
Rossi, Massimiliano
Marin, Alvaro
Cevheri, Necmettin
Kähler, Christian J.
and
Yoda, Minami
2019.
Particle distribution and velocity in electrokinetically induced banding.
Microfluidics and Nanofluidics,
Vol. 23,
Issue. 5,
Liebl, Maik
Gleich, Bernhard
Eberbeck, Dietmar
Radon, Patricia
Rahmer, Jürgen
Trahms, Lutz
and
Wiekhorst, Frank
2019.
Noninvasive monitoring of blood flow using a single magnetic microsphere.
Scientific Reports,
Vol. 9,
Issue. 1,
Lochab, V.
Yee, A.
Yoda, M.
Conlisk, A. T.
and
Prakash, S.
2019.
Dynamics of colloidal particles in microchannels under combined pressure and electric potential gradients.
Microfluidics and Nanofluidics,
Vol. 23,
Issue. 12,
Nizkaya, Tatiana V.
Asmolov, Evgeny S.
Harting, Jens
and
Vinogradova, Olga I.
2020.
Inertial migration of neutrally buoyant particles in superhydrophobic channels.
Physical Review Fluids,
Vol. 5,
Issue. 1,
Razavi Bazaz, Sajad
Mashhadian, Ali
Ehsani, Abbas
Saha, Suvash Chandra
Krüger, Timm
and
Ebrahimi Warkiani, Majid
2020.
Computational inertial microfluidics: a review.
Lab on a Chip,
Vol. 20,
Issue. 6,
p.
1023.
Luo, Mengxi
Law, Junhui
Wang, Xian
Xin, Liming
Shan, Guanqiao
Badiwala, Mitesh
Huang, Xi
and
Sun, Yu
2020.
Robotic Swarm Control for Precise and On-Demand Embolization.
p.
4470.
Xiang, Nan
and
Ni, Zhonghua
2020.
Handbook of Single Cell Technologies.
p.
1.
Rühle, Felix
Schaaf, Christian
and
Stark, Holger
2020.
Optimal Control of Colloidal Trajectories in Inertial Microfluidics Using the Saffman Effect.
Micromachines,
Vol. 11,
Issue. 6,
p.
592.
Hafemann, T.
Tschisgale, S.
and
Fröhlich, J.
2020.
A simulation method for particle migration in microfluidic spirals with application to small and medium particle concentrations.
Physics of Fluids,
Vol. 32,
Issue. 12,
Nizkaya, Tatiana V.
Gekova, Anna S.
Harting, Jens
Asmolov, Evgeny S.
and
Vinogradova, Olga I.
2020.
Inertial migration of oblate spheroids in a plane channel.
Physics of Fluids,
Vol. 32,
Issue. 11,
Esipov, Denis V.
Chirkov, Denis V.
Kuranakov, Dmitriy S.
and
Lapin, Vasiliy N.
2020.
Direct Numerical Simulation of the Segre–Silberberg Effect Using Immersed Boundary Method.
Journal of Fluids Engineering,
Vol. 142,
Issue. 11,
Ekanayake, Nilanka I. K.
Berry, Joseph D.
Stickland, Anthony D.
Dunstan, David E.
Muir, Ineke L.
Dower, Steven K.
and
Harvie, Dalton J. E.
2020.
Lift and drag forces acting on a particle moving with zero slip in a linear shear flow near a wall.
Journal of Fluid Mechanics,
Vol. 904,
Issue. ,
Harding, Brendan
and
Stokes, Yvonne M.
2020.
Inertial focusing of non-neutrally buoyant spherical particles in curved microfluidic ducts.
Journal of Fluid Mechanics,
Vol. 902,
Issue. ,
Huang, Yuanding
Zhao, Xuezeng
and
Pan, Yunlu
2020.
Slip-shear and inertial migration of finite-size spheres in plane Poiseuille flow.
Computational Materials Science,
Vol. 176,
Issue. ,
p.
109542.
Shi, Pengyu
and
Rzehak, Roland
2020.
Lift forces on solid spherical particles in wall-bounded flows.
Chemical Engineering Science,
Vol. 211,
Issue. ,
p.
115264.
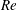 $Re$, particles migrate across laminar flow streamlines to their equilibrium positions in microchannels. This migration is attributed to a lift force, and the balance between this lift and gravity determines the location of particles in channels. Here we demonstrate that velocity of finite-size particles located near a channel wall differs significantly from that of an undisturbed flow, and that their equilibrium position depends on this, referred to as slip velocity, difference. We then present theoretical arguments, which allow us to generalize expressions for a lift force, originally suggested for some limiting cases and
$Re$, particles migrate across laminar flow streamlines to their equilibrium positions in microchannels. This migration is attributed to a lift force, and the balance between this lift and gravity determines the location of particles in channels. Here we demonstrate that velocity of finite-size particles located near a channel wall differs significantly from that of an undisturbed flow, and that their equilibrium position depends on this, referred to as slip velocity, difference. We then present theoretical arguments, which allow us to generalize expressions for a lift force, originally suggested for some limiting cases and 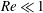 $Re\ll 1$, to finite-size particles in a channel flow at
$Re\ll 1$, to finite-size particles in a channel flow at 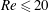 $Re\leqslant 20$. Our theoretical model, validated by lattice Boltzmann simulations, provides considerable insight into inertial migration of finite-size particles in a microchannel and suggests some novel microfluidic approaches to separate them by size or density at a moderate
$Re\leqslant 20$. Our theoretical model, validated by lattice Boltzmann simulations, provides considerable insight into inertial migration of finite-size particles in a microchannel and suggests some novel microfluidic approaches to separate them by size or density at a moderate 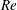 $Re$.
$Re$.