Published online by Cambridge University Press: 11 November 2019
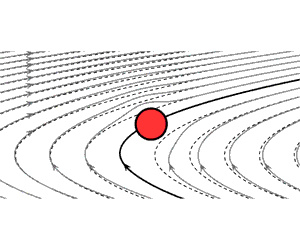
The present study is focused on obtaining the inviscid flow solution for a circular cylinder traversing steadily across an unbounded uniform-shear flow. The work is motivated by understanding the aerodynamics of bodies traversing across a shear flow, as well as by developing an understanding of fundamental concepts that are well understood for uniform free stream but not in the presence of shear. The results show that, in general, the presence of shear makes it impossible to define a unique approach-stream incidence angle  $\unicode[STIX]{x1D6FC}$ relative to the cylinder. However, in the limit of, what we have termed ‘quasi-uniform’ flow, such an angle can be defined. We show that in this limit, the flow is also quasi-steady, and the static-cylinder solution can be used to solve for the moving-cylinder problem with good accuracy. This ‘quasi-uniform and quasi-steady’ (QUS) condition is attained when a single unsteadiness parameter
$\unicode[STIX]{x1D6FC}$ relative to the cylinder. However, in the limit of, what we have termed ‘quasi-uniform’ flow, such an angle can be defined. We show that in this limit, the flow is also quasi-steady, and the static-cylinder solution can be used to solve for the moving-cylinder problem with good accuracy. This ‘quasi-uniform and quasi-steady’ (QUS) condition is attained when a single unsteadiness parameter  $\dot{U}_{o}^{+}$ approaches zero. For small values of the cylinder-to-free-stream velocity ratio
$\dot{U}_{o}^{+}$ approaches zero. For small values of the cylinder-to-free-stream velocity ratio  $V_{r}$,
$V_{r}$,  $\dot{U}_{o}^{+}\approx K_{eff}V_{r}$, where
$\dot{U}_{o}^{+}\approx K_{eff}V_{r}$, where  $K_{eff}$ is the effective non-dimensional shear rate. Away from the QUS flow limit, the flow field and the surface pressure distribution are significantly different between the moving and the static cylinders. However, a surprising result is that regardless of whether QUS conditions hold, the force acting on the moving cylinder in a Galilean frame of reference is always the same as that on a static cylinder in uniform-shear free stream but with non-dimensional shear rate and incidence angle equal to the moving cylinder’s instantaneous
$K_{eff}$ is the effective non-dimensional shear rate. Away from the QUS flow limit, the flow field and the surface pressure distribution are significantly different between the moving and the static cylinders. However, a surprising result is that regardless of whether QUS conditions hold, the force acting on the moving cylinder in a Galilean frame of reference is always the same as that on a static cylinder in uniform-shear free stream but with non-dimensional shear rate and incidence angle equal to the moving cylinder’s instantaneous  $K_{eff}$ and
$K_{eff}$ and  $\tan ^{-1}(V_{r})$, respectively.
$\tan ^{-1}(V_{r})$, respectively.