Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T07:38:11.511Z Has data issue: false hasContentIssue false
  • English
  • Français

Mechanism of frequency lock-in in vortex-induced vibrations at low Reynolds numbers

Published online by Cambridge University Press:  14 October 2015

Weiwei Zhang ,
Xintao Li ,
Zhengyin Ye  and
Yuewen Jiang
Weiwei Zhang*
Affiliation:
School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China
Xintao Li
Affiliation:
School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China
Zhengyin Ye
Affiliation:
School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China
Yuewen Jiang
Affiliation:
School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China
*
†Email address for correspondence: aeroelastic@nwpu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this study, a CFD-based linear dynamics model combined with the direct Computational Fluid Dynamics/Computational Structural Dynamics (CFD/CSD) simulation method is utilized to study the physical mechanisms underlying frequency lock-in in vortex-induced vibrations (VIVs). An identification method is employed to construct the reduced-order models (ROMs) of unsteady aerodynamics for the incompressible flow past a vibrating cylinder at low Reynolds numbers (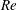$Re$). Reduced-order-model-based fluid–structure interaction models for VIV are also constructed by coupling ROMs and structural motion equations. The effects of the natural frequency of the cylinder, mass ratio and structural damping coefficient on the dynamics of the coupled system at 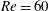$Re=60$ are investigated. The results show that the frequency lock-in phenomenon at low Reynolds numbers can be divided into two patterns according to different induced mechanisms. The two patterns are ‘resonance-induced lock-in’ and ‘flutter-induced lock-in’. When the natural frequency of the cylinder is in the vicinity of the eigenfrequency of the uncoupled wake mode (WM), only the WM is unstable. The dynamics of the coupled system is dominated by resonance. Meanwhile, for relatively high natural frequencies (i.e. greater than the eigenfrequency of the uncoupled WM), the structure mode becomes unstable, and the coupling between the two unstable modes eventually leads to flutter. Flutter is the root cause of frequency lock-in and the higher vibration amplitude of the cylinder than that of the resonance region. This result provides evidence for the finding of De Langre (J. Fluids Struct., vol. 22, 2006, pp. 783–791) that frequency lock-in is caused by coupled-mode flutter. The linear model exactly predicts the onset reduced velocity of frequency lock-in compared with that of direct numerical simulations. In addition, the transition frequency predicted by the linear model is in close coincidence with the amplitude of the lift coefficient of a fixed cylinder for high mass ratios. Therefore, it confirms that linear models can capture a significant part of the inherent physics of the frequency lock-in phenomenon.

JFM classification

Aerodynamics: Flow-structure interactions Nonlinear Dynamical Systems: Low-dimensional models Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 783 , 25 November 2015 , pp. 72 - 102
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baranyi, L. & Lewis, R. I. 2006 Comparison of a grid-based CFD method and vortex dynamics predictions of low Reynolds number cylinder flows. Aeronautical J. 110 (1103), 63.CrossRefGoogle Scholar
Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75 (5), 750–756.CrossRefGoogle Scholar
Bearman, P. W. 2011 Circular cylinder wakes and vortex-induced vibrations. J. Fluids Struct. 27, 648–658.Google Scholar
Blevins, R. D. 1990 Flow-Induced Vibration. Van Nostrand Reinhold.Google Scholar
Brunton, S. L., Rowley, C. W. & Williams, D. R. 2013 Reduced-order unsteady aerodynamic models at low Reynolds numbers. J. Fluid Mech. 724, 203–233.Google Scholar
Buffoni, E. 2003 Vortex shedding in subcritical conditions. Phys. Fluids 15 (3), 814–816.CrossRefGoogle Scholar
Cai, J., Liu, F. & Luo, S. 2003 Stability of symmetric vortices in two dimensions and over three-dimensional slender conical bodies. J. Fluid Mech. 480, 65–94.Google Scholar
Chen, S. S., Zhu, S. & Cai, Y. 1995 An unsteady flow theory for vortex-induced vibration. J. Sound Vib. 184 (1), 73–92.Google Scholar
Cossu, C. & Morino, L. 2000 On the instability of a spring-mounted circular cylinder in a viscous flow at low Reynolds numbers. J. Fluids Struct. 14 (2), 183–196.CrossRefGoogle Scholar
Crouch, J. D., Garbaruk, A. & Magidov, D. 2007 Predicting the onset of flow unsteadiness based on global instability. J. Comput Phys. 224 (2), 924–940.Google Scholar
Crouch, J. D., Garbaruk, A., Magidov, D. & Travin, A. 2009 Origin of transonic buffet on aerofoils. J. Fluid Mech. 628, 357–369.Google Scholar
Dahan, J. A., Morgans, A. S. & Lardeau, S. 2012 Feedback control for form-drag reduction on a bluff body with a blunt trailing edge. J. Fluid Mech. 704, 360–387.Google Scholar
De Boer, A., Van der Schoot, M. S. & Bijl, H. 2007 Mesh deformation based on radial basis function interpolation. Comput. Struct. 85 (11), 784–795.Google Scholar
De Langre, E. 2006 Frequency lock-in is caused by coupled-mode flutter. J. Fluids Struct. 22 (6), 783–791.Google Scholar
Den Hartog, J. P. 1934 Mechanical Vibrations. Courier Corporation.Google Scholar
Dowell, E. H. 1980 A Modern Course in Aeroelasticity. Springer.Google Scholar
Facchinetti, M. L., De Langre, E. & Biolley, F. 2002 Vortex shedding modeling using diffusive van der Pol oscillators. C. R. Mec. 330 (7), 451–456.Google Scholar
Facchinetti, M. L., De Langre, E. & Biolley, F. 2004a Coupling of structure and wake oscillators in vortex-induced vibrations. J. Fluids Struct. 19 (2), 123–140.Google Scholar
Facchinetti, M. L., De Langre, E. & Biolley, F. 2004b Vortex-induced travelling waves along a cable. Eur. J. Mech. (B/Fluids) 23 (1), 199–208.Google Scholar
Feng, C. C.1968 The measurement of vortex induced effects in flow past stationary and oscillating circular and D-section cylinders. Master’s Thesis, University of British Columbia, Vancouver, B.C., Canada.Google Scholar
Gabbai, R. D. & Benaroya, H. 2005. An overview of modeling and experiments of vortex-induced vibration of circular cylinders. J. Sound Vib. 282 (3), 575–616.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2002 Resonance forever: existence of a critical mass and an infinite regime of resonance in vortex-induced vibration. J. Fluid Mech. 473, 147–166.Google Scholar
Govardhan, R. N. & Williamson, C. H. K. 2006 Defining the ‘modified Griffin plot’ in vortex-induced vibration: revealing the effect of Reynolds number using controlled damping. J. Fluid Mech. 561, 147–180.Google Scholar
Grouthier, C., Michelin, S., Modarres-Sadeghi, Y. & De, E. 2013 Self-similar vortex-induced vibrations of a hanging string. J. Fluid Mech. 724, R2.Google Scholar
Hartlen, R. T. & Currie, I. G. 1970 Lift-oscillator model of vortex-induced vibration. J. Engng Mech. Div. 96 (5), 577–591.Google Scholar
He, J. W., Glowinski, R., Metcalfe, R., Nordlander, A. & Periaux, J. 2000 Active control and drag optimization for flow past a circular cylinder: I. oscillatory cylinder rotation. J. Comput. Phys. 163 (1), 83–117.Google Scholar
Illingworth, S. J., Morgans, A. S. & Rowley, C. W. 2012 Feedback control of cavity flow oscillations using simple linear models. J. Fluid Mech. 709, 223–248.Google Scholar
Jiang, Y.2013 Numerical solution of Navier–Stokes equations on generalized mesh and its applications. PhD thesis, NWPU, Xi’an, China.Google Scholar
Le, D. V., Khoo, B. C. & Lim, K. M. 2008 An implicit-forcing immersed boundary method for simulating viscous flows in irregular domains. Comput. Meth. Appl. Mech. Engng 197 (25), 2119–2130.CrossRefGoogle Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2010 A numerical study of global frequency selection in the time-mean wake of a circular cylinder. J. Fluid Mech. 645, 435–446.CrossRefGoogle Scholar
Lu, L., Qin, J. M., Teng, B. & Li, Y. C. 2011 Numerical investigations of lift suppression by feedback rotary oscillation of circular cylinder at low Reynolds number. Phys. Fluids 23 (3), 033601.Google Scholar
Lucia, D. J., Beran, P. S. & Silva, W. A. 2004 Reduced-order modeling: new approaches for computational physics. Prog. Aerosp. Sci. 40 (1), 51–117.Google Scholar
Meliga, P. & Chomaz, J. 2011 An asymptotic expansion for the vortex-induced vibrations of a circular cylinder. J. Fluid Mech. 671, 137–167.Google Scholar
Mittal, S. 2008 Global linear stability analysis of time-averaged flows. Intl J. Numer. Meth. Fluids. 58, 111–118.Google Scholar
Mittal, S. & Singh, S. 2005 Vortex-induced vibrations at subcritical Re . J. Fluid Mech. 534, 185–194.Google Scholar
Nguyen, T., Koide, M., Yamada, S., Takahashi, T. & Shirakashi, M. 2012 Influence of mass and damping ratios on VIVs of a cylinder with a downstream counterpart in cruciform arrangement. J. Fluids Struct. 28, 40–55.CrossRefGoogle Scholar
Prasanth, T. K., Premchandran, V. & Mittal, S. 2011 Hysteresis in vortex-induced vibrations: critical blockage and effect of $m^{\ast }$ . J. Fluid Mech. 671, 207–225.Google Scholar
Sarpkaya, T. 1978 Fluid forces on oscillating cylinders. NASA STI/Recon Tech. Rep. A, 78 46523.Google Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19 (4), 389–447.Google Scholar
Singh, S. P. & Mittal, S. 2005 Vortex-induced oscillations at low Reynolds numbers: hysteresis and vortex-shedding modes. J. Fluids Struct. 20 (8), 1085–1104.CrossRefGoogle Scholar
Violette, R., De Langre, E. & Szydlowski, J. 2010 A linear stability approach to vortex-induced vibrations and waves. J. Fluids Struct. 26 (3), 442–466.Google Scholar
Wang, Z., Fan, J. & Cen, K. 2009 Immersed boundary method for the simulation of 2D viscous flow based on vorticity–velocity formulations. J. Comput. Phys. 228 (5), 1504–1520.Google Scholar
Willden, R. H. J. & Graham, J. M. R. 2006 Three distinct response regimes for the transverse vortex-induced vibrations of circular cylinders at low Reynolds numbers. J. Fluids Struct. 22 (6), 885–895.Google Scholar
Williamson, C. H. K. 1989 Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 206, 579–627.CrossRefGoogle Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.Google Scholar
Zhang, W., Jiang, Y. & Ye, Z. 2007 Two better loosely coupled solution algorithms of CFD based aeroelastic simulation. Engng Appl. Comput. Fluid 1 (4), 253–262.Google Scholar
Zhang, W. & Ye, Z. 2007 Reduced-order-model-based flutter analysis at high angle of attack. J. Aircraft 44 (6), 2086–2089.Google Scholar
Zhou, C. Y., So, R. M. C. & Lam, K. 1999 Vortex-induced vibrations of an elastic circular cylinder. J. Fluids Struct. 13 (2), 165–189.CrossRefGoogle Scholar
Zhu, J., Wang, X. Q., Xie, W. C. & So, R. M. 2008 Flow-induced instability under bounded noise excitation in cross-flow. J. Sound Vib. 312 (3), 476–495.Google Scholar