Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang, Min
Yang, Yunchao
Zhang, Duan Z.
and
Balachandar, S.
2021.
Numerical calculation of the particle–fluid–particle stress in random arrays of fixed particles.
Physical Review Fluids,
Vol. 6,
Issue. 10,
Seyed-Ahmadi, Arman
and
Wachs, Anthony
2021.
Sedimentation of inertial monodisperse suspensions of cubes and spheres.
Physical Review Fluids,
Vol. 6,
Issue. 4,
Tavanashad, Vahid
Passalacqua, Alberto
and
Subramaniam, Shankar
2021.
Particle-resolved simulation of freely evolving particle suspensions: Flow physics and modeling.
International Journal of Multiphase Flow,
Vol. 135,
Issue. ,
p.
103533.
Pakseresht, Pedram
and
Apte, Sourabh V.
2021.
A disturbance corrected point-particle approach for two-way coupled particle-laden flows on arbitrary shaped grids.
Journal of Computational Physics,
Vol. 439,
Issue. ,
p.
110381.
Vowinckel, Bernhard
2021.
Incorporating grain-scale processes in macroscopic sediment transport models.
Acta Mechanica,
Vol. 232,
Issue. 6,
p.
2023.
Euzenat, Florian
Hammouti, Abdelkader
Climent, Eric
Fede, Pascal
and
Wachs, Anthony
2021.
Effect of spatial filter features on local heat transfer coefficients obtained from particle-resolved simulations of a flow through a fixed random array of rigid spherical particles.
International Journal of Heat and Fluid Flow,
Vol. 92,
Issue. ,
p.
108873.
Zhao, Li
Chen, Xiao
and
Zhou, Qiang
2021.
Inhomogeneous drag models for gas-solid suspensions based on sub-grid quantities.
Powder Technology,
Vol. 385,
Issue. ,
p.
170.
Domínguez-Vázquez, Daniel
Jacobs, Gustaaf B.
and
Tartakovsky, Daniel M.
2021.
Lagrangian models of particle-laden flows with stochastic forcing: Monte Carlo, moment equations, and method of distributions analyses.
Physics of Fluids,
Vol. 33,
Issue. 3,
Seyed-Ahmadi, Arman
and
Wachs, Anthony
2022.
Physics-inspired architecture for neural network modeling of forces and torques in particle-laden flows.
Computers & Fluids,
Vol. 238,
Issue. ,
p.
105379.
Lattanzi, Aaron M.
Tavanashad, Vahid
Subramaniam, Shankar
and
Capecelatro, Jesse
2022.
Stochastic model for the hydrodynamic force in Euler–Lagrange simulations of particle-laden flows.
Physical Review Fluids,
Vol. 7,
Issue. 1,
Xia, Yan
Yu, Zhaosheng
Pan, Dingyi
Lin, Zhaowu
and
Guo, Yu
2022.
Drag model from interface-resolved simulations of particle sedimentation in a periodic domain and vertical turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 944,
Issue. ,
Capecelatro, Jesse
2022.
Modeling high-speed gas–particle flows relevant to spacecraft landings.
International Journal of Multiphase Flow,
Vol. 150,
Issue. ,
p.
104008.
Fong, Kee Onn
and
Coletti, Filippo
2022.
Experimental analysis of particle clustering in moderately dense gas–solid flow.
Journal of Fluid Mechanics,
Vol. 933,
Issue. ,
Zhu, Li-Tao
Chen, Xi-Zhong
Ouyang, Bo
Yan, Wei-Cheng
Lei, He
Chen, Zhe
and
Luo, Zheng-Hong
2022.
Review of Machine Learning for Hydrodynamics, Transport, and Reactions in Multiphase Flows and Reactors.
Industrial & Engineering Chemistry Research,
Vol. 61,
Issue. 28,
p.
9901.
Hardy, Baptiste
Simonin, Olivier
De Wilde, Juray
and
Winckelmans, Grégoire
2022.
Simulation of the flow past random arrays of spherical particles: Microstructure-based tensor quantities as a tool to predict fluid–particle forces.
International Journal of Multiphase Flow,
Vol. 149,
Issue. ,
p.
103970.
Zhu, Li-Tao
Lei, He
Ouyang, Bo
and
Luo, Zheng-Hong
2022.
Using mesoscale drag model-augmented coarse-grid simulation to design fluidized bed reactor: Effect of bed internals and sizes.
Chemical Engineering Science,
Vol. 253,
Issue. ,
p.
117547.
Du, Shaohua
Zhao, Li
Chen, Xihao
Yang, Bolun
and
Zhou, Qiang
2022.
Effect of Stefan flow on the drag force of single reactive particle surrounded by a sea of inert particles.
Chemical Engineering Science,
Vol. 253,
Issue. ,
p.
117546.
Zhao, Li
Zhou, Qiang
Yang, Bolun
and
Chen, Xiao
2022.
Inhomogeneous drag correction based on surrounding solid volume fraction in low-Reynolds-number regime.
Powder Technology,
Vol. 401,
Issue. ,
p.
117292.
Balachandar, S.
and
Maxey, Martin R.
2023.
Modeling Approaches and Computational Methods for Particle-Laden Turbulent Flows.
p.
299.
Gai, Guodong
and
Wachs, Anthony
2023.
Dynamics, wakes, and regime transitions of a fixed angular particle in an unbounded inertial flow. I. Regular tetrahedron angular position.
Physical Review Fluids,
Vol. 8,
Issue. 6,
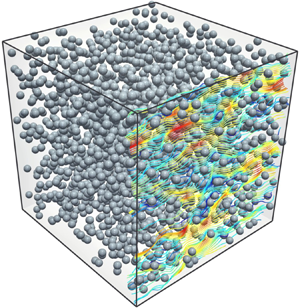
 $2 \leq \textit {Re} \leq 150$ and a solid volume fraction range of
$2 \leq \textit {Re} \leq 150$ and a solid volume fraction range of  $0.1 \leq \phi \leq 0.4$. The key idea exploited by our model is that, while the arrangement of neighbours around each particle is uniform and random, conditioning forces or torques exerted on a reference sphere to specific ranges of values results in the emergence of significantly non-uniform distributions of neighbouring particles. Based on probabilistic arguments, we take advantage of the statistical information extracted from PR-DNS to construct force/torque-conditioned probability distribution maps, which are ultimately used as basis functions for regression. Given the locations of surrounding particles as input to the model, our results demonstrate that the present probability-driven framework is capable of predicting up to 85 % of the actual observed force and torque variation in the best cases. Since the precise location of each particle is known in an Eulerian–Lagrangian (EL) simulation, our model would be able to estimate the unresolved subgrid force and torque fluctuations reasonably well, and thereby considerably enhance the fidelity of EL simulations via improved interphase coupling.
$0.1 \leq \phi \leq 0.4$. The key idea exploited by our model is that, while the arrangement of neighbours around each particle is uniform and random, conditioning forces or torques exerted on a reference sphere to specific ranges of values results in the emergence of significantly non-uniform distributions of neighbouring particles. Based on probabilistic arguments, we take advantage of the statistical information extracted from PR-DNS to construct force/torque-conditioned probability distribution maps, which are ultimately used as basis functions for regression. Given the locations of surrounding particles as input to the model, our results demonstrate that the present probability-driven framework is capable of predicting up to 85 % of the actual observed force and torque variation in the best cases. Since the precise location of each particle is known in an Eulerian–Lagrangian (EL) simulation, our model would be able to estimate the unresolved subgrid force and torque fluctuations reasonably well, and thereby considerably enhance the fidelity of EL simulations via improved interphase coupling.