Article contents
Modelling the decay of finite-span starting and stopping wall jets in an external stream
Published online by Cambridge University Press: 08 November 2022
Abstract
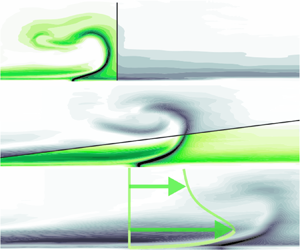
The flow under consideration is a wall jet that results from an inclined jet in cross-flow emitted into a zero-pressure-gradient turbulent boundary layer from a slot-like outlet of width  $b=0.5\,\mathrm {mm}$ and span
$b=0.5\,\mathrm {mm}$ and span  $L=20\,\mathrm {mm}$. Despite the finite jet span, the velocity decay and wall-normal spreading rate in the symmetry plane can be described with power laws almost identical to those for the two-dimensional flow determined by Zhou & Wygnanski (AIAA J., vol. 31, 1993, pp. 848–853). This is explained by the lack of significant lateral spreading found in the present configuration due to a self-amplifying inward-directed fluid motion, fundamentally differing from conditions found in the absence of an external stream. Regions with ‘approximately self-similar’ properties also exist in the case of unsteady velocity programmes where the fluid is ejected in a pulsatile fashion. Here, the wall jet is enclosed by a leading vortex structure and a deceleration wave, for which the time-dependent locations can be predicted by means of empirical constants. This yields models for the major properties inside the advancing and diffusing wall jet that only require knowledge regarding the velocity ratio, the ejected momentum flux and the kinematic viscosity, representing an extension to scaling laws for steady wall jets in still ambience established by Narasimha et al. (Aeronaut. Q., vol. 77, 1973, pp. 355–359).
$L=20\,\mathrm {mm}$. Despite the finite jet span, the velocity decay and wall-normal spreading rate in the symmetry plane can be described with power laws almost identical to those for the two-dimensional flow determined by Zhou & Wygnanski (AIAA J., vol. 31, 1993, pp. 848–853). This is explained by the lack of significant lateral spreading found in the present configuration due to a self-amplifying inward-directed fluid motion, fundamentally differing from conditions found in the absence of an external stream. Regions with ‘approximately self-similar’ properties also exist in the case of unsteady velocity programmes where the fluid is ejected in a pulsatile fashion. Here, the wall jet is enclosed by a leading vortex structure and a deceleration wave, for which the time-dependent locations can be predicted by means of empirical constants. This yields models for the major properties inside the advancing and diffusing wall jet that only require knowledge regarding the velocity ratio, the ejected momentum flux and the kinematic viscosity, representing an extension to scaling laws for steady wall jets in still ambience established by Narasimha et al. (Aeronaut. Q., vol. 77, 1973, pp. 355–359).
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
Steinfurth and Weiss supplementary movie 1
Steinfurth and Weiss supplementary movie 2
Visualisation of the extraction of time-dependent deceleration wave location $x_d/b$; upper diagram: FTLE field with $x_d/b$ marked by red dashed vertical line, lower diagram: maximum jet velocities for steady and starting wall jets with $x_d/b$ marked by red circle
- 3
- Cited by


