Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Steen, Paul H.
Chang, Chun-Ti
and
Bostwick, Joshua B.
2019.
Droplet motions fill a periodic table.
Proceedings of the National Academy of Sciences,
Vol. 116,
Issue. 11,
p.
4849.
Lee, Yaerim
Matsushima, Naoto
Yada, Susumu
Nita, Satoshi
Kodama, Takashi
Amberg, Gustav
and
Shiomi, Junichiro
2019.
Revealing How Topography of Surface Microstructures Alters Capillary Spreading.
Scientific Reports,
Vol. 9,
Issue. 1,
Wesson, Elizabeth
and
Steen, Paul
2020.
Steiner triangular drop dynamics.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 30,
Issue. 2,
Wei, Yanju
Zhang, Yajie
Yang, Yajing
Zhang, Jie
Deng, Shengcai
and
Liu, Shenghua
2020.
Coalescence of a soap film into a pool.
Physics of Fluids,
Vol. 32,
Issue. 2,
Costalonga, Maxime
and
Brunet, Philippe
2020.
Directional motion of vibrated sessile drops: A quantitative study.
Physical Review Fluids,
Vol. 5,
Issue. 2,
Xia, Yi
and
Steen, Paul H.
2020.
Dissipation of oscillatory contact lines using resonant mode scanning.
npj Microgravity,
Vol. 6,
Issue. 1,
Shikhmurzaev, Yulii D.
2020.
Moving contact lines and dynamic contact angles: a ‘litmus test’ for mathematical models, accomplishments and new challenges.
The European Physical Journal Special Topics,
Vol. 229,
Issue. 10,
p.
1945.
Kern, Vanessa R.
Bostwick, Joshua B.
and
Steen, Paul H.
2021.
Drop impact on solids: contact-angle hysteresis filters impact energy into modal vibrations.
Journal of Fluid Mechanics,
Vol. 923,
Issue. ,
Liu, Jing
Wei, Ruihua
Lin, Shiji
Chen, Longquan
and
Wei, Zheng
2021.
Elastic film modelling and experimental research of the first-order vibration frequencies of sessile micro-droplets.
Fluid Dynamics Research,
Vol. 53,
Issue. 3,
p.
035505.
Yada, Susumu
Allais, Blandine
van der Wijngaart, Wouter
Lundell, Fredrik
Amberg, Gustav
and
Bagheri, Shervin
2021.
Droplet Impact on Surfaces with Asymmetric Microscopic Features.
Langmuir,
Vol. 37,
Issue. 36,
p.
10849.
Driscoll, Michelle M.
2022.
Microgravity makes fully mobile droplets measurable.
Nature,
Vol. 609,
Issue. 7926,
p.
247.
McCraney, J.
Kern, V.
Bostwick, J. B.
Daniel, S.
and
Steen, P. H.
2022.
Oscillations of Drops with Mobile Contact Lines on the International Space Station: Elucidation of Terrestrial Inertial Droplet Spreading.
Physical Review Letters,
Vol. 129,
Issue. 8,
McCraney, J.
Ludwicki, J.
Bostwick, J.
Daniel, S.
and
Steen, P.
2022.
Coalescence-induced droplet spreading: Experiments aboard the International Space Station.
Physics of Fluids,
Vol. 34,
Issue. 12,
Amberg, Gustav
2022.
Detailed modelling of contact line motion in oscillatory wetting.
npj Microgravity,
Vol. 8,
Issue. 1,
Ludwicki, Jonathan M.
Kern, Vanessa R.
McCraney, Joshua
Bostwick, Joshua B.
Daniel, Susan
and
Steen, Paul H.
2022.
Is contact-line mobility a material parameter?.
npj Microgravity,
Vol. 8,
Issue. 1,
Brunet, P.
and
Baudoin, M.
2022.
Unstationary dynamics of drops subjected to MHz-surface acoustic waves modulated at low frequency.
Experiments in Fluids,
Vol. 63,
Issue. 1,
Fiorini, Domenico
Mendez, Miguel Alfonso
Simonini, Alessia
Steelant, Johan
and
Seveno, David
2022.
Effect of inertia on the dynamic contact angle in oscillating menisci.
Physics of Fluids,
Vol. 34,
Issue. 10,
Scott, Julian F.
2022.
The response of a spherical droplet on a wall executing small sinusoidal vibrations.
Meccanica,
Vol. 57,
Issue. 8,
p.
1879.
Lee, Yaerim
Amberg, Gustav
Shiomi, Junichiro
and
Żur, Krzysztof
2022.
Vibration sorting of small droplets on hydrophilic surface by asymmetric contact-line friction.
PNAS Nexus,
Vol. 1,
Issue. 2,
Fiorini, Domenico
Simonini, Alessia
Steelant, Johan
Seveno, David
and
Mendez, Miguel Alfonso
2023.
Dynamic wetting experiments with nitrogen in a quasi-capillary tube.
Physical Review Fluids,
Vol. 8,
Issue. 12,
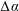 $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FC}$ to the contact-line speed
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FC}$ to the contact-line speed 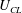 $U_{CL}$. The contact angle changes dynamically with contact-line speeds during rapid movement of liquid across a solid. Speeds beyond the region of stick–slip are the focus of this experimental paper. For these speeds, liquid inertia and surface tension compete while damping is weak. The mobility parameter
$U_{CL}$. The contact angle changes dynamically with contact-line speeds during rapid movement of liquid across a solid. Speeds beyond the region of stick–slip are the focus of this experimental paper. For these speeds, liquid inertia and surface tension compete while damping is weak. The mobility parameter 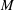 $M$ is defined empirically as the proportionality, when it exists, between
$M$ is defined empirically as the proportionality, when it exists, between  $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FC}$ and 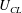 $U_{CL}$,
$U_{CL}$, 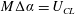 $M\unicode[STIX]{x0394}\unicode[STIX]{x1D6FC}=U_{CL}$. We discover that
$M\unicode[STIX]{x0394}\unicode[STIX]{x1D6FC}=U_{CL}$. We discover that 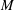 $M$ exists and measure it. The experimental approach is to drive the contact line of a sessile drop by a plane-normal oscillation of the drop’s support. Contact angles, displacements and speeds of the contact line are measured. To unmask the mobility away from stick–slip, the diagram of
$M$ exists and measure it. The experimental approach is to drive the contact line of a sessile drop by a plane-normal oscillation of the drop’s support. Contact angles, displacements and speeds of the contact line are measured. To unmask the mobility away from stick–slip, the diagram of 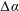 $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FC}$ against
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FC}$ against 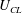 $U_{CL}$, the traditional diagram, is remapped to a new diagram by rescaling with displacement. This new diagram reveals a regime where
$U_{CL}$, the traditional diagram, is remapped to a new diagram by rescaling with displacement. This new diagram reveals a regime where  $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FC}$ is proportional to
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FC}$ is proportional to 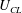 $U_{CL}$ and the slope yields the mobility
$U_{CL}$ and the slope yields the mobility 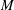 $M$. The experimental approach reported introduces the cyclically dynamic contact angle goniometer. The concept and method of the goniometer are illustrated with data mappings for water on a low-hysteresis non-wetting substrate.
$M$. The experimental approach reported introduces the cyclically dynamic contact angle goniometer. The concept and method of the goniometer are illustrated with data mappings for water on a low-hysteresis non-wetting substrate.