Published online by Cambridge University Press: 08 February 2017
In this experimental study, we investigate the interaction of gravity–capillary solitary waves generated by two surface pressure sources moving side by side at constant speed. The nonlinear response of a water surface to a single source moving at a speed just below the minimum phase speed of linear gravity–capillary waves in deep water (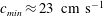 $c_{min}\approx 23~\text{cm}~\text{s}^{-1}$) consists of periodic generation of pairs of three-dimensional solitary waves (or lumps) in a V-shaped pattern downstream of the source. In the reference frame of the laboratory, these unsteady lumps propagate in a direction oblique to the motion of the source. In the present experiments, the strengths of the two sources are adjusted to produce nearly identical responses and the free-surface deformations are visualized using photography-based techniques. The first lumps generated by the two sources move in intersecting directions that make a half-angle of approximately
$c_{min}\approx 23~\text{cm}~\text{s}^{-1}$) consists of periodic generation of pairs of three-dimensional solitary waves (or lumps) in a V-shaped pattern downstream of the source. In the reference frame of the laboratory, these unsteady lumps propagate in a direction oblique to the motion of the source. In the present experiments, the strengths of the two sources are adjusted to produce nearly identical responses and the free-surface deformations are visualized using photography-based techniques. The first lumps generated by the two sources move in intersecting directions that make a half-angle of approximately 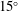 $15^{\circ }$ and collide in the centreplane between the sources. A steep depression is formed during the collision, but this depression quickly decreases in amplitude while radiating small-amplitude radial waves. After the collision, a quasi-stable pattern is formed with several rows of localized depressions that are qualitatively similar to lumps but exhibit periodic amplitude oscillations, similar to a breather. The shape of the wave pattern and the period of oscillations depend strongly on the distance between the sources.
$15^{\circ }$ and collide in the centreplane between the sources. A steep depression is formed during the collision, but this depression quickly decreases in amplitude while radiating small-amplitude radial waves. After the collision, a quasi-stable pattern is formed with several rows of localized depressions that are qualitatively similar to lumps but exhibit periodic amplitude oscillations, similar to a breather. The shape of the wave pattern and the period of oscillations depend strongly on the distance between the sources.
Refraction movie with 1 active air-jet located on the top-left of the images (corresponding to figure 2).
Refraction movie with 2 air-jets separated by 8 cm (corresponding to figure 3).
Refraction movie with 2 air-jets separated by 12 cm (corresponding to figure 4).
Refraction movies with 2 air-jets separated by 12 cm (reference frame of the lab, before the first collision)
Refraction movies with 2 air-jets separated by 12 cm (reference frame of the lab, before the first collision)
LIF movies in the center-plane of the tubes (corresponding to figures 9 and 10). From the top: one air jet tube active (light sheet 4 cm from air-jet), 2 air-jets with 4 cm separation, 2 air-jets with 8 cm separation, and 2 air-jets with 12 cm separation.