Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mons, V.
Meldi, M.
and
Sagaut, P.
2014.
Numerical investigation on the partial return to isotropy of freely decaying homogeneous axisymmetric turbulence.
Physics of Fluids,
Vol. 26,
Issue. 2,
Mons, Vincent
Cambon, Claude
and
Sagaut, Pierre
2016.
A spectral model for homogeneous shear-driven anisotropic turbulence in terms of spherically averaged descriptors.
Journal of Fluid Mechanics,
Vol. 788,
Issue. ,
p.
147.
Briard, Antoine
Gomez, Thomas
Mons, Vincent
and
Sagaut, Pierre
2016.
Decay and growth laws in homogeneous shear turbulence.
Journal of Turbulence,
Vol. 17,
Issue. 7,
p.
699.
Clay, M. P.
and
Yeung, P. K.
2016.
A numerical study of turbulence under temporally evolving axisymmetric contraction and subsequent relaxation.
Journal of Fluid Mechanics,
Vol. 805,
Issue. ,
p.
460.
Yoshimatsu, Katsunori
and
Kaneda, Yukio
2018.
Large-scale structure of velocity and passive scalar fields in freely decaying homogeneous anisotropic turbulence.
Physical Review Fluids,
Vol. 3,
Issue. 10,
Soulard, Olivier
Guillois, Florian
Griffond, Jérôme
Sabelnikov, Vladimir
and
Simoëns, Serge
2018.
Permanence of large eddies in Richtmyer-Meshkov turbulence with a small Atwood number.
Physical Review Fluids,
Vol. 3,
Issue. 10,
Yoshimatsu, Katsunori
and
Kaneda, Yukio
2019.
No return to reflection symmetry in freely decaying homogeneous turbulence.
Physical Review Fluids,
Vol. 4,
Issue. 2,
Sur, Sharanya
2019.
Decaying turbulence and magnetic fields in galaxy clusters.
Monthly Notices of the Royal Astronomical Society,
Vol. 488,
Issue. 3,
p.
3439.
Yoshimatsu, Katsunori
and
Ariki, Taketo
2019.
Error Growth in Three-Dimensional Homogeneous Turbulence.
Journal of the Physical Society of Japan,
Vol. 88,
Issue. 12,
p.
124401.
Yoshimatsu, Katsunori
and
Kaneda, Yukio
2020.
Anisotropy freezing of passive scalar fields in anisotropy growing homogeneous turbulence.
Physical Review Fluids,
Vol. 5,
Issue. 1,
Soulard, Olivier
Guillois, Florian
Griffond, Jérôme
Sabelnikov, Vladimir
and
Simoëns, Serge
2020.
A two-scale Langevin PDF model for Richtmyer–Meshkov turbulence with a small Atwood number.
Physica D: Nonlinear Phenomena,
Vol. 403,
Issue. ,
p.
132276.
Anas, Mohammad
Joshi, Pranav
and
Verma, Mahendra K.
2020.
Freely decaying turbulence in a finite domain at finite Reynolds number.
Physics of Fluids,
Vol. 32,
Issue. 9,
Hosking, David N.
and
Schekochihin, Alexander A.
2021.
Reconnection-Controlled Decay of Magnetohydrodynamic Turbulence and the Role of Invariants.
Physical Review X,
Vol. 11,
Issue. 4,
Gorce, Jean-Baptiste
and
Falcon, Eric
2022.
Statistical Equilibrium of Large Scales in Three-Dimensional Hydrodynamic Turbulence.
Physical Review Letters,
Vol. 129,
Issue. 5,
Panickacheril John, John
Donzis, Diego A.
and
Sreenivasan, Katepalli R.
2022.
Laws of turbulence decay from direct numerical simulations.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 380,
Issue. 2218,
Yoshimatsu, Katsunori
and
Kaneda, Yukio
2022.
Dynamical Invariance and Self-Similarity of Freely Decaying Homogeneous Nonaxisymmetric Turbulence.
Journal of the Physical Society of Japan,
Vol. 91,
Issue. 5,
Davidson, Peter A.
2023.
The Decay of Energy and Scalar Variance in Axisymmetric Turbulence.
Atmosphere,
Vol. 14,
Issue. 6,
p.
1019.
Gorce, Jean-Baptiste
and
Falcon, Eric
2024.
Freely Decaying Saffman Turbulence Experimentally Generated by Magnetic Stirrers.
Physical Review Letters,
Vol. 132,
Issue. 26,
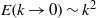 , where
, where 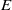 is the energy spectrum and
is the energy spectrum and  the wavenumber. We note that such turbulence possesses two statistical invariants which are related to the form of the spectral tensor
the wavenumber. We note that such turbulence possesses two statistical invariants which are related to the form of the spectral tensor 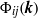 at small
at small 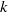 . These are
. These are 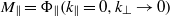 and
and 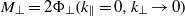 , where the subscripts
, where the subscripts  and
and  indicate quantities parallel and perpendicular to the axis of symmetry. Since
indicate quantities parallel and perpendicular to the axis of symmetry. Since  and
and  ,
,  and
and 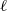 being integral scales, self-similarity of the large scales (when it applies) demands
being integral scales, self-similarity of the large scales (when it applies) demands 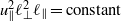 and
and 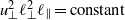 . This, in turn, requires that
. This, in turn, requires that 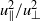 is constant, contrary to the popular belief that freely decaying turbulence should exhibit a ‘return to isotropy’. Numerical simulations performed in large periodic domains, with different types and levels of initial anisotropy, confirm that
is constant, contrary to the popular belief that freely decaying turbulence should exhibit a ‘return to isotropy’. Numerical simulations performed in large periodic domains, with different types and levels of initial anisotropy, confirm that 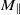 and
and 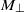 are indeed invariants and that, in the fully developed state,
are indeed invariants and that, in the fully developed state, 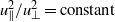 . Somewhat surprisingly, the same simulations also show that
. Somewhat surprisingly, the same simulations also show that 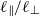 is more or less constant in the fully developed state. Simple theoretical arguments are given which suggest that, when
is more or less constant in the fully developed state. Simple theoretical arguments are given which suggest that, when 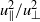 and
and 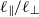 are both constant, the integral scales should evolve as
are both constant, the integral scales should evolve as 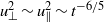 and
and  , irrespective of the level of anisotropy and of the presence of helicity. These decay laws, first proposed by Saffman (Phys. Fluids, vol. 10, 1967, p. 1349), are verified by the numerical simulations.
, irrespective of the level of anisotropy and of the presence of helicity. These decay laws, first proposed by Saffman (Phys. Fluids, vol. 10, 1967, p. 1349), are verified by the numerical simulations.