Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Liang, Jin-Hu
Wang, Su
Zhang, Sheng-Tao
Yue, Lian-Jie
Fan, Bing-Cheng
Zhang, Xin-Yu
and
Cui, Ji-Ping
2014.
The vitiation effects of water vapor and carbon dioxide on the autoignition characteristics of kerosene.
Acta Mechanica Sinica,
Vol. 30,
Issue. 4,
p.
485.
Liu Yu
Zhou Jin
and
Lin Zhi-Yong
2014.
Ramp-induced oblique detonation wave with an incoming boudary layer effect.
Acta Physica Sinica,
Vol. 63,
Issue. 20,
p.
204701.
Teng, Honghui
Zhang, Yining
and
Jiang, Zonglin
2014.
Numerical investigation on the induction zone structure of the oblique detonation waves.
Computers & Fluids,
Vol. 95,
Issue. ,
p.
127.
Liu, Yu
Han, Xu
Lin, Zhiyong
and
Zhou, Jin
2014.
Parallel Computational Fluid Dynamics.
Vol. 405,
Issue. ,
p.
504.
Teng, Hong Hui
Jiang, Zong Lin
and
Ng, Hoi Dick
2014.
Numerical study on unstable surfaces of oblique detonations.
Journal of Fluid Mechanics,
Vol. 744,
Issue. ,
p.
111.
Wang, Tao
Zhang, Yining
Teng, Honghui
Jiang, Zonglin
and
Ng, Hoi Dick
2015.
Numerical study of oblique detonation wave initiation in a stoichiometric hydrogen-air mixture.
Physics of Fluids,
Vol. 27,
Issue. 9,
Teng, Honghui
Ng, Hoi Dick
Li, Kang
Luo, Changtong
and
Jiang, Zonglin
2015.
Evolution of cellular structures on oblique detonation surfaces.
Combustion and Flame,
Vol. 162,
Issue. 2,
p.
470.
Wang, Tao
Zhang, Yining
Teng, Honghui
and
Jiang, Zonglin
2015.
Oblique Shock to Detonation Transition in Hydrogen-air Mixtures.
Procedia Engineering,
Vol. 126,
Issue. ,
p.
209.
Zhang, Bo
Shen, Xiaobo
Pang, Lei
and
Gao, Yuan
2016.
Methane–oxygen detonation characteristics near their propagation limits in ducts.
Fuel,
Vol. 177,
Issue. ,
p.
1.
Zhang, Bo
2016.
The influence of wall roughness on detonation limits in hydrogen–oxygen mixture.
Combustion and Flame,
Vol. 169,
Issue. ,
p.
333.
Wang, Cheng
Zhao, Yongyao
and
Zhang, Bo
2016.
Numerical simulation of flame acceleration and deflagration-to-detonation transition of ethylene in channels.
Journal of Loss Prevention in the Process Industries,
Vol. 43,
Issue. ,
p.
120.
Liu, Yan
Han, Xudong
Yao, Songbai
and
Wang, Jianping
2016.
A numerical investigation of the prompt oblique detonation wave sustained by a finite-length wedge.
Shock Waves,
Vol. 26,
Issue. 6,
p.
729.
Zhang, Yining
Gong, Jishuang
and
Wang, Tao
2016.
Numerical study on initiation of oblique detonations in hydrogen–air mixtures with various equivalence ratios.
Aerospace Science and Technology,
Vol. 49,
Issue. ,
p.
130.
Zhang, Bo
Pang, Lei
Shen, Xiaobo
and
Gao, Yuan
2016.
Measurement and prediction of detonation cell size in binary fuel blends of methane/hydrogen mixtures.
Fuel,
Vol. 172,
Issue. ,
p.
196.
Fang, Yishen
Hu, Zongmin
Teng, Honghui
Jiang, Zonglin
and
Ng, Hoi Dick
2017.
Numerical study of inflow equivalence ratio inhomogeneity on oblique detonation formation in hydrogen–air mixtures.
Aerospace Science and Technology,
Vol. 71,
Issue. ,
p.
256.
Teng, Honghui
Ng, Hoi Dick
and
Jiang, Zonglin
2017.
Initiation characteristics of wedge-induced oblique detonation waves in a stoichiometric hydrogen-air mixture.
Proceedings of the Combustion Institute,
Vol. 36,
Issue. 2,
p.
2735.
Bhattrai, Sudip
and
Tang, Hao
2017.
Formation of near-Chapman–Jouguet oblique detonation wave over a dual-angle ramp.
Aerospace Science and Technology,
Vol. 63,
Issue. ,
p.
1.
Zhang, Bo
Liu, Hong
and
Wang, Cheng
2017.
On the detonation propagation behavior in hydrogen-oxygen mixture under the effect of spiral obstacles.
International Journal of Hydrogen Energy,
Vol. 42,
Issue. 33,
p.
21392.
Ren, Zhaoxin
and
Wang, Bing
2017.
Transition of oblique detonation wave in a two-phase hydrocarbon-air mixture.
Teng, Honghui
Yang, Pengfei
and
Jiang, Zonglin
2017.
Numerical study of oblique detonation initiations with chain-branching kinetics.
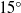 $1{5}^{\ensuremath{\circ} } $–
$1{5}^{\ensuremath{\circ} } $–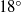 $1{8}^{\ensuremath{\circ} } $. The previously proposed criterion using the characteristic time ratio is also examined and compared with the present angle difference criterion, and the latter is proved to provide better results.
$1{8}^{\ensuremath{\circ} } $. The previously proposed criterion using the characteristic time ratio is also examined and compared with the present angle difference criterion, and the latter is proved to provide better results.