Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hinman, W. Schuyler
and
Johansen, Craig T.
2018.
Mechanisms in the hypersonic laminar near wake of a blunt body.
Journal of Fluid Mechanics,
Vol. 839,
Issue. ,
p.
33.
Xu, Chang-Yue
and
Ni, Zhu-Qing
2018.
Novel characteristics of wavy cylinder in supersonic turbulent flow.
European Journal of Mechanics - B/Fluids,
Vol. 67,
Issue. ,
p.
158.
Zhang, Zhiyu
Li, Zhufei
Huang, Rong
and
Yang, Jiming
2019.
Experimental investigation of shock oscillations on V-shaped blunt leading edges.
Physics of Fluids,
Vol. 31,
Issue. 2,
Hinman, W. S.
and
Johansen, C. T.
2019.
31st International Symposium on Shock Waves 1.
p.
1135.
Wu, Juliana
Deijlen, Lisa
Bhatt, Anubhav
Ganesh, Harish
and
Ceccio, Steven L.
2021.
Cavitation dynamics and vortex shedding in the wake of a bluff body.
Journal of Fluid Mechanics,
Vol. 917,
Issue. ,
Burtsev, Anton
Quintanilha, Helio Ricardo d.
Theofilis, Vassilios
Santos, Ricardo D.
and
Alves, Leonardo S.
2021.
Linear Instability Mechanisms of Supersonic Flow Past Blunt Bodies.
Blanco-Casares, A.
and
Jacobs, G. B.
2022.
Wall roughness effects on the supersonic flow over a circular cylinder.
Shock Waves,
Vol. 32,
Issue. 7,
p.
643.
Awasthi, M.
McCreton, S.
Moreau, D.J.
and
Doolan, C.J.
2022.
Supersonic cylinder wake dynamics.
Journal of Fluid Mechanics,
Vol. 945,
Issue. ,
Mejia, Nicholas
Smith, Joshua
Stenta, William
Maxwell, Brian
and
Schmidt, Bryan E.
2022.
Numerical Investigation of Aerodynamic Interference in Supersonic Retropropulsion.
Thasu, Premika S.
and
Duvvuri, Subrahmanyam
2022.
Strouhal number universality in high-speed cylinder wake flows.
Physical Review Fluids,
Vol. 7,
Issue. 8,
Yanhao, Luo
Hua, Liang
Jun, Li
Shanguang, Guo
Mengxiao, Tang
and
Weiliang, Kong
2022.
Experimental investigation of incident shock wave/boundary layer interaction controlled by pulsed spark discharge array.
Experimental Thermal and Fluid Science,
Vol. 132,
Issue. ,
p.
110515.
Karpuzcu, Irmak T.
and
Levin, Deborah A.
2023.
Study of Side-Jet Interactions over a Hypersonic Cone Flow Using Kinetic Methods.
AIAA Journal,
Vol. 61,
Issue. 11,
p.
4741.
Oliver, Timothy K.
2023.
Aerodynamic Interactions and Turbulence Mitigation by Unidentified Aerospace-undersea Phenomena.
Baidya, Rio
Scharnowski, Sven
de Silva, Charitha M.
Awasthi, Manuj
and
Kähler, Christian J.
2023.
Investigation of a Near-Field Cylinder Wake in the Subsonic, Transonic, and Supersonic Regimes.
AIAA Journal,
Vol. 61,
Issue. 12,
p.
5415.
Zhang, Huiying
Wallace, James M.
and
Wu, Xiaohua
2023.
Quantifying instantaneous flow reversal of tracer particles in subsonic, transonic and supersonic flows past a circular cylinder.
Journal of Turbulence,
Vol. 24,
Issue. 11-12,
p.
613.
Talluru, Murali Krishna
and
Gai, Sudhir
2023.
On oscillations in cylinder wakes at high speeds.
Gan, Tian
Wang, Qiong
Gan, Wenjun
and
Jieming, Zhang
2023.
Visualization study of perturbations induced by plasma actuators and its effect on shock wave/boundary-layer interaction.
Journal of Visualization,
Vol. 26,
Issue. 3,
p.
517.
Tumuklu, Ozgur
and
Hanquist, Kyle M.
2024.
Hypersonic turbulence wake modeling from rarefied to continuum regimes.
Vol. 3050,
Issue. ,
p.
080013.
Lax, Philip A.
Elliott, Skye
Gordeyev, Stanislav
Kemnetz, Matthew R.
and
Leonov, Sergey B.
2024.
Flow Structure behind Spanwise Pin Array in Supersonic Flow.
Aerospace,
Vol. 11,
Issue. 1,
p.
93.
Zhang, Dongsheng
Yang, Hesen
Su, Zhi
and
Liang, Hua
2024.
Hypersonic shock–shock interaction over double wedge controlled by a supermultichannel high-energy pulsed arc discharge array.
Physics of Fluids,
Vol. 36,
Issue. 9,
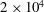 $2\times 10^{4}$ to
$2\times 10^{4}$ to 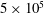 $5\times 10^{5}$ . Periodic oscillations of the sliplines in the wake are observed. The Strouhal number of the oscillations based on the diameter of the cylinder is found to increase monotonically from 0.30 to 0.50 with increasing Reynolds number. If the Strouhal number is formed using the length of the sliplines, however, it has a constant value of approximately 0.48 for all Reynolds numbers studied. This scaling indicates that the oscillations in supersonic flow are likely driven by acoustic signals propagating back and forth through the subsonic region between the separation points on the cylinder and the neck where the sliplines converge, unlike in subsonic flow where oscillations are caused by vortices shed from the cylinder surface.
$5\times 10^{5}$ . Periodic oscillations of the sliplines in the wake are observed. The Strouhal number of the oscillations based on the diameter of the cylinder is found to increase monotonically from 0.30 to 0.50 with increasing Reynolds number. If the Strouhal number is formed using the length of the sliplines, however, it has a constant value of approximately 0.48 for all Reynolds numbers studied. This scaling indicates that the oscillations in supersonic flow are likely driven by acoustic signals propagating back and forth through the subsonic region between the separation points on the cylinder and the neck where the sliplines converge, unlike in subsonic flow where oscillations are caused by vortices shed from the cylinder surface.

