Published online by Cambridge University Press: 22 May 2013
We present experimental results for the Reynolds number 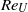 ${\mathit{Re}}_{U} $ based on the horizontal mean-flow velocity
${\mathit{Re}}_{U} $ based on the horizontal mean-flow velocity 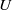 $U$ and for
$U$ and for 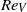 ${\mathit{Re}}_{V} $ based on the root-mean-square horizontal fluctuation velocity
${\mathit{Re}}_{V} $ based on the root-mean-square horizontal fluctuation velocity 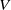 $V$ for turbulent Rayleigh–Bénard convection in a cylindrical sample of aspect ratio
$V$ for turbulent Rayleigh–Bénard convection in a cylindrical sample of aspect ratio 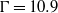 $\Gamma = 10. 9$ over the Prandtl number range
$\Gamma = 10. 9$ over the Prandtl number range 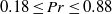 $0. 18\leq \mathit{Pr}\leq 0. 88$. The results were derived from space–time cross-correlation functions of shadowgraph images, using the elliptic approximation of He & Zhang (Phys. Rev. E, vol. 73, 2006, 055303). The data cover the Rayleigh number range from
$0. 18\leq \mathit{Pr}\leq 0. 88$. The results were derived from space–time cross-correlation functions of shadowgraph images, using the elliptic approximation of He & Zhang (Phys. Rev. E, vol. 73, 2006, 055303). The data cover the Rayleigh number range from 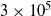 $3\times 1{0}^{5} $ to
$3\times 1{0}^{5} $ to 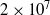 $2\times 1{0}^{7} $. We find that
$2\times 1{0}^{7} $. We find that 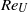 ${\mathit{Re}}_{U} $ is nearly two orders of magnitude smaller than the values given by the Grossmann–Lohse (GL) model (Grossmann & Lohse, Phys. Rev. E, vol. 66, 2002, 016305) for
${\mathit{Re}}_{U} $ is nearly two orders of magnitude smaller than the values given by the Grossmann–Lohse (GL) model (Grossmann & Lohse, Phys. Rev. E, vol. 66, 2002, 016305) for 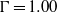 $\Gamma = 1. 00$ and attribute this difference to averaging caused by lateral random diffusion of the large-scale circulation cells in large-
$\Gamma = 1. 00$ and attribute this difference to averaging caused by lateral random diffusion of the large-scale circulation cells in large-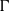 $\Gamma $ samples. For the fluctuations we found
$\Gamma $ samples. For the fluctuations we found 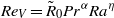 ${\mathit{Re}}_{V} = {\tilde {R} }_{0} {\mathit{Pr}}^{\alpha } {\mathit{Ra}}^{\eta } $, with
${\mathit{Re}}_{V} = {\tilde {R} }_{0} {\mathit{Pr}}^{\alpha } {\mathit{Ra}}^{\eta } $, with 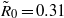 ${\tilde {R} }_{0} = 0. 31$,
${\tilde {R} }_{0} = 0. 31$, 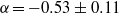 $\alpha = - 0. 53\pm 0. 11$ and
$\alpha = - 0. 53\pm 0. 11$ and 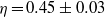 $\eta = 0. 45\pm 0. 03$. That result agrees well with the GL model. The close agreement of the coefficient
$\eta = 0. 45\pm 0. 03$. That result agrees well with the GL model. The close agreement of the coefficient 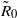 ${\tilde {R} }_{0} $ must be regarded as a coincidence because the GL model was for
${\tilde {R} }_{0} $ must be regarded as a coincidence because the GL model was for 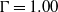 $\Gamma = 1. 00$ and for a mean-flow velocity
$\Gamma = 1. 00$ and for a mean-flow velocity 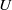 $U$.
$U$.
Movie 1 corresponding to Fig. 1a of the main document, running at approximately half of real-time speed. 11 mm square in the center of the cell, with Pr = 0.18, Ra = 1x10^{6}, 11 pixels/mm
Movie 2 corresponding to Fig. 1b of the main document, running at approximately real-time speed. 94 mm square, with Pr=0.88, Ra=2x10^{7}, 5 pixels/mm.
Movie 3 corresponding to Fig. 7a of the main document, running at approximately real-time speed. It shows processed shadowgraph images corresponding to Fig. 1b for Pr = 0.88 and Ra = 2x10^{7}. Only the dark (relatively warm) structures near the bottom of the sample remain. A 94 mm square was used with a resolution of 5 pixels/mm.
Movie 4 corresponding to Fig. 7b of the main document, running at approximately real-time speed. It shows processed shadowgraph images corresponding to Fig. 1b for Pr = 0.88 and Ra = 2x10^{7}. Only the light (relatively cold) structures near the top of the sample remain. A 94 mm square was used with a resolution of 5 pixels/mm.