Article contents
Robust features of a turbulent boundary layer subjected to high-intensity free-stream turbulence
Published online by Cambridge University Press: 20 July 2018
Abstract
The influence of the large scale organisation of free-stream turbulence on a turbulent boundary layer is investigated experimentally in a wind tunnel through hot-wire measurements. An active grid is used to generate high-intensity free-stream turbulence with turbulence intensities and local turbulent Reynolds numbers in the ranges 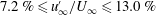 $7.2\,\%\leqslant u_{\infty }^{\prime }/U_{\infty }\leqslant 13.0\,\%$ and
$7.2\,\%\leqslant u_{\infty }^{\prime }/U_{\infty }\leqslant 13.0\,\%$ and 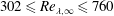 $302\leqslant Re_{\unicode[STIX]{x1D706},\infty }\leqslant 760$, respectively. In particular, several cases are produced with fixed
$302\leqslant Re_{\unicode[STIX]{x1D706},\infty }\leqslant 760$, respectively. In particular, several cases are produced with fixed 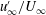 $u_{\infty }^{\prime }/U_{\infty }$ and
$u_{\infty }^{\prime }/U_{\infty }$ and 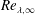 $Re_{\unicode[STIX]{x1D706},\infty }$, but up to a 65 % change in the free-stream integral scale
$Re_{\unicode[STIX]{x1D706},\infty }$, but up to a 65 % change in the free-stream integral scale 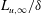 $L_{u,\infty }/\unicode[STIX]{x1D6FF}$. It is shown that, while qualitatively the spectra at various wall-normal positions in the boundary layer look similar, there are quantifiable differences at the large wavelengths all the way to the wall. Nonetheless, profiles of the longitudinal statistics up to fourth order are well collapsed between cases at the same
$L_{u,\infty }/\unicode[STIX]{x1D6FF}$. It is shown that, while qualitatively the spectra at various wall-normal positions in the boundary layer look similar, there are quantifiable differences at the large wavelengths all the way to the wall. Nonetheless, profiles of the longitudinal statistics up to fourth order are well collapsed between cases at the same 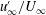 $u_{\infty }^{\prime }/U_{\infty }$. It is argued that a larger separation of the integral scale would not yield a different result, nor would it be physically realisable. Comparing cases across the wide range of turbulence intensities and free-stream Reynolds numbers tested, it is demonstrated that the near-wall spectral peak is independent of the free-stream turbulence, and seemingly universal. The outer peak was also found to be described by a set of global scaling laws, and hence both the near-wall and outer spectral peaks can be predicted a priori with only knowledge of the free-stream spectrum, the boundary layer thickness (
$u_{\infty }^{\prime }/U_{\infty }$. It is argued that a larger separation of the integral scale would not yield a different result, nor would it be physically realisable. Comparing cases across the wide range of turbulence intensities and free-stream Reynolds numbers tested, it is demonstrated that the near-wall spectral peak is independent of the free-stream turbulence, and seemingly universal. The outer peak was also found to be described by a set of global scaling laws, and hence both the near-wall and outer spectral peaks can be predicted a priori with only knowledge of the free-stream spectrum, the boundary layer thickness ( $\unicode[STIX]{x1D6FF}$) and the friction velocity (
$\unicode[STIX]{x1D6FF}$) and the friction velocity (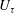 $U_{\unicode[STIX]{x1D70F}}$). Finally, a conceptual model is suggested that attributes the increase in
$U_{\unicode[STIX]{x1D70F}}$). Finally, a conceptual model is suggested that attributes the increase in 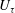 $U_{\unicode[STIX]{x1D70F}}$ as
$U_{\unicode[STIX]{x1D70F}}$ as  $u_{\infty }^{\prime }/U_{\infty }$ increases to the build-up of energy at large wavelengths near the wall because that energy cannot be transferred to the universal near-wall spectral peak.
$u_{\infty }^{\prime }/U_{\infty }$ increases to the build-up of energy at large wavelengths near the wall because that energy cannot be transferred to the universal near-wall spectral peak.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 14
- Cited by



