Published online by Cambridge University Press: 28 November 2017
A singular perturbation theory is developed for the steady, inertialess motion of a lipid-bilayer vesicle flowing through a narrow tube. The vesicle is treated as a sac of fluid enclosed by an inextensible membrane that admits a bending stiffness. Matched asymptotic expansions are developed in terms of a clearance parameter 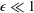 $\unicode[STIX]{x1D716}\ll 1$ in order to calculate the flow field and vesicle shape. Mild restrictions are applied to the ratio of viscosities
$\unicode[STIX]{x1D716}\ll 1$ in order to calculate the flow field and vesicle shape. Mild restrictions are applied to the ratio of viscosities  $\unicode[STIX]{x1D705}$ and the ratio of bending stresses to viscous stresses
$\unicode[STIX]{x1D705}$ and the ratio of bending stresses to viscous stresses 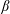 $\unicode[STIX]{x1D6FD}$; in particular, the theory holds for
$\unicode[STIX]{x1D6FD}$; in particular, the theory holds for 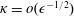 $\unicode[STIX]{x1D705}=o(\unicode[STIX]{x1D716}^{-1/2})$ and
$\unicode[STIX]{x1D705}=o(\unicode[STIX]{x1D716}^{-1/2})$ and 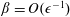 $\unicode[STIX]{x1D6FD}=O(\unicode[STIX]{x1D716}^{-1})$. The ratio of the vesicle length to the tube radius
$\unicode[STIX]{x1D6FD}=O(\unicode[STIX]{x1D716}^{-1})$. The ratio of the vesicle length to the tube radius 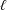 $\ell$ is included as a parameter and asymptotic solutions in the limit of negligible bending stiffness are developed for long, cylindrical vesicles and short, spherical vesicles. The main result of the theory is a prediction for the vesicle speed and extra pressure drop due to the presence of the vesicle in the tube. The effects of confinement, vesicle length, and membrane bending elasticity are examined. The theoretical predictions show good agreement with experimental measurements reported for vesicles and red blood cells in highly confined channel flow. Previously reported models for red blood cells (Secomb et al., J. Fluid Mech., vol. 163, 1986, pp. 405–423; Halpern & Secomb, J. Fluid Mech., vol. 203, 1989, pp. 381–400) are clarified and extended in light of the new theory.
$\ell$ is included as a parameter and asymptotic solutions in the limit of negligible bending stiffness are developed for long, cylindrical vesicles and short, spherical vesicles. The main result of the theory is a prediction for the vesicle speed and extra pressure drop due to the presence of the vesicle in the tube. The effects of confinement, vesicle length, and membrane bending elasticity are examined. The theoretical predictions show good agreement with experimental measurements reported for vesicles and red blood cells in highly confined channel flow. Previously reported models for red blood cells (Secomb et al., J. Fluid Mech., vol. 163, 1986, pp. 405–423; Halpern & Secomb, J. Fluid Mech., vol. 203, 1989, pp. 381–400) are clarified and extended in light of the new theory.