Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T18:53:04.177Z Has data issue: false hasContentIssue false
  • English
  • Français

Transient force generation during impulsive rotation of wall-mounted panels

Published online by Cambridge University Press:  13 March 2013

Alexis Pierides ,
Amir Elzawawy  and
Yiannis Andreopoulos
Alexis Pierides
Affiliation:
Experimental Aerodynamics and Fluid Mechanics Laboratory, Mechanical Engineering, The City College of the City University of New York, New York, NY 10031, USA
Amir Elzawawy*
Affiliation:
Experimental Aerodynamics and Fluid Mechanics Laboratory, Mechanical Engineering, The City College of the City University of New York, New York, NY 10031, USA
Yiannis Andreopoulos
Affiliation:
Experimental Aerodynamics and Fluid Mechanics Laboratory, Mechanical Engineering, The City College of the City University of New York, New York, NY 10031, USA
*
†Email address for correspondence: amir.elzawawy@vaughn.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Square and triangular shape actuator panels mounted on the wall of a wind tunnel beneath an air flow have been impulsively rotated with an angular velocity between 3 and 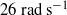$26~\mathrm{rad} ~{\mathrm{s} }^{- 1} $. A custom-designed balance was used to measure the time-dependent lift and drag forces during the deployment of the actuator, the position of which was monitored by a digital encoder. The measured forces have been compensated for inertia effects which are significant. The results indicated that all lift and drag force coefficients during the transient deployment are different than the corresponding coefficients under stationary conditions at the same deployment angle. It was found that these dynamic effects are augmented with increasing velocity ratio 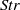$\mathit{Str}$. The square actuator was found to have better aerodynamic performance than the triangular ones. Additional experiments within different boundary layers reveal that the generated unsteady forces on the moving panels are affected by the characteristics of the incoming boundary layers. The results showed that the thinner the boundary layer is the higher the forces are. Time-resolved flow visualization studies indicated that during the deployment of the panel the upstream turbulent boundary layer structures and the free stream fluid are decelerated and squeezed in the longitudinal direction as they approach the moving plate. A very thin and highly sheared wall layer develops over the moving panel, it generates a substantial amount of vorticity and it subsequently separates from the three edges of the panel to form a large-scale ring-like vortical structure which is responsible for the transient augmentation of the aerodynamic forces. This structure consists of wrapped around separated shear layers which contain pockets of compressed eddies and free stream fluid originated in the upstream incoming boundary layer and free stream. A horseshoe vortex starts to form over the moving plate and during the final stages of deployment it has been moved upstream while the incoming boundary layer turbulent structures are pushed and diverted upwards.

JFM classification

Aerodynamics: Aerodynamics Biological Fluid Dynamics: Swimming/flying Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 721 , 25 April 2013 , pp. 403 - 437
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agui, J. H. & Andreopoulos, J. 1992 Experimental investigation of a three-dimensional boundary layer flow in the vicinity of an upright wall mounted cylinder. Trans. ASME J. Fluids Engng 114 (4), 566–576.Google Scholar
Akaydin, D. H., Elvin, N. & Andreopoulos, Y. 2010 Wake of a cylinder: a paradigm for energy harvesting with piezoelectric materials. Exp. Fluids 49 (1), 291–304.Google Scholar
Anderson, J. M., Streitlien, K., Barrett, D. S. & Triantafyllou, M. S. 1998 Oscillating foils of high propulsive efficiency. J. Fluid Mech. 360, 41–72.Google Scholar
Andreopoulos, J. & Agui, J. 1996 Wall vorticity flux dynamics in a two-dimensional turbulent boundary layer. J. Fluid Mech. 309, 45–84.Google Scholar
Birch, J. M. & Dickinson, M. H. 2001 Spanwise flow and the attachment of the leading-edge vortex on insect wings. Nature 412 (6848), 729–733.Google Scholar
Borazjani, I. & Sotiropoulos, F. 2010 On the role of form and kinematics on the hydrodynamics of body/caudal fin swimming. J. Expl Biol. 213, 89–107.Google Scholar
Buckholtz, J. H. J. & Smits, A. J. 2006 On the evolution of the wake structure produced by a low-aspect-ratio pitching panel. J. Fluid Mech. 546, 433–443.Google Scholar
Buckholtz, J. H. J. & Smits, A. J. 2008 The wake structure and thrust performance of a rigid low-aspect-ratio pitching panel. J. Fluid Mech. 603, 331–365.Google Scholar
Dickinson, M. H., Lehmann, F. O. & Sane, S. P. 1999 Wing rotation and the aerodynamic basics of insect flight. Science 284, 1954–1960.Google Scholar
Dong, S., Karniadakis, G. E., Ekmekci, A. & Rockwell, D. 2006 A combined DNS-PIV study of the turbulent near wake. J. Fluid Mech. 569, 185–207.Google Scholar
von Ellenrieder, K. D., Parker, K. & Soria, J. 2003 Flow structures behind a heaving and pitching finite-span wing. J. Fluid Mech. 490, 129–138.Google Scholar
Ellington, C. P. 1984 The aerodynamics of hovering insect flight. II. Morphological parameters. Phil. Trans. R. Soc. Lond. 305, 17–40.Google Scholar
Ellington, C. P., van den Berg, C., Willmott, A. P. & Thomas, A. L. R. 1996 Leading-edge vortices in insect flight. Nature 384 (6610), 626–630.CrossRefGoogle Scholar
Elzawawy, A. 2012 Time resolved particle image velocimetry techniques with continuous wave laser and their application to transient flows. PhD thesis, The City University of New York.Google Scholar
Freymuth, P. 1988 Propulsive vortical signature of plunging and pitching aerofoils. AIAA J. 23, 881–883.Google Scholar
Green, M. A. & Smits, A. J. 2008 Effects of three-dimensionality on thrust production by a pitching panel. J. Fluid Mech. 615, 211–220.Google Scholar
Ho, C. H. & Tai, Y.-C. 1998 Micro-electro-mechanical systems (MEMS) and fluid flows. Annu. Rev. Fluid. Mech. 30, 579–612.Google Scholar
Ho, S., Nassefa, H., Pornsin-Sirirak, N., Tai, Y.-C. & Ho, C.-M. 2003 Unsteady aerodynamics and flow control for flapping wing flyers. Prog. Aeronaut. Sci. 39, 635–681.Google Scholar
Kim, D. & Gharib, M. 2010 Experimental study of three-dimensional vortex structures in translating and rotating plates. Exp. Fluids 49 (1), 329–339.Google Scholar
Koumoutsakos, P. & Shiels, D. 1996 Simulations of the viscous flow normal to an impulsively started and uniformly accelerated flat plate. J. Fluid Mech. 328, 177–227.Google Scholar
Maxworthy, T. 1981 The fluid-dynamics of insect flight. Annu. Rev. Fluid Mech. (13), 329–350.Google Scholar
Paik, J., Escauriaza, C. & Sotiropoulos, F. 2007 On the bimodal dynamics of the turbulent horseshoe vortex system in a wing-body junction. Phys. Fluids 19, 045107.Google Scholar
Pierides, A. 2011 An experimental study on the characteristics of transient deployment of hinged wing actuators within a boundary layer. PhD thesis, The City University of New York.Google Scholar
Ringuette, M. J., Milano, M. & Gharib, M. 2007 Role of tip vortex in the force generation of low-aspect-ratio normal flat plates. J. Fluid Mech. 581, 453–468.Google Scholar
Sarpkaya, T & Kline, H. K. 1982 Impulsively-started flow about four types of bluff body. Trans. ASME I: J. Fluids Engng 104, 207–213.Google Scholar
Suryadi, A., Ishil, T. & Obl, S. 2010 Stereo PIV measurement of infinite, flapping rigid plate in hovering condition. Exp. Fluids 49 (2), 447–460.CrossRefGoogle Scholar
Taira, K., Dickson, W. B, Colonious, T., Dickinson, M. H. & Rowley, C. W. 2007 Unsteadiness in a flow over a flat plate at angle-of-attack at low Reynolds numbers, AIAA-65342 conference paper.Google Scholar
Triantafyllou, M. S., Techet, A. H., Zhu, Q., Beal, D. N., Hover, F. S. & Yue, D. K. P. 2003 Vorticity control in fish-like propulsion and control. J. Integ. Comp. Biol 42, 1026–1031.Google Scholar
Triantafyllou, M. S., Triantafyllou, G. S. & Gopalkrishnan, R. 1991 Wake mechanics for thrust generation in oscillating foils. Phys. Fluids A 3 (12), 2835–2837.Google Scholar
Vikestad, K., Vandiver, J. K. & Larsen, C. M. 2000 Added mass and oscillation frequency for a circular cylinder subjected to vortex-induced vibrations and external disturbance. J. Fluids Struct. 14, 1071–1088.Google Scholar
Wang, Z. J. 2005 Dissecting insect flight. Annu. Rev. Fluid Mech. 37, 183–198.Google Scholar

Pierides et al. supplementary movie

Flow visualization shows vortical structures shed off the tip of the actuator, during deployment, taken at x3=0 plane (Reθ=3,400; Reh=68,200; Str=0.24).

Download Pierides et al. supplementary movie(Video)
Video 2.2 MB

Pierides et al. supplementary movie

Flow visualization shows vortical structures shed off the tip of the actuator, during deployment, taken at x2=9 plane (Reθ=3,400; Reh=68,200; Str=0.24).

Download Pierides et al. supplementary movie(Video)
Video 2.5 MB

Pierides et al. supplementary movie

Flow visualization of the upstream interaction of the deploying actuator with the incoming boundary layer flow, (Reθ=3,400; Reh=68,200; Str=0.24).

Download Pierides et al. supplementary movie(Video)
Video 2.7 MB